ऑनलाइन कैलकुलेटर. किसी दिए गए बिंदु पर किसी फ़ंक्शन के ग्राफ़ की सीधी स्पर्शरेखा का समीकरण

व्युत्पन्न के चिह्न और फ़ंक्शन की एकरसता की प्रकृति के बीच संबंध दिखाना।

कृपया निम्नलिखित के बारे में अत्यधिक सावधान रहें। देखिए, आपको क्या दिया गया है इसका शेड्यूल! कार्य या उसका व्युत्पन्न

यदि व्युत्पन्न का एक ग्राफ दिया गया है, तो हमें केवल फलन चिन्हों और शून्यों में रुचि होगी। हमें सैद्धांतिक रूप से किसी भी "पहाड़ियों" या "खोखले" में कोई दिलचस्पी नहीं है!

कार्य 1।

यह चित्र अंतराल पर परिभाषित किसी फ़ंक्शन का ग्राफ़ दिखाता है। उन पूर्णांक बिंदुओं की संख्या निर्धारित करें जिन पर फ़ंक्शन का व्युत्पन्न नकारात्मक है।

समाधान:

चित्र में, घटते फ़ंक्शन के क्षेत्रों को रंग में हाइलाइट किया गया है:

फ़ंक्शन के इन घटते क्षेत्रों में 4 पूर्णांक मान होते हैं।

कार्य 2.

यह चित्र अंतराल पर परिभाषित किसी फ़ंक्शन का ग्राफ़ दिखाता है। उन बिंदुओं की संख्या ज्ञात करें जिन पर फ़ंक्शन के ग्राफ़ की स्पर्श रेखा रेखा के समानांतर या संपाती है।

समाधान:

एक बार किसी फ़ंक्शन के ग्राफ़ की स्पर्शरेखा एक सीधी रेखा के समानांतर (या संपाती) होती है (या, जो एक ही चीज़ है), होने पर ढलान, शून्य के बराबर, तो स्पर्शरेखा का एक कोणीय गुणांक होता है।

बदले में इसका मतलब है कि स्पर्शरेखा अक्ष के समानांतर है, क्योंकि ढलान अक्ष के स्पर्शरेखा के झुकाव के कोण की स्पर्शरेखा है।

इसलिए, हम ग्राफ़ पर चरम बिंदु (अधिकतम और न्यूनतम बिंदु) पाते हैं - यह इन बिंदुओं पर है कि ग्राफ़ के स्पर्शरेखा वाले कार्य अक्ष के समानांतर होंगे।

ऐसे 4 बिंदु हैं.

कार्य 3.

यह आंकड़ा अंतराल पर परिभाषित फ़ंक्शन के व्युत्पन्न का एक ग्राफ दिखाता है। उन बिंदुओं की संख्या ज्ञात करें जिन पर फ़ंक्शन के ग्राफ़ की स्पर्श रेखा रेखा के समानांतर या संपाती है।

समाधान:

चूँकि किसी फ़ंक्शन के ग्राफ़ की स्पर्श रेखा उस रेखा के समानांतर (या संपाती) होती है जिसका ढलान होता है, तो स्पर्श रेखा का भी ढलान होता है।

बदले में इसका मतलब है कि स्पर्श बिंदुओं पर।

इसलिए, हम देखते हैं कि ग्राफ़ पर कितने बिंदुओं की कोटि बराबर है।

जैसा कि आप देख सकते हैं, ऐसे चार बिंदु हैं।

कार्य 4.

यह चित्र अंतराल पर परिभाषित किसी फ़ंक्शन का ग्राफ़ दिखाता है। उन बिंदुओं की संख्या ज्ञात करें जिन पर फ़ंक्शन का व्युत्पन्न 0 है।

समाधान:

चरम बिंदुओं पर व्युत्पन्न शून्य के बराबर है। हमारे पास उनमें से 4 हैं:

कार्य 5.

चित्र एक फ़ंक्शन का ग्राफ़ और x-अक्ष पर ग्यारह बिंदु दिखाता है:। इनमें से कितने बिंदुओं पर फ़ंक्शन का व्युत्पन्न नकारात्मक है?

समाधान:

घटते फ़ंक्शन के अंतराल पर, इसका व्युत्पन्न नकारात्मक मान लेता है। तथा बिन्दुओं पर फलन घटता जाता है। ऐसे 4 बिंदु हैं.

कार्य 6.

यह चित्र अंतराल पर परिभाषित किसी फ़ंक्शन का ग्राफ़ दिखाता है। फ़ंक्शन के चरम बिंदुओं का योग ज्ञात करें।

समाधान:

चरम बिंदु– ये अधिकतम अंक (-3, -1, 1) और न्यूनतम अंक (-2, 0, 3) हैं।

चरम बिंदुओं का योग: -3-1+1-2+0+3=-2.

कार्य 7.

यह आंकड़ा अंतराल पर परिभाषित फ़ंक्शन के व्युत्पन्न का एक ग्राफ दिखाता है। फलन की वृद्धि के अंतराल ज्ञात कीजिए। अपने उत्तर में, इन अंतरालों में शामिल पूर्णांक बिंदुओं का योग इंगित करें।

समाधान:

यह आंकड़ा उन अंतरालों को उजागर करता है जहां फ़ंक्शन का व्युत्पन्न गैर-नकारात्मक है।

छोटे बढ़ते अंतराल पर कोई पूर्णांक बिंदु नहीं हैं; बढ़ते अंतराल पर चार पूर्णांक मान हैं: , , और ।

उनका योग:

कार्य 8.

यह आंकड़ा अंतराल पर परिभाषित फ़ंक्शन के व्युत्पन्न का एक ग्राफ दिखाता है। फलन की वृद्धि के अंतराल ज्ञात कीजिए। अपने उत्तर में, उनमें से सबसे बड़े की लंबाई बताएं।

समाधान:

चित्र में, सभी अंतराल जिन पर व्युत्पन्न सकारात्मक है, रंग में हाइलाइट किए गए हैं, जिसका अर्थ है कि इन अंतरालों पर फ़ंक्शन स्वयं बढ़ता है।

इनमें से सबसे बड़े की लंबाई 6 है.

कार्य 9.

यह आंकड़ा अंतराल पर परिभाषित फ़ंक्शन के व्युत्पन्न का एक ग्राफ दिखाता है। खंड पर किस बिंदु पर यह सबसे बड़ा मूल्य लेता है?

समाधान:

आइए देखें कि ग्राफ़ उस खंड पर कैसा व्यवहार करता है, जिसमें हमारी रुचि है केवल व्युत्पन्न का चिह्न .

व्युत्पन्न का चिह्न ऋणात्मक है, क्योंकि इस खंड पर ग्राफ़ अक्ष के नीचे है।

मान लीजिए कि एक फलन f दिया गया है, जिसका किसी बिंदु x 0 पर एक परिमित अवकलज f (x 0) है। फिर कोणीय गुणांक f'(x 0) वाले बिंदु (x 0 ; f (x 0)) से गुजरने वाली सीधी रेखा स्पर्शरेखा कहलाती है।

यदि व्युत्पन्न बिंदु x 0 पर मौजूद नहीं है तो क्या होगा? दो विकल्प हैं:

1. ग्राफ़ में कोई स्पर्शरेखा भी नहीं है। एक क्लासिक उदाहरण फ़ंक्शन y = |x | है बिंदु पर (0; 0).
2. स्पर्शरेखा ऊर्ध्वाधर हो जाती है. यह सच है, उदाहरण के लिए, बिंदु (1; π /2) पर फ़ंक्शन y = आर्क्सिन x के लिए।

स्पर्शरेखा समीकरण

कोई भी गैर-ऊर्ध्वाधर सीधी रेखा y = kx + b रूप के समीकरण द्वारा दी जाती है, जहां k ढलान है। स्पर्शरेखा कोई अपवाद नहीं है, और किसी बिंदु x 0 पर इसका समीकरण बनाने के लिए, इस बिंदु पर फ़ंक्शन और व्युत्पन्न का मान जानना पर्याप्त है।

तो, मान लीजिए कि एक फ़ंक्शन y = f (x) दिया गया है, जिसका खंड पर व्युत्पन्न y = f '(x) है। फिर किसी भी बिंदु x 0 ∈ (a ; b) पर इस फ़ंक्शन के ग्राफ़ पर एक स्पर्शरेखा खींची जा सकती है, जो समीकरण द्वारा दी गई है:

y = f '(x 0) (x − x 0) + f (x 0)

यहां f '(x 0) बिंदु x 0 पर व्युत्पन्न का मान है, और f (x 0) स्वयं फ़ंक्शन का मान है।

काम। फ़ंक्शन y = x 3 दिया गया है। बिंदु x 0 = 2 पर इस फ़ंक्शन के ग्राफ़ की स्पर्शरेखा के लिए एक समीकरण लिखें।

स्पर्शरेखा समीकरण: y = f '(x 0) · (x − x 0) + f (x 0). बिंदु x 0 = 2 हमें दिया गया है, लेकिन मान f (x 0) और f '(x 0) की गणना करनी होगी।

सबसे पहले, आइए फ़ंक्शन का मान ज्ञात करें। यहां सब कुछ आसान है: एफ (एक्स 0) = एफ (2) = 2 3 = 8;
आइए अब व्युत्पन्न खोजें: f '(x) = (x 3)' = 3x 2;
हम व्युत्पन्न में x 0 = 2 प्रतिस्थापित करते हैं: f '(x 0) = f'(2) = 3 2 2 = 12;
कुल मिलाकर हमें मिलता है: y = 12 · (x - 2) + 8 = 12x - 24 + 8 = 12x - 16।
यह स्पर्शरेखा समीकरण है.

काम। फ़ंक्शन f (x) = 2sin x + 5 के ग्राफ़ की स्पर्शरेखा के लिए बिंदु x 0 = π /2 पर एक समीकरण लिखें।

इस बार हम प्रत्येक क्रिया का विस्तार से वर्णन नहीं करेंगे - हम केवल मुख्य चरणों का संकेत देंगे। हमारे पास है:

एफ (एक्स 0) = एफ (π /2) = 2सिन (π /2) + 5 = 2 + 5 = 7;
f '(x) = (2sin x + 5)' = 2cos x;
एफ ’(एक्स 0) = एफ ’(π /2) = 2cos (π /2) = 0;

स्पर्शरेखा समीकरण:

y = 0 · (x − π /2) + 7 ⇒ y = 7

बाद के मामले में, सीधी रेखा क्षैतिज हो गई, क्योंकि इसका कोणीय गुणांक k = 0 है। इसमें कुछ भी गलत नहीं है - हम बस एक चरम बिंदु पर पहुँच गए हैं।

लेख ग्राफिक नोटेशन के साथ परिभाषाओं, व्युत्पन्न के ज्यामितीय अर्थ का विस्तृत विवरण प्रदान करता है। स्पर्शरेखा रेखा के समीकरण पर उदाहरण सहित विचार किया जाएगा, द्वितीय क्रम के वक्रों की स्पर्शरेखा के समीकरण मिलेंगे।

Yandex.RTB R-A-339285-1 परिभाषा 1

सीधी रेखा y = k x + b के झुकाव के कोण को कोण α कहा जाता है, जिसे x अक्ष की सकारात्मक दिशा से सीधी रेखा y = k x + b तक सकारात्मक दिशा में मापा जाता है।

चित्र में, x दिशा को हरे तीर और हरे चाप द्वारा और झुकाव के कोण को लाल चाप द्वारा दर्शाया गया है। नीली रेखा सीधी रेखा को संदर्भित करती है।

परिभाषा 2

सीधी रेखा y = k x + b की ढलान को संख्यात्मक गुणांक k कहा जाता है।

कोणीय गुणांक सीधी रेखा की स्पर्शरेखा के बराबर है, दूसरे शब्दों में k = t g α।

• एक सीधी रेखा के झुकाव का कोण केवल 0 के बराबर होता है यदि वह x के समानांतर हो और ढलान शून्य के बराबर हो, क्योंकि शून्य की स्पर्श रेखा 0 के बराबर होती है। इसका मतलब है कि समीकरण का रूप y = b होगा.
• यदि सीधी रेखा y = k x + b का झुकाव कोण न्यून कोण है, तो स्थितियाँ 0 संतुष्ट होती हैं< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0, और ग्राफ़ में वृद्धि हुई है।
• यदि α = π 2, तो रेखा का स्थान x पर लंबवत है। समानता x = c द्वारा निर्दिष्ट की जाती है, जिसका मान c एक वास्तविक संख्या है।
• यदि सीधी रेखा y = k x + b का झुकाव कोण अधिक है, तो यह शर्तों π 2 के अनुरूप है< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

सेकेंट एक रेखा है जो फ़ंक्शन f (x) के 2 बिंदुओं से होकर गुजरती है। दूसरे शब्दों में, एक छेदक एक सीधी रेखा है जो किसी दिए गए फ़ंक्शन के ग्राफ़ पर किन्हीं दो बिंदुओं से होकर खींची जाती है।

चित्र से पता चलता है कि A B एक छेदक है, और f (x) एक काला वक्र है, α एक लाल चाप है, जो छेदक के झुकाव के कोण को दर्शाता है।

जब एक सीधी रेखा का कोणीय गुणांक झुकाव के कोण के स्पर्शरेखा के बराबर होता है, तो यह स्पष्ट है कि एक समकोण त्रिभुज A B C की स्पर्शरेखा को आसन्न भुजा के विपरीत पक्ष के अनुपात से पाया जा सकता है।

परिभाषा 4

हमें प्रपत्र का छेदक ज्ञात करने का एक सूत्र मिलता है:

k = t g α = B C A C = f (x B) - f x A x B - x A, जहां बिंदु A और B के भुज x A, x B, और f (x A), f (x) के मान हैं बी) इन बिंदुओं पर मान कार्य हैं।

जाहिर है, छेदक का कोणीय गुणांक समानता k = f (x B) - f (x A) x B - x A या k = f (x A) - f (x B) x A - x B का उपयोग करके निर्धारित किया जाता है। , और समीकरण को y = f (x B) - f (x A) x B - x A x - x A + f (x A) या के रूप में लिखा जाना चाहिए
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

सेकेंट ग्राफ़ को दृश्य रूप से 3 भागों में विभाजित करता है: बिंदु A के बाईं ओर, A से B तक, B के दाईं ओर। नीचे दिए गए चित्र से पता चलता है कि तीन सेकेंट हैं जिन्हें संपाती माना जाता है, अर्थात, उन्हें a का उपयोग करके सेट किया गया है समान समीकरण.

परिभाषा के अनुसार, यह स्पष्ट है कि इस मामले में सीधी रेखा और उसकी छेदक रेखा संपाती हैं।

एक सेकेंट किसी दिए गए फ़ंक्शन के ग्राफ़ को कई बार काट सकता है। यदि किसी छेदक के लिए y = 0 के रूप का समीकरण है, तो साइनसॉइड के साथ प्रतिच्छेदन बिंदुओं की संख्या अनंत है।

परिभाषा 5

बिंदु x 0 पर फ़ंक्शन f (x) के ग्राफ़ की स्पर्शरेखा; f (x 0) किसी दिए गए बिंदु x 0 से गुजरने वाली एक सीधी रेखा है; f (x 0), एक खंड की उपस्थिति के साथ जिसमें x 0 के करीब कई x मान हैं।

उदाहरण 1

आइए नीचे दिए गए उदाहरण पर करीब से नज़र डालें। तब यह स्पष्ट है कि फ़ंक्शन y = x + 1 द्वारा परिभाषित रेखा को निर्देशांक (1; 2) वाले बिंदु पर y = 2 x की स्पर्शरेखा माना जाता है। स्पष्टता के लिए, (1; 2) के करीब मान वाले ग्राफ़ पर विचार करना आवश्यक है। फ़ंक्शन y = 2 x को काले रंग में दिखाया गया है, नीली रेखा स्पर्शरेखा रेखा है, और लाल बिंदु प्रतिच्छेदन बिंदु है।

जाहिर है, y = 2 x रेखा y = x + 1 के साथ विलीन हो जाता है।

स्पर्शरेखा निर्धारित करने के लिए, हमें स्पर्शरेखा A B के व्यवहार पर विचार करना चाहिए क्योंकि बिंदु B बिंदु A पर अनंत रूप से पहुंचता है। स्पष्टता के लिए, हम एक चित्र प्रस्तुत करते हैं।

नीली रेखा द्वारा दर्शाया गया छेदक A B, स्वयं स्पर्शरेखा की स्थिति की ओर झुकता है, और छेदक α के झुकाव का कोण स्वयं स्पर्शरेखा α x के झुकाव के कोण की ओर झुकना शुरू कर देगा।

परिभाषा 6

बिंदु A पर फ़ंक्शन y = f (x) के ग्राफ़ की स्पर्शरेखा को छेदक A B की सीमित स्थिति माना जाता है क्योंकि B, A की ओर झुकता है, अर्थात B → A।

आइए अब एक बिंदु पर किसी फ़ंक्शन के व्युत्पन्न के ज्यामितीय अर्थ पर विचार करें।

आइए फ़ंक्शन f (x) के लिए छेदक A B पर विचार करने के लिए आगे बढ़ें, जहां A और B निर्देशांक x 0, f (x 0) और x 0 + ∆ x, f (x 0 + ∆ x), और ∆ x के साथ है तर्क की वृद्धि के रूप में दर्शाया गया है। अब फलन ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) का रूप लेगा। स्पष्टता के लिए, आइए एक चित्र का उदाहरण दें।

परिणामी समकोण त्रिभुज A B C पर विचार करें। हम हल करने के लिए स्पर्शरेखा की परिभाषा का उपयोग करते हैं, अर्थात, हम संबंध ∆ y ∆ x = t g α प्राप्त करते हैं। स्पर्शरेखा की परिभाषा से यह पता चलता है कि lim ∆ x → 0 ∆ y ∆ x = t g α x। एक बिंदु पर व्युत्पन्न के नियम के अनुसार, हमारे पास यह है कि बिंदु x 0 पर व्युत्पन्न f (x) को तर्क की वृद्धि के लिए फ़ंक्शन की वृद्धि के अनुपात की सीमा कहा जाता है, जहां ∆ x → 0 , तो हम इसे f (x 0) = lim ∆ x → 0 ∆ y ∆ x के रूप में निरूपित करते हैं।

यह इस प्रकार है कि f" (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, जहां k x को स्पर्श रेखा के ढलान के रूप में दर्शाया गया है।

अर्थात्, हम पाते हैं कि f' (x) बिंदु x 0 पर मौजूद हो सकता है, और x 0 के बराबर स्पर्शरेखा के बिंदु पर फ़ंक्शन के दिए गए ग्राफ़ की स्पर्शरेखा की तरह, f 0 (x 0), जहां का मान बिंदु पर स्पर्श रेखा का ढलान बिंदु x 0 पर अवकलज के बराबर है। तब हमें वह मिलता है k x = f " (x 0) .

किसी बिंदु पर किसी फ़ंक्शन के व्युत्पन्न का ज्यामितीय अर्थ यह है कि यह उसी बिंदु पर ग्राफ़ के स्पर्शरेखा के अस्तित्व की अवधारणा देता है।

किसी समतल पर किसी सीधी रेखा का समीकरण लिखने के लिए उस बिंदु के साथ कोणीय गुणांक का होना आवश्यक है जिससे वह गुजरती है। चौराहे पर इसका अंकन x 0 माना जाता है।

बिंदु x 0, f 0 (x 0) पर फ़ंक्शन y = f (x) के ग्राफ़ का स्पर्शरेखा समीकरण y = f "(x 0) x - x 0 + f (x 0) का रूप लेता है।

इसका मतलब यह है कि व्युत्पन्न f "(x 0) का अंतिम मान स्पर्शरेखा की स्थिति निर्धारित कर सकता है, अर्थात लंबवत, बशर्ते कि lim x → x 0 + 0 f "(x) = ∞ और lim x → x 0 - 0 f "(x ) = ∞ या स्थिति lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) के तहत बिल्कुल भी अनुपस्थिति।

स्पर्शरेखा का स्थान उसके कोणीय गुणांक k x = f "(x 0) के मान पर निर्भर करता है। जब o x अक्ष के समानांतर होता है, तो हमें वह k k = 0 प्राप्त होता है, जब o y - k x = ∞ के समानांतर होता है, और का रूप स्पर्श रेखा समीकरण x = x 0 k x > 0 के साथ बढ़ता है, k x के साथ घटता है< 0 .

उदाहरण 2

निर्देशांक (1; 3) वाले बिंदु पर फ़ंक्शन y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 के ग्राफ के स्पर्शरेखा के लिए एक समीकरण संकलित करें और झुकाव का कोण निर्धारित करें।

समाधान

शर्त के अनुसार, हमारे पास यह है कि फ़ंक्शन सभी वास्तविक संख्याओं के लिए परिभाषित है। हम पाते हैं कि शर्त द्वारा निर्दिष्ट निर्देशांक वाला बिंदु, (1; 3) स्पर्शरेखा का एक बिंदु है, तो x 0 = - 1, f (x 0) = - 3.

मान-1 वाले बिंदु पर अवकलज ज्ञात करना आवश्यक है। हमें वह मिल गया

y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

स्पर्शरेखा के बिंदु पर f' (x) का मान स्पर्शरेखा का ढलान है, जो ढलान की स्पर्शरेखा के बराबर है।

फिर k x = t g α x = y " (x 0) = 3 3

यह इस प्रकार है कि α x = a r c t g 3 3 = π 6

उत्तर:स्पर्श रेखा समीकरण का रूप ले लेती है

y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

स्पष्टता के लिए, हम ग्राफिक चित्रण में एक उदाहरण देते हैं।

मूल फ़ंक्शन के ग्राफ़ के लिए काले रंग का उपयोग किया जाता है, नीला रंग स्पर्शरेखा की छवि है, और लाल बिंदु स्पर्शरेखा का बिंदु है। दाईं ओर का चित्र एक विस्तृत दृश्य दिखाता है।

उदाहरण 3

किसी दिए गए फ़ंक्शन के ग्राफ़ के स्पर्शरेखा के अस्तित्व का निर्धारण करें
y = 3 · x - 1 5 + 1 निर्देशांक वाले बिंदु पर (1 ; 1) . एक समीकरण लिखें और झुकाव का कोण निर्धारित करें।

समाधान

शर्त के अनुसार, हमारे पास यह है कि किसी दिए गए फ़ंक्शन की परिभाषा का क्षेत्र सभी वास्तविक संख्याओं का सेट माना जाता है।

आइए व्युत्पन्न खोजने के लिए आगे बढ़ें

y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

यदि x 0 = 1, तो f' (x) अपरिभाषित है, लेकिन सीमाएं lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 के रूप में लिखी जाती हैं · 1 + 0 = + ∞ और lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , जिसका अर्थ है बिंदु (1; 1) पर ऊर्ध्वाधर स्पर्शरेखा का अस्तित्व।

उत्तर:समीकरण x = 1 का रूप लेगा, जहां झुकाव का कोण π 2 के बराबर होगा।

स्पष्टता के लिए, आइए इसे ग्राफ़िक रूप से चित्रित करें।

उदाहरण 4

फ़ंक्शन y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 के ग्राफ़ पर बिंदु खोजें, जहां

1. कोई स्पर्शरेखा नहीं है;
2. स्पर्शरेखा x के समानांतर है;
3. स्पर्शरेखा रेखा y = 8 5 x + 4 के समानांतर है।

समाधान

परिभाषा के दायरे पर ध्यान देना जरूरी है. शर्त के अनुसार, हमारे पास यह है कि फ़ंक्शन सभी वास्तविक संख्याओं के सेट पर परिभाषित किया गया है। हम मॉड्यूल का विस्तार करते हैं और सिस्टम को अंतराल x ∈ - ∞ के साथ हल करते हैं; 2 और [-2 ; + ∞) . हमें वह मिल गया

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)

कार्य में अंतर करना आवश्यक है। हमारे पास वह है

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)

जब x = − 2, तब व्युत्पन्न मौजूद नहीं होता क्योंकि उस बिंदु पर एकतरफा सीमाएँ समान नहीं होती हैं:

लिम x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 लिम x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

हम बिंदु x = - 2 पर फ़ंक्शन के मान की गणना करते हैं, जहां हमें वह मिलता है

1. y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, अर्थात् बिंदु पर स्पर्श रेखा ( - 2; - 2) अस्तित्व में नहीं होगा.
2. जब ढलान शून्य हो तो स्पर्शरेखा x के समानांतर होती है। तब k x = t g α x = f''(x 0)। यानी, ऐसे x के मान ज्ञात करना आवश्यक है जब फ़ंक्शन का व्युत्पन्न इसे शून्य में बदल देता है। अर्थात, f' का मान (x) स्पर्शरेखा के बिंदु होंगे, जहां स्पर्शरेखा x के समानांतर है।

जब x ∈ - ∞ ; - 2, तो - 1 5 (x 2 + 12 x + 35) = 0, और x ∈ (- 2; + ∞) के लिए हमें 1 5 (x 2 - 4 x + 3) = 0 मिलता है।

1 5 (x 2 + 12 x + 35) = 0 डी = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

संगत फ़ंक्शन मानों की गणना करें

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 वाई 3 = वाई (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 वाई 4 = वाई (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

अतः - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 को फ़ंक्शन ग्राफ़ के आवश्यक बिंदु माना जाता है।

आइए समाधान का चित्रमय प्रतिनिधित्व देखें।

काली रेखा फ़ंक्शन का ग्राफ़ है, लाल बिंदु स्पर्शरेखा बिंदु हैं।

1. जब रेखाएँ समानांतर होती हैं, तो कोणीय गुणांक बराबर होते हैं। फिर फ़ंक्शन ग्राफ़ पर उन बिंदुओं की खोज करना आवश्यक है जहां ढलान मान 8 5 के बराबर होगा। ऐसा करने के लिए, आपको फॉर्म y "(x) = 8 5 के समीकरण को हल करने की आवश्यकता है। फिर, यदि x ∈ - ∞; - 2, तो हम प्राप्त करते हैं - 1 5 (x 2 + 12 x + 35) = 8 5, और यदि x ∈ ( - 2 ; + ∞), तो 1 5 (x 2 - 4 x + 3) = 8 5.

पहले समीकरण का कोई मूल नहीं है क्योंकि विवेचक शून्य से कम है। चलो उसे लिख लें

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 डी = 12 2 - 4 43 = - 28< 0

तो फिर, एक अन्य समीकरण की दो वास्तविक जड़ें हैं

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

आइए फ़ंक्शन के मान ज्ञात करने के लिए आगे बढ़ें। हमें वह मिल गया

वाई 1 = वाई (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 वाई 2 = वाई (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

मान वाले अंक - 1; 4 15, 5; 8 3 वे बिंदु हैं जिन पर स्पर्शरेखाएँ रेखा y = 8 5 x + 4 के समानांतर हैं।

उत्तर:काली रेखा - फ़ंक्शन का ग्राफ, लाल रेखा - y = 8 5 x + 4 का ग्राफ, नीली रेखा - बिंदुओं पर स्पर्शरेखा - 1; 4 15, 5; 8 3.

दिए गए फलन के लिए स्पर्शरेखाओं की अनंत संख्या हो सकती है।

उदाहरण 5

फ़ंक्शन y = 3 cos 3 2 x - π 4 - 1 3 की सभी उपलब्ध स्पर्शरेखाओं के समीकरण लिखें, जो सीधी रेखा y = - 2 x + 1 2 के लंबवत स्थित हैं।

समाधान

स्पर्शरेखा समीकरण संकलित करने के लिए रेखाओं की लंबवतता की स्थिति के आधार पर स्पर्शरेखा बिंदु के गुणांक और निर्देशांक ज्ञात करना आवश्यक है। परिभाषा इस प्रकार है: कोणीय गुणांकों का गुणनफल जो सीधी रेखाओं के लंबवत होते हैं - 1 के बराबर होते हैं, अर्थात k x · k ⊥ = - 1 के रूप में लिखा जाता है। शर्त से हमारे पास यह है कि कोणीय गुणांक रेखा के लंबवत स्थित है और k ⊥ = - 2 के बराबर है, तो k x = - 1 k ⊥ = - 1 - 2 = 1 2.

अब आपको स्पर्श बिंदुओं के निर्देशांक खोजने की आवश्यकता है। आपको किसी दिए गए फ़ंक्शन के लिए x और फिर उसका मान ढूंढना होगा। ध्यान दें कि बिंदु पर व्युत्पन्न के ज्यामितीय अर्थ से
x 0 से हम पाते हैं कि k x = y "(x 0)। इस समानता से हम संपर्क बिंदुओं के लिए x का मान पाते हैं।

हमें वह मिल गया

y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - पाप 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 पाप 3 2 x 0 - π 4 3 2 = - 9 2 पाप 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 पाप 3 2 x 0 - π 4 = 1 2 ⇒ पाप 3 2 x 0 - π 4 = - 1 9

इस त्रिकोणमितीय समीकरण का उपयोग स्पर्शरेखा बिंदुओं के निर्देशांक की गणना के लिए किया जाएगा।

3 2 x 0 - π 4 = ए आर सी पाप - 1 9 + 2 πk या 3 2 x 0 - π 4 = π - ए आर सी पाप - 1 9 + 2 πk

3 2 x 0 - π 4 = - ए आर सी पाप 1 9 + 2 πk या 3 2 x 0 - π 4 = π + ए आर सी पाप 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c पाप 1 9 + 2 πk या x 0 = 2 3 5 π 4 + a r c पाप 1 9 + 2 πk , k ∈ Z

Z पूर्णांकों का एक समूह है.

संपर्क के x बिंदु पाए गए हैं. अब आपको y के मानों की खोज के लिए आगे बढ़ना होगा:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - पाप 2 3 2 x 0 - π 4 - 1 3 या y 0 = 3 - 1 - पाप 2 3 2 x 0 - π 4 - 1 3

वाई 0 = 3 1 - - 1 9 2 - 1 3 या वाई 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 या y 0 = - 4 5 + 1 3

इससे हमें यह प्राप्त होता है कि 2 3 π 4 - a r c syn 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + ए आर सी पाप 1 9 + 2 πk ; - 4 5 + 1 3 स्पर्शरेखा के बिंदु हैं।

उत्तर:आवश्यक समीकरण इस प्रकार लिखे जायेंगे

y = 1 2 x - 2 3 π 4 - a r c पाप 1 9 + 2 πk + 4 5 - 1 3, y = 1 2 x - 2 3 5 π 4 + a r c पाप 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

एक दृश्य प्रतिनिधित्व के लिए, एक समन्वय रेखा पर एक फ़ंक्शन और एक स्पर्शरेखा पर विचार करें।

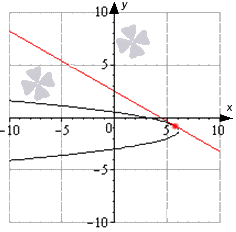
चित्र से पता चलता है कि फ़ंक्शन अंतराल पर स्थित है [-10; 10 ], जहां काली रेखा फ़ंक्शन का ग्राफ है, नीली रेखाएं स्पर्शरेखाएं हैं, जो फॉर्म y = - 2 x + 1 2 की दी गई रेखा के लंबवत स्थित हैं। लाल बिंदु स्पर्श बिंदु हैं.

दूसरे क्रम के वक्रों के विहित समीकरण एकल-मूल्य वाले फ़ंक्शन नहीं हैं। उनके लिए स्पर्शरेखा समीकरण ज्ञात योजनाओं के अनुसार संकलित किए जाते हैं।

एक वृत्त की स्पर्शरेखा

बिंदु x c e n t e r पर केन्द्रित एक वृत्त को परिभाषित करना; y c e n t e r और त्रिज्या R, सूत्र x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 लागू करें।

इस समानता को दो कार्यों के मिलन के रूप में लिखा जा सकता है:

वाई = आर 2 - एक्स - एक्स सी ई एन टी ई आर 2 + वाई सी ई एन टी ई आर वाई = - आर 2 - एक्स - एक्स सी ई एन टी ई आर 2 + वाई सी ई एन टी ई आर

पहला फ़ंक्शन शीर्ष पर स्थित है, और दूसरा नीचे, जैसा कि चित्र में दिखाया गया है।

बिंदु x 0 पर एक वृत्त का समीकरण संकलित करने के लिए; y 0, जो ऊपरी या निचले अर्धवृत्त में स्थित है, आपको फॉर्म y = R 2 - x - x c e n t e r 2 + y c e n t e r या y = - R 2 - x - x c e n t e r 2 + के फ़ंक्शन के ग्राफ़ का समीकरण ढूंढना चाहिए संकेतित बिंदु पर वाई सी ई एन टी ई आर।

जब बिंदुओं पर x c e n t e r ; वाई सी ई एन टी ई आर + आर और एक्स सी ई एन टी ई आर; y c e n t e r - R स्पर्श रेखाएं समीकरण y = y c e n t e r + R और y = y c e n t e r - R द्वारा दी जा सकती हैं, और बिंदुओं x c e n t e r + R पर; वाई सी ई एन टी ई आर और
एक्स सी ई एन टी ई आर - आर ; y c e n t e r, o y के समानांतर होगा, तो हमें x = x c e n t e r + R और x = x c e n t e r - R के रूप के समीकरण प्राप्त होते हैं।

एक दीर्घवृत्त की स्पर्शरेखा

जब दीर्घवृत्त का केंद्र x c e n t e r पर हो; y c e n t e r अर्ध-अक्ष a और b के साथ, तो इसे समीकरण x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 का उपयोग करके निर्दिष्ट किया जा सकता है।

एक दीर्घवृत्त और एक वृत्त को दो कार्यों, अर्थात् ऊपरी और निचले आधे-दीर्घवृत्त को मिलाकर निरूपित किया जा सकता है। तब हमें वह मिलता है

y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

यदि स्पर्शरेखाएँ दीर्घवृत्त के शीर्षों पर स्थित हैं, तो वे x के बारे में या y के बारे में समानांतर हैं। स्पष्टता के लिए नीचे दिए गए आंकड़े पर विचार करें।

उदाहरण 6

दीर्घवृत्त x - 3 2 4 + y - 5 2 25 = 1 की स्पर्शरेखा का समीकरण x = 2 के बराबर x के मान वाले बिंदुओं पर लिखें।

समाधान

उन स्पर्शरेखा बिंदुओं को खोजना आवश्यक है जो मान x = 2 के अनुरूप हों। हम दीर्घवृत्त के मौजूदा समीकरण को प्रतिस्थापित करते हैं और उसे पाते हैं

एक्स - 3 2 4 एक्स = 2 + वाई - 5 2 25 = 1 1 4 + वाई - 5 2 25 = 1 ⇒ वाई - 5 2 = 3 4 25 ⇒ वाई = ± 5 3 2 + 5

फिर 2 ; 5 3 2 + 5 और 2; - 5 3 2 + 5 स्पर्शरेखा बिंदु हैं जो ऊपरी और निचले आधे-दीर्घवृत्त से संबंधित हैं।

आइए y के संबंध में दीर्घवृत्त के समीकरण को खोजने और हल करने के लिए आगे बढ़ें। हमें वह मिल गया

एक्स - 3 2 4 + वाई - 5 2 25 = 1 वाई - 5 2 25 = 1 - एक्स - 3 2 4 (वाई - 5) 2 = 25 1 - एक्स - 3 2 4 वाई - 5 = ± 5 1 - एक्स - 3 2 4 वाई = 5 ± 5 2 4 - एक्स - 3 2

जाहिर है, ऊपरी अर्ध-दीर्घवृत्त को y = 5 + 5 2 4 - x - 3 2 के रूप के एक फ़ंक्शन का उपयोग करके निर्दिष्ट किया जाता है, और निचला आधा दीर्घवृत्त y = 5 - 5 2 4 - x - 3 2 के रूप में निर्दिष्ट किया जाता है।

आइए एक बिंदु पर किसी फ़ंक्शन के ग्राफ़ के स्पर्शरेखा के लिए एक समीकरण बनाने के लिए एक मानक एल्गोरिदम लागू करें। आइए हम लिखते हैं कि बिंदु 2 पर पहली स्पर्शरेखा के लिए समीकरण; 5 3 2 + 5 जैसा दिखेगा

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

हम पाते हैं कि बिंदु पर एक मान के साथ दूसरे स्पर्शरेखा का समीकरण
2 ; - 5 3 2 + 5 का रूप लेता है

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

ग्राफ़िक रूप से, स्पर्शरेखाओं को इस प्रकार निर्दिष्ट किया गया है:

अतिशयोक्ति का स्पर्शरेखा

जब हाइपरबोला का केंद्र x c e n t e r पर होता है; y c e n t e r और शीर्ष x c e n t e r + α ; वाई सी ई एन टी ई आर और एक्स सी ई एन टी ई आर - α ; y c e n t e r , असमानता x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 होती है, यदि शीर्ष x c e n t e r के साथ; वाई सी ई एन टी ई आर + बी और एक्स सी ई एन टी ई आर; y c e n t e r - b , फिर असमानता x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 का उपयोग करके निर्दिष्ट किया जाता है।

एक हाइपरबोला को फॉर्म के दो संयुक्त कार्यों के रूप में दर्शाया जा सकता है

y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r या y = b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r y = - b a · (एक्स - एक्स सी ई एन टी ई आर) 2 + ए 2 + वाई सी ई एन टी ई आर

पहले मामले में हमारे पास यह है कि स्पर्शरेखाएँ y के समानांतर हैं, और दूसरे में वे x के समानांतर हैं।

इसका तात्पर्य यह है कि हाइपरबोला के स्पर्शरेखा के समीकरण को खोजने के लिए, यह पता लगाना आवश्यक है कि स्पर्शरेखा का बिंदु किस फ़ंक्शन से संबंधित है। इसे निर्धारित करने के लिए, समीकरणों में स्थानापन्न करना और पहचान की जांच करना आवश्यक है।

उदाहरण 7

बिंदु 7 पर अतिपरवलय x - 3 2 4 - y + 3 2 9 = 1 की स्पर्शरेखा के लिए एक समीकरण लिखें; - 3 3 - 3 .

समाधान

2 फ़ंक्शंस का उपयोग करके हाइपरबोला खोजने के लिए समाधान रिकॉर्ड को बदलना आवश्यक है। हमें वह मिल गया

एक्स - 3 2 4 - वाई + 3 2 9 = 1 ⇒ वाई + 3 2 9 = एक्स - 3 2 4 - 1 ⇒ वाई + 3 2 = 9 एक्स - 3 2 4 - 1 ⇒ वाई + 3 = 3 2 एक्स - 3 2 - 4 और y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

यह पहचानना आवश्यक है कि निर्देशांक 7 वाला दिया गया बिंदु किस फ़ंक्शन से संबंधित है; - 3 3 - 3 .

जाहिर है, पहले फ़ंक्शन की जांच करने के लिए यह आवश्यक है y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, तो बिंदु ग्राफ़ से संबंधित नहीं है, चूंकि समानता कायम नहीं है.

दूसरे फ़ंक्शन के लिए हमारे पास है कि y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, जिसका अर्थ है कि बिंदु दिए गए ग्राफ़ से संबंधित है। यहां से आपको ढलान ढूंढनी चाहिए.

हमें वह मिल गया

y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

उत्तर:स्पर्शरेखा समीकरण को इस प्रकार दर्शाया जा सकता है

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

इसे इस प्रकार स्पष्ट रूप से दर्शाया गया है:

एक परवलय की स्पर्शरेखा

बिंदु x 0, y (x 0) पर परवलय y = a x 2 + b x + c की स्पर्शरेखा के लिए एक समीकरण बनाने के लिए, आपको एक मानक एल्गोरिदम का उपयोग करना होगा, फिर समीकरण y = y "(x) का रूप लेगा 0) x - x 0 + y ( x 0)। शीर्ष पर ऐसी स्पर्शरेखा x के समानांतर है।

आपको परवलय x = a y 2 + b y + c को दो कार्यों के मिलन के रूप में परिभाषित करना चाहिए। इसलिए, हमें y के समीकरण को हल करने की आवश्यकता है। हमें वह मिल गया

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - बी - बी 2 - 4 ए (सी - एक्स) 2 ए

रेखांकन के रूप में दर्शाया गया है:

यह पता लगाने के लिए कि क्या कोई बिंदु x 0, y (x 0) किसी फ़ंक्शन से संबंधित है, मानक एल्गोरिदम के अनुसार धीरे से आगे बढ़ें। ऐसी स्पर्शरेखा परवलय के सापेक्ष y के समानांतर होगी।

उदाहरण 8

ग्राफ़ x - 2 y 2 - 5 y + 3 की स्पर्शरेखा का समीकरण लिखें जब हमारे पास 150° का स्पर्शरेखा कोण हो।

समाधान

हम परवलय को दो कार्यों के रूप में निरूपित करके समाधान शुरू करते हैं। हमें वह मिल गया

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

ढलान का मान इस फ़ंक्शन के बिंदु x 0 पर व्युत्पन्न के मान के बराबर है और झुकाव के कोण के स्पर्शरेखा के बराबर है।

हम पाते हैं:

के एक्स = वाई "(एक्स 0) = टी जी α एक्स = टी जी 150 ° = - 1 3

यहां से हम संपर्क बिंदुओं के लिए x मान निर्धारित करते हैं।

पहला फ़ंक्शन इस प्रकार लिखा जाएगा

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

जाहिर है, कोई वास्तविक जड़ें नहीं हैं, क्योंकि हमें नकारात्मक मूल्य मिला है। हम यह निष्कर्ष निकालते हैं कि ऐसे फलन के लिए 150° के कोण वाली कोई स्पर्शरेखा नहीं है।

दूसरा फ़ंक्शन इस प्रकार लिखा जाएगा

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ वाई (एक्स 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

हमारे पास यह है कि संपर्क के बिंदु 23 4 हैं; - 5 + 3 4 .

उत्तर:स्पर्श रेखा समीकरण का रूप ले लेती है

y = - 1 3 x - 23 4 + - 5 + 3 4

आइए इसे आलेखीय रूप से इस प्रकार चित्रित करें:

यदि आपको पाठ में कोई त्रुटि दिखाई देती है, तो कृपया उसे हाइलाइट करें और Ctrl+Enter दबाएँ

वीडियो पाठ "फ़ंक्शन के ग्राफ़ के स्पर्शरेखा का समीकरण" विषय में महारत हासिल करने के लिए शैक्षिक सामग्री प्रदर्शित करता है। वीडियो पाठ के दौरान, किसी दिए गए बिंदु पर किसी फ़ंक्शन के ग्राफ़ के स्पर्शरेखा के समीकरण की अवधारणा तैयार करने के लिए आवश्यक सैद्धांतिक सामग्री, ऐसी स्पर्शरेखा खोजने के लिए एक एल्गोरिदम, और अध्ययन की गई सैद्धांतिक सामग्री का उपयोग करके समस्याओं को हल करने के उदाहरणों का वर्णन किया गया है। .

वीडियो ट्यूटोरियल उन तरीकों का उपयोग करता है जो सामग्री की स्पष्टता में सुधार करते हैं। प्रस्तुतिकरण में चित्र, आरेख, महत्वपूर्ण ध्वनि टिप्पणियाँ, एनीमेशन, हाइलाइटिंग और अन्य उपकरण शामिल हैं।

वीडियो पाठ पाठ के विषय की प्रस्तुति और बिंदु M(a;f(a)) पर कुछ फ़ंक्शन y=f(x) के ग्राफ की स्पर्श रेखा की छवि के साथ शुरू होता है। यह ज्ञात है कि किसी दिए गए बिंदु पर ग्राफ़ पर खींची गई स्पर्शरेखा का कोणीय गुणांक इस बिंदु पर फ़ंक्शन f΄(a) के व्युत्पन्न के बराबर है। बीजगणित पाठ्यक्रम से भी हम सीधी रेखा y=kx+m का समीकरण जानते हैं। एक बिंदु पर स्पर्शरेखा समीकरण खोजने की समस्या का समाधान योजनाबद्ध रूप से प्रस्तुत किया गया है, जो गुणांक k, m को खोजने के लिए कम हो जाता है। फ़ंक्शन के ग्राफ़ से संबंधित एक बिंदु के निर्देशांक को जानने के बाद, हम स्पर्शरेखा समीकरण f(a)=ka+m में निर्देशांक मान को प्रतिस्थापित करके m पा सकते हैं। इससे हमें m=f(a)-ka मिलता है। इस प्रकार, किसी दिए गए बिंदु पर व्युत्पन्न का मान और बिंदु के निर्देशांक को जानकर, हम स्पर्शरेखा समीकरण को इस प्रकार निरूपित कर सकते हैं y=f(a)+f΄(a)(x-a)।

निम्नलिखित आरेख के बाद स्पर्शरेखा समीकरण बनाने का एक उदाहरण है। फलन y=x 2 , x=-2 दिया गया है। a=-2 लेते हुए, हम दिए गए बिंदु f(a)= f(-2)=(-2) 2 =4 पर फ़ंक्शन का मान पाते हैं। हम फलन f΄(x)=2x का अवकलज निर्धारित करते हैं। इस बिंदु पर व्युत्पन्न f΄(a)= f΄(-2)=2·(-2)=-4 के बराबर है। समीकरण बनाने के लिए, सभी गुणांक a=-2, f(a)=4, f΄(a)=-4 पाए गए, इसलिए स्पर्शरेखा समीकरण y=4+(-4)(x+2) है। समीकरण को सरल करने पर, हमें y = -4-4x मिलता है।

निम्नलिखित उदाहरण फ़ंक्शन y=tgx के ग्राफ़ के मूल बिंदु पर स्पर्शरेखा के लिए एक समीकरण बनाने का सुझाव देता है। किसी दिए गए बिंदु पर a=0, f(0)=0, f΄(x)=1/cos 2 x, f΄(0)=1. तो स्पर्शरेखा समीकरण y=x जैसा दिखता है।

सामान्यीकरण के रूप में, एक निश्चित बिंदु पर किसी फ़ंक्शन के ग्राफ़ के स्पर्शरेखा समीकरण को बनाने की प्रक्रिया को 4 चरणों वाले एल्गोरिदम के रूप में औपचारिक रूप दिया जाता है:

• स्पर्शरेखा बिंदु के भुज के लिए पदनाम a दर्ज करें;
• एफ(ए) की गणना की जाती है;
• f΄(x) निर्धारित किया जाता है और f΄(a) की गणना की जाती है। A, f(a), f΄(a) के पाए गए मानों को स्पर्शरेखा समीकरण सूत्र y=f(a)+f΄(a)(x-a) में प्रतिस्थापित किया जाता है।

उदाहरण 1 बिंदु x=1 पर फ़ंक्शन y=1/x के ग्राफ़ के स्पर्शरेखा समीकरण की रचना करने पर विचार करता है। समस्या को हल करने के लिए हम एक एल्गोरिदम का उपयोग करते हैं। बिंदु a=1 पर दिए गए फ़ंक्शन के लिए, फ़ंक्शन का मान f(a)=-1 है। फलन f΄(x)=1/x 2 का व्युत्पन्न। बिंदु a=1 पर व्युत्पन्न f΄(a)= f΄(1)=1. प्राप्त डेटा का उपयोग करके, स्पर्शरेखा समीकरण y=-1+(x-1), या y=x-2, तैयार किया जाता है।

उदाहरण 2 में, फ़ंक्शन y=x 3 +3x 2 -2x-2 के ग्राफ़ की स्पर्शरेखा का समीकरण खोजना आवश्यक है। मुख्य शर्त स्पर्शरेखा और सीधी रेखा y=-2x+1 की समानता है। सबसे पहले, हम स्पर्शरेखा का कोणीय गुणांक ज्ञात करते हैं, जो सीधी रेखा y=-2x+1 के कोणीय गुणांक के बराबर है। चूँकि किसी दी गई रेखा के लिए f΄(a)=-2, वांछित स्पर्शरेखा के लिए k=-2 है। हम फ़ंक्शन का व्युत्पन्न पाते हैं (x 3 +3x 2 -2x-2)΄=3x 2 +6x-2. यह जानते हुए कि f΄(a)=-2, हम बिंदु 3a 2 +6a-2=-2 के निर्देशांक पाते हैं। समीकरण को हल करने पर, हमें 1 =0, और 2 =-2 प्राप्त होता है। पाए गए निर्देशांक का उपयोग करके, आप एक प्रसिद्ध एल्गोरिदम का उपयोग करके स्पर्शरेखा समीकरण पा सकते हैं। हम बिंदुओं f(a 1)=-2, f(a 2)=-18 पर फ़ंक्शन का मान पाते हैं। बिंदु f΄(а 1)=f΄(а 2)=-2 पर अवकलज का मान। पाए गए मानों को स्पर्शरेखा समीकरण में प्रतिस्थापित करते हुए, हम पहले बिंदु a 1 =0 y=-2x-2 के लिए प्राप्त करते हैं, और दूसरे बिंदु a 2 =-2 के लिए स्पर्शरेखा समीकरण y=-2x-22 प्राप्त करते हैं।

उदाहरण 3 फ़ंक्शन y=√x के ग्राफ़ के बिंदु (0;3) पर खींचने के लिए स्पर्शरेखा समीकरण की संरचना का वर्णन करता है। समाधान एक सुविख्यात एल्गोरिथम का उपयोग करके बनाया गया है। स्पर्शरेखा बिंदु के निर्देशांक x=a हैं, जहां a>0। बिंदु f(a)=√x पर फ़ंक्शन का मान। फ़ंक्शन f΄(х)=1/2√х का व्युत्पन्न, इसलिए किसी दिए गए बिंदु पर f΄(а)=1/2√а। सभी प्राप्त मानों को स्पर्शरेखा समीकरण में प्रतिस्थापित करने पर, हम y = √a + (x-a)/2√a प्राप्त करते हैं। समीकरण को बदलने पर, हमें y=x/2√а+√а/2 मिलता है। यह जानते हुए कि स्पर्शरेखा बिंदु (0;3) से होकर गुजरती है, हम a का मान ज्ञात करते हैं। हम 3=√a/2 से a पाते हैं। अत: √a=6, a=36। हम स्पर्शरेखा समीकरण y=x/12+3 पाते हैं। यह आंकड़ा विचाराधीन फ़ंक्शन का ग्राफ़ और निर्मित वांछित स्पर्शरेखा दिखाता है।

छात्रों को अनुमानित समानताएं Δy=≈f΄(x)Δxand f(x+Δx)-f(x)≈f΄(x)Δx याद दिलाई जाती हैं। x=a, x+Δx=x, Δx=x-a लेते हुए, हमें f(x)- f(a)≈f΄(a)(x-a) मिलता है, इसलिए f(x)≈f(a)+ f΄( ए)(एक्स-ए)।

उदाहरण 4 में, व्यंजक 2.003 6 का अनुमानित मान ज्ञात करना आवश्यक है। चूँकि बिंदु x=2.003 पर फ़ंक्शन f(x)=x 6 का मान ज्ञात करना आवश्यक है, हम f(x)=x 6, a=2, f(a) लेते हुए प्रसिद्ध सूत्र का उपयोग कर सकते हैं )= f(2)=64, f ΄(x)=6x 5. बिंदु f΄(2)=192 पर व्युत्पन्न। इसलिए, 2.003 6 ≈65-192·0.003. अभिव्यक्ति की गणना करने पर, हमें 2.003 6 ≈64.576 मिलता है।

स्कूल में पारंपरिक गणित पाठ में उपयोग के लिए वीडियो पाठ "किसी फ़ंक्शन के ग्राफ़ के स्पर्शरेखा का समीकरण" की अनुशंसा की जाती है। दूर से पढ़ाने वाले शिक्षक के लिए, वीडियो सामग्री विषय को अधिक स्पष्ट रूप से समझाने में मदद करेगी। यदि आवश्यक हो तो विषय की समझ को गहरा करने के लिए छात्रों को स्वतंत्र रूप से समीक्षा करने के लिए वीडियो की अनुशंसा की जा सकती है।

पाठ डिकोडिंग:

हम जानते हैं कि यदि एक बिंदु M (a; f(a)) (ए से निर्देशांक a और ef के साथ em) फ़ंक्शन y = f (x) के ग्राफ़ से संबंधित है और यदि इस बिंदु पर एक स्पर्शरेखा खींचना संभव है फ़ंक्शन के ग्राफ़ पर जो अक्ष भुज के लंबवत नहीं है, तो स्पर्शरेखा का कोणीय गुणांक f"(a) (a से eff prime) के बराबर होता है।

मान लीजिए कि एक फ़ंक्शन y = f(x) और एक बिंदु M (a; f(a)) दिया गया है, और यह भी ज्ञात है कि f´(a) मौजूद है। आइए किसी दिए गए बिंदु पर दिए गए फ़ंक्शन के ग्राफ़ की स्पर्शरेखा के लिए एक समीकरण बनाएं। यह समीकरण, किसी भी सीधी रेखा के समीकरण की तरह, जो कोटि अक्ष के समानांतर नहीं है, का रूप y = kx+m है (y, ka x प्लस em के बराबर है), इसलिए कार्य का मान ज्ञात करना है गुणांक k और m. (ka और em)

कोण गुणांक k= f"(a)। m के मान की गणना करने के लिए, हम इस तथ्य का उपयोग करते हैं कि वांछित सीधी रेखा बिंदु M(a; f (a)) से होकर गुजरती है। इसका मतलब यह है कि यदि हम के निर्देशांक को प्रतिस्थापित करते हैं सीधी रेखा के समीकरण में बिंदु M पर, हमें सही समानता प्राप्त होती है: f(a) = ka+m, जहां से हम पाते हैं कि m = f(a) - ka।

यह गुणांक Ki और m के पाए गए मानों को सीधी रेखा के समीकरण में प्रतिस्थापित करना बाकी है:

y = kx+(f(a) -ka);

y = f(a)+k(x-a);

य= एफ(ए)+ एफ"(ए) (एक्स- ए). ( y, a से ef के बराबर है और a से ef prime, x घटा a से गुणा किया गया है)।

हमने बिंदु x=a पर फ़ंक्शन y = f(x) के ग्राफ़ की स्पर्श रेखा के लिए समीकरण प्राप्त कर लिया है।

यदि, मान लीजिए, y = x 2 और x = -2 (अर्थात a = -2), तो f (a) = f (-2) = (-2) 2 = 4; f´(x) = 2x, जिसका अर्थ है f"(a) = f´(-2) = 2·(-2) = -4. (तब a का ef चार के बराबर है, अभाज्य का ef x दो x के बराबर है, जिसका अर्थ है कि a से ef अभाज्य शून्य से चार के बराबर है)

समीकरण में पाए गए मान a = -2, f(a) = 4, f"(a) = -4 को प्रतिस्थापित करने पर, हम प्राप्त करते हैं: y = 4+(-4)(x+2), अर्थात। y = -4x -4.

(ई शून्य से चार x शून्य से चार के बराबर है)

आइए मूल बिंदु पर फ़ंक्शन y = tanx (y स्पर्शरेखा x के बराबर है) के ग्राफ़ की स्पर्शरेखा के लिए एक समीकरण बनाएं। हमारे पास: a = 0, f(0) = tan0=0;

f"(x)= , जिसका अर्थ है f"(0) = l. समीकरण में पाए गए मान a=0, f(a)=0, f´(a) = 1 को प्रतिस्थापित करने पर, हमें मिलता है: y=x।

आइए हम एक एल्गोरिदम का उपयोग करके बिंदु x पर किसी फ़ंक्शन के ग्राफ़ के स्पर्शरेखा के समीकरण को खोजने में अपने चरणों को संक्षेप में प्रस्तुत करें।

फ़ंक्शन y = f(x) के ग्राफ़ की स्पर्शरेखा के लिए एक समीकरण विकसित करने के लिए एल्गोरिदम:

1) स्पर्शरेखा बिंदु के भुज को अक्षर a से निर्दिष्ट करें।

2) f(a) की गणना करें।

3) f´(x) खोजें और f´(a) की गणना करें।

4) सूत्र में प्राप्त संख्याओं a, f(a), f´(a) को प्रतिस्थापित करें य= एफ(ए)+ एफ"(ए) (एक्स- ए).

उदाहरण 1. फ़ंक्शन y = - in के ग्राफ़ की स्पर्शरेखा के लिए एक समीकरण बनाएं

बिंदु x = 1.

समाधान। आइए इस उदाहरण में इसे ध्यान में रखते हुए एल्गोरिदम का उपयोग करें

2) f(a)=f(1)=- =-1

3)f´(x)=; f´(a)= f´(1)= =1.

4) प्राप्त तीन संख्याओं को प्रतिस्थापित करें: a = 1, f(a) = -1, f"(a) = 1 सूत्र में। हमें मिलता है: y = -1+(x-1), y = x-2 .

उत्तर: y = x-2.

उदाहरण 2. फलन y = दिया गया है एक्स 3 +3एक्स 2 -2एक्स-2. फ़ंक्शन y = f(x) के ग्राफ़ की स्पर्श रेखा का समीकरण, सीधी रेखा y = -2x +1 के समानांतर लिखें।

स्पर्शरेखा समीकरण की रचना के लिए एल्गोरिदम का उपयोग करते हुए, हम इस बात को ध्यान में रखते हैं कि इस उदाहरण में f(x) = एक्स 3 +3एक्स 2 -2एक्स-2, लेकिन स्पर्शरेखा बिंदु का भुज यहां इंगित नहीं किया गया है।

आइए इस तरह सोचना शुरू करें। वांछित स्पर्शरेखा सीधी रेखा y = -2x+1 के समानांतर होनी चाहिए। और समानांतर रेखाओं में समान कोणीय गुणांक होते हैं। इसका मतलब यह है कि स्पर्शरेखा का कोणीय गुणांक दी गई सीधी रेखा के कोणीय गुणांक के बराबर है: k स्पर्शरेखा। = -2. होक कैस. = f"(a)। इस प्रकार, हम समीकरण f ´(a) = -2 से a का मान ज्ञात कर सकते हैं।

आइए फ़ंक्शन का व्युत्पन्न खोजें आप=एफ(एक्स):

एफ"(एक्स)= (x 3 +3x 2 -2x-2)´ =3x 2 +6x-2;एफ"(ए)= 3ए 2 +6ए-2.

समीकरण f"(a) = -2 से, अर्थात। 3ए 2 +6ए-2=-2 हमें a 1 =0, a 2 =-2 मिलता है। इसका मतलब यह है कि दो स्पर्शरेखाएं हैं जो समस्या की शर्तों को पूरा करती हैं: एक एब्सिस्सा 0 वाले बिंदु पर, दूसरी एब्सिस्सा -2 वाले बिंदु पर।

अब आप एल्गोरिथम का पालन कर सकते हैं।

1) ए 1 =0, और 2 =-2.

2) एफ(ए 1)= 0 3 +3·0 2 -2∙0-2=-2; एफ(ए 2)= (-2) 3 +3·(-2) 2 -2·(-2)-2=6;

3) एफ"(ए 1) = एफ"(ए 2) = -2.

4) मान a 1 = 0, f(a 1) = -2, f"(a 1) = -2 को सूत्र में प्रतिस्थापित करने पर, हमें मिलता है:

y=-2-2(x-0), y=-2x-2.

मान a 2 = -2, f(a 2) =6, f"(a 2) = -2 को सूत्र में प्रतिस्थापित करने पर, हमें मिलता है:

y=6-2(x+2), y=-2x+2.

उत्तर: y=-2x-2, y=-2x+2.

उदाहरण 3. बिंदु (0; 3) से फ़ंक्शन y = के ग्राफ़ पर एक स्पर्शरेखा खींचें। समाधान। आइए इस उदाहरण में f(x) = को ध्यान में रखते हुए, स्पर्शरेखा समीकरण बनाने के लिए एल्गोरिदम का उपयोग करें। ध्यान दें कि यहां, उदाहरण 2 की तरह, स्पर्शरेखा बिंदु का भुज स्पष्ट रूप से इंगित नहीं किया गया है। फिर भी, हम एल्गोरिथम का पालन करते हैं।

1) मान लीजिए x = a स्पर्शरेखा बिंदु का भुज है; यह स्पष्ट है कि a >0.

3)f´(x)=()´=; f´(ए) =.

4) सूत्र में a, f(a) = , f"(a) = के मानों को प्रतिस्थापित करना

y=f (a) +f "(a) (x-a), हम पाते हैं:

शर्त के अनुसार, स्पर्शरेखा बिंदु (0; 3) से होकर गुजरती है। समीकरण में x = 0, y = 3 मानों को प्रतिस्थापित करने पर, हमें मिलता है: 3 =, और फिर =6, a =36।

जैसा कि आप देख सकते हैं, इस उदाहरण में, एल्गोरिदम के केवल चौथे चरण में हम स्पर्शरेखा बिंदु का भुज खोजने में कामयाब रहे। समीकरण में मान a =36 रखने पर, हमें मिलता है: y=+3

चित्र में. चित्र 1 विचारित उदाहरण का एक ज्यामितीय चित्रण दिखाता है: फ़ंक्शन y = का एक ग्राफ़ बनाया गया है, एक सीधी रेखा y = +3 खींची गई है।

उत्तर: y = +3.

हम जानते हैं कि एक फ़ंक्शन y = f(x) के लिए, जिसका बिंदु x पर व्युत्पन्न है, अनुमानित समानता मान्य है: Δyf´(x)Δx (डेल्टा y लगभग x के eff अभाज्य को डेल्टा x से गुणा करने के बराबर है)

या, अधिक विस्तार से, f(x+Δx)-f(x) f´(x) Δx (x से eff प्लस डेल्टा x घटा ef, x से डेल्टा x द्वारा eff प्राइम के लगभग बराबर है)।

आगे की चर्चा की सुविधा के लिए, आइए संकेतन बदलें:

x की जगह हम लिखेंगे ए,

x+Δx के स्थान पर हम x लिखेंगे

Δx के स्थान पर हम x-a लिखेंगे।

तब ऊपर लिखी अनुमानित समानता का रूप ले लेगी:

f(x)-f(a)f´(a)(x-a)

f(x)f(a)+f´(a)(x-a). (x से eff लगभग a से ef के बराबर है और a से ef prime, x और a के बीच के अंतर से गुणा किया गया है)।

उदाहरण 4. संख्यात्मक अभिव्यक्ति 2.003 6 का अनुमानित मान ज्ञात कीजिए।

समाधान। हम बिंदु x = 2.003 पर फ़ंक्शन y = x 6 का मान ज्ञात करने के बारे में बात कर रहे हैं। आइए सूत्र f(x)f(a)+f´(a)(x-a) का उपयोग करें, यह ध्यान में रखते हुए कि इस उदाहरण में f(x)=x 6, a = 2,f(a) = f(2) = 2 6 =64; x = 2.003, f"(x) = 6x 5 और, इसलिए, f"(a) = f"(2) = 6 2 5 =192।

परिणामस्वरूप हमें मिलता है:

2.003 6 64+192· 0.003, यानी। 2.003 6 =64.576.

यदि हम कैलकुलेटर का उपयोग करते हैं, तो हमें मिलता है:

2,003 6 = 64,5781643...

जैसा कि आप देख सकते हैं, सन्निकटन सटीकता काफी स्वीकार्य है।

निम्नलिखित चित्र पर विचार करें:

यह एक निश्चित फ़ंक्शन y = f(x) को दर्शाता है, जो बिंदु a पर भिन्न है। बिंदु M को निर्देशांक (a; f(a)) के साथ चिह्नित किया गया है। ग्राफ़ के एक मनमाने बिंदु P(a + ∆x; f(a + ∆x)) से होकर एक छेदक MR खींचा जाता है।

यदि अब बिंदु P को ग्राफ़ के अनुदिश बिंदु M पर स्थानांतरित कर दिया जाता है, तो सीधी रेखा MR बिंदु M के चारों ओर घूमेगी। इस स्थिति में, ∆x शून्य की ओर प्रवृत्त होगा। यहां से हम किसी फ़ंक्शन के ग्राफ़ की स्पर्शरेखा की परिभाषा तैयार कर सकते हैं।

किसी फ़ंक्शन के ग्राफ़ की स्पर्श रेखा

किसी फ़ंक्शन के ग्राफ़ का स्पर्शरेखा छेदक की सीमित स्थिति है क्योंकि तर्क की वृद्धि शून्य हो जाती है। यह समझा जाना चाहिए कि बिंदु x0 पर फ़ंक्शन f के व्युत्पन्न के अस्तित्व का मतलब है कि ग्राफ़ के इस बिंदु पर है स्पर्शरेखाउसे।

इस मामले में, स्पर्शरेखा का कोणीय गुणांक इस बिंदु f'(x0) पर इस फ़ंक्शन के व्युत्पन्न के बराबर होगा। यह व्युत्पत्ति का ज्यामितीय अर्थ है। बिंदु x0 पर अवकलनीय फ़ंक्शन f के ग्राफ़ की स्पर्श रेखा बिंदु (x0;f(x0)) से गुजरने वाली एक निश्चित सीधी रेखा है और इसमें कोणीय गुणांक f'(x0) होता है।

स्पर्शरेखा समीकरण

आइए बिंदु A(x0; f(x0)) पर किसी फ़ंक्शन f के ग्राफ़ की स्पर्श रेखा का समीकरण प्राप्त करने का प्रयास करें। ढलान k वाली एक सीधी रेखा के समीकरण का निम्नलिखित रूप है:

चूँकि हमारा ढलान गुणांक व्युत्पन्न के बराबर है च'(x0), तो समीकरण निम्नलिखित रूप लेगा: y = च'(x0)*एक्स + बी.

अब आइए b के मान की गणना करें। ऐसा करने के लिए, हम इस तथ्य का उपयोग करते हैं कि फ़ंक्शन बिंदु A से होकर गुजरता है।

f(x0) = f'(x0)*x0 + b, यहां से हम b को व्यक्त करते हैं और b = f(x0) - f'(x0)*x0 प्राप्त करते हैं।

हम परिणामी मान को स्पर्शरेखा समीकरण में प्रतिस्थापित करते हैं:

y = f'(x0)*x + b = f'(x0)*x + f(x0) - f'(x0)*x0 = f(x0) + f'(x0)*(x - x0).

y = f(x0) + f'(x0)*(x - x0).

निम्नलिखित उदाहरण पर विचार करें: बिंदु x = 2 पर फ़ंक्शन f(x) = x 3 - 2*x 2 + 1 के ग्राफ़ की स्पर्शरेखा का समीकरण खोजें।

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f'(x) = 3*x 2 - 4*x.

4. f'(x0) = f'(2) = 3*2 2 - 4*2 = 4.

5. प्राप्त मानों को स्पर्शरेखा सूत्र में रखें, हमें मिलता है: y = 1 + 4*(x - 2)। कोष्ठक खोलने और समान पद लाने पर हमें प्राप्त होता है: y = 4*x - 7.

उत्तर: y = 4*x - 7.

स्पर्शरेखा समीकरण बनाने की सामान्य योजनाफ़ंक्शन के ग्राफ़ पर y = f(x):

1. x0 निर्धारित करें।

2. f(x0) की गणना करें।

3. f'(x) की गणना करें