ഓൺലൈൻ കാൽക്കുലേറ്റർ. ഒരു നിശ്ചിത പോയിന്റിലെ ഒരു ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള നേരായ ടാൻജന്റ് സമവാക്യം

ഡെറിവേറ്റീവിന്റെ ചിഹ്നവും ഫംഗ്‌ഷന്റെ ഏകതാനതയുടെ സ്വഭാവവും തമ്മിലുള്ള ബന്ധം കാണിക്കുന്നു.

താഴെ പറയുന്ന കാര്യങ്ങളിൽ അതീവ ജാഗ്രത പുലർത്തുക. നോക്കൂ, നിങ്ങൾക്ക് നൽകിയിരിക്കുന്നതിന്റെ ഷെഡ്യൂൾ! ഫംഗ്ഷൻ അല്ലെങ്കിൽ അതിന്റെ ഡെറിവേറ്റീവ്

ഡെറിവേറ്റീവിന്റെ ഒരു ഗ്രാഫ് നൽകിയാൽ, അപ്പോൾ നമുക്ക് ഫംഗ്ഷൻ ചിഹ്നങ്ങളിലും പൂജ്യങ്ങളിലും മാത്രം താൽപ്പര്യമുണ്ടാകും. തത്വത്തിൽ "കുന്നുകൾ" അല്ലെങ്കിൽ "പൊള്ളകൾ" എന്നിവയിൽ ഞങ്ങൾക്ക് താൽപ്പര്യമില്ല!

ടാസ്ക് 1.

ഇടവേളയിൽ നിർവചിച്ചിരിക്കുന്ന ഒരു ഫംഗ്ഷന്റെ ഗ്രാഫ് ചിത്രം കാണിക്കുന്നു. ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് നെഗറ്റീവ് ആയ പൂർണ്ണസംഖ്യ പോയിന്റുകളുടെ എണ്ണം നിർണ്ണയിക്കുക.

പരിഹാരം:

ചിത്രത്തിൽ, പ്രവർത്തനം കുറയുന്ന മേഖലകൾ നിറത്തിൽ ഹൈലൈറ്റ് ചെയ്തിരിക്കുന്നു:

ഫംഗ്‌ഷന്റെ ഈ കുറയുന്ന മേഖലകളിൽ 4 പൂർണ്ണസംഖ്യ മൂല്യങ്ങൾ അടങ്ങിയിരിക്കുന്നു.

ടാസ്ക് 2.

ഇടവേളയിൽ നിർവചിച്ചിരിക്കുന്ന ഒരു ഫംഗ്ഷന്റെ ഗ്രാഫ് ചിത്രം കാണിക്കുന്നു. ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റ് സമാന്തരമായോ അല്ലെങ്കിൽ വരിയുമായി പൊരുത്തപ്പെടുന്നതോ ആയ പോയിന്റുകളുടെ എണ്ണം കണ്ടെത്തുക.

പരിഹാരം:

ഒരു ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റ് ഒരു നേർരേഖയ്‌ക്ക് സമാന്തരമായി (അല്ലെങ്കിൽ യോജിക്കുന്നു) ഒരിക്കൽ (അല്ലെങ്കിൽ, അത് തന്നെയാണ്), ചരിവ്, പൂജ്യത്തിന് തുല്യമാണ്, അപ്പോൾ ടാൻജെന്റിന് ഒരു കോണീയ ഗുണകം ഉണ്ട്.

ഇത് അർത്ഥമാക്കുന്നത് ടാൻജെന്റ് അക്ഷത്തിന് സമാന്തരമാണെന്നാണ്, കാരണം ചരിവ് അക്ഷത്തിലേക്കുള്ള ടാൻജെന്റിന്റെ ചെരിവിന്റെ കോണിന്റെ ടാൻജെന്റാണ്.

അതിനാൽ, ഗ്രാഫിൽ ഞങ്ങൾ എക്സ്ട്രീം പോയിന്റുകൾ (പരമാവധി കുറഞ്ഞതും കുറഞ്ഞതുമായ പോയിന്റുകൾ) കണ്ടെത്തുന്നു - ഈ പോയിന്റുകളിലാണ് ഗ്രാഫിലേക്കുള്ള ടാൻജന്റ് ഫംഗ്‌ഷനുകൾ അക്ഷത്തിന് സമാന്തരമാകുന്നത്.

അത്തരം 4 പോയിന്റുകൾ ഉണ്ട്.

ടാസ്ക് 3.

ഇടവേളയിൽ നിർവചിച്ചിരിക്കുന്ന ഒരു ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവിന്റെ ഒരു ഗ്രാഫ് ചിത്രം കാണിക്കുന്നു. ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റ് സമാന്തരമായോ അല്ലെങ്കിൽ വരിയുമായി പൊരുത്തപ്പെടുന്നതോ ആയ പോയിന്റുകളുടെ എണ്ണം കണ്ടെത്തുക.

പരിഹാരം:

ഒരു ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റ് ഒരു ചരിവുള്ള ഒരു രേഖയ്‌ക്ക് സമാന്തരമായതിനാൽ (അല്ലെങ്കിൽ ഒത്തുചേരുന്നു), അപ്പോൾ ടാൻജന്റിനും ഒരു ചരിവുണ്ട്.

ഇത് അർത്ഥമാക്കുന്നത് ടച്ച് പോയിന്റുകളിൽ എന്നാണ്.

അതിനാൽ, ഗ്രാഫിലെ എത്ര പോയിന്റുകൾക്ക് തുല്യമായ ഒരു ഓർഡിനേറ്റ് ഉണ്ടെന്ന് ഞങ്ങൾ നോക്കുന്നു.

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, അത്തരം നാല് പോയിന്റുകൾ ഉണ്ട്.

ടാസ്ക് 4.

ഇടവേളയിൽ നിർവചിച്ചിരിക്കുന്ന ഒരു ഫംഗ്ഷന്റെ ഗ്രാഫ് ചിത്രം കാണിക്കുന്നു. ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് 0 ആയ പോയിന്റുകളുടെ എണ്ണം കണ്ടെത്തുക.

പരിഹാരം:

ഡെറിവേറ്റീവ് എക്സ്ട്രീം പോയിന്റുകളിൽ പൂജ്യത്തിന് തുല്യമാണ്. ഞങ്ങൾക്ക് അവയിൽ 4 ഉണ്ട്:

ടാസ്ക് 5.

ചിത്രം ഒരു ഫംഗ്‌ഷന്റെ ഗ്രാഫും x-അക്ഷത്തിൽ പതിനൊന്ന് പോയിന്റുകളും കാണിക്കുന്നു:. ഈ പോയിന്റുകളിൽ എത്രയെണ്ണത്തിൽ ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് നെഗറ്റീവ് ആണ്?

പരിഹാരം:

ഫംഗ്ഷൻ കുറയുന്നതിന്റെ ഇടവേളകളിൽ, അതിന്റെ ഡെറിവേറ്റീവ് നെഗറ്റീവ് മൂല്യങ്ങൾ എടുക്കുന്നു. കൂടാതെ പോയിന്റുകളിൽ പ്രവർത്തനം കുറയുന്നു. അത്തരം 4 പോയിന്റുകൾ ഉണ്ട്.

ടാസ്ക് 6.

ഇടവേളയിൽ നിർവചിച്ചിരിക്കുന്ന ഒരു ഫംഗ്ഷന്റെ ഗ്രാഫ് ചിത്രം കാണിക്കുന്നു. ഫംഗ്‌ഷന്റെ എക്‌സ്ട്രീം പോയിന്റുകളുടെ ആകെത്തുക കണ്ടെത്തുക.

പരിഹാരം:

എക്സ്ട്രീം പോയിന്റുകൾ– ഇവയാണ് പരമാവധി പോയിന്റുകളും (-3, -1, 1) ഏറ്റവും കുറഞ്ഞ പോയിന്റുകളും (-2, 0, 3).

എക്സ്ട്രീം പോയിന്റുകളുടെ ആകെത്തുക: -3-1+1-2+0+3=-2.

ടാസ്ക് 7.

ഇടവേളയിൽ നിർവചിച്ചിരിക്കുന്ന ഒരു ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവിന്റെ ഒരു ഗ്രാഫ് ചിത്രം കാണിക്കുന്നു. പ്രവർത്തനത്തിന്റെ വർദ്ധനവിന്റെ ഇടവേളകൾ കണ്ടെത്തുക. നിങ്ങളുടെ ഉത്തരത്തിൽ, ഈ ഇടവേളകളിൽ ഉൾപ്പെടുത്തിയിരിക്കുന്ന പൂർണ്ണസംഖ്യകളുടെ ആകെത്തുക സൂചിപ്പിക്കുക.

പരിഹാരം:

ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് നോൺ-നെഗറ്റീവ് ആയ ഇടവേളകളെ ചിത്രം എടുത്തുകാണിക്കുന്നു.

വർദ്ധിച്ചുവരുന്ന ചെറിയ ഇടവേളയിൽ പൂർണ്ണസംഖ്യാ പോയിന്റുകളൊന്നുമില്ല; വർദ്ധിച്ചുവരുന്ന ഇടവേളയിൽ നാല് പൂർണ്ണസംഖ്യ മൂല്യങ്ങളുണ്ട്: , , കൂടാതെ .

അവയുടെ ആകെത്തുക:

ടാസ്ക് 8.

ഇടവേളയിൽ നിർവചിച്ചിരിക്കുന്ന ഒരു ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവിന്റെ ഒരു ഗ്രാഫ് ചിത്രം കാണിക്കുന്നു. പ്രവർത്തനത്തിന്റെ വർദ്ധനവിന്റെ ഇടവേളകൾ കണ്ടെത്തുക. നിങ്ങളുടെ ഉത്തരത്തിൽ, അവയിൽ ഏറ്റവും വലുത് നീളം സൂചിപ്പിക്കുക.

പരിഹാരം:

ചിത്രത്തിൽ, ഡെറിവേറ്റീവ് പോസിറ്റീവ് ആയ എല്ലാ ഇടവേളകളും നിറത്തിൽ ഹൈലൈറ്റ് ചെയ്തിട്ടുണ്ട്, അതായത് ഈ ഇടവേളകളിൽ പ്രവർത്തനം തന്നെ വർദ്ധിക്കുന്നു.

അവയിൽ ഏറ്റവും വലുത് 6 ആണ്.

ടാസ്ക് 9.

ഇടവേളയിൽ നിർവചിച്ചിരിക്കുന്ന ഒരു ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവിന്റെ ഒരു ഗ്രാഫ് ചിത്രം കാണിക്കുന്നു. സെഗ്‌മെന്റിന്റെ ഏത് ഘട്ടത്തിലാണ് അത് ഏറ്റവും വലിയ മൂല്യം കൈക്കൊള്ളുന്നത്?

പരിഹാരം:

സെഗ്‌മെന്റിൽ ഗ്രാഫ് എങ്ങനെ പ്രവർത്തിക്കുന്നുവെന്ന് നോക്കാം, അതാണ് ഞങ്ങൾക്ക് താൽപ്പര്യമുള്ളത് ഡെറിവേറ്റീവിന്റെ അടയാളം മാത്രം .

ഈ സെഗ്‌മെന്റിലെ ഗ്രാഫ് അക്ഷത്തിന് താഴെയായതിനാൽ ഓൺ എന്ന ഡെറിവേറ്റീവിന്റെ അടയാളം മൈനസ് ആണ്.

ഒരു ഫംഗ്ഷൻ എഫ് നൽകട്ടെ, ചില ഘട്ടങ്ങളിൽ x 0 ന് ഒരു ഫിനിറ്റ് ഡെറിവേറ്റീവ് f (x 0) ഉണ്ട്. അപ്പോൾ കോണീയ ഗുണകം f '(x 0) ഉള്ള ബിന്ദുവിലൂടെ കടന്നുപോകുന്ന നേർരേഖയെ (x 0 ; f (x 0) ടാൻജന്റ് എന്ന് വിളിക്കുന്നു.

x 0 എന്ന ബിന്ദുവിൽ ഡെറിവേറ്റീവ് നിലവിലില്ലെങ്കിൽ എന്ത് സംഭവിക്കും? രണ്ട് ഓപ്ഷനുകൾ ഉണ്ട്:

1. ഗ്രാഫിനും സ്പർശനമില്ല. y = |x | എന്ന ഫംഗ്‌ഷൻ ഒരു മികച്ച ഉദാഹരണമാണ് പോയിന്റിൽ (0; 0).
2. ടാൻജെന്റ് ലംബമായി മാറുന്നു. ഇത് ശരിയാണ്, ഉദാഹരണത്തിന്, പോയിന്റിലെ y = arcsin x എന്ന ഫംഗ്‌ഷന് (1; π /2).

ടാൻജന്റ് സമവാക്യം

ലംബമല്ലാത്ത ഏതൊരു നേർരേഖയും y = kx + b എന്ന ഫോമിന്റെ ഒരു സമവാക്യമാണ് നൽകുന്നത്, ഇവിടെ k എന്നത് ചരിവാണ്. ടാൻജെന്റ് ഒരു അപവാദമല്ല, x 0 എന്ന ബിന്ദുവിൽ അതിന്റെ സമവാക്യം സൃഷ്ടിക്കുന്നതിന്, ഈ ഘട്ടത്തിൽ ഫംഗ്‌ഷന്റെയും ഡെറിവേറ്റീവിന്റെയും മൂല്യം അറിഞ്ഞാൽ മതിയാകും.

അതിനാൽ, സെഗ്‌മെന്റിൽ ഒരു ഡെറിവേറ്റീവ് y = f ’(x) ഉള്ള ഒരു ഫംഗ്‌ഷൻ y = f (x) നൽകട്ടെ. തുടർന്ന് ഏത് ഘട്ടത്തിലും x 0 ∈ (a ; b) ഈ ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്ക് ഒരു ടാൻജെന്റ് വരയ്ക്കാം, അത് സമവാക്യം നൽകുന്നു:

y = f '(x 0) (x - x 0) + f (x 0)

ഇവിടെ f ’(x 0) എന്നത് x 0 പോയിന്റിലെ ഡെറിവേറ്റീവിന്റെ മൂല്യവും f (x 0) എന്നത് ഫംഗ്‌ഷന്റെ തന്നെ മൂല്യവുമാണ്.

ടാസ്ക്. y = x 3 എന്ന ഫംഗ്ഷൻ നൽകിയിരിക്കുന്നു. x 0 = 2 എന്ന പോയിന്റിൽ ഈ ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റിനായി ഒരു സമവാക്യം എഴുതുക.

ടാൻജന്റ് സമവാക്യം: y = f ’(x 0) · (x - x 0) + f (x 0). x 0 = 2 എന്ന പോയിന്റ് ഞങ്ങൾക്ക് നൽകിയിരിക്കുന്നു, എന്നാൽ f (x 0), f '(x 0) എന്നീ മൂല്യങ്ങൾ കണക്കാക്കേണ്ടതുണ്ട്.

ആദ്യം, നമുക്ക് ഫംഗ്ഷന്റെ മൂല്യം കണ്ടെത്താം. ഇവിടെ എല്ലാം എളുപ്പമാണ്: f (x 0) = f (2) = 2 3 = 8;
ഇനി നമുക്ക് ഡെറിവേറ്റീവ് കണ്ടെത്താം: f '(x) = (x 3)' = 3x 2;
ഡെറിവേറ്റീവിലേക്ക് ഞങ്ങൾ x 0 = 2 മാറ്റിസ്ഥാപിക്കുന്നു: f '(x 0) = f '(2) = 3 2 2 = 12;
മൊത്തത്തിൽ നമുക്ക് ലഭിക്കുന്നത്: y = 12 · (x - 2) + 8 = 12x - 24 + 8 = 12x - 16.
ഇതാണ് ടാൻജെന്റ് സമവാക്യം.

ടാസ്ക്. x 0 = π /2 എന്ന പോയിന്റിൽ f (x) = 2sin x + 5 എന്ന ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റിനായി ഒരു സമവാക്യം എഴുതുക.

ഈ സമയം ഞങ്ങൾ ഓരോ പ്രവർത്തനവും വിശദമായി വിവരിക്കില്ല - ഞങ്ങൾ പ്രധാന ഘട്ടങ്ങൾ മാത്രം സൂചിപ്പിക്കും. നമുക്ക് ഉണ്ട്:

f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f '(x) = (2sin x + 5)' = 2cos x;
f ’(x 0) = f ’(π /2) = 2cos (π /2) = 0;

ടാൻജെന്റ് സമവാക്യം:

y = 0 · (x - π /2) + 7 ⇒ y = 7

പിന്നീടുള്ള സന്ദർഭത്തിൽ, നേർരേഖ തിരശ്ചീനമായി മാറി, കാരണം അതിന്റെ കോണീയ ഗുണകം k = 0. ഇതിൽ തെറ്റൊന്നുമില്ല - ഞങ്ങൾ ഒരു എക്സ്ട്രീം പോയിന്റിൽ ഇടറി.

ലേഖനം നിർവചനങ്ങളുടെ വിശദമായ വിശദീകരണം നൽകുന്നു, ഗ്രാഫിക് നൊട്ടേഷനുകളുള്ള ഡെറിവേറ്റീവിന്റെ ജ്യാമിതീയ അർത്ഥം. ഒരു ടാൻജെന്റ് ലൈനിന്റെ സമവാക്യം ഉദാഹരണങ്ങൾക്കൊപ്പം പരിഗണിക്കും, ഒരു ടാൻജെന്റ് മുതൽ 2nd ഓർഡർ കർവുകൾ വരെയുള്ള സമവാക്യങ്ങൾ കണ്ടെത്തും.

Yandex.RTB R-A-339285-1 നിർവ്വചനം 1

y = k x + b എന്ന നേർരേഖയുടെ ചെരിവിന്റെ കോണിനെ ആംഗിൾ α എന്ന് വിളിക്കുന്നു, ഇത് x അക്ഷത്തിന്റെ പോസിറ്റീവ് ദിശയിൽ നിന്ന് y = k x + b എന്ന നേർരേഖയിലേക്ക് പോസിറ്റീവ് ദിശയിലേക്ക് അളക്കുന്നു.

ചിത്രത്തിൽ, x ദിശയെ ഒരു പച്ച അമ്പടയാളവും പച്ച കമാനവും, ചെരിവിന്റെ കോണും ചുവന്ന ആർക്ക് ഉപയോഗിച്ചും സൂചിപ്പിക്കുന്നു. നീല വര നേർരേഖയെ സൂചിപ്പിക്കുന്നു.

നിർവ്വചനം 2

y = k x + b എന്ന നേർരേഖയുടെ ചരിവിനെ സംഖ്യാ ഗുണകം k എന്ന് വിളിക്കുന്നു.

കോണീയ ഗുണകം നേർരേഖയുടെ ടാൻജെന്റിന് തുല്യമാണ്, മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ k = t g α.

• ഒരു നേർരേഖയുടെ ചെരിവിന്റെ കോൺ 0 ന് തുല്യമായിരിക്കും, അത് x ന് സമാന്തരവും ചരിവ് പൂജ്യത്തിന് തുല്യവുമാണ്, കാരണം പൂജ്യത്തിന്റെ ടാൻജെന്റ് 0 ന് തുല്യമാണ്. ഇതിനർത്ഥം സമവാക്യത്തിന്റെ രൂപം y = b ആയിരിക്കും എന്നാണ്.
• y = k x + b എന്ന നേർരേഖയുടെ ചെരിവിന്റെ കോൺ നിശിതമാണെങ്കിൽ, വ്യവസ്ഥകൾ 0 തൃപ്തികരമാണ്< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0, ഒപ്പം ഗ്രാഫിൽ വർദ്ധനവുമുണ്ട്.
• α = π 2 ആണെങ്കിൽ, വരിയുടെ സ്ഥാനം x ന് ലംബമാണ്. തുല്യതയെ x = c ആണ് സൂചിപ്പിക്കുന്നത്, മൂല്യം c ഒരു യഥാർത്ഥ സംഖ്യയാണ്.
• y = k x + b എന്ന നേർരേഖയുടെ ചെരിവിന്റെ ആംഗിൾ അവ്യക്തമാണെങ്കിൽ, അത് π 2 വ്യവസ്ഥകളുമായി പൊരുത്തപ്പെടുന്നു.< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

f (x) ഫംഗ്‌ഷന്റെ 2 പോയിന്റുകളിലൂടെ കടന്നുപോകുന്ന ഒരു വരിയാണ് സെക്കന്റ്. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, ഒരു നിശ്ചിത ഫംഗ്ഷന്റെ ഗ്രാഫിലെ ഏതെങ്കിലും രണ്ട് പോയിന്റുകളിലൂടെ കടന്നുപോകുന്ന ഒരു നേർരേഖയാണ് സെക്കന്റ്.

A B ഒരു സെക്കന്റാണെന്നും f (x) ഒരു കറുത്ത വക്രമാണെന്നും α ഒരു ചുവന്ന ചാപമാണെന്നും ചിത്രം കാണിക്കുന്നു, ഇത് സെക്കന്റിന്റെ ചെരിവിന്റെ കോണിനെ സൂചിപ്പിക്കുന്നു.

ഒരു നേർരേഖയുടെ കോണീയ ഗുണകം ചെരിവിന്റെ കോണിന്റെ ടാൻജെന്റിന് തുല്യമായിരിക്കുമ്പോൾ, A B C എന്ന വലത് ത്രികോണത്തിന്റെ ടാൻജെന്റ് എതിർവശവും തൊട്ടടുത്തുള്ളതുമായ അനുപാതത്തിൽ കണ്ടെത്താനാകുമെന്ന് വ്യക്തമാണ്.

നിർവ്വചനം 4

ഫോമിന്റെ ഒരു സെക്കന്റ് കണ്ടെത്തുന്നതിനുള്ള ഒരു ഫോർമുല നമുക്ക് ലഭിക്കും:

k = t g α = B C A C = f (x B) - f x A x B - x A, ഇവിടെ A, B എന്നീ പോയിന്റുകളുടെ അബ്സിസ്സകൾ x A, x B, f (x A), f (x) എന്നീ മൂല്യങ്ങളാണ് ബി) ഈ പോയിന്റുകളിലെ മൂല്യങ്ങളുടെ പ്രവർത്തനങ്ങളാണ്.

വ്യക്തമായും, k = f (x B) - f (x A) x B - x A അല്ലെങ്കിൽ k = f (x A) - f (x B) x A - x B എന്ന തുല്യത ഉപയോഗിച്ചാണ് സെക്കന്റിന്റെ കോണീയ ഗുണകം നിർണ്ണയിക്കുന്നത്. , കൂടാതെ സമവാക്യം y = f (x B) - f (x A) x B - x A x - x A + f (x A) അല്ലെങ്കിൽ
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

സെക്കന്റ് ഗ്രാഫിനെ ദൃശ്യപരമായി 3 ഭാഗങ്ങളായി വിഭജിക്കുന്നു: പോയിന്റ് A യുടെ ഇടതുവശത്ത്, A മുതൽ B വരെ, B യുടെ വലത് വരെ. യാദൃശ്ചികമായി കണക്കാക്കുന്ന മൂന്ന് സെക്കന്റുകളുണ്ടെന്ന് ചുവടെയുള്ള ചിത്രം കാണിക്കുന്നു, അതായത്, അവ ഒരു ഉപയോഗിച്ച് സജ്ജീകരിച്ചിരിക്കുന്നു. സമാനമായ സമവാക്യം.

നിർവചനം അനുസരിച്ച്, ഈ കേസിൽ നേർരേഖയും അതിന്റെ സെക്കന്റും യോജിക്കുന്നുവെന്ന് വ്യക്തമാണ്.

തന്നിരിക്കുന്ന ഫംഗ്‌ഷന്റെ ഗ്രാഫിനെ ഒരു സെക്കന്റിന് ഒന്നിലധികം തവണ വിഭജിക്കാൻ കഴിയും. ഒരു സെക്കന്റിന് y = 0 എന്ന ഫോമിന്റെ ഒരു സമവാക്യം ഉണ്ടെങ്കിൽ, സൈനസോയിഡുമായി വിഭജിക്കുന്ന പോയിന്റുകളുടെ എണ്ണം അനന്തമാണ്.

നിർവ്വചനം 5

x 0 പോയിന്റിലെ f (x) ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റ്; f (x 0) എന്നത് ഒരു നിശ്ചിത പോയിന്റിലൂടെ കടന്നുപോകുന്ന ഒരു നേർരേഖയാണ് x 0; f (x 0), x 0 ന് അടുത്തുള്ള നിരവധി x മൂല്യങ്ങളുള്ള ഒരു സെഗ്‌മെന്റിന്റെ സാന്നിധ്യമുണ്ട്.

ഉദാഹരണം 1

ചുവടെയുള്ള ഉദാഹരണം നമുക്ക് സൂക്ഷ്മമായി പരിശോധിക്കാം. y = x + 1 എന്ന ഫംഗ്‌ഷൻ നിർവചിച്ചിരിക്കുന്ന രേഖ കോർഡിനേറ്റുകളുള്ള (1; 2) പോയിന്റിൽ y = 2 x ലേക്ക് ടാൻജന്റ് ആയി കണക്കാക്കുന്നത് വ്യക്തമാണ്. വ്യക്തതയ്ക്കായി, (1; 2) അടുത്ത മൂല്യങ്ങളുള്ള ഗ്രാഫുകൾ പരിഗണിക്കേണ്ടത് ആവശ്യമാണ്. y = 2 x എന്ന ഫംഗ്‌ഷൻ കറുപ്പിൽ കാണിച്ചിരിക്കുന്നു, നീല വരയാണ് ടാൻജെന്റ് ലൈൻ, ചുവന്ന ഡോട്ട് ഇന്റർസെക്ഷൻ പോയിന്റാണ്.

വ്യക്തമായും, y = 2 x y = x + 1 എന്ന വരിയുമായി ലയിക്കുന്നു.

ടാൻജെന്റ് നിർണ്ണയിക്കാൻ, ബി പോയിന്റ് എയെ അനന്തമായി സമീപിക്കുമ്പോൾ, എ ബിയുടെ സ്വഭാവം നാം പരിഗണിക്കണം, വ്യക്തതയ്ക്കായി, ഞങ്ങൾ ഒരു ഡ്രോയിംഗ് അവതരിപ്പിക്കുന്നു.

നീല വരയാൽ സൂചിപ്പിച്ചിരിക്കുന്ന സെക്കന്റ് എ ബി, ടാൻജെന്റിന്റെ സ്ഥാനത്തേക്ക് തന്നെ ചായുന്നു, കൂടാതെ സെക്കന്റ് α ന്റെ ചെരിവിന്റെ കോൺ α x ന്റെ ചെരിവിന്റെ കോണിലേക്ക് ചായാൻ തുടങ്ങും.

നിർവ്വചനം 6

A പോയിന്റിലെ y = f (x) എന്ന ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റ്, B, A ലേക്ക് പ്രവണത കാണിക്കുന്നതിനാൽ, A B യുടെ പരിമിതപ്പെടുത്തുന്ന സ്ഥാനമായി കണക്കാക്കപ്പെടുന്നു, അതായത്, B → A.

ഇനി നമുക്ക് ഒരു പോയിന്റിലെ ഒരു ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവിന്റെ ജ്യാമിതീയ അർത്ഥം പരിഗണിക്കാം.

x 0, f (x 0), x 0 + ∆ x, f (x 0 + ∆ x), ∆ x എന്നീ കോർഡിനേറ്റുകളുള്ള A, B എന്നിവ f (x) ഫംഗ്‌ഷനുള്ള A B എന്ന സെക്കന്റ് പരിഗണിക്കുന്നതിലേക്ക് പോകാം. വാദത്തിന്റെ വർദ്ധനവായി സൂചിപ്പിച്ചിരിക്കുന്നു. ഇപ്പോൾ ഫംഗ്ഷൻ ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) എന്ന ഫോം എടുക്കും. വ്യക്തതയ്ക്കായി, ഒരു ഡ്രോയിംഗിന്റെ ഒരു ഉദാഹരണം നൽകാം.

തത്ഫലമായുണ്ടാകുന്ന വലത് ത്രികോണം A B C പരിഗണിക്കുക. പരിഹരിക്കാൻ ഞങ്ങൾ ടാൻജെന്റിന്റെ നിർവചനം ഉപയോഗിക്കുന്നു, അതായത്, നമുക്ക് ∆ y ∆ x = t g α എന്ന ബന്ധം ലഭിക്കും. ഒരു സ്പർശനത്തിന്റെ നിർവചനത്തിൽ നിന്ന് അത് പിന്തുടരുന്നത് lim ∆ x → 0 ∆ y ∆ x = t g α x . ഒരു ബിന്ദുവിലെ ഡെറിവേറ്റീവിന്റെ നിയമമനുസരിച്ച്, x 0 എന്ന ബിന്ദുവിലെ derivative f (x) എന്നത് ഫംഗ്‌ഷന്റെ ഇൻക്രിമെന്റിന്റെയും ആർഗ്യുമെന്റിന്റെ ഇൻക്രിമെന്റിന്റെയും അനുപാതത്തിന്റെ പരിധി എന്ന് വിളിക്കപ്പെടുന്നു, ഇവിടെ ∆ x → 0 , അപ്പോൾ നമ്മൾ അതിനെ f (x 0) = lim ∆ x → 0 ∆ y ∆ x ആയി സൂചിപ്പിക്കുന്നു.

ഇത് പിന്തുടരുന്നത് f "(x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, ഇവിടെ k x എന്നത് സ്പർശനത്തിന്റെ ചരിവായി സൂചിപ്പിക്കുന്നു.

അതായത്, x 0 പോയിന്റിൽ f ' (x) നിലനിൽക്കുമെന്നും, x 0, f 0 (x 0) ന് തുല്യമായ സ്പർശനബിന്ദുവിൽ ഫംഗ്‌ഷന്റെ ഒരു നിശ്ചിത ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റ് പോലെ, അതിന്റെ മൂല്യം പോയിന്റിലെ ടാൻജെന്റിന്റെ ചരിവ് പോയിന്റ് x 0 ലെ ഡെറിവേറ്റീവിന് തുല്യമാണ്. അപ്പോൾ നമുക്ക് ആ k x = f " (x 0) ലഭിക്കും.

ഒരു ബിന്ദുവിലെ ഒരു ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവിന്റെ ജ്യാമിതീയ അർത്ഥം, അതേ ബിന്ദുവിലെ ഗ്രാഫിലേക്ക് ഒരു ടാൻജന്റിന്റെ അസ്തിത്വം എന്ന ആശയം അത് നൽകുന്നു എന്നതാണ്.

ഒരു തലത്തിൽ ഏതെങ്കിലും നേർരേഖയുടെ സമവാക്യം എഴുതാൻ, അത് കടന്നുപോകുന്ന പോയിന്റുമായി ഒരു കോണീയ ഗുണകം ഉണ്ടായിരിക്കേണ്ടത് ആവശ്യമാണ്. കവലയിൽ അതിന്റെ നൊട്ടേഷൻ x 0 ആയി കണക്കാക്കുന്നു.

x 0, f 0 (x 0) എന്ന പോയിന്റിലെ y = f (x) എന്ന ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റ് സമവാക്യം y = f "(x 0) x - x 0 + f (x 0) എന്ന ഫോം എടുക്കുന്നു.

ഇതിനർത്ഥം f "(x 0) എന്ന ഡെറിവേറ്റീവിന്റെ അന്തിമ മൂല്യത്തിന് ടാൻജന്റെ സ്ഥാനം നിർണ്ണയിക്കാൻ കഴിയും, അതായത് ലംബമായി, നൽകിയിരിക്കുന്ന lim x → x 0 + 0 f "(x) = ∞, lim x → x 0 - 0 f "(x ) = ∞ അല്ലെങ്കിൽ lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) എന്ന വ്യവസ്ഥയ്ക്ക് കീഴിലുള്ള അഭാവം.

ടാൻജെന്റിന്റെ സ്ഥാനം അതിന്റെ കോണീയ ഗുണകമായ k x = f "(x 0) മൂല്യത്തെ ആശ്രയിച്ചിരിക്കുന്നു. o x അക്ഷത്തിന് സമാന്തരമാകുമ്പോൾ, നമുക്ക് k k = 0, o y - k x = ∞ ന് സമാന്തരമാകുമ്പോൾ, അതിന്റെ രൂപവും ലഭിക്കും. ടാൻജെന്റ് സമവാക്യം x = x 0, k x > 0-നൊപ്പം വർദ്ധിക്കുന്നു, k x ആയി കുറയുന്നു< 0 .

ഉദാഹരണം 2

കോർഡിനേറ്റുകൾ (1; 3) ഉപയോഗിച്ച് പോയിന്റിൽ y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 എന്ന ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്ക് ടാൻജെന്റിനായി ഒരു സമവാക്യം കംപൈൽ ചെയ്യുകയും ചെരിവിന്റെ ആംഗിൾ നിർണ്ണയിക്കുകയും ചെയ്യുക.

പരിഹാരം

വ്യവസ്ഥ പ്രകാരം, എല്ലാ യഥാർത്ഥ സംഖ്യകൾക്കും ഫംഗ്ഷൻ നിർവചിച്ചിരിക്കുന്നു. വ്യവസ്ഥയിൽ വ്യക്തമാക്കിയ കോർഡിനേറ്റുകളുള്ള പോയിന്റ്, (1; 3) സ്പർശനത്തിന്റെ ഒരു പോയിന്റാണെന്ന് ഞങ്ങൾ കണ്ടെത്തുന്നു, തുടർന്ന് x 0 = - 1, f (x 0) = - 3.

മൂല്യമുള്ള പോയിന്റിൽ ഡെറിവേറ്റീവ് കണ്ടെത്തേണ്ടത് ആവശ്യമാണ് - 1. ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

സ്‌പർശനബിന്ദുവിലുള്ള f' (x) ന്റെ മൂല്യം സ്‌പർശകത്തിന്റെ ചരിവാണ്, അത് ചരിവിന്റെ ടാൻജെന്റിന് തുല്യമാണ്.

അപ്പോൾ k x = t g α x = y "(x 0) = 3 3

അത് പിന്തുടരുന്നത് α x = a r c t g 3 3 = π 6 ആണ്

ഉത്തരം:ടാൻജെന്റ് സമവാക്യം രൂപമെടുക്കുന്നു

y = f "(x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

വ്യക്തതയ്ക്കായി, ഞങ്ങൾ ഒരു ഗ്രാഫിക് ചിത്രീകരണത്തിൽ ഒരു ഉദാഹരണം നൽകുന്നു.

ഒറിജിനൽ ഫംഗ്‌ഷന്റെ ഗ്രാഫിന് കറുപ്പ് നിറം ഉപയോഗിക്കുന്നു, നീല നിറം ടാൻജെന്റിന്റെ ചിത്രമാണ്, ചുവന്ന ഡോട്ട് സ്പർശനത്തിന്റെ പോയിന്റാണ്. വലതുവശത്തുള്ള ചിത്രം വിപുലീകരിച്ച കാഴ്ച കാണിക്കുന്നു.

ഉദാഹരണം 3

തന്നിരിക്കുന്ന ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്ക് ഒരു ടാൻജന്റിന്റെ അസ്തിത്വം നിർണ്ണയിക്കുക
y = 3 · x - 1 5 + 1 പോയിന്റിൽ കോർഡിനേറ്റുകൾ (1 ; 1) . ഒരു സമവാക്യം എഴുതുക, ചെരിവിന്റെ കോൺ നിർണ്ണയിക്കുക.

പരിഹാരം

വ്യവസ്ഥയനുസരിച്ച്, നൽകിയിരിക്കുന്ന ഫംഗ്‌ഷന്റെ നിർവചനത്തിന്റെ ഡൊമെയ്‌ൻ എല്ലാ യഥാർത്ഥ സംഖ്യകളുടെയും ഗണമായി കണക്കാക്കുന്നു.

നമുക്ക് ഡെറിവേറ്റീവ് കണ്ടെത്തുന്നതിലേക്ക് പോകാം

y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

x 0 = 1 ആണെങ്കിൽ, f' (x) നിർവചിക്കപ്പെട്ടിട്ടില്ല, എന്നാൽ പരിധികൾ lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 എന്നാണ് എഴുതിയിരിക്കുന്നത്. · 1 + 0 = + ∞, ലിം x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , അതായത് പോയിന്റിൽ (1; 1) അസ്തിത്വം ലംബമായ ടാൻജെന്റ്.

ഉത്തരം:സമവാക്യം x = 1 എന്ന രൂപമെടുക്കും, അവിടെ ചെരിവിന്റെ കോൺ π 2 ന് തുല്യമായിരിക്കും.

വ്യക്തതയ്ക്കായി, നമുക്ക് അത് ഗ്രാഫിക്കായി ചിത്രീകരിക്കാം.

ഉദാഹരണം 4

y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 എന്ന ഫംഗ്‌ഷന്റെ ഗ്രാഫിൽ പോയിന്റുകൾ കണ്ടെത്തുക.

1. ടാൻജെന്റ് ഇല്ല;
2. ടാൻജെന്റ് x ന് സമാന്തരമാണ്;
3. ടാൻജെന്റ് y = 8 5 x + 4 എന്ന വരിക്ക് സമാന്തരമാണ്.

പരിഹാരം

നിർവചനത്തിന്റെ വ്യാപ്തിയിൽ ശ്രദ്ധിക്കേണ്ടത് ആവശ്യമാണ്. വ്യവസ്ഥ പ്രകാരം, എല്ലാ യഥാർത്ഥ സംഖ്യകളുടെയും ഗണത്തിൽ ഫംഗ്ഷൻ നിർവചിച്ചിരിക്കുന്നു. ഞങ്ങൾ മൊഡ്യൂൾ വികസിപ്പിക്കുകയും സിസ്റ്റം പരിഹരിക്കുകയും ചെയ്യുന്നു x ∈ - ∞ ; 2 ഒപ്പം [- 2 ; +∞) . ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12, x ∈ [ - 2 ; +∞)

പ്രവർത്തനത്തെ വേർതിരിക്കേണ്ടത് ആവശ്യമാണ്. ഞങ്ങൾക്ക് അത് ഉണ്ട്

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3, x ∈ [ - 2 ; +∞)

x = − 2 ആയിരിക്കുമ്പോൾ, ഡെറിവേറ്റീവ് നിലവിലില്ല, കാരണം ആ ഘട്ടത്തിൽ ഏകപക്ഷീയമായ പരിധികൾ തുല്യമല്ല:

ലിം x → - 2 - 0 y " (x) = ലിം x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 ലിം x → - 2 + 0 y " (x) = ലിം x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

x = - 2 എന്ന പോയിന്റിൽ ഫംഗ്‌ഷന്റെ മൂല്യം ഞങ്ങൾ കണക്കാക്കുന്നു, അവിടെ നമുക്ക് അത് ലഭിക്കും

1. y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, അതായത് ബിന്ദുവിലെ ടാൻജെന്റ് ( - 2; - 2) നിലനിൽക്കില്ല.
2. ചരിവ് പൂജ്യമാകുമ്പോൾ ടാൻജെന്റ് x ന് സമാന്തരമാണ്. അപ്പോൾ k x = t g α x = f "(x 0). അതായത്, ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് അതിനെ പൂജ്യത്തിലേക്ക് മാറ്റുമ്പോൾ അത്തരം x ന്റെ മൂല്യങ്ങൾ കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്. അതായത്, f 'ന്റെ മൂല്യങ്ങൾ. (x) സ്പർശനത്തിന്റെ പോയിന്റുകളായിരിക്കും, അവിടെ ടാൻജെന്റ് x ന് സമാന്തരമാണ്.

എപ്പോൾ x ∈ - ∞ ; - 2, തുടർന്ന് - 1 5 (x 2 + 12 x + 35) = 0, കൂടാതെ x ∈ (- 2; + ∞) ന് നമുക്ക് 1 5 (x 2 - 4 x + 3) = 0 ലഭിക്കും.

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

അനുബന്ധ ഫംഗ്ഷൻ മൂല്യങ്ങൾ കണക്കാക്കുക

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

അതിനാൽ - 5; 8 5, - 4; 4 3, 1; 8 5, 3; ഫംഗ്ഷൻ ഗ്രാഫിന്റെ ആവശ്യമായ പോയിന്റുകളായി 4 3 കണക്കാക്കപ്പെടുന്നു.

പരിഹാരത്തിന്റെ ഗ്രാഫിക്കൽ പ്രാതിനിധ്യം നോക്കാം.

കറുത്ത വര ഫംഗ്ഷന്റെ ഗ്രാഫ് ആണ്, ചുവന്ന ഡോട്ടുകൾ ടാൻജെൻസി പോയിന്റുകളാണ്.

1. വരികൾ സമാന്തരമാകുമ്പോൾ, കോണീയ ഗുണകങ്ങൾ തുല്യമായിരിക്കും. ഫംഗ്ഷൻ ഗ്രാഫിലെ പോയിന്റുകൾക്കായി തിരയേണ്ടത് ആവശ്യമാണ്, അവിടെ ചരിവ് മൂല്യം 8 5 ന് തുല്യമായിരിക്കും. ഇത് ചെയ്യുന്നതിന്, നിങ്ങൾ y "(x) = 8 5 എന്ന ഫോമിന്റെ ഒരു സമവാക്യം പരിഹരിക്കേണ്ടതുണ്ട്. തുടർന്ന്, x ∈ - ∞; - 2 ആണെങ്കിൽ, നമുക്ക് അത് ലഭിക്കും - 1 5 (x 2 + 12 x + 35) = 8 5, x ∈ (- 2 ; + ∞) ആണെങ്കിൽ 1 5 (x 2 - 4 x + 3) = 8 5.

വിവേചനം പൂജ്യത്തേക്കാൾ കുറവായതിനാൽ ആദ്യ സമവാക്യത്തിന് വേരുകളില്ല. നമുക്ക് അത് എഴുതാം

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

മറ്റൊരു സമവാക്യത്തിന് രണ്ട് യഥാർത്ഥ വേരുകളുണ്ട്, അപ്പോൾ

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

ഫംഗ്ഷന്റെ മൂല്യങ്ങൾ കണ്ടെത്തുന്നതിലേക്ക് പോകാം. ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

മൂല്യങ്ങളുള്ള പോയിന്റുകൾ - 1; 4 15, 5; 8 3 എന്നത് y = 8 5 x + 4 എന്ന രേഖയ്ക്ക് സമാന്തരമായി സ്പർശിക്കുന്ന പോയിന്റുകളാണ്.

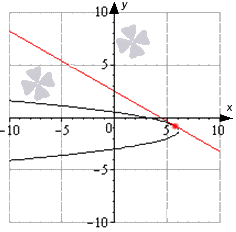
ഉത്തരം:ബ്ലാക്ക് ലൈൻ - ഫംഗ്ഷന്റെ ഗ്രാഫ്, റെഡ് ലൈൻ - y = 8 5 x + 4 എന്ന ഗ്രാഫ്, നീല വര - പോയിന്റുകളിലെ ടാൻജെന്റുകൾ - 1; 4 15, 5; 8 3.

തന്നിരിക്കുന്ന ഫംഗ്‌ഷനുകൾക്ക് അനന്തമായ ടാൻജന്റുകൾ ഉണ്ടായിരിക്കാം.

ഉദാഹരണം 5

y = - 2 x + 1 2 എന്ന നേർരേഖയ്ക്ക് ലംബമായി സ്ഥിതി ചെയ്യുന്ന y = 3 cos 3 2 x - π 4 - 1 3 എന്ന ഫംഗ്‌ഷന്റെ ലഭ്യമായ എല്ലാ ടാൻജെന്റുകളുടെയും സമവാക്യങ്ങൾ എഴുതുക.

പരിഹാരം

ടാൻജെന്റ് സമവാക്യം കംപൈൽ ചെയ്യുന്നതിന്, വരികളുടെ ലംബതയുടെ അവസ്ഥയെ അടിസ്ഥാനമാക്കി, ടാൻജെന്റ് പോയിന്റിന്റെ ഗുണകവും കോർഡിനേറ്റുകളും കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്. നിർവചനം ഇപ്രകാരമാണ്: നേർരേഖകൾക്ക് ലംബമായ കോണീയ ഗുണകങ്ങളുടെ ഗുണനഫലം തുല്യമാണ് - 1, അതായത് k x · k ⊥ = - 1 എന്ന് എഴുതിയിരിക്കുന്നു. വ്യവസ്ഥയിൽ നിന്ന് നമുക്ക് കോണീയ ഗുണകം രേഖയ്ക്ക് ലംബമായി സ്ഥിതിചെയ്യുന്നു, അത് k ⊥ = - 2 ന് തുല്യമാണ്, തുടർന്ന് k x = - 1 k ⊥ = - 1 - 2 = 1 2.

ഇപ്പോൾ നിങ്ങൾ ടച്ച് പോയിന്റുകളുടെ കോർഡിനേറ്റുകൾ കണ്ടെത്തേണ്ടതുണ്ട്. തന്നിരിക്കുന്ന ഫംഗ്‌ഷനുവേണ്ടി നിങ്ങൾ x ഉം അതിന്റെ മൂല്യവും കണ്ടെത്തേണ്ടതുണ്ട്. പോയിന്റിലെ ഡെറിവേറ്റീവിന്റെ ജ്യാമിതീയ അർത്ഥത്തിൽ നിന്ന് ശ്രദ്ധിക്കുക
x 0 നമുക്ക് k x = y "(x 0) ലഭിക്കുന്നു. ഈ സമത്വത്തിൽ നിന്ന് കോൺടാക്റ്റ് പോയിന്റുകൾക്കായി x ന്റെ മൂല്യങ്ങൾ കണ്ടെത്തുന്നു.

ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

y "(x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 sin 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9

ടാൻജെന്റ് പോയിന്റുകളുടെ ഓർഡിനേറ്റുകൾ കണക്കാക്കാൻ ഈ ത്രികോണമിതി സമവാക്യം ഉപയോഗിക്കും.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk അല്ലെങ്കിൽ 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk അല്ലെങ്കിൽ 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk അല്ലെങ്കിൽ x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z എന്നത് പൂർണ്ണസംഖ്യകളുടെ ഒരു കൂട്ടമാണ്.

x കോൺടാക്റ്റ് പോയിന്റുകൾ കണ്ടെത്തി. ഇപ്പോൾ നിങ്ങൾ y യുടെ മൂല്യങ്ങൾക്കായി തിരയുന്നതിലേക്ക് പോകേണ്ടതുണ്ട്:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 അല്ലെങ്കിൽ y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 അല്ലെങ്കിൽ y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 അല്ലെങ്കിൽ y 0 = - 4 5 + 1 3

ഇതിൽ നിന്ന് നമുക്ക് ലഭിക്കുന്നത് 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3, 2 3 5 π 4 + a r c sin 1 9 + 2 πk; - 4 5 + 1 3 ആണ് സ്പർശനത്തിന്റെ പോയിന്റുകൾ.

ഉത്തരം:ആവശ്യമായ സമവാക്യങ്ങൾ ഇങ്ങനെ എഴുതും

y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3, y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

ഒരു വിഷ്വൽ പ്രാതിനിധ്യത്തിനായി, ഒരു കോർഡിനേറ്റ് ലൈനിൽ ഒരു ഫംഗ്ഷനും ഒരു ടാൻജെന്റും പരിഗണിക്കുക.

ഫംഗ്ഷൻ ഇടവേളയിൽ സ്ഥിതി ചെയ്യുന്നതായി ചിത്രം കാണിക്കുന്നു [ - 10 ; 10 ], ബ്ലാക്ക് ലൈൻ ഫംഗ്‌ഷന്റെ ഗ്രാഫ് ആണെങ്കിൽ, നീല വരകൾ സ്‌പർശകങ്ങളാണ്, അവ y = - 2 x + 1 2 എന്ന രൂപത്തിന്റെ തന്നിരിക്കുന്ന വരിക്ക് ലംബമായി സ്ഥിതി ചെയ്യുന്നു. ചുവന്ന ഡോട്ടുകൾ ടച്ച് പോയിന്റുകളാണ്.

2nd ഓർഡർ കർവുകളുടെ കാനോനിക്കൽ സമവാക്യങ്ങൾ ഒറ്റ മൂല്യമുള്ള ഫംഗ്ഷനുകളല്ല. അറിയപ്പെടുന്ന സ്കീമുകൾ അനുസരിച്ച് അവയ്ക്കുള്ള സ്പർശന സമവാക്യങ്ങൾ സമാഹരിച്ചിരിക്കുന്നു.

ഒരു വൃത്തത്തിലേക്കുള്ള ടാൻജന്റ്

x c e n t e r എന്ന ബിന്ദുവിൽ കേന്ദ്രമുള്ള ഒരു വൃത്തം നിർവ്വചിക്കാൻ; y c e n t e r ഉം R ആരവും, x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 എന്ന ഫോർമുല പ്രയോഗിക്കുക.

ഈ സമത്വം രണ്ട് പ്രവർത്തനങ്ങളുടെ ഒരു യൂണിയൻ ആയി എഴുതാം:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

ചിത്രത്തിൽ കാണിച്ചിരിക്കുന്നതുപോലെ ആദ്യ ഫംഗ്ഷൻ മുകളിലും രണ്ടാമത്തേത് താഴെയുമാണ്.

x 0 എന്ന ബിന്ദുവിൽ ഒരു സർക്കിളിന്റെ സമവാക്യം കംപൈൽ ചെയ്യാൻ; y 0 , മുകളിലോ താഴെയോ ഉള്ള അർദ്ധവൃത്തത്തിൽ സ്ഥിതിചെയ്യുന്നു, y = R 2 - x - x c e n t e r 2 + y c e n t e r അല്ലെങ്കിൽ y = - R 2 - x - x c e r 2 ഫോമിന്റെ ഒരു ഫംഗ്ഷന്റെ ഗ്രാഫിന്റെ സമവാക്യം നിങ്ങൾ കണ്ടെത്തണം. സൂചിപ്പിച്ച പോയിന്റിൽ y c e n t e r.

x c e n t e r എന്ന പോയിന്റുകളിൽ ആയിരിക്കുമ്പോൾ; y c e n t e r + R, x c e n t e r; y = y c e n t e r + R, y = y c e n t e r - R എന്നീ സമവാക്യങ്ങളാൽ y c e n t e r - R ടാൻജന്റുകൾ നൽകാം, കൂടാതെ x c e n t e r + R എന്ന പോയിന്റുകളിലും; y c e n t e r ഉം
x c e n t e r - R; y c e n t e r o y ന് സമാന്തരമായിരിക്കും, അപ്പോൾ നമുക്ക് x = x c e n t e r + R, x = x c e n t e r - R എന്നീ രൂപങ്ങളുടെ സമവാക്യങ്ങൾ ലഭിക്കും.

ദീർഘവൃത്തത്തിലേക്കുള്ള ടാൻജന്റ്

ദീർഘവൃത്തത്തിന് x c e n t e r-ൽ ഒരു കേന്ദ്രം ഉള്ളപ്പോൾ; y c e n t e r അർദ്ധ അക്ഷങ്ങൾ a, b എന്നിവ ഉപയോഗിച്ച്, അത് x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 എന്ന സമവാക്യം ഉപയോഗിച്ച് വ്യക്തമാക്കാം.

ഒരു ദീർഘവൃത്തത്തെയും വൃത്തത്തെയും രണ്ട് ഫംഗ്ഷനുകൾ സംയോജിപ്പിച്ച് സൂചിപ്പിക്കാം, അതായത് മുകളിലും താഴെയുമുള്ള അർദ്ധ-ദീർഘവൃത്തം. അപ്പോൾ നമുക്ക് അത് ലഭിക്കും

y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

ദീർഘവൃത്തത്തിന്റെ ശിഖരങ്ങളിലാണ് ടാൻജെന്റുകൾ സ്ഥിതി ചെയ്യുന്നതെങ്കിൽ, അവ ഏകദേശം x അല്ലെങ്കിൽ ഏകദേശം y ന് സമാന്തരമാണ്. ചുവടെ, വ്യക്തതയ്ക്കായി, ചിത്രം പരിഗണിക്കുക.

ഉദാഹരണം 6

x = 2 ന് തുല്യമായ x മൂല്യങ്ങളുള്ള പോയിന്റുകളിൽ ദീർഘവൃത്താകൃതിയിലുള്ള x - 3 2 4 + y - 5 2 25 = 1 ലേക്ക് സ്പർശനത്തിന്റെ സമവാക്യം എഴുതുക.

പരിഹാരം

x = 2 മൂല്യവുമായി പൊരുത്തപ്പെടുന്ന ടാൻജെന്റ് പോയിന്റുകൾ കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്. ദീർഘവൃത്തത്തിന്റെ നിലവിലുള്ള സമവാക്യത്തിലേക്ക് ഞങ്ങൾ പകരം വയ്ക്കുകയും അത് കണ്ടെത്തുകയും ചെയ്യുന്നു

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

അപ്പോൾ 2; 5 3 2 + 5 ഒപ്പം 2; - 5 3 2 + 5 എന്നത് മുകളിലും താഴെയുമുള്ള അർദ്ധ-ദീർഘവൃത്തത്തിൽ പെടുന്ന ടാൻജെന്റ് പോയിന്റുകളാണ്.

y യുമായി ബന്ധപ്പെട്ട് ദീർഘവൃത്തത്തിന്റെ സമവാക്യം കണ്ടെത്തുന്നതിലേക്കും പരിഹരിക്കുന്നതിലേക്കും നമുക്ക് പോകാം. ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

വ്യക്തമായും, y = 5 + 5 2 4 - x - 3 2, താഴത്തെ പകുതി ദീർഘവൃത്തം y = 5 - 5 2 4 - x - 3 2 എന്നിവയുടെ ഒരു ഫംഗ്ഷൻ ഉപയോഗിച്ചാണ് മുകളിലെ അർദ്ധ-ദീർഘവൃത്തം വ്യക്തമാക്കിയിരിക്കുന്നത്.

ഒരു പോയിന്റിലെ ഒരു ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്ക് ഒരു ടാൻജന്റിന് ഒരു സമവാക്യം സൃഷ്‌ടിക്കാൻ നമുക്ക് ഒരു സ്റ്റാൻഡേർഡ് അൽഗോരിതം പ്രയോഗിക്കാം. പോയിന്റ് 2-ൽ ആദ്യത്തെ ടാൻജെന്റിനുള്ള സമവാക്യം എന്ന് നമുക്ക് എഴുതാം; 5 3 2 + 5 പോലെ കാണപ്പെടും

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

പോയിന്റിലെ ഒരു മൂല്യമുള്ള രണ്ടാമത്തെ ടാൻജെന്റിന്റെ സമവാക്യം ഞങ്ങൾ കണ്ടെത്തുന്നു
2 ; - 5 3 2 + 5 ഫോം എടുക്കുന്നു

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

ഗ്രാഫിക്കലായി, ടാൻജന്റുകൾ ഇനിപ്പറയുന്ന രീതിയിൽ നിയുക്തമാക്കിയിരിക്കുന്നു:

ഹൈപ്പർബോളിലേക്കുള്ള ടാൻജന്റ്

ഒരു ഹൈപ്പർബോളയ്ക്ക് x c e n t e r ൽ ഒരു കേന്ദ്രം ഉള്ളപ്പോൾ; y c e n t e r ഉം വെർട്ടീസുകളും x c e n t e r + α; y c e n t e r, x c e n t e r - α; y c e n t e r , അസമത്വം x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 നടക്കുന്നു, x c e n t e r ലംബങ്ങളോടെയാണെങ്കിൽ; y c e n t e r + b, x c e n t e r; y c e n t e r -b , അപ്പോൾ അസമത്വം ഉപയോഗിച്ച് വ്യക്തമാക്കുന്നു x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

ഒരു ഹൈപ്പർബോളയെ ഫോമിന്റെ രണ്ട് സംയുക്ത പ്രവർത്തനങ്ങളായി പ്രതിനിധീകരിക്കാം

y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r അല്ലെങ്കിൽ y = x a · 2 e n t e r y = - b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r

ആദ്യ സന്ദർഭത്തിൽ നമുക്ക് സ്പർശനങ്ങൾ y ന് സമാന്തരമാണ്, രണ്ടാമത്തേതിൽ അവ x ന് സമാന്തരമാണ്.

ഒരു ഹൈപ്പർബോളയിലേക്കുള്ള ടാൻജെന്റിന്റെ സമവാക്യം കണ്ടെത്തുന്നതിന്, സ്പർശനബിന്ദു ഏത് പ്രവർത്തനത്തിലാണെന്ന് കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്. ഇത് നിർണ്ണയിക്കാൻ, സമവാക്യങ്ങളിൽ പകരം വയ്ക്കുകയും ഐഡന്റിറ്റി പരിശോധിക്കുകയും ചെയ്യേണ്ടത് ആവശ്യമാണ്.

ഉദാഹരണം 7

പോയിന്റ് 7-ൽ ഹൈപ്പർബോള x - 3 2 4 - y + 3 2 9 = 1 വരെയുള്ള ടാൻജെന്റിന് ഒരു സമവാക്യം എഴുതുക; - 3 3 - 3 .

പരിഹാരം

2 ഫംഗ്ഷനുകൾ ഉപയോഗിച്ച് ഒരു ഹൈപ്പർബോള കണ്ടെത്തുന്നതിനുള്ള പരിഹാര റെക്കോർഡ് രൂപാന്തരപ്പെടുത്തേണ്ടത് ആവശ്യമാണ്. ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 ഒപ്പം y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

കോർഡിനേറ്റുകൾ 7 ഉള്ള ഒരു നിശ്ചിത പോയിന്റ് ഏത് ഫംഗ്‌ഷനുടേതാണെന്ന് തിരിച്ചറിയേണ്ടത് ആവശ്യമാണ്; - 3 3 - 3 .

വ്യക്തമായും, ആദ്യ ഫംഗ്ഷൻ പരിശോധിക്കുന്നതിന് അത് ആവശ്യമാണ് y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, അപ്പോൾ പോയിന്റ് ഗ്രാഫിൽ ഉൾപ്പെടുന്നില്ല, കാരണം സമത്വം നിലനിൽക്കില്ല.

രണ്ടാമത്തെ ഫംഗ്‌ഷനായി നമുക്ക് y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 ഉണ്ട്, അതായത് പോയിന്റ് നൽകിയിരിക്കുന്ന ഗ്രാഫിൽ പെടുന്നു. ഇവിടെ നിന്ന് നിങ്ങൾ ചരിവ് കണ്ടെത്തണം.

ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

ഉത്തരം:ടാൻജെന്റ് സമവാക്യം ഇങ്ങനെ പ്രതിനിധീകരിക്കാം

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

ഇത് ഇതുപോലെ വ്യക്തമായി ചിത്രീകരിച്ചിരിക്കുന്നു:

ഒരു പരവലയത്തിലേക്കുള്ള ടാൻജന്റ്

x 0, y (x 0) എന്ന പോയിന്റിൽ പരാബോള y = a x 2 + b x + c എന്നതിലേക്കുള്ള ടാൻജെന്റിനായി ഒരു സമവാക്യം സൃഷ്ടിക്കാൻ, നിങ്ങൾ ഒരു സാധാരണ അൽഗോരിതം ഉപയോഗിക്കണം, തുടർന്ന് സമവാക്യം y = y "(x" എന്ന ഫോം എടുക്കും. 0) x - x 0 + y ( x 0). ശീർഷത്തിലെ അത്തരമൊരു ടാൻജെന്റ് x ന് സമാന്തരമാണ്.

നിങ്ങൾ പരവലയ x = a y 2 + b y + c രണ്ട് ഫംഗ്‌ഷനുകളുടെ യൂണിയൻ ആയി നിർവ്വചിക്കണം. അതിനാൽ, നമ്മൾ y യുടെ സമവാക്യം പരിഹരിക്കേണ്ടതുണ്ട്. ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

ഗ്രാഫിക്കായി ചിത്രീകരിച്ചിരിക്കുന്നത്:

ഒരു പോയിന്റ് x 0, y (x 0) ഒരു ഫംഗ്‌ഷനുടേതാണോ എന്ന് കണ്ടെത്താൻ, സ്റ്റാൻഡേർഡ് അൽഗോരിതം അനുസരിച്ച് മൃദുവായി തുടരുക. അത്തരം ഒരു സ്പർശനം പരവലയവുമായി താരതമ്യപ്പെടുത്തുമ്പോൾ o y ന് സമാന്തരമായിരിക്കും.

ഉദാഹരണം 8

നമുക്ക് 150 ° ടാൻജെന്റ് കോൺ ഉള്ളപ്പോൾ x - 2 y 2 - 5 y + 3 എന്ന ഗ്രാഫിലേക്ക് ടാൻജെന്റിന്റെ സമവാക്യം എഴുതുക.

പരിഹാരം

പരാബോളയെ രണ്ട് ഫംഗ്ഷനുകളായി പ്രതിനിധീകരിച്ച് ഞങ്ങൾ പരിഹാരം ആരംഭിക്കുന്നു. ഞങ്ങൾക്ക് അത് ലഭിക്കുന്നു

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

ചരിവിന്റെ മൂല്യം ഈ ഫംഗ്‌ഷന്റെ പോയിന്റ് x 0 ലെ ഡെറിവേറ്റീവിന്റെ മൂല്യത്തിന് തുല്യമാണ്, ഇത് ചെരിവിന്റെ കോണിന്റെ ടാൻജെന്റിന് തുല്യമാണ്.

നമുക്ക് ലഭിക്കുന്നത്:

k x = y "(x 0) = t g α x = t g 150 ° = - 1 3

ഇവിടെ നിന്ന് ഞങ്ങൾ കോൺടാക്റ്റ് പോയിന്റുകളുടെ x മൂല്യം നിർണ്ണയിക്കുന്നു.

ആദ്യ ഫംഗ്ഷൻ ഇങ്ങനെ എഴുതപ്പെടും

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

വ്യക്തമായും, ഞങ്ങൾക്ക് ഒരു നെഗറ്റീവ് മൂല്യം ലഭിച്ചതിനാൽ യഥാർത്ഥ വേരുകളൊന്നുമില്ല. അത്തരമൊരു പ്രവർത്തനത്തിന് 150° കോണുള്ള ടാൻജെന്റ് ഇല്ലെന്ന് ഞങ്ങൾ നിഗമനം ചെയ്യുന്നു.

രണ്ടാമത്തെ ഫംഗ്‌ഷൻ ഇങ്ങനെ എഴുതപ്പെടും

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

ഞങ്ങൾക്ക് കോൺടാക്റ്റ് പോയിന്റുകൾ 23 4 ആണ്; - 5 + 3 4 .

ഉത്തരം:ടാൻജെന്റ് സമവാക്യം രൂപമെടുക്കുന്നു

y = - 1 3 x - 23 4 + - 5 + 3 4

നമുക്ക് ഇത് ഗ്രാഫിക്കായി ഈ രീതിയിൽ ചിത്രീകരിക്കാം:

ടെക്‌സ്‌റ്റിൽ ഒരു പിശക് നിങ്ങൾ ശ്രദ്ധയിൽപ്പെട്ടാൽ, അത് ഹൈലൈറ്റ് ചെയ്‌ത് Ctrl+Enter അമർത്തുക

വീഡിയോ പാഠം "ഒരു ഫംഗ്ഷന്റെ ഗ്രാഫിലേക്കുള്ള ഒരു സ്പർശനത്തിന്റെ സമവാക്യം" വിഷയം മാസ്റ്റേഴ്സ് ചെയ്യുന്നതിനുള്ള വിദ്യാഭ്യാസ സാമഗ്രികൾ കാണിക്കുന്നു. വീഡിയോ പാഠത്തിനിടയിൽ, ഒരു നിശ്ചിത പോയിന്റിലെ ഒരു ഫംഗ്ഷന്റെ ഗ്രാഫിലേക്ക് ഒരു ടാൻജെന്റിന്റെ സമവാക്യം എന്ന ആശയം രൂപപ്പെടുത്തുന്നതിന് ആവശ്യമായ സൈദ്ധാന്തിക മെറ്റീരിയൽ, അത്തരമൊരു ടാൻജെന്റ് കണ്ടെത്തുന്നതിനുള്ള ഒരു അൽഗോരിതം, പഠിച്ച സൈദ്ധാന്തിക മെറ്റീരിയൽ ഉപയോഗിച്ച് പ്രശ്നങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ഉദാഹരണങ്ങൾ എന്നിവ വിവരിക്കുന്നു. .

വീഡിയോ ട്യൂട്ടോറിയൽ മെറ്റീരിയലിന്റെ വ്യക്തത മെച്ചപ്പെടുത്തുന്ന രീതികൾ ഉപയോഗിക്കുന്നു. അവതരണത്തിൽ ഡ്രോയിംഗുകൾ, ഡയഗ്രമുകൾ, പ്രധാനപ്പെട്ട വോയ്‌സ് കമന്റുകൾ, ആനിമേഷൻ, ഹൈലൈറ്റിംഗ്, മറ്റ് ടൂളുകൾ എന്നിവ അടങ്ങിയിരിക്കുന്നു.

വീഡിയോ പാഠം ആരംഭിക്കുന്നത് പാഠത്തിന്റെ വിഷയത്തിന്റെ അവതരണവും M(a;f(a)) എന്ന ബിന്ദുവിലുള്ള ചില ഫംഗ്‌ഷന്റെ y=f(x) ഗ്രാഫിലേക്കുള്ള ഒരു ടാൻജന്റിന്റെ ചിത്രവും ഉപയോഗിച്ചാണ്. ഒരു നിശ്ചിത പോയിന്റിൽ ഗ്രാഫിലേക്ക് പ്ലോട്ട് ചെയ്‌തിരിക്കുന്ന ടാൻജെന്റിന്റെ കോണീയ ഗുണകം ഈ പോയിന്റിലെ ഫംഗ്‌ഷൻ f΄(a) ന്റെ ഡെറിവേറ്റീവിന് തുല്യമാണെന്ന് അറിയാം. ബീജഗണിതത്തിൽ നിന്ന് y=kx+m എന്ന നേർരേഖയുടെ സമവാക്യം നമുക്കറിയാം. ഒരു ബിന്ദുവിൽ ടാൻജെന്റ് സമവാക്യം കണ്ടെത്തുന്നതിനുള്ള പ്രശ്നത്തിനുള്ള പരിഹാരം സ്കീമാറ്റിക്കായി അവതരിപ്പിച്ചിരിക്കുന്നു, ഇത് ഗുണകങ്ങൾ k, m കണ്ടെത്തുന്നതിലേക്ക് കുറയ്ക്കുന്നു. ഫംഗ്‌ഷന്റെ ഗ്രാഫിൽ ഉൾപ്പെടുന്ന ഒരു ബിന്ദുവിന്റെ കോർഡിനേറ്റുകൾ അറിയുമ്പോൾ, കോർഡിനേറ്റ് മൂല്യത്തെ f(a)=ka+m എന്ന സമവാക്യത്തിലേക്ക് മാറ്റി പകരം വയ്ക്കുന്നതിലൂടെ m കണ്ടെത്താം. അതിൽ നിന്ന് m=f(a)-ka കണ്ടെത്തുന്നു. അങ്ങനെ, ഒരു നിശ്ചിത പോയിന്റിലെ ഡെറിവേറ്റീവിന്റെ മൂല്യവും പോയിന്റിന്റെ കോർഡിനേറ്റുകളും അറിയുന്നതിലൂടെ, നമുക്ക് y=f(a)+f΄(a)(x-a) എന്ന രീതിയിൽ ടാൻജെന്റ് സമവാക്യത്തെ പ്രതിനിധീകരിക്കാം.

ഡയഗ്രം പിന്തുടരുന്ന ഒരു ടാൻജെന്റ് സമവാക്യം രചിക്കുന്നതിനുള്ള ഒരു ഉദാഹരണം താഴെ കൊടുക്കുന്നു. y=x 2, x=-2 എന്ന ഫംഗ്‌ഷൻ നൽകിയിരിക്കുന്നു. a=-2 എടുക്കുമ്പോൾ, തന്നിരിക്കുന്ന പോയിന്റിൽ f(a)= f(-2)=(-2) 2 =4 എന്നതിൽ ഫംഗ്‌ഷന്റെ മൂല്യം ഞങ്ങൾ കണ്ടെത്തുന്നു. f΄(x)=2x എന്ന ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് ഞങ്ങൾ നിർണ്ണയിക്കുന്നു. ഈ ഘട്ടത്തിൽ ഡെറിവേറ്റീവ് f΄(a)= f΄(-2)=2·(-2)=-4 ന് തുല്യമാണ്. സമവാക്യം രചിക്കുന്നതിന്, എല്ലാ ഗുണകങ്ങളും a=-2, f(a)=4, f΄(a)=-4 എന്നിവ കണ്ടെത്തി, അതിനാൽ ടാൻജെന്റ് സമവാക്യം y=4+(-4)(x+2) ആണ്. സമവാക്യം ലളിതമാക്കുമ്പോൾ, നമുക്ക് y = -4-4x ലഭിക്കും.

y=tgx ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ഉത്ഭവസ്ഥാനത്ത് ടാൻജെന്റിനായി ഒരു സമവാക്യം നിർമ്മിക്കാൻ ഇനിപ്പറയുന്ന ഉദാഹരണം നിർദ്ദേശിക്കുന്നു. ഒരു നിശ്ചിത പോയിന്റിൽ a=0, f(0)=0, f΄(x)=1/cos 2 x, f΄(0)=1. അതിനാൽ ടാൻജെന്റ് സമവാക്യം y=x പോലെ കാണപ്പെടുന്നു.

ഒരു സാമാന്യവൽക്കരണം എന്ന നിലയിൽ, ഒരു നിശ്ചിത ഘട്ടത്തിൽ ഒരു ഫംഗ്ഷന്റെ ഗ്രാഫിലേക്ക് ഒരു സമവാക്യ ടാൻജെന്റ് രചിക്കുന്ന പ്രക്രിയ 4 ഘട്ടങ്ങൾ അടങ്ങുന്ന ഒരു അൽഗോരിതം രൂപത്തിൽ ഔപചാരികമാക്കുന്നു:

• ടാൻജെന്റ് പോയിന്റിന്റെ abscissa യുടെ പദവി a നൽകുക;
• f (a) കണക്കാക്കുന്നു;
• f΄(x) നിർണ്ണയിക്കുകയും f΄(a) കണക്കാക്കുകയും ചെയ്യുന്നു. a, f(a), f΄(a) എന്നിവയുടെ കണ്ടെത്തിയ മൂല്യങ്ങൾ y=f(a)+f΄(a)(x-a) എന്ന ടാൻജെന്റ് സമവാക്യ ഫോർമുലയിലേക്ക് മാറ്റിസ്ഥാപിക്കുന്നു.

x=1 എന്ന പോയിന്റിലെ y=1/x എന്ന ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്ക് ടാൻജെന്റ് സമവാക്യം രചിക്കുന്നത് ഉദാഹരണം 1 പരിഗണിക്കുന്നു. പ്രശ്നം പരിഹരിക്കാൻ ഞങ്ങൾ ഒരു അൽഗോരിതം ഉപയോഗിക്കുന്നു. പോയിന്റ് a=1-ൽ നൽകിയിരിക്കുന്ന ഒരു ഫംഗ്‌ഷന്, f(a)=-1 എന്ന ഫംഗ്‌ഷന്റെ മൂല്യം. f΄(x)=1/x 2 എന്ന ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ്. പോയിന്റ് a=1-ൽ f΄(a)= f΄(1)=1 എന്ന ഡെറിവേറ്റീവ്. ലഭിച്ച ഡാറ്റ ഉപയോഗിച്ച്, ടാൻജെന്റ് സമവാക്യം y=-1+(x-1), അല്ലെങ്കിൽ y=x-2, വരയ്ക്കുന്നു.

ഉദാഹരണം 2-ൽ, y=x 3 +3x 2 -2x-2 എന്ന ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജന്റിന്റെ സമവാക്യം കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്. y=-2x+1 എന്ന ടാൻജെന്റിന്റെയും നേർരേഖയുടെയും സമാന്തരതയാണ് പ്രധാന വ്യവസ്ഥ. ആദ്യം, y=-2x+1 എന്ന നേർരേഖയുടെ കോണീയ ഗുണകത്തിന് തുല്യമായ സ്പർശനത്തിന്റെ കോണീയ ഗുണകം ഞങ്ങൾ കണ്ടെത്തുന്നു. തന്നിരിക്കുന്ന ലൈനിന് f΄(a)=-2 ആയതിനാൽ, ആവശ്യമുള്ള ടാൻജെന്റിന് k=-2. ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് ഞങ്ങൾ കണ്ടെത്തുന്നു (x 3 +3x 2 -2x-2)΄=3x 2 +6x-2. f΄(a)=-2 എന്നറിയുമ്പോൾ, പോയിന്റ് 3a 2 +6a-2=-2 ന്റെ കോർഡിനേറ്റുകൾ ഞങ്ങൾ കണ്ടെത്തുന്നു. സമവാക്യം പരിഹരിച്ചുകഴിഞ്ഞാൽ, നമുക്ക് 1 =0, 2 =-2 എന്നിവ ലഭിക്കും. കണ്ടെത്തിയ കോർഡിനേറ്റുകൾ ഉപയോഗിച്ച്, അറിയപ്പെടുന്ന അൽഗോരിതം ഉപയോഗിച്ച് നിങ്ങൾക്ക് ടാൻജെന്റ് സമവാക്യം കണ്ടെത്താനാകും. f(a 1)=-2, f(a 2)=-18 എന്നീ പോയിന്റുകളിൽ ഫംഗ്‌ഷന്റെ മൂല്യം ഞങ്ങൾ കണ്ടെത്തുന്നു. f΄(а 1)= f΄(а 2)=-2 എന്ന പോയിന്റിലെ ഡെറിവേറ്റീവിന്റെ മൂല്യം. കണ്ടെത്തിയ മൂല്യങ്ങളെ ടാൻജെന്റ് സമവാക്യത്തിലേക്ക് മാറ്റിസ്ഥാപിക്കുമ്പോൾ, ആദ്യ പോയിന്റിന് 1 =0 y=-2x-2, രണ്ടാമത്തെ പോയിന്റിന് ഒരു 2 =-2 ടാൻജെന്റ് സമവാക്യം y=-2x-22 എന്നിവ ലഭിക്കും.

y=√x എന്ന ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്ക് (0;3) പോയിന്റിൽ വരയ്‌ക്കുന്നതിനുള്ള ടാൻജെന്റ് സമവാക്യത്തിന്റെ ഘടനയെ ഉദാഹരണം 3 വിവരിക്കുന്നു. അറിയപ്പെടുന്ന അൽഗോരിതം ഉപയോഗിച്ചാണ് പരിഹാരം നിർമ്മിച്ചിരിക്കുന്നത്. ടാൻജെന്റ് പോയിന്റിന് x=a കോർഡിനേറ്റുകൾ ഉണ്ട്, ഇവിടെ a>0. f(a)=√x എന്ന പോയിന്റിലെ ഫംഗ്‌ഷന്റെ മൂല്യം. ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് f΄(х)=1/2√х, അതിനാൽ തന്നിരിക്കുന്ന പോയിന്റിൽ f΄(а)=1/2√а. ലഭിച്ച എല്ലാ മൂല്യങ്ങളും ടാൻജെന്റ് സമവാക്യത്തിലേക്ക് മാറ്റി, നമുക്ക് y = √a + (x-a)/2√a ലഭിക്കും. സമവാക്യം രൂപാന്തരപ്പെടുത്തുമ്പോൾ, നമുക്ക് y=x/2√а+√а/2 ലഭിക്കും. പോയിന്റ് (0;3) വഴിയാണ് ടാൻജെന്റ് കടന്നുപോകുന്നത് എന്നറിയുമ്പോൾ, a യുടെ മൂല്യം നമ്മൾ കണ്ടെത്തുന്നു. 3=√a/2 എന്നതിൽ നിന്ന് ഞങ്ങൾ a കണ്ടെത്തുന്നു. അതിനാൽ √a=6, a=36. y=x/12+3 എന്ന ടാൻജെന്റ് സമവാക്യം ഞങ്ങൾ കണ്ടെത്തുന്നു. പരിഗണനയിലുള്ള ഫംഗ്‌ഷന്റെ ഗ്രാഫും നിർമ്മിച്ച ആവശ്യമുള്ള ടാൻജെന്റും ചിത്രം കാണിക്കുന്നു.

Δy=≈f΄(x)Δxand f(x+Δx)-f(x)≈f΄(x)Δx എന്ന ഏകദേശ തുല്യതകൾ വിദ്യാർത്ഥികളെ ഓർമ്മിപ്പിക്കുന്നു. x=a, x+Δx=x, Δx=x-a എടുക്കുമ്പോൾ, നമുക്ക് f(x)- f(a)≈f΄(a)(x-a), അതിനാൽ f(x)≈f(a)+ f΄( a)(x-a).

ഉദാഹരണം 4-ൽ, 2.003 6 എന്ന പദപ്രയോഗത്തിന്റെ ഏകദേശ മൂല്യം കണ്ടെത്തേണ്ടത് ആവശ്യമാണ്. x=2.003 എന്ന പോയിന്റിൽ f(x)=x 6 എന്ന ഫംഗ്‌ഷന്റെ മൂല്യം കണ്ടെത്തേണ്ടത് അത്യാവശ്യമായതിനാൽ, f(x)=x 6, a=2, f(a) എടുത്ത് നമുക്ക് അറിയപ്പെടുന്ന ഫോർമുല ഉപയോഗിക്കാം. )= f(2)=64, f ΄(x)=6x 5. f΄(2)=192 എന്ന പോയിന്റിലെ ഡെറിവേറ്റീവ്. അതിനാൽ, 2.003 6 ≈65-192·0.003. എക്സ്പ്രഷൻ കണക്കാക്കിയ ശേഷം, നമുക്ക് 2.003 6 ≈64.576 ലഭിക്കും.

"ഒരു ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ഒരു സ്പർശനത്തിന്റെ സമവാക്യം" എന്ന വീഡിയോ പാഠം സ്കൂളിലെ ഒരു പരമ്പരാഗത ഗണിത പാഠത്തിൽ ഉപയോഗിക്കാൻ ശുപാർശ ചെയ്യുന്നു. വിദൂരമായി പഠിപ്പിക്കുന്ന ഒരു അധ്യാപകന്, വിഷയം കൂടുതൽ വ്യക്തമായി വിശദീകരിക്കാൻ വീഡിയോ മെറ്റീരിയൽ സഹായിക്കും. വിഷയത്തെക്കുറിച്ചുള്ള അവരുടെ ഗ്രാഹ്യം ആഴത്തിലാക്കാൻ ആവശ്യമെങ്കിൽ സ്വതന്ത്രമായി അവലോകനം ചെയ്യാൻ വിദ്യാർത്ഥികൾക്ക് വീഡിയോ ശുപാർശ ചെയ്യാവുന്നതാണ്.

ടെക്സ്റ്റ് ഡീകോഡിംഗ്:

ഒരു പോയിന്റ് M (a; f(a)) (a-ൽ നിന്നുള്ള കോർഡിനേറ്റുകളുള്ള em, a-ൽ നിന്നുള്ള ef) y = f (x) എന്ന ഫംഗ്‌ഷന്റെ ഗ്രാഫിൽ പെടുന്നുവെന്നും ഈ ഘട്ടത്തിൽ ഒരു ടാൻജെന്റ് വരയ്ക്കാൻ സാധിക്കുമെന്നും നമുക്കറിയാം. അച്ചുതണ്ട് abscissa ന് ലംബമല്ലാത്ത ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്ക്, അപ്പോൾ ടാൻജന്റെ കോണീയ ഗുണകം f"(a) (a-ൽ നിന്നുള്ള eff പ്രൈം) ന് തുല്യമാണ്.

ഒരു ഫംഗ്‌ഷൻ y = f(x), ഒരു പോയിന്റ് M (a; f(a)) നൽകട്ടെ, കൂടാതെ f´(a) നിലവിലുണ്ടെന്നും അറിയാം. ഒരു നിശ്ചിത പോയിന്റിൽ തന്നിരിക്കുന്ന ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റിനായി നമുക്ക് ഒരു സമവാക്യം ഉണ്ടാക്കാം. ഈ സമവാക്യത്തിന്, ഓർഡിനേറ്റ് അക്ഷത്തിന് സമാന്തരമല്ലാത്ത ഏതെങ്കിലും നേർരേഖയുടെ സമവാക്യം പോലെ, y = kx+m (y എന്നത് ka x പ്ലസ് em ന് തുല്യമാണ്), അതിനാൽ ഇതിന്റെ മൂല്യങ്ങൾ കണ്ടെത്തുക എന്നതാണ് ചുമതല. ഗുണകങ്ങൾ k, m. (ka, em)

ആംഗിൾ കോഫിഫിഷ്യന്റ് k= f"(a) m ന്റെ മൂല്യം കണക്കാക്കാൻ, ആവശ്യമുള്ള നേർരേഖ M(a; f (a) എന്ന ബിന്ദുവിലൂടെ കടന്നുപോകുന്നു എന്ന വസ്തുത ഉപയോഗിക്കുന്നു. ഇതിനർത്ഥം നമ്മൾ കോർഡിനേറ്റുകൾ മാറ്റിസ്ഥാപിക്കുകയാണെങ്കിൽ പോയിന്റ് M നേർരേഖയുടെ സമവാക്യത്തിലേക്ക്, നമുക്ക് ശരിയായ തുല്യത ലഭിക്കും: f(a) = ka+m, അവിടെ നിന്ന് m = f(a) - ka എന്ന് കണ്ടെത്തുന്നു.

ki, m എന്നീ ഗുണകങ്ങളുടെ കണ്ടെത്തിയ മൂല്യങ്ങളെ നേർരേഖയുടെ സമവാക്യത്തിലേക്ക് മാറ്റിസ്ഥാപിക്കാൻ ഇത് ശേഷിക്കുന്നു:

y = kx+(f(a) -ka);

y = f(a)+k(x-a);

വൈ= എഫ്(എ)+ എഫ്"(എ) (x- എ). ( y എന്നത് a യിൽ നിന്നുള്ള ഒരു പ്ലസ് ef പ്രൈമിൽ നിന്നുള്ള ef ന് തുല്യമാണ്, x മൈനസ് a കൊണ്ട് ഗുണിച്ചാൽ).

x=a എന്ന ബിന്ദുവിൽ y = f(x) ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റിനുള്ള സമവാക്യം നമുക്ക് ലഭിച്ചു.

പറയുകയാണെങ്കിൽ, y = x 2 ഉം x = -2 (അതായത് a = -2), പിന്നെ f (a) = f (-2) = (-2) 2 = 4; f´(x) = 2x, അതായത് f"(a) = f´(-2) = 2·(-2) = -4. (അപ്പോൾ a യുടെ ef നാലിന് തുല്യമാണ്, പ്രൈം ന്റെ ef x രണ്ട് x ന് തുല്യമാണ്, അതായത് എഫ് പ്രൈം ഒരു മൈനസ് നാലിൽ നിന്ന് തുല്യമാണ്)

കണ്ടെത്തിയ മൂല്യങ്ങൾ a = -2, f(a) = 4, f"(a) = -4 എന്നിവ സമവാക്യത്തിലേക്ക് മാറ്റിസ്ഥാപിക്കുമ്പോൾ, നമുക്ക് ലഭിക്കുന്നത്: y = 4+(-4)(x+2), അതായത് y = -4x -4.

(E എന്നത് മൈനസ് നാല് x മൈനസ് നാലിന് തുല്യമാണ്)

ഉത്ഭവസ്ഥാനത്ത് y = tanx (y എന്നത് ടാൻജെന്റിന് തുല്യമാണ് x) എന്ന ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റിനായി നമുക്ക് ഒരു സമവാക്യം ഉണ്ടാക്കാം. നമുക്കുണ്ട്: a = 0, f(0) = tan0=0;

f"(x)= , അതായത് f"(0) = l. കണ്ടെത്തിയ മൂല്യങ്ങൾ a=0, f(a)=0, f´(a) = 1 എന്നിവ സമവാക്യത്തിലേക്ക് മാറ്റിസ്ഥാപിക്കുമ്പോൾ നമുക്ക് ലഭിക്കുന്നത്: y=x.

ഒരു അൽഗോരിതം ഉപയോഗിച്ച് പോയിന്റ് x-ലെ ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജന്റിന്റെ സമവാക്യം കണ്ടെത്തുന്നതിനുള്ള നമ്മുടെ ഘട്ടങ്ങൾ നമുക്ക് സംഗ്രഹിക്കാം.

y = f(x):

1) ടാൻജെന്റ് പോയിന്റിന്റെ abscissa എന്ന അക്ഷരം ഉപയോഗിച്ച് നിശ്ചയിക്കുക.

2) f(a) കണക്കാക്കുക.

3) f´(x) കണ്ടെത്തി f´(a) കണക്കാക്കുക.

4) കണ്ടെത്തിയ സംഖ്യകൾ a, f(a), f´(a) ഫോർമുലയിൽ പകരം വയ്ക്കുക വൈ= എഫ്(എ)+ എഫ്"(എ) (x- എ).

ഉദാഹരണം 1. ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റിന് ഒരു സമവാക്യം സൃഷ്ടിക്കുക y = - in

പോയിന്റ് x = 1.

പരിഹാരം. ഈ ഉദാഹരണത്തിൽ അത് കണക്കിലെടുത്ത് നമുക്ക് അൽഗോരിതം ഉപയോഗിക്കാം

2) f(a)=f(1)=- =-1

3) f´(x)=; f´(a)= f´(1)= =1.

4) കണ്ടെത്തിയ മൂന്ന് സംഖ്യകൾ മാറ്റിസ്ഥാപിക്കുക: a = 1, f(a) = -1, f"(a) = 1 ഫോർമുലയിലേക്ക്. നമുക്ക് ലഭിക്കുന്നത്: y = -1+(x-1), y = x-2 .

ഉത്തരം: y = x-2.

ഉദാഹരണം 2. ഫംഗ്ഷൻ y = നൽകിയിരിക്കുന്നു x 3 +3x 2 -2x-2. y = -2x +1 എന്ന നേർരേഖയ്ക്ക് സമാന്തരമായി y = f(x) ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്ക് ടാൻജന്റ് സമവാക്യം എഴുതുക.

ടാൻജെന്റ് സമവാക്യം രചിക്കുന്നതിനുള്ള അൽഗോരിതം ഉപയോഗിച്ച്, ഈ ഉദാഹരണത്തിൽ f(x) = എന്ന് ഞങ്ങൾ കണക്കിലെടുക്കുന്നു. x 3 +3x 2 -2x-2, എന്നാൽ ടാൻജെന്റ് പോയിന്റിന്റെ abscissa ഇവിടെ സൂചിപ്പിച്ചിട്ടില്ല.

നമുക്ക് ഇങ്ങനെ ചിന്തിക്കാൻ തുടങ്ങാം. ആവശ്യമുള്ള ടാൻജെന്റ് y = -2x+1 എന്ന നേർരേഖയ്ക്ക് സമാന്തരമായിരിക്കണം. സമാന്തര രേഖകൾക്ക് തുല്യ കോണീയ ഗുണകങ്ങൾ ഉണ്ട്. ഇതിനർത്ഥം, സ്പർശനത്തിന്റെ കോണീയ ഗുണകം നൽകിയിരിക്കുന്ന നേർരേഖയുടെ കോണീയ ഗുണകത്തിന് തുല്യമാണ്: k tangent. = -2. ഹോക്ക് കാസ്. = f"(a) അങ്ങനെ, f´(a) = -2 എന്ന സമവാക്യത്തിൽ നിന്ന് a യുടെ മൂല്യം നമുക്ക് കണ്ടെത്താം.

ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവ് കണ്ടെത്താം y=എഫ്(x):

എഫ്"(x)= (x 3 +3x 2 -2x-2)´ =3x 2 +6x-2;എഫ്"(a)= 3a 2 +6a-2.

f"(a) = -2 എന്ന സമവാക്യത്തിൽ നിന്ന്, അതായത്. 3a 2 +6a-2=-2 ഞങ്ങൾ ഒരു 1 =0, a 2 =-2 കണ്ടെത്തുന്നു. ഇതിനർത്ഥം പ്രശ്നത്തിന്റെ വ്യവസ്ഥകളെ തൃപ്തിപ്പെടുത്തുന്ന രണ്ട് സ്പർശനങ്ങളുണ്ട്: ഒന്ന് abscissa 0 ഉള്ള പോയിന്റിൽ, മറ്റൊന്ന് abscissa -2 ഉള്ള പോയിന്റിൽ.

ഇപ്പോൾ നിങ്ങൾക്ക് അൽഗോരിതം പിന്തുടരാം.

1) a 1 =0, 2 =-2.

2) f(a 1)= 0 3 +3·0 2 -2∙0-2=-2; f(a 2)= (-2) 3 +3·(-2) 2 -2·(-2)-2=6;

3) f"(a 1) = f"(a 2) = -2.

4) a 1 = 0, f(a 1) = -2, f"(a 1) = -2 എന്ന മൂല്യങ്ങൾ ഫോർമുലയിലേക്ക് മാറ്റി, നമുക്ക് ലഭിക്കുന്നത്:

y=-2-2(x-0), y=-2x-2.

ഫോർമുലയിൽ a 2 = -2, f(a 2) =6, f"(a 2) = -2 എന്ന മൂല്യങ്ങൾ മാറ്റിസ്ഥാപിക്കുമ്പോൾ, നമുക്ക് ലഭിക്കുന്നത്:

y=6-2(x+2), y=-2x+2.

ഉത്തരം: y=-2x-2, y=-2x+2.

ഉദാഹരണം 3. പോയിന്റിൽ നിന്ന് (0; 3) y = ഫംഗ്ഷന്റെ ഗ്രാഫിലേക്ക് ഒരു ടാൻജെന്റ് വരയ്ക്കുക. പരിഹാരം. ഈ ഉദാഹരണത്തിൽ f(x) = എന്നത് കണക്കിലെടുത്ത് ടാൻജെന്റ് സമവാക്യം രചിക്കുന്നതിന് നമുക്ക് അൽഗോരിതം ഉപയോഗിക്കാം. ഇവിടെ, ഉദാഹരണം 2 പോലെ, ടാൻജെന്റ് പോയിന്റിന്റെ abscissa വ്യക്തമായി സൂചിപ്പിച്ചിട്ടില്ല. എന്നിരുന്നാലും, ഞങ്ങൾ അൽഗോരിതം പിന്തുടരുന്നു.

1) x = a എന്നത് സ്പർശനബിന്ദുവിന്റെ abscissa ആയിരിക്കട്ടെ; ഒരു >0 എന്ന് വ്യക്തമാണ്.

3) f´(x)=()´=; f´(a) =.

4) a, f(a) = , f"(a) = എന്നതിന്റെ മൂല്യങ്ങൾ ഫോർമുലയിലേക്ക് മാറ്റിസ്ഥാപിക്കുന്നു

y=f (a) +f "(a) (x-a), നമുക്ക് ലഭിക്കുന്നത്:

വ്യവസ്ഥ പ്രകാരം, ടാൻജെന്റ് പോയിന്റിലൂടെ കടന്നുപോകുന്നു (0; 3). സമവാക്യത്തിലേക്ക് x = 0, y = 3 മൂല്യങ്ങൾ മാറ്റിസ്ഥാപിക്കുമ്പോൾ, നമുക്ക് ലഭിക്കുന്നത്: 3 = , തുടർന്ന് =6, a =36.

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, ഈ ഉദാഹരണത്തിൽ, അൽഗോരിതത്തിന്റെ നാലാമത്തെ ഘട്ടത്തിൽ മാത്രമാണ് ഞങ്ങൾക്ക് ടാൻജെന്റ് പോയിന്റിന്റെ അബ്സിസ്സ കണ്ടെത്താൻ കഴിഞ്ഞത്. a =36 എന്ന മൂല്യം സമവാക്യത്തിലേക്ക് മാറ്റി, നമുക്ക് ലഭിക്കുന്നത്: y=+3

ചിത്രത്തിൽ. പരിഗണിക്കപ്പെട്ട ഉദാഹരണത്തിന്റെ ജ്യാമിതീയ ചിത്രീകരണം ചിത്രം 1 കാണിക്കുന്നു: y = ഫംഗ്‌ഷന്റെ ഒരു ഗ്രാഫ് നിർമ്മിച്ചിരിക്കുന്നു, ഒരു നേർരേഖ y = +3 വരയ്ക്കുന്നു.

ഉത്തരം: y = +3.

പോയിന്റ് x-ൽ ഡെറിവേറ്റീവ് ഉള്ള y = f(x) എന്ന ഫംഗ്‌ഷന്, ഏകദേശ തുല്യത സാധുവാണെന്ന് നമുക്കറിയാം: Δyf´(x)Δx (ഡെൽറ്റ y എന്നത് ഡെൽറ്റ x കൊണ്ട് ഗുണിച്ച x ന്റെ eff പ്രൈമിന് ഏകദേശം തുല്യമാണ്)

അല്ലെങ്കിൽ, കൂടുതൽ വിശദമായി പറഞ്ഞാൽ, f(x+Δx)-f(x) f´(x) Δx (x-ൽ നിന്നുള്ള eff പ്ലസ് ഡെൽറ്റ x മൈനസ് ef, x-ൽ നിന്നുള്ള ef പ്രൈം, ഡെൽറ്റ x-ൽ നിന്നുള്ള ef പ്രൈമിന് ഏകദേശം തുല്യമാണ്).

കൂടുതൽ ചർച്ചയുടെ സൗകര്യത്തിനായി, നമുക്ക് നൊട്ടേഷൻ മാറ്റാം:

x ന് പകരം ഞങ്ങൾ എഴുതും എ,

x+Δx എന്നതിന് പകരം നമ്മൾ x എന്ന് എഴുതും

Δx ന് പകരം നമ്മൾ x-a എന്ന് എഴുതും.

അപ്പോൾ മുകളിൽ എഴുതിയ ഏകദേശ സമത്വം ഫോം എടുക്കും:

f(x)-f(a)f´(a)(x-a)

f(x)f(a)+f´(a)(x-a). (x-ൽ നിന്നുള്ള eff, a യിൽ നിന്നുള്ള ഒരു പ്ലസ് ef പ്രൈമിൽ നിന്നുള്ള ef-ന് ഏകദേശം തുല്യമാണ്, x ഉം a ഉം തമ്മിലുള്ള വ്യത്യാസം കൊണ്ട് ഗുണിച്ചാൽ).

ഉദാഹരണം 4. സംഖ്യാ പദപ്രയോഗത്തിന്റെ ഏകദേശ മൂല്യം കണ്ടെത്തുക 2.003 6.

പരിഹാരം. x = 2.003 എന്ന പോയിന്റിൽ y = x 6 എന്ന ഫംഗ്ഷന്റെ മൂല്യം കണ്ടെത്തുന്നതിനെക്കുറിച്ചാണ് നമ്മൾ സംസാരിക്കുന്നത്. നമുക്ക് f(x)f(a)+f´(a)(x-a) ഫോർമുല ഉപയോഗിക്കാം, ഈ ഉദാഹരണത്തിൽ f(x)=x 6, a = 2,f(a) = f(2) = 2 6 =64; x = 2.003, f"(x) = 6x 5, അതിനാൽ, f"(a) = f"(2) = 6 2 5 =192.

ഫലമായി നമുക്ക് ലഭിക്കുന്നത്:

2.003 6 64+192· 0.003, അതായത്. 2.003 6 =64.576.

ഞങ്ങൾ ഒരു കാൽക്കുലേറ്റർ ഉപയോഗിക്കുകയാണെങ്കിൽ, നമുക്ക് ലഭിക്കുന്നത്:

2,003 6 = 64,5781643...

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, ഏകദേശ കൃത്യത തികച്ചും സ്വീകാര്യമാണ്.

ഇനിപ്പറയുന്ന ചിത്രം പരിഗണിക്കുക:

ഇത് ഒരു നിശ്ചിത ഫംഗ്‌ഷൻ y = f(x) ചിത്രീകരിക്കുന്നു, അത് പോയിന്റ് a-ൽ വ്യത്യാസപ്പെട്ടിരിക്കുന്നു. കോർഡിനേറ്റുകളുള്ള പോയിന്റ് M (a; f(a)) അടയാളപ്പെടുത്തിയിരിക്കുന്നു. ഗ്രാഫിന്റെ പി(a + ∆x; f(a + ∆x)) എന്ന അനിയന്ത്രിതമായ പോയിന്റിലൂടെ ഒരു സെക്കന്റ് MR വരയ്ക്കുന്നു.

ഇപ്പോൾ പോയിന്റ് P ഗ്രാഫിനൊപ്പം പോയിന്റ് M ലേക്ക് മാറ്റുകയാണെങ്കിൽ, MR നേർരേഖ MR പോയിന്റിന് ചുറ്റും കറങ്ങും. ഈ സാഹചര്യത്തിൽ, ∆x പൂജ്യമായി മാറും. ഇവിടെ നിന്ന് നമുക്ക് ഒരു ഫംഗ്ഷന്റെ ഗ്രാഫിലേക്കുള്ള ഒരു ടാൻജന്റിന്റെ നിർവചനം രൂപപ്പെടുത്താം.

ഒരു ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജന്റ്

ഒരു ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റ്, ആർഗ്യുമെന്റിന്റെ ഇൻക്രിമെന്റ് പൂജ്യത്തിലേക്ക് പോകുന്നതിനാൽ സെക്കന്റിന്റെ പരിമിതപ്പെടുത്തുന്ന സ്ഥാനമാണ്. x0 എന്ന പോയിന്റിൽ f ഫംഗ്‌ഷന്റെ ഡെറിവേറ്റീവിന്റെ അസ്തിത്വം ഗ്രാഫിന്റെ ഈ പോയിന്റിൽ ഉണ്ടെന്നാണ് അർത്ഥമാക്കുന്നത് എന്ന് മനസ്സിലാക്കണം. ടാൻജെന്റ്അവന്.

ഈ സാഹചര്യത്തിൽ, ടാൻജെന്റിന്റെ കോണീയ ഗുണകം ഈ ഘട്ടത്തിൽ f'(x0) ഈ ഫംഗ്ഷന്റെ ഡെറിവേറ്റീവിന് തുല്യമായിരിക്കും. ഇതാണ് ഡെറിവേറ്റീവിന്റെ ജ്യാമിതീയ അർത്ഥം. പോയിന്റ് x0-ൽ വ്യത്യസ്‌തമായ ഒരു ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജെന്റ് എന്നത് പോയിന്റിലൂടെ കടന്നുപോകുന്ന ഒരു നിശ്ചിത നേർരേഖയാണ് (x0;f(x0)) കൂടാതെ ഒരു കോണീയ ഗുണകം f'(x0).

ടാൻജന്റ് സമവാക്യം

പോയിന്റ് A(x0; f(x0)) ചില ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്ക് ടാൻജന്റിന്റെ സമവാക്യം നേടാൻ ശ്രമിക്കാം. ചരിവുള്ള ഒരു നേർരേഖയുടെ സമവാക്യത്തിന് ഇനിപ്പറയുന്ന രൂപമുണ്ട്:

ഞങ്ങളുടെ ചരിവ് ഗുണകം ഡെറിവേറ്റീവിന് തുല്യമായതിനാൽ f'(x0), അപ്പോൾ സമവാക്യം ഇനിപ്പറയുന്ന ഫോം എടുക്കും: y = f'(x0)*x + ബി.

ഇനി ബിയുടെ മൂല്യം കണക്കാക്കാം. ഇത് ചെയ്യുന്നതിന്, ഫംഗ്ഷൻ പോയിന്റ് എയിലൂടെ കടന്നുപോകുന്നു എന്ന വസ്തുത ഞങ്ങൾ ഉപയോഗിക്കുന്നു.

f(x0) = f'(x0)*x0 + b, ഇവിടെ നിന്ന് നമ്മൾ b പ്രകടിപ്പിക്കുകയും b = f(x0) - f'(x0)*x0 നേടുകയും ചെയ്യുന്നു.

തത്ഫലമായുണ്ടാകുന്ന മൂല്യം ഞങ്ങൾ ടാൻജെന്റ് സമവാക്യത്തിലേക്ക് മാറ്റിസ്ഥാപിക്കുന്നു:

y = f'(x0)*x + b = f'(x0)*x + f(x0) - f'(x0)*x0 = f(x0) + f'(x0)*(x - x0).

y = f(x0) + f'(x0)*(x - x0).

ഇനിപ്പറയുന്ന ഉദാഹരണം പരിഗണിക്കുക: x = 2 എന്ന പോയിന്റിൽ f(x) = x 3 - 2*x 2 + 1 എന്ന ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്കുള്ള ടാൻജന്റിന്റെ സമവാക്യം കണ്ടെത്തുക.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f'(x) = 3*x 2 - 4*x.

4. f'(x0) = f'(2) = 3*2 2 - 4*2 = 4.

5. ലഭിച്ച മൂല്യങ്ങൾ ടാൻജെന്റ് ഫോർമുലയിലേക്ക് മാറ്റിസ്ഥാപിക്കുക, നമുക്ക് ലഭിക്കും: y = 1 + 4*(x - 2). ബ്രാക്കറ്റുകൾ തുറന്ന് സമാനമായ പദങ്ങൾ കൊണ്ടുവരുമ്പോൾ നമുക്ക് ലഭിക്കുന്നു: y = 4*x - 7.

ഉത്തരം: y = 4*x - 7.

ടാൻജെന്റ് സമവാക്യം രചിക്കുന്നതിനുള്ള പൊതു സ്കീം y = f(x) ഫംഗ്‌ഷന്റെ ഗ്രാഫിലേക്ക്:

1. x0 നിർണ്ണയിക്കുക.

2. f(x0) കണക്കാക്കുക.

3. f'(x) കണക്കാക്കുക