एक वृत्त के अनुभागीय क्षेत्र का सूत्र। एक वृत्त का क्षेत्रफल: सूत्र

अनुदेश

वृत्त के ज्ञात क्षेत्रफल के आधार पर त्रिज्या ज्ञात करने के लिए पाई का प्रयोग करें। यह स्थिरांक वृत्त के व्यास और उसकी सीमा (वृत्त) की लंबाई के बीच का अनुपात निर्धारित करता है। एक सर्कल की लंबाई एक विमान का अधिकतम क्षेत्र है जिसे इसके साथ कवर किया जा सकता है, और व्यास दो त्रिज्या के बराबर है, इसलिए त्रिज्या वाला क्षेत्र भी एक दूसरे के साथ एक अनुपात के साथ सहसंबद्ध होता है जिसे के माध्यम से व्यक्त किया जा सकता है संख्या पाई। इस स्थिरांक (π) को वृत्त के क्षेत्रफल (S) और वर्ग त्रिज्या (r) के रूप में परिभाषित किया गया है। इससे यह निष्कर्ष निकलता है कि त्रिज्या को क्षेत्र को संख्या Pi: r = (S / ) से विभाजित करने वाले भागफल के वर्गमूल के रूप में व्यक्त किया जा सकता है।

लंबे समय तक, एरास्टोफेनिस ने प्राचीन दुनिया के सबसे प्रसिद्ध पुस्तकालय, अलेक्जेंड्रिया पुस्तकालय का नेतृत्व किया। हमारे ग्रह के आकार की गणना के अलावा, उन्होंने कई महत्वपूर्ण आविष्कार और खोजें कीं। उन्होंने अभाज्य संख्याओं को निर्धारित करने के लिए एक सरल विधि का आविष्कार किया, जिसे अब "एरास्टोफेन चलनी" कहा जाता है।

उन्होंने "दुनिया का नक्शा" बनाया जिसमें उन्होंने उस समय के प्राचीन यूनानियों को ज्ञात दुनिया के सभी हिस्सों को दिखाया। नक्शा अपने समय के लिए सर्वश्रेष्ठ में से एक माना जाता था। देशांतर और अक्षांश की एक प्रणाली और एक कैलेंडर विकसित किया जिसमें लीप वर्ष शामिल थे। शस्त्रागार क्षेत्र का आविष्कार किया, एक यांत्रिक उपकरण जिसका उपयोग प्रारंभिक खगोलविदों द्वारा आकाश में तारों की स्पष्ट गति को प्रदर्शित करने और भविष्यवाणी करने के लिए किया जाता था। उन्होंने 675 सितारों की एक तारकीय सूची भी संकलित की।

स्रोत:

• साइरेन के यूनानी वैज्ञानिक एराटोस्थनीज ने दुनिया में पहली बार पृथ्वी की त्रिज्या की गणना की
• एराटोस्थनीज "पृथ्वी की गणना" की परिधि
• एरेटोस्थेनेज

एक सपाट आकृति है जो केंद्र से समान दूरी पर बिंदुओं का एक समूह है। वे सभी समान दूरी पर हैं और एक वृत्त बनाते हैं।

वह खंड जो वृत्त के केंद्र को उसके वृत्त के बिंदुओं से जोड़ता है, कहलाता है RADIUS... प्रत्येक वृत्त में, सभी त्रिज्याएँ एक दूसरे के बराबर होती हैं। एक वृत्त पर दो बिंदुओं को जोड़ने वाली और केंद्र से गुजरने वाली सीधी रेखा कहलाती है व्यास... एक वृत्त के क्षेत्रफल के सूत्र की गणना एक गणितीय स्थिरांक - संख्या का उपयोग करके की जाती है।

यह दिलचस्प है : संख्या . एक वृत्त की परिधि और उसके व्यास की लंबाई का अनुपात है और स्थिर है। 1737 में एल यूलर के कार्यों के बाद मूल्य π = 3.1415926 लागू किया गया था।

एक वृत्त के क्षेत्रफल की गणना स्थिरांक का उपयोग करके की जा सकती है। और वृत्त की त्रिज्या। त्रिज्या के संदर्भ में एक वृत्त के क्षेत्रफल का सूत्र इस प्रकार है:

आइए त्रिज्या के माध्यम से एक वृत्त के क्षेत्रफल की गणना के एक उदाहरण पर विचार करें। मान लीजिए R = 4 cm त्रिज्या वाला एक वृत्त दिया गया है, आइए आकृति का क्षेत्रफल ज्ञात करें।

हमारी परिधि 50.24 वर्ग मीटर होगी। से। मी।

एक सूत्र है व्यास के माध्यम से एक वृत्त का क्षेत्रफल... यह आवश्यक मापदंडों की गणना के लिए भी व्यापक रूप से उपयोग किया जाता है। इन सूत्रों का पता लगाने के लिए इस्तेमाल किया जा सकता है।

व्यास के माध्यम से एक वृत्त के क्षेत्रफल की गणना करने के एक उदाहरण पर विचार करें, इसकी त्रिज्या जानकर। मान लीजिए कि R = 4 cm त्रिज्या वाला एक वृत्त दिया गया है। आरंभ करने के लिए, हम व्यास ज्ञात करते हैं, जैसा कि आप जानते हैं, त्रिज्या का दोगुना है।


अब हम उपरोक्त सूत्र का उपयोग करके एक वृत्त के क्षेत्रफल की गणना के उदाहरण के लिए डेटा का उपयोग करते हैं:

जैसा कि आप देख सकते हैं, परिणाम वही उत्तर है जो पहली गणना में है।

किसी वृत्त के क्षेत्रफल की गणना के लिए मानक सूत्रों का ज्ञान भविष्य में आसानी से निर्धारित करने में मदद करेगा क्षेत्र क्षेत्रऔर लापता मात्राओं को खोजना आसान है।

हम पहले से ही जानते हैं कि वृत्त के क्षेत्रफल के सूत्र की गणना वृत्त की त्रिज्या के वर्ग द्वारा अचर के गुणनफल से की जाती है। त्रिज्या को परिधि के संदर्भ में व्यक्त किया जा सकता है और अभिव्यक्ति को परिधि के संदर्भ में एक वृत्त के क्षेत्रफल के सूत्र में प्रतिस्थापित किया जा सकता है:
अब हम इस समानता को एक वृत्त के क्षेत्रफल की गणना के सूत्र में प्रतिस्थापित करते हैं और परिधि के माध्यम से एक वृत्त का क्षेत्रफल ज्ञात करने का सूत्र प्राप्त करते हैं

परिधि के संदर्भ में एक वृत्त के क्षेत्रफल की गणना के एक उदाहरण पर विचार करें। मान लीजिए l = 8 cm लंबा एक वृत्त दिया गया है। हम व्युत्पन्न सूत्र में मान को प्रतिस्थापित करते हैं:

वृत्त का कुल क्षेत्रफल 5 वर्ग मीटर होगा। से। मी।

एक वर्ग के चारों ओर परिचालित एक वृत्त का क्षेत्रफल

एक वर्ग के चारों ओर घिरे वृत्त का क्षेत्रफल ज्ञात करना बहुत आसान है।

इसके लिए केवल वर्ग की भुजा और सरल सूत्रों के ज्ञान की आवश्यकता होती है। वर्ग का विकर्ण परिवृत्त के विकर्ण के बराबर होगा। पक्ष को जानने के बाद, यह पाइथागोरस प्रमेय द्वारा पाया जा सकता है: यहां से।
विकर्ण खोजने के बाद, हम त्रिज्या की गणना कर सकते हैं:।
और फिर हम एक वर्ग के चारों ओर वर्णित एक वृत्त के क्षेत्र के लिए मूल सूत्र में सब कुछ प्रतिस्थापित करते हैं:

एक वृत्त कई बिंदुओं का एक दृश्य संग्रह है जो केंद्र से समान दूरी पर हैं। इसका क्षेत्रफल ज्ञात करने के लिए, आपको यह जानना होगा कि त्रिज्या, व्यास, संख्या और परिधि क्या हैं।

एक वृत्त के क्षेत्रफल की गणना में शामिल मात्रा quantities

वृत्त के केंद्र बिंदु और वृत्त के किसी भी बिंदु द्वारा सीमित दूरी को इस ज्यामितीय आकृति की त्रिज्या कहा जाता है। एक वृत्त की सभी त्रिज्याओं की लंबाई समान होती है। वृत्त के किन्हीं 2 बिंदुओं के बीच का खंड जो केंद्र बिंदु से होकर गुजरता है, व्यास कहलाता है। व्यास की लंबाई त्रिज्या 2 गुणा की लंबाई के बराबर है।

वृत्त का क्षेत्रफल निकालने के लिए के मान का प्रयोग करें। यह मान वृत्त के व्यास की परिधि के अनुपात के बराबर है और इसका एक स्थिर मान है। = 3.1415926। परिधि की गणना सूत्र L = 2πR द्वारा की जाती है।

त्रिज्या के माध्यम से एक वृत्त का क्षेत्रफल ज्ञात कीजिए

इसलिए, एक वृत्त का क्षेत्रफल वृत्त की त्रिज्या से संख्या के गुणनफल के बराबर होता है, जिसे दूसरी शक्ति तक बढ़ा दिया जाता है। उदाहरण के तौर पर, हम वृत्त की त्रिज्या की लंबाई 5 सेमी के बराबर लेते हैं। तब वृत्त S का क्षेत्रफल 3.14 * 5 ^ 2 = 78.5 वर्ग मीटर के बराबर होगा। से। मी।

व्यास से वृत्त का क्षेत्रफल

किसी वृत्त के क्षेत्रफल की गणना वृत्त के व्यास के आकार को जानकर भी की जा सकती है। इस स्थिति में, S = (π / 4) * d ^ 2, जहाँ d वृत्त का व्यास है। आइए एक ही उदाहरण लेते हैं, जहां त्रिज्या 5 सेमी है, तो इसका व्यास 5 * 2 = 10 सेमी होगा। वृत्त का क्षेत्रफल S = 3.14 / 4 * 10 ^ 2 = 78.5 वर्ग सेमी। पहले उदाहरण में कुल गणना के बराबर परिणाम दोनों मामलों में गणना की शुद्धता की पुष्टि करता है।

परिधि के माध्यम से एक वृत्त का क्षेत्रफल

यदि वृत्त की त्रिज्या को परिधि के पदों में दर्शाया जाता है, तो सूत्र इस प्रकार दिखाई देगा: R = (L/2) . हम इस व्यंजक को वृत्त के क्षेत्रफल के सूत्र में प्रतिस्थापित करते हैं और परिणामस्वरूप हमें S = (L ^ 2) / 4π मिलता है। एक उदाहरण पर विचार करें जिसमें परिधि 10 सेमी है तो वृत्त का क्षेत्रफल S = (10 ^ 2) / 4 * 3.14 = 7.96 वर्ग है। से। मी।

एक वृत्त का क्षेत्रफल एक उत्कीर्ण वर्ग की एक भुजा की लंबाई के माध्यम से

यदि एक वृत्त में एक वर्ग अंकित है, तो वृत्त के व्यास की लंबाई वर्ग के विकर्ण की लंबाई के बराबर होती है। वर्ग की भुजा के आकार को जानकर, आप वृत्त के व्यास को सूत्र द्वारा आसानी से ज्ञात कर सकते हैं: d ^ 2 = 2a ^ 2। दूसरे शब्दों में, 2 शक्ति व्यास वर्ग गुणा 2 का दूसरा शक्ति पक्ष है।

किसी वृत्त के व्यास की लंबाई की गणना करने के बाद, आप इसकी त्रिज्या का पता लगा सकते हैं, और फिर वृत्त का क्षेत्रफल निर्धारित करने के लिए किसी एक सूत्र का उपयोग कर सकते हैं।

सर्किल सेक्टर क्षेत्र

एक त्रिज्यखंड एक वृत्त का वह भाग होता है जो 2 त्रिज्याओं से घिरा होता है और उनके बीच एक चाप होता है। इसका क्षेत्रफल ज्ञात करने के लिए, आपको त्रिज्यखंड का कोण मापने की आवश्यकता है। उसके बाद, आपको एक अंश बनाने की आवश्यकता है, जिसके अंश में सेक्टर के कोण का मान होगा, और हर में - 360। सेक्टर के क्षेत्र की गणना करने के लिए, परिणामस्वरूप प्राप्त मूल्य उपरोक्त सूत्रों में से किसी एक का उपयोग करके गणना की गई वृत्त के क्षेत्रफल से अंश को विभाजित करने पर गुणा किया जाना चाहिए।

मंडलियों को अधिक सावधान दृष्टिकोण की आवश्यकता होती है और B5 वस्तुओं में बहुत कम आम हैं। साथ ही, सामान्य समाधान योजना बहुभुज के मामले की तुलना में और भी सरल है (पाठ "एक समन्वय ग्रिड पर बहुभुज के क्षेत्र" देखें)।

ऐसे कार्यों में केवल वृत्त R की त्रिज्या ज्ञात करना आवश्यक है। फिर आप सूत्र S = R 2 का उपयोग करके वृत्त के क्षेत्रफल की गणना कर सकते हैं। इस सूत्र से यह भी पता चलता है कि समाधान के लिए R 2 को खोजना पर्याप्त है।

संकेतित मानों को खोजने के लिए, ग्रिड लाइनों के चौराहे पर स्थित बिंदु पर वृत्त को इंगित करना पर्याप्त है। और फिर पाइथागोरस प्रमेय का प्रयोग करें। आइए त्रिज्या की गणना के विशिष्ट उदाहरणों पर विचार करें:

एक कार्य। आकृति में दिखाए गए तीन वृत्तों की त्रिज्याएँ ज्ञात कीजिए:

आइए प्रत्येक सर्कल में अतिरिक्त निर्माण करें:

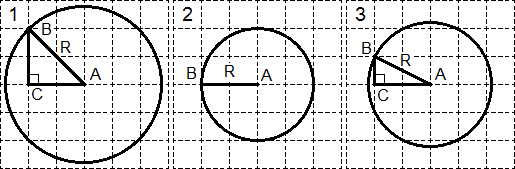
प्रत्येक मामले में, बिंदु बी को सर्कल पर चुना जाता है ताकि यह ग्रिड लाइनों के चौराहे पर स्थित हो। वृत्त 1 और 3 में बिंदु C एक समकोण त्रिभुज की आकृति को पूरा करता है। यह त्रिज्या खोजना बाकी है:

पहले वृत्त में एक त्रिभुज ABC पर विचार करें। पाइथागोरस प्रमेय द्वारा: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.

दूसरे सर्कल के लिए, सब कुछ स्पष्ट है: आर = एबी = 2।

तीसरा मामला पहले जैसा ही है। पाइथागोरस प्रमेय द्वारा त्रिभुज ABC से: R 2 = AB 2 = AC 2 + BC 2 = 1 2 + 2 2 = 5।

अब हम जानते हैं कि किसी वृत्त (या कम से कम उसके वर्ग) की त्रिज्या कैसे ज्ञात की जाती है। इसलिए, हम क्षेत्र का पता लगा सकते हैं। ऐसे कार्य हैं जहां आपको एक क्षेत्र का क्षेत्र खोजने की जरूरत है, न कि पूरे सर्कल को। ऐसे मामलों में, यह पता लगाना आसान है कि यह क्षेत्र वृत्त का कौन सा भाग है, और इस प्रकार क्षेत्रफल ज्ञात करें।

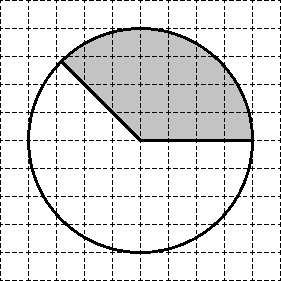
एक कार्य। भरे हुए त्रिज्यखंड का क्षेत्रफल S ज्ञात कीजिए। कृपया अपने उत्तर में S/π इंगित करें।

जाहिर है, सेक्टर एक सर्कल का एक चौथाई हिस्सा है। इसलिए, एस = 0.25 · एस सर्कल।

यह सर्कल के एस - सर्कल के क्षेत्र को खोजने के लिए बनी हुई है। ऐसा करने के लिए, हम एक अतिरिक्त निर्माण करेंगे:

त्रिभुज ABC आयताकार है। पाइथागोरस प्रमेय से हमें प्राप्त होता है: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8।

अब हम वृत्त और त्रिज्यखंड के क्षेत्रफल ज्ञात करते हैं: वृत्त का S = R 2 = 8π; एस = 0.25 एस सर्कल = 2π।

अंत में, मांगा गया मान S / = 2 है।

अज्ञात दायरे में सेक्टर क्षेत्र

यह बिल्कुल नए प्रकार का कार्य है, 2010-2011 में ऐसा कुछ भी नहीं था। शर्त के अनुसार, हमें एक निश्चित क्षेत्र का एक वृत्त दिया जाता है (अर्थात् क्षेत्र, त्रिज्या नहीं!)। फिर, इस सर्कल के अंदर, एक सेक्टर को हाइलाइट किया जाता है, जिसका क्षेत्र पाया जाना है।

अच्छी खबर यह है कि ऐसी समस्याएं वर्ग की सभी समस्याओं में सबसे आसान होती हैं, जो गणित की परीक्षा में होती हैं। इसके अलावा, सर्कल और सेक्टर को हमेशा ग्रिड पर रखा जाता है। इसलिए, ऐसी समस्याओं को हल करने का तरीका जानने के लिए, बस तस्वीर पर एक नज़र डालें:

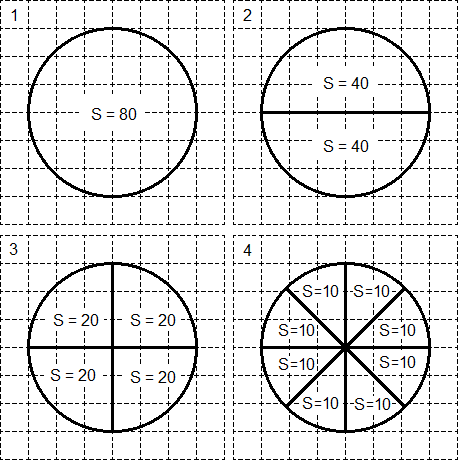
माना मूल वृत्त का क्षेत्रफल S वृत्त का क्षेत्रफल = 80 है। फिर इसे दो त्रिज्यखंडों में विभाजित किया जा सकता है जिनका क्षेत्रफल S = 40 प्रत्येक है (चरण 2 देखें)। इसी तरह, इन "आधा" क्षेत्रों में से प्रत्येक को फिर से आधे में विभाजित किया जा सकता है - हमें चार क्षेत्र मिलते हैं जिनमें प्रत्येक क्षेत्र S = 20 होता है (चरण 3 देखें)। अंत में, हम इनमें से प्रत्येक सेक्टर को दो और में विभाजित कर सकते हैं - हमें 8 "स्क्रैप" सेक्टर मिलते हैं। इनमें से प्रत्येक "स्क्रैप" का क्षेत्रफल S = 10 होगा।

कृपया ध्यान दें: गणित में किसी भी USE समस्या में कोई बारीक विभाजन नहीं है! इस प्रकार, समस्या B-3 को हल करने के लिए एल्गोरिथ्म इस प्रकार है:

1. मूल सर्कल को 8 "स्क्रैप" क्षेत्रों में काटें। उनमें से प्रत्येक का क्षेत्रफल पूरे वृत्त के क्षेत्रफल का ठीक 1/8 है। उदाहरण के लिए, यदि स्थिति के अनुसार वृत्त का क्षेत्रफल वृत्त का S = 240 है, तो "स्क्रैप" का क्षेत्रफल S = 240: 8 = 30 है;
2. पता करें कि मूल क्षेत्र में कितने "स्क्रैप" रखे गए हैं, जिस क्षेत्र का आप पता लगाना चाहते हैं। उदाहरण के लिए, यदि हमारे क्षेत्र में 30 के क्षेत्रफल के साथ 3 "टुकड़े" हैं, तो वांछित क्षेत्र का क्षेत्रफल एस = 3 · 30 = 90 है। यह उत्तर होगा।

बस इतना ही! समस्या को व्यावहारिक रूप से मौखिक रूप से हल किया जाता है। अगर आपको अभी भी कुछ समझ में नहीं आ रहा है, तो एक पिज्जा खरीदें और उसके 8 टुकड़े कर लें। ऐसा प्रत्येक टुकड़ा वही "स्क्रैप" सेक्टर होगा जिसे बड़े टुकड़ों में जोड़ा जा सकता है।

आइए अब परीक्षण परीक्षा के उदाहरण देखें:

एक कार्य। चेकर्ड पेपर पर एक वृत्त खींचा जाता है, जिसका क्षेत्रफल 40 है। छायांकित आकृति का क्षेत्रफल ज्ञात कीजिए।

तो, वृत्त का क्षेत्रफल 40 है। आइए इसे 8 सेक्टरों में विभाजित करें - प्रत्येक क्षेत्र S = 40: 5 = 8 के साथ। हमें मिलता है:

जाहिर है, भरे हुए सेक्टर में ठीक दो "स्क्रैप" सेक्टर होते हैं। इसलिए, इसका क्षेत्रफल 2 · 5 = 10 है। यही संपूर्ण समाधान है!

एक कार्य। चेकर पेपर पर एक वृत्त खींचा जाता है, जिसका क्षेत्रफल 64 है। छायांकित आकृति का क्षेत्रफल ज्ञात कीजिए।

पूरे वृत्त को फिर से 8 समान त्रिज्यखंडों में विभाजित करें। जाहिर है, उनमें से एक का क्षेत्र वही है जो आपको खोजने की जरूरत है। अतः इसका क्षेत्रफल S = 64: 8 = 8 है।

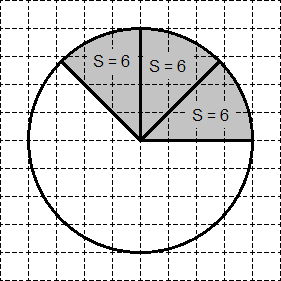
एक कार्य। चेकर पेपर पर एक वृत्त खींचा जाता है, जिसका क्षेत्रफल 48 है। छायांकित आकृति का क्षेत्रफल ज्ञात कीजिए।

सर्कल को फिर से 8 बराबर सेक्टरों में विभाजित करें। उनमें से प्रत्येक का क्षेत्रफल S = 48: 8 = 6 के बराबर है। ठीक तीन सेक्टरों को मांगे गए सेक्टर में रखा गया है - एक "टुकड़ा" (आंकड़ा देखें)। अतः वांछित त्रिज्यखंड का क्षेत्रफल 3 6 = 18 है।