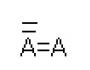ab ಮತ್ತು bc ರೇಖೆಗಳು ಸಮಾನಾಂತರವಾಗಿರುತ್ತವೆ, ಛೇದಿಸುತ್ತವೆ ಮತ್ತು ದಾಟುತ್ತವೆ. ವ್ಯಾಖ್ಯಾನ

ಪ್ರಮೇಯ. ಒಂದು ರೇಖೆಯು ನಿರ್ದಿಷ್ಟ ಸಮತಲದಲ್ಲಿ ಇದ್ದರೆ ಮತ್ತು ಇನ್ನೊಂದು ರೇಖೆಯು ಈ ಸಮತಲವನ್ನು ಮೊದಲ ಸಾಲಿಗೆ ಸೇರದ ಹಂತದಲ್ಲಿ ಛೇದಿಸಿದರೆ, ಈ ಎರಡು ಸಾಲುಗಳು ಛೇದಿಸುತ್ತವೆ. ದಾಟುವ ರೇಖೆಗಳ ಚಿಹ್ನೆ ಪುರಾವೆ. ಸಮತಲದಲ್ಲಿ ಒಂದು ಸುಳ್ಳು ರೇಖೆಯನ್ನು ಬಿಡಿ, ಮತ್ತು ಬಿ ರೇಖೆಯು ಸಮತಲವನ್ನು ಬಿ ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತದೆ, ಅದು ಸಾಲಿಗೆ ಸೇರಿಲ್ಲ. a ಮತ್ತು b ರೇಖೆಗಳು ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಇದ್ದರೆ, ನಂತರ B ಬಿಂದುವು ಈ ಸಮತಲದಲ್ಲಿ ಇರುತ್ತದೆ. ಈ ರೇಖೆಯ ಮೂಲಕ ಒಂದೇ ಒಂದು ಸಮತಲವು ಹಾದುಹೋಗುವುದರಿಂದ ಮತ್ತು ಈ ರೇಖೆಯ ಹೊರಗೆ ಒಂದು ಬಿಂದು ಇರುವುದರಿಂದ, ಈ ಸಮತಲವು ಸಮತಲವಾಗಿರಬೇಕು. ಆದರೆ ನಂತರ ಸರಳ ರೇಖೆಯು ಸಮತಲದಲ್ಲಿ ಇರುತ್ತದೆ, ಇದು ಸ್ಥಿತಿಗೆ ವಿರುದ್ಧವಾಗಿದೆ. ಪರಿಣಾಮವಾಗಿ, ನೇರ ರೇಖೆಗಳು a ಮತ್ತು b ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಇರುವುದಿಲ್ಲ, ಅಂದರೆ. ಅಂತರ್ಜಾತಿ.

ನಿಯಮಿತ ತ್ರಿಕೋನ ಪ್ರಿಸ್ಮ್‌ನ ಅಂಚುಗಳನ್ನು ಹೊಂದಿರುವ ಎಷ್ಟು ಜೋಡಿ ಓರೆ ರೇಖೆಗಳಿವೆ? ಪರಿಹಾರ: ಬೇಸ್‌ಗಳ ಪ್ರತಿ ಅಂಚಿಗೆ ಅದರೊಂದಿಗೆ ಛೇದಿಸುವ ಮೂರು ಅಂಚುಗಳಿವೆ. ಪ್ರತಿ ಪಾರ್ಶ್ವದ ಅಂಚಿಗೆ ಅದರೊಂದಿಗೆ ಛೇದಿಸುವ ಎರಡು ಪಕ್ಕೆಲುಬುಗಳಿವೆ. ಆದ್ದರಿಂದ, ಅಗತ್ಯವಿರುವ ಜೋಡಿಗಳ ಓರೆ ಸಾಲುಗಳು ವ್ಯಾಯಾಮ 5 ಆಗಿದೆ

ನಿಯಮಿತ ಷಡ್ಭುಜೀಯ ಪ್ರಿಸ್ಮ್ನ ಅಂಚುಗಳನ್ನು ಹೊಂದಿರುವ ಎಷ್ಟು ಜೋಡಿ ಓರೆ ರೇಖೆಗಳಿವೆ? ಪರಿಹಾರ: ಬೇಸ್ಗಳ ಪ್ರತಿಯೊಂದು ಅಂಚು 8 ಜೋಡಿ ಕ್ರಾಸಿಂಗ್ ಲೈನ್ಗಳಲ್ಲಿ ಭಾಗವಹಿಸುತ್ತದೆ. ಪ್ರತಿ ಲ್ಯಾಟರಲ್ ಎಡ್ಜ್ 8 ಜೋಡಿ ಕ್ರಾಸಿಂಗ್ ಲೈನ್‌ಗಳಲ್ಲಿ ಭಾಗವಹಿಸುತ್ತದೆ. ಆದ್ದರಿಂದ, ಅಗತ್ಯವಿರುವ ಜೋಡಿಗಳ ಓರೆ ಸಾಲುಗಳು ವ್ಯಾಯಾಮ 6 ಆಗಿದೆ

ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಎರಡು ರೇಖೆಗಳು ಸಾಮಾನ್ಯ ಬಿಂದುವನ್ನು ಹೊಂದಿದ್ದರೆ, ಈ ಎರಡು ಸಾಲುಗಳು ಛೇದಿಸುತ್ತವೆ ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ. ಕೆಳಗಿನ ಚಿತ್ರದಲ್ಲಿ, A ಮತ್ತು b ರೇಖೆಗಳು A ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತವೆ. a ಮತ್ತು c ರೇಖೆಗಳು ಛೇದಿಸುವುದಿಲ್ಲ.

ಯಾವುದೇ ಎರಡು ಸರಳ ರೇಖೆಗಳು ಕೇವಲ ಒಂದು ಸಾಮಾನ್ಯ ಬಿಂದುವನ್ನು ಹೊಂದಿರುತ್ತವೆ ಅಥವಾ ಯಾವುದೇ ಸಾಮಾನ್ಯ ಬಿಂದುಗಳನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ.

ಸಮಾನಾಂತರ ರೇಖೆಗಳು

ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಎರಡು ರೇಖೆಗಳು ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಮಲಗಿದ್ದರೆ ಮತ್ತು ಛೇದಿಸದಿದ್ದರೆ ಸಮಾನಾಂತರ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಸಮಾನಾಂತರ ರೇಖೆಗಳನ್ನು ಸೂಚಿಸಲು, ವಿಶೇಷ ಐಕಾನ್ ಬಳಸಿ - ||.

a||b ಎಂಬ ಸಂಕೇತ ಎಂದರೆ a ಸಾಲು b ಗೆ ಸಮಾನಾಂತರವಾಗಿರುತ್ತದೆ. ಮೇಲೆ ಪ್ರಸ್ತುತಪಡಿಸಿದ ಚಿತ್ರದಲ್ಲಿ, a ಮತ್ತು c ಸಾಲುಗಳು ಸಮಾನಾಂತರವಾಗಿರುತ್ತವೆ.

ಸಮಾನಾಂತರ ರೇಖೆಗಳ ಪ್ರಮೇಯ

ನಿರ್ದಿಷ್ಟ ರೇಖೆಯ ಮೇಲೆ ಇರದ ಬಾಹ್ಯಾಕಾಶದ ಯಾವುದೇ ಬಿಂದುವಿನ ಮೂಲಕ, ನಿರ್ದಿಷ್ಟ ರೇಖೆಗೆ ಸಮಾನಾಂತರವಾಗಿ ಒಂದು ರೇಖೆಯನ್ನು ಹಾದುಹೋಗುತ್ತದೆ ಮತ್ತು ಮೇಲಾಗಿ ಒಂದೇ ಒಂದು.

ಕ್ರಾಸಿಂಗ್ ಲೈನ್ಸ್

ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಇರುವ ಎರಡು ಸಾಲುಗಳು ಛೇದಿಸಬಹುದು ಅಥವಾ ಸಮಾನಾಂತರವಾಗಿರಬಹುದು. ಆದರೆ ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ, ಎರಡು ಸರಳ ರೇಖೆಗಳು ಈ ಸಮತಲಕ್ಕೆ ಸೇರಿರುವುದಿಲ್ಲ. ಅವುಗಳನ್ನು ಎರಡು ವಿಭಿನ್ನ ವಿಮಾನಗಳಲ್ಲಿ ಇರಿಸಬಹುದು.

ವಿಭಿನ್ನ ವಿಮಾನಗಳಲ್ಲಿ ಇರುವ ರೇಖೆಗಳು ಛೇದಿಸುವುದಿಲ್ಲ ಮತ್ತು ಸಮಾನಾಂತರ ರೇಖೆಗಳಲ್ಲ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ. ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಇರದ ಎರಡು ಸಾಲುಗಳನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ನೇರ ರೇಖೆಗಳನ್ನು ದಾಟುವುದು.

ಕೆಳಗಿನ ಚಿತ್ರವು ಎರಡು ಛೇದಿಸುವ ನೇರ ರೇಖೆಗಳನ್ನು ತೋರಿಸುತ್ತದೆ a ಮತ್ತು b , ಇದು ವಿಭಿನ್ನ ಸಮತಲಗಳಲ್ಲಿ ಇರುತ್ತದೆ.

ಓರೆ ರೇಖೆಗಳಲ್ಲಿ ಪರೀಕ್ಷೆ ಮತ್ತು ಪ್ರಮೇಯ

ಎರಡು ರೇಖೆಗಳಲ್ಲಿ ಒಂದು ನಿರ್ದಿಷ್ಟ ಸಮತಲದಲ್ಲಿದ್ದರೆ, ಮತ್ತು ಇನ್ನೊಂದು ರೇಖೆಯು ಈ ಸಮತಲವನ್ನು ಮೊದಲ ಸಾಲಿನಲ್ಲಿರದೆ ಒಂದು ಹಂತದಲ್ಲಿ ಛೇದಿಸಿದರೆ, ಈ ಸಾಲುಗಳು ಛೇದಿಸುತ್ತವೆ.

ಓರೆ ರೇಖೆಗಳ ಮೇಲೆ ಪ್ರಮೇಯ: ಪ್ರತಿ ಎರಡು ಛೇದಿಸುವ ರೇಖೆಗಳ ಮೂಲಕ ಇತರ ರೇಖೆಗೆ ಸಮಾನಾಂತರವಾಗಿ ಸಮತಲವನ್ನು ಹಾದುಹೋಗುತ್ತದೆ ಮತ್ತು ಮೇಲಾಗಿ ಕೇವಲ ಒಂದು.

ಹೀಗಾಗಿ, ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ರೇಖೆಗಳ ಸಂಬಂಧಿತ ಸ್ಥಾನಗಳ ಎಲ್ಲಾ ಸಂಭವನೀಯ ಪ್ರಕರಣಗಳನ್ನು ನಾವು ಪರಿಗಣಿಸಿದ್ದೇವೆ. ಅವುಗಳಲ್ಲಿ ಮೂರು ಮಾತ್ರ ಇವೆ.

1. ಸಾಲುಗಳು ಛೇದಿಸುತ್ತವೆ. (ಅಂದರೆ, ಅವರಿಗೆ ಒಂದೇ ಒಂದು ಸಾಮಾನ್ಯ ಅಂಶವಿದೆ.)

2. ಸಾಲುಗಳು ಸಮಾನಾಂತರವಾಗಿರುತ್ತವೆ. (ಅಂದರೆ, ಅವುಗಳು ಸಾಮಾನ್ಯ ಬಿಂದುಗಳನ್ನು ಹೊಂದಿಲ್ಲ ಮತ್ತು ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಇರುತ್ತವೆ.)

3. ನೇರ ರೇಖೆಗಳು ದಾಟುತ್ತವೆ. (ಅಂದರೆ, ಅವು ವಿಭಿನ್ನ ವಿಮಾನಗಳಲ್ಲಿವೆ.)

ನಾನು ಹೊಸ ವರ್ಡೋವ್ ಫೈಲ್ ಅನ್ನು ರಚಿಸುವ ಮೊದಲು ಮತ್ತು ಅಂತಹ ಆಕರ್ಷಕ ವಿಷಯವನ್ನು ಮುಂದುವರಿಸುವ ಮೊದಲು ಒಂದು ನಿಮಿಷವೂ ಕಳೆದಿಲ್ಲ. ನೀವು ಕೆಲಸದ ಮನಸ್ಥಿತಿಯ ಕ್ಷಣಗಳನ್ನು ಸೆರೆಹಿಡಿಯಬೇಕು, ಆದ್ದರಿಂದ ಯಾವುದೇ ಸಾಹಿತ್ಯದ ಪರಿಚಯವಿರುವುದಿಲ್ಲ. ಗದ್ಯದ ಹೊಡೆತ ಇರುತ್ತದೆ =)

ಎರಡು ನೇರ ಸ್ಥಳಗಳು ಮಾಡಬಹುದು:

1) ಅಂತರ್ಜಾತಿ;

2) ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸಿ;

3) ಸಮಾನಾಂತರವಾಗಿರಿ;

4) ಹೊಂದಾಣಿಕೆ.

ಪ್ರಕರಣ ಸಂಖ್ಯೆ 1 ಮೂಲಭೂತವಾಗಿ ಇತರ ಪ್ರಕರಣಗಳಿಗಿಂತ ಭಿನ್ನವಾಗಿದೆ. ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಮಲಗದಿದ್ದರೆ ಎರಡು ಸರಳ ರೇಖೆಗಳು ಛೇದಿಸುತ್ತವೆ. ಒಂದು ತೋಳನ್ನು ಮೇಲಕ್ಕೆತ್ತಿ ಮತ್ತು ಇನ್ನೊಂದು ತೋಳನ್ನು ಮುಂದಕ್ಕೆ ವಿಸ್ತರಿಸಿ - ರೇಖೆಗಳನ್ನು ದಾಟುವ ಉದಾಹರಣೆ ಇಲ್ಲಿದೆ. ಅಂಕ ಸಂಖ್ಯೆ 2-4 ರಲ್ಲಿ ನೇರ ರೇಖೆಗಳು ಸುಳ್ಳು ಮಾಡಬೇಕು ಒಂದು ವಿಮಾನದಲ್ಲಿ.

ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ರೇಖೆಗಳ ಸಂಬಂಧಿತ ಸ್ಥಾನಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಹೇಗೆ?

ಎರಡು ನೇರ ಸ್ಥಳಗಳನ್ನು ಪರಿಗಣಿಸಿ:

- ಒಂದು ಬಿಂದು ಮತ್ತು ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ಮೂಲಕ ವ್ಯಾಖ್ಯಾನಿಸಲಾದ ನೇರ ರೇಖೆ;
- ಒಂದು ಬಿಂದು ಮತ್ತು ದಿಕ್ಕಿನ ವೆಕ್ಟರ್‌ನಿಂದ ವ್ಯಾಖ್ಯಾನಿಸಲಾದ ನೇರ ರೇಖೆ.

ಉತ್ತಮ ತಿಳುವಳಿಕೆಗಾಗಿ, ಸ್ಕೀಮ್ಯಾಟಿಕ್ ಡ್ರಾಯಿಂಗ್ ಮಾಡೋಣ:

ರೇಖಾಚಿತ್ರವು ಛೇದಿಸುವ ನೇರ ರೇಖೆಗಳನ್ನು ಉದಾಹರಣೆಯಾಗಿ ತೋರಿಸುತ್ತದೆ.

ಈ ಸರಳ ರೇಖೆಗಳನ್ನು ಹೇಗೆ ಎದುರಿಸುವುದು?

ಅಂಕಗಳು ತಿಳಿದಿರುವುದರಿಂದ, ವೆಕ್ಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಸುಲಭ.

ನೇರವಾಗಿದ್ದರೆ ಅಂತರ್ಜಾತಿ, ನಂತರ ವಾಹಕಗಳು ಕೋಪ್ಲಾನರ್ ಅಲ್ಲ(ಪಾಠ ನೋಡಿ ವಾಹಕಗಳ ರೇಖೀಯ (ಅಲ್ಲದ) ಅವಲಂಬನೆ. ವಾಹಕಗಳ ಆಧಾರ), ಮತ್ತು, ಆದ್ದರಿಂದ, ಅವುಗಳ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ ಕೂಡಿದ ನಿರ್ಣಾಯಕವು ಶೂನ್ಯವಲ್ಲ. ಅಥವಾ, ವಾಸ್ತವವಾಗಿ ಅದೇ ವಿಷಯ, ಅದು ಶೂನ್ಯವಲ್ಲ: .

ಸಂದರ್ಭಗಳಲ್ಲಿ ಸಂಖ್ಯೆ 2-4, ನಮ್ಮ ರಚನೆಯು ಒಂದು ಸಮತಲಕ್ಕೆ "ಬೀಳುತ್ತದೆ", ಮತ್ತು ವಾಹಕಗಳು ಕೋಪ್ಲಾನರ್, ಮತ್ತು ರೇಖೀಯವಾಗಿ ಅವಲಂಬಿತ ವೆಕ್ಟರ್‌ಗಳ ಮಿಶ್ರ ಉತ್ಪನ್ನವು ಶೂನ್ಯಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ: .

ಅಲ್ಗಾರಿದಮ್ ಅನ್ನು ಮತ್ತಷ್ಟು ವಿಸ್ತರಿಸೋಣ. ಹಾಗೆ ನಟಿಸೋಣ ಆದ್ದರಿಂದ, ರೇಖೆಗಳು ಛೇದಿಸುತ್ತವೆ, ಸಮಾನಾಂತರವಾಗಿರುತ್ತವೆ ಅಥವಾ ಹೊಂದಿಕೆಯಾಗುತ್ತವೆ.

ದಿಕ್ಕು ವಾಹಕಗಳಾಗಿದ್ದರೆ ಕೊಲಿನಿಯರ್, ನಂತರ ಸಾಲುಗಳು ಸಮಾನಾಂತರವಾಗಿರುತ್ತವೆ ಅಥವಾ ಕಾಕತಾಳೀಯವಾಗಿರುತ್ತವೆ. ಅಂತಿಮ ಉಗುರುಗಾಗಿ, ನಾನು ಈ ಕೆಳಗಿನ ತಂತ್ರವನ್ನು ಪ್ರಸ್ತಾಪಿಸುತ್ತೇನೆ: ಒಂದು ಸಾಲಿನಲ್ಲಿ ಯಾವುದೇ ಬಿಂದುವನ್ನು ತೆಗೆದುಕೊಂಡು ಅದರ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಎರಡನೇ ಸಾಲಿನ ಸಮೀಕರಣಕ್ಕೆ ಬದಲಿಸಿ; ನಿರ್ದೇಶಾಂಕಗಳು "ಸರಿಹೊಂದಿದರೆ", ನಂತರ ಸಾಲುಗಳು ಸೇರಿಕೊಳ್ಳುತ್ತವೆ; ಅವರು "ಹೊಂದಿಕೊಳ್ಳದಿದ್ದರೆ" ನಂತರ ಸಾಲುಗಳು ಸಮಾನಾಂತರವಾಗಿರುತ್ತವೆ.

ಅಲ್ಗಾರಿದಮ್ ಸರಳವಾಗಿದೆ, ಆದರೆ ಪ್ರಾಯೋಗಿಕ ಉದಾಹರಣೆಗಳು ಇನ್ನೂ ಸಹಾಯ ಮಾಡುತ್ತವೆ:

ಉದಾಹರಣೆ 11

ಎರಡು ಸಾಲುಗಳ ಸಂಬಂಧಿತ ಸ್ಥಾನವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ

ಪರಿಹಾರ: ಅನೇಕ ಜ್ಯಾಮಿತಿ ಸಮಸ್ಯೆಗಳಂತೆ, ಬಿಂದುವಿನ ಮೂಲಕ ಪರಿಹಾರ ಬಿಂದುವನ್ನು ರೂಪಿಸಲು ಅನುಕೂಲಕರವಾಗಿದೆ:

1) ನಾವು ಸಮೀಕರಣಗಳಿಂದ ಬಿಂದುಗಳು ಮತ್ತು ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತೇವೆ:

2) ವೆಕ್ಟರ್ ಅನ್ನು ಹುಡುಕಿ:

ಹೀಗಾಗಿ, ವಾಹಕಗಳು ಕೋಪ್ಲಾನಾರ್ ಆಗಿರುತ್ತವೆ, ಅಂದರೆ ರೇಖೆಗಳು ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಇರುತ್ತವೆ ಮತ್ತು ಛೇದಿಸಬಹುದು, ಸಮಾನಾಂತರವಾಗಿರಬಹುದು ಅಥವಾ ಹೊಂದಿಕೆಯಾಗಬಹುದು.

4) ಕೋಲಿನಿಯರಿಟಿಗಾಗಿ ದಿಕ್ಕಿನ ವೆಕ್ಟರ್‌ಗಳನ್ನು ಪರಿಶೀಲಿಸೋಣ.

ಈ ವೆಕ್ಟರ್‌ಗಳ ಅನುಗುಣವಾದ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ ವ್ಯವಸ್ಥೆಯನ್ನು ರಚಿಸೋಣ:

ಇಂದ ಎಲ್ಲರೂಇದು ಅನುಸರಿಸುವ ಸಮೀಕರಣಗಳು, ಆದ್ದರಿಂದ, ವ್ಯವಸ್ಥೆಯು ಸ್ಥಿರವಾಗಿರುತ್ತದೆ, ವೆಕ್ಟರ್‌ಗಳ ಅನುಗುಣವಾದ ನಿರ್ದೇಶಾಂಕಗಳು ಅನುಪಾತದಲ್ಲಿರುತ್ತವೆ ಮತ್ತು ವೆಕ್ಟರ್‌ಗಳು ಕಾಲಿನಿಯರ್ ಆಗಿರುತ್ತವೆ.

ತೀರ್ಮಾನ: ಸಾಲುಗಳು ಸಮಾನಾಂತರವಾಗಿರುತ್ತವೆ ಅಥವಾ ಹೊಂದಿಕೆಯಾಗುತ್ತವೆ.

5) ಸಾಲುಗಳು ಸಾಮಾನ್ಯ ಅಂಕಗಳನ್ನು ಹೊಂದಿದೆಯೇ ಎಂದು ಕಂಡುಹಿಡಿಯಿರಿ. ಮೊದಲ ಸಾಲಿಗೆ ಸೇರಿದ ಬಿಂದುವನ್ನು ತೆಗೆದುಕೊಳ್ಳೋಣ ಮತ್ತು ಅದರ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ರೇಖೆಯ ಸಮೀಕರಣಗಳಾಗಿ ಬದಲಿಸೋಣ:

ಹೀಗಾಗಿ, ಸಾಲುಗಳಿಗೆ ಯಾವುದೇ ಸಾಮಾನ್ಯ ಬಿಂದುಗಳಿಲ್ಲ, ಮತ್ತು ಸಮಾನಾಂತರವಾಗಿರುವುದನ್ನು ಹೊರತುಪಡಿಸಿ ಅವುಗಳಿಗೆ ಯಾವುದೇ ಆಯ್ಕೆಯಿಲ್ಲ.

ಉತ್ತರ:

ನೀವೇ ಪರಿಹರಿಸಲು ಆಸಕ್ತಿದಾಯಕ ಉದಾಹರಣೆ:

ಉದಾಹರಣೆ 12

ರೇಖೆಗಳ ಸಂಬಂಧಿತ ಸ್ಥಾನಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ

ನೀವೇ ಪರಿಹರಿಸಲು ಇದು ಒಂದು ಉದಾಹರಣೆಯಾಗಿದೆ. ಎರಡನೇ ಸಾಲಿನಲ್ಲಿ ಅಕ್ಷರವನ್ನು ನಿಯತಾಂಕವಾಗಿ ಹೊಂದಿದೆ ಎಂಬುದನ್ನು ದಯವಿಟ್ಟು ಗಮನಿಸಿ. ತಾರ್ಕಿಕ. ಸಾಮಾನ್ಯ ಸಂದರ್ಭದಲ್ಲಿ, ಇವು ಎರಡು ವಿಭಿನ್ನ ಸಾಲುಗಳಾಗಿವೆ, ಆದ್ದರಿಂದ ಪ್ರತಿ ಸಾಲು ತನ್ನದೇ ಆದ ನಿಯತಾಂಕವನ್ನು ಹೊಂದಿದೆ.

ಮತ್ತು ಉದಾಹರಣೆಗಳನ್ನು ಬಿಟ್ಟುಬಿಡಬೇಡಿ ಎಂದು ನಾನು ಮತ್ತೊಮ್ಮೆ ನಿಮ್ಮನ್ನು ಒತ್ತಾಯಿಸುತ್ತೇನೆ, ನಾನು ಪ್ರಸ್ತಾಪಿಸುವ ಕಾರ್ಯಗಳು ಯಾದೃಚ್ಛಿಕತೆಯಿಂದ ದೂರವಿದೆ ;-)

ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಒಂದು ಸಾಲಿನ ತೊಂದರೆಗಳು

ಪಾಠದ ಅಂತಿಮ ಭಾಗದಲ್ಲಿ, ಪ್ರಾದೇಶಿಕ ರೇಖೆಗಳೊಂದಿಗೆ ಗರಿಷ್ಠ ಸಂಖ್ಯೆಯ ವಿವಿಧ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಗಣಿಸಲು ನಾನು ಪ್ರಯತ್ನಿಸುತ್ತೇನೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಕಥೆಯ ಮೂಲ ಕ್ರಮವನ್ನು ಗಮನಿಸಬಹುದು: ಮೊದಲು ನಾವು ದಾಟುವ ರೇಖೆಗಳೊಂದಿಗೆ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಗಣಿಸುತ್ತೇವೆ, ನಂತರ ಛೇದಿಸುವ ರೇಖೆಗಳೊಂದಿಗೆ ಮತ್ತು ಕೊನೆಯಲ್ಲಿ ನಾವು ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಸಮಾನಾಂತರ ರೇಖೆಗಳ ಬಗ್ಗೆ ಮಾತನಾಡುತ್ತೇವೆ. ಆದಾಗ್ಯೂ, ಈ ಪಾಠದ ಕೆಲವು ಕಾರ್ಯಗಳನ್ನು ರೇಖೆಗಳ ಸ್ಥಳದ ಹಲವಾರು ಪ್ರಕರಣಗಳಿಗೆ ಏಕಕಾಲದಲ್ಲಿ ರೂಪಿಸಬಹುದು ಎಂದು ನಾನು ಹೇಳಲೇಬೇಕು ಮತ್ತು ಈ ನಿಟ್ಟಿನಲ್ಲಿ, ವಿಭಾಗವನ್ನು ಪ್ಯಾರಾಗಳಾಗಿ ವಿಂಗಡಿಸುವುದು ಸ್ವಲ್ಪಮಟ್ಟಿಗೆ ಅನಿಯಂತ್ರಿತವಾಗಿದೆ. ಸರಳವಾದ ಉದಾಹರಣೆಗಳಿವೆ, ಹೆಚ್ಚು ಸಂಕೀರ್ಣ ಉದಾಹರಣೆಗಳಿವೆ, ಮತ್ತು ಪ್ರತಿಯೊಬ್ಬರೂ ತಮಗೆ ಬೇಕಾದುದನ್ನು ಕಂಡುಕೊಳ್ಳುತ್ತಾರೆ ಎಂದು ಭಾವಿಸುತ್ತೇವೆ.

ಕ್ರಾಸಿಂಗ್ ಲೈನ್ಸ್

ಇವೆರಡೂ ಇರುವ ಯಾವುದೇ ಸಮತಲವಿಲ್ಲದಿದ್ದರೆ ಸರಳ ರೇಖೆಗಳು ಛೇದಿಸುತ್ತವೆ ಎಂದು ನಾನು ನಿಮಗೆ ನೆನಪಿಸುತ್ತೇನೆ. ನಾನು ಅಭ್ಯಾಸದ ಮೂಲಕ ಯೋಚಿಸುತ್ತಿರುವಾಗ, ದೈತ್ಯಾಕಾರದ ಸಮಸ್ಯೆಯು ಮನಸ್ಸಿಗೆ ಬಂದಿತು, ಮತ್ತು ಈಗ ನಿಮ್ಮ ಗಮನಕ್ಕೆ ನಾಲ್ಕು ತಲೆಗಳನ್ನು ಹೊಂದಿರುವ ಡ್ರ್ಯಾಗನ್ ಅನ್ನು ಪ್ರಸ್ತುತಪಡಿಸಲು ನನಗೆ ಸಂತೋಷವಾಗಿದೆ:

ಉದಾಹರಣೆ 13

ನೇರ ರೇಖೆಗಳನ್ನು ನೀಡಲಾಗಿದೆ. ಅಗತ್ಯವಿದೆ:

ಎ) ರೇಖೆಗಳು ಛೇದಿಸುತ್ತವೆ ಎಂದು ಸಾಬೀತುಪಡಿಸಿ;

ಬಿ) ಕೊಟ್ಟಿರುವ ರೇಖೆಗಳಿಗೆ ಲಂಬವಾಗಿರುವ ಬಿಂದುವಿನ ಮೂಲಕ ಹಾದುಹೋಗುವ ರೇಖೆಯ ಸಮೀಕರಣಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ;

ಸಿ) ಒಳಗೊಂಡಿರುವ ನೇರ ರೇಖೆಯ ಸಮೀಕರಣಗಳನ್ನು ರಚಿಸಿ ಸಾಮಾನ್ಯ ಲಂಬದಾಟುವ ಸಾಲುಗಳು;

ಡಿ) ರೇಖೆಗಳ ನಡುವಿನ ಅಂತರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.

ಪರಿಹಾರ: ನಡೆಯುವವನು ರಸ್ತೆಯನ್ನು ಕರಗತ ಮಾಡಿಕೊಳ್ಳುತ್ತಾನೆ:

ಎ) ರೇಖೆಗಳು ಛೇದಿಸುತ್ತವೆ ಎಂದು ನಾವು ಸಾಬೀತುಪಡಿಸೋಣ. ಈ ರೇಖೆಗಳ ಬಿಂದುಗಳು ಮತ್ತು ದಿಕ್ಕಿನ ವೆಕ್ಟರ್‌ಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:

ವೆಕ್ಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:

ಲೆಕ್ಕ ಹಾಕೋಣ ವಾಹಕಗಳ ಮಿಶ್ರ ಉತ್ಪನ್ನ:

ಹೀಗಾಗಿ, ವಾಹಕಗಳು ಕೋಪ್ಲಾನರ್ ಅಲ್ಲ, ಅಂದರೆ ರೇಖೆಗಳು ಛೇದಿಸುತ್ತವೆ, ಇದು ಸಾಬೀತುಪಡಿಸಬೇಕಾದದ್ದು.

ರೇಖೆಗಳನ್ನು ದಾಟಲು ಪರಿಶೀಲನಾ ಅಲ್ಗಾರಿದಮ್ ಚಿಕ್ಕದಾಗಿದೆ ಎಂದು ಬಹುಶಃ ಪ್ರತಿಯೊಬ್ಬರೂ ಬಹಳ ಹಿಂದೆಯೇ ಗಮನಿಸಿದ್ದಾರೆ.

ಬಿ) ಬಿಂದುವಿನ ಮೂಲಕ ಹಾದುಹೋಗುವ ಮತ್ತು ರೇಖೆಗಳಿಗೆ ಲಂಬವಾಗಿರುವ ರೇಖೆಯ ಸಮೀಕರಣಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. ಸ್ಕೀಮ್ಯಾಟಿಕ್ ಡ್ರಾಯಿಂಗ್ ಮಾಡೋಣ:

ಬದಲಾವಣೆಗಾಗಿ ನಾನು ನೇರವಾಗಿ ಪೋಸ್ಟ್ ಮಾಡಿದ್ದೇನೆ ಹಿಂದೆನೇರವಾಗಿ, ಕ್ರಾಸಿಂಗ್ ಪಾಯಿಂಟ್‌ಗಳಲ್ಲಿ ಅದು ಹೇಗೆ ಸ್ವಲ್ಪ ಅಳಿಸಲ್ಪಟ್ಟಿದೆ ಎಂಬುದನ್ನು ನೋಡಿ. ಮಿಶ್ರ ತಳಿ? ಹೌದು, ಸಾಮಾನ್ಯವಾಗಿ, ನೇರ ರೇಖೆ "ಡಿ" ಅನ್ನು ಮೂಲ ನೇರ ರೇಖೆಗಳೊಂದಿಗೆ ದಾಟಲಾಗುತ್ತದೆ. ಈ ಕ್ಷಣದಲ್ಲಿ ನಮಗೆ ಆಸಕ್ತಿಯಿಲ್ಲದಿದ್ದರೂ, ನಾವು ಲಂಬವಾದ ರೇಖೆಯನ್ನು ನಿರ್ಮಿಸಬೇಕಾಗಿದೆ ಮತ್ತು ಅದು ಅಷ್ಟೆ.

ನೇರ "ಡಿ" ಬಗ್ಗೆ ಏನು ತಿಳಿದಿದೆ? ಅದಕ್ಕೆ ಸೇರಿದ ಬಿಂದು ಗೊತ್ತಾಗಿದೆ. ಸಾಕಷ್ಟು ಮಾರ್ಗದರ್ಶಿ ವೆಕ್ಟರ್ ಇಲ್ಲ.

ಸ್ಥಿತಿಯ ಪ್ರಕಾರ, ನೇರ ರೇಖೆಯು ನೇರ ರೇಖೆಗಳಿಗೆ ಲಂಬವಾಗಿರಬೇಕು, ಅಂದರೆ ಅದರ ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ಗಳಿಗೆ ಆರ್ಥೋಗೋನಲ್ ಆಗಿರುತ್ತದೆ. ಉದಾಹರಣೆ ಸಂಖ್ಯೆ 9 ರಿಂದ ಈಗಾಗಲೇ ಪರಿಚಿತವಾಗಿದೆ, ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:

ಬಿಂದು ಮತ್ತು ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ಅನ್ನು ಬಳಸಿಕೊಂಡು "ಡಿ" ನೇರ ರೇಖೆಯ ಸಮೀಕರಣಗಳನ್ನು ರಚಿಸೋಣ:

ಸಿದ್ಧವಾಗಿದೆ. ತಾತ್ವಿಕವಾಗಿ, ನೀವು ಛೇದಗಳಲ್ಲಿ ಚಿಹ್ನೆಗಳನ್ನು ಬದಲಾಯಿಸಬಹುದು ಮತ್ತು ರೂಪದಲ್ಲಿ ಉತ್ತರವನ್ನು ಬರೆಯಬಹುದು , ಆದರೆ ಇದರ ಅಗತ್ಯವಿಲ್ಲ.

ಪರಿಶೀಲಿಸಲು, ನೀವು ಪಾಯಿಂಟ್‌ನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಪರಿಣಾಮವಾಗಿ ನೇರ ರೇಖೆಯ ಸಮೀಕರಣಗಳಾಗಿ ಬದಲಿಸಬೇಕು, ನಂತರ ಬಳಸಿ ವಾಹಕಗಳ ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನವೆಕ್ಟರ್ "pe one" ಮತ್ತು "pe two" ದಿಕ್ಕಿನ ವೆಕ್ಟರ್‌ಗಳಿಗೆ ನಿಜವಾಗಿಯೂ ಆರ್ಥೋಗೋನಲ್ ಆಗಿದೆ ಎಂದು ಖಚಿತಪಡಿಸಿಕೊಳ್ಳಿ.

ಸಾಮಾನ್ಯ ಲಂಬವಾಗಿರುವ ರೇಖೆಯ ಸಮೀಕರಣಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಹೇಗೆ?

ಸಿ) ಈ ಸಮಸ್ಯೆಯು ಹೆಚ್ಚು ಕಷ್ಟಕರವಾಗಿರುತ್ತದೆ. ಡಮ್ಮೀಸ್ ಈ ಹಂತವನ್ನು ಬಿಟ್ಟುಬಿಡಬೇಕೆಂದು ನಾನು ಶಿಫಾರಸು ಮಾಡುತ್ತೇವೆ, ವಿಶ್ಲೇಷಣಾತ್ಮಕ ರೇಖಾಗಣಿತದ ಬಗ್ಗೆ ನಿಮ್ಮ ಪ್ರಾಮಾಣಿಕ ಸಹಾನುಭೂತಿಯನ್ನು ತಣ್ಣಗಾಗಲು ನಾನು ಬಯಸುವುದಿಲ್ಲ =) ಮೂಲಕ, ಹೆಚ್ಚು ಸಿದ್ಧಪಡಿಸಿದ ಓದುಗರು ಸಹ ತಡೆಹಿಡಿಯುವುದು ಉತ್ತಮವಾಗಿದೆ, ವಾಸ್ತವವೆಂದರೆ ಸಂಕೀರ್ಣತೆಯ ವಿಷಯದಲ್ಲಿ ಉದಾಹರಣೆಯಾಗಿದೆ ಲೇಖನದಲ್ಲಿ ಕೊನೆಯದಾಗಿ ಇಡಬೇಕು, ಆದರೆ ಪ್ರಸ್ತುತಿಯ ತರ್ಕದ ಪ್ರಕಾರ ಅದು ಇಲ್ಲಿ ನೆಲೆಗೊಂಡಿರಬೇಕು.

ಆದ್ದರಿಂದ, ಓರೆ ರೇಖೆಗಳ ಸಾಮಾನ್ಯ ಲಂಬವಾಗಿರುವ ರೇಖೆಯ ಸಮೀಕರಣಗಳನ್ನು ನೀವು ಕಂಡುಹಿಡಿಯಬೇಕು.

- ಇದು ಈ ಸಾಲುಗಳನ್ನು ಸಂಪರ್ಕಿಸುವ ಮತ್ತು ಈ ಸಾಲುಗಳಿಗೆ ಲಂಬವಾಗಿರುವ ಒಂದು ವಿಭಾಗವಾಗಿದೆ:

ಇಲ್ಲಿ ನಮ್ಮ ಸುಂದರ ವ್ಯಕ್ತಿ: - ಛೇದಿಸುವ ರೇಖೆಗಳ ಸಾಮಾನ್ಯ ಲಂಬ. ಅವನು ಒಬ್ಬನೇ. ಅದರಂತೆ ಮತ್ತೊಂದಿಲ್ಲ. ಈ ವಿಭಾಗವನ್ನು ಒಳಗೊಂಡಿರುವ ಸಾಲಿಗೆ ನಾವು ಸಮೀಕರಣಗಳನ್ನು ರಚಿಸಬೇಕಾಗಿದೆ.

ನೇರ "ಉಮ್" ಬಗ್ಗೆ ಏನು ತಿಳಿದಿದೆ? ಅದರ ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ತಿಳಿದಿದೆ, ಹಿಂದಿನ ಪ್ಯಾರಾಗ್ರಾಫ್ನಲ್ಲಿ ಕಂಡುಬರುತ್ತದೆ. ಆದರೆ, ದುರದೃಷ್ಟವಶಾತ್, "ಎಮ್" ಎಂಬ ಸರಳ ರೇಖೆಗೆ ಸೇರಿದ ಒಂದು ಬಿಂದುವೂ ನಮಗೆ ತಿಳಿದಿಲ್ಲ, ಅಥವಾ ಲಂಬವಾಗಿರುವ ಬಿಂದುಗಳ ತುದಿಗಳು ನಮಗೆ ತಿಳಿದಿಲ್ಲ. ಈ ಲಂಬ ರೇಖೆಯು ಎರಡು ಮೂಲ ರೇಖೆಗಳನ್ನು ಎಲ್ಲಿ ಛೇದಿಸುತ್ತದೆ? ಆಫ್ರಿಕಾದಲ್ಲಿ, ಅಂಟಾರ್ಟಿಕಾದಲ್ಲಿ? ಸ್ಥಿತಿಯ ಆರಂಭಿಕ ವಿಮರ್ಶೆ ಮತ್ತು ವಿಶ್ಲೇಷಣೆಯಿಂದ, ಸಮಸ್ಯೆಯನ್ನು ಹೇಗೆ ಪರಿಹರಿಸುವುದು ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿಲ್ಲ. ಆದರೆ ಸರಳ ರೇಖೆಯ ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ಸಮೀಕರಣಗಳ ಬಳಕೆಗೆ ಸಂಬಂಧಿಸಿದ ಒಂದು ಟ್ರಿಕಿ ಟ್ರಿಕ್ ಇದೆ.

ನಾವು ನಿರ್ಧಾರವನ್ನು ಪಾಯಿಂಟ್ ಮೂಲಕ ರೂಪಿಸುತ್ತೇವೆ:

1) ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ರೂಪದಲ್ಲಿ ಮೊದಲ ಸಾಲಿನ ಸಮೀಕರಣಗಳನ್ನು ಪುನಃ ಬರೆಯೋಣ:

ಬಿಂದುವನ್ನು ಪರಿಗಣಿಸೋಣ. ನಮಗೆ ನಿರ್ದೇಶಾಂಕಗಳು ತಿಳಿದಿಲ್ಲ. ಆದರೆ. ಒಂದು ಬಿಂದುವು ನಿರ್ದಿಷ್ಟ ಸಾಲಿಗೆ ಸೇರಿದ್ದರೆ, ಅದರ ನಿರ್ದೇಶಾಂಕಗಳು ಗೆ ಸಂಬಂಧಿಸಿವೆ, ನಾವು ಅದನ್ನು ಸೂಚಿಸೋಣ. ನಂತರ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ರೂಪದಲ್ಲಿ ಬರೆಯಲಾಗುತ್ತದೆ:

ಜೀವನವು ಉತ್ತಮಗೊಳ್ಳುತ್ತಿದೆ, ಒಬ್ಬ ಅಪರಿಚಿತ ಇನ್ನೂ ಮೂರು ಅಪರಿಚಿತನಲ್ಲ.

2) ಎರಡನೇ ಅಂಶದ ಮೇಲೆ ಅದೇ ಆಕ್ರೋಶವನ್ನು ನಡೆಸಬೇಕು. ಎರಡನೇ ಸಾಲಿನ ಸಮೀಕರಣಗಳನ್ನು ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ರೂಪದಲ್ಲಿ ಪುನಃ ಬರೆಯೋಣ:

ಒಂದು ಬಿಂದುವು ನಿರ್ದಿಷ್ಟ ಸಾಲಿಗೆ ಸೇರಿದ್ದರೆ, ಆಗ ಒಂದು ನಿರ್ದಿಷ್ಟ ಅರ್ಥದೊಂದಿಗೆಅದರ ನಿರ್ದೇಶಾಂಕಗಳು ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ಸಮೀಕರಣಗಳನ್ನು ಪೂರೈಸಬೇಕು:

ಅಥವಾ:

3) ವೆಕ್ಟರ್, ಹಿಂದೆ ಕಂಡುಕೊಂಡ ವೆಕ್ಟರ್‌ನಂತೆ, ನೇರ ರೇಖೆಯ ನಿರ್ದೇಶನ ವೆಕ್ಟರ್ ಆಗಿರುತ್ತದೆ. ಎರಡು ಬಿಂದುಗಳಿಂದ ವೆಕ್ಟರ್ ಅನ್ನು ಹೇಗೆ ನಿರ್ಮಿಸುವುದು ಎಂದು ತರಗತಿಯಲ್ಲಿ ಅನಾದಿ ಕಾಲದಲ್ಲಿ ಚರ್ಚಿಸಲಾಗಿದೆ ಡಮ್ಮೀಸ್‌ಗಾಗಿ ವೆಕ್ಟರ್‌ಗಳು. ಈಗ ವ್ಯತ್ಯಾಸವೆಂದರೆ ವೆಕ್ಟರ್‌ಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಅಜ್ಞಾತ ನಿಯತಾಂಕ ಮೌಲ್ಯಗಳೊಂದಿಗೆ ಬರೆಯಲಾಗಿದೆ. ಏನೀಗ? ವೆಕ್ಟರ್‌ನ ಪ್ರಾರಂಭದ ಅನುಗುಣವಾದ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ವೆಕ್ಟರ್‌ನ ಅಂತ್ಯದ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ ಕಳೆಯುವುದನ್ನು ಯಾರೂ ನಿಷೇಧಿಸುವುದಿಲ್ಲ.

ಎರಡು ಅಂಶಗಳಿವೆ: .

ವೆಕ್ಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯುವುದು:

4) ದಿಕ್ಕಿನ ವೆಕ್ಟರ್‌ಗಳು ಕಾಲಿನಿಯರ್ ಆಗಿರುವುದರಿಂದ, ಒಂದು ವೆಕ್ಟರ್ ಅನ್ನು ರೇಖೀಯವಾಗಿ ಇನ್ನೊಂದರ ಮೂಲಕ ನಿರ್ದಿಷ್ಟ ಅನುಪಾತದ ಗುಣಾಂಕ "ಲ್ಯಾಂಬ್ಡಾ" ನೊಂದಿಗೆ ವ್ಯಕ್ತಪಡಿಸಲಾಗುತ್ತದೆ:

ಅಥವಾ ಸಮನ್ವಯದಿಂದ ನಿರ್ದೇಶಾಂಕ:

ಇದು ಅತ್ಯಂತ ಸಾಮಾನ್ಯವಾಗಿದೆ ಎಂದು ಬದಲಾಯಿತು ರೇಖೀಯ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಮೂರು ಅಪರಿಚಿತರೊಂದಿಗೆ, ಇದು ಪ್ರಮಾಣಿತವಾಗಿ ಪರಿಹರಿಸಬಹುದಾದ, ಉದಾಹರಣೆಗೆ, ಕ್ರಾಮರ್ ವಿಧಾನ. ಆದರೆ ಇಲ್ಲಿ ಸ್ವಲ್ಪ ನಷ್ಟದಿಂದ ಹೊರಬರಲು ಸಾಧ್ಯವಿದೆ; ಮೂರನೇ ಸಮೀಕರಣದಿಂದ ನಾವು "ಲ್ಯಾಂಬ್ಡಾ" ಅನ್ನು ವ್ಯಕ್ತಪಡಿಸುತ್ತೇವೆ ಮತ್ತು ಅದನ್ನು ಮೊದಲ ಮತ್ತು ಎರಡನೆಯ ಸಮೀಕರಣಗಳಾಗಿ ಬದಲಿಸುತ್ತೇವೆ:

ಹೀಗೆ: , ಮತ್ತು ನಮಗೆ "ಲ್ಯಾಂಬ್ಡಾ" ಅಗತ್ಯವಿಲ್ಲ. ನಿಯತಾಂಕದ ಮೌಲ್ಯಗಳು ಒಂದೇ ಆಗಿವೆ ಎಂಬ ಅಂಶವು ಸಂಪೂರ್ಣವಾಗಿ ಅಪಘಾತವಾಗಿದೆ.

5) ಆಕಾಶವು ಸಂಪೂರ್ಣವಾಗಿ ತೆರವುಗೊಳಿಸುತ್ತಿದೆ, ನಾವು ಕಂಡುಕೊಂಡ ಮೌಲ್ಯಗಳನ್ನು ಬದಲಿಸೋಣ ನಮ್ಮ ಅಂಕಗಳಿಗೆ:

ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ನಿರ್ದಿಷ್ಟವಾಗಿ ಅಗತ್ಯವಿಲ್ಲ, ಏಕೆಂದರೆ ಅದರ ಪ್ರತಿರೂಪವು ಈಗಾಗಲೇ ಕಂಡುಬಂದಿದೆ.

ದೀರ್ಘ ಪ್ರಯಾಣದ ನಂತರ ಪರಿಶೀಲಿಸಲು ಯಾವಾಗಲೂ ಆಸಕ್ತಿದಾಯಕವಾಗಿದೆ.

:

ಸರಿಯಾದ ಸಮಾನತೆಗಳನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ.

ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಸಮೀಕರಣಗಳಾಗಿ ಬದಲಿಸೋಣ :

ಸರಿಯಾದ ಸಮಾನತೆಗಳನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ.

6) ಅಂತಿಮ ಸ್ವರಮೇಳ: ಒಂದು ಬಿಂದು (ನೀವು ಅದನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು) ಮತ್ತು ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ಅನ್ನು ಬಳಸಿಕೊಂಡು ಸರಳ ರೇಖೆಯ ಸಮೀಕರಣಗಳನ್ನು ರಚಿಸೋಣ:

ತಾತ್ವಿಕವಾಗಿ, ನೀವು ಅಖಂಡ ನಿರ್ದೇಶಾಂಕಗಳೊಂದಿಗೆ "ಉತ್ತಮ" ಬಿಂದುವನ್ನು ಆಯ್ಕೆ ಮಾಡಬಹುದು, ಆದರೆ ಇದು ಕಾಸ್ಮೆಟಿಕ್ ಆಗಿದೆ.

ಛೇದಿಸುವ ರೇಖೆಗಳ ನಡುವಿನ ಅಂತರವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಹೇಗೆ?

ಡಿ) ನಾವು ಡ್ರ್ಯಾಗನ್‌ನ ನಾಲ್ಕನೇ ತಲೆಯನ್ನು ಕತ್ತರಿಸಿದ್ದೇವೆ.

ವಿಧಾನ ಒಂದು. ಒಂದು ವಿಧಾನವೂ ಅಲ್ಲ, ಆದರೆ ಒಂದು ಸಣ್ಣ ವಿಶೇಷ ಪ್ರಕರಣ. ದಾಟುವ ರೇಖೆಗಳ ನಡುವಿನ ಅಂತರವು ಅವುಗಳ ಸಾಮಾನ್ಯ ಲಂಬವಾಗಿರುವ ಉದ್ದಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ: .

ಸಾಮಾನ್ಯ ಲಂಬವಾದ ತೀವ್ರ ಬಿಂದುಗಳು ಹಿಂದಿನ ಪ್ಯಾರಾಗ್ರಾಫ್ನಲ್ಲಿ ಕಂಡುಬರುತ್ತದೆ, ಮತ್ತು ಕಾರ್ಯವು ಪ್ರಾಥಮಿಕವಾಗಿದೆ:

ವಿಧಾನ ಎರಡು. ಪ್ರಾಯೋಗಿಕವಾಗಿ, ಸಾಮಾನ್ಯವಾಗಿ ಸಾಮಾನ್ಯ ಲಂಬವಾದ ತುದಿಗಳು ತಿಳಿದಿಲ್ಲ, ಆದ್ದರಿಂದ ವಿಭಿನ್ನ ವಿಧಾನವನ್ನು ಬಳಸಲಾಗುತ್ತದೆ. ಸಮಾನಾಂತರ ಸಮತಲಗಳನ್ನು ಎರಡು ಛೇದಿಸುವ ನೇರ ರೇಖೆಗಳ ಮೂಲಕ ಎಳೆಯಬಹುದು ಮತ್ತು ಈ ವಿಮಾನಗಳ ನಡುವಿನ ಅಂತರವು ಈ ನೇರ ರೇಖೆಗಳ ನಡುವಿನ ಅಂತರಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ನಿರ್ದಿಷ್ಟವಾಗಿ ಹೇಳುವುದಾದರೆ, ಈ ವಿಮಾನಗಳ ನಡುವೆ ಸಾಮಾನ್ಯ ಲಂಬವಾದ ಅಂಟಿಕೊಳ್ಳುತ್ತದೆ.

ವಿಶ್ಲೇಷಣಾತ್ಮಕ ರೇಖಾಗಣಿತದ ಸಂದರ್ಭದಲ್ಲಿ, ಮೇಲಿನ ಪರಿಗಣನೆಗಳಿಂದ, ಛೇದಿಸುವ ನೇರ ರೇಖೆಗಳ ನಡುವಿನ ಅಂತರವನ್ನು ಕಂಡುಹಿಡಿಯಲು ಸೂತ್ರವನ್ನು ಪಡೆಯಲಾಗಿದೆ:
(ನಮ್ಮ ಅಂಕಗಳ ಬದಲಿಗೆ "ಉಮ್ ಒಂದು, ಎರಡು" ನೀವು ಸಾಲುಗಳ ಅನಿಯಂತ್ರಿತ ಅಂಕಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು).

ವಾಹಕಗಳ ಮಿಶ್ರ ಉತ್ಪನ್ನ"a" ಪಾಯಿಂಟ್‌ನಲ್ಲಿ ಈಗಾಗಲೇ ಕಂಡುಬಂದಿದೆ: .

ವಾಹಕಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನ"ಆಗಿದೆ" ಪ್ಯಾರಾಗ್ರಾಫ್ನಲ್ಲಿ ಕಂಡುಬರುತ್ತದೆ: , ಅದರ ಉದ್ದವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡೋಣ:

ಹೀಗೆ:

ಟ್ರೋಫಿಗಳನ್ನು ಒಂದೇ ಸಾಲಿನಲ್ಲಿ ಹೆಮ್ಮೆಯಿಂದ ಪ್ರದರ್ಶಿಸೋಣ:

ಉತ್ತರ:
ಎ) , ಅಂದರೆ ಸರಳ ರೇಖೆಗಳು ಛೇದಿಸುತ್ತವೆ, ಇದು ಸಾಬೀತುಪಡಿಸಲು ಅಗತ್ಯವಾಗಿತ್ತು;
b) ;
ವಿ) ;
ಜಿ)

ದಾಟುವ ರೇಖೆಗಳ ಬಗ್ಗೆ ನೀವು ಇನ್ನೇನು ಹೇಳಬಹುದು? ಅವುಗಳ ನಡುವೆ ಒಂದು ನಿರ್ದಿಷ್ಟ ಕೋನವಿದೆ. ಆದರೆ ಮುಂದಿನ ಪ್ಯಾರಾಗ್ರಾಫ್ನಲ್ಲಿ ನಾವು ಸಾರ್ವತ್ರಿಕ ಕೋನ ಸೂತ್ರವನ್ನು ಪರಿಗಣಿಸುತ್ತೇವೆ:

ನೇರ ಸ್ಥಳಗಳನ್ನು ಛೇದಿಸುವುದು ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಅಗತ್ಯವಾಗಿ ಇರುತ್ತದೆ:

ನಿಮ್ಮ ಎಲ್ಲಾ ಶಕ್ತಿಯೊಂದಿಗೆ ಛೇದಕ ಬಿಂದುವಿನ ಮೇಲೆ ಒಲವು ತೋರುವುದು ಮೊದಲ ಆಲೋಚನೆ. ಮತ್ತು ನಾನು ತಕ್ಷಣ ಯೋಚಿಸಿದೆ, ಸರಿಯಾದ ಆಸೆಗಳನ್ನು ನೀವೇ ಏಕೆ ನಿರಾಕರಿಸುತ್ತೀರಿ?! ಈಗಲೇ ಅವಳ ಮೇಲೆ ಬರೋಣ!

ಪ್ರಾದೇಶಿಕ ರೇಖೆಗಳ ಛೇದನದ ಬಿಂದುವನ್ನು ಹೇಗೆ ಕಂಡುಹಿಡಿಯುವುದು?

ಉದಾಹರಣೆ 14

ರೇಖೆಗಳ ಛೇದನದ ಬಿಂದುವನ್ನು ಹುಡುಕಿ

ಪರಿಹಾರ: ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ರೂಪದಲ್ಲಿ ಸಾಲುಗಳ ಸಮೀಕರಣಗಳನ್ನು ಪುನಃ ಬರೆಯೋಣ:

ಈ ಕಾರ್ಯವನ್ನು ಈ ಪಾಠದ ಉದಾಹರಣೆ ಸಂಖ್ಯೆ 7 ರಲ್ಲಿ ವಿವರವಾಗಿ ಚರ್ಚಿಸಲಾಗಿದೆ (ನೋಡಿ. ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ರೇಖೆಯ ಸಮೀಕರಣಗಳು) ಮತ್ತು ಮೂಲಕ, ನಾನು ಉದಾಹರಣೆ ಸಂಖ್ಯೆ 12 ರಿಂದ ನೇರ ರೇಖೆಗಳನ್ನು ಸ್ವತಃ ತೆಗೆದುಕೊಂಡಿದ್ದೇನೆ. ನಾನು ಸುಳ್ಳು ಹೇಳುವುದಿಲ್ಲ, ಹೊಸದರೊಂದಿಗೆ ಬರಲು ನಾನು ತುಂಬಾ ಸೋಮಾರಿಯಾಗಿದ್ದೇನೆ.

ಪರಿಹಾರವು ಪ್ರಮಾಣಿತವಾಗಿದೆ ಮತ್ತು ಛೇದಿಸುವ ರೇಖೆಗಳ ಸಾಮಾನ್ಯ ಲಂಬವಾಗಿರುವ ಸಮೀಕರಣಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ನಾವು ಪ್ರಯತ್ನಿಸುತ್ತಿರುವಾಗ ಈಗಾಗಲೇ ಎದುರಾಗಿದೆ.

ರೇಖೆಗಳ ಛೇದನದ ಬಿಂದುವು ರೇಖೆಗೆ ಸೇರಿದೆ, ಆದ್ದರಿಂದ ಅದರ ನಿರ್ದೇಶಾಂಕಗಳು ಈ ರೇಖೆಯ ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ಸಮೀಕರಣಗಳನ್ನು ಪೂರೈಸುತ್ತವೆ ಮತ್ತು ಅವುಗಳಿಗೆ ಅನುಗುಣವಾಗಿರುತ್ತವೆ ಒಂದು ನಿರ್ದಿಷ್ಟ ನಿಯತಾಂಕ ಮೌಲ್ಯ:

ಆದರೆ ಇದೇ ಹಂತವು ಎರಡನೇ ಸಾಲಿಗೆ ಸೇರಿದೆ, ಆದ್ದರಿಂದ:

ನಾವು ಅನುಗುಣವಾದ ಸಮೀಕರಣಗಳನ್ನು ಸಮೀಕರಿಸುತ್ತೇವೆ ಮತ್ತು ಸರಳೀಕರಣಗಳನ್ನು ಕೈಗೊಳ್ಳುತ್ತೇವೆ:

ಎರಡು ಅಜ್ಞಾತಗಳೊಂದಿಗೆ ಮೂರು ರೇಖೀಯ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಯನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ. ಸಾಲುಗಳು ಛೇದಿಸಿದರೆ (ಉದಾಹರಣೆ ಸಂಖ್ಯೆ 12 ರಲ್ಲಿ ಇದು ಸಾಬೀತಾಗಿದೆ), ನಂತರ ಸಿಸ್ಟಮ್ ಅಗತ್ಯವಾಗಿ ಸ್ಥಿರವಾಗಿರುತ್ತದೆ ಮತ್ತು ಅನನ್ಯ ಪರಿಹಾರವನ್ನು ಹೊಂದಿದೆ. ಅದನ್ನು ಪರಿಹರಿಸಬಹುದು ಗಾಸಿಯನ್ ವಿಧಾನ, ಆದರೆ ಅಂತಹ ಶಿಶುವಿಹಾರದ ಮಾಂತ್ರಿಕತೆಯೊಂದಿಗೆ ನಾವು ಪಾಪ ಮಾಡುವುದಿಲ್ಲ, ನಾವು ಅದನ್ನು ಸರಳವಾಗಿ ಮಾಡುತ್ತೇವೆ: ಮೊದಲ ಸಮೀಕರಣದಿಂದ ನಾವು "ಟಿ ಸೊನ್ನೆ" ಅನ್ನು ವ್ಯಕ್ತಪಡಿಸುತ್ತೇವೆ ಮತ್ತು ಅದನ್ನು ಎರಡನೇ ಮತ್ತು ಮೂರನೇ ಸಮೀಕರಣಗಳಾಗಿ ಬದಲಿಸುತ್ತೇವೆ:

ಕೊನೆಯ ಎರಡು ಸಮೀಕರಣಗಳು ಮೂಲಭೂತವಾಗಿ ಒಂದೇ ಆಗಿವೆ, ಮತ್ತು ಅದು ಅವರಿಂದ ಅನುಸರಿಸುತ್ತದೆ . ನಂತರ:

ನಿಯತಾಂಕದ ಕಂಡುಬರುವ ಮೌಲ್ಯವನ್ನು ಸಮೀಕರಣಗಳಾಗಿ ಬದಲಿಸೋಣ:

ಉತ್ತರ:

ಪರಿಶೀಲಿಸಲು, ನಾವು ನಿಯತಾಂಕದ ಕಂಡುಬರುವ ಮೌಲ್ಯವನ್ನು ಸಮೀಕರಣಗಳಾಗಿ ಬದಲಿಸುತ್ತೇವೆ:
ಪರಿಶೀಲಿಸಬೇಕಾದ ಅದೇ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಪಡೆಯಲಾಗಿದೆ. ನಿಖರವಾದ ಓದುಗರು ಪಾಯಿಂಟ್‌ನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ರೇಖೆಗಳ ಮೂಲ ಅಂಗೀಕೃತ ಸಮೀಕರಣಗಳಾಗಿ ಬದಲಿಸಬಹುದು.

ಮೂಲಕ, ಇದಕ್ಕೆ ವಿರುದ್ಧವಾಗಿ ಮಾಡಲು ಸಾಧ್ಯವಾಯಿತು: "es zero" ಮೂಲಕ ಪಾಯಿಂಟ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ ಮತ್ತು ಅದನ್ನು "te zero" ಮೂಲಕ ಪರಿಶೀಲಿಸಿ.

ಪ್ರಸಿದ್ಧ ಗಣಿತದ ಮೂಢನಂಬಿಕೆಯು ಹೇಳುತ್ತದೆ: ಅಲ್ಲಿ ರೇಖೆಗಳ ಛೇದನವನ್ನು ಚರ್ಚಿಸಲಾಗಿದೆ, ಯಾವಾಗಲೂ ಲಂಬವಾಗಿರುವ ವಾಸನೆ ಇರುತ್ತದೆ.

ಕೊಟ್ಟಿರುವ ಒಂದಕ್ಕೆ ಲಂಬವಾಗಿರುವ ಜಾಗದ ರೇಖೆಯನ್ನು ಹೇಗೆ ನಿರ್ಮಿಸುವುದು?

(ರೇಖೆಗಳು ಛೇದಿಸುತ್ತವೆ)

ಉದಾಹರಣೆ 15

ಎ) ರೇಖೆಗೆ ಲಂಬವಾಗಿರುವ ಬಿಂದುವಿನ ಮೂಲಕ ಹಾದುಹೋಗುವ ರೇಖೆಯ ಸಮೀಕರಣಗಳನ್ನು ಬರೆಯಿರಿ (ರೇಖೆಗಳು ಛೇದಿಸುತ್ತವೆ).

ಬಿ) ಬಿಂದುವಿನಿಂದ ರೇಖೆಯ ಅಂತರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.

ಸೂಚನೆ : ಷರತ್ತು "ರೇಖೆಗಳು ಛೇದಿಸುತ್ತವೆ" - ಗಮನಾರ್ಹ. ಪಾಯಿಂಟ್ ಮೂಲಕ
"el" ನೇರ ರೇಖೆಯೊಂದಿಗೆ ಛೇದಿಸುವ ಅನಂತ ಸಂಖ್ಯೆಯ ಲಂಬ ರೇಖೆಗಳನ್ನು ನೀವು ಸೆಳೆಯಬಹುದು. ನಿರ್ದಿಷ್ಟ ಬಿಂದುವಿಗೆ ಲಂಬವಾಗಿರುವ ನೇರ ರೇಖೆಯನ್ನು ಎಳೆಯುವಾಗ ಮಾತ್ರ ಪರಿಹಾರವು ಸಂಭವಿಸುತ್ತದೆ ಎರಡುನೇರ ರೇಖೆಯಿಂದ ನೀಡಲಾಗಿದೆ (ಉದಾಹರಣೆ ಸಂಖ್ಯೆ 13, ಪಾಯಿಂಟ್ "ಬಿ" ನೋಡಿ).

ಎ) ಪರಿಹಾರ: ನಾವು ಅಜ್ಞಾತ ರೇಖೆಯನ್ನು ಮೂಲಕ ಸೂಚಿಸುತ್ತೇವೆ. ಸ್ಕೀಮ್ಯಾಟಿಕ್ ಡ್ರಾಯಿಂಗ್ ಮಾಡೋಣ:

ನೇರ ರೇಖೆಯ ಬಗ್ಗೆ ಏನು ತಿಳಿದಿದೆ? ಸ್ಥಿತಿಯ ಪ್ರಕಾರ, ಒಂದು ಬಿಂದುವನ್ನು ನೀಡಲಾಗುತ್ತದೆ. ನೇರ ರೇಖೆಯ ಸಮೀಕರಣಗಳನ್ನು ಸಂಯೋಜಿಸಲು, ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಅವಶ್ಯಕ. ವೆಕ್ಟರ್ ಅಂತಹ ವೆಕ್ಟರ್ ಆಗಿ ಸಾಕಷ್ಟು ಸೂಕ್ತವಾಗಿದೆ, ಆದ್ದರಿಂದ ನಾವು ಅದನ್ನು ನಿಭಾಯಿಸುತ್ತೇವೆ. ಹೆಚ್ಚು ನಿಖರವಾಗಿ, ಕುತ್ತಿಗೆಯ ಸ್ಕ್ರಫ್ನಿಂದ ವೆಕ್ಟರ್ನ ಅಜ್ಞಾತ ಅಂತ್ಯವನ್ನು ತೆಗೆದುಕೊಳ್ಳೋಣ.

1) "ಎಲ್" ನೇರ ರೇಖೆಯ ಸಮೀಕರಣಗಳಿಂದ ಅದರ ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ಅನ್ನು ಹೊರತೆಗೆಯೋಣ ಮತ್ತು ಸಮೀಕರಣಗಳನ್ನು ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ರೂಪದಲ್ಲಿ ಪುನಃ ಬರೆಯೋಣ:

ಪಾಠದ ಸಮಯದಲ್ಲಿ ಈಗ ಮೂರನೇ ಬಾರಿಗೆ ಜಾದೂಗಾರನು ತನ್ನ ಟೋಪಿಯಿಂದ ಬಿಳಿ ಹಂಸವನ್ನು ಎಳೆಯುತ್ತಾನೆ ಎಂದು ಹಲವರು ಊಹಿಸಿದ್ದಾರೆ. ಅಜ್ಞಾತ ನಿರ್ದೇಶಾಂಕಗಳೊಂದಿಗೆ ಒಂದು ಬಿಂದುವನ್ನು ಪರಿಗಣಿಸಿ. ಪಾಯಿಂಟ್ ಆಗಿರುವುದರಿಂದ, ಅದರ ನಿರ್ದೇಶಾಂಕಗಳು "el" ನೇರ ರೇಖೆಯ ಪ್ಯಾರಾಮೆಟ್ರಿಕ್ ಸಮೀಕರಣಗಳನ್ನು ಪೂರೈಸುತ್ತವೆ ಮತ್ತು ಅವು ನಿರ್ದಿಷ್ಟ ನಿಯತಾಂಕ ಮೌಲ್ಯಕ್ಕೆ ಸಂಬಂಧಿಸಿವೆ:

ಅಥವಾ ಒಂದು ಸಾಲಿನಲ್ಲಿ:

2) ಸ್ಥಿತಿಯ ಪ್ರಕಾರ, ರೇಖೆಗಳು ಲಂಬವಾಗಿರಬೇಕು, ಆದ್ದರಿಂದ, ಅವುಗಳ ದಿಕ್ಕಿನ ವಾಹಕಗಳು ಆರ್ಥೋಗೋನಲ್ ಆಗಿರುತ್ತವೆ. ಮತ್ತು ವಾಹಕಗಳು ಆರ್ಥೋಗೋನಲ್ ಆಗಿದ್ದರೆ, ನಂತರ ಅವರ ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನಶೂನ್ಯಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ:

ಏನಾಯಿತು? ಅಜ್ಞಾತ ಒಂದನ್ನು ಹೊಂದಿರುವ ಸರಳ ರೇಖೀಯ ಸಮೀಕರಣ:

3) ನಿಯತಾಂಕದ ಮೌಲ್ಯವು ತಿಳಿದಿದೆ, ನಾವು ಪಾಯಿಂಟ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:

ಮತ್ತು ದಿಕ್ಕಿನ ವೆಕ್ಟರ್:
.

4) ಬಿಂದು ಮತ್ತು ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ಅನ್ನು ಬಳಸಿಕೊಂಡು ಸರಳ ರೇಖೆಯ ಸಮೀಕರಣಗಳನ್ನು ರಚಿಸೋಣ:

ಅನುಪಾತದ ಛೇದಗಳು ಭಿನ್ನರಾಶಿಗಳಾಗಿ ಹೊರಹೊಮ್ಮಿದವು, ಮತ್ತು ಭಿನ್ನರಾಶಿಗಳನ್ನು ತೊಡೆದುಹಾಕಲು ಸೂಕ್ತವಾದಾಗ ಇದು ನಿಖರವಾಗಿ ಸಂಭವಿಸುತ್ತದೆ. ನಾನು ಅವುಗಳನ್ನು -2 ರಿಂದ ಗುಣಿಸುತ್ತೇನೆ:

ಉತ್ತರ:

ಸೂಚನೆ : ಪರಿಹಾರಕ್ಕೆ ಹೆಚ್ಚು ಕಠಿಣವಾದ ಅಂತ್ಯವನ್ನು ಈ ಕೆಳಗಿನಂತೆ ಔಪಚಾರಿಕಗೊಳಿಸಲಾಗಿದೆ: ಒಂದು ಬಿಂದು ಮತ್ತು ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ಅನ್ನು ಬಳಸಿಕೊಂಡು ಸರಳ ರೇಖೆಯ ಸಮೀಕರಣಗಳನ್ನು ರಚಿಸೋಣ. ವಾಸ್ತವವಾಗಿ, ವೆಕ್ಟರ್ ನೇರ ರೇಖೆಯ ಮಾರ್ಗದರ್ಶಕ ವೆಕ್ಟರ್ ಆಗಿದ್ದರೆ, ಕೊಲಿನಿಯರ್ ವೆಕ್ಟರ್, ಸ್ವಾಭಾವಿಕವಾಗಿ, ಈ ಸರಳ ರೇಖೆಯ ಮಾರ್ಗದರ್ಶಿ ವೆಕ್ಟರ್ ಆಗಿರುತ್ತದೆ.

ಪರಿಶೀಲನೆಯು ಎರಡು ಹಂತಗಳನ್ನು ಒಳಗೊಂಡಿದೆ:

1) ಆರ್ಥೋಗೋನಾಲಿಟಿಗಾಗಿ ರೇಖೆಗಳ ದಿಕ್ಕಿನ ವಾಹಕಗಳನ್ನು ಪರಿಶೀಲಿಸಿ;

2) ನಾವು ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಪ್ರತಿ ಸಾಲಿನ ಸಮೀಕರಣಗಳಾಗಿ ಬದಲಿಸುತ್ತೇವೆ, ಅವರು ಅಲ್ಲಿ ಮತ್ತು ಅಲ್ಲಿ ಎರಡೂ "ಹೊಂದಿಕೊಳ್ಳಬೇಕು".

ವಿಶಿಷ್ಟ ಕ್ರಿಯೆಗಳ ಕುರಿತು ಸಾಕಷ್ಟು ಚರ್ಚೆಗಳು ನಡೆದಿವೆ, ಆದ್ದರಿಂದ ನಾನು ಡ್ರಾಫ್ಟ್ ಅನ್ನು ಪರಿಶೀಲಿಸಿದೆ.

ಅಂದಹಾಗೆ, ನಾನು ಇನ್ನೊಂದು ಬಿಂದುವನ್ನು ಮರೆತಿದ್ದೇನೆ - "el" ಎಂಬ ನೇರ ರೇಖೆಗೆ ಹೋಲಿಸಿದರೆ "en" ಬಿಂದುವಿಗೆ ಸಮ್ಮಿತೀಯವಾಗಿ "zyu" ಬಿಂದುವನ್ನು ನಿರ್ಮಿಸಲು. ಆದಾಗ್ಯೂ, ಉತ್ತಮವಾದ "ಫ್ಲಾಟ್ ಅನಲಾಗ್" ಇದೆ, ಅದನ್ನು ಲೇಖನದಲ್ಲಿ ಕಾಣಬಹುದು ಸಮತಲದಲ್ಲಿ ನೇರ ರೇಖೆಯೊಂದಿಗೆ ಸರಳವಾದ ಸಮಸ್ಯೆಗಳು. ಇಲ್ಲಿ ವ್ಯತ್ಯಾಸವು ಹೆಚ್ಚುವರಿ "Z" ನಿರ್ದೇಶಾಂಕದಲ್ಲಿ ಮಾತ್ರ ಇರುತ್ತದೆ.

ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಒಂದು ಬಿಂದುವಿನಿಂದ ರೇಖೆಯ ಅಂತರವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಹೇಗೆ?

b) ಪರಿಹಾರ: ಒಂದು ಬಿಂದುವಿನಿಂದ ರೇಖೆಯ ಅಂತರವನ್ನು ಕಂಡುಹಿಡಿಯೋಣ.

ವಿಧಾನ ಒಂದು. ಈ ಅಂತರವು ಲಂಬವಾಗಿರುವ ಉದ್ದಕ್ಕೆ ನಿಖರವಾಗಿ ಸಮನಾಗಿರುತ್ತದೆ: . ಪರಿಹಾರವು ಸ್ಪಷ್ಟವಾಗಿದೆ: ಅಂಕಗಳು ತಿಳಿದಿದ್ದರೆ , ಅದು:

ವಿಧಾನ ಎರಡು. ಪ್ರಾಯೋಗಿಕ ಸಮಸ್ಯೆಗಳಲ್ಲಿ, ಲಂಬವಾದ ಮೂಲವು ಸಾಮಾನ್ಯವಾಗಿ ಮೊಹರು ರಹಸ್ಯವಾಗಿದೆ, ಆದ್ದರಿಂದ ಸಿದ್ಧ ಸೂತ್ರವನ್ನು ಬಳಸಲು ಇದು ಹೆಚ್ಚು ತರ್ಕಬದ್ಧವಾಗಿದೆ.

ಒಂದು ಬಿಂದುವಿನಿಂದ ರೇಖೆಯ ಅಂತರವನ್ನು ಸೂತ್ರದಿಂದ ವ್ಯಕ್ತಪಡಿಸಲಾಗುತ್ತದೆ:
, "el" ನೇರ ರೇಖೆಯ ನಿರ್ದೇಶನ ವೆಕ್ಟರ್ ಎಲ್ಲಿದೆ, ಮತ್ತು - ಉಚಿತನಿರ್ದಿಷ್ಟ ಸಾಲಿಗೆ ಸೇರಿದ ಬಿಂದು.

1) ರೇಖೆಯ ಸಮೀಕರಣಗಳಿಂದ ನಾವು ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ಮತ್ತು ಹೆಚ್ಚು ಪ್ರವೇಶಿಸಬಹುದಾದ ಬಿಂದುವನ್ನು ಹೊರತೆಗೆಯುತ್ತೇವೆ.

2) ಸ್ಥಿತಿಯಿಂದ ಪಾಯಿಂಟ್ ತಿಳಿದಿದೆ, ವೆಕ್ಟರ್ ಅನ್ನು ತೀಕ್ಷ್ಣಗೊಳಿಸಿ:

3) ಕಂಡುಹಿಡಿಯೋಣ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನಮತ್ತು ಅದರ ಉದ್ದವನ್ನು ಲೆಕ್ಕಹಾಕಿ:

4) ಮಾರ್ಗದರ್ಶಿ ವೆಕ್ಟರ್‌ನ ಉದ್ದವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಿ:

5) ಹೀಗಾಗಿ, ಒಂದು ಬಿಂದುವಿನಿಂದ ರೇಖೆಯ ಅಂತರ:

l1 ಮತ್ತು l2 ಸಾಲುಗಳು ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಇರದಿದ್ದರೆ ಅವುಗಳನ್ನು ಓರೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. a ಮತ್ತು b ಈ ರೇಖೆಗಳ ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ಆಗಿರಲಿ ಮತ್ತು M1 ಮತ್ತು M2 ಅಂಕಗಳು ಕ್ರಮವಾಗಿ l1 ಮತ್ತು l2 ರೇಖೆಗಳಿಗೆ ಸೇರಿರಲಿ.

ನಂತರ ವಾಹಕಗಳು a, b, M1M2> coplanar ಅಲ್ಲ, ಮತ್ತು ಆದ್ದರಿಂದ ಅವುಗಳ ಮಿಶ್ರಿತ ಉತ್ಪನ್ನವು ಶೂನ್ಯಕ್ಕೆ ಸಮನಾಗಿರುವುದಿಲ್ಲ, ಅಂದರೆ (a, b, M1M2>) =/= 0. ಸಂವಾದ ಹೇಳಿಕೆಯು ಸಹ ನಿಜವಾಗಿದೆ: ವೇಳೆ (a, b , M1M2> ) =/= 0, ನಂತರ ವೆಕ್ಟರ್‌ಗಳು a, b, M1M2> ಕಾಪ್ಲಾನರ್ ಆಗಿರುವುದಿಲ್ಲ ಮತ್ತು ಆದ್ದರಿಂದ, l1 ​​ಮತ್ತು l2 ರೇಖೆಗಳು ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಇರುವುದಿಲ್ಲ, ಅಂದರೆ ಅವು ಛೇದಿಸುತ್ತವೆ. ಹೀಗಾಗಿ, ಎರಡು ಸಾಲುಗಳು ಛೇದಿಸುತ್ತವೆ. ಪರಿಸ್ಥಿತಿ (a, b, M1M2>) =/= 0, ಇಲ್ಲಿ a ಮತ್ತು b ರೇಖೆಗಳ ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ಆಗಿದ್ದರೆ ಮತ್ತು M1 ಮತ್ತು M2 ಕ್ರಮವಾಗಿ ಈ ಸಾಲುಗಳಿಗೆ ಸೇರಿದ ಬಿಂದುಗಳಾಗಿವೆ. ಷರತ್ತು (a, b, M1M2>) = 0 ರೇಖೆಗಳು ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಇರುವುದಕ್ಕೆ ಅಗತ್ಯವಾದ ಮತ್ತು ಸಾಕಷ್ಟು ಸ್ಥಿತಿಯಾಗಿದೆ. ರೇಖೆಗಳನ್ನು ಅವುಗಳ ಅಂಗೀಕೃತ ಸಮೀಕರಣಗಳಿಂದ ನೀಡಿದರೆ

ನಂತರ a = (a1; a2; a3), b = (b1; b2; b3), M1 (x1; y1; z1), M2(x2; y2; z2) ಮತ್ತು ಷರತ್ತು (2) ಅನ್ನು ಈ ಕೆಳಗಿನಂತೆ ಬರೆಯಲಾಗಿದೆ:

ದಾಟುವ ರೇಖೆಗಳ ನಡುವಿನ ಅಂತರ

ಇದು ಛೇದಿಸುವ ರೇಖೆಗಳಲ್ಲಿ ಒಂದು ಮತ್ತು ಅದಕ್ಕೆ ಸಮಾನಾಂತರವಾಗಿರುವ ಸಮತಲದ ನಡುವಿನ ಅಂತರವಾಗಿದೆ, ಇನ್ನೊಂದು ರೇಖೆಯ ಮೂಲಕ ಹಾದುಹೋಗುತ್ತದೆ, ಛೇದಿಸುವ ರೇಖೆಗಳ ನಡುವಿನ ಅಂತರವು ಛೇದಿಸುವ ರೇಖೆಗಳ ಕೆಲವು ಬಿಂದುವಿನಿಂದ ಮೊದಲನೆಯದಕ್ಕೆ ಸಮಾನಾಂತರವಾಗಿ ಮತ್ತೊಂದು ರೇಖೆಯ ಮೂಲಕ ಹಾದುಹೋಗುವ ಸಮತಲಕ್ಕೆ ಇರುವ ಅಂತರವಾಗಿದೆ. ಸಾಲು.

26. ದೀರ್ಘವೃತ್ತದ ವ್ಯಾಖ್ಯಾನ, ಅಂಗೀಕೃತ ಸಮೀಕರಣ. ಅಂಗೀಕೃತ ಸಮೀಕರಣದ ವ್ಯುತ್ಪನ್ನ. ಗುಣಲಕ್ಷಣಗಳು.

ದೀರ್ಘವೃತ್ತವು ಸಮತಲದ ಮೇಲಿನ ಬಿಂದುಗಳ ಜ್ಯಾಮಿತೀಯ ಸ್ಥಳವಾಗಿದೆ, ಇದಕ್ಕಾಗಿ ಈ ಸಮತಲದ ಎರಡು ಕೇಂದ್ರೀಕೃತ ಬಿಂದುಗಳಿಗೆ ದೂರದ ಮೊತ್ತ F1 ಮತ್ತು F2 ಸ್ಥಿರ ಮೌಲ್ಯವಾಗಿದೆ, ಈ ಸಂದರ್ಭದಲ್ಲಿ, ದೀರ್ಘವೃತ್ತದ ಫೋಸಿಯ ಕಾಕತಾಳೀಯತೆ ಹೊರಗಿಡಲಾಗಿಲ್ಲ. ಸುವಾಸನೆಗಳು ಹೊಂದಿಕೆಯಾದರೆ, ದೀರ್ಘವೃತ್ತವು ವೃತ್ತವಾಗಿದೆ. ಯಾವುದೇ ದೀರ್ಘವೃತ್ತಕ್ಕೆ ನೀವು ಕಾರ್ಟೇಶಿಯನ್ ಅನ್ನು ಒಂದು ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯನ್ನು ಕಾಣಬಹುದು, ಉದಾಹರಣೆಗೆ ದೀರ್ಘವೃತ್ತವನ್ನು ಸಮೀಕರಣದಿಂದ ವಿವರಿಸಲಾಗುತ್ತದೆ (ದೀರ್ಘವೃತ್ತದ ಅಂಗೀಕೃತ ಸಮೀಕರಣ):

ಇದು ಮೂಲದಲ್ಲಿ ಕೇಂದ್ರೀಕೃತವಾಗಿರುವ ದೀರ್ಘವೃತ್ತವನ್ನು ವಿವರಿಸುತ್ತದೆ, ಅದರ ಅಕ್ಷಗಳು ನಿರ್ದೇಶಾಂಕ ಅಕ್ಷಗಳೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾಗುತ್ತವೆ.

ಬಲಭಾಗದಲ್ಲಿ ಮೈನಸ್ ಚಿಹ್ನೆಯೊಂದಿಗೆ ಘಟಕವಿದ್ದರೆ, ಪರಿಣಾಮವಾಗಿ ಸಮೀಕರಣವು ಹೀಗಿರುತ್ತದೆ:

ಕಾಲ್ಪನಿಕ ದೀರ್ಘವೃತ್ತವನ್ನು ವಿವರಿಸುತ್ತದೆ. ನೈಜ ಸಮತಲದಲ್ಲಿ ಅಂತಹ ದೀರ್ಘವೃತ್ತವನ್ನು ಚಿತ್ರಿಸುವುದು ಅಸಾಧ್ಯ.ನಾವು F1 ಮತ್ತು F2 ನಿಂದ ಫೋಸಿಯನ್ನು ಸೂಚಿಸೋಣ, ಮತ್ತು ಅವುಗಳ ನಡುವಿನ ಅಂತರವನ್ನು 2c ಯಿಂದ ಸೂಚಿಸೋಣ ಮತ್ತು ದೀರ್ಘವೃತ್ತದ ಅನಿಯಂತ್ರಿತ ಬಿಂದುವಿನಿಂದ ಫೋಸಿಗೆ ಇರುವ ಅಂತರಗಳ ಮೊತ್ತವನ್ನು 2a ಯಿಂದ ಸೂಚಿಸೋಣ.

ದೀರ್ಘವೃತ್ತದ ಸಮೀಕರಣವನ್ನು ಪಡೆಯಲು, ನಾವು ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯನ್ನು Oxy ಅನ್ನು ಆರಿಸಿಕೊಳ್ಳುತ್ತೇವೆ ಇದರಿಂದ foci F1 ಮತ್ತು F2 ಆಕ್ಸ್ ಅಕ್ಷದ ಮೇಲೆ ಇರುತ್ತದೆ ಮತ್ತು ಮೂಲವು F1F2 ವಿಭಾಗದ ಮಧ್ಯದಲ್ಲಿ ಹೊಂದಿಕೆಯಾಗುತ್ತದೆ. ನಂತರ foci ಕೆಳಗಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ: ಮತ್ತು M(x;y) ದೀರ್ಘವೃತ್ತದ ಅನಿಯಂತ್ರಿತ ಬಿಂದುವಾಗಿರಲಿ. ನಂತರ, ದೀರ್ಘವೃತ್ತದ ವ್ಯಾಖ್ಯಾನದ ಪ್ರಕಾರ, ಅಂದರೆ.

ಇದು ಮೂಲಭೂತವಾಗಿ, ದೀರ್ಘವೃತ್ತದ ಸಮೀಕರಣವಾಗಿದೆ.

27. ಹೈಪರ್ಬೋಲಾ, ಅಂಗೀಕೃತ ಸಮೀಕರಣದ ವ್ಯಾಖ್ಯಾನ. ಅಂಗೀಕೃತ ಸಮೀಕರಣದ ವ್ಯುತ್ಪನ್ನ. ಗುಣಲಕ್ಷಣಗಳು

ಹೈಪರ್ಬೋಲಾ ಎಂಬುದು ಸಮತಲದಲ್ಲಿನ ಬಿಂದುಗಳ ಜ್ಯಾಮಿತೀಯ ಸ್ಥಾನವಾಗಿದ್ದು, ಈ ಸಮತಲದ ಎರಡು ಸ್ಥಿರ ಬಿಂದುಗಳಿಗೆ ದೂರದಲ್ಲಿರುವ ವ್ಯತ್ಯಾಸದ ಸಂಪೂರ್ಣ ಮೌಲ್ಯವು ಫೋಸಿ ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ, ಇದು ಸ್ಥಿರ ಮೌಲ್ಯವಾಗಿದೆ. M(x;y) ಅನಿಯಂತ್ರಿತವಾಗಿರಲಿ ಹೈಪರ್ಬೋಲಾದ ಬಿಂದು. ನಂತರ, ಹೈಪರ್ಬೋಲಾದ ವ್ಯಾಖ್ಯಾನದ ಪ್ರಕಾರ |MF 1 – MF 2 |=2a ಅಥವಾ MF 1 – MF 2 =±2a,

28. ಪ್ಯಾರಾಬೋಲಾದ ವ್ಯಾಖ್ಯಾನ, ಅಂಗೀಕೃತ ಸಮೀಕರಣ. ಅಂಗೀಕೃತ ಸಮೀಕರಣದ ವ್ಯುತ್ಪನ್ನ. ಗುಣಲಕ್ಷಣಗಳು. ಪ್ಯಾರಾಬೋಲಾ ಎಂಬುದು ಸಮತಲದ HMT ಆಗಿದ್ದು, ಈ ಸಮತಲದ ಕೆಲವು ಸ್ಥಿರ ಬಿಂದು F ಗೆ ಇರುವ ಅಂತರವು ಕೆಲವು ಸ್ಥಿರ ಸರಳ ರೇಖೆಯ ಅಂತರಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಇದು ಪರಿಗಣನೆಯಲ್ಲಿರುವ ಸಮತಲದಲ್ಲಿದೆ. ಎಫ್ - ಪ್ಯಾರಾಬೋಲಾದ ಗಮನ; ಸ್ಥಿರ ರೇಖೆಯು ಪ್ಯಾರಾಬೋಲಾದ ಡೈರೆಕ್ಟ್ರಿಕ್ಸ್ ಆಗಿದೆ. r=d,

ಆರ್=; d=x+p/2; (x-p/2) 2 +y 2 =(x+p/2) 2 ; x 2 -xp+p 2 /4+y 2 =x 2 +px+p 2/4; ವೈ 2 =2px;

ಗುಣಲಕ್ಷಣಗಳು: 1. ಒಂದು ಪ್ಯಾರಾಬೋಲಾ ಸಮ್ಮಿತಿಯ ಅಕ್ಷವನ್ನು ಹೊಂದಿದೆ (ಪ್ಯಾರಾಬೋಲಾ ಆಕ್ಸಿಸ್); 2.ಎಲ್ಲಾ

ಪ್ಯಾರಾಬೋಲಾವು ಆಕ್ಸಿ ಪ್ಲೇನ್‌ನ ಬಲ ಅರ್ಧ ಸಮತಲದಲ್ಲಿ p>0 ನಲ್ಲಿ ಮತ್ತು ಎಡಭಾಗದಲ್ಲಿದೆ

ಒಂದು ವೇಳೆ p<0. 3.Директриса параболы, определяемая каноническим уравнением, имеет уравнение x= -p/2.