ऑनलाइन कॅल्क्युलेटर. दिलेल्या बिंदूवर फंक्शनच्या आलेखाला सरळ स्पर्शिकेचे समीकरण

व्युत्पन्नाचे चिन्ह आणि फंक्शनच्या मोनोटोनिसिटीचे स्वरूप यांच्यातील संबंध दर्शवित आहे.

कृपया खालील गोष्टींबद्दल अत्यंत सावधगिरी बाळगा. बघा, तुम्हाला काय दिले आहे त्याचे वेळापत्रक! कार्य किंवा त्याचे व्युत्पन्न

व्युत्पन्नाचा आलेख दिला तर, तर आपल्याला फक्त फंक्शन चिन्हे आणि शून्यांमध्ये रस असेल. आम्हाला तत्वतः कोणत्याही “टेकड्या” किंवा “पोकळ” मध्ये स्वारस्य नाही!

कार्य १.

आकृती मध्यांतरावर परिभाषित केलेल्या कार्याचा आलेख दर्शविते. पूर्णांक बिंदूंची संख्या निश्चित करा ज्यावर फंक्शनचे व्युत्पन्न ऋण आहे.

उपाय:

आकृतीमध्ये, कमी होणार्‍या कार्याचे क्षेत्र रंगात हायलाइट केले आहेत:

फंक्शनच्या या कमी होणाऱ्या प्रदेशांमध्ये 4 पूर्णांक मूल्ये असतात.

कार्य २.

आकृती मध्यांतरावर परिभाषित केलेल्या कार्याचा आलेख दर्शविते. फंक्शनच्या आलेखाची स्पर्शिका ज्या रेषेला समांतर आहे किंवा त्याच्याशी एकरूप आहे अशा बिंदूंची संख्या शोधा.

उपाय:

एकदा फंक्शनच्या आलेखाची स्पर्शिका एका सरळ रेषेशी समांतर (किंवा एकरूप) झाली (किंवा, जी समान आहे), उतार, शून्याच्या बरोबरीने, नंतर स्पर्शिकेला कोनीय गुणांक असतो.

याचा अर्थ असा होतो की स्पर्शिका अक्षाला समांतर असते, कारण उतार ही स्पर्शिकेच्या अक्षाकडे झुकण्याच्या कोनाची स्पर्शिका असते.

म्हणून, आम्हाला आलेखावर टोकाचे बिंदू (जास्तीत जास्त आणि किमान बिंदू) आढळतात - या बिंदूंवर आलेखाला स्पर्श करणारी फंक्शन्स अक्षाच्या समांतर असतील.

असे 4 गुण आहेत.

कार्य 3.

आकृती मध्यांतरावर परिभाषित केलेल्या फंक्शनच्या व्युत्पन्नाचा आलेख दर्शविते. फंक्शनच्या आलेखाची स्पर्शिका ज्या रेषेला समांतर आहे किंवा त्याच्याशी एकरूप आहे अशा बिंदूंची संख्या शोधा.

उपाय:

फंक्शनच्या आलेखाची स्पर्शिका उतार असलेल्या रेषेशी समांतर (किंवा एकरूप) असल्याने, स्पर्शिकेलाही उतार असतो.

या बदल्यात याचा अर्थ असा की स्पर्श बिंदूंवर.

म्हणून, आपण आलेखावरील किती बिंदूंचे समतुल्य ऑर्डिनेट आहे ते पाहतो.

तुम्ही बघू शकता, असे चार मुद्दे आहेत.

कार्य 4.

आकृती मध्यांतरावर परिभाषित केलेल्या कार्याचा आलेख दर्शविते. फंक्शनचे व्युत्पन्न 0 असलेल्या बिंदूंची संख्या शोधा.

उपाय:

डेरिव्हेटिव्ह एक्स्ट्रीम पॉइंट्सवर शून्याच्या बरोबरीचे आहे. आमच्याकडे त्यापैकी 4 आहेत:

कार्य 5.

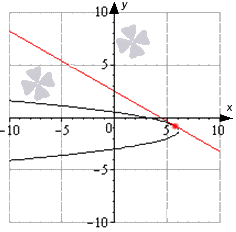
आकृती फंक्शनचा आलेख आणि x-अक्षावरील अकरा बिंदू दर्शवते:. यापैकी किती बिंदूंवर फंक्शनचे व्युत्पन्न ऋण असते?

उपाय:

घटत्या फंक्शनच्या अंतरावर, त्याचे व्युत्पन्न नकारात्मक मूल्ये घेते. आणि फंक्शन पॉइंट्सवर कमी होते. असे 4 गुण आहेत.

कार्य 6.

आकृती मध्यांतरावर परिभाषित केलेल्या कार्याचा आलेख दर्शविते. फंक्शनच्या एक्स्ट्रीम पॉइंट्सची बेरीज शोधा.

उपाय:

एक्स्ट्रीम पॉइंट्स- हे कमाल गुण (-3, -1, 1) आणि किमान गुण (-2, 0, 3) आहेत.

एक्स्ट्रीम पॉइंट्सची बेरीज: -3-1+1-2+0+3=-2.

कार्य 7.

आकृती मध्यांतरावर परिभाषित केलेल्या फंक्शनच्या व्युत्पन्नाचा आलेख दर्शविते. फंक्शनच्या वाढीचे अंतर शोधा. तुमच्या उत्तरामध्ये, या मध्यांतरांमध्ये समाविष्ट असलेल्या पूर्णांक बिंदूंची बेरीज दर्शवा.

उपाय:

आकृती मध्यांतरांना हायलाइट करते जेथे फंक्शनचे व्युत्पन्न गैर-ऋणात्मक आहे.

लहान वाढत्या मध्यांतरावर कोणतेही पूर्णांक बिंदू नाहीत; वाढत्या मध्यांतरावर चार पूर्णांक मूल्ये आहेत: , , आणि .

त्यांची बेरीज:

कार्य 8.

आकृती मध्यांतरावर परिभाषित केलेल्या फंक्शनच्या व्युत्पन्नाचा आलेख दर्शविते. फंक्शनच्या वाढीचे अंतर शोधा. तुमच्या उत्तरात, त्यापैकी सर्वात मोठ्याची लांबी दर्शवा.

उपाय:

आकृतीमध्ये, सर्व अंतराल ज्यावर व्युत्पन्न धनात्मक आहे ते रंगाने हायलाइट केले आहेत, याचा अर्थ या मध्यांतरांवर कार्य स्वतःच वाढते.

त्यापैकी सर्वात मोठ्याची लांबी 6 आहे.

कार्य ९.

आकृती मध्यांतरावर परिभाषित केलेल्या फंक्शनच्या व्युत्पन्नाचा आलेख दर्शविते. विभागातील कोणत्या टप्प्यावर ते सर्वात मोठे मूल्य घेते?

उपाय:

चला पाहू या सेगमेंटवर आलेख कसा वागतो, ज्यामध्ये आपल्याला स्वारस्य आहे केवळ व्युत्पन्नाचे चिन्ह .

व्युत्पन्न ऑनचे चिन्ह वजा आहे, कारण या विभागावरील आलेख अक्षाच्या खाली आहे.

फंक्शन f देऊ द्या, ज्यामध्ये काही बिंदू x 0 ला मर्यादित व्युत्पन्न f (x 0) असेल. नंतर बिंदू (x 0 ; f (x 0)) मधून जाणारी सरळ रेषा, कोनीय गुणांक f’ (x 0) असलेली, स्पर्शिका म्हणतात.

जर व्युत्पन्न x 0 बिंदूवर अस्तित्वात नसेल तर काय होईल? दोन पर्याय आहेत:

1. आलेखाला स्पर्शिकाही नाही. एक उत्कृष्ट उदाहरण म्हणजे फंक्शन y = |x | बिंदूवर (0; 0).
2. स्पर्शिका उभी होते. हे सत्य आहे, उदाहरणार्थ, बिंदूवर y = arcsin x फंक्शनसाठी (1; π /2).

स्पर्शिका समीकरण

कोणतीही अनुलंब सरळ रेषा y = kx + b या स्वरूपाच्या समीकरणाद्वारे दिली जाते, जेथे k हा उतार आहे. स्पर्शिका अपवाद नाही आणि त्याचे समीकरण x ० बिंदूवर तयार करण्यासाठी, या बिंदूवर फंक्शन आणि व्युत्पन्नाचे मूल्य जाणून घेणे पुरेसे आहे.

तर, एक फंक्शन y = f (x) देऊ, ज्याचे व्युत्पन्न y = f’ (x) खंडावर आहे. नंतर कोणत्याही बिंदूवर x 0 ∈ (a; b) या फंक्शनच्या आलेखावर स्पर्शिका काढली जाऊ शकते, जे समीकरणाद्वारे दिले जाते:

y = f’ (x 0) (x − x 0) + f (x 0)

येथे f’ (x 0) हे बिंदू x 0 वरील व्युत्पन्नाचे मूल्य आहे आणि f (x 0) हे फंक्शनचे मूल्य आहे.

कार्य. फंक्शन y = x 3 दिले आहे. x 0 = 2 बिंदूवर या फंक्शनच्या आलेखाच्या स्पर्शिकेसाठी समीकरण लिहा.

स्पर्शिका समीकरण: y = f’ (x 0) · (x − x 0) + f (x 0). बिंदू x 0 = 2 आपल्याला दिलेला आहे, परंतु f (x 0) आणि f’ (x 0) ही मूल्ये मोजावी लागतील.

प्रथम, फंक्शनची व्हॅल्यू शोधू. येथे सर्व काही सोपे आहे: f (x 0) = f (2) = 2 3 = 8;
आता व्युत्पन्न शोधू: f ’(x) = (x 3)’ = 3x 2;
आम्ही डेरिव्हेटिव्हमध्ये x 0 = 2 ला बदलतो: f’ (x 0) = f’ (2) = 3 2 2 = 12;
एकूण आपल्याला मिळते: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
हे स्पर्शिका समीकरण आहे.

कार्य. बिंदू x 0 = π /2 येथे f (x) = 2sin x + 5 या फंक्शनच्या आलेखाच्या स्पर्शिकेसाठी समीकरण लिहा.

यावेळी आम्ही प्रत्येक क्रियेचे तपशीलवार वर्णन करणार नाही - आम्ही फक्त मुख्य चरण सूचित करू. आमच्याकडे आहे:

f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f ’(x) = (2sin x + 5)’ = 2cos x;
f’ (x 0) = f’ (π /2) = 2cos (π /2) = 0;

स्पर्शिका समीकरण:

y = 0 · (x − π /2) + 7 ⇒ y = 7

नंतरच्या प्रकरणात, सरळ रेषा क्षैतिज असल्याचे बाहेर वळले, कारण त्याचे कोनीय गुणांक k = 0. यात काहीही चुकीचे नाही - आम्ही फक्त एका टोकाच्या बिंदूवर अडखळलो.

लेख व्याख्यांचे तपशीलवार स्पष्टीकरण, ग्राफिक नोटेशनसह व्युत्पन्नाचा भौमितीय अर्थ प्रदान करतो. स्पर्शरेषेचे समीकरण उदाहरणांसह विचारात घेतले जाईल, स्पर्शरेषेपासून दुसऱ्या क्रमाच्या वक्रांची समीकरणे सापडतील.

Yandex.RTB R-A-339285-1 व्याख्या 1

y = k x + b या सरळ रेषेच्या झुकावच्या कोनास कोन α म्हणतात, जो x अक्षाच्या सकारात्मक दिशेपासून सरळ रेषेपर्यंत y = k x + b या सकारात्मक दिशेने मोजला जातो.

आकृतीमध्ये, x दिशा हिरव्या बाणाने आणि हिरव्या कमानीने आणि लाल कमानीने झुकण्याचा कोन दर्शविला आहे. निळी रेषा सरळ रेषेला सूचित करते.

व्याख्या २

y = k x + b या सरळ रेषेच्या उताराला संख्यात्मक गुणांक k म्हणतात.

कोनीय गुणांक सरळ रेषेच्या स्पर्शिकेइतका असतो, दुसऱ्या शब्दांत k = t g α.

• सरळ रेषेच्या कलतेचा कोन ० च्या समान असेल तरच तो x च्या समांतर असेल आणि उतार शून्य असेल, कारण शून्याची स्पर्शिका ० असेल. याचा अर्थ समीकरणाचे स्वरूप y = b असेल.
• सरळ रेषेचा झुकाव कोन y = k x + b तीव्र असल्यास, अटी 0 पूर्ण होतात< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0, आणि आलेख मध्ये वाढ आहे.
• जर α = π 2 असेल, तर रेषेचे स्थान x ला लंब असेल. समानता x = c ने निर्दिष्‍ट केली आहे आणि c ही खरी संख्या आहे.
• y = k x + b या सरळ रेषेचा कलतेचा कोन स्थूल असेल तर तो π 2 च्या परिस्थितीशी जुळतो.< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

सेकंट म्हणजे फंक्शन f(x) च्या 2 बिंदूंमधून जाणारी रेषा. दुस-या शब्दात, सेकंट ही सरळ रेषा आहे जी दिलेल्या फंक्शनच्या आलेखावरील कोणत्याही दोन बिंदूंमधून काढली जाते.

आकृती दाखवते की A B एक सेकंट आहे, आणि f (x) एक काळा वक्र आहे, α लाल चाप आहे, जो सेकंटच्या झुकावचा कोन दर्शवितो.

जेव्हा सरळ रेषेचा कोनीय गुणांक झुकाव कोनाच्या स्पर्शिकेइतका असतो, तेव्हा हे स्पष्ट होते की काटकोन त्रिकोण A B C ची स्पर्शिका समीप बाजूच्या विरुद्ध बाजूच्या गुणोत्तराने शोधली जाऊ शकते.

व्याख्या 4

आम्हाला फॉर्मचा सीकंट शोधण्यासाठी एक सूत्र मिळते:

k = t g α = B C A C = f (x B) - f x A x B - x A, जेथे बिंदू A आणि B चे abscissas ही मूल्ये x A, x B, आणि f (x A), f (x) आहेत ब) या बिंदूंवरील मूल्यांची कार्ये आहेत.

स्पष्टपणे, सेकंटचा कोनीय गुणांक k = f (x B) - f (x A) x B - x A किंवा k = f (x A) - f (x B) x A - x B समानता वापरून निर्धारित केला जातो. , आणि समीकरण y = f (x B) - f (x A) x B - x A x - x A + f (x A) किंवा असे लिहिले पाहिजे
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

सेकंट आलेखाला दृष्यदृष्ट्या 3 भागांमध्ये विभाजित करतो: बिंदू A च्या डावीकडे, A पासून B पर्यंत, B च्या उजवीकडे. खालील आकृती दर्शवते की तीन भाग आहेत जे योगायोग मानले जातात, म्हणजेच ते a वापरून सेट केले जातात. समान समीकरण.

व्याख्येनुसार, हे स्पष्ट आहे की या प्रकरणात सरळ रेषा आणि त्याचा भाग एकरूप आहे.

सेकंट दिलेल्या फंक्शनचा आलेख अनेक वेळा छेदू शकतो. जर सेकंटसाठी y = 0 फॉर्मचे समीकरण असेल, तर सायनसॉइडसह छेदनबिंदूंच्या बिंदूंची संख्या अनंत आहे.

व्याख्या 5

बिंदू x 0 येथे फंक्शन f(x) च्या आलेखाला स्पर्शिका; f (x 0) ही दिलेल्या बिंदू x 0 मधून जाणारी सरळ रेषा आहे; f (x 0), x 0 च्या जवळ अनेक x मूल्ये असलेल्या खंडाच्या उपस्थितीसह.

उदाहरण १

खाली दिलेल्या उदाहरणावर बारकाईने नजर टाकूया. मग हे स्पष्ट होते की फंक्शन y = x + 1 द्वारे परिभाषित केलेली रेषा निर्देशांक (1; 2) सह बिंदूवर y = 2 x ला स्पर्शिका मानली जाते. स्पष्टतेसाठी, (1; 2) जवळील मूल्यांसह आलेख विचारात घेणे आवश्यक आहे. फंक्शन y = 2 x काळ्या रंगात दाखवले आहे, निळी रेषा स्पर्शरेषा आहे आणि लाल बिंदू छेदनबिंदू आहे.

अर्थात, y = 2 x y = x + 1 या रेषेत विलीन होते.

स्पर्शिका निश्चित करण्यासाठी, बिंदू B बिंदू A च्या जवळ येत असताना स्पर्शिका A B चे वर्तन विचारात घेतले पाहिजे. स्पष्टतेसाठी, आम्ही एक रेखाचित्र सादर करतो.

निळ्या रेषेने दर्शविलेले सीकंट A B, स्पर्शिकेच्याच स्थितीकडे झुकते आणि α चे झुकाव कोन स्पर्शिकेच्या स्वतःच्या α x कडे कलते.

व्याख्या 6

बिंदू A वरील फंक्शन y = f (x) च्या आलेखाची स्पर्शिका ही सीकंट A B चे मर्यादित स्थान मानली जाते कारण B हा A कडे झुकतो, म्हणजेच B → A.

आता एका बिंदूवर फंक्शनच्या व्युत्पन्नाचा भौमितिक अर्थ विचारात घेऊ.

चला f (x) फंक्शनसाठी सीकंट A B चा विचार करूया, जिथे A आणि B सह निर्देशांक x 0, f (x 0) आणि x 0 + ∆ x, f (x 0 + ∆ x), आणि ∆ x आहे युक्तिवादाची वाढ म्हणून दर्शविले जाते. आता फंक्शन ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) फॉर्म घेईल. स्पष्टतेसाठी, रेखांकनाचे उदाहरण देऊ.

परिणामी काटकोन त्रिकोण A B C विचारात घ्या. सोडवण्यासाठी आपण स्पर्शिकेची व्याख्या वापरतो, म्हणजेच आपल्याला ∆ y ∆ x = t g α हा संबंध प्राप्त होतो. स्पर्शिकेच्या व्याख्येवरून ते lim ∆ x → 0 ∆ y ∆ x = t g α x खालीलप्रमाणे आहे. एका बिंदूवरील व्युत्पन्नाच्या नियमानुसार, आपल्याकडे x 0 या बिंदूवरील व्युत्पन्न f(x) ला वितर्काच्या वाढीच्या फंक्शनच्या वाढीच्या गुणोत्तराची मर्यादा म्हणतात, जेथे ∆ x → 0 , नंतर आपण ते f (x 0) = lim ∆ x → 0 ∆ y ∆ x असे दर्शवू.

हे खालीलप्रमाणे आहे की f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, जेथे k x स्पर्शिकेचा उतार म्हणून दर्शविला जातो.

म्हणजेच, आम्हाला आढळले की f ' (x) बिंदू x 0 वर अस्तित्वात असू शकते आणि फंक्शनच्या दिलेल्या आलेखाप्रमाणे स्पर्शिकेच्या बिंदूवर x 0, f 0 (x 0) च्या बरोबरीचे मूल्य बिंदूवरील स्पर्शिकेचा उतार बिंदू x 0 वरील व्युत्पन्न बरोबर असतो. मग आपल्याला ते k x = f " (x 0) मिळेल.

एका बिंदूवर फंक्शनच्या व्युत्पन्नाचा भौमितिक अर्थ असा आहे की ते त्याच बिंदूवर आलेखाला स्पर्शिकेच्या अस्तित्वाची संकल्पना देते.

विमानावरील कोणत्याही सरळ रेषेचे समीकरण लिहिण्यासाठी, तो ज्या बिंदूतून जातो त्या बिंदूसह कोनीय गुणांक असणे आवश्यक आहे. त्याचे नोटेशन छेदनबिंदूवर x 0 मानले जाते.

x 0, f 0 (x 0) बिंदूवरील फंक्शन y = f (x) च्या आलेखाचे स्पर्शिका समीकरण y = f "(x 0) x - x 0 + f (x 0) असे रूप घेते.

याचा अर्थ असा की व्युत्पन्न f "(x 0) चे अंतिम मूल्य स्पर्शिकेचे स्थान निर्धारित करू शकते, म्हणजे, lim x → x 0 + 0 f "(x) = ∞ आणि lim x → x 0 - प्रदान केले आहे. 0 f "(x ) = ∞ किंवा अजिबात अनुपस्थिती lim x → x 0 + 0 f " (x) ≠ लिम x → x 0 - 0 f " (x) .

स्पर्शिकेचे स्थान त्याच्या कोनीय गुणांक k x = f "(x 0) च्या मूल्यावर अवलंबून असते. o x अक्षाच्या समांतर असताना, k k = 0, o y - k x = ∞ च्या समांतर असताना, आणि त्याचे स्वरूप स्पर्शिका समीकरण x = x 0 k x > 0 ने वाढते, k x म्हणून कमी होते< 0 .

उदाहरण २

y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 या बिंदूवर निर्देशांकांसह (1; 3) फंक्शनच्या आलेखासाठी स्पर्शिकेसाठी समीकरण संकलित करा आणि कलतेचा कोन निश्चित करा.

उपाय

अटीनुसार, आमच्याकडे फंक्शन सर्व वास्तविक संख्यांसाठी परिभाषित केले आहे. आम्हाला असे आढळून आले की अटी, (1; 3) द्वारे निर्दिष्ट केलेल्या निर्देशांकांसह बिंदू हा स्पर्शिकेचा बिंदू आहे, नंतर x 0 = - 1, f (x 0) = - 3.

मूल्य - 1 सह बिंदूवर व्युत्पन्न शोधणे आवश्यक आहे. आम्हाला ते मिळते

y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

स्पर्शिकेच्या बिंदूवर f'(x) चे मूल्य स्पर्शिकेचा उतार आहे, जो उताराच्या स्पर्शिकेइतका आहे.

नंतर k x = t g α x = y " (x 0) = 3 3

हे खालीलप्रमाणे आहे की α x = a r c t g 3 3 = π 6

उत्तर:स्पर्शिका समीकरण फॉर्म घेते

y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

स्पष्टतेसाठी, आम्ही ग्राफिक चित्रात एक उदाहरण देतो.

मूळ फंक्शनच्या आलेखासाठी काळा रंग वापरला जातो, निळा रंग स्पर्शिकेची प्रतिमा आहे आणि लाल बिंदू स्पर्शिकेचा बिंदू आहे. उजवीकडील आकृती एक मोठे दृश्य दर्शवते.

उदाहरण ३

दिलेल्या फंक्शनच्या आलेखाला स्पर्शिकेचे अस्तित्व निश्चित करा
y = 3 · x - 1 5 + 1 निर्देशांकासह बिंदूवर (1 ; 1) . एक समीकरण लिहा आणि झुकाव कोन निश्चित करा.

उपाय

अटीनुसार, दिलेल्या फंक्शनच्या व्याख्येचे डोमेन सर्व वास्तविक संख्यांचा संच मानले जाते.

चला व्युत्पन्न शोधण्यासाठी पुढे जाऊया

y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

जर x 0 = 1 असेल, तर f' (x) अपरिभाषित आहे, परंतु मर्यादा लिम x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 म्हणून लिहील्या आहेत · 1 + 0 = + ∞ आणि लिम x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , ज्याचा अर्थ बिंदूवर उभ्या स्पर्शिकेचे अस्तित्व (1; 1).

उत्तर:समीकरण x = 1 फॉर्म घेईल, जेथे झुकाव कोन π 2 असेल.

स्पष्टतेसाठी, ते ग्राफिक पद्धतीने चित्रित करूया.

उदाहरण ४

y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 फंक्शनच्या आलेखावरील बिंदू शोधा, जेथे

1. स्पर्शिका नाही;
2. स्पर्शिका x ला समांतर आहे;
3. स्पर्शिका y = 8 5 x + 4 या रेषेला समांतर आहे.

उपाय

व्याख्येच्या व्याप्तीकडे लक्ष देणे आवश्यक आहे. अटीनुसार, आमच्याकडे फंक्शन सर्व वास्तविक संख्यांच्या सेटवर परिभाषित केले आहे. आम्ही मॉड्यूल विस्तृत करतो आणि मध्यांतराने सिस्टम सोडवतो x ∈ - ∞ ; 2 आणि [ - 2 ; + ∞). आम्हाला ते मिळते

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)

फंक्शन वेगळे करणे आवश्यक आहे. आमच्याकडे ते आहे

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)

जेव्हा x = − 2, तेव्हा व्युत्पन्न अस्तित्वात नाही कारण त्या बिंदूवर एकतर्फी मर्यादा समान नसतात:

लिम x → - 2 - 0 y " (x) = लिम x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 लिम x → - 2 + 0 y " (x) = लिम x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

आपण x = - 2 या बिंदूवर फंक्शनचे मूल्य मोजतो, जिथे आपल्याला ते मिळते

1. y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, म्हणजेच बिंदूवरील स्पर्शिका ( - 2; - 2) अस्तित्वात नाही.
2. उतार शून्य असताना स्पर्शिका x ला समांतर असते. नंतर k x = t g α x = f "(x 0). म्हणजे, फंक्शनचे व्युत्पन्न जेव्हा शून्यावर वळते तेव्हा अशा x ची मूल्ये शोधणे आवश्यक आहे. म्हणजेच f ' ची मूल्ये. (x) स्पर्शिकेचे बिंदू असतील, जेथे स्पर्शिका x ला समांतर असते.

जेव्हा x ∈ - ∞ ; - 2, नंतर - 1 5 (x 2 + 12 x + 35) = 0, आणि x ∈ (- 2; + ∞) साठी आपल्याला 1 5 (x 2 - 4 x + 3) = 0 मिळेल.

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

संबंधित कार्य मूल्यांची गणना करा

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

म्हणून - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 हे फंक्शन आलेखाचे आवश्यक बिंदू मानले जातात.

चला सोल्यूशनचे ग्राफिकल प्रतिनिधित्व पाहू.

काळी रेषा फंक्शनचा आलेख आहे, लाल ठिपके स्पर्शिका बिंदू आहेत.

1. जेव्हा रेषा समांतर असतात, तेव्हा कोनीय गुणांक समान असतात. नंतर फंक्शन आलेखावरील बिंदू शोधणे आवश्यक आहे जेथे उतार 8 5 मूल्याच्या बरोबरीचा असेल. हे करण्यासाठी, तुम्हाला y "(x) = 8 5 फॉर्मचे समीकरण सोडवावे लागेल. नंतर, जर x ∈ - ∞; - 2 असेल, तर आम्हाला ते - 1 5 (x 2 + 12 x + 35) = 8 मिळेल. 5, आणि जर x ∈ ( - 2; + ∞), तर 1 5 (x 2 - 4 x + 3) = 8 5.

भेदभाव शून्यापेक्षा कमी असल्याने पहिल्या समीकरणाला मूळ नाही. चला ते लिहूया

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

दुसर्‍या समीकरणाची दोन खरी मुळे आहेत

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

फंक्शनची व्हॅल्यू शोधण्यासाठी पुढे जाऊ या. आम्हाला ते मिळते

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

मूल्यांसह गुण - 1; 4 15, 5; 8 3 हे बिंदू आहेत ज्यावर स्पर्शरेषा y = 8 5 x + 4 या रेषेच्या समांतर असतात.

उत्तर:काळी रेषा – फंक्शनचा आलेख, लाल रेषा – y चा आलेख = 8 5 x + 4, निळी रेषा – बिंदूंवरील स्पर्शिका - 1; 4 15, 5; ८ ३.

दिलेल्या फंक्शन्ससाठी अनंत संख्येने स्पर्शिका असू शकतात.

उदाहरण 5

y = 3 cos 3 2 x - π 4 - 1 3 फंक्शनच्या सर्व उपलब्ध स्पर्शिकेची समीकरणे लिहा, जी सरळ रेषेला लंब स्थित आहेत y = - 2 x + 1 2.

उपाय

स्पर्शिका समीकरण संकलित करण्यासाठी, रेषांच्या लंबाच्या स्थितीवर आधारित स्पर्शिका बिंदूचे गुणांक आणि समन्वय शोधणे आवश्यक आहे. व्याख्या खालीलप्रमाणे आहे: सरळ रेषांना लंब असलेल्या कोनीय गुणांकांचे गुणांक - 1 च्या बरोबरीचे आहे, म्हणजेच k x · k ⊥ = - 1 असे लिहिले आहे. स्थितीवरून आपल्याकडे कोनीय गुणांक रेषेला लंब स्थित आहे आणि k ⊥ = - 2 च्या समान आहे, नंतर k x = - 1 k ⊥ = - 1 - 2 = 1 2 आहे.

आता आपल्याला स्पर्श बिंदूंचे निर्देशांक शोधण्याची आवश्यकता आहे. दिलेल्या फंक्शनसाठी तुम्हाला x आणि नंतर त्याचे मूल्य शोधण्याची आवश्यकता आहे. बिंदूवरील व्युत्पन्नाच्या भूमितीय अर्थावरून लक्षात घ्या
x 0 आपल्याला k x = y "(x 0) मिळते. या समानतेवरून आपल्याला संपर्काच्या बिंदूंसाठी x ची मूल्ये सापडतात.

आम्हाला ते मिळते

y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - पाप 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 पाप 3 2 x 0 - π 4 3 2 = - 9 2 पाप 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 पाप 3 2 x 0 - π 4 = 1 2 ⇒ पाप 3 2 x 0 - π 4 = - 1 9

हे त्रिकोणमितीय समीकरण स्पर्शिका बिंदूंच्या निर्देशांकांची गणना करण्यासाठी वापरले जाईल.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk किंवा 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk किंवा 3 2 x 0 - π 4 = π + a r c पाप 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk किंवा x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z हा पूर्णांकांचा संच आहे.

संपर्काचे x बिंदू सापडले आहेत. आता तुम्हाला y ची मूल्ये शोधण्यासाठी पुढे जाण्याची आवश्यकता आहे:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - पाप 2 3 2 x 0 - π 4 - 1 3 किंवा y 0 = 3 - 1 - पाप 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 किंवा y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 किंवा y 0 = - 4 5 + 1 3

यावरून आपल्याला प्राप्त होते की 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 हे स्पर्शिकेचे बिंदू आहेत.

उत्तर:आवश्यक समीकरणे म्हणून लिहिली जातील

y = 1 2 x - 2 3 π 4 - a r c पाप 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c पाप 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

व्हिज्युअल प्रतिनिधित्वासाठी, समन्वय रेषेवरील फंक्शन आणि स्पर्शिका विचारात घ्या.

आकृती दर्शवते की फंक्शन मध्यांतरावर स्थित आहे [ - 10 ; 10], जिथे काळी रेषा फंक्शनचा आलेख आहे, तिथे निळ्या रेषा स्पर्शरेषा आहेत, ज्या y = - 2 x + 1 2 फॉर्मच्या दिलेल्या रेषेला लंब आहेत. लाल ठिपके स्पर्श बिंदू आहेत.

2ऱ्या क्रमाच्या वक्रांची प्रमाणिक समीकरणे एकल-मूल्य असलेली कार्ये नाहीत. त्यांच्यासाठी स्पर्शिका समीकरणे ज्ञात योजनांनुसार संकलित केली जातात.

वर्तुळाला स्पर्शिका

x c e n t e r बिंदूवर केंद्र असलेले वर्तुळ परिभाषित करण्यासाठी; y c e n t e r आणि त्रिज्या R, x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 हे सूत्र लागू करा.

ही समानता दोन कार्यांचे संघटन म्हणून लिहिली जाऊ शकते:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

आकृतीत दाखवल्याप्रमाणे पहिले फंक्शन शीर्षस्थानी आणि दुसरे तळाशी आहे.

बिंदू x 0 वर वर्तुळाचे समीकरण संकलित करण्यासाठी; y 0 , जे वरच्या किंवा खालच्या अर्धवर्तुळात स्थित आहे, तुम्हाला y = R 2 - x - x c e n t e r 2 + y c e n t e r किंवा y = - R 2 - x - x - x c e n t e r 2 + फॉर्मच्या फंक्शनच्या आलेखाचे समीकरण शोधावे. सूचित बिंदूवर y c e n t e r.

जेव्हा x c e n t e r बिंदूंवर; y c e n t e r + R आणि x c e n t e r ; y c e n t e r - R स्पर्शरेषा y = y c e n t e r + R आणि y = y c e n t e r - R या समीकरणांद्वारे दिली जाऊ शकतात आणि x c e n t e r + R बिंदूंवर; y c e n t e r आणि
x c e n t e r - R ; y c e n t e r o y ला समांतर असेल, नंतर आपल्याला x = x c e n t e r + R आणि x = x c e n t e r - R या स्वरूपाची समीकरणे प्राप्त होतील.

लंबवर्तुळाला स्पर्शिका

जेव्हा लंबवर्तुळाचे केंद्र x c e n t e r वर असते; y c e n t e r अर्ध-अक्ष a आणि b सह, नंतर x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 हे समीकरण वापरून निर्दिष्ट केले जाऊ शकते.

लंबवर्तुळ आणि वर्तुळ हे दोन फंक्शन्स एकत्रित करून दर्शविले जाऊ शकते, म्हणजे वरचा आणि खालचा अर्ध-लंबवृत्त. मग आम्हाला ते मिळते

y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

जर स्पर्शिका लंबवर्तुळाच्या शिरोबिंदूंवर स्थित असतील, तर ते x किंवा y बद्दल समांतर असतात. खाली, स्पष्टतेसाठी, आकृतीचा विचार करा.

उदाहरण 6

स्पर्शिकेचे समीकरण लंबवर्तुळाकार x - 3 2 4 + y - 5 2 25 = 1 या बिंदूंवर x = 2 च्या मूल्यांसह लिहा.

उपाय

x = 2 या मूल्याशी संबंधित स्पर्शक बिंदू शोधणे आवश्यक आहे. आम्ही लंबवर्तुळाच्या विद्यमान समीकरणामध्ये बदलतो आणि ते शोधतो

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

नंतर 2; 5 3 2 + 5 आणि 2; - 5 3 2 + 5 हे स्पर्श बिंदू आहेत जे वरच्या आणि खालच्या अर्ध-लंबवृत्ताशी संबंधित आहेत.

y च्या संदर्भात लंबवर्तुळाचे समीकरण शोधणे आणि सोडवण्याकडे वळू. आम्हाला ते मिळते

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

अर्थात, वरचा अर्धावृत्त y = 5 + 5 2 4 - x - 3 2, आणि खालचा अर्धा लंबवर्तुळ y = 5 - 5 2 4 - x - 3 2 या फॉर्मचे फंक्शन वापरून निर्दिष्ट केला आहे.

एका बिंदूवर फंक्शनच्या आलेखाला स्पर्शिकेसाठी समीकरण तयार करण्यासाठी मानक अल्गोरिदम लागू करू. बिंदू 2 वरील पहिल्या स्पर्शिकेचे समीकरण असे लिहूया; 5 3 2 + 5 असे दिसेल

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

बिंदूवर मूल्य असलेल्या दुसऱ्या स्पर्शिकेचे समीकरण आपल्याला आढळते
2; - 5 3 2 + 5 फॉर्म घेते

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

ग्राफिकदृष्ट्या, स्पर्शिका खालीलप्रमाणे नियुक्त केल्या आहेत:

स्पर्शिका ते हायपरबोल

जेव्हा हायपरबोलाचे केंद्र x c e n t e r वर असते; y c e n t e r आणि शिरोबिंदू x c e n t e r + α ; y c e n t e r आणि x c e n t e r - α ; y c e n t e r , असमानता x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 घडते, जर शिरोबिंदू x c e n t e r सह ; y c e n t e r + b आणि x c e n t e r ; y c e n t e r - b , नंतर असमानता x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 वापरून निर्दिष्ट केले आहे.

हायपरबोला फॉर्मची दोन एकत्रित कार्ये म्हणून प्रस्तुत केले जाऊ शकते

y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r किंवा y = b a · (x - x c e n t e r) 2 + e + y + y + + + + + (x - x c e n t e r) 2 + a 2 + y c e n t e r

पहिल्या प्रकरणात आपल्याला स्पर्शिका y च्या समांतर आहेत आणि दुसऱ्या प्रकरणात ते x ला समांतर आहेत.

हे असे आहे की अतिपरवल्याच्या स्पर्शिकेचे समीकरण शोधण्यासाठी, स्पर्शिकेचा बिंदू कोणत्या कार्याशी संबंधित आहे हे शोधणे आवश्यक आहे. हे निश्चित करण्यासाठी, समीकरणांमध्ये बदलणे आणि ओळख तपासणे आवश्यक आहे.

उदाहरण 7

हायपरबोला x - 3 2 4 - y + 3 2 9 = 1 बिंदू 7 वर स्पर्शिकेसाठी समीकरण लिहा; - ३ ३ - ३ .

उपाय

2 फंक्शन्स वापरून हायपरबोला शोधण्यासाठी सोल्यूशन रेकॉर्डचे रूपांतर करणे आवश्यक आहे. आम्हाला ते मिळते

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 आणि y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

निर्देशांक 7 सह दिलेला बिंदू कोणत्या फंक्शनचा आहे हे ओळखणे आवश्यक आहे; - ३ ३ - ३ .

अर्थात, पहिले कार्य तपासण्यासाठी y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3 आवश्यक आहे, तर बिंदू आलेखाशी संबंधित नाही, कारण समानता टिकत नाही.

दुसऱ्या फंक्शनसाठी आपल्याकडे y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 आहे, म्हणजे बिंदू दिलेल्या आलेखाचा आहे. इथून उतार शोधावा.

आम्हाला ते मिळते

y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

उत्तर:स्पर्शिका समीकरण असे दर्शविले जाऊ शकते

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

हे स्पष्टपणे असे चित्रित केले आहे:

पॅराबोलाला स्पर्शिका

x 0, y (x 0) बिंदूवर पॅराबोला y = a x 2 + b x + c या स्पर्शिकेसाठी एक समीकरण तयार करण्यासाठी, आपण एक मानक अल्गोरिदम वापरणे आवश्यक आहे, नंतर समीकरण y = y "(x) फॉर्म घेईल 0) x - x 0 + y ( x 0). शिरोबिंदूवरील अशी स्पर्शिका x ला समांतर असते.

तुम्ही पॅराबोला x = a y 2 + b y + c हे दोन फंक्शन्सचे मिलन म्हणून परिभाषित केले पाहिजे. म्हणून, आपल्याला y चे समीकरण सोडवावे लागेल. आम्हाला ते मिळते

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

ग्राफिकरित्या असे चित्रित केले आहे:

बिंदू x 0, y (x 0) फंक्शनचा आहे की नाही हे शोधण्यासाठी, मानक अल्गोरिदमनुसार हळूवारपणे पुढे जा. अशी स्पर्शिका पॅराबोलाच्या सापेक्ष o y च्या समांतर असेल.

उदाहरण 8

जेव्हा आपल्याकडे 150 ° चा स्पर्शिका कोन असेल तेव्हा स्पर्शिकेचे समीकरण x - 2 y 2 - 5 y + 3 या आलेखावर लिहा.

उपाय

आपण पॅराबोला दोन फंक्शन्स म्हणून प्रस्तुत करून सोल्युशन सुरू करतो. आम्हाला ते मिळते

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

उताराचे मूल्य या फंक्शनच्या बिंदू x 0 वरील व्युत्पन्न मूल्याच्या बरोबरीचे आहे आणि झुकाव कोनाच्या स्पर्शिकेइतके आहे.

आम्हाला मिळते:

k x = y "(x 0) = t g α x = t g 150 ° = - 1 3

येथून आपण संपर्काच्या बिंदूंसाठी x मूल्य निर्धारित करतो.

पहिले फंक्शन असे लिहिले जाईल

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

स्पष्टपणे, कोणतीही वास्तविक मुळे नाहीत, कारण आम्हाला नकारात्मक मूल्य मिळाले आहे. आम्ही असा निष्कर्ष काढतो की अशा फंक्शनसाठी 150° कोन असलेली स्पर्शिका नाही.

दुसरे फंक्शन असे लिहिले जाईल

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

आमच्याकडे संपर्काचे बिंदू आहेत 23 4 ; - ५ + ३ ४ .

उत्तर:स्पर्शिका समीकरण फॉर्म घेते

y = - 1 3 x - 23 4 + - 5 + 3 4

चला ते या प्रकारे चित्रित करूया:

तुम्हाला मजकुरात त्रुटी आढळल्यास, कृपया ते हायलाइट करा आणि Ctrl+Enter दाबा

व्हिडिओ धडा "फंक्शनच्या आलेखासाठी स्पर्शिकेचे समीकरण" विषयावर प्रभुत्व मिळवण्यासाठी शैक्षणिक साहित्य प्रदर्शित करते. व्हिडिओ धड्यादरम्यान, दिलेल्या बिंदूवर फंक्शनच्या आलेखाच्या स्पर्शिकेच्या समीकरणाची संकल्पना तयार करण्यासाठी आवश्यक सैद्धांतिक सामग्री, अशी स्पर्शिका शोधण्यासाठी अल्गोरिदम आणि अभ्यासलेल्या सैद्धांतिक सामग्रीचा वापर करून समस्या सोडवण्याच्या उदाहरणांचे वर्णन केले आहे. .

व्हिडिओ ट्यूटोरियल अशा पद्धती वापरते ज्या सामग्रीची स्पष्टता सुधारतात. सादरीकरणामध्ये रेखाचित्रे, आकृत्या, महत्त्वाच्या व्हॉइस टिप्पण्या, अॅनिमेशन, हायलाइटिंग आणि इतर साधने आहेत.

व्हिडिओ धडा धड्याच्या विषयाच्या सादरीकरणाने आणि M(a;f(a)) बिंदूवरील काही फंक्शन y=f(x) च्या आलेखाच्या स्पर्शिकेच्या प्रतिमेसह सुरू होतो. हे ज्ञात आहे की दिलेल्या बिंदूवर आलेखावर प्लॉट केलेल्या स्पर्शिकेचा कोनीय गुणांक या बिंदूवर f΄(a) फंक्शनच्या व्युत्पन्नाइतका असतो. तसेच बीजगणित अभ्यासक्रमावरून आपल्याला y=kx+m या सरळ रेषेचे समीकरण कळते. एका बिंदूवर स्पर्शिका समीकरण शोधण्याच्या समस्येचे निराकरण योजनाबद्धपणे सादर केले जाते, जे k, m गुणांक शोधण्यासाठी कमी करते. फंक्शनच्या आलेखाशी संबंधित बिंदूचे निर्देशांक जाणून घेतल्यास, आपण f(a)=ka+m या स्पर्शिका समीकरणामध्ये समन्वय मूल्य बदलून m शोधू शकतो. त्यातून आपल्याला m=f(a)-ka सापडतो. अशा प्रकारे, दिलेल्या बिंदूवरील व्युत्पन्नाचे मूल्य आणि बिंदूचे समन्वय जाणून घेतल्यास, आपण स्पर्शिका समीकरण y=f(a)+f΄(a)(x-a) अशा प्रकारे दर्शवू शकतो.

आकृतीच्या अनुषंगाने स्पर्शिका समीकरण तयार करण्याचे उदाहरण खालीलप्रमाणे आहे. y=x 2 , x=-2 फंक्शन दिले. a=-2 घेतल्यास, f(a)= f(-2)=(-2) 2 = 4 दिलेल्या बिंदूवर फंक्शनचे मूल्य सापडते. आम्ही f΄(x)=2x या फंक्शनचे व्युत्पन्न ठरवतो. या टप्प्यावर व्युत्पन्न f΄(a)= f΄(-2)=2·(-2)=-4 समान आहे. समीकरण तयार करण्यासाठी, सर्व गुणांक a=-2, f(a)=4, f΄(a)=-4 आढळले, त्यामुळे स्पर्शिका समीकरण y=4+(-4)(x+2) आहे. समीकरण सरलीकृत केल्यास आपल्याला y = -4-4x मिळेल.

खालील उदाहरण y=tgx या फंक्शनच्या आलेखाच्या उगमस्थानी स्पर्शिकेसाठी समीकरण तयार करण्याचे सुचवते. दिलेल्या बिंदूवर a=0, f(0)=0, f΄(x)=1/cos 2 x, f΄(0)=1. त्यामुळे स्पर्शिका समीकरण y=x सारखे दिसते.

सामान्यीकरण म्हणून, एका विशिष्ट बिंदूवर फंक्शनच्या आलेखावर समीकरण स्पर्शिका तयार करण्याची प्रक्रिया 4 चरणांचा समावेश असलेल्या अल्गोरिदमच्या स्वरूपात औपचारिक केली जाते:

• स्पर्शिका बिंदूच्या abscissa साठी पदनाम a प्रविष्ट करा;
• f(a) ची गणना केली जाते;
• f΄(x) निर्धारित केले जाते आणि f΄(a) ची गणना केली जाते. a, f(a), f΄(a) ची सापडलेली मूल्ये स्पर्शिका समीकरण सूत्र y=f(a)+f΄(a)(x-a) मध्ये बदलली जातात.

उदाहरण 1 बिंदू x=1 वर y=1/x या फंक्शनच्या आलेखावर स्पर्शिका समीकरण तयार करण्याचा विचार करते. समस्येचे निराकरण करण्यासाठी आम्ही अल्गोरिदम वापरतो. बिंदू a=1 वर दिलेल्या फंक्शनसाठी, फंक्शनचे मूल्य f(a)=-1. फंक्शनचे व्युत्पन्न f΄(x)=1/x 2. बिंदू a=1 व्युत्पन्न f΄(a)= f΄(1)=1. प्राप्त डेटा वापरून, स्पर्शिका समीकरण y=-1+(x-1), किंवा y=x-2, काढले आहे.

उदाहरण 2 मध्ये, y=x 3 +3x 2 -2x-2 फंक्शनच्या आलेखाच्या स्पर्शिकेचे समीकरण शोधणे आवश्यक आहे. मुख्य स्थिती म्हणजे स्पर्शिकेची समांतरता आणि सरळ रेषा y=-2x+1. प्रथम, आपल्याला स्पर्शिकेचा कोनीय गुणांक y=-2x+1 या सरळ रेषेच्या कोनीय गुणांकाएवढा आहे. दिलेल्या रेषेसाठी f΄(a)=-2 असल्याने, इच्छित स्पर्शिकेसाठी k=-2. आपल्याला फंक्शनचे व्युत्पन्न सापडते (x 3 +3x 2 -2x-2)΄=3x 2 +6x-2. f΄(a)=-2 हे जाणून घेतल्यास, आपल्याला बिंदू 3a 2 +6a-2=-2 चे समन्वय सापडतात. समीकरण सोडवल्यानंतर, आपल्याला 1 =0 आणि 2 =-2 मिळेल. सापडलेल्या निर्देशांकांचा वापर करून, तुम्ही सुप्रसिद्ध अल्गोरिदम वापरून स्पर्शिका समीकरण शोधू शकता. फंक्शनचे मूल्य f(a 1)=-2, f(a 2)=-18 या बिंदूंवर सापडते. f΄(а 1)= f΄(а 2)=-2 बिंदूवरील व्युत्पन्नाचे मूल्य. सापडलेल्या मूल्यांना स्पर्शिका समीकरणामध्ये बदलून, पहिल्या बिंदूसाठी 1 =0 y=-2x-2 आणि दुसऱ्या बिंदूसाठी 2 =-2 स्पर्शिका समीकरण y=-2x-22 प्राप्त होते.

उदाहरण 3 y=√x या फंक्शनच्या आलेखावर बिंदू (0;3) वर काढण्यासाठी स्पर्शिका समीकरणाच्या रचनेचे वर्णन करते. समाधान सुप्रसिद्ध अल्गोरिदम वापरून केले जाते. स्पर्शिका बिंदूमध्ये x=a समन्वय असतात, जेथे a>0. f(a)=√x बिंदूवरील फंक्शनचे मूल्य. f΄(х)=1/2√х फंक्शनचे व्युत्पन्न, म्हणून दिलेल्या बिंदूवर f΄(а)=1/2√а. सर्व प्राप्त मूल्यांना स्पर्शिका समीकरणामध्ये बदलून, आपल्याला y = √a + (x-a)/2√a प्राप्त होते. समीकरण बदलल्यास आपल्याला y=x/2√а+√а/2 मिळेल. स्पर्शिका बिंदू (0;3) मधून जाते हे जाणून, आपल्याला a चे मूल्य सापडते. आम्हाला 3=√a/2 वरून a सापडतो. म्हणून √a=6, a=36. आपल्याला स्पर्शिका समीकरण y=x/12+3 सापडते. आकृती विचाराधीन कार्याचा आलेख आणि तयार केलेली इच्छित स्पर्शिका दर्शवते.

विद्यार्थ्यांना अंदाजे समानता Δy=≈f΄(x)Δxand f(x+Δx)-f(x)≈f΄(x)Δx ची आठवण करून दिली जाते. x=a, x+Δx=x, Δx=x-a घेतल्यास, आपल्याला f(x)- f(a)≈f΄(a)(x-a) मिळते, म्हणून f(x)≈f(a)+ f΄( a)(x-a).

उदाहरण 4 मध्ये, 2.003 6 या अभिव्यक्तीचे अंदाजे मूल्य शोधणे आवश्यक आहे. x=2.003 बिंदूवर f(x)=x 6 चे मूल्य शोधणे आवश्यक असल्याने, आपण f(x)=x 6, a=2, f(a घेऊन सुप्रसिद्ध सूत्र वापरू शकतो. )= f(2)=64, f ΄(x)=6x 5. f΄(2)=192 बिंदूवर व्युत्पन्न. म्हणून, 2.003 6 ≈65-192·0.003. अभिव्यक्तीची गणना केल्यावर, आपल्याला 2.003 6 ≈64.576 मिळेल.

शाळेत पारंपारिक गणिताच्या धड्यात वापरण्यासाठी "फंक्शनच्या आलेखाला स्पर्शिकेचे समीकरण" या व्हिडिओ धड्याची शिफारस केली जाते. दूरस्थपणे शिकवणाऱ्या शिक्षकासाठी, व्हिडिओ सामग्री विषय अधिक स्पष्टपणे स्पष्ट करण्यात मदत करेल. विद्यार्थ्‍यांनी त्‍यांच्‍या विषयाची समज वाढवण्‍यासाठी आवश्‍यकता असल्‍यास स्‍वतंत्रपणे पुनरावलोकन करण्‍यासाठी व्हिडिओची शिफारस केली जाऊ शकते.

मजकूर डीकोडिंग:

आम्हाला माहित आहे की जर बिंदू M (a; f(a)) (em मधील a आणि ef समन्वयांसह) y = f (x) फंक्शनच्या आलेखाशी संबंधित असेल आणि या बिंदूवर स्पर्शिका काढणे शक्य असेल तर अक्ष abscissa ला लंब नसलेल्या फंक्शनच्या आलेखाला, नंतर स्पर्शिकेचा कोनीय गुणांक f"(a) (a वरून eff प्राइम) बरोबर असतो.

फंक्शन y = f(x) आणि एक बिंदू M (a; f(a)) द्या, आणि हे देखील ज्ञात आहे की f´(a) अस्तित्वात आहे. दिलेल्या बिंदूवर दिलेल्या फंक्शनच्या आलेखाच्या स्पर्शिकेचे समीकरण बनवू. या समीकरणाला, ऑर्डिनेट अक्षाच्या समांतर नसलेल्या कोणत्याही सरळ रेषेच्या समीकरणाप्रमाणे, त्याचे स्वरूप y = kx+m (y हे ka x अधिक em च्या बरोबरीचे आहे), त्यामुळे त्याची मूल्ये शोधण्याचे कार्य आहे गुणांक k आणि m. (ka आणि em)

कोन गुणांक k = f"(a). m चे मूल्य मोजण्यासाठी, आपण इच्छित सरळ रेषा M(a; f (a) बिंदूमधून जाते हे तथ्य वापरतो). याचा अर्थ असा की जर आपण बिंदूच्या निर्देशांकांची जागा घेतली तर सरळ रेषेच्या समीकरणामध्ये M बिंदू करा, आपल्याला योग्य समानता मिळते : f(a) = ka+m, जिथून आपल्याला m = f(a) - ka असे आढळते.

सरळ रेषेच्या समीकरणामध्ये ki आणि m गुणांकांची सापडलेली मूल्ये बदलणे बाकी आहे:

y = kx+(f(a)-ka);

y = f(a)+k(x-a);

y= f(a)+ f"(a) (x- a). ( y हे ef च्या बरोबर आहे a वरून अधिक ef प्राइम पासून, x वजा a ने गुणाकार).

आपण x=a बिंदूवर फंक्शन y = f(x) च्या आलेखाच्या स्पर्शिकेचे समीकरण प्राप्त केले आहे.

जर, म्हणा, y = x 2 आणि x = -2 (म्हणजे a = -2), तर f (a) = f (-2) = (-2) 2 = 4; f´(x) = 2x, म्हणजे f"(a) = f´(-2) = 2·(-2) = -4. x हे दोन x च्या बरोबरीचे आहे, याचा अर्थ ef प्राइम वरून इक्वल वजा चार)

आढळलेली मूल्ये a = -2, f(a) = 4, f"(a) = -4 समीकरणात बदलून, आम्हाला मिळते: y = 4+(-4)(x+2), म्हणजे y = -4x -4.

(ई म्हणजे उणे चार x वजा चार)

मूळ y = tanx (y स्पर्शिका x च्या समान आहे) फंक्शनच्या आलेखाच्या स्पर्शिकेसाठी एक समीकरण तयार करू. आमच्याकडे आहे: a = 0, f(0) = tan0=0;

f"(x)= , म्हणजे f"(0) = l. a=0, f(a)=0, f´(a) = 1 ही मूल्ये समीकरणात बदलल्यास, आपल्याला मिळते: y=x.

अल्गोरिदम वापरून बिंदू x वरील फंक्शनच्या आलेखाच्या स्पर्शिकेचे समीकरण शोधण्याच्या आपल्या चरणांचा सारांश घेऊ.

फंक्शन y = f(x) च्या आलेखाच्या स्पर्शिकेसाठी समीकरण विकसित करण्यासाठी अल्गोरिदम:

1) स्पर्शिका बिंदूचा abscissa अक्षर a सह नियुक्त करा.

2) f(a) ची गणना करा.

3) f´(x) शोधा आणि f´(a) ची गणना करा.

4) सापडलेल्या संख्या a, f(a), f´(a) सूत्रामध्ये बदला y= f(a)+ f"(a) (x- a).

उदाहरण 1. फंक्शन y = - in च्या आलेखाच्या स्पर्शिकेसाठी समीकरण तयार करा

बिंदू x = 1.

उपाय. या उदाहरणात ते लक्षात घेऊन अल्गोरिदम वापरू

२) f(a)=f(1)=- =-1

३) f´(x)=; f´(a)= f´(1)= =1.

4) सापडलेल्या तीन संख्यांची जागा घ्या: a = 1, f(a) = -1, f"(a) = 1 सूत्रामध्ये. आम्हाला मिळते: y = -1+(x-1), y = x-2 .

उत्तर: y = x-2.

उदाहरण 2. फंक्शन y = दिले आहे x 3 +3x 2 -2x-2. y = f(x) फंक्शनच्या आलेखावर स्पर्शिकेचे समीकरण लिहा, सरळ रेषेला y = -2x +1 समांतर.

स्पर्शिका समीकरण तयार करण्यासाठी अल्गोरिदम वापरून, आम्ही हे लक्षात घेतो की या उदाहरणात f(x) = x 3 +3x 2 -2x-2, परंतु स्पर्शिका बिंदूचा abscissa येथे दर्शविला नाही.

असा विचार करूया. इच्छित स्पर्शिका y = -2x+1 या सरळ रेषेच्या समांतर असणे आवश्यक आहे. आणि समांतर रेषांमध्ये समान कोनीय गुणांक असतात. याचा अर्थ स्पर्शिकेचा कोनीय गुणांक दिलेल्या सरळ रेषेच्या कोनीय गुणांकाच्या बरोबरीचा आहे: k स्पर्शिका. = -2. होक केस. = f"(a). अशा प्रकारे, f ´(a) = -2 या समीकरणातून a चे मूल्य शोधू शकतो.

फंक्शनचे व्युत्पन्न शोधू y =f(x):

f"(x)= (x 3 +3x 2 -2x-2)´ = 3x 2 +6x-2;f"(a)= 3a 2 +6a-2.

f"(a) = -2 या समीकरणावरून, i.e. 3a 2 +6a-2=-2 आपल्याला 1 =0, a 2 =-2 सापडतो. याचा अर्थ असा की दोन स्पर्शरेषा आहेत जी समस्येच्या अटी पूर्ण करतात: एक abscissa 0 सह बिंदूवर, दुसरा abscissa -2 सह बिंदूवर.

आता तुम्ही अल्गोरिदम फॉलो करू शकता.

1) a 1 =0, आणि 2 =-2.

2) f(a 1) = 0 ३ +३·० २ -२∙०-२=-२; f(a 2) = (-2) 3 +3·(-2) 2 -2·(-2)-2=6;

3) f"(a 1) = f"(a 2) = -2.

4) a 1 = 0, f(a 1) = -2, f"(a 1) = -2 ही मूल्ये सूत्रामध्ये बदलल्यास, आपल्याला मिळते:

y=-2-2(x-0), y=-2x-2.

a 2 = -2, f(a 2) =6, f"(a 2) = -2 ही मूल्ये सूत्रामध्ये बदलल्यास, आपल्याला मिळते:

y=6-2(x+2), y=-2x+2.

उत्तर: y=-2x-2, y=-2x+2.

उदाहरण 3. बिंदूपासून (0; 3) फंक्शन y = च्या आलेखावर स्पर्शिका काढा. उपाय. या उदाहरणात f(x) = हे लक्षात घेऊन स्पर्शिका समीकरण तयार करण्यासाठी अल्गोरिदम वापरू. लक्षात घ्या की येथे, उदाहरण 2 प्रमाणे, स्पर्शिका बिंदूचा abscissa स्पष्टपणे सूचित केलेला नाही. तरीही, आम्ही अल्गोरिदमचे अनुसरण करतो.

1) x = a हे स्पर्शिकेच्या बिंदूचे abscissa असू द्या; हे स्पष्ट आहे की a >0.

३) f´(x)=()´=; f´(a) =.

4) a, f(a) = , f"(a) = ची मूल्ये सूत्रामध्ये बदलणे

y=f (a) +f "(a) (x-a), आम्हाला मिळते:

स्थितीनुसार, स्पर्शिका बिंदू (0; 3) मधून जाते. समीकरणामध्ये x = 0, y = 3 ही मूल्ये बदलल्यास, आपल्याला मिळते: 3 = , आणि नंतर =6, a =36.

जसे आपण पाहू शकता, या उदाहरणात, अल्गोरिदमच्या केवळ चौथ्या चरणावर आम्ही स्पर्शिका बिंदूचा abscissa शोधण्यात व्यवस्थापित केले. समीकरणामध्ये a =36 मूल्य बदलल्यास, आपल्याला मिळेल: y=+3

अंजीर मध्ये. आकृती 1 विचारात घेतलेल्या उदाहरणाचे भौमितिक चित्रण दाखवते: y = फंक्शनचा आलेख तयार केला आहे, y = +3 ही सरळ रेषा काढली आहे.

उत्तर: y = +3.

आम्हाला माहित आहे की y = f(x), ज्याचे बिंदू x वर व्युत्पन्न आहे, अंदाजे समानता वैध आहे: Δyf´(x)Δx (डेल्टा y हा डेल्टा x ने गुणाकार केलेल्या x च्या eff प्राइमच्या जवळपास समान आहे)

किंवा, अधिक तपशीलात, f(x+Δx)-f(x) f´(x) Δx (x वरून eff अधिक डेल्टा x वजा ef x वरून x वरून डेल्टा x च्या ef प्राइमच्या जवळपास आहे).

पुढील चर्चेच्या सोयीसाठी, नोटेशन बदलूया:

x च्या ऐवजी आपण लिहू ए,

x+Δx ऐवजी x लिहू

Δx च्या ऐवजी x-a लिहू.

मग वर लिहिलेली अंदाजे समानता फॉर्म घेईल:

f(x)-f(a)f´(a)(x-a)

f(x)f(a)+f´(a)(x-a). (x मधील eff हे a मधील अधिक ef प्राइम मधील ef च्या जवळपास समान आहे, x आणि a मधील फरकाने गुणाकार केला आहे).

उदाहरण 4. संख्यात्मक अभिव्यक्ती 2.003 6 चे अंदाजे मूल्य शोधा.

उपाय. आपण x = 2.003 बिंदूवर y = x 6 फंक्शनचे मूल्य शोधण्याबद्दल बोलत आहोत. या उदाहरणात f(x)=x 6, a = 2,f(a) = f(2) हे लक्षात घेऊन f(x)f(a)+f´(a)(x-a) हे सूत्र वापरू. = 2 6 = 64; x = 2.003, f"(x) = 6x 5 आणि म्हणून, f"(a) = f"(2) = 6 2 5 =192.

परिणामी आम्हाला मिळते:

2.003 6 64+192· 0.003, म्हणजे २.००३ ६ = ६४.५७६.

आम्ही कॅल्क्युलेटर वापरल्यास, आम्हाला मिळेल:

2,003 6 = 64,5781643...

तुम्ही बघू शकता, अंदाजे अचूकता अगदी स्वीकार्य आहे.

खालील आकृतीचा विचार करा:

हे विशिष्ट फंक्शन y = f(x) दर्शविते, जे बिंदू a वर भिन्न आहे. बिंदू M सह निर्देशांक (a; f(a)) चिन्हांकित आहे. आलेखाच्या एका अनियंत्रित बिंदू P(a + ∆x; f(a + ∆x)) द्वारे सेकंट MR काढला जातो.

जर आता बिंदू P आलेखाच्या बाजूने M बिंदूकडे हलविला असेल, तर सरळ रेषा MR बिंदू M भोवती फिरेल. या प्रकरणात, ∆x शून्याकडे झुकेल. येथून आपण फंक्शनच्या आलेखापर्यंत स्पर्शिकेची व्याख्या तयार करू शकतो.

फंक्शनच्या आलेखाला स्पर्शिका

फंक्शनच्या आलेखाची स्पर्शिका ही सीकंटची मर्यादित स्थिती असते कारण वितर्काची वाढ शून्याकडे असते. हे समजले पाहिजे की x0 बिंदूवर फंक्शनच्या व्युत्पन्नाचे अस्तित्व म्हणजे आलेखाच्या या बिंदूवर आहे स्पर्शिकात्याला.

या प्रकरणात, स्पर्शिकेचा कोनीय गुणांक f’(x0) या बिंदूवर या फंक्शनच्या व्युत्पन्नाइतका असेल. हा व्युत्पन्नाचा भौमितिक अर्थ आहे. बिंदू x0 वर भिन्नता असलेल्या फंक्शनच्या आलेखाची स्पर्शिका ही बिंदू (x0;f(x0)) मधून जाणारी आणि कोनीय गुणांक f’(x0) असलेली विशिष्ट सरळ रेषा आहे.

स्पर्शिका समीकरण

बिंदू A(x0; f(x0)) वरील काही फंक्शन f च्या आलेखाशी स्पर्शिकेचे समीकरण मिळवण्याचा प्रयत्न करूया. उतार k सह सरळ रेषेच्या समीकरणाचे खालील रूप आहे:

आमचा उतार गुणांक डेरिव्हेटिव्हच्या बरोबरीचा असल्याने f’(x0), नंतर समीकरण खालील फॉर्म घेईल: y = f’(x0)*x + b.

आता b ची किंमत काढू. हे करण्यासाठी, आम्ही फंक्शन बिंदू A मधून जातो हे तथ्य वापरतो.

f(x0) = f’(x0)*x0 + b, येथून आपण b व्यक्त करतो आणि b = f(x0) - f’(x0)*x0 मिळवतो.

आम्ही परिणामी मूल्य स्पर्शिका समीकरणात बदलतो:

y = f’(x0)*x + b = f’(x0)*x + f(x0) - f’(x0)*x0 = f(x0) + f’(x0)*(x - x0).

y = f(x0) + f’(x0)*(x - x0).

खालील उदाहरणाचा विचार करा: बिंदू x = 2 वर f(x) = x 3 - 2*x 2 + 1 फंक्शनच्या आलेखाच्या स्पर्शिकेचे समीकरण शोधा.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f’(x) = 3*x 2 - 4*x.

4. f’(x0) = f’(2) = 3*2 2 - 4*2 = 4.

5. प्राप्त मूल्यांना स्पर्शिका सूत्रामध्ये बदला, आम्हाला मिळेल: y = 1 + 4*(x - 2). कंस उघडणे आणि तत्सम संज्ञा आणणे आपल्याला मिळते: y = 4*x - 7.

उत्तर: y = 4*x - 7.

स्पर्शिका समीकरण तयार करण्यासाठी सामान्य योजनाफंक्शन y = f(x) च्या आलेखापर्यंत:

1. x0 निश्चित करा.

2. f(x0) ची गणना करा.

3. f’(x) ची गणना करा