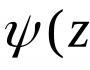What are called zeros of a function? Function zeros rule
Argument values z at which f(z) goes to zero called. zero point, i.e. If f(a) = 0, then a - zero point.
Def. Dot A called zero ordern
, If
The FKP can be represented in the form f(z) = , where 
analytical function and 
0.
In this case, in the Taylor series expansion of the function (43), the first n coefficients are zero
=
=
Etc. Determine the order of zero for 
and (1 –cos z) at z
=
0
=
=
zero 1st order
1 – cos z
=
=
zero 2nd order
Def. Dot z
=
called point at infinity And zero functions f(z), If f(
) = 0. Such a function can be expanded into a series in negative powers z
: f(z)
=
. If
first n
coefficients are equal to zero, then we arrive at zero order n
at a point at infinity: f(z)
= z
-
n
.
Isolated singular points are divided into: a) removable singular points; b) poles of ordern; V) essentially singular points.
Dot A called removable singular point functions f(z) if at z 
a
lim f(z)
= With - final number .
Dot A called pole of ordern
(n
1) functions f(z), if the inverse function 
=
1/
f(z) has zero order n at the point A. Such a function can always be represented as f(z)
=
, Where 
- analytical function and 
.
Dot A called essentially a special point functions f(z), if at z 
a
lim f(z) does not exist.
Laurent series
Let us consider the case of a ring convergence region r < | z 0 – a| < R centered at a point A for function f(z). Let's introduce two new circles L 1 (r) And L 2 (R) near the boundaries of the ring with a point z 0 between them. Let's make a cut of the ring, connect the circles along the edges of the cut, move on to a simply connected region and in
Cauchy integral formula (39) we obtain two integrals over the variable z
f(z 0)
=
+
,
(42)
where integration goes in opposite directions.
For the integral over L 1 condition is met | z 0 – a | > | z – a |, and for the integral over L 2 inverse condition | z 0 – a | < | z – a |. Therefore, the factor 1/( z – z 0) expand into series (a) in the integral over L 2 and in series (b) in the integral over L 1 . As a result, we obtain the expansion f(z) in the ring area in Laurent series by positive and negative powers ( z 0 – a)
f(z 0)
=
A n
(z 0 -a) n
(43)
Where A n
=
=
;A -n
=
Expansion in positive powers (z 0 - A) called the right part Laurent series (Taylor series), and expansion in negative powers is called. main part Laurent series.
If inside the circle L 1 there are no singular points and the function is analytic, then in (44) the first integral is equal to zero by Cauchy’s theorem and only the correct part remains in the expansion of the function. Negative powers in expansion (45) appear only when analyticity is violated within the inner circle and serve to describe the function near isolated singular points.
To construct the Laurent series (45) for f(z) you can calculate expansion coefficients using a general formula or use expansions of elementary functions included in f(z).
Number of terms ( n) of the main part of the Laurent series depends on the type of singular point: removable singular point
(n
=
0)
; essentially singular point
(n 
);
polen- wow order(n
-
final number).
and for f(z)
=
dot z
= 0 removable singular point, because there is no main part. f(z)
=
(z
-
) = 1 -
b) For f(z)
=
dot z
= 0 -
1st order pole
f(z)
=
(z
-
) =
-
c) For f(z) = e 1 / z dot z = 0 - essentially singular point
f(z)
=
e 1 /
z =
If f(z) is analytical in the domain D with the exception of m isolated singular points 
and | z 1 |
< |z 2 |
< . . . < |z m| , then when expanding the function in powers z the entire plane is divided into m+ 1 ring | z i |
< | z
| < | z i+ 1 | and the Laurent series has a different appearance for each ring. When expanding in powers ( z
–
z i
) the region of convergence of the Laurent series is the circle | z
–
z i
| < r, Where r
– distance to the nearest singular point.
Etc. Let's expand the function f(z)
=
in the Laurent series in powers z And ( z
-
1).
Solution. Let's represent the function in the form f(z)
= - z 2
. We use the formula for the sum of a geometric progression 
. In the circle |z|< 1 ряд сходится и f(z)
= - z 2
(1 + z
+ z 2
+ z 3
+ z 4
+ . . .) = - z 2
- z 3
- z 4 - . . . , i.e. the decomposition contains only correct Part. Let us move to the outer region of the circle |z| > 1. Let's represent the function in the form 
, where 1/| z|
< 1, и получим разложение f(z)
= z
=z
+ 1 +
Because , expansion of a function in powers ( z
-
1) looks like f(z)
= (z
-
1) -1
+ 2 + (z
-
1) for everyone 
1.
Etc. Expand the function into a Laurent series f(z)
=
:
a) by degrees z in a circle | z|
< 1; b)
по степеням z
ring 1<
|z|
< 3 ; c)
по степеням (z
–
2).Solution. Let's decompose the function into simple fractions
=
=
+
=
.
From the conditions z
=1
A
= -1/2 , z
=3
B
= ½.
A) f(z)
=
½ [ 
]
= ½ [ 
-(1/3)
], with | z|<
1.
b) f(z)
= - ½ [ 
+
]
= -
(
), at 1< |z|
< 3.
With) f(z)
=
½ [ 
]= -
½
[ 
]
=
=
- ½
= -
, with |2 - z|
< 1
It is a circle of radius 1 centered at z = 2 .
In some cases, power series can be reduced to a set of geometric progressions, and after this it is easy to determine the region of their convergence.
Etc. Investigate the convergence of the series
.
. . +
+
+
+
1
+ ()
+ ()
2
+ ()
3
+ . . .
Solution. This is the sum of two geometric progressions with q 1
=
, q 2 = () . From the conditions of their convergence it follows 
< 1 ,
< 1 или |z|
> 1 , |z|
< 2 , т.е. область сходимости ряда кольцо
1 < |z|
< 2 .
Function zeros are the argument values at which the function is equal to zero.
To find the zeros of the function given by the formula y=f(x), you need to solve the equation f(x)=0.
If the equation has no roots, the function has no zeros.
Examples.
1) Find the zeros of the linear function y=3x+15.
To find the zeros of the function, solve the equation 3x+15=0.
Thus, the zero of the function y=3x+15 is x= -5.
Answer: x= -5.
2) Find the zeros of the quadratic function f(x)=x²-7x+12.
To find the zeros of the function, solve the quadratic equation
Its roots x1=3 and x2=4 are zeros of this function.
Answer: x=3; x=4.
Instructions
1. The zero of a function is the value of the argument x at which the value of the function is equal to zero. However, only those arguments that are within the scope of the definition of the function under study can be zeros. That is, there are a lot of values for which the function f(x) is useful. 2. Write down the given function and equate it to zero, say f(x) = 2x?+5x+2 = 0. Solve the resulting equation and find its real roots. The roots of a quadratic equation are calculated with support for finding the discriminant. 2x?+5x+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0.5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. Thus, in this case, two roots of the quadratic equation are obtained, corresponding to the arguments of the initial function f(x). 3. Check all detected x values for belonging to the domain of definition of the given function. Find out the OOF, to do this, check the initial expression for the presence of even roots of the form?f (x), for the presence of fractions in the function with an argument in the denominator, for the presence of logarithmic or trigonometric expressions. 4. When considering a function with an expression under a root of an even degree, take as the domain of definition all the arguments x, the values of which do not turn the radical expression into a negative number (on the contrary, the function does not make sense). Check whether the detected zeros of the function fall within a certain range of acceptable x values. 5. The denominator of the fraction cannot go to zero; therefore, exclude those arguments x that lead to such a result. For logarithmic quantities, only those values of the argument should be considered for which the expression itself is greater than zero. Zeros of the function that turn the sublogarithmic expression into zero or a negative number must be discarded from the final result. Note! When finding the roots of an equation, extra roots may appear. This is easy to check: just substitute the resulting value of the argument into the function and make sure whether the function turns to zero. Helpful advice Occasionally a function is not expressed in an obvious way through its argument, then it is easy to know what this function is. An example of this is the equation of a circle.
Function zeros The abscissa value at which the value of the function is equal to zero is called.
If a function is given by its equation, then the zeros of the function will be the solutions to the equation. If a graph of a function is given, then the zeros of the function are the values at which the graph intersects the x-axis.
Content:
The zero of a function is the value of x at which the value of the function is zero. Typically, finding the zeros of a function is done by solving a polynomial equation, such as x 2 + 4x +3 = 0. Here are several ways to find the zeros of a function.
Steps
1 Factorization
- 1
Write the equation so it looks something like x 2 + 5x + 4. Start with a higher order term (such as x 2) and then work down to a free term (a constant without a variable; a number). Equate the resulting expression to 0.
- Polynomials (equations) written correctly:
- x 2 + 5x + 6 = 0
- x 2 - 2x – 3 = 0
- Polynomials (equations) written incorrectly:
- 5x + 6 = -x 2
- x 2 = 2x + 3
- Polynomials (equations) written correctly:
- 2
a", "b", "c".
This will simplify the factorization problem. Write the equation in this format: a x 2 ± b x ± c = 0. Now find a, b, c from the equation given to you. Here are some examples:
- x 2 + 5x + 6 = 0
- a
- b = 5
- c = 6
- x 2 - 2x – 3 = 0
- a= 1 (there is no coefficient before “x”, so coefficient = 1)
- b = -2
- c = -3
- x 2 + 5x + 6 = 0
- 3
Write down all pairs of coefficient factors " With".
A pair of factors of a given number are two numbers that, when multiplied, give that number. Pay special attention to negative numbers. Two negative numbers, when multiplied, give a positive number. The order of the multiplication does not matter ("1 x 4" is the same as "4 x 1").
- Equation: x 2 + 5x + 6 = 0
- Multiplier pairs 6, or c:
- 1 x 6 = 6
- -1 x -6 = 6
- 2 x 3 = 6
- -2 x -3 = 6
- 4
Find a pair of factors whose sum is " b" .
Look at the meaning b and find which of the pairs, when summed, will give this number.
- b = 5
- A pair of multipliers whose sum is 5 is 2 and 3
- 2 + 3 = 5
- 5
From this pair of factors, make 2 binomials and combine them into a binomial. A binomial is the product of binomials of the form (x ± number)(x ± number). How do you know which sign (plus or minus) to choose? Just look at the sign of the numbers from a pair of factors: a positive number is a plus sign, a negative number is a minus sign. Here are a couple of factors with which we made the binomial:
- (x + 2)(x + 3) = 0
- 6
Solve each binomial by moving the unknown to the other side of the equation. Equate each binomial to 0: (x + 2) = 0 and (x + 3) = 0, and then solve the equation:
- (x + 2) = 0; x = -2
- (x + 3) = 0; x = -3
- 7 These are the zeros of the function.
2 Solving a quadratic equation
- 1 The quadratic equation looks like this:
- 2 Denote the coefficients in your equation by " a", "b", "c". This will simplify the problem of solving the equation. Write the equation in this format: a x 2 ± b x ± c = 0.
- 3 Now find a, b, c from the equation given to you.
- 4
Solve the equation. To solve a quadratic equation, you need to know the formula for solving such an equation. Everything else is just substitution and calculation.
- Another option for solving a quadratic equation is a perfect square. Some people consider this method simpler than solving by formula.
- 5 The result of solving a quadratic equation using the formula will be the “zeros” of the function that you are looking for. The formula gives the answer in the form of two numbers, which are the solution (zeros) of this function.
3 Graph of a quadratic equation
- 1 Graph the function. The function is written as x 2 + 8x + 12 = 0.
- 2 Find the x-intercepts. These two points will be the zeros of the function.
- 3 Use the graph as a way to check, not as a way to solve an equation. If you are plotting to show the zeros of a function, use this to double check your results.
- You can check your calculations by substituting the solutions found into the initial equation. If the equation is equal to zero, then the solutions are correct.
The mathematical representation of a function clearly shows how one quantity completely determines the value of another quantity. Traditionally, numerical functions are considered that assign one number to another. The zero of a function is usually the value of the argument at which the function becomes zero.
Instructions
1. In order to detect the zeros of a function, you need to equate its right side to zero and solve the resulting equation. Let's imagine you are given a function f(x)=x-5.
2. To find the zeros of this function, let’s take and equate its right side to zero: x-5=0.
3. Having solved this equation, we find that x=5 and this value of the argument will be the zero of the function. That is, when the argument value is 5, the function f(x) becomes zero.
Under the view functions in mathematics we understand the connection between the elements of sets. To put it more correctly, this is a “law” according to which the entire element of one set (called the domain of definition) is associated with a certain element of another set (called the domain of values).
You will need
- Knowledge of algebra and mathematical review.
Instructions
1. Values functions This is a certain area from which a function can take values. Let's say the range of values functions f(x)=|x| from 0 to infinity. In order to discover meaning functions at a certain point you need to substitute the argument functions its numerical equivalent, the resulting number will be meaning m functions. Let the function f(x)=|x| – 10 + 4x. Let's find out meaning functions at point x=-2. Let's replace x with the number -2: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16. That is meaning functions at point -2 is equal to -16.
Note!
Before looking for the value of a function at a point, make sure that it is within the domain of the function.
Helpful advice
A similar method allows one to discover the meaning of the function of several arguments. The difference is that instead of one number you will need to substitute several - according to the number of arguments of the function.
The function represents the established connection between the variable y and the variable x. Moreover, all the values of x, called the argument, correspond to the exceptional value of y - the function. In graphical form, a function is depicted on a Cartesian coordinate system in the form of a graph. The points of intersection of the graph with the abscissa axis, on which the arguments x are plotted, are called zeros of the function. Finding acceptable zeros is one of the tasks of finding a given function. In this case, all permissible values of the independent variable x that form the domain of definition of the function (DOF) are taken into account.
Instructions
1. The zero of a function is the value of the argument x at which the value of the function is equal to zero. However, only those arguments that are within the scope of the definition of the function under study can be zeros. That is, there are a lot of values for which the function f(x) is useful.
2. Write down the given function and equate it to zero, say f(x) = 2x?+5x+2 = 0. Solve the resulting equation and find its real roots. The roots of a quadratic equation are calculated with support for finding the discriminant. 2x?+5x+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0.5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. Thus, in this case, two roots of the quadratic equation are obtained, corresponding to the arguments of the initial function f(x).
3. Check all detected x values for belonging to the domain of definition of the given function. Find out the OOF, to do this, check the initial expression for the presence of even roots of the form?f (x), for the presence of fractions in the function with an argument in the denominator, for the presence of logarithmic or trigonometric expressions.
4. When considering a function with an expression under a root of an even degree, take as the domain of definition all the arguments x, the values of which do not turn the radical expression into a negative number (on the contrary, the function does not make sense). Check whether the detected zeros of the function fall within a certain range of acceptable x values.
5. The denominator of the fraction cannot go to zero; therefore, exclude those arguments x that lead to such a result. For logarithmic quantities, only those values of the argument should be considered for which the expression itself is greater than zero. Zeros of the function that turn the sublogarithmic expression into zero or a negative number must be discarded from the final result.
Note!
When finding the roots of an equation, extra roots may appear. This is easy to check: just substitute the resulting value of the argument into the function and make sure whether the function turns to zero.
Helpful advice
Occasionally a function is not expressed in an obvious way through its argument, then it is easy to know what this function is. An example of this is the equation of a circle.
In which it takes the value zero. For example, for a function given by the formula
Is zero because
.The zeros of a function are also called roots of the function.
The concept of zeros of a function can be considered for any functions whose range of values contains zero or the zero element of the corresponding algebraic structure.
For a function of a real variable, zeros are the values at which the graph of the function intersects the x-axis.
Finding the zeros of a function often requires the use of numerical methods (for example, Newton's method, gradient methods).
One of the unsolved mathematical problems is finding the zeros of the Riemann zeta function.
Root of a polynomial
see also
Literature
Wikimedia Foundation. 2010.
See what “Function Zero” is in other dictionaries:
The point where a given function f(z) vanishes; thus, N. f. f (z) is the same as the roots of the equation f (z) = 0. For example, the points 0, π, π, 2π, 2π,... are zeros of the function sinz. Zeros of an analytical function (See Analytical... ...
Zero function, zero function... Spelling dictionary-reference book
This term has other meanings, see Zero. The contents of this article should be moved to the "Function Null" article. You can help the project by combining articles. If it is necessary to discuss the feasibility of merging, replace this ... Wikipedia
Or C string (from the name of the C language) or ASCIZ string (from the name of the assembler directive.asciz) a method of representing strings in programming languages, in which, instead of introducing a special string type, an array of characters is used, and at the end ... ... Wikipedia
In quantum field theory, the accepted (jargon) name for the property of vanishing the renormalization factor of the coupling constant is where g0 is the bare coupling constant from the interaction Lagrangian, physical. coupling constant dressed up as interaction. Equality Z... Physical encyclopedia
Null mutation n-allele- Null mutation, n. allele * null mutation, n. allele * null mutation or n. allel or silent a. a mutation leading to complete loss of function in the DNA sequence in which it occurred... Genetics. encyclopedic Dictionary
The statement in probability theory that any event (the so-called residual event), the occurrence of which is determined only by arbitrarily distant elements of a sequence of independent random events or random variables, has... ... Mathematical Encyclopedia
1) A number that has the property that any (real or complex) number does not change when added to it. Denoted by the symbol 0. The product of any number by N. is equal to N.: If the product of two numbers is equal to N., then one of the factors ... Mathematical Encyclopedia
Functions defined by relationships between independent variables that are not resolved relative to the latter; these relations are one of the ways to specify a function. For example, the relation x2 + y2 1 = 0 defines the N.f. ... Great Soviet Encyclopedia
The set of those and only those points in which in no neighborhood of the generalized function vanishes. The generalized function of vanishes in the open set if for all. Using the expansion of unity, it is shown that if a generalized function ... Mathematical Encyclopedia
