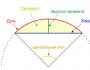
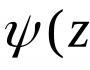Calculation of the length of a circular arc by radius. Circle geometry
The circle, its parts, their sizes and relationships are things that a jeweler constantly encounters. Rings, bracelets, castes, tubes, balls, spirals - a lot of round things have to be made. How can you calculate all this, especially if you were lucky enough to skip geometry classes at school?..
Let's first look at what parts a circle has and what they are called.
- A circle is a line that encloses a circle.
- An arc is a part of a circle.
- Radius is a segment connecting the center of a circle with any point on the circle.
- A chord is a segment connecting two points on a circle.
- A segment is a part of a circle bounded by a chord and an arc.
- A sector is a part of a circle bounded by two radii and an arc.
The quantities we are interested in and their designations:

Now let's see what problems related to parts of a circle have to be solved.
- Find the length of the development of any part of the ring (bracelet). Given the diameter and chord (option: diameter and central angle), find the length of the arc.
- There is a drawing on a plane, you need to find out its size in projection after bending it into an arc. Given the arc length and diameter, find the chord length.
- Find out the height of the part obtained by bending a flat workpiece into an arc. Source data options: arc length and diameter, arc length and chord; find the height of the segment.
Life will give you other examples, but I gave these only to show the need to set some two parameters to find all the others. This is what we will do. Namely, we will take five parameters of the segment: D, L, X, φ and H. Then, choosing all possible pairs from them, we will consider them as initial data and find all the rest by brainstorming.
In order not to unnecessarily burden the reader, I will not give detailed solutions, but will present only the results in the form of formulas (those cases where there is no formal solution, I will discuss along the way).
And one more note: about units of measurement. All quantities, except the central angle, are measured in the same abstract units. This means that if, for example, you specify one value in millimeters, then the other does not need to be specified in centimeters, and the resulting values will be measured in the same millimeters (and areas in square millimeters). The same can be said for inches, feet and nautical miles.
And only the central angle in all cases is measured in degrees and nothing else. Because, as a rule of thumb, people who design something round don't tend to measure angles in radians. The phrase “angle pi by four” confuses many, while “angle forty-five degrees” is understandable to everyone, since it is only five degrees higher than normal. However, in all formulas there will be one more angle - α - present as an intermediate value. In meaning, this is half the central angle, measured in radians, but you can safely not delve into this meaning.
1. Given the diameter D and arc length L
; chord length  ;
;
segment height ![]() ; central angle
; central angle ![]() .
.
2. Given diameter D and chord length X
![]() ; arc length ;
; arc length ;
segment height ![]() ; central angle
; central angle ![]() .
.
Since the chord divides the circle into two segments, this problem has not one, but two solutions. To get the second, you need to replace the angle α in the above formulas with the angle .
3. Given the diameter D and central angle φ
![]() ; arc length ;
; arc length ;
chord length  ; segment height
; segment height ![]() .
.
4. Given the diameter D and height of the segment H
 ; arc length ;
; arc length ;
chord length  ; central angle
; central angle ![]() .
.
6. Given arc length L and central angle φ
![]() ; diameter ;
; diameter ;
chord length  ; segment height
; segment height ![]() .
.
8. Given the chord length X and the central angle φ
![]() ; arc length
; arc length ![]() ;
;
diameter ; segment height ![]() .
.
9. Given the length of the chord X and the height of the segment H
![]() ; arc length
; arc length ![]() ;
;
diameter ; central angle ![]() .
.
10. Given the central angle φ and the height of the segment H
![]() ; diameter
; diameter ![]() ;
;
arc length ; chord length  .
.
The attentive reader could not help but notice that I missed two options:
5. Given arc length L and chord length X
7. Given the length of the arc L and the height of the segment H
These are just those two unpleasant cases when the problem does not have a solution that could be written in the form of a formula. And the task is not so rare. For example, you have a flat piece of length L, and you want to bend it so that its length becomes X (or its height becomes H). What diameter should I take the mandrel (crossbar)?
This problem comes down to solving the equations: ![]() ; - in option 5
; - in option 5
; - in option 7
and although they cannot be solved analytically, they can be easily solved programmatically. And I even know where to get such a program: on this very site, under the name . Everything that I am telling you here at length, she does in microseconds.
To complete the picture, let’s add to the results of our calculations the circumference and three area values - circle, sector and segment. (Areas will help us a lot when calculating the mass of all round and semicircular parts, but more on this in a separate article.) All these quantities are calculated using the same formulas:
circumference ;
area of a circle  ;
;
sector area ![]() ;
;
segment area ![]() ;
;
And in conclusion, let me remind you once again about the existence of an absolutely free program that performs all of the above calculations, freeing you from the need to remember what an arctangent is and where to look for it.
Circumference called a closed, plane curve, all points of which, lying in the same plane, are located at the same distance from the center.
Dot ABOUT is the center of the circle, R is the radius of the circle - the distance from any point on the circle to the center. By definition, all radii of a closed
 rice. 1
rice. 1
the curves have the same length.
The distance between two points on a circle is called a chord. A segment of a circle passing through its center and connecting two of its points is called a diameter. The midpoint of the diameter is the center of the circle. Points on a circle divide a closed curve into two parts, each part is called a circular arc. If the ends of the arc belong to the diameter, then such a circle is called a semicircle, the length of which is usually denoted π . The degree measure of two circles that have common ends is 360 degrees.
Concentric circles are circles that have a common center. Orthogonal circles are circles that intersect at an angle of 90 degrees.
The plane enclosed by a circle is called a circle. One part of the circle, which is limited by two radii and an arc, is a circular sector. A sector arc is an arc that bounds a sector.
 Rice. 2
Rice. 2
The relative position of a circle and a straight line (Fig. 2).
A circle and a straight line have two points in common if the distance from the straight line to the center of the circle is less than the radius of the circle. In this case, the straight line in relation to the circle is called a secant.
A circle and a straight line have one common point if the distance from the straight line to the center of the circle is equal to the radius of the circle. In this case, the line in relation to the circle is called tangent to the circle. Their common point is called the tangency point of the circle and the line.
Basic circle formulas:

- C = 2πR , Where C - circumference
- R = С/(2π) = D/2 , Where С/(2π) — length of the arc of a circle
- D = C/π = 2R , Where D - diameter
- S = πR2 , Where S - area of a circle
- S = ((πR2)/360)α , Where S — area of the circular sector
The circumference and circle got their name in Ancient Greece. Already in ancient times, people were interested in round bodies, so the circle became the crown of perfection. The fact that a round body could move on its own was the impetus for the invention of the wheel. It would seem, what is special about this invention? But imagine if in an instant the wheels disappear from our lives. This invention later gave rise to the mathematical concept of a circle.
The video course “Get an A” includes all the topics necessary to successfully pass the Unified State Exam in mathematics with 60-65 points. Completely all tasks 1-13 of the Profile Unified State Exam in mathematics. Also suitable for passing the Basic Unified State Examination in mathematics. If you want to pass the Unified State Exam with 90-100 points, you need to solve part 1 in 30 minutes and without mistakes!
Preparation course for the Unified State Exam for grades 10-11, as well as for teachers. Everything you need to solve Part 1 of the Unified State Exam in mathematics (the first 12 problems) and Problem 13 (trigonometry). And this is more than 70 points on the Unified State Exam, and neither a 100-point student nor a humanities student can do without them.
All the necessary theory. Quick solutions, pitfalls and secrets of the Unified State Exam. All current tasks of part 1 from the FIPI Task Bank have been analyzed. The course fully complies with the requirements of the Unified State Exam 2018.
The course contains 5 large topics, 2.5 hours each. Each topic is given from scratch, simply and clearly.
Hundreds of Unified State Exam tasks. Word problems and probability theory. Simple and easy to remember algorithms for solving problems. Geometry. Theory, reference material, analysis of all types of Unified State Examination tasks. Stereometry. Tricky solutions, useful cheat sheets, development of spatial imagination. Trigonometry from scratch to problem 13. Understanding instead of cramming. Clear explanations of complex concepts. Algebra. Roots, powers and logarithms, function and derivative. A basis for solving complex problems of Part 2 of the Unified State Exam.
How well do you remember all the names associated with the circle? Just in case, let us remind you - look at the pictures - refresh your knowledge.
Firstly - The center of a circle is a point from which the distances from all points on the circle are the same.
Secondly - radius - a line segment connecting the center and a point on the circle.

There are a lot of radii (as many as there are points on the circle), but All radii have the same length.
Sometimes for short radius they call it exactly length of the segment“the center is a point on the circle,” and not the segment itself.
And here's what happens if you connect two points on a circle? Also a segment?
So, this segment is called "chord".


Just as in the case of radius, diameter is often the length of a segment connecting two points on a circle and passing through the center. By the way, how are diameter and radius related? Look carefully. Of course, the radius is equal to half the diameter.

In addition to chords, there are also secants.

Remember the simplest thing?
Central angle is the angle between two radii.

And now - the inscribed angle
Inscribed angle - the angle between two chords that intersect at a point on a circle.

In this case, they say that the inscribed angle rests on an arc (or on a chord).
Look at the picture:


Measurements of arcs and angles.
Circumference. Arcs and angles are measured in degrees and radians. First, about degrees. There are no problems for angles - you need to learn how to measure the arc in degrees.

The degree measure (arc size) is the value (in degrees) of the corresponding central angle
What does the word “appropriate” mean here? Let's look carefully:

Do you see two arcs and two central angles? Well, a larger arc corresponds to a larger angle (and it’s okay that it’s larger), and a smaller arc corresponds to a smaller angle.
So, we agreed: the arc contains the same number of degrees as the corresponding central angle.
And now about the scary thing - about radians!
What kind of beast is this “radian”?
Imagine this: Radians are a way of measuring angles... in radii!
An angle of radians is a central angle whose arc length is equal to the radius of the circle.
Then the question arises - how many radians are there in a straight angle?

In other words: how many radii “fit” in half a circle? Or in another way: how many times is the length of half a circle greater than the radius?
Scientists asked this question back in Ancient Greece.
And so, after a long search, they discovered that the ratio of the circumference to the radius does not want to be expressed in “human” numbers like, etc.
And it’s not even possible to express this attitude through roots. That is, it turns out that it is impossible to say that half a circle is times or times larger than the radius! Can you imagine how amazing it was for people to discover this for the first time?! For the ratio of the length of half a circle to the radius, “normal” numbers were not enough. I had to enter a letter.
So, - this is a number expressing the ratio of the length of the semicircle to the radius.
Now we can answer the question: how many radians are there in a straight angle? It contains radians. Precisely because half the circle is times larger than the radius.
Ancient (and not so ancient) people throughout the centuries (!) tried to more accurately calculate this mysterious number, to better express it (at least approximately) through “ordinary” numbers. And now we are incredibly lazy - two signs after a busy day are enough for us, we are used to
Think about it, this means, for example, that the length of a circle with a radius of one is approximately equal, but this exact length is simply impossible to write down with a “human” number - you need a letter. And then this circumference will be equal. And of course, the circumference of the radius is equal.
Let's go back to radians.
We have already found out that a straight angle contains radians.

What we have:
That means I'm glad, that is, I'm glad. In the same way, a plate with the most popular angles is obtained.
The relationship between the values of the inscribed and central angles.
There is an amazing fact:
The inscribed angle is half the size of the corresponding central angle.

Look how this statement looks in the picture. A “corresponding” central angle is one whose ends coincide with the ends of the inscribed angle, and the vertex is at the center. And at the same time, the “corresponding” central angle must “look” at the same chord () as the inscribed angle.
Why is this so? Let's look at a simple case first. Let one of the chords pass through the center. It happens like that sometimes, right?

What happens here? Let's consider. It is isosceles - after all, and - radii. So, (labeled them).
Now let's look at. This is the outer corner for! We recall that an external angle is equal to the sum of two internal angles not adjacent to it, and write:
That is! Unexpected effect. But there is also a central angle for the inscribed.

This means that for this case they proved that the central angle is twice the inscribed angle. But it’s a painfully special case: isn’t it true that the chord doesn’t always go straight through the center? But it’s okay, now this particular case will help us a lot. Look: second case: let the center lie inside.

Let's do this: draw the diameter. And then... we see two pictures that were already analyzed in the first case. Therefore we already have that
This means (in the drawing, a)
Well, that leaves the last case: the center is outside the corner.

We do the same thing: draw the diameter through the point. Everything is the same, but instead of a sum there is a difference.
That's all!
Let's now form two main and very important consequences from the statement that the inscribed angle is half the central angle.
Corollary 1
All inscribed angles based on one arc are equal to each other.
We illustrate:

There are countless inscribed angles based on the same arc (we have this arc), they may look completely different, but they all have the same central angle (), which means that all these inscribed angles are equal between themselves.
Corollary 2
The angle subtended by the diameter is a right angle.
Look: what angle is central to?

Certainly, . But he is equal! Well, therefore (as well as many more inscribed angles resting on) and is equal.
Angle between two chords and secants
But what if the angle we are interested in is NOT inscribed and NOT central, but, for example, like this:

or like this?

Is it possible to somehow express it through some central angles? It turns out that it is possible. Look: we are interested.
a) (as an external corner for). But - inscribed, rests on the arc -. - inscribed, rests on the arc - .

For beauty they say:

The angle between the chords is equal to half the sum of the angular values of the arcs enclosed in this angle.
They write this for brevity, but of course, when using this formula you need to keep in mind the central angles
b) And now - “outside”! How to be? Yes, almost the same! Only now (again we apply the property of the external angle for). That is now.

And that means... Let’s bring beauty and brevity to the notes and wording:

The angle between the secants is equal to half the difference in the angular values of the arcs enclosed in this angle.
Well, now you are armed with all the basic knowledge about angles related to a circle. Go ahead, take on the challenges!
CIRCLE AND INSINALED ANGLE. AVERAGE LEVEL
Even a five-year-old child knows what a circle is, right? Mathematicians, as always, have an abstruse definition on this subject, but we will not give it (see), but rather let us remember what the points, lines and angles associated with a circle are called.
Important Terms
Firstly:
| center of the circle- a point from which all points on the circle are the same distance. |
Secondly:
There is another accepted expression: “the chord contracts the arc.” Here in the figure, for example, the chord subtends the arc. And if a chord suddenly passes through the center, then it has a special name: “diameter”.
By the way, how are diameter and radius related? Look carefully. Of course,
And now - the names for the corners.
Natural, isn't it? The sides of the angle extend from the center - which means the angle is central.
This is where difficulties sometimes arise. Pay attention - NOT ANY angle inside a circle is inscribed, but only one whose vertex “sits” on the circle itself.
Let's see the difference in the pictures:
Another way they say:
There is one tricky point here. What is the “corresponding” or “own” central angle? Just an angle with the vertex at the center of the circle and the ends at the ends of the arc? Not certainly in that way. Look at the drawing.
One of them, however, doesn’t even look like a corner - it’s bigger. But a triangle cannot have more angles, but a circle may well! So: the smaller arc AB corresponds to a smaller angle (orange), and the larger arc corresponds to a larger one. Just like that, isn't it?
The relationship between the magnitudes of the inscribed and central angles
Remember this very important statement:
In textbooks they like to write this same fact like this:
Isn’t it true that the formulation is simpler with a central angle?
But still, let’s find a correspondence between the two formulations, and at the same time learn to find in the drawings the “corresponding” central angle and the arc on which the inscribed angle “rests”.
Look: here is a circle and an inscribed angle:
Where is its “corresponding” central angle?
Let's look again:
What is the rule?
But! In this case, it is important that the inscribed and central angles “look” at the arc from one side. For example:
Oddly enough, blue! Because the arc is long, longer than half the circle! So don’t ever get confused!
What consequence can be deduced from the “halfness” of the inscribed angle?
But, for example:
Angle subtended by diameter
Have you already noticed that mathematicians love to talk about the same thing in different words? Why do they need this? You see, the language of mathematics, although formal, is alive, and therefore, as in ordinary language, every time you want to say it in a way that is more convenient. Well, we have already seen what “an angle rests on an arc” means. And imagine, the same picture is called “an angle rests on a chord.” On what? Yes, of course, to the one that tightens this arc!
When is it more convenient to rely on a chord than on an arc?
Well, in particular, when this chord is a diameter.
There is a surprisingly simple, beautiful and useful statement for such a situation!
Look: here is the circle, the diameter and the angle that rests on it.
CIRCLE AND INSINALED ANGLE. BRIEFLY ABOUT THE MAIN THINGS
1. Basic concepts.
3. Measurements of arcs and angles.
An angle of radians is a central angle whose arc length is equal to the radius of the circle.
This is a number that expresses the ratio of the length of a semicircle to its radius.
The circumference of the radius is equal to.
4. The relationship between the values of the inscribed and central angles.
Well, the topic is over. If you are reading these lines, it means you are very cool.
Because only 5% of people are able to master something on their own. And if you read to the end, then you are in this 5%!
Now the most important thing.
You have understood the theory on this topic. And, I repeat, this... this is just super! You are already better than the vast majority of your peers.
The problem is that this may not be enough...
For what?
For successfully passing the Unified State Exam, for entering college on a budget and, MOST IMPORTANTLY, for life.
I won’t convince you of anything, I’ll just say one thing...
People who have received a good education earn much more than those who have not received it. This is statistics.
But this is not the main thing.
The main thing is that they are MORE HAPPY (there are such studies). Perhaps because many more opportunities open up before them and life becomes brighter? Don't know...
But think for yourself...
What does it take to be sure to be better than others on the Unified State Exam and ultimately be... happier?
GAIN YOUR HAND BY SOLVING PROBLEMS ON THIS TOPIC.
You won't be asked for theory during the exam.
You will need solve problems against time.
And, if you haven’t solved them (A LOT!), you’ll definitely make a stupid mistake somewhere or simply won’t have time.
It's like in sports - you need to repeat it many times to win for sure.
Find the collection wherever you want, necessarily with solutions, detailed analysis and decide, decide, decide!
You can use our tasks (optional) and we, of course, recommend them.
In order to get better at using our tasks, you need to help extend the life of the YouClever textbook you are currently reading.
How? There are two options:
- Unlock all hidden tasks in this article -
- Unlock access to all hidden tasks in all 99 articles of the textbook - Buy a textbook - 899 RUR
Yes, we have 99 such articles in our textbook and access to all tasks and all hidden texts in them can be opened immediately.
Access to all hidden tasks is provided for the ENTIRE life of the site.
In conclusion...
If you don't like our tasks, find others. Just don't stop at theory.
“Understood” and “I can solve” are completely different skills. You need both.
Find problems and solve them!
Problem 10 (OGE - 2015)
On a circle with center O, points A and B are marked so that ∠ AOB = 18°. The length of the smaller arc AB is 5. Find the length of the larger arc of the circle.
Solution
∠ AOB = 18°. The entire circle is 360°. Therefore ∠ AOB is 18/360 = 1/20 of a circle.
This means that the smaller arc AB is 1/20 of the entire circle, so the larger arc is the rest, i.e. 19/20 circumference.
1/20 of a circle corresponds to an arc length of 5. Then the length of the larger arc is 5 * 19 = 95.
Problem 10 (OGE - 2015)
On a circle with center O, points A and B are marked so that ∠ AOB = 40°. The length of the smaller arc AB is 50. Find the length of the larger arc of the circle.
Solution
∠ AOB = 40°. The entire circle is 360°. Therefore ∠ AOB is 40/360 = 1/9 of a circle.
This means that the smaller arc AB is 1/9 of the entire circle, so the larger arc is the rest, i.e. 8/9 circle.
1/9 of a circle corresponds to an arc length of 50. Then the length of the larger arc is 50*8 = 400.
Answer: 400.
Task 10 (GIA - 2014)
The length of a chord of a circle is 72, and the distance from the center of the circle to this chord is 27. Find the diameter of the circle.

Solution

Using the Pythagorean theorem, from the right triangle AOB we obtain:
AO 2 = OB 2 +AB 2,
AO 2 = 27 2 +36 2 = 729+1296 = 2025,
Then the diameter is 2R = 2*45 = 90.
Task 10 (GIA - 2014)
Point O is the center of the circle on which points A, B and C lie. It is known that ∠ABC = 134° and ∠OAB = 75°. Find angle BCO. Give your answer in degrees.