1 funktion derivaatta pisteessä. Johdannainen funktiosta

Määritelmä. Olkoon funktio \ (y = f (x) \) määritelty jossain välissä, joka sisältää pisteen \ (x_0 \). Anna argumentille inkrementti \ (\ Delta x \), jotta se ei poistu tästä intervallista. Etsi funktion \ (\ Delta y \) vastaava lisäys (siirrettäessä pisteestä \ (x_0 \) pisteeseen \ (x_0 + \ Delta x \)) ja muodosta suhde \ (\ frac (\ Delta y) ( \ Delta x) \). Jos tälle suhteelle on raja \ (\ Delta x \ oikea nuoli 0 \), niin määritetty raja kutsutaan johdannainen funktio\ (y = f (x) \) pisteessä \ (x_0 \) ja merkitse \ (f "(x_0) \).

$$ \ lim _ (\ Delta x \ to 0) \ frac (\ Delta y) (\ Delta x) = f "(x_0) $$

Symbolia y " käytetään usein merkitsemään derivaatta. Huomaa, että y" = f (x) on uusi funktio, mutta liittyy luonnollisesti funktioon y = f (x), joka on määritelty kaikissa pisteissä x, joissa yllä oleva raja on olemassa. ... Tätä funktiota kutsutaan seuraavasti: funktion y = f (x) derivaatta.

Johdannan geometrinen merkitys on seuraava. Jos funktion y = f (x) kuvaaja pisteessä, jossa abskissa x = a voidaan piirtää tangentti, ei yhdensuuntainen y-akselin kanssa, niin f (a) ilmaisee tangentin kulmakertoimen:
\ (k = f "(a) \)

Koska \ (k = tg (a) \), yhtälö \ (f "(a) = tg (a) \) on tosi.

Tulkikaamme nyt derivaatan määritelmää likimääräisten yhtälöiden näkökulmasta. Olkoon funktiolla \ (y = f (x) \) derivaatta tietyssä pisteessä \ (x \):
$$ \ lim _ (\ Delta x \ to 0) \ frac (\ Delta y) (\ Delta x) = f "(x) $$
Tämä tarkoittaa, että likimääräinen yhtälö \ (\ frac (\ Delta y) (\ Delta x) \ likimain f "(x) \) toteutuu lähellä pistettä x, eli \ (\ Delta y \ liki f" (x) \ cdot \ Delta x \). Saadun likimääräisen yhtälön merkityksellinen merkitys on seuraava: funktion inkrementti on "melkein verrannollinen" argumentin kasvuun ja suhteellisuuskerroin on derivaatan arvo tietyssä pisteessä x. Esimerkiksi funktio \ (y = x ^ 2 \) täyttää likimääräisen yhtälön \ (\ Delta y \ noin 2x \ cdot \ Delta x \). Jos analysoimme derivaatan määritelmää huolellisesti, huomaamme, että se sisältää algoritmin sen löytämiseksi.

Muotoillaan se.

Kuinka löytää funktion y = f (x) derivaatta?

1. Korjaa arvo \ (x \), etsi \ (f (x) \)
2. Anna argumentille \ (x \) lisäys \ (\ Delta x \), siirry uuteen pisteeseen \ (x + \ Delta x \), etsi \ (f (x + \ Delta x) \)
3. Etsi funktion lisäys: \ (\ Delta y = f (x + \ Delta x) - f (x) \)
4. Muodosta relaatio \ (\ frac (\ Delta y) (\ Delta x) \)
5. Laske $$ \ lim _ (\ Delta x \ to 0) \ frac (\ Delta y) (\ Delta x) $$
Tämä raja on funktion derivaatta pisteessä x.

Jos funktiolla y = f (x) on derivaatta pisteessä x, niin sitä kutsutaan differentioituvaksi pisteessä x. Kutsutaan menetelmää funktion y = f (x) derivaatan löytämiseksi erilaistuminen funktio y = f (x).

Tarkastellaanpa seuraavaa kysymystä: miten funktion jatkuvuus ja differentioituvuus tietyssä pisteessä liittyvät toisiinsa?

Olkoon funktio y = f (x) differentioituva pisteessä x. Tällöin funktion kuvaajalle voidaan piirtää tangentti pisteessä M (x; f (x)), ja muistaakseni tangentin kaltevuus on f "(x). Tällainen kuvaaja ei voi" katketa ​​"pisteessä piste M, eli funktion on oltava jatkuva pisteessä x.

Se oli "sormenpään" perustelu. Esitetään tiukempi perustelu. Jos funktio y = f (x) on differentioituva pisteessä x, niin likimääräinen yhtälö \ (\ Delta y \ liki f "(x) \ cdot \ Delta x \) pätee. Jos tässä yhtälössä \ (\ Delta x \) pyrkii nollaan, sitten \ (\ Delta y \) pyrkii nollaan, ja tämä on funktion jatkuvuuden ehto pisteessä.

Niin, jos funktio on differentioituva pisteessä x, niin se on myös jatkuva tässä pisteessä.

Päinvastoin ei pidä paikkaansa. Esimerkiksi: funktio y = | x | on jatkuva kaikkialla, erityisesti pisteessä x = 0, mutta funktion kaavion tangenttia "liitospisteessä" (0; 0) ei ole olemassa. Jos jossain kohdassa funktion kuvaajalle on mahdotonta piirtää tangenttia, niin tässä vaiheessa ei ole derivaattia.

Vielä yksi esimerkki. Funktio \ (y = \ sqrt (x) \) on jatkuva koko lukuviivalla, mukaan lukien pisteessä x = 0. Ja funktion kaavion tangentti on olemassa missä tahansa pisteessä, myös pisteessä x = 0 Mutta tässä kohdassa tangentti osuu yhteen y-akselin kanssa, eli se on kohtisuorassa abskissa-akselia vastaan, sen yhtälö on muotoa x = 0. Tällaisella suoralla ei ole kaltevuutta, joten ei ole \ ( f "(0) \)

Joten tutustuimme funktion uuteen ominaisuuteen - differentiaatioon. Ja kuinka voimme päätellä funktion kaaviosta sen differentiatiivisuudesta?

Vastaus on itse asiassa saatu yllä. Jos jossain kohdassa funktion kuvaajalle on mahdollista piirtää tangentti, joka ei ole kohtisuorassa abskissa-akselia vastaan, niin tässä vaiheessa funktio on differentioituva. Jos jossain vaiheessa funktion kuvaajan tangenttia ei ole olemassa tai se on kohtisuorassa abskissa-akselia vastaan, niin funktio ei tässä vaiheessa ole differentioituva.

Erottamisen säännöt

Operaatiota derivaatan löytämiseksi kutsutaan erilaistuminen... Tätä toimintoa suoritettaessa joudut usein työskentelemään osamääräjen, summien, funktioiden tulojen sekä "funktioiden funktioiden" eli monimutkaisten funktioiden kanssa. Johdannan määritelmän perusteella on mahdollista johtaa tätä työtä helpottavia differentiointisääntöjä. Jos C on vakioluku ja f = f (x), g = g (x) ovat joitain differentioituvia funktioita, niin seuraavat ovat totta eriyttämissäännöt:

Joidenkin funktioiden johdannainen taulukko

Kun ratkaistiin erilaisia ​​geometrian, mekaniikan, fysiikan ja muiden tiedonhaarojen ongelmia, tuli tarpeelliseksi käyttää samaa analyyttistä prosessia tästä funktiosta y = f (x) hanki uusi funktio nimeltä johdettu toiminto(tai yksinkertaisesti funktion f (x) derivaatta ja ne on merkitty symbolilla

Prosessi, jolla annetusta funktiosta f (x) hanki uusi toiminto f "(x) kutsutaan erilaistuminen ja se koostuu seuraavista kolmesta vaiheesta: 1) annamme argumentin x lisäys  x ja määritä funktion vastaava lisäys  y = f (x + x) -f (x); 2) muodosta suhde

3) harkitsee x vakio, ja  x0, löydämme
, jota merkitsemme f "(x), ikään kuin korostaen, että tuloksena oleva funktio riippuu vain arvosta x jossa mennään rajalle. Määritelmä: Johdannainen y "= f" (x) tämä funktio y = f (x) tietylle x:lle kutsutaan funktion inkrementin ja argumentin inkrementin suhteen rajaksi edellyttäen, että argumentin inkrementti pyrkii nollaan, jos tämä raja tietysti on olemassa, ts. on rajallinen. Täten,
, tai

Huomaa, että jos jollain arvolla x, esimerkiksi klo x = a, asenne
klo  x0 ei pyri äärelliseen rajaan, niin tässä tapauksessa sanotaan, että funktio f (x) klo x = a(tai pisteessä x = a) ei ole johdannaista tai se ei ole differentioituva pisteessä x = a.

2. Derivaatan geometrinen merkitys.

Tarkastellaan funktion y = f (x) kuvaajaa, joka on differentioituva pisteen x 0 läheisyydessä

f (x)

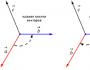
Tarkastellaan mielivaltaista suoraa, joka kulkee funktion kuvaajan pisteen läpi - piste A (x 0, f (x 0)) ja leikkaa kuvaajan jossakin pisteessä B (x; f (x)). Tällaista suoraa (AB) kutsutaan sekantiksi. ∆ABS:sta: AC = ∆x; ВС = ∆у; tgβ = ∆y / ∆x.

Koska AC || Ox, sitten ALO = BAC = β (vastaa rinnakkain). Mutta ALO on sekantin AB kaltevuuskulma Ox-akselin positiiviseen suuntaan. Siten tgβ = k on suoran AB kaltevuus.

Nyt vähennämme ∆х, ts. ∆х → 0. Tässä tapauksessa piste B lähestyy pistettä A käyrän mukaan ja sekantti AB pyörii. Sekantin AB raja-asema kohdassa ∆x → 0 on suora (a), jota kutsutaan funktion y = f (x) kuvaajan tangentiksi pisteessä A.

Jos siirrytään rajalle ∆х → 0 yhtälössä tanβ = ∆y / ∆x, niin saadaan
tai tg = f "(x 0), koska
-Ox-akselin positiivisen suunnan tangentin kaltevuuskulma
, johdannaisen määritelmän mukaan. Mutta tg = k on tangentin kulmakerroin, mikä tarkoittaa, että k = tg = f "(x 0).

Joten derivaatan geometrinen merkitys on seuraava:

Pisteessä x olevan funktion derivaatta 0 on yhtä suuri kuin funktion kaavion tangentin kaltevuus, joka on piirretty pisteeseen, jossa on abskissa x 0 .

3. Johdannan fyysinen merkitys.

Harkitse pisteen liikettä suoraa pitkin. Olkoon pisteen koordinaatti annettu milloin tahansa x (t). Tiedetään (fysiikkakurssilta), että keskinopeus tietyn ajanjakson aikana on yhtä suuri kuin tämän ajanjakson aikana kuljetun matkan suhde aikaväliin, ts.

Vav = ∆x / ∆t. Siirrytään viimeisen yhtälön rajaan muodossa ∆t → 0.

lim Vav (t) =  (t 0) - hetkellinen nopeus hetkellä t 0, ∆t → 0.

ja lim = ∆x / ∆t = x "(t 0) (derivaatan määritelmän mukaan).

Joten  (t) = x "(t).

Derivaatan fyysinen merkitys on seuraava: funktion derivaattay = f(x) pisteessäx 0 on funktion muutosnopeusf(x) kohdassax 0

Derivaattaa käytetään fysiikassa nopeuden löytämiseen tunnetun koordinaatin funktion perusteella ajasta, kiihtyvyyttä tunnetun nopeuden funktion perusteella ajasta.

 (t) = x "(t) - nopeus,

a (f) =  "(t) - kiihtyvyys tai

Jos ympyrän materiaalin pisteen liikelaki tunnetaan, voit löytää kulmanopeuden ja kulmakiihtyvyyden pyörimisliikkeen aikana:

φ = φ (t) - kulman muutos ajan myötä,

ω = φ "(t) - kulmanopeus,

ε = φ "(t) - kulmakiihtyvyys tai ε = φ" (t).

Jos epähomogeenisen sauvan massan jakautumislaki tunnetaan, niin epähomogeenisen sauvan lineaaritiheys löytyy:

m = m (x) - massa,

x , l - tangon pituus,

p = m "(x) - lineaarinen tiheys.

Derivaattaa käytetään kimmoisuuden ja harmonisten värähtelyjen teorian tehtävien ratkaisemiseen. Siis Hooken lain mukaan

F = -kx, x on muuttuva koordinaatti, k on jousen kimmokerroin. Asettamalla ω 2 = k / m, saadaan jousiheilurin differentiaaliyhtälö x "(t) + ω 2 x (t) = 0,

missä ω = √k / √m on värähtelytaajuus (l / c), k on jousen jäykkyys (H / m).

Yhtälöä, jonka muoto on у "+ ω 2 y = 0, kutsutaan harmonisten värähtelyjen yhtälöksi (mekaaninen, sähköinen, sähkömagneettinen). Tällaisten yhtälöiden ratkaisu on funktio.

у = Asin (ωt + φ 0) tai у = Acos (ωt + φ 0), jossa

А - värähtelyjen amplitudi, ω - syklinen taajuus,

φ 0 - alkuvaihe.

On täysin mahdotonta ratkaista fyysisiä ongelmia tai esimerkkejä matematiikassa ilman tietoa derivaatista ja sen laskentamenetelmistä. Johdannainen on yksi matemaattisen analyysin tärkeimmistä käsitteistä. Päätimme omistaa tämän päivän artikkelin tälle perustavanlaatuiselle aiheelle. Mikä on derivaatta, mikä on sen fysikaalinen ja geometrinen merkitys, miten lasketaan funktion derivaatta? Kaikki nämä kysymykset voidaan yhdistää yhdeksi: kuinka ymmärtää johdannainen?

Johdannan geometrinen ja fyysinen merkitys

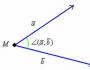
Olkoon toiminto f (x) annetaan jossain välissä (a, b) ... Pisteet х ja х0 kuuluvat tähän väliin. Kun x muuttuu, itse funktio muuttuu. Argumentin muuttaminen - ero sen arvojen välillä x-x0 ... Tämä ero on kirjoitettu muodossa delta x ja sitä kutsutaan argumentin lisäykseksi. Toiminnon muutos tai lisäys on funktion arvojen ero kahdessa pisteessä. Johdannainen määritelmä:

Funktion derivaatta pisteessä on raja funktion inkrementin tietyssä pisteessä suhteessa argumentin lisäykseen, kun jälkimmäinen pyrkii nollaan.

Muuten se voidaan kirjoittaa näin:

Mitä järkeä on löytää tällainen raja? Ja tässä mitä:

funktion derivaatta pisteessä on yhtä suuri kuin OX-akselin välisen kulman tangentti ja funktion kaavion tangentti tässä pisteessä.

Johdannan fyysinen merkitys: reitin derivaatta ajan suhteen on yhtä suuri kuin suoraviivaisen liikkeen nopeus.

Todellakin, kouluajoista lähtien kaikki ovat ymmärtäneet, että nopeus on yksityinen tie. x = f (t) ja aikaa t ... Keskinopeus tietyn ajanjakson aikana:

Selvittääksesi liikkeen nopeuden kerrallaan t0 sinun on laskettava raja:

Sääntö yksi: ota vakio

Vakio voidaan siirtää derivaatan etumerkin ulkopuolelle. Lisäksi se on tehtävä. Kun ratkaiset esimerkkejä matematiikassa, ota sääntönä - Jos voit yksinkertaistaa ilmaisua, muista yksinkertaistaa .

Esimerkki. Lasketaan derivaatta:

Sääntö kaksi: funktioiden summan derivaatta

Kahden funktion summan derivaatta on yhtä suuri kuin näiden funktioiden derivaattojen summa. Sama pätee funktioiden eron johdannaiseen.

Emme todista tätä lausetta, vaan harkitsemme käytännön esimerkkiä.

Etsi funktion derivaatta:

Kolmas sääntö: funktioiden tulon derivaatta

Kahden differentioituvan funktion tulon derivaatta lasketaan kaavalla:

Esimerkki: etsi funktion derivaatta:

Ratkaisu:

Tässä on tärkeää sanoa monimutkaisten funktioiden derivaattojen laskemisesta. Kompleksisen funktion derivaatta on yhtä suuri kuin tämän funktion derivaatan tulo väliargumentin suhteen väliargumentin derivaatalla riippumattoman muuttujan suhteen.

Yllä olevassa esimerkissä tapaamme lausekkeen:

Tässä tapauksessa väliargumentti on 8x viidenteen potenssiin nähden. Laskeaksemme tällaisen lausekkeen derivaatan laskemme ensin ulkoisen funktion derivaatan väliargumentin suhteen ja kerromme sitten välittömän väliargumentin derivaatalla riippumattoman muuttujan suhteen.

Sääntö neljä: kahden funktion osamääräderivaata

Kaava kahden funktion osamäärän derivaatan määrittämiseksi:

Yritimme kertoa sinulle nukkejen johdannaisista tyhjästä. Tämä aihe ei ole niin yksinkertainen kuin miltä se kuulostaa, joten varoita: esimerkeissä on usein sudenkuoppia, joten ole varovainen laskeessasi johdannaisia.

Jos sinulla on kysyttävää tästä ja muista aiheista, voit ottaa yhteyttä opiskelijapalveluun. Lyhyessä ajassa autamme sinua ratkaisemaan vaikeimman testin ja selviytymään tehtävistä, vaikka et olisi koskaan aiemmin laskenut johdannaisia.

Kun ihminen on ottanut ensimmäiset itsenäiset askeleet matemaattisen analyysin opiskelussa ja alkaa kysyä epämiellyttäviä kysymyksiä, ei ole enää niin helppoa päästää irti lauseesta, että "kaalista löydettiin differentiaalilaskentaa". Siksi on aika saada päättäväisyyttä ja paljastaa syntymän salaisuus. johdannaistaulukot ja differentiointisäännöt... Aloitettu artikkelissa johdannaisen merkityksestä, jota suosittelen lämpimästi opiskeluun, koska siellä mietimme juuri johdannaisen käsitettä ja aloimme klikata aiheeseen liittyviä ongelmia. Samalla oppitunnilla on selkeä käytännönläheisyys, lisäksi

alla käsitellyt esimerkit voidaan periaatteessa hallita ja puhtaasti muodollisesti (esimerkiksi kun ei ole aikaa/halua syventyä johdannaisen olemukseen). On myös erittäin toivottavaa (mutta ei taaskaan välttämätöntä) pystyä löytämään johdannaisia ​​"tavanomaisella" menetelmällä - ainakin kahden perusopetuksen tasolla: Kuinka löytää johdannainen ja monimutkaisen funktion johdannainen.

Mutta jotain, jota ilman et varmasti tule toimeen nyt, on ilman sitä toimintojen rajat... Sinun täytyy YMMÄRTÄ, mikä on raja ja pystyä ratkaisemaan ne ainakin keskitasolla. Ja kaikki johdannaisen takia

funktio pisteessä määritetään kaavalla:

Muistan nimitykset ja termit: he kutsuvat argumentin lisäys;

- funktion lisäys;

- nämä ovat YKSI symboleja ("deltaa" ei voi "revitä" pois "x":stä tai "pelistä").

Ilmeisesti se on "dynaaminen" muuttuja, - vakio ja rajan laskemisen tulos - numero (joskus - "plus" tai "miinus" ääretön).

Voit ottaa huomioon MITÄ tahansa arvoa, johon kuuluu määrittelyalueita funktio, jossa derivaatta esiintyy.

Huomautus: lauseke "jossa johdannainen on olemassa" - yleensä välttämätön! Joten esimerkiksi piste ja sisältyy funktion määritelmäalueeseen, mutta derivaatta

ei ole olemassa siellä. Siksi kaava

ei sovelleta tässä kohdassa

ja lyhennetty sanamuoto ilman tarkennusta olisi virheellinen. Samanlaiset tosiasiat pätevät myös muille funktioille, joissa on graafin "raja", erityisesti käänteissinille ja käänteiskosinille.

Siten vaihdon jälkeen saamme toisen toimintakaavan:

Kiinnitä huomiota salakavalaan seikkaan, joka voi hämmentää teekannua: tässä rajassa "x", joka on itsenäinen muuttuja, toimii ylimääräisenä, ja "dynamiikka" asetetaan jälleen lisäyksen mukaan. Rajan laskemisen tulos

on johdettu funktio.

Yllä olevan perusteella muotoilemme ehdot kahdelle tyypilliselle ongelmalle:

- Löytö johdannainen pisteessä käyttämällä johdannaisen määritelmää.

- Löytö johdannainen funktio käyttämällä johdannaisen määritelmää. Tämä versio on havaintojeni mukaan paljon yleisempi ja se tulee olemaan pääpaino.

Perusteellinen ero tehtävien välillä on, että ensimmäisessä tapauksessa on löydettävä numero (valinnaisesti ääretön) ja toisessa -

toiminto. Lisäksi johdannaista ei välttämättä ole ollenkaan.

Miten ?

Piirrä suhde ja laske raja.

Mistä se tuli johdannaisten taulukko ja differentiointisäännöt ? Ainoan rajan ansiosta

Se näyttää taikalta, mutta sisään

todellisuus - taikausko ja ei petoksia. Oppitunnilla Mikä on johdannainen? Aloin pohtia konkreettisia esimerkkejä, joissa määritelmää käyttäen löysin lineaarisen ja toisen asteen funktion derivaatat. Koulutuksellisen lämmittelyn vuoksi jatkamme häirintää johdannaisten taulukko Algoritmin ja teknisten ratkaisujen hiominen:

Itse asiassa on todistettava tehofunktion derivaatan erikoistapaus, joka yleensä esiintyy taulukossa:.

Ratkaisu on teknisesti muotoiltu kahdella tavalla. Aloitetaan ensimmäisestä, jo tutusta lähestymistavasta: tikkaat alkavat plankista ja johdettu funktio alkaa derivaatalla pisteessä.

Harkitse jotakin (erityistä) pistettä, joka kuuluu määrittelyalueita funktio, jossa derivaatta esiintyy. Asetetaan tässä vaiheessa lisäys (ei tietenkään mene pidemmälle o / o -ya) ja muodosta vastaava funktion lisäys:

Lasketaan raja:

Epävarmuus 0:0 eliminoidaan standarditekniikalla, jota pidetään jo ensimmäisellä vuosisadalla eKr. Kerrotaan

osoittaja ja nimittäjä konjugaattilauseketta kohti :

Tekniikkaa tällaisen rajan ratkaisemiseksi käsitellään yksityiskohtaisesti johdantotunnilla. toimintojen rajoista.

Koska voit valita MILLOIN pisteen intervallista

Sitten kun vaihto on suoritettu, saamme:

Iloitkaamme vielä kerran logaritmeista:

Etsi funktion derivaatta käyttämällä derivaatan määritelmää

Ratkaisu: Harkitse erilaista lähestymistapaa saman ongelman edistämiseen. Se on täsmälleen sama, mutta suunnittelun kannalta järkevämpi. Ajatuksena on päästä eroon

alaindeksi ja käytä kirjainta kirjaimen sijaan.

Harkitse mielivaltaista pistettä, joka kuuluu määrittelyalueita funktio (intervalli) ja aseta sen lisäys. Ja tässä muuten, kuten useimmissa tapauksissa, voit tehdä ilman varauksia, koska logaritminen funktio on differentioitavissa missä tahansa määrittelyalueen kohdassa.

Sitten vastaava funktion lisäys:

Etsitään johdannainen:

Suunnittelun helppoutta tasapainottaa vallitseva hämmennys

ilmaantuu aloittelijoille (eikä vain). Loppujen lopuksi olemme tottuneet siihen, että kirjain "X" muuttuu rajassa! Mutta täällä kaikki on erilaista: - antiikkipatsas, mutta - elävä vierailija, joka kävelee reippaasti pitkin museon käytävää. Eli "x" on "eräänlainen vakio".

Kommentoin epävarmuuden poistamista askel askeleelta:

(1) Käytämme logaritmin ominaisuutta.

(2) Jaa osoittaja suluissa olevalla nimittäjällä.

(3) Nimittäjässä kerromme ja jaamme keinotekoisesti "x":llä niin, että

hyödynnä ihmeellinen raja , kun taas as äärettömän pieni puhuu ääneen.

Vastaus: johdannaisen määritelmän mukaan:

Tai lyhennettynä:

Ehdotan, että suunnitellaan itsenäisesti kaksi muuta taulukkokaavaa:

Etsi johdannainen määritelmän mukaan

Tässä tapauksessa on kätevää tuoda koottu lisäys välittömästi yhteiseen nimittäjään. Likimääräinen esimerkki tehtävästä oppitunnin lopussa (ensimmäinen menetelmä).

Etsi johdannainen määritelmän mukaan

Ja tässä kaikki on vähennettävä merkittävään rajaan. Päätös virallistetaan toisella tavalla.

Useita muita näytetään samalla tavalla. taulukkojohdannaiset... Täydellinen luettelo löytyy koulun oppikirjasta tai esimerkiksi Fichtengolzin 1. osasta. En näe paljon järkeä kirjoittaa uudelleen todisteita erottelusäännöistä kirjoista - niitä myös syntyy

kaava.

Siirtyminen tosielämän tehtäviin: Esimerkki 5

Etsi funktion derivaatta käyttämällä johdannaisen määritelmää

Ratkaisu: käytä ensimmäistä suunnittelutyyliä. Harkitse jotakin pistettä, joka kuuluu, ja aseta siihen argumentin lisäys. Sitten vastaava funktion lisäys:

Ehkä jotkut lukijat eivät ole vielä täysin ymmärtäneet periaatetta, jonka mukaan lisäys tulisi tehdä. Otamme pisteen (luvun) ja etsimme siitä funktion arvon: , eli funktioon

"x" tulee korvata. Nyt otamme

Käännetty funktion lisäys voi olla hyödyllistä yksinkertaistaa välittömästi... Mitä varten? Helpota ja lyhennä ratkaisua lisärajaan.

Käytämme kaavoja, laajennamme sulkeita ja lyhennämme kaikkea, mitä voidaan lyhentää:

Kalkkuna on perattu, ei ongelmia paistin kanssa:

Lopulta:

Koska voit valita minkä tahansa oikean luvun, suoritamme vaihdon ja saamme .

Vastaus: a-priory.

Tarkistamista varten löydämme johdannaisen sääntöjen avulla

erottelu ja taulukot:

Oikea vastaus on aina hyödyllistä ja miellyttävää tietää etukäteen, joten on parempi mielessään tai luonnoksessa erottaa ehdotettu toiminto "nopeasti" heti ratkaisun alussa.

Etsi funktion derivaatta derivaatan määritelmän mukaan

Tämä on esimerkki tee-se-itse-ratkaisusta. Tulos on pinnalla:

Takaisin tyyliin 2: Esimerkki 7

Otetaan heti selvää, mitä pitäisi tapahtua. Tekijä: monimutkaisen funktion erottamisen sääntö:

Ratkaisu: harkitse mielivaltaista pistettä, joka kuuluu, aseta siihen argumentin inkrementti ja muodosta inkrementti

Etsitään johdannainen:

(1) Käytämme trigonometristä kaavaa

(2) Avaamme sulut sinin alle ja annamme samanlaiset termit kosinin alle.

(3) Sinin alla kumotaan termit, kosinin alla jaetaan osoittaja termi kerrallaan nimittäjällä.

(4) Parittoman sinin takia laitamme "miinus". Kosinuksen alla

osoittavat, että termi.

(5) Teemme keinotekoisen kertolaskun nimittäjässä käyttääksemme ensimmäinen ihana raja... Siten epävarmuus eliminoituu, kampaamme tuloksen.

Vastaus: määritelmän mukaan Kuten näette, tarkasteltavan ongelman päävaikeus perustuu

itse rajan monimutkaisuus + pakkauksen pieni erikoisuus. Käytännössä suunnittelumenetelmiä on molempia, joten kuvailen molemmat lähestymistavat mahdollisimman yksityiskohtaisesti. Ne ovat samanarvoisia, mutta silti subjektiivisen vaikutelmani mukaan teekannujen on tarkoituksenmukaisempaa noudattaa vaihtoehtoa 1 "x nollalla".

Etsi määritelmän avulla funktion derivaatta

Tämä on itsenäinen tehtävä. Malli on suunniteltu samassa hengessä kuin edellinen esimerkki.

Analysoidaan harvinaisempaa versiota ongelmasta:

Etsi funktion derivaatta pisteessä käyttämällä derivaatan määritelmää.

Ensinnäkin, mikä pitäisi olla lopputulos? Numero Lasketaan vastaus tavallisella tavalla:

Ratkaisu: selkeyden kannalta tämä tehtävä on paljon helpompi, koska kaavassa sen sijaan

tarkka merkitys otetaan huomioon.

Asetetaan pisteen lisäys ja laaditaan vastaava funktion inkrementti:

Lasketaan derivaatta pisteessä:

Käytämme erittäin harvinaista kaavaa tangenttien erolle ja jälleen kerran vähennämme ratkaisun ensimmäiseen

ihana raja:

Vastaus: pisteen derivaatan määritelmän mukaan.

Ongelma ei ole niin vaikea ratkaista ja "yleensä" - riittää, kun korvataan yksinkertaiset suunnittelumenetelmästä riippuen. Tässä tapauksessa et tietenkään saa numeroa, vaan johdetun funktion.

Esimerkki 10 Etsi määritelmän avulla funktion derivaatta pisteessä

Tämä on esimerkki tee-se-itse-ratkaisusta.

Lopullinen bonustehtävä on tarkoitettu ensisijaisesti matemaattisen analyysin syventävälle opiskelijoille, mutta se ei haittaa kaikkia muitakaan:

Onko funktio erotettavissa pisteessä?

Ratkaisu: on selvää, että paloittain määritelty funktio on jatkuva pisteessä, mutta onko se siellä differentioituva?

Ratkaisun algoritmi, ei vain paloittainen funktioiden, on seuraava:

1) Etsi vasemmanpuoleinen derivaatta tästä pisteestä:.

2) Etsi oikeanpuoleinen derivaatta tästä pisteestä:.

3) Jos yksipuoliset derivaatat ovat äärellisiä ja yhtyvät:

, niin funktio on differentioituva pisteessä ja

geometrisesti on olemassa yhteinen tangentti (katso oppitunnin teoreettinen osa Johdannan määritelmä ja merkitys).

Jos vastaanotetaan kaksi eri arvoa: (joista yksi voi osoittautua äärettömäksi), silloin funktio ei ole differentioituva pisteessä.

Jos molemmat yksipuoliset derivaatat ovat yhtä suuria kuin ääretön

(jopa eri merkeillä), toiminto ei toimi

pisteessä differentioituva, mutta kaaviolla on ääretön derivaatta ja yhteinen pystytangentti (katso oppitunnin esimerkki 5Normaali yhtälö) .

Tällä oppitunnilla opimme soveltamaan erottelukaavoja ja -sääntöjä.

Esimerkkejä. Etsi funktioiden derivaatat.

1. y = x 7 + x 5 - x 4 + x 3 - x 2 + x-9. Käytä sääntöä minä, kaavat 4, 2 ja 1... Saamme:

y' = 7x 6 + 5x 4 -4x 3 + 3x 2 -2x + 1.

2. y = 3x 6 -2x + 5. Ratkaisemme samalla tavalla käyttäen samoja kaavoja ja kaavaa 3.

y ’= 3 ∙ 6x 5 -2 = 18x 5 -2.

Käytä sääntöä minä, kaavat 3, 5 ja 6 ja 1.

Käytä sääntöä IV, kaavat 5 ja 1 .

Viidennessä esimerkissä säännön mukaan minä summan derivaatta on yhtä suuri kuin johdannaisten summa, ja olemme juuri löytäneet 1. termin derivaatan (esimerkki 4 ), siksi löydämme johdannaiset 2 ja 3 ehdot ja 1:lle termi, voimme heti kirjoittaa tuloksen.

Erottava 2 ja 3 termejä kaavan mukaan 4 ... Tätä varten muunnamme kolmannen ja neljännen asteen juuret nimittäjissä asteiksi, joilla on negatiivinen eksponentti, ja sitten 4 kaava, löydämme potenssien derivaatat.

Katsokaa tätä esimerkkiä ja tulosta. Onko sinulla mallia? Hyvä. Tämä tarkoittaa, että meillä on uusi kaava ja voimme lisätä sen johdannaistaulukkoomme.

Ratkaistaan ​​kuudes esimerkki ja johdetaan toinen kaava.

Käytämme sääntöä IV ja kaava 4 ... Pienennä tuloksena olevia fraktioita.

Tarkastellaan tätä funktiota ja sen johdannaista. Tietenkin ymmärsit kuvion ja olet valmis nimeämään kaavan:

Opi uusia kaavoja!

Esimerkkejä.

1. Etsi argumentin inkrementti ja funktion inkrementti y = x 2 jos argumentin alkuarvo oli 4 ja uusi - 4,01 .

Ratkaisu.

Uusi argumentin arvo x = x 0 + Δx... Korvaa tiedot: 4.01 = 4 + Δx, tästä syystä argumentin lisäys Δx= 4,01-4 = 0,01. Funktion inkrementti on määritelmän mukaan yhtä suuri kuin funktion uusien ja aiempien arvojen erotus, ts. Δy = f (x 0 + Δx) - f (x 0). Koska meillä on toiminto y = x 2, sitten Δy= (x 0 + Δx) 2 - (x 0) 2 = (x 0) 2 + 2x 0 · Δx + (Δx) 2 - (x 0) 2 = 2x 0 · Δx + (Δx) 2 =

2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.

Vastaus: argumentin lisäys Δx= 0,01; funktion lisäys Δy=0,0801.

Toiminnon inkrementti oli mahdollista löytää eri tavalla: Δy= y (x 0 + Δx) -y (x 0) = y (4,01) -y (4) = 4,01 2 - 4 2 = 16,0801-16 = 0,0801.

2. Etsi funktion kuvaajan tangentin kaltevuuskulma y = f (x) pisteessä x 0, jos f "(x 0) = 1.

Ratkaisu.

Johdannainen arvo tangenttipisteessä x 0 ja siellä on tangentin kaltevuuskulman tangentin arvo (derivaatan geometrinen merkitys). Meillä on: f "(x 0) = tanα = 1 → α = 45 °, koska tg45 ° = 1.

Vastaus: tämän funktion kaavion tangentti muodostaa kulman Ox-akselin positiivisen suunnan kanssa, joka on yhtä suuri kuin 45 °.

3. Johda funktion derivaatan kaava y = x n.

Erilaistuminen Onko funktion derivaatan löytäminen.

Derivaataita etsittäessä käytetään kaavoja, jotka on johdettu derivaatan määritelmän perusteella, samalla tavalla kuin johdettiin johdetun asteen kaava: (x n) "= nx n-1.

Nämä ovat kaavat.

Johdannaisten taulukko se on helpompi muistaa lausumalla sanalliset sanamuodot:

1. Vakion derivaatta on nolla.

2. X-viiva on yhtä suuri kuin yksi.

3. Vakiotekijä voidaan ottaa pois derivaatan etumerkistä.

4. Asteen derivaatta on yhtä suuri kuin tämän asteen eksponentin tulo samalla kantalla, mutta eksponentti on yksi vähemmän.

5. Juuren derivaatta on yhtä kuin yksi jaettuna kahdella samalla juurella.

6. Yksikön derivaatta jaettuna x:llä on yhtä suuri kuin miinus yksi jaettuna x:llä.

7. Siniderivaata on yhtä suuri kuin kosini.

8. Kosinin derivaatta on yhtä suuri kuin miinussini.

9. Tangentin derivaatta on yhtä suuri kuin yksi jaettuna kosinin neliöllä.

10. Kotangenttiderivaata on yhtä kuin miinus yksi jaettuna sinineliöllä.

Me opetamme eriyttämissäännöt.

1. Algebrallisen summan derivaatta on yhtä suuri kuin termien derivaattojen algebrallinen summa.

2. Tuloksen derivaatta on yhtä suuri kuin ensimmäisen tekijän derivaatan tulo toisella plus ensimmäisen tekijän tulo toisen derivaatalla.

3. "Y":n derivaatta jaettuna "ve":llä on yhtä suuri kuin murtoluku, jonka osoittajassa "y on veto kerrottuna" ve "miinus" y kerrottuna alkuluvulla ", ja nimittäjässä -"ve neliö". .

4. Kaavan erikoistapaus 3.

Opetamme yhdessä!

Sivu 1/1 1