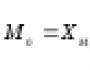Kulman tangentin merkitys. Sini, kosini, tangentti: mikä se on? Kuinka löytää sini, kosini ja tangentti? Sini trigonometriassa
Esimerkkejä:
\(\cos(30^°)=\)\(\frac(\sqrt(3))(2)\)
\(\cos\)\(\frac(π)(3)\) \(=\)\(\frac(1)(2)\)
\(\cos2=-0,416…\)
Argumentti ja arvo
Terävän kulman kosini
Terävän kulman kosini voidaan määrittää käyttämällä suorakulmaista kolmiota - se on yhtä suuri kuin viereisen jalan suhde hypotenuusaan.
Esimerkki :
1) Olkoon kulma annettu ja sinun on määritettävä tämän kulman kosini.

2) Täydennetään mikä tahansa suorakulmainen kolmio tähän kulmaan.

3) Mitattuaan tarvittavat sivut voimme laskea kosinin.

Terävän kulman kosini on suurempi kuin \(0\) ja pienempi kuin \(1\)
Jos ongelmaa ratkaistaessa terävän kulman kosini osoittautui suuremmiksi kuin 1 tai negatiivinen, niin jossain ratkaisussa on virhe.
Luvun kosini
Numeroympyrän avulla voit määrittää minkä tahansa luvun kosinin, mutta yleensä löytää lukujen kosinin, jotka liittyvät jotenkin seuraaviin: \(\frac(π)(2)\) , \(\frac(3π)(4)\) , \(-2π\ ).
Esimerkiksi luvun \(\frac(π)(6)\) kosini on yhtä suuri kuin \(\frac(\sqrt(3))(2)\) . Ja luvulle \(-\)\(\frac(3π)(4)\) se on yhtä suuri kuin \(-\)\(\frac(\sqrt(2))(2)\) (noin \ (-0 ,71\)).

Kosini muille käytännössä usein tavallisille lukuille, katso.
Kosiniarvo on aina välillä \(-1\) ja \(1\). Tässä tapauksessa kosini voidaan laskea täysin mille tahansa kulmille ja numeroille.
Minkä tahansa kulman kosini
Numeerisen ympyrän ansiosta on mahdollista määrittää ei vain terävän kulman, vaan myös tylpän, negatiivisen ja jopa suuremman kuin \ (360 ° \) (täysi käännös) kosini. Kuinka tehdä se - on helpompi nähdä kerran kuin kuulla \(100\) kertaa, joten katso kuvaa.

Nyt selitys: olkoon tarpeen määrittää kulman kosini KOA astemitta \(150°\). Yhdistämme pointin O ympyrän keskipisteen ja sivun kanssa OK- \(x\)-akselilla. Aseta sen jälkeen sivuun \ (150 ° \) vastapäivään. Sitten pisteen ordinaatat MUTTA näyttää meille tämän kulman kosinin.
Jos olemme kiinnostuneita kulmasta, jossa on astemitta, esimerkiksi \ (-60 ° \) (kulma KOV), teemme samoin, mutta \(60°\) laitetaan sivuun myötäpäivään.

Ja lopuksi, kulma on suurempi kuin \(360°\) (kulma KOS) - kaikki on samanlaista kuin tylsä, vasta täyden kierroksen jälkeen myötäpäivään siirrymme toiselle kierrokselle ja "saamme asteiden puutteen". Tarkemmin sanottuna meidän tapauksessamme kulma \(405°\) piirretään muodossa \(360° + 45°\).

On helppo arvata, että jos haluat asettaa kulman esimerkiksi \ (960 ° \), sinun on tehtävä kaksi käännöstä (\ (360 ° + 360 ° + 240 ° \)) ja kulma \ (2640 ° \) - kokonaiset seitsemän.
Kannattaa muistaa, että:
Suoran kulman kosini on nolla. Tylsän kulman kosini on negatiivinen.
Kosinimerkit neljänneksissä
Käyttämällä kosiniakselia (eli kuvassa punaisella korostettua abskissa-akselia) on helppo määrittää kosinien merkit numeerista (trigonometristä) ympyrää pitkin:
Kun akselin arvot ovat \(0\) - \(1\), kosinissa on plusmerkki (I ja IV neljännekset ovat viheralueita),
- jos akselin arvot ovat \(0\) - \(-1\), kosinissa on miinusmerkki (II ja III neljännes - violetti alue).

Esimerkki.
Määritä merkki \(\cos 1\).
Ratkaisu:
Etsitään \(1\) trigonometriseltä ympyrältä. Aloitamme siitä tosiasiasta, että \ (π \u003d 3,14 \). Tämä tarkoittaa, että yksi on noin kolme kertaa lähempänä nollaa ("aloituspiste").

Jos piirretään kohtisuora kosiniakseliin nähden, käy ilmi, että \(\cos1\) on positiivinen.
Vastaus:
Plussa.
Suhde muihin trigonometrisiin funktioihin:
- sama kulma (tai numero): trigonometrinen perusidentiteetti \(\sin^2x+\cos^2x=1\)- sama kulma (tai luku): kaavalla \(1+tg^2x=\)\(\frac(1)(\cos^2x)\)
- ja saman kulman (tai luvun) sini: \(ctgx=\)\(\frac(\cos(x))(\sinx)\)
Katso muut yleisimmin käytetyt kaavat.
Funktio \(y=\cos(x)\)
Jos piirrämme kulmat radiaaneina \(x\)-akselille ja näitä kulmia vastaavat kosiniarvot \(y\)-akselille, saadaan seuraava kaavio:

Tätä kuvaajaa kutsutaan ja sillä on seuraavat ominaisuudet:
Määritelmäalue on mikä tahansa x:n arvo: \(D(\cos(x))=R\)
- arvoalue - \(-1\) - \(1\) mukaan lukien: \(E(\cos(x))=[-1;1]\)
- parillinen: \(\cos(-x)=\cos(x)\)
- jaksollinen jaksolla \(2π\): \(\cos(x+2π)=\cos(x)\)
- leikkauspisteet koordinaattiakselien kanssa:
abskissa: \((\)\(\frac(π)(2)\) \(+πn\),\(;0)\), missä \(n ϵ Z\)
y-akseli: \((0;1)\)
- merkkivälit:
funktio on positiivinen aikaväleillä: \((-\)\(\frac(π)(2)\) \(+2πn;\) \(\frac(π)(2)\) \(+2πn) \), jossa \(n ϵ Z\)
funktio on negatiivinen aikaväleillä: \((\)\(\frac(π)(2)\) \(+2πn;\)\(\frac(3π)(2)\) \(+2πn)\ ), jossa \(n ϵ Z\)
- lisäys- ja laskuvälit:
funktio kasvaa aikaväleillä: \((π+2πn;2π+2πn)\), missä \(n ϵ Z\)
funktio pienenee aikaväleillä: \((2πn;π+2πn)\), missä \(n ϵ Z\)
- funktion maksimi ja minimi:
funktiolla on maksimiarvo \(y=1\) pisteissä \(x=2πn\), missä \(n ϵ Z\)
funktiolla on minimiarvo \(y=-1\) pisteissä \(x=π+2πn\), missä \(n ϵ Z\).
Mikä on kulman sini, kosini, tangentti, kotangentti, auttaa sinua ymmärtämään suorakulmaisen kolmion.
Mitä kutsutaan suorakulmaisen kolmion sivuiksi? Aivan oikein, hypotenuusa ja jalat: hypotenuusa on oikeaa kulmaa vastapäätä oleva sivu (esimerkissämme tämä on sivu \ (AC \) ); jalat ovat kaksi jäljellä olevaa sivua \ (AB \) ja \ (BC \) (ne, jotka ovat oikean kulman vieressä), lisäksi, jos tarkastelemme jalkoja kulman \ (BC \) suhteen, niin jalka \ (AB \) on viereinen haara ja jalka \ (BC \) on vastakkainen. Joten, nyt vastataan kysymykseen: mitkä ovat kulman sini, kosini, tangentti ja kotangentti?
Kulman sini- tämä on vastakkaisen (kaukaisen) jalan suhde hypotenuusaan.
Meidän kolmiossa:
\[ \sin \beta =\dfrac(BC)(AC) \]
Kulman kosini- tämä on viereisen (läheisen) jalan suhde hypotenuusaan.
Meidän kolmiossa:
\[ \cos \beta =\dfrac(AB)(AC) \]
Kulman tangentti- tämä on vastakkaisen (kaukaisen) jalan suhde viereiseen (läheiseen).
Meidän kolmiossa:
\[ tg\beta =\dfrac(BC)(AB) \]
Kulman kotangentti- tämä on viereisen (läheisen) jalan suhde vastakkaiseen (kaumaan).
Meidän kolmiossa:
\[ ctg\beta =\dfrac(AB)(BC) \]
Nämä määritelmät ovat välttämättömiä muistaa! Jotta olisi helpompi muistaa, mikä jalka jakaa millä, sinun on ymmärrettävä se selvästi tangentti ja kotangentti vain jalat istuvat, ja hypotenuusa ilmestyy vain sisään sinus ja kosini. Ja sitten voit keksiä assosiaatioketjun. Esimerkiksi tämä:
kosini→kosketus→kosketus→viereinen;
Kotangentti→kosketus→kosketus→viereinen.
Ensinnäkin on muistettava, että sini, kosini, tangentti ja kotangentti kolmion sivujen suhteina eivät riipu näiden sivujen pituuksista (yhdessä kulmassa). Älä luota? Varmista sitten katsomalla kuvaa:

Otetaan esimerkiksi kulman \(\beta \) kosini. Määritelmän mukaan kolmiosta \(ABC \) : \(\cos \beta =\dfrac(AB)(AC)=\dfrac(4)(6)=\dfrac(2)(3) \), mutta voimme laskea kulman \(\beta \) kosinin kolmiosta \(AHI \) : \(\cos \beta =\dfrac(AH)(AI)=\dfrac(6)(9)=\dfrac(2)(3) \). Katsos, sivujen pituudet ovat erilaisia, mutta yhden kulman kosinin arvo on sama. Siten sinin, kosinin, tangentin ja kotangentin arvot riippuvat yksinomaan kulman suuruudesta.
Jos ymmärrät määritelmät, mene eteenpäin ja korjaa ne!
Alla olevassa kuvassa näkyvälle kolmiolle \(ABC \) löydämme \(\sin \ \alpha ,\ \cos \ \alpha ,\ tg\ \alpha ,\ ctg\ \alpha \).

\(\begin(array)(l)\sin \ \alpha =\dfrac(4)(5)=0,8\\\cos \ \alpha =\dfrac(3)(5)=0,6\\ tg\ \alpha =\dfrac(4)(3)\\ctg\ \alpha =\dfrac(3)(4)=0,75\end(array) \)
No, saitko sen? Kokeile sitten itse: laske sama kulmalle \(\beta \) .
Vastaukset: \(\sin \ \beta =0.6;\ \cos \ \beta =0.8;\ tg\ \beta =0.75;\ ctg\ \beta =\dfrac(4)(3) \).
Yksikkö (trigonometrinen) ympyrä
Ymmärtääksemme asteen ja radiaanin käsitteet tarkastelimme ympyrää, jonka säde on yhtä suuri kuin \ (1 \) . Sellaista ympyrää kutsutaan yksittäinen. Se on erittäin hyödyllinen trigonometrian tutkimuksessa. Siksi käsittelemme sitä hieman yksityiskohtaisemmin.

Kuten näet, tämä ympyrä on rakennettu suorakulmaiseen koordinaattijärjestelmään. Ympyrän säde on yhtä suuri kuin yksi, kun taas ympyrän keskipiste on origossa, sädevektorin alkusijainti on kiinteä \(x \)-akselin positiivista suuntaa pitkin (esimerkissämme tämä on säde \(AB \) ).
Jokainen ympyrän piste vastaa kahta numeroa: koordinaatti akselilla \(x \) ja koordinaatti akselilla \(y \) . Mitä nämä koordinaattiluvut ovat? Ja ylipäätään, mitä tekemistä niillä on käsillä olevan aiheen kanssa? Muista tätä varten harkittu suorakulmainen kolmio. Yllä olevassa kuvassa näet kaksi kokonaista suorakulmaista kolmiota. Tarkastellaan kolmiota \(ACG \) . Se on suorakaiteen muotoinen, koska \(CG \) on kohtisuorassa \(x \)-akselia vastaan.
Mikä on \(\cos \ \alpha \) kolmiosta \(ACG \)? Oikein \(\cos \ \alpha =\dfrac(AG)(AC) \). Lisäksi tiedämme, että \(AC \) on yksikköympyrän säde, joten \(AC=1 \) . Korvaa tämä arvo kosinikaavaamme. Tässä on mitä tapahtuu:
\(\cos \ \alpha =\dfrac(AG)(AC)=\dfrac(AG)(1)=AG \).
Ja mikä on \(\sin \ \alpha \) kolmiosta \(ACG \)? No tottakai, \(\sin \alpha =\dfrac(CG)(AC) \)! Korvaa säteen arvo \ (AC \) tässä kaavassa ja saa:
\(\sin \alpha =\dfrac(CG)(AC)=\dfrac(CG)(1)=CG \)
Joten, voitko kertoa minulle, mitkä ovat ympyrään kuuluvan pisteen \(C \) koordinaatit? No ei mitenkään? Mutta entä jos ymmärrät, että \(\cos \ \alpha \) ja \(\sin \alpha \) ovat vain numeroita? Mitä koordinaattia \(\cos \alpha \) vastaa? No, tietysti koordinaatti \(x \) ! Ja mitä koordinaattia \(\sin \alpha \) vastaa? Aivan oikein, \(y \) koordinaatti! Eli pointti \(C(x;y)=C(\cos \alpha ;\sin \alpha) \).

Mitä sitten ovat \(tg \alpha \) ja \(ctg \alpha \) ? Se on oikein, käytetään sopivia tangentin ja kotangentin määritelmiä ja saadaan se \(tg \alpha =\dfrac(\sin \alpha )(\cos \alpha )=\dfrac(y)(x) \), a \(ctg \alpha =\dfrac(\cos \alpha )(\sin \alpha )=\dfrac(x)(y) \).
Entä jos kulma on suurempi? Tässä esimerkiksi, kuten tässä kuvassa:

Mikä tässä esimerkissä on muuttunut? Selvitetään se. Tätä varten käännymme jälleen suorakulmaiseen kolmioon. Tarkastellaan suorakulmaista kolmiota \(((A)_(1))((C)_(1))G \) : kulma (kulman \(\beta \) vieressä). Mikä on kulman sinin, kosinin, tangentin ja kotangentin arvo \(((C)_(1))((A)_(1))G=180()^\circ -\beta \ \)? Aivan oikein, noudatamme vastaavia trigonometristen funktioiden määritelmiä:
\(\begin(array)(l)\sin \angle ((C)_(1))((A)_(1))G=\dfrac(((C)_(1))G)(( (A)_(1))((C)_(1)))=\dfrac(((C)_(1))G)(1)=((C)_(1))G=y; \\\cos \angle ((C)_(1))((A)_(1))G=\dfrac(((A)_(1))G)(((A)_(1)) ((C)_(1)))=\dfrac(((A)_(1))G)(1)=((A)_(1))G=x;\\tg\kulma ((C) )_(1))((A)_(1))G=\dfrac(((C)_(1))G)(((A)_(1))G)=\dfrac(y)( x);\\ctg\kulma ((C)_(1))((A)_(1))G=\dfrac(((A)_(1))G)(((C)_(1 ))G)=\dfrac(x)(y)\end(array) \)
No, kuten näet, kulman sinin arvo vastaa edelleen koordinaattia \ (y \) ; kulman kosinin arvo - koordinaatti \ (x \) ; ja tangentin ja kotangentin arvot vastaaviin suhteisiin. Siten nämä suhteet ovat sovellettavissa mihin tahansa sädevektorin kiertoon.
On jo mainittu, että sädevektorin alkusijainti on \(x \)-akselin positiivisessa suunnassa. Toistaiseksi olemme kiertäneet tätä vektoria vastapäivään, mutta mitä tapahtuu, jos käännämme sitä myötäpäivään? Ei mitään poikkeuksellista, saat myös tietyn kokoisen kulman, mutta vain se on negatiivinen. Siten, kun kierretään sädevektoria vastapäivään, saamme positiiviset kulmat, ja kun käännetään myötäpäivään - negatiivinen.
Tiedämme siis, että sädevektorin koko kierros ympyrän ympäri on \(360()^\circ \) tai \(2\pi \) . Onko mahdollista kiertää sädevektoria \(390()^\circ \) tai \(-1140()^\circ \)? No tietysti voit! Ensimmäisessä tapauksessa \(390()^\circ =360()^\circ +30()^\circ \), joten sädevektori tekee yhden täyden kierroksen ja pysähtyy kohtaan \(30()^\circ \) tai \(\dfrac(\pi )(6) \) .
Toisessa tapauksessa \(-1140()^\circ =-360()^\circ \cdot 3-60()^\circ \), eli sädevektori tekee kolme täydellistä kierrosta ja pysähtyy kohtaan \(-60()^\circ \) tai \(-\dfrac(\pi )(3) \) .
Siten yllä olevista esimerkeistä voimme päätellä, että kulmat, jotka eroavat toisistaan \(360()^\circ \cdot m \) tai \(2\pi \cdot m \) (jossa \(m \) on mikä tahansa kokonaisluku ) vastaavat sädevektorin samaa sijaintia.
Alla olevassa kuvassa näkyy kulma \(\beta =-60()^\circ \) . Sama kuva vastaa nurkkaa \(-420()^\circ ,-780()^\circ ,\ 300()^\circ ,660()^\circ \) jne. Tätä listaa voi jatkaa loputtomiin. Kaikki nämä kulmat voidaan kirjoittaa yleisellä kaavalla \(\beta +360()^\circ \cdot m \) tai \(\beta +2\pi \cdot m \) (jossa \(m \) on mikä tahansa kokonaisluku)
\(\begin(array)(l)-420()^\circ =-60+360\cdot (-1);\\-780()^\circ =-60+360\cdot (-2); \\300()^\circ =-60+360\cdot 1;\\660()^\circ =-60+360\cdot 2.\end(array) \)

Nyt, kun tiedät trigonometristen perusfunktioiden määritelmät ja käyttämällä yksikköympyrää, yritä vastata, mitä arvot ovat yhtä suuria:
\(\begin(array)(l)\sin \ 90()^\circ =?\\\cos \ 90()^\circ =?\\\text(tg)\ 90()^\circ =? \\\text(ctg)\ 90()^\circ =?\\\sin \ 180()^\circ =\sin \ \pi =?\\\cos \ 180()^\circ =\cos \ \pi =?\\\teksti(tg)\ 180()^\circ =\text(tg)\ \pi =?\\\teksti(ctg)\ 180()^\circ =\text(ctg)\ \pi =?\\\sin \ 270()^\circ =?\\\cos \ 270()^\circ =?\\\text(tg)\ 270()^\circ =?\\\teksti (ctg)\ 270()^\circ =?\\\sin \ 360()^\circ =?\\\cos \ 360()^\circ =?\\\text(tg)\ 360()^ \circ =?\\\text(ctg)\ 360()^\circ =?\\\sin \ 450()^\circ =?\\\cos \ 450()^\circ =?\\\teksti (tg)\ 450()^\circ =?\\\text(ctg)\ 450()^\circ =?\end(array) \)
Tässä on yksikköympyrä avuksi:

Onko vaikeuksia? Otetaanpa sitten selvää. Tiedämme siis, että:
\(\begin(array)(l)\sin \alpha =y;\\cos\alpha =x;\\tg\alpha =\dfrac(y)(x);\\ctg\alpha =\dfrac(x) )(y).\end(array) \)
Täältä määritämme tiettyjä kulman mittaa vastaavien pisteiden koordinaatit. No, aloitetaan järjestyksessä: kulma sisään \(90()^\circ =\dfrac(\pi )(2) \) vastaa pistettä, jonka koordinaatit \(\left(0;1 \right) \) , joten:
\(\sin 90()^\circ =y=1 \) ;
\(\cos 90()^\circ =x=0 \) ;
\(\text(tg)\ 90()^\circ =\dfrac(y)(x)=\dfrac(1)(0)\Rightarrow \text(tg)\ 90()^\circ \)- ei ole olemassa;
\(\text(ctg)\ 90()^\circ =\dfrac(x)(y)=\dfrac(0)(1)=0 \).
Lisäksi samaa logiikkaa noudattaen saamme selville, että kulmat sisäänpäin \(180()^\circ ,\ 270()^\circ ,\ 360()^\circ ,\ 450()^\circ (=360()^\circ +90()^\circ)\ \ ) vastaavat pisteitä, joissa on koordinaatit \(\left(-1;0 \right),\text( )\left(0;-1 \right),\text( )\left(1;0 \right),\text( )\left(0 ;1 \oikea) \), vastaavasti. Tämän tietäen on helppo määrittää trigonometristen funktioiden arvot vastaavissa pisteissä. Kokeile ensin itse ja tarkista sitten vastaukset.
Vastaukset:
\(\displaystyle \sin \ 180()^\circ =\sin \ \pi =0 \)
\(\displaystyle \cos \ 180()^\circ =\cos \ \pi =-1 \)
\(\text(tg)\ 180()^\circ =\text(tg)\ \pi =\dfrac(0)(-1)=0 \)
\(\text(ctg)\ 180()^\circ =\text(ctg)\ \pi =\dfrac(-1)(0)\Rightarrow \text(ctg)\ \pi \)- ei ole olemassa
\(\sin \ 270()^\circ =-1 \)
\(\cos \ 270()^\circ =0 \)
\(\text(tg)\ 270()^\circ =\dfrac(-1)(0)\Rightarrow \text(tg)\ 270()^\circ \)- ei ole olemassa
\(\text(ctg)\ 270()^\circ =\dfrac(0)(-1)=0 \)
\(\sin \ 360()^\circ =0 \)
\(\cos \ 360()^\circ =1 \)
\(\text(tg)\ 360()^\circ =\dfrac(0)(1)=0 \)
\(\text(ctg)\ 360()^\circ =\dfrac(1)(0)\Rightarrow \text(ctg)\ 2\pi \)- ei ole olemassa
\(\sin \ 450()^\circ =\sin \ \left(360()^\circ +90()^\circ \right)=\sin \ 90()^\circ =1 \)
\(\cos \ 450()^\circ =\cos \ \left(360()^\circ +90()^\circ \right)=\cos \ 90()^\circ =0 \)
\(\text(tg)\ 450()^\circ =\text(tg)\ \left(360()^\circ +90()^\circ \right)=\text(tg)\ 90() ^\circ =\dfrac(1)(0)\Rightarrow \text(tg)\ 450()^\circ \)- ei ole olemassa
\(\text(ctg)\ 450()^\circ =\text(ctg)\left(360()^\circ +90()^\circ \right)=\text(ctg)\ 90()^ \circ =\dfrac(0)(1)=0 \).
Näin ollen voimme tehdä seuraavan taulukon:

Kaikkia näitä arvoja ei tarvitse muistaa. Riittää, kun muistat yksikköympyrän pisteiden koordinaattien ja trigonometristen funktioiden arvojen välisen vastaavuuden:
\(\left. \begin(array)(l)\sin \alpha =y;\\cos \alpha =x;\\tg \alpha =\dfrac(y)(x);\\ctg \alpha =\ dfrac(x)(y).\end(array) \right\)\ \text(Täytyy muistaa tai pystyä tulostamaan!! \) !}
Ja tässä ovat kulmien trigonometristen funktioiden arvot ja \(30()^\circ =\dfrac(\pi )(6),\ 45()^\circ =\dfrac(\pi )(4) \) alla olevan taulukon mukaisesti, sinun on muistettava:

Ei tarvitse pelätä, nyt näytämme yhden esimerkin vastaavien arvojen melko yksinkertaisesta muistamisesta:

Tämän menetelmän käyttämiseksi on tärkeää muistaa siniarvot kaikille kolmelle kulmamitalle ( \(30()^\circ =\dfrac(\pi )(6),\ 45()^\circ =\dfrac(\pi )(4),\ 60()^\circ =\dfrac(\pi )(3) \)), sekä kulman tangentin arvo muodossa \(30()^\circ \) . Kun tiedät nämä \(4\) arvot, koko taulukko on melko helppo palauttaa - kosiniarvot siirretään nuolien mukaisesti, eli:
\(\begin(array)(l)\sin 30()^\circ =\cos \ 60()^\circ =\dfrac(1)(2)\ \ \\\sin 45()^\circ = \cos \ 45()^\circ =\dfrac(\sqrt(2))(2)\\\sin 60()^\circ =\cos \ 30()^\circ =\dfrac(\sqrt(3) ))(2)\ \end(array) \)
\(\text(tg)\ 30()^\circ \ =\dfrac(1)(\sqrt(3)) \), tämän tietäen on mahdollista palauttaa arvot \(\teksti(tg)\ 45()^\circ , \text(tg)\ 60()^\circ \). Osoittaja "\(1 \) " vastaa \(\text(tg)\ 45()^\circ \ \) ja nimittäjä "\(\sqrt(\text(3)) \)" vastaa \ (\teksti (tg)\ 60()^\circ \ \) . Kotangenttiarvot siirretään kuvassa olevien nuolien mukaisesti. Jos ymmärrät tämän ja muistat kaavion nuolilla, riittää, että muistat vain \(4 \) arvot taulukosta.
Ympyrän pisteen koordinaatit
Onko mahdollista löytää piste (sen koordinaatit) ympyrästä, kun tiedetään ympyrän keskipisteen koordinaatit, säde ja kiertokulma? No tietysti voit! Johdetaan yleinen kaava pisteen koordinaattien löytämiseksi. Tässä meillä on esimerkiksi tällainen ympyrä:

Se piste meille on annettu \(K(((x)_(0));((y)_(0)))=K(3;2) \) on ympyrän keskipiste. Ympyrän säde on \(1,5 \) . On tarpeen löytää pisteen \(P \) koordinaatit, jotka saadaan kiertämällä pistettä \(O \) \(\delta \) astetta.
Kuten kuvasta näkyy, pisteen \ (P \) koordinaatti \ (x \) vastaa janan \ pituutta (TP=UQ=UK+KQ \) . Janan \ (UK \) pituus vastaa ympyrän keskipisteen koordinaattia \ (x \), eli se on yhtä suuri kuin \ (3 \) . Janan \(KQ \) pituus voidaan ilmaista käyttämällä kosinin määritelmää:
\(\cos \ \delta =\dfrac(KQ)(KP)=\dfrac(KQ)(r)\Rightarrow KQ=r\cdot \cos \ \delta \).
Sitten meillä on pisteen \(P \) koordinaatti \(x=((x)_(0))+r\cdot \cos \ \delta =3+1,5\cdot \cos \ \delta \).
Samalla logiikalla löydämme pisteen \(P \) y-koordinaatin arvon. Tällä tavalla,
\(y=((y)_(0))+r\cdot \sin \ \delta =2+1,5\cdot \sin \delta \).
Joten yleisesti ottaen pisteiden koordinaatit määritetään kaavoilla:
\(\begin(array)(l)x=((x)_(0))+r\cdot \cos \ \delta \\y=((y)_(0))+r\cdot \sin \ \delta \end(array) \), missä
\(((x)_(0)),((y)_(0)) \) - ympyrän keskipisteen koordinaatit,
\(r\) - ympyrän säde,
\(\delta \) - vektorin säteen kiertokulma.
Kuten näette, harkitsemamme yksikköympyrän osalta nämä kaavat pienenevät merkittävästi, koska keskustan koordinaatit ovat nolla ja säde on yhtä suuri:
\(\begin(array)(l)x=((x)_(0))+r\cdot \cos \ \delta =0+1\cdot \cos \ \delta =\cos \ \delta \\y =((y)_(0))+r\cdot \sin \ \delta =0+1\cdot \sin \ \delta =\sin \ \delta \end(array) \)
Javascript on poistettu käytöstä selaimessasi.ActiveX-komponentit on otettava käyttöön, jotta voit tehdä laskelmia!
Kosini on hyvin tunnettu trigonometrinen funktio, joka on myös yksi trigonometrian pääfunktioista. Kulman kosini suorakulmaisessa kolmiossa on kolmion viereisen haaran suhde kolmion hypotenuusaan. Useimmiten kosinin määritelmä liittyy kolmioon, joka on täsmälleen suorakaiteen muotoinen. Mutta tapahtuu myös niin, että kulma, jolle on tarpeen laskea kosini suorakaiteen muotoisessa kolmiossa, ei sijaitse tässä suorakaiteen muotoisessa kolmiossa. Mitä sitten tehdä? Kuinka löytää kolmion kulman kosini?
Jos haluat laskea kulman kosinin suorakulmaisessa kolmiossa, kaikki on hyvin yksinkertaista. Sinun tarvitsee vain muistaa kosinin määritelmä, jossa on ratkaisu tähän ongelmaan. Sinun tarvitsee vain löytää sama suhde viereisen jalan sekä kolmion hypotenuusan välillä. Tässä ei todellakaan ole vaikeaa ilmaista kulman kosinia. Kaava näyttää tältä: - cosα = a/c, tässä "a" on jalan pituus ja sivu "c" on vastaavasti hypotenuusan pituus. Esimerkiksi suorakulmaisen kolmion terävän kulman kosini voidaan löytää tällä kaavalla.
Jos olet kiinnostunut siitä, mikä on mielivaltaisen kolmion kulman kosini, niin kosinilause tulee apuun, jota tulisi käyttää tällaisissa tapauksissa. Kosinilause sanoo, että kolmion sivun neliö on a priori yhtä suuri kuin saman kolmion muiden sivujen neliöiden summa, mutta ilman näiden sivujen tuloa kahdesti sen kulman kosinilla, joka sijaitsee niitä.
- Jos sinun on löydettävä terävän kulman kosini kolmiosta, sinun on käytettävä seuraavaa kaavaa: cosα \u003d (a 2 + b 2 - c 2) / (2ab).
- Jos kolmiossa on tarpeen löytää tylpän kulman kosini, sinun on käytettävä seuraavaa kaavaa: cosα \u003d (c 2 - a 2 - b 2) / (2ab). Kaavan merkinnät - a ja b - ovat halutun kulman vieressä olevien sivujen pituuksia, c on halutun kulman vastakkaisen sivun pituus.
Myös kulman kosini voidaan laskea sinilauseen avulla. Se sanoo, että kolmion kaikki sivut ovat verrannollisia vastakkaisten kulmien sineihin. Sinilauseen avulla voit laskea kolmion jäljellä olevat alkiot, kun tiedät vain kaksi sivua ja kulman, joka on vastakkainen toiselle sivulle, tai kaksi kulmaa ja yksi sivu. Harkitse esimerkkiä. Ongelmaehdot: a=1; b = 2; c = 3. Kulma, joka on vastakkainen sivun "A" kanssa, merkitsee - α, niin meillä on kaavojen mukaan: cosα \u003d (b² + c²-a²) / (2 * b * c) \u003d (2² + 3²) -1²) / (2 * 2 *3)=(4+9-1)/12=12/12=1. Vastaus: 1.
Jos kulman kosini ei tarvitse laskea kolmiossa, vaan jossain muussa mielivaltaisessa geometrisessa kuviossa, kaikki muuttuu hieman monimutkaisemmaksi. Kulman arvo on ensin määritettävä radiaaneina tai asteina ja vasta sitten laskettava kosini tästä arvosta. Numeerisen arvon kosini määritetään käyttämällä Bradis-taulukoita, teknisiä laskimia tai erityisiä matemaattisia sovelluksia.
Erityisissä matemaattisissa sovelluksissa voi olla toimintoja, kuten kulmien kosinien automaattinen laskeminen tietyssä kuviossa. Tällaisten sovellusten kauneus on, että ne antavat oikean vastauksen, ja käyttäjä ei käytä aikaansa joskus melko monimutkaisten ongelmien ratkaisemiseen. Toisaalta, kun käytetään jatkuvasti yksinomaan sovelluksia ongelmien ratkaisemiseen, kaikki taidot työskennellä matemaattisten ongelmien ratkaisemiseksi kolmioiden kulmien kosinien ja muiden mielivaltaisten lukujen löytämiseksi menetetään.
Yksi matematiikan haaroista, joiden kanssa koululaiset selviävät suurimmista vaikeuksista, on trigonometria. Ei ihme: tämän tietoalueen hallitsemiseksi vapaasti tarvitset spatiaalista ajattelua, kykyä löytää sinejä, kosineja, tangentteja, kotangentteja kaavoilla, yksinkertaistaa lausekkeita ja pystyä käyttämään numeroa pi laskelmissa. Lisäksi sinun tulee osata soveltaa trigonometriaa lauseiden todistamisessa, mikä edellyttää joko kehittynyttä matemaattista muistia tai kykyä päätellä monimutkaisia loogisia ketjuja.
Trigonometrian alkuperä
Tutustuminen tähän tieteeseen tulisi aloittaa kulman sinin, kosinin ja tangentin määrittelyllä, mutta ensin sinun on selvitettävä, mitä trigonometria yleensä tekee.
Historiallisesti suorakulmaiset kolmiot ovat olleet pääasiallinen tutkimuskohde tässä matemaattisen tieteen osassa. 90 asteen kulman läsnäolo mahdollistaa erilaisten toimintojen suorittamisen, joiden avulla voidaan määrittää tarkasteltavan kuvan kaikkien parametrien arvot käyttämällä kahta sivua ja yhtä kulmaa tai kahta kulmaa ja yhtä sivua. Aiemmin ihmiset huomasivat tämän kuvion ja alkoivat käyttää sitä aktiivisesti rakennusten rakentamisessa, navigoinnissa, tähtitiedossa ja jopa taiteessa.
Ensimmäinen taso
Aluksi ihmiset puhuivat kulmien ja sivujen suhteesta yksinomaan suorakulmaisten kolmioiden esimerkissä. Sitten löydettiin erityisiä kaavoja, jotka mahdollistivat tämän matematiikan osan arkielämän käytön rajojen laajentamisen.
Trigonometrian opiskelu koulussa alkaa nykyään suorakulmaisilla kolmioilla, minkä jälkeen opiskelijoiden käytössä on fysiikka ja abstraktien trigonometristen yhtälöiden ratkaiseminen, joiden parissa työ alkaa lukiossa.
Pallomainen trigonometria
Myöhemmin, kun tiede saavutti seuraavan kehitystason, kaavoja, joissa on sini, kosini, tangentti, kotangentti, alettiin käyttää pallogeometriassa, jossa pätevät muut säännöt, ja kolmion kulmien summa on aina yli 180 astetta. Tätä osiota ei opeteta koulussa, mutta sen olemassaolosta on tiedettävä ainakin siksi, että maan pinta ja minkä tahansa muun planeetan pinta on kupera, mikä tarkoittaa, että kaikki pintamerkinnät ovat "kaaren muotoisia" kolmiulotteinen tila.

Ota maapallo ja lanka. Kiinnitä lanka mihin tahansa kahteen maapallon pisteeseen niin, että se on kireällä. Kiinnitä huomiota - se on saanut kaaren muodon. Juuri tällaisilla muodoilla käsittelee pallogeometriaa, jota käytetään geodesiassa, tähtitiedessä ja muilla teoreettisilla ja soveltavilla aloilla.
Suorakulmainen kolmio
Kun olet oppinut hieman trigonometrian käyttötapoja, palataan perustrigonometriaan ymmärtääksemme paremmin, mitä sini, kosini, tangentti ovat, mitä laskelmia niiden avulla voidaan tehdä ja mitä kaavoja käyttää.
Ensimmäinen askel on ymmärtää suorakulmaiseen kolmioon liittyvät käsitteet. Ensinnäkin hypotenuusa on 90 asteen kulman vastainen puoli. Hän on pisin. Muistamme, että Pythagoraan lauseen mukaan sen numeerinen arvo on yhtä suuri kuin kahden muun sivun neliöiden summan juuri.
Esimerkiksi jos kaksi sivua ovat 3 ja 4 senttimetriä vastaavasti, hypotenuusan pituus on 5 senttimetriä. Muuten, muinaiset egyptiläiset tiesivät tästä noin neljä ja puoli tuhatta vuotta sitten.
Kahta jäljellä olevaa sivua, jotka muodostavat suoran kulman, kutsutaan jaloiksi. Lisäksi on muistettava, että kolmion kulmien summa suorakaiteen muotoisessa koordinaattijärjestelmässä on 180 astetta.
Määritelmä
Lopuksi, kun ymmärrämme geometrisen perustan, voimme siirtyä kulman sinin, kosinin ja tangentin määritelmään.
Kulman sini on vastakkaisen haaran (eli halutun kulman vastakkaisen sivun) suhde hypotenuusaan. Kulman kosini on viereisen jalan suhde hypotenuusaan.

Muista, ettei sini eikä kosini voi olla suurempi kuin yksi! Miksi? Koska hypotenuusa on oletuksena pisin, riippumatta siitä, kuinka pitkä jalka on, se on lyhyempi kuin hypotenuusa, mikä tarkoittaa, että niiden suhde on aina pienempi kuin yksi. Joten jos saat tehtävän vastauksessa sinin tai kosinin, jonka arvo on suurempi kuin 1, etsi virhettä laskelmissa tai päättelyssä. Tämä vastaus on selvästi väärä.
Lopuksi kulman tangentti on vastakkaisen sivun suhde viereiseen sivuun. Sama tulos antaa sinin jaon kosinilla. Katso: kaavan mukaan jaamme sivun pituuden hypotenuusalla, jonka jälkeen jaamme toisen sivun pituudella ja kerromme hypotenuusalla. Siten saamme saman suhteen kuin tangentin määritelmässä.
Kotangentti on kulman vieressä olevan sivun suhde vastakkaiseen sivuun. Saamme saman tuloksen jakamalla yksikön tangentilla.
Joten olemme pohtineet määritelmiä siitä, mitä sini, kosini, tangentti ja kotangentti ovat, ja voimme käsitellä kaavoja.
Yksinkertaisimmat kaavat
Trigonometriassa ei tule toimeen ilman kaavoja - kuinka löytää sini, kosini, tangentti, kotangentti ilman niitä? Ja juuri tätä vaaditaan ongelmien ratkaisemisessa.
Ensimmäinen kaava, joka sinun tulee tietää aloittaessasi trigonometrian opiskelun, sanoo, että kulman sinin ja kosinin neliöiden summa on yhtä suuri kuin yksi. Tämä kaava on suora seuraus Pythagoraan lauseesta, mutta se säästää aikaa, jos haluat tietää kulman arvon, ei sivun.
Monet opiskelijat eivät muista toista kaavaa, joka on myös erittäin suosittu koulutehtäviä ratkaistaessa: ykkösen ja kulman tangentin neliön summa on yhtä suuri kuin yksi jaettuna kulman kosinin neliöllä. Katso tarkemmin: loppujen lopuksi tämä on sama väite kuin ensimmäisessä kaavassa, vain identiteetin molemmat puolet jaettiin kosinin neliöllä. Osoittautuu, että yksinkertainen matemaattinen operaatio tekee trigonometrisesta kaavasta täysin tunnistamattoman. Muista: kun tiedät, mitä sini, kosini, tangentti ja kotangentti ovat, muunnossäännöt ja muutama peruskaava, voit milloin tahansa itsenäisesti johtaa tarvittavat monimutkaisemmat kaavat paperiarkille.
Kaksoiskulmakaavat ja argumenttien lisääminen
Kaksi muuta kaavaa, jotka sinun on opittava, liittyvät kulmien summan ja eron sinin ja kosinin arvoihin. Ne on esitetty alla olevassa kuvassa. Huomaa, että ensimmäisessä tapauksessa sini ja kosini kerrotaan molemmat kertaa, ja toisessa lisätään sinin ja kosinin paritulo.

Kaksikulma-argumentteihin liittyy myös kaavoja. Ne ovat täysin johdettu aiemmista - käytännössä yritä saada ne itse ottamalla alfa-kulma yhtä suureksi kuin beeta-kulma.
Lopuksi huomaa, että kaksoiskulmakaavat voidaan muuntaa alentamaan sinin, kosinin ja tangentin alfa-astetta.
Lauseet
Perustrigonometrian kaksi päälausetta ovat sinilause ja kosinilause. Näiden lauseiden avulla voit helposti ymmärtää, kuinka löytää sini, kosini ja tangentti, ja siten kuvion pinta-ala ja kummankin sivun koko jne.
Sinilause sanoo, että jakamalla kolmion kunkin sivun pituus vastakkaisen kulman arvolla, saadaan sama luku. Lisäksi tämä luku on yhtä suuri kuin kaksi rajatun ympyrän sädettä, toisin sanoen ympyrää, joka sisältää kaikki annetun kolmion pisteet.

Kosinilause yleistää Pythagoraan lauseen projisoimalla sen mihin tahansa kolmioon. Osoittautuu, että vähennä kahden sivun neliöiden summasta niiden tulo kerrottuna niiden viereisen kulman kaksoiskosinuksella - tuloksena oleva arvo on yhtä suuri kuin kolmannen sivun neliö. Siten Pythagoraan lause osoittautuu kosinilauseen erikoistapaukseksi.
Virheitä huolimattomuudesta
Tietäenkin, mitä sini, kosini ja tangentti ovat, on helppo tehdä virhe hajamielisyyden tai yksinkertaisimpien laskelmien virheen vuoksi. Tällaisten virheiden välttämiseksi tutustutaan suosituimpiin niistä.
Ensinnäkin tavallisia murtolukuja ei pidä muuntaa desimaaliluvuiksi ennen kuin lopputulos on saatu - voit jättää vastauksen tavalliseksi murtoluvuksi, ellei ehto toisin mainita. Tällaista muutosta ei voida kutsua virheeksi, mutta on muistettava, että ongelman jokaisessa vaiheessa voi ilmaantua uusia juuria, joita kirjoittajan idean mukaan pitäisi vähentää. Tässä tapauksessa tuhlaat aikaa tarpeettomiin matemaattisiin operaatioihin. Tämä pätee erityisesti arvoihin, kuten kolmen tai kahden juureen, koska niitä esiintyy tehtävissä jokaisessa vaiheessa. Sama koskee "rumien" numeroiden pyöristämistä.

Huomaa lisäksi, että kosinilause pätee mihin tahansa kolmioon, mutta ei Pythagoraan lauseeseen! Jos unohdat vahingossa vähentää sivujen tulon kaksinkertaisena kerrottuna niiden välisen kulman kosinilla, et saa vain täysin väärää tulosta, vaan myös osoitat aiheen täydellisen väärinymmärryksen. Tämä on pahempaa kuin huolimaton virhe.
Kolmanneksi, älä sekoita 30 ja 60 asteen kulmien arvoja sineille, kosineille, tangenteille ja kotangenteille. Muista nämä arvot, koska 30 asteen sini on yhtä suuri kuin 60:n kosini ja päinvastoin. Ne on helppo sekoittaa, minkä seurauksena saat väistämättä virheellisen tuloksen.
Sovellus
Monilla opiskelijoilla ei ole kiirettä aloittaa trigonometrian opiskelu, koska he eivät ymmärrä sen soveltavaa merkitystä. Mikä on sini, kosini, tangentti insinöörille tai tähtitieteilijälle? Nämä ovat käsitteitä, joiden avulla voit laskea etäisyyden kaukaisiin tähtiin, ennustaa meteoriitin putoamisen, lähettää tutkimusluotaimen toiselle planeetalle. Ilman niitä on mahdotonta rakentaa rakennusta, suunnitella autoa, laskea pinnan kuormitusta tai kohteen liikerataa. Ja nämä ovat vain ilmeisimpiä esimerkkejä! Loppujen lopuksi trigonometriaa muodossa tai toisessa käytetään kaikkialla musiikista lääketieteeseen.
Lopulta
Olet siis sini, kosini, tangentti. Voit käyttää niitä laskelmissa ja ratkaista koulutehtäviä onnistuneesti.

Trigonometrian koko olemus tiivistyy siihen tosiasiaan, että tuntemattomat parametrit on laskettava kolmion tunnetuista parametreista. Parametreja on yhteensä kuusi: kolmen sivun pituudet ja kolmen kulman suuruudet. Koko ero tehtävien välillä on siinä, että syötetiedot annetaan eri tavalla.
Kuinka löytää sini, kosini, tangentti jalkojen tai hypotenuusan tunnettujen pituuksien perusteella, tiedät nyt. Koska nämä termit tarkoittavat vain suhdetta ja suhdeluku on murto-osa, trigonometrisen ongelman päätavoitteena on löytää tavallisen yhtälön tai yhtälöjärjestelmän juuret. Ja täällä sinua auttaa tavallinen koulumatematiikka.
Käsitteet sini, kosini, tangentti ja kotangentti ovat trigonometrian pääluokat - matematiikan haara, ja ne liittyvät erottamattomasti kulman määritelmään. Tämän matemaattisen tieteen hallussapito edellyttää kaavojen ja lauseiden ulkoa oppimista ja ymmärtämistä sekä kehittynyttä tilaajattelua. Siksi trigonometriset laskelmat aiheuttavat usein vaikeuksia koululaisille ja opiskelijoille. Voit voittaa ne tutustumalla trigonometrisiin funktioihin ja kaavoihin.
Käsitteet trigonometriassa
Ymmärtääksesi trigonometrian peruskäsitteet, sinun on ensin päätettävä, mitä suorakulmainen kolmio ja kulma ympyrässä ovat ja miksi kaikki trigonometriset peruslaskut liittyvät niihin. Kolmio, jonka yksi kulmista on 90 astetta, on suorakulmainen kolmio. Historiallisesti ihmiset käyttivät tätä lukua usein arkkitehtuurissa, navigoinnissa, taiteessa, tähtitiedossa. Näin ollen, tutkiessaan ja analysoimalla tämän luvun ominaisuuksia, ihmiset tulivat laskemaan sen parametrien vastaavat suhteet.
Suorakulmaisiin kolmioihin liittyvät pääluokat ovat hypotenuusa ja jalat. Hypotenuusa on kolmion sivu, joka on oikeaa kulmaa vastapäätä. Jalat ovat vastaavasti kaksi muuta puolta. Minkä tahansa kolmion kulmien summa on aina 180 astetta.
Pallotrigonometria on trigonometrian osa, jota ei opeteta koulussa, mutta tutkijat käyttävät sitä soveltavissa tieteissä, kuten tähtitiedeessä ja geodesiassa. Kolmion ominaisuus pallomaisessa trigonometriassa on, että sen kulmien summa on aina suurempi kuin 180 astetta.
Kolmion kulmat
 Suorakulmaisessa kolmiossa kulman sini on halutun kulman vastakkaisen jalan suhde kolmion hypotenuusaan. Vastaavasti kosini on viereisen jalan ja hypotenuusan suhde. Molemmilla arvoilla on aina arvo pienempi kuin yksi, koska hypotenuusa on aina pidempi kuin jalka.
Suorakulmaisessa kolmiossa kulman sini on halutun kulman vastakkaisen jalan suhde kolmion hypotenuusaan. Vastaavasti kosini on viereisen jalan ja hypotenuusan suhde. Molemmilla arvoilla on aina arvo pienempi kuin yksi, koska hypotenuusa on aina pidempi kuin jalka.
Kulman tangentti on arvo, joka on yhtä suuri kuin halutun kulman vastakkaisen haaran suhde viereiseen haaraan tai sinistä kosiniin. Kotangentti puolestaan on halutun kulman viereisen haaran suhde vastakkaiseen kakettiin. Kulman kotangentti voidaan saada myös jakamalla yksikkö tangentin arvolla.
yksikköympyrä
Yksikköympyrä geometriassa on ympyrä, jonka säde on yhtä suuri kuin yksi. Tällainen ympyrä muodostetaan suorakulmaisessa koordinaatistossa, jossa ympyrän keskipiste osuu yhteen alkupisteen kanssa, ja sädevektorin alkusijainti määräytyy X-akselin positiivisen suunnan (abskissa-akselin) mukaan. Jokaisella ympyrän pisteellä on kaksi koordinaattia: XX ja YY, eli abskissan ja ordinaatin koordinaatit. Valitsemalla mikä tahansa ympyrän piste XX-tasossa ja pudottamalla siitä kohtisuora abskissa-akselille, saadaan suorakulmainen kolmio, jonka säde on valittuun pisteeseen (merkitkäämme sitä kirjaimella C), joka on piirretty kohtisuoraan X-akseli (leikkauspiste on merkitty kirjaimella G) ja jana abskissa-akselilla origon (piste merkitään kirjaimella A) ja leikkauspisteen G välillä. Tuloksena oleva kolmio ACG on suorakulmainen kolmio, joka on merkitty ympyrä, jossa AG on hypotenuusa ja AC ja GC ovat jalkoja. Ympyrän AC säteen ja abskissa-akselin segmentin välinen kulma, jossa on merkintä AG, määritellään α:ksi (alfa). Joten cos α = AG/AC. Koska AC on yksikköympyrän säde ja se on yhtä suuri kuin yksi, käy ilmi, että cos α=AG. Samoin sin α=CG.
Lisäksi näiden tietojen tiedossa on mahdollista määrittää ympyrän pisteen C koordinaatti, koska cos α=AG ja sin α=CG, mikä tarkoittaa, että pisteellä C on annetut koordinaatit (cos α; sin α). Tietäen, että tangentti on yhtä suuri kuin sinin ja kosinin suhde, voimme määrittää, että tg α \u003d y / x ja ctg α \u003d x / y. Kun otetaan huomioon negatiivisen koordinaatiston kulmat, voidaan laskea, että joidenkin kulmien sini- ja kosiniarvot voivat olla negatiivisia.
Laskelmat ja peruskaavat
Trigonometristen funktioiden arvot
Otettuaan huomioon trigonometristen funktioiden olemuksen yksikköympyrän kautta, voimme johtaa näiden funktioiden arvot joillekin kulmille. Arvot on lueteltu alla olevassa taulukossa.
Yksinkertaisimmat trigonometriset identiteetit
Yhtälöitä, joissa trigonometrisen funktion etumerkin alla on tuntematon arvo, kutsutaan trigonometrisiksi. Identiteetit, joiden arvo on sin x = α, k on mikä tahansa kokonaisluku:
- sin x = 0, x = πk.
- 2. sin x \u003d 1, x \u003d π / 2 + 2πk.
- sin x \u003d -1, x \u003d -π / 2 + 2πk.
- sin x = a, |a| > 1, ei ratkaisuja.
- sin x = a, |a| ≦ 1, x = (-1)^k * arcsin α + πk.
Identiteetit arvolla cos x = a, jossa k on mikä tahansa kokonaisluku:
- cos x = 0, x = π/2 + πk.
- cos x = 1, x = 2πk.
- cos x \u003d -1, x \u003d π + 2πk.
- cos x = a, |a| > 1, ei ratkaisuja.
- cos x = a, |a| ≦ 1, х = ±arccos α + 2πk.
Identiteetit arvolla tg x = a, jossa k on mikä tahansa kokonaisluku:
- tg x = 0, x = π/2 + πk.
- tg x \u003d a, x \u003d arctg α + πk.
Identiteetit, joiden arvo on ctg x = a, jossa k on mikä tahansa kokonaisluku:
- ctg x = 0, x = π/2 + πk.
- ctg x \u003d a, x \u003d arcctg α + πk.
Valokaavat
Tämä vakiokaavojen luokka tarkoittaa menetelmiä, joilla voit siirtyä muodon trigonometrisista funktioista argumentin funktioihin, toisin sanoen muuntaa minkä tahansa arvon kulman sini, kosini, tangentti ja kotangentti kulman vastaaviksi indikaattoreiksi. väli 0 - 90 astetta laskennan helpottamiseksi.
Kaavat pienennysfunktioiden kulman sinille näyttävät tältä:
- sin(900 - α) = α;
- sin(900 + α) = cos α;
- sin(1800 - α) = sin α;
- sin(1800 + α) = -sin α;
- sin(2700 - α) = -cos a;
- sin(2700 + α) = -cos α;
- sin(3600 - α) = -sin α;
- sin(3600 + α) = sin α.
Kulman kosinille:
- cos(900 - α) = sin α;
- cos(900 + a) = -sin a;
- cos(1800 - a) = -cos a;
- cos(1800 + a) = -cos a;
- cos(2700 - a) = -sin a;
- cos(2700 + α) = sin α;
- cos(3600 - a) = cos a;
- cos(3600 + α) = cos α.
Yllä olevien kaavojen käyttö on mahdollista kahdella säännöllä. Ensinnäkin, jos kulma voidaan esittää arvona (π/2 ± a) tai (3π/2 ± a), funktion arvo muuttuu:
- synnistä cosiin;
- cosista syntiin;
- tg:stä ctg:hen;
- ctg:stä tg:hen.
Funktion arvo pysyy muuttumattomana, jos kulma voidaan esittää muodossa (π ± a) tai (2π ± a).
Toiseksi pelkistetyn funktion merkki ei muutu: jos se oli alun perin positiivinen, se pysyy sellaisena. Sama pätee negatiivisiin funktioihin.
Lisäyskaavat
Nämä kaavat ilmaisevat kahden kiertokulman summan ja eron sinin, kosinin, tangentin ja kotangentin arvot trigonometristen funktioidensa suhteen. Kulmat merkitään yleensä α:na ja β:na.
Kaavat näyttävät tältä:
- sin(α ± β) = sin α * cos β ± cos α * sin.
- cos(α ± β) = cos α * cos β ∓ sin α * sin.
- tan(α ± β) = (tan α ± tan β) / (1 ∓ tan α * tan β).
- ctg(a ± β) = (-1 ± ctg a * ctg β) / (ctg a ± ctg β).
Nämä kaavat pätevät kaikille kulmille α ja β.
Kaksois- ja kolmoiskulmakaavat
Kaksois- ja kolmoiskulman trigonometriset kaavat ovat kaavoja, jotka yhdistävät kulmien 2α ja 3α funktiot kulman α trigonometrisiin funktioihin. Johdettu summauskaavoista:
- sin2α = 2sinα*cosα.
- cos2α = 1 - 2sin^2α.
- tg2a = 2tga/(1 - tg^2a).
- sin3α = 3sinα - 4sin^3α.
- cos3α = 4cos^3α - 3cosα.
- tg3a = (3tgα - tg^3a)/(1-tg^2a).
Siirtyminen summasta tuotteeseen
Kun otetaan huomioon, että 2sinx*cosy = sin(x+y) + sin(x-y), tätä kaavaa yksinkertaistamalla saadaan identiteetti sinα + sinβ = 2sin(α + β)/2 * cos(α − β)/2. Samoin sina - sinp = 2sin(a - β)/2 * cos(a + β)/2; cosα + cosβ = 2cos(α + β)/2 * cos(α − β)/2; cosα - cosβ = 2sin(α + β)/2 * sin(α - β)/2; tgα + tgβ = sin(a + β) / cosa * cosβ; tga-tgp = sin(a-p)/cosa*cosp; cosα + sinα = √2sin(π/4 ∓ α) = √2cos(π/4 ± α).
Siirtyminen tuotteesta summaan
Nämä kaavat seuraavat summan tuloksi siirtymisen identiteetistä:
- sinα * sinβ = 1/2*;
- cosa * cosβ = 1/2*;
- sinα * cosβ = 1/2*.
Vähennyskaavat
Näissä identiteeteissä sinin ja kosinin neliö- ja kuutiopotenssit voidaan ilmaista monikulmaisen ensimmäisen potenssin sininä ja kosinina:
- sin^2 a = (1 - cos2a)/2;
- cos^2a = (1 + cos2a)/2;
- sin^3 α = (3 * sinα - sin3α)/4;
- cos^3 a = (3 * cosa + cos3a)/4;
- sin^4 a = (3 - 4cos2a + cos4a)/8;
- cos^4 α = (3 + 4cos2α + cos4α)/8.
Universaali korvaus
Universaalit trigonometriset korvauskaavat ilmaisevat trigonometriset funktiot puolikulman tangentin muodossa.
- sin x \u003d (2tgx / 2) * (1 + tg ^ 2 x / 2), kun taas x \u003d π + 2πn;
- cos x = (1 - tg^2 x/2) / (1 + tg^2 x/2), missä x = π + 2πn;
- tg x \u003d (2tgx / 2) / (1 - tg ^ 2 x / 2), missä x \u003d π + 2πn;
- ctg x \u003d (1 - tg ^ 2 x / 2) / (2tgx / 2), kun taas x \u003d π + 2πn.
Erikoistapaukset
Yksinkertaisimpien trigonometristen yhtälöiden erityistapaukset on annettu alla (k on mikä tahansa kokonaisluku).
Yksityinen sine:
| sin x arvo | x arvo |
|---|---|
| 0 | pk |
| 1 | π/2 + 2πk |
| -1 | -π/2 + 2πk |
| 1/2 | π/6 + 2πk tai 5π/6 + 2πk |
| -1/2 | -π/6 + 2πk tai -5π/6 + 2πk |
| √2/2 | π/4 + 2πk tai 3π/4 + 2πk |
| -√2/2 | -π/4 + 2πk tai -3π/4 + 2πk |
| √3/2 | π/3 + 2πk tai 2π/3 + 2πk |
| -√3/2 | -π/3 + 2πk tai -2π/3 + 2πk |
Kosiniosamäärät:
| cos x arvo | x arvo |
|---|---|
| 0 | π/2 + 2πk |
| 1 | 2πk |
| -1 | 2 + 2πk |
| 1/2 | ±π/3 + 2πk |
| -1/2 | ±2π/3 + 2πk |
| √2/2 | ±π/4 + 2πk |
| -√2/2 | ±3π/4 + 2πk |
| √3/2 | ±π/6 + 2πk |
| -√3/2 | ±5π/6 + 2πk |
Yksityinen tangentille:
| tg x arvo | x arvo |
|---|---|
| 0 | pk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3/3 | π/6 + πk |
| -√3/3 | -π/6 + πk |
| √3 | π/3 + πk |
| -√3 | -π/3 + πk |
Kotangenttiosamäärät:
| ctg x arvo | x arvo |
|---|---|
| 0 | π/2 + πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3 | π/6 + πk |
| -√3 | -π/3 + πk |
| √3/3 | π/3 + πk |
| -√3/3 | -π/3 + πk |
Lauseet
Sinilause
Lauseena on kaksi versiota - yksinkertainen ja laajennettu. Yksinkertainen sinilause: a/sin α = b/sin β = c/sin γ. Tässä tapauksessa a, b, c ovat kolmion sivut ja α, β, γ ovat vastaavasti vastakkaisia kulmia.
Laajennettu sinilause mielivaltaiselle kolmiolle: a/sin α = b/sin β = c/sin γ = 2R. Tässä identiteetissä R tarkoittaa ympyrän sädettä, johon annettu kolmio on merkitty.
Kosinilause
Identiteetti näytetään seuraavasti: a^2 = b^2 + c^2 - 2*b*c*cos α. Kaavassa a, b, c ovat kolmion sivut ja α on sivun a vastakkainen kulma.
Tangenttilause
Kaava ilmaisee kahden kulman tangenttien ja niitä vastakkaisten sivujen pituuden välisen suhteen. Sivut on merkitty a, b, c ja vastaavat vastakkaiset kulmat ovat α, β, γ. Tangenttilauseen kaava: (a - b) / (a+b) = tg((α - β)/2) / tg((α + β)/2).
Kotangenttilause
Yhdistää kolmioon piirretyn ympyrän säteen sen sivujen pituuteen. Jos a, b, c ovat kolmion sivut ja vastaavasti A, B, C ovat niiden vastakkaiset kulmat, r on piirretyn ympyrän säde ja p on kolmion puolikehä, seuraavat identiteetit pidä:
- ctg A/2 = (p-a)/r;
- ctg B/2 = (p-b)/r;
- ctg C/2 = (p-c)/r.
Sovellukset

Trigonometria ei ole vain teoreettinen tiede, joka liittyy matemaattisiin kaavoihin. Sen ominaisuuksia, lauseita ja sääntöjä käyttävät käytännössä useat ihmisen toiminnan alat - tähtitiede, lento- ja merinavigointi, musiikin teoria, geodesia, kemia, akustiikka, optiikka, elektroniikka, arkkitehtuuri, taloustiede, konetekniikka, mittaustyöt, tietokonegrafiikka, kartografia, valtameri ja monet muut.
Sini, kosini, tangentti ja kotangentti ovat trigonometrian peruskäsitteitä, joilla voit matemaattisesti ilmaista kolmion kulmien ja sivujen pituuksien välistä suhdetta ja löytää halutut suureet identiteettien, lauseiden ja sääntöjen avulla.