මාර්ගගත ගණක යන්ත්‍රය. දී ඇති ලක්ෂ්‍යයක ශ්‍රිතයක ප්‍රස්ථාරයට සෘජු ස්පර්ශක සමීකරණය

ව්‍යුත්පන්නයේ ලකුණ සහ ශ්‍රිතයේ ඒකාකාරී බවේ ස්වභාවය අතර සම්බන්ධය පෙන්වයි.

කරුණාකර පහත සඳහන් දේ ගැන අතිශයින්ම සැලකිලිමත් වන්න. බලන්න, ඔබට ලබා දී ඇති දේවල කාලසටහන! කාර්යය හෝ එහි ව්යුත්පන්නය

ව්යුත්පන්නයේ ප්රස්ථාරයක් ලබා දෙන්නේ නම්, එවිට අපි ශ්රිත සංඥා සහ ශුන්ය ගැන පමණක් උනන්දු වනු ඇත. අපි ප්‍රතිපත්තිමය වශයෙන් කිසිදු “කඳු” හෝ “කුහර” ගැන උනන්දු නොවෙමු!

කාර්යය 1.

රූපයේ දැක්වෙන්නේ අන්තරය මත අර්ථ දක්වා ඇති ශ්‍රිතයක ප්‍රස්තාරයකි. ශ්‍රිතයේ ව්‍යුත්පන්නය සෘණ වන නිඛිල ලක්ෂ්‍ය ගණන නිර්ණය කරන්න.

විසඳුමක්:

රූපයේ, ක්‍රියාකාරිත්වය අඩු වන ප්‍රදේශ වර්ණයෙන් උද්දීපනය කර ඇත:

ශ්‍රිතයේ මෙම අඩුවන කලාපවල නිඛිල අගයන් 4ක් අඩංගු වේ.

කාර්යය 2.

රූපයේ දැක්වෙන්නේ අන්තරය මත අර්ථ දක්වා ඇති ශ්‍රිතයක ප්‍රස්තාරයකි. ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශක රේඛාවට සමාන්තරව හෝ සමපාත වන ලක්ෂ්‍ය ගණන සොයන්න.

විසඳුමක්:

ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශකය සරල රේඛාවක් සමඟ (හෝ, එය එකම දෙය) සමග සමාන්තරව (හෝ සමපාත වූ විට) බෑවුම, ශුන්‍යයට සමාන වේ, එවිට ස්පර්ශකයට කෝණික සංගුණකයක් ඇත.

මෙය අනෙක් අතට ස්පර්ශය අක්ෂයට සමාන්තර වේ, බෑවුම යනු අක්ෂයේ ස්පර්ශකයේ ආනතියේ කෝණයේ ස්පර්ශකය වන බැවිනි.

එබැවින්, අපි ප්‍රස්ථාරයේ අන්ත ලක්ෂ්‍ය (උපරිම සහ අවම ලක්ෂ්‍ය) සොයා ගනිමු - ප්‍රස්ථාරයට ස්පර්ශක ශ්‍රිත අක්ෂයට සමාන්තර වන්නේ මෙම ලක්ෂ්‍යවල ය.

එවැනි කරුණු 4 ක් ඇත.

කාර්යය 3.

පරතරය මත අර්ථ දක්වා ඇති ශ්‍රිතයක ව්‍යුත්පන්නයේ ප්‍රස්ථාරයක් රූපයේ දැක්වේ. ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශක රේඛාවට සමාන්තරව හෝ සමපාත වන ලක්ෂ්‍ය ගණන සොයන්න.

විසඳුමක්:

ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශකය බෑවුමක් ඇති රේඛාවක් සමග සමාන්තරව (හෝ සමපාත වන බැවින්) ස්පර්ශයට ද බෑවුමක් ඇත.

මෙයින් අදහස් කරන්නේ ස්පර්ශක ස්ථානවල බවයි.

එබැවින්, ප්‍රස්ථාරයේ ලක්ෂ්‍ය කීයකට සමාන ඕඩිනේට් තිබේදැයි අපි බලමු.

ඔබට පෙනෙන පරිදි, එවැනි කරුණු හතරක් තිබේ.

කාර්යය 4.

රූපයේ දැක්වෙන්නේ අන්තරය මත අර්ථ දක්වා ඇති ශ්‍රිතයක ප්‍රස්තාරයකි. ශ්‍රිතයේ ව්‍යුත්පන්නය 0 වන ලක්ෂ්‍ය ගණන සොයන්න.

විසඳුමක්:

ව්‍යුත්පන්නය අන්ත ලක්ෂ්‍යවල ශුන්‍යයට සමාන වේ. අපට ඒවායින් 4 ක් ඇත:

කාර්යය 5.

රූපයේ දැක්වෙන්නේ ශ්‍රිතයක ප්‍රස්ථාරයක් සහ x-අක්ෂයේ ලක්ෂ්‍ය එකොළහක්:. මෙම ලක්ෂ්‍යවලින් කීයකින් ශ්‍රිතයේ ව්‍යුත්පන්නය සෘණ වන්නේද?

විසඳුමක්:

අඩුවන ශ්‍රිතයේ කාල පරතරයන්හිදී, එහි ව්‍යුත්පන්නය සෘණ අගයන් ගනී. තවද ලක්ෂ්යවලදී කාර්යය අඩු වේ. එවැනි කරුණු 4 ක් ඇත.

කාර්යය 6.

රූපයේ දැක්වෙන්නේ අන්තරය මත අර්ථ දක්වා ඇති ශ්‍රිතයක ප්‍රස්තාරයකි. ශ්‍රිතයේ අන්ත ලක්ෂ්‍යවල එකතුව සොයන්න.

විසඳුමක්:

අන්ත ලකුණු– මේවා උපරිම ලකුණු (-3, -1, 1) සහ අවම ලකුණු (-2, 0, 3) වේ.

අන්ත ලක්ෂ්‍යවල එකතුව: -3-1+1-2+0+3=-2.

කාර්යය 7.

පරතරය මත අර්ථ දක්වා ඇති ශ්‍රිතයක ව්‍යුත්පන්නයේ ප්‍රස්ථාරයක් රූපයේ දැක්වේ. ශ්‍රිතයේ වැඩි වීමේ කාල අන්තරයන් සොයන්න. ඔබේ පිළිතුරෙහි, මෙම කාල අන්තරයන්ට ඇතුළත් කර ඇති පූර්ණ සංඛ්‍යා ලක්ෂ්‍යවල එකතුව දක්වන්න.

විසඳුමක්:

ශ්‍රිතයේ ව්‍යුත්පන්නය සෘණ නොවන විරාමයන් රූපයෙන් ඉස්මතු කරයි.

කුඩා වැඩිවන පරතරය මත නිඛිල ලක්ෂ්‍ය නොමැත; වැඩිවන පරතරය මත පූර්ණ සංඛ්‍යා හතරක් ඇත: , , සහ .

ඔවුන්ගේ එකතුව:

කාර්යය 8.

පරතරය මත අර්ථ දක්වා ඇති ශ්‍රිතයක ව්‍යුත්පන්නයේ ප්‍රස්ථාරයක් රූපයේ දැක්වේ. ශ්‍රිතයේ වැඩි වීමේ කාල අන්තරයන් සොයන්න. ඔබේ පිළිතුරෙහි, ඒවායින් විශාලතම දිග සඳහන් කරන්න.

විසඳුමක්:

රූපයේ, ව්‍යුත්පන්නය ධනාත්මක වන සියලුම කාල අන්තරයන් වර්ණයෙන් උද්දීපනය කර ඇත, එයින් අදහස් කරන්නේ මෙම කාල පරතරයන් මත ශ්‍රිතය වැඩි වන බවයි.

ඒවායින් විශාලතම දිග 6 කි.

කාර්යය 9.

පරතරය මත අර්ථ දක්වා ඇති ශ්‍රිතයක ව්‍යුත්පන්නයේ ප්‍රස්ථාරයක් රූපයේ දැක්වේ. කොටසෙහි කුමන අවස්ථාවේදී එය විශාලතම අගයක් ගනීද?

විසඳුමක්:

අපි උනන්දුව දක්වන කොටසෙහි ප්‍රස්ථාරය හැසිරෙන්නේ කෙසේදැයි බලමු ව්යුත්පන්නයේ ලකුණ පමණි .

මෙම කොටසෙහි ප්‍රස්ථාරය අක්ෂයට පහළින් ඇති බැවින් on ව්‍යුත්පන්නයේ ලකුණ සෘණ වේ.

යම් අවස්ථාවක x 0 හි පරිමිත ව්‍යුත්පන්නයක් ඇති f (x 0) ශ්‍රිතයක් ලබා දෙමු. එවිට කෝණික සංගුණකය f’(x 0) සහිත ලක්ෂ්‍යය (x 0 ; f (x 0)) හරහා ගමන් කරන සරල රේඛාව ස්පර්ශකයක් ලෙස හැඳින්වේ.

ව්‍යුත්පන්නය x 0 ලක්ෂ්‍යයේ නොමැති නම් කුමක් සිදුවේද? විකල්ප දෙකක් තිබේ:

1. ප්‍රස්ථාරයට ද ස්පර්ශකයක් නොමැත. සම්භාව්‍ය උදාහරණයක් වන්නේ y = |x | ශ්‍රිතයයි ලක්ෂ්යයේ (0; 0).
2. ස්පර්ශකය සිරස් අතට හැරේ. උදාහරණයක් ලෙස, ලක්ෂ්‍යයේ (1; π /2) y = arcsin x ශ්‍රිතය සඳහා මෙය සත්‍ය වේ.

ස්පර්ශක සමීකරණය

ඕනෑම සිරස් නොවන සරල රේඛාවක් y = kx + b ආකෘතියේ සමීකරණයකින් ලබා දී ඇත, මෙහි k යනු බෑවුම වේ. ස්පර්ශකයද ව්‍යතිරේකයක් නොවන අතර, x 0 යම් අවස්ථාවක එහි සමීකරණය නිර්මාණය කිරීම සඳහා, මෙම ලක්ෂ්‍යයේ ශ්‍රිතයේ සහ ව්‍යුත්පන්නයේ අගය දැනගැනීම ප්‍රමාණවත් වේ.

එබැවින්, කොටසෙහි y = f ’(x) ව්‍යුත්පන්නයක් ඇති y = f (x) ශ්‍රිතයක් ලබා දෙන්න. එවිට ඕනෑම අවස්ථාවක x 0 ∈ (a ; b) මෙම ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශකයක් ඇද ගත හැක, එය සමීකරණය මගින් ලබා දී ඇත:

y = f ’(x 0) (x - x 0) + f (x 0)

මෙහි f ’(x 0) යනු x 0 ලක්ෂයේ ව්‍යුත්පන්නයේ අගය වන අතර f (x 0) යනු ශ්‍රිතයේම අගයයි.

කාර්ය. y = x 3 ශ්‍රිතය ලබා දී ඇත. x 0 = 2 ලක්ෂ්‍යයේ මෙම ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශකය සඳහා සමීකරණයක් ලියන්න.

ස්පර්ශක සමීකරණය: y = f ’(x 0) · (x - x 0) + f (x 0). x 0 = 2 ලක්ෂ්‍යය අපට ලබා දී ඇත, නමුත් f (x 0) සහ f '(x 0) අගයන් ගණනය කිරීමට සිදුවේ.

පළමුව, අපි කාර්යයේ අගය සොයා ගනිමු. මෙහි සෑම දෙයක්ම පහසුය: f (x 0) = f (2) = 2 3 = 8;
දැන් අපි ව්‍යුත්පන්නය සොයා ගනිමු: f '(x) = (x 3)' = 3x 2;
අපි x 0 = 2 ව්‍යුත්පන්නයට ආදේශ කරමු: f ’(x 0) = f ’(2) = 3 2 2 = 12;
සමස්තයක් වශයෙන් අපට ලැබෙන්නේ: y = 12 · (x - 2) + 8 = 12x - 24 + 8 = 12x - 16.
මෙය ස්පර්ශක සමීකරණයයි.

කාර්ය. x 0 = π /2 ලක්ෂ්‍යයේ f (x) = 2sin x + 5 ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශකය සඳහා සමීකරණයක් ලියන්න.

මෙවර අපි සෑම ක්‍රියාවක්ම විස්තරාත්මකව විස්තර නොකරමු - අපි ප්‍රධාන පියවර පමණක් දක්වන්නෙමු. අපිට තියෙනවා:

f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f ’(x) = (2sin x + 5)’ = 2cos x;
f ’(x 0) = f ’(π /2) = 2cos (π /2) = 0;

ස්පර්ශක සමීකරණය:

y = 0 · (x - π /2) + 7 ⇒ y = 7

අවසාන අවස්ථාවේ දී, සරල රේඛාව තිරස් අතට හැරුනේ, මන්ද එහි කෝණික සංගුණකය k = 0. මෙහි වරදක් නැත - අපි අන්ත ලක්ෂ්‍යයක් මත පැකිළෙමු.

ලිපිය අර්ථ දැක්වීම් පිළිබඳ සවිස්තරාත්මක පැහැදිලි කිරීමක් සපයයි, චිත්රක අංකන සහිත ව්යුත්පන්නයේ ජ්යාමිතික අර්ථය. ස්පර්ශක රේඛාවක සමීකරණය උදාහරණ සමඟ සලකා බලනු ඇත, 2 වන අනුපිළිවෙලෙහි වක්‍ර දක්වා ස්පර්ශකයක සමීකරණ සොයා ගනු ඇත.

Yandex.RTB R-A-339285-1 අර්ථ දැක්වීම 1

y = k x + b සරල රේඛාවේ ආනතිය කෝණය α ලෙස හැඳින්වේ, එය x අක්ෂයේ ධනාත්මක දිශාවේ සිට y = k x + b දක්වා ධනාත්මක දිශාවට මනිනු ලැබේ.

රූපයේ, x දිශාව හරිත ඊතලයකින් සහ හරිත චාපයකින් ද, ආනතියේ කෝණය රතු චාපයකින් ද දැක්වේ. නිල් රේඛාව සරල රේඛාවට යොමු කරයි.

අර්ථ දැක්වීම 2

y = k x + b සරල රේඛාවේ බෑවුම සංඛ්‍යාත්මක සංගුණකය k ලෙස හැඳින්වේ.

කෝණික සංගුණකය සරල රේඛාවේ ස්පර්ශයට සමාන වේ, වෙනත් වචන වලින් කිවහොත් k = t g α.

• සරල රේඛාවක ආනතියේ කෝණය 0 ට සමාන වන්නේ එය x ට සමාන්තර නම් සහ බෑවුම ශුන්‍යයට සමාන නම් පමණි, මන්ද ශුන්‍යයේ ස්පර්ශකය 0 ට සමාන වේ. මෙයින් අදහස් කරන්නේ සමීකරණයේ ස්වරූපය y = b වනු ඇති බවයි.
• y = k x + b සරල රේඛාවේ ආනතියේ කෝණය තියුණු නම්, කොන්දේසි 0 තෘප්තිමත් වේ.< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0, සහ ප්රස්ථාරයේ වැඩි වීමක් ඇත.
• α = π 2 නම්, රේඛාවේ පිහිටීම x ට ලම්බක වේ. සමානාත්මතාවය x = c මගින් නියම කර ඇති අගය c තාත්වික අංකයක් වේ.
• y = k x + b සරල රේඛාවේ ආනතියේ කෝණය නොපැහැදිලි නම්, එය π 2 කොන්දේසි වලට අනුරූප වේ.< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

secant යනු f (x) ශ්‍රිතයේ ලක්ෂ්‍ය 2ක් හරහා ගමන් කරන රේඛාවකි. වෙනත් වචන වලින් කිවහොත්, secant යනු දී ඇති ශ්‍රිතයක ප්‍රස්ථාරයේ ඕනෑම ලක්ෂ්‍ය දෙකක් හරහා ගමන් කරන සරල රේඛාවකි.

රූපයේ දැක්වෙන්නේ A B යනු තත්පරයක් වන අතර f (x) යනු කළු වක්‍රයක් වන අතර α යනු රතු චාපයක් වන අතර එය තත්පරයේ ආනතියේ කෝණය පෙන්නුම් කරයි.

සෘජු රේඛාවක කෝණික සංගුණකය ආනතියේ කෝණයේ ස්පර්ශකයට සමාන වන විට, A B C සෘජුකෝණාශ්‍රය ත්‍රිකෝණයක ස්පර්ශකය ප්‍රතිවිරුද්ධ පැත්තට යාබදව ඇති අනුපාතයෙන් සොයාගත හැකි බව පැහැදිලිය.

අර්ථ දැක්වීම 4

පෝරමයේ සෙකන්ට් එකක් සොයා ගැනීම සඳහා අපට සූත්‍රයක් ලැබේ:

k = t g α = B C A C = f (x B) - f x A x B - x A, මෙහි A සහ ​​B යන ලක්ෂ්‍යවල abscissas යනු x A, x B, සහ f (x A), f (x) අගයන් වේ. B) මෙම ලක්ෂ්යවල අගයන් ශ්රිත වේ.

පැහැදිලිවම, තත්පරයේ කෝණික සංගුණකය k = f (x B) - f (x A) x B - x A හෝ k = f (x A) - f (x B) x A - x B සමානාත්මතාවය භාවිතයෙන් තීරණය වේ. , සහ සමීකරණය ලිවිය යුත්තේ y = f (x B) - f (x A) x B - x A x - x A + f (x A) හෝ
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

secant මගින් ප්‍රස්ථාරය දෘශ්‍යමය වශයෙන් කොටස් 3 කට බෙදා ඇත: A ලක්ෂ්‍යයේ වම් පසින්, A සිට B දක්වා, B සිට දකුණට. පහත රූපයේ දැක්වෙන්නේ අහඹු ලෙස සලකනු ලබන තත්පර තුනක් ඇති බවයි, එනම් ඒවා a භාවිතයෙන් සකසා ඇත. සමාන සමීකරණය.

නිර්වචනය අනුව, මෙම නඩුවේ සරල රේඛාව සහ එහි secant සමපාත වන බව පැහැදිලිය.

තත්පරයකට දී ඇති ශ්‍රිතයක ප්‍රස්ථාරය කිහිප වතාවක් ඡේදනය කළ හැක. secant සඳහා y = 0 ආකාරයේ සමීකරණයක් තිබේ නම්, sinusoid සමඟ ඡේදනය වන ලක්ෂ්ය ගණන අනන්තය.

අර්ථ දැක්වීම 5

x 0 ලක්ෂයේ f (x) ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශක; f (x 0) යනු ලබා දී ඇති ලක්ෂ්‍යයක් හරහා ගමන් කරන සරල රේඛාවකි x 0; f (x 0), x 0 ට ආසන්න බොහෝ x අගයන් ඇති ඛණ්ඩයක් තිබීමත් සමඟ.

උදාහරණ 1

පහත උදාහරණය දෙස සමීපව බලමු. එවිට y = x + 1 ශ්‍රිතයෙන් අර්ථ දක්වා ඇති රේඛාව ඛණ්ඩාංක (1; 2) සහිත ලක්ෂ්‍යයේ දී y = 2 x ට ස්පර්ශක ලෙස සලකන බව පැහැදිලිය. පැහැදිලිකම සඳහා, (1; 2) ට ආසන්න අගයන් සහිත ප්‍රස්ථාර සලකා බැලීම අවශ්‍ය වේ. y = 2 x ශ්‍රිතය කළු පැහැයෙන් පෙන්වා ඇත, නිල් රේඛාව ස්පර්ශක රේඛාව වන අතර රතු තිත ඡේදනය වන ලක්ෂ්‍යය වේ.

පැහැදිලිවම, y = 2 x y = x + 1 රේඛාව සමඟ ඒකාබද්ධ වේ.

ස්පර්ශකය නිර්ණය කිරීම සඳහා, අපි A B ලක්ෂ්‍යය A ලක්ෂ්‍යයට අසීමිතව ළඟා වන විට A B හි හැසිරීම සලකා බැලිය යුතුය.පැහැදිලි භාවය සඳහා, අපි චිත්‍රයක් ඉදිරිපත් කරමු.

නිල් රේඛාවෙන් දැක්වෙන A B, ස්පර්ශකයේ පිහිටීම වෙත නැඹුරු වන අතර, α හි ආනතියේ කෝණය ස්පර්ශකයේම α x ආනතියේ කෝණයට නැඹුරු වීමට පටන් ගනී.

අර්ථ දැක්වීම 6

A ලක්ෂ්‍යයේ ඇති y = f (x) ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශකය A B ට නැඹුරු වන බැවින් A B හි සීමාකාරී ස්ථානය ලෙස සැලකේ, එනම් B → A.

දැන් අපි ලක්ෂ්‍යයක ශ්‍රිතයක ව්‍යුත්පන්නයේ ජ්‍යාමිතික අර්ථය සලකා බලමු.

අපි f (x) ශ්‍රිතය සඳහා A B යන දෙවන කොටස සලකා බලමු, එහිදී A සහ ​​B ඛණ්ඩාංක x 0, f (x 0) සහ x 0 + ∆ x, f (x 0 + ∆ x), සහ ∆ x වේ තර්කයේ වැඩිවීමක් ලෙස දැක්වේ. දැන් ශ්‍රිතය ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) පෝරමය ගනී. පැහැදිලිකම සඳහා, අපි චිත්රයක් සඳහා උදාහරණයක් දෙන්නෙමු.

ප්‍රතිඵලයක් ලෙස ලැබෙන සෘජුකෝණ ත්‍රිකෝණය සලකා බලන්න A B C. අපි ස්පර්ශක නිර්වචනය විසඳීමට භාවිතා කරමු, එනම්, අපි සම්බන්ධය ∆ y ∆ x = t g α ලබා ගනිමු. ස්පර්ශකයේ නිර්වචනය අනුව එය ලිම් ∆ x → 0 ∆ y ∆ x = t g α x . ලක්ෂ්‍යයක ව්‍යුත්පන්නයේ රීතියට අනුව, අපට ඇත්තේ x 0 ලක්ෂ්‍යයේ ඇති f (x) ව්‍යුත්පන්නය ශ්‍රිතයේ වර්ධකයේ සහ තර්කයේ වර්ධකයේ අනුපාතයේ සීමාව ලෙස හැඳින්වේ, එහිදී ∆ x → 0 , එවිට අපි එය f (x 0) = lim ∆ x → 0 ∆ y ∆ x ලෙස දක්වන්නෙමු.

එය පහත දැක්වෙන්නේ f "(x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, එහිදී k x ස්පර්ශකයේ බෑවුම ලෙස දැක්වේ.

එනම්, f '(x) x 0 ලක්ෂ්‍යයේ පැවතිය හැකි අතර, x 0, f 0 (x 0) ට සමාන ස්පර්ශක ලක්ෂ්‍යයේ දී ශ්‍රිතයේ දී ඇති ප්‍රස්ථාරයකට ස්පර්ශකයක් මෙන්, එහි අගය ලක්ෂ්‍යයේ ස්පර්ශකයේ බෑවුම x 0 ලක්ෂයේ ව්‍යුත්පන්නයට සමාන වේ. එවිට අපට එම k x = f " (x 0) ලැබේ.

ලක්ෂ්‍යයක ශ්‍රිතයක ව්‍යුත්පන්නයේ ජ්‍යාමිතික අර්ථය වන්නේ එය එම ලක්ෂ්‍යයේම ප්‍රස්ථාරයට ස්පර්ශක පැවැත්ම පිළිබඳ සංකල්පය ලබා දීමයි.

තලයක ඕනෑම සරල රේඛාවක සමීකරණය ලිවීමට, එය ගමන් කරන ලක්ෂ්‍යය සමඟ කෝණික සංගුණකයක් තිබීම අවශ්‍ය වේ. එහි අංකනය ඡේදනය වන විට x 0 ලෙස ගනු ලැබේ.

x 0, f 0 (x 0) ලක්ෂ්‍යයේ y = f (x) ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශක සමීකරණය y = f "(x 0) x - x 0 + f (x 0) ආකාරය ගනී.

මෙයින් අදහස් කරන්නේ f "(x 0) ව්‍යුත්පන්නයේ අවසාන අගයට ස්පර්ශකයේ පිහිටීම තීරණය කළ හැකි බවයි, එනම් සිරස් අතට, සපයා ඇති lim x → x 0 + 0 f "(x) = ∞ සහ lim x → x 0 - 0 f "(x ) = ∞ හෝ නොමැති වීම lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .

ස්පර්ශකයේ පිහිටීම එහි කෝණික සංගුණකයේ අගය මත රඳා පවතී k x = f "(x 0). o x අක්ෂයට සමාන්තරව, අපි k k = 0 ලබා ගනිමු, o y - k x = ∞ ට සමාන්තර වන විට, සහ ආකෘතියේ ආකාරය ස්පර්ශක සමීකරණය x = x 0 k x > 0 සමඟ වැඩි වේ, k x ලෙස අඩු වේ< 0 .

උදාහරණ 2

ඛණ්ඩාංක (1; 3) සමඟ ලක්ෂ්‍යයේ දී y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශකය සඳහා සමීකරණයක් සම්පාදනය කර ආනතියේ කෝණය තීරණය කරන්න.

විසඳුමක්

කොන්දේසිය අනුව, සියලුම තාත්වික සංඛ්‍යා සඳහා ශ්‍රිතය අර්ථ දක්වා ඇති බව අපට ඇත. කොන්දේසිය මගින් නිශ්චිතව දක්වා ඇති ඛණ්ඩාංක සහිත ලක්ෂ්‍යය, (1; 3) ස්පර්ශක ලක්ෂ්‍යයක් බව අපට පෙනී යයි, එවිට x 0 = - 1, f (x 0) = - 3.

අගය සහිත ලක්ෂ්‍යයේ ව්‍යුත්පන්නය සොයා ගැනීම අවශ්‍ය වේ - 1. අපිට ඒක ලැබෙනවා

y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

ස්පර්ශක ලක්ෂ්‍යයේ f' (x) අගය වන්නේ ස්පර්ශකයේ බෑවුම වන අතර එය බෑවුමේ ස්පර්ශයට සමාන වේ.

එවිට k x = t g α x = y "(x 0) = 3 3

එය පහත දැක්වෙන්නේ α x = a r c t g 3 3 = π 6 ය

පිළිතුර:ස්පර්ශක සමීකරණය ස්වරූපය ගනී

y = f "(x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

පැහැදිලිකම සඳහා, අපි චිත්රක නිදර්ශනයක උදාහරණයක් දෙන්නෙමු.

මුල් ශ්‍රිතයේ ප්‍රස්ථාරය සඳහා කළු වර්ණය භාවිතා වේ, නිල් වර්ණය ස්පර්ශකයේ රූපය වන අතර රතු තිත ස්පර්ශක ලක්ෂ්‍යය වේ. දකුණු පස ඇති රූපය විශාල කළ දර්ශනයක් පෙන්වයි.

උදාහරණය 3

දී ඇති ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශක පැවැත්ම නිර්ණය කරන්න
y = 3 · x - 1 5 + 1 ඛණ්ඩාංක සහිත ලක්ෂ්‍යයේ (1 ; 1) . සමීකරණයක් ලියන්න සහ ආනතියේ කෝණය තීරණය කරන්න.

විසඳුමක්

කොන්දේසිය අනුව, දී ඇති ශ්‍රිතයක අර්ථ දැක්වීමේ වසම සියලු තාත්වික සංඛ්‍යා සමූහය ලෙස සලකනු ලැබේ.

අපි ව්‍යුත්පන්නය සෙවීමට යමු

y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

x 0 = 1 නම්, f' (x) නිර්වචනය කර නොමැති නමුත්, සීමාවන් ලිම් x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 ලෙස ලියා ඇත. · 1 + 0 = + ∞ සහ lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , එනම් ලක්ෂ්‍යයේ සිරස් ස්පර්ශක පැවැත්ම (1; 1).

පිළිතුර:සමීකරණය x = 1 ස්වරූපය ගනී, එහිදී ආනතියේ කෝණය π 2 ට සමාන වේ.

පැහැදිලිකම සඳහා, අපි එය චිත්රක ලෙස නිරූපණය කරමු.

උදාහරණය 4

y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 ශ්‍රිතයේ ප්‍රස්ථාරයේ ලක්ෂ්‍ය සොයන්න

1. ස්පර්ශකයක් නොමැත;
2. ස්පර්ශකය x ට සමාන්තර වේ;
3. ස්පර්ශකය y = 8 5 x + 4 රේඛාවට සමාන්තර වේ.

විසඳුමක්

අර්ථ දැක්වීමේ විෂය පථය කෙරෙහි අවධානය යොමු කිරීම අවශ්ය වේ. කොන්දේසිය අනුව, සියලු තාත්වික සංඛ්යා කට්ටලය මත ශ්රිතය අර්ථ දක්වා ඇත. අපි මොඩියුලය පුළුල් කර පද්ධතිය x ∈ - ∞ පරතරයන් සමඟ විසඳන්නෙමු ; 2 සහ [ - 2 ; +∞) . අපිට ඒක ලැබෙනවා

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; +∞)

කාර්යය වෙනස් කිරීම අවශ්ය වේ. අපිට ඒක තියෙනවා

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; +∞)

x = - 2 වූ විට, එම අවස්ථාවේ දී ඒකපාර්ශ්වික සීමාවන් සමාන නොවන නිසා ව්‍යුත්පන්නය නොපවතී:

lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

අපි x = - 2 ලක්ෂ්‍යයෙන් ශ්‍රිතයේ අගය ගණනය කරමු, එහිදී අපට එය ලැබේ

1. y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, එනම් ලක්ෂ්‍යයේ ස්පර්ශකය ( - 2; - 2) නොපවතියි.
2. බෑවුම ශුන්‍ය වූ විට ස්පර්ශකය x ට සමාන්තර වේ. එවිට k x = t g α x = f "(x 0). එනම්, ශ්‍රිතයේ ව්‍යුත්පන්නය එය ශුන්‍යයට හරවන විට එවැනි x හි අගයන් සොයා ගැනීම අවශ්‍ය වේ. එනම් f' හි අගයන්. (x) ස්පර්ශක ලක්ෂ්‍ය වනු ඇත, එහිදී ස්පර්ශකය x ට සමාන්තර වේ.

විට x ∈ - ∞ ; - 2, පසුව - 1 5 (x 2 + 12 x + 35) = 0, සහ x ∈ (- 2; + ∞) සඳහා අපට 1 5 (x 2 - 4 x + 3) = 0 ලැබේ.

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

අනුරූප ශ්‍රිත අගයන් ගණනය කරන්න

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

එබැවින් - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 ශ්‍රිත ප්‍රස්ථාරයේ අවශ්‍ය ලක්ෂ්‍ය ලෙස සැලකේ.

විසඳුමේ චිත්රක නිරූපණයක් දෙස බලමු.

කළු රේඛාව ශ්‍රිතයේ ප්‍රස්ථාරය, රතු තිත් ස්පර්ශක ලක්ෂ්‍ය වේ.

1. රේඛා සමාන්තර වන විට කෝණික සංගුණක සමාන වේ. එවිට ශ්‍රිත ප්‍රස්ථාරයේ බෑවුම 8 5 අගයට සමාන වන ලකුණු සෙවීම අවශ්‍ය වේ. මෙය සිදු කිරීම සඳහා, ඔබ y "(x) = 8 5 පෝරමයේ සමීකරණයක් විසඳිය යුතුය. එවිට, x ∈ - ∞; - 2 නම්, අපි එය ලබා ගනිමු - 1 5 (x 2 + 12 x + 35) = 8 5, සහ x ∈ (- 2 ; + ∞) නම් 1 5 (x 2 - 4 x + 3) = 8 5.

වෙනස්කම් කිරීම ශුන්‍යයට වඩා අඩු බැවින් පළමු සමීකරණයට මූලයන් නොමැත. අපි ඒක ලියමු

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

තවත් සමීකරණයකට සැබෑ මූලයන් දෙකක් ඇත, එසේ නම්

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

අපි ශ්‍රිතයේ අගයන් සෙවීමට යමු. අපිට ඒක ලැබෙනවා

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

අගයන් සහිත ලකුණු - 1; 4 15, 5; 8 3 යනු ස්පර්ශක y = 8 5 x + 4 රේඛාවට සමාන්තර වන ලක්ෂ්‍ය වේ.

පිළිතුර:කළු රේඛාව - ශ්රිතයේ ප්රස්ථාරය, රතු රේඛාව - y = 8 5 x + 4 හි ප්රස්ථාරය, නිල් රේඛාව - ලක්ෂ්යවල ස්පර්ශක - 1; 4 15, 5; 8 3.

දී ඇති ශ්‍රිත සඳහා ස්පර්ශක අනන්ත සංඛ්‍යාවක් තිබිය හැක.

උදාහරණ 5

y = - 2 x + 1 2 සරල රේඛාවට ලම්බකව පිහිටා ඇති y = 3 cos 3 2 x - π 4 - 1 3 ශ්‍රිතයේ පවතින සියලුම ස්පර්ශකවල සමීකරණ ලියන්න.

විසඳුමක්

ස්පර්ශක සමීකරණය සම්පාදනය කිරීම සඳහා, රේඛාවල ලම්බක තත්ත්වය මත පදනම්ව ස්පර්ශක ලක්ෂ්‍යයේ සංගුණකය සහ ඛණ්ඩාංක සොයා ගැනීම අවශ්‍ය වේ. නිර්වචනය පහත පරිදි වේ: සරල රේඛා වලට ලම්බක වන කෝණික සංගුණකවල ගුණිතය සමාන වේ - 1, එනම් k x · k ⊥ = - 1 ලෙස ලියා ඇත. අපට ඇති කොන්දේසියෙන් කෝණික සංගුණකය රේඛාවට ලම්බකව පිහිටා ඇති අතර k ⊥ = - 2 ට සමාන වේ, පසුව k x = - 1 k ⊥ = - 1 - 2 = 1 2.

දැන් ඔබට ස්පර්ශ ලක්ෂ්යවල ඛණ්ඩාංක සොයාගත යුතුය. දී ඇති ශ්‍රිතයක් සඳහා ඔබ x සහ පසුව එහි අගය සොයා ගත යුතුය. ලක්ෂ්‍යයේ ව්‍යුත්පන්නයේ ජ්‍යාමිතික අර්ථයෙන් බව සලකන්න
x 0 අපි k x = y "(x 0) ලබා ගනිමු. මෙම සමානාත්මතාවයෙන් අපි සම්බන්ධතා ස්ථාන සඳහා x හි අගයන් සොයා ගනිමු.

අපිට ඒක ලැබෙනවා

y "(x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 sin 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9

මෙම ත්‍රිකෝණමිතික සමීකරණය ස්පර්ශක ලක්ෂ්‍යවල ඕඩිනේට් ගණනය කිරීමට භාවිතා කරනු ඇත.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk හෝ 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk හෝ 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk හෝ x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z යනු පූර්ණ සංඛ්‍යා සමූහයකි.

x සම්බන්ධතා ස්ථාන සොයාගෙන ඇත. දැන් ඔබ y හි අගයන් සෙවීමට යා යුතුය:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 හෝ y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 හෝ y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 හෝ y 0 = - 4 5 + 1 3

මෙයින් අපට ලැබෙන්නේ 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3, 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 ස්පර්ශක ලක්ෂ්‍ය වේ.

පිළිතුර:අවශ්ය සමීකරණ ලෙස ලියා ඇත

y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3, y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

දෘශ්‍ය නිරූපණයක් සඳහා, ඛණ්ඩාංක රේඛාවක් මත ශ්‍රිතයක් සහ ස්පර්ශකයක් සලකා බලන්න.

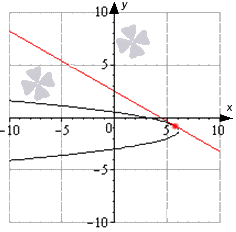
රූපයේ දැක්වෙන්නේ ශ්රිතය [-10 ; 10 ], කළු රේඛාව ශ්‍රිතයේ ප්‍රස්ථාරය වන අතර, නිල් රේඛා ස්පර්ශක වේ, ඒවා y = - 2 x + 1 2 ආකෘතියේ දී ඇති රේඛාවට ලම්බකව පිහිටා ඇත. රතු තිත් ස්පර්ශක ස්ථාන වේ.

2 වන අනුපිළිවෙලෙහි වක්‍රවල කැනොනිකල් සමීකරණ තනි අගයක් සහිත ශ්‍රිත නොවේ. ඔවුන් සඳහා ස්පර්ශක සමීකරණ දන්නා යෝජනා ක්රම අනුව සම්පාදනය කර ඇත.

කවයකට ස්පර්ශක

x c e n t e r ලක්ෂ්‍යයේ කේන්ද්‍රය සහිත කවයක් අර්ථ දැක්වීමට; y c e n t e r සහ අරය R, x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 සූත්‍රය යොදන්න.

මෙම සමානාත්මතාවය කාර්යයන් දෙකක එකතුවක් ලෙස ලිවිය හැකිය:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

රූපයේ දැක්වෙන පරිදි පළමු කාර්යය ඉහළින් පිහිටා ඇති අතර දෙවැන්න පහළින් පිහිටා ඇත.

x 0 ලක්ෂයේ වෘත්තයක සමීකරණය සම්පාදනය කිරීමට; y 0 , ඉහළ හෝ පහළ අර්ධ වෘත්තාකාරයේ පිහිටා ඇති අතර, ඔබ y = R 2 - x - x c e n t e r 2 + y c e n t e r හෝ y = - R 2 - x - x c e n 2 ආකෘතියේ ශ්රිතයක ප්රස්ථාරයේ සමීකරණය සොයාගත යුතුය. y c e n t e r දක්වා ඇති ස්ථානයේ.

x c e n t e r ලක්ෂ්‍යවල සිටින විට; y c e n t e r + R සහ x c e n t e r; y c e n t e r - R ස්පර්ශක y = y c e n t e r + R සහ y = y c e n t e r - R , සහ ලක්ෂ්‍ය x c e n t e r + R යන සමීකරණ මගින් ලබා දිය හැක; y c e n t e r සහ
x c e n t e r - R ; y c e n t e r o y ට සමාන්තර වනු ඇත, එවිට අපි x = x c e n t e r + R සහ x = x c e n t e r - R ආකෘතියේ සමීකරණ ලබා ගනිමු.

ඉලිප්සයකට ස්පර්ශක

ඉලිප්සයට x c e n t e r හි කේන්ද්‍රයක් ඇති විට; y c e n t e r අර්ධ අක්ෂ සහිත a සහ b, එවිට එය x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 සමීකරණය භාවිතයෙන් නියම කළ හැක.

ඉහළ සහ පහළ අර්ධ-ඉලිප්ස යන ශ්‍රිත දෙකක් එකතු කිරීමෙන් ඉලිප්සයක් සහ වෘත්තයක් දැක්විය හැක. එතකොට අපිට ඒක ලැබෙනවා

y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

ස්පර්ශක පිහිටා ඇත්තේ ඉලිප්සයේ සිරස්වල නම්, ඒවා x හෝ y පමණ සමාන්තර වේ. පහත, පැහැදිලිකම සඳහා, රූපය සලකා බලන්න.

උදාහරණ 6

x = 2 ට සමාන x අගයන් සහිත ලක්ෂ්‍යවල x - 3 2 4 + y - 5 2 25 = 1 ඉලිප්සයට ස්පර්ශක සමීකරණය ලියන්න.

විසඳුමක්

x = 2 අගයට අනුරූප වන ස්පර්ශක ලක්ෂ්ය සොයා ගැනීම අවශ්ය වේ. අපි ඉලිප්සයේ පවතින සමීකරණයට ආදේශ කර එය සොයා ගනිමු

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

එවිට 2; 5 3 2 + 5 සහ 2; - 5 3 2 + 5 යනු ඉහළ සහ පහළ අර්ධ ඉලිප්සයට අයත් වන ස්පර්ශක ලක්ෂ්‍ය වේ.

y සම්බන්ධයෙන් ඉලිප්සයේ සමීකරණය සොයා ගැනීමට සහ විසඳීමට අපි ඉදිරියට යමු. අපිට ඒක ලැබෙනවා

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

පැහැදිලිවම, ඉහළ අර්ධ-ඉලිප්සය y = 5 + 5 2 4 - x - 3 2 ආකෘතියේ ශ්‍රිතයක් භාවිතයෙන් සහ පහළ අර්ධ ඉලිප්සය y = 5 - 5 2 4 - x - 3 2 ලෙස දක්වා ඇත.

ලක්ෂ්‍යයක ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශකයක් සඳහා සමීකරණයක් සෑදීමට සම්මත ඇල්ගොරිතමයක් යොදමු. අපි 2 ලක්ෂයේ පළමු ස්පර්ශකය සඳහා සමීකරණය ලියන්නෙමු; 5 3 2 + 5 වගේ පෙනේවි

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

ලක්ෂ්‍යයේ අගයක් සහිත දෙවන ස්පර්ශකයේ සමීකරණය බව අපට පෙනී යයි
2 ; - 5 3 2 + 5 පෝරමය ගනී

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y "(x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

රූපමය වශයෙන්, ස්පර්ශක පහත පරිදි නම් කර ඇත:

අධිබෝලයට ස්පර්ශක

හයිපර්බෝලා x c e n t e r හි කේන්ද්‍රයක් ඇති විට; y c e n t e r සහ vertices x c e n t e r + α ; y c e n t e r සහ x c e n t e r - α ; y c e n t e r , අසමානතාවය x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 සිදු වේ, සිරස් x c e n t e r සමඟ නම්; y c e n t e r + b සහ x c e n t e r; y c e n t e r -b , පසුව x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 අසමානතාවය භාවිතා කර නියම කර ඇත.

හයිපර්බෝලා ආකෘතියේ ඒකාබද්ධ ශ්‍රිත දෙකක් ලෙස දැක්විය හැක

y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r හෝ y = x a · (x - x c e n t e r) e n t e r y = - b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r

පළමු අවස්ථාවෙහිදී අපට ස්පර්ශක y ට සමාන්තර වන අතර දෙවැන්න x ට සමාන්තර වේ.

එහි දැක්වෙන්නේ ස්පර්ශකයේ සමීකරණය හයිපර්බෝලාවකට සොයා ගැනීමට නම්, ස්පර්ශක ලක්ෂ්‍යය අයත් වන්නේ කුමන කාර්යයට දැයි සොයා බැලිය යුතු බවයි. මෙය තීරණය කිරීම සඳහා, සමීකරණවලට ආදේශ කිරීම සහ අනන්යතාව පරීක්ෂා කිරීම අවශ්ය වේ.

උදාහරණ 7

7 ලක්ෂයේ දී හයිපර්බෝලා x - 3 2 4 - y + 3 2 9 = 1 වෙත ස්පර්ශකය සඳහා සමීකරණයක් ලියන්න; - 3 3 - 3 .

විසඳුමක්

ශ්‍රිත 2ක් භාවිතා කරමින් අධිබලයක් සොයා ගැනීම සඳහා විසඳුම් වාර්තාව පරිවර්තනය කිරීම අවශ්‍ය වේ. අපිට ඒක ලැබෙනවා

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 සහ y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

ඛණ්ඩාංක 7 සහිත දී ඇති ලක්ෂ්‍යයක් අයත් වන්නේ කුමන කාර්යයටදැයි හඳුනා ගැනීම අවශ්‍ය වේ; - 3 3 - 3 .

නිසැකවම, පළමු ශ්‍රිතය පරීක්ෂා කිරීම සඳහා එය අවශ්‍ය වේ y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, එවිට ලක්ෂ්‍යය ප්‍රස්ථාරයට අයත් නොවේ, සමානාත්මතාවය නොපවතින බැවිනි.

දෙවන ශ්‍රිතය සඳහා අපට ඇත්තේ y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, එනම් ලක්ෂ්‍යය ලබා දී ඇති ප්‍රස්ථාරයට අයත් වේ. මෙතැන් සිට ඔබ බෑවුම සොයාගත යුතුය.

අපිට ඒක ලැබෙනවා

y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

පිළිතුර:ස්පර්ශක සමීකරණය මෙසේ නිරූපණය කළ හැක

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

එය පැහැදිලිව නිරූපණය කරන්නේ මෙසේය.

පරාවලයකට ස්පර්ශක

x 0, y (x 0) ලක්ෂ්‍යයේ දී පරාවලය y = a x 2 + b x + c වෙත ස්පර්ශකය සඳහා සමීකරණයක් නිර්මාණය කිරීම සඳහා, ඔබ සම්මත ඇල්ගොරිතමයක් භාවිතා කළ යුතුය, එවිට සමීකරණය y = y "(x 0) x - x 0 + y ( x 0).ශීර්ෂයේ ඇති එවැනි ස්පර්ශකයක් x ට සමාන්තර වේ.

ඔබ පරාවලය x = a y 2 + b y + c ශ්‍රිත දෙකක එකතුවක් ලෙස අර්ථ දැක්විය යුතුය. එබැවින්, අපි y සඳහා සමීකරණය විසඳිය යුතුය. අපිට ඒක ලැබෙනවා

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

චිත්‍රක ලෙස නිරූපණය කර ඇත:

ලක්ෂ්‍යයක් x 0, y (x 0) ශ්‍රිතයකට අයත් වේද යන්න සොයා ගැනීමට, සම්මත ඇල්ගොරිතමයට අනුව මෘදු ලෙස ඉදිරියට යන්න. එවැනි ස්පර්ශකයක් පැරබෝලාවට සාපේක්ෂව o y ට සමාන්තර වේ.

උදාහරණ 8

අපට ස්පර්ශක කෝණය 150 ° ඇති විට x - 2 y 2 - 5 y + 3 ප්‍රස්ථාරයට ස්පර්ශක සමීකරණය ලියන්න.

විසඳුමක්

පැරබෝලා කාර්යයන් දෙකක් ලෙස නිරූපණය කිරීමෙන් අපි විසඳුම ආරම්භ කරමු. අපිට ඒක ලැබෙනවා

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

බෑවුමේ අගය මෙම ශ්‍රිතයේ x 0 ලක්ෂයේ ව්‍යුත්පන්නයේ අගයට සමාන වන අතර ආනතියේ කෝණයේ ස්පර්ශයට සමාන වේ.

අපට ලැබෙන්නේ:

k x = y "(x 0) = t g α x = t g 150 ° = - 1 3

මෙතැන් සිට අපි සම්බන්ධතා ස්ථාන සඳහා x අගය තීරණය කරමු.

පළමු කාර්යය ලෙස ලියා ඇත

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

නිසැකවම, අපට සෘණ අගයක් ලැබුණු බැවින් සැබෑ මූලයන් නොමැත. එවැනි ශ්රිතයක් සඳහා 150 ° ක කෝණයක් සහිත ස්පර්ශකයක් නොමැති බව අපි නිගමනය කරමු.

දෙවන කාර්යය ලෙස ලියා ඇත

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

අපට සම්බන්ධතා ඇති ස්ථාන 23 4 ; - 5 + 3 4 .

පිළිතුර:ස්පර්ශක සමීකරණය ස්වරූපය ගනී

y = - 1 3 x - 23 4 + - 5 + 3 4

අපි එය මේ ආකාරයෙන් චිත්‍රක ලෙස නිරූපණය කරමු:

ඔබ පෙළෙහි දෝෂයක් දුටුවහොත්, කරුණාකර එය උද්දීපනය කර Ctrl+Enter ඔබන්න

“ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශක සමීකරණය” වීඩියෝ පාඩම මාතෘකාව ප්‍රගුණ කිරීම සඳහා අධ්‍යාපනික ද්‍රව්‍ය විදහා දක්වයි. වීඩියෝ පාඩම අතරතුර, දී ඇති ලක්ෂ්‍යයක ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශක සමීකරණයේ සංකල්පය සැකසීමට අවශ්‍ය න්‍යායාත්මක ද්‍රව්‍ය, එවැනි ස්පර්ශකයක් සොයා ගැනීම සඳහා ඇල්ගොරිතමයක් සහ අධ්‍යයනය කරන ලද න්‍යායාත්මක ද්‍රව්‍ය භාවිතයෙන් ගැටළු විසඳීමේ උදාහරණ විස්තර කෙරේ. .

වීඩියෝ නිබන්ධනය ද්රව්යයේ පැහැදිලි බව වැඩි දියුණු කරන ක්රම භාවිතා කරයි. ඉදිරිපත් කිරීමෙහි චිත්‍ර, රූප සටහන්, වැදගත් හඬ අදහස්, සජීවිකරණය, උද්දීපනය සහ වෙනත් මෙවලම් අඩංගු වේ.

වීඩියෝ පාඩම ආරම්භ වන්නේ පාඩමේ මාතෘකාව ඉදිරිපත් කිරීම සහ M(a;f(a)) ලක්ෂ්‍යයේ y=f(x) යම් ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශක රූපයක් සමඟිනි. දී ඇති ලක්ෂ්‍යයක ප්‍රස්ථාරයට සැලසුම් කර ඇති ස්පර්ශකයේ කෝණික සංගුණකය මෙම ලක්ෂ්‍යයේ f΄(a) ශ්‍රිතයේ ව්‍යුත්පන්නයට සමාන බව දන්නා කරුණකි. එසේම වීජ ගණිත පාඨමාලාවෙන් අපි y=kx+m සරල රේඛාවේ සමීකරණය දනිමු. ලක්ෂ්‍යයක ස්පර්ශක සමීකරණය සෙවීමේ ගැටලුවට විසඳුම ක්‍රමානුකූලව ඉදිරිපත් කර ඇති අතර, එය සංගුණක k, m සොයා ගැනීම දක්වා අඩු කරයි. ශ්‍රිතයේ ප්‍රස්ථාරයට අයත් ලක්ෂ්‍යයක ඛණ්ඩාංක දැනගැනීමෙන්, අපට ඛණ්ඩාංක අගය f(a)=ka+m යන ස්පර්ශක සමීකරණයට ආදේශ කිරීමෙන් m සෙවිය හැක. ඒකෙන් අපිට හම්බෙනවා m=f(a)-ka. මේ අනුව, ලබා දී ඇති ලක්ෂ්‍යයක ව්‍යුත්පන්නයේ අගය සහ ලක්ෂ්‍යයේ ඛණ්ඩාංක දැන ගැනීමෙන්, අපට ස්පර්ශක සමීකරණය මේ ආකාරයෙන් නිරූපණය කළ හැකිය y=f(a)+f΄(a)(x-a).

පහත දැක්වෙන්නේ රූප සටහනට අනුව ස්පර්ශක සමීකරණයක් සම්පාදනය කිරීමේ උදාහරණයකි. y=x 2, x=-2 ශ්‍රිතය ලබා දී ඇත. a=-2 ගත් විට, අපි යම් ලක්ෂ්‍යයක දී ශ්‍රිතයේ අගය සොයා ගනිමු f(a)= f(-2)=(-2) 2 =4. f΄(x)=2x ශ්‍රිතයේ ව්‍යුත්පන්නය අපි තීරණය කරමු. මෙම අවස්ථාවේදී ව්‍යුත්පන්නය f΄(a)= f΄(-2)=2·(-2)=-4 ට සමාන වේ. සමීකරණය සෑදීම සඳහා, සියලු සංගුණක a=-2, f(a)=4, f΄(a)=-4 සොයා ගන්නා ලදී, එබැවින් ස්පර්ශක සමීකරණය y=4+(-4)(x+2) වේ. සමීකරණය සරල කිරීම, අපි y = -4-4x ලබා ගනිමු.

පහත උදාහරණය y=tgx ශ්‍රිතයේ ප්‍රස්ථාරයට මූලාරම්භයේ ඇති ස්පර්ශකය සඳහා සමීකරණයක් තැනීම යෝජනා කරයි. දී ඇති ලක්ෂ්‍යයක a=0, f(0)=0, f΄(x)=1/cos 2 x, f΄(0)=1. එබැවින් ස්පර්ශක සමීකරණය y=x ලෙස පෙනේ.

සාමාන්‍යකරණයක් ලෙස, කිසියම් ලක්ෂ්‍යයක ශ්‍රිතයක ප්‍රස්ථාරයට සමීකරණ ස්පර්ශකයක් සම්පාදනය කිරීමේ ක්‍රියාවලිය පියවර 4 කින් සමන්විත ඇල්ගොරිතමයක් ආකාරයෙන් විධිමත් කර ඇත:

• ස්පර්ශක ලක්ෂ්‍යයේ abscissa සඳහා නම් a ඇතුලත් කරන්න;
• f (a) ගණනය කරනු ලැබේ;
• f΄(x) තීරණය වන අතර f΄(a) ගණනය කෙරේ. a, f(a), f΄(a) හි සොයාගත් අගයන් y=f(a)+f΄(a)(x-a) ස්පර්ශක සමීකරණ සූත්‍රයට ආදේශ කර ඇත.

උදාහරණ 1 x=1 ලක්ෂ්‍යයේ y=1/x ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශක සමීකරණය සම්පාදනය කිරීම සලකා බලයි. ගැටළුව විසඳීම සඳහා අපි ඇල්ගොරිතමයක් භාවිතා කරමු. a=1 ලක්ෂ්‍යයේ දී ඇති ශ්‍රිතයක් සඳහා, f(a)=-1 ශ්‍රිතයේ අගය. f΄(x)=1/x 2 ශ්‍රිතයේ ව්‍යුත්පන්නය. a=1 ලක්ෂ්‍යයේදී f΄(a)= f΄(1)=1 ව්‍යුත්පන්නය. ලබාගත් දත්ත භාවිතා කරමින්, ස්පර්ශක සමීකරණය y=-1+(x-1), හෝ y=x-2, අඳිනු ලැබේ.

උදාහරණ 2 හි, y=x 3 +3x 2 -2x-2 ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශක සමීකරණය සොයා ගැනීම අවශ්‍ය වේ. ප්‍රධාන කොන්දේසිය වන්නේ ස්පර්ශක සහ සරල රේඛාව y=-2x+1 හි සමාන්තරතාවයයි. පළමුව, අපි y=-2x+1 සරල රේඛාවේ කෝණික සංගුණකයට සමාන ස්පර්ශකයේ කෝණික සංගුණකය සොයා ගනිමු. ලබා දී ඇති රේඛාවක් සඳහා f΄(a)=-2 බැවින්, අපේක්ෂිත ස්පර්ශකය සඳහා k=-2. අපි ශ්‍රිතයේ ව්‍යුත්පන්නය සොයා ගනිමු (x 3 +3x 2 -2x-2)΄=3x 2 +6x-2. f΄(a)=-2 බව දැන ගැනීමෙන්, අපි 3a 2 +6a-2=-2 ලක්ෂ්‍යයේ ඛණ්ඩාංක සොයා ගනිමු. සමීකරණය විසඳා ගත් පසු, අපට 1 =0, සහ 2 =-2 ලැබේ. සොයාගත් ඛණ්ඩාංක භාවිතා කරමින්, ඔබට සුප්‍රසිද්ධ ඇල්ගොරිතමයක් භාවිතයෙන් ස්පර්ශක සමීකරණය සොයාගත හැකිය. අපි f(a 1)=-2, f(a 2)=-18 යන ලක්ෂ්‍ය වලින් ශ්‍රිතයේ අගය සොයා ගනිමු. f΄(а 1)= f΄(а 2)=-2 ලක්ෂ්‍යයේ ව්‍යුත්පන්නයේ අගය. සොයාගත් අගයන් ස්පර්ශක සමීකරණයට ආදේශ කිරීමෙන්, අපි පළමු ලක්ෂ්‍යය සඳහා 1 =0 y=-2x-2 සහ දෙවන ලක්ෂ්‍යය සඳහා 2 =-2 ස්පර්ශක සමීකරණය y=-2x-22 ලබා ගනිමු.

උදාහරණ 3 y=√x ශ්‍රිතයේ ප්‍රස්ථාරයට (0;3) ලක්ෂ්‍යයේ දී එය ඇඳීම සඳහා ස්පර්ශක සමීකරණයේ සංයුතිය විස්තර කරයි. විසඳුම සෑදී ඇත්තේ සුප්රසිද්ධ ඇල්ගොරිතමයක් භාවිතා කරමිනි. ස්පර්ශක ලක්ෂ්‍යයේ ඛණ්ඩාංක x=a ඇත, එහිදී a>0. f(a)=√x ලක්ෂ්‍යයේ ශ්‍රිතයේ අගය. f΄(х)=1/2√х ශ්‍රිතයේ ව්‍යුත්පන්නය, එබැවින් දී ඇති ලක්ෂ්‍යයක f΄(а)=1/2√а. ලබාගත් සියලුම අගයන් ස්පර්ශක සමීකරණයට ආදේශ කිරීමෙන්, අපි y = √a + (x-a)/2√a ලබා ගනිමු. සමීකරණය පරිවර්තනය කිරීමෙන් අපට y=x/2√а+√а/2 ලැබේ. ස්පර්ශකය ලක්ෂ්‍යය (0;3) හරහා ගමන් කරන බව දැන ගැනීමෙන්, අපි a හි අගය සොයා ගනිමු. අපි 3=√a/2 සිට සොයා ගනිමු. එබැවින් √a=6, a=36. අපි y=x/12+3 ස්පර්ශක සමීකරණය සොයා ගනිමු. රූපයේ දැක්වෙන්නේ සලකා බලනු ලබන ශ්‍රිතයේ ප්‍රස්ථාරය සහ ඉදිකරන ලද අපේක්ෂිත ස්පර්ශකයයි.

Δy=≈f΄(x)Δxand f(x+Δx)-f(x)≈f΄(x)Δx යන ආසන්න සමානාත්මතා සිසුන්ට මතක් කර දෙයි. x=a, x+Δx=x, Δx=x-a ගත්තම අපිට f(x)- f(a)≈f΄(a)(x-a), ඒ නිසා f(x)≈f(a)+ f΄( a)(x-a).

උදාහරණ 4 හි, 2.003 6 ප්‍රකාශනයේ ආසන්න අගය සොයා ගැනීම අවශ්‍ය වේ. x=2.003 ලක්ෂ්‍යයේදී f(x)=x 6 ශ්‍රිතයේ අගය සෙවීමට අවශ්‍ය වන බැවින්, f(x)=x 6, a=2, f(a යන ප්‍රකට සූත්‍රය භාවිතා කළ හැක. )= f(2)=64, f ΄(x)=6x 5. f΄(2)=192 ලක්ෂ්‍යයේ ව්‍යුත්පන්න. එබැවින්, 2.003 6 ≈65-192·0.003. ප්‍රකාශනය ගණනය කිරීමෙන් පසුව, අපට 2.003 6 ≈64.576 ලැබේ.

“ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශක සමීකරණය” යන වීඩියෝ පාඩම පාසලේ සාම්ප්‍රදායික ගණිත පාඩමක භාවිතය සඳහා නිර්දේශ කෙරේ. දුරස්ථව උගන්වන ගුරුවරයෙකු සඳහා, මාතෘකාව වඩාත් පැහැදිලිව පැහැදිලි කිරීමට වීඩියෝ ද්රව්ය උපකාර වනු ඇත. විෂය පිළිබඳ ඔවුන්ගේ අවබෝධය ගැඹුරු කිරීම සඳහා අවශ්‍ය නම් ස්වාධීනව සමාලෝචනය කිරීමට සිසුන්ට වීඩියෝව නිර්දේශ කළ හැකිය.

පෙළ විකේතනය:

ලක්ෂ්‍යයක් M (a; f(a)) (em ඛණ්ඩාංක a සහ ef සිට ef) අයත් වන්නේ නම්, y = f (x) ශ්‍රිතයේ ප්‍රස්ථාරයට අයත් වන බවත්, මෙම අවස්ථාවේදී ස්පර්ශකයක් ඇඳීමට හැකි බවත් අපි දනිමු. අක්ෂය abscissa ට ලම්බක නොවන ශ්‍රිතයේ ප්‍රස්ථාරයට, එවිට ස්පර්ශකයේ කෝණික සංගුණකය f"(a) (eff prime සිට a) ට සමාන වේ.

y = f(x) ශ්‍රිතයක් සහ M (a; f(a)) ලක්ෂ්‍යයක් ලබා දෙන්න, f´(a) පවතින බව ද දනී. දී ඇති ලක්ෂ්‍යයක දී ඇති ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශක සඳහා සමීකරණයක් නිර්මාණය කරමු. මෙම සමීකරණය, ආදි අක්ෂයට සමාන්තර නොවන ඕනෑම සරල රේඛාවක සමීකරණයක් මෙන්, y = kx+m (y යනු ka x plus em ට සමාන වේ), එබැවින් කාර්යය වන්නේ අගයන් සොයා ගැනීමයි. සංගුණක k සහ m. (ka සහ em)

කෝණ සංගුණකය k= f"(a) m හි අගය ගණනය කිරීම සඳහා, අපි අපේක්ෂිත සරල රේඛාව M(a; f (a) ලක්ෂ්‍යය හරහා ගමන් කරන බව භාවිතා කරමු. මෙයින් අදහස් කරන්නේ අප ඛණ්ඩාංක ආදේශ කරන්නේ නම්, M ලක්ෂ්‍යය සරල රේඛාවේ සමීකරණයට, අපි නිවැරදි සමානාත්මතාවය ලබා ගනිමු: f(a) = ka+m, m = f(a) - ka බව සොයා ගන්නා ස්ථානයෙන්.

ki සහ m සංගුණකවල සොයාගත් අගයන් සරල රේඛාවේ සමීකරණයට ආදේශ කිරීමට ඉතිරිව ඇත:

y = kx+(f(a) -ka);

y = f(a)+k(x-a);

වයි= f(ඒ)+ f"(ඒ) (x- ඒ). ( y සමාන වන්නේ a වෙතින් plus ef ප්‍රයිම් එකකින් ef ට සමාන වන අතර, x minus a වලින් ගුණ කරනු ලැබේ).

අපි x=a ලක්ෂ්‍යයේ y = f(x) ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශකය සඳහා සමීකරණය ලබා ගෙන ඇත.

y = x 2 සහ x = -2 (එනම් a = -2) නම්, f (a) = f (-2) = (-2) 2 = 4; f´(x) = 2x, එනම් f"(a) = f´(-2) = 2·(-2) = -4. (එවිට a හි ef හතරට සමාන වේ, ප්‍රථමකයේ ef x යනු x දෙකට සමාන වේ, එයින් අදහස් වන්නේ ef ප්‍රයිම් සිට සෘණ හතරට සමාන වේ)

සොයාගත් අගයන් a = -2, f(a) = 4, f"(a) = -4 සමීකරණයට ආදේශ කිරීම, අපි ලබා ගනිමු: y = 4+(-4)(x+2), i.e. -4x -4.

(E යනු සෘණ හතර x සෘණ හතරට සමාන වේ)

y = tanx (y යනු ස්පර්ශක x ට සමාන) ශ්‍රිතයේ ප්‍රස්ථාරයට මූලාරම්භයේ දී ස්පර්ශකය සඳහා සමීකරණයක් නිර්මාණය කරමු. අපට ඇත්තේ: a = 0, f(0) = tan0=0;

f"(x)= , එනම් f"(0) = l. සොයාගත් අගයන් a=0, f(a)=0, f´(a) = 1 සමීකරණයට ආදේශ කිරීමෙන් අපට ලැබෙන්නේ: y=x.

ඇල්ගොරිතමයක් භාවිතයෙන් x ලක්ෂයේ ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශක සමීකරණය සෙවීමේ අපගේ පියවර සාරාංශ කරමු.

y = f(x) ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශකයක් සඳහා සමීකරණයක් සංවර්ධනය කිරීමේ ඇල්ගොරිතම:

1) ස්පර්ශක ලක්ෂ්‍යයේ abscissa අකුර a සමඟ නම් කරන්න.

2) f(a) ගණනය කරන්න.

3) f´(x) සොයාගෙන f´(a) ගණනය කරන්න.

4) සොයාගත් අංක a, f(a), f´(a) සූත්‍රයට ආදේශ කරන්න වයි= f(ඒ)+ f"(ඒ) (x- ඒ).

උදාහරණ 1. y = - in ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශක සඳහා සමීකරණයක් සාදන්න

ලක්ෂ්‍යය x = 1.

විසඳුමක්. මෙම උදාහරණයේ දී එය සැලකිල්ලට ගනිමින් ඇල්ගොරිතම භාවිතා කරමු

2) f(a)=f(1)=- =-1

3) f´(x)=; f´(a)= f´(1)= =1.

4) සොයාගත් අංක තුන ආදේශ කරන්න: a = 1, f(a) = -1, f"(a) = 1 සූත්‍රය තුළට. අපට ලැබෙන්නේ: y = -1+(x-1), y = x-2 .

පිළිතුර: y = x-2.

උදාහරණ 2. y = ශ්‍රිතය ලබා දී ඇත x 3 +3x 2 -2x-2. y = -2x +1 යන සරල රේඛාවට සමාන්තරව, y = f(x) ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශක සමීකරණය ලියන්න.

ස්පර්ශක සමීකරණය සම්පාදනය කිරීම සඳහා ඇල්ගොරිතම භාවිතා කරමින්, අපි මෙම උදාහරණයේ f(x) = බව සැලකිල්ලට ගනිමු. x 3 +3x 2 -2x-2, නමුත් ස්පර්ශක ලක්ෂ්‍යයේ abscissa මෙහි දක්වා නැත.

අපි මෙහෙම හිතන්න පටන් ගමු. අපේක්ෂිත ස්පර්ශකය y = -2x+1 සරල රේඛාවට සමාන්තර විය යුතුය. සමාන්තර රේඛා සමාන කෝණික සංගුණක ඇත. මෙයින් අදහස් කරන්නේ ස්පර්ශකයේ කෝණික සංගුණකය ලබා දී ඇති සරල රේඛාවේ කෝණික සංගුණකයට සමාන වන බවයි: k ස්පර්ශක. = -2. හොක් කැස්. = f"(a) මේ අනුව, අපට f´(a) = -2 සමීකරණයෙන් a හි අගය සොයාගත හැක.

ශ්‍රිතයේ ව්‍යුත්පන්නය සොයා ගනිමු y=f(x):

f"(x)= (x 3 +3x 2 -2x-2)´ =3x 2 +6x-2;f"(අ)= 3a 2 +6a-2.

f"(a) = -2 සමීකරණයෙන්, i.e. 3a 2 +6a-2=-2 අපි 1 =0, a 2 =-2 සොයා ගනිමු. මෙයින් අදහස් කරන්නේ ගැටලුවේ කොන්දේසි තෘප්තිමත් කරන ස්පර්ශක දෙකක් ඇති බවයි: එකක් abscissa 0 සමඟ, අනෙක abscissa -2 සමඟ.

දැන් ඔබට ඇල්ගොරිතම අනුගමනය කළ හැකිය.

1) a 1 =0, සහ 2 =-2.

2) f(a 1)= 0 3 +3·0 2 -2∙0-2=-2; f(a 2)= (-2) 3 +3·(-2) 2 -2·(-2)-2=6;

3) f"(a 1) = f"(a 2) = -2.

4) a 1 = 0, f (a 1) = -2, f"(a 1) = -2 යන අගයන් සූත්‍රයට ආදේශ කිරීමෙන් අපට ලැබෙන්නේ:

y=-2-2(x-0), y=-2x-2.

a 2 = -2, f(a 2) =6, f"(a 2) = -2 යන අගයන් සූත්‍රයට ආදේශ කිරීමෙන් අපට ලැබෙන්නේ:

y=6-2(x+2), y=-2x+2.

පිළිතුර: y=-2x-2, y=-2x+2.

උදාහරණ 3. ලක්ෂ්‍යයෙන් (0; 3) y = ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශකයක් අඳින්න. විසඳුමක්. මෙම උදාහරණයේ f(x) = බව සැලකිල්ලට ගනිමින් ස්පර්ශක සමීකරණය සෑදීම සඳහා ඇල්ගොරිතම භාවිතා කරමු. මෙහිදී, උදාහරණ 2 හි මෙන්, ස්පර්ශක ලක්ෂ්‍යයේ abscissa පැහැදිලිව දක්වා නොමැති බව සලකන්න. කෙසේ වෙතත්, අපි ඇල්ගොරිතම අනුගමනය කරමු.

1) x = a ස්පර්ශක ලක්ෂ්‍යයේ abscissa විය යුතුය; >0 බව පැහැදිලිය.

3) f´(x)=()´=; f´(a) =.

4) a, f(a) = , f"(a) = හි අගයන් සූත්‍රයට ආදේශ කිරීම

y=f (a) +f "(a) (x-a), අපට ලැබෙන්නේ:

කොන්දේසිය අනුව, ස්පර්ශකය ලක්ෂ්‍යය හරහා ගමන් කරයි (0; 3). x = 0, y = 3 යන අගයන් සමීකරණයට ආදේශ කිරීමෙන්, අපට ලැබෙන්නේ: 3 = , ඉන්පසු =6, a =36.

ඔබට පෙනෙන පරිදි, මෙම උදාහරණයේදී, ඇල්ගොරිතමයේ සිව්වන පියවරේදී පමණක් ස්පර්ශක ලක්ෂ්‍යයේ abscissa සොයා ගැනීමට අපට හැකි විය. අගය a =36 සමීකරණයට ආදේශ කිරීම, අපට ලැබෙන්නේ: y=+3

රූපයේ. රූපය 1 සලකා බැලූ උදාහරණයේ ජ්යාමිතික නිදර්ශනයක් පෙන්වයි: y = ශ්රිතයේ ප්රස්ථාරයක් ඉදි කර ඇත, සරල රේඛාවක් y = +3 අඳිනු ලැබේ.

පිළිතුර: y = +3.

x ලක්ෂ්‍යයේ ව්‍යුත්පන්නයක් ඇති y = f(x) ශ්‍රිතයක් සඳහා, ආසන්න සමානාත්මතාවය වලංගු බව අපි දනිමු: Δyf´(x)Δx (ඩෙල්ටා y යනු ඩෙල්ටා x න් ගුණ කළ x හි eff ප්‍රථමකයට ආසන්න වශයෙන් සමාන වේ)

හෝ, වඩාත් විස්තරාත්මකව, f(x+Δx)-f(x) f´(x) Δx (x සිට eff x ප්ලස් ඩෙල්ටා x minus ef x වෙතින් ef ප්‍රයිම් ඩෙල්ටා x මගින් x ට ආසන්න වශයෙන් සමාන වේ).

වැඩිදුර සාකච්ඡාවේ පහසුව සඳහා, අපි අංකනය වෙනස් කරමු:

x වෙනුවට අපි ලියන්නෙමු ඒ,

x+Δx වෙනුවට අපි x ලියන්නෙමු

Δx වෙනුවට අපි x-a ලියන්නෙමු.

එවිට ඉහත ලියා ඇති ආසන්න සමානාත්මතාවය ස්වරූපය ගනී:

f(x)-f(a)f´(a)(x-a)

f(x)f(a)+f´(a)(x-a). (x සිට eff යනු a වෙතින් plus ef ප්‍රයිම් එකකින් ef ට ආසන්න වශයෙන් සමාන වේ, x සහ a අතර වෙනස මගින් ගුණ කරනු ලැබේ).

උදාහරණ 4. සංඛ්‍යාත්මක ප්‍රකාශනයේ ආසන්න අගය සොයන්න 2.003 6.

විසඳුමක්. අපි කතා කරන්නේ x = 2.003 ලක්ෂ්‍යයේ y = x 6 ශ්‍රිතයේ අගය සොයා ගැනීමයි. මෙම උදාහරණයේ f(x)=x 6, a = 2,f(a) = f(2) බව සැලකිල්ලට ගනිමින් f(x)f(a)+f´(a)(x-a) සූත්‍රය භාවිතා කරමු. = 2 6 =64; x = 2.003, f"(x) = 6x 5 සහ, එබැවින්, f"(a) = f"(2) = 6 2 5 =192.

ප්රතිඵලයක් වශයෙන් අපට ලැබෙන්නේ:

2.003 6 64+192· 0.003, i.e. 2.003 6 =64.576.

අපි ගණක යන්ත්‍රයක් භාවිතා කරන්නේ නම්, අපට ලැබෙන්නේ:

2,003 6 = 64,5781643...

ඔබට පෙනෙන පරිදි, ආසන්න නිරවද්යතාව බෙහෙවින් පිළිගත හැකිය.

පහත රූපය සලකා බලන්න:

එය a ලක්ෂ්‍යයේ දී අවකලනය කළ හැකි y = f(x) යම් ශ්‍රිතයක් නිරූපණය කරයි. ඛණ්ඩාංක සහිත M ලක්ෂ්‍යය (a; f(a)) සලකුණු කර ඇත. දෙවන MR ප්‍රස්ථාරයේ අත්තනෝමතික ලක්ෂ්‍යයක් හරහා P(a + ∆x; f(a + ∆x)) ඇද ගනු ලැබේ.

දැන් P ලක්ෂ්‍යය ප්‍රස්ථාරය දිගේ M ලක්ෂ්‍යයට මාරු කරන්නේ නම්, MR සරල රේඛාව M ලක්ෂ්‍යය වටා භ්‍රමණය වේ. මෙම අවස්ථාවේදී ∆x ශුන්‍යයට නැඹුරු වේ. මෙතැන් සිට අපට ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශක නිර්වචනය සකස් කළ හැක.

ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශක

ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශකය යනු තර්කයේ වර්ධකය ශුන්‍යයට නැඹුරු වන බැවින් තත්පරයේ සීමාකාරී පිහිටීමයි. x0 ලක්ෂ්‍යයේ f ශ්‍රිතයේ ව්‍යුත්පන්නයේ පැවැත්මෙන් අදහස් වන්නේ ප්‍රස්ථාරයේ මෙම ලක්ෂ්‍යයේ පවතින බවයි. ස්පර්ශකඔහුට.

මෙම අවස්ථාවෙහිදී, ස්පර්ශකයේ කෝණික සංගුණකය f'(x0) මෙම ලක්ෂ්‍යයේ දී මෙම ශ්‍රිතයේ ව්‍යුත්පන්නයට සමාන වේ. ව්යුත්පන්නයේ ජ්යාමිතික අර්ථය මෙයයි. x0 ලක්ෂ්‍යයේදී f අවකලනය කළ හැකි ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශකය යනු ලක්ෂ්‍යය (x0;f(x0)) හරහා ගමන් කරන සහ කෝණික සංගුණකයක් සහිත f'(x0) නිශ්චිත සරල රේඛාවකි.

ස්පර්ශක සමීකරණය

A(x0; f(x0)) ලක්ෂ්‍යයේ f යම් ශ්‍රිතයක ප්‍රස්ථාරයට ස්පර්ශක සමීකරණය ලබා ගැනීමට උත්සාහ කරමු. බෑවුම k සමඟ සරල රේඛාවක සමීකරණයට පහත ස්වරූපය ඇත:

අපගේ බෑවුම් සංගුණකය ව්‍යුත්පන්නයට සමාන බැවින් f'(x0), එවිට සමීකරණය පහත ස්වරූපය ගනී: y = f'(x0)*x + b.

දැන් අපි b හි අගය ගණනය කරමු. මෙය සිදු කිරීම සඳහා, ශ්‍රිතය A ලක්ෂ්‍යය හරහා ගමන් කරන බව අපි භාවිතා කරමු.

f(x0) = f’(x0)*x0 + b, මෙතැන් සිට අපි b ප්‍රකාශ කර b = f(x0) - f’(x0)*x0 ලබා ගනිමු.

ලැබෙන අගය ස්පර්ශක සමීකරණයට අපි ආදේශ කරමු:

y = f'(x0)*x + b = f'(x0)*x + f(x0) - f'(x0)*x0 = f(x0) + f'(x0)*(x - x0).

y = f(x0) + f'(x0)*(x - x0).

පහත උදාහරණය සලකා බලන්න: x = 2 ලක්ෂ්‍යයේදී f(x) = x 3 - 2*x 2 + 1 ශ්‍රිතයේ ප්‍රස්ථාරයට ස්පර්ශකයේ සමීකරණය සොයා ගන්න.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f’(x) = 3*x 2 - 4*x.

4. f’(x0) = f’(2) = 3*2 2 - 4*2 = 4.

5. ලබාගත් අගයන් ස්පර්ශක සූත්‍රයට ආදේශ කරන්න, අපට ලැබෙන්නේ: y = 1 + 4*(x - 2). වරහන් විවෘත කර සමාන පද ගෙන ඒමෙන් අපට ලැබේ: y = 4*x - 7.

පිළිතුර: y = 4*x - 7.

ස්පර්ශක සමීකරණය සම්පාදනය කිරීම සඳහා පොදු යෝජනා ක්රමය y = f(x) ශ්‍රිතයේ ප්‍රස්ථාරයට:

1. x0 නිර්ණය කරන්න.

2. f(x0) ගණනය කරන්න.

3. f’(x) ගණනය කරන්න