Multiplicer simple brøker med et heltal. Regler for at gange og dividere brøker med et heltal

hjem / Tidligere

Sidste gang lærte vi at lægge til og trække brøker fra (se lektionen "Addition og subtraktion af brøker"). Det sværeste øjeblik i disse handlinger var at bringe brøker til en fællesnævner.

Nu er det tid til at beskæftige sig med multiplikation og division. Den gode nyhed er, at disse operationer er endnu nemmere end addition og subtraktion. Til at begynde med skal du overveje det enkleste tilfælde, når der er to positive brøker uden en fornem heltal.

For at gange to brøker skal du gange deres tællere og nævnere hver for sig. Det første tal vil være tælleren for den nye brøk, og det andet vil være nævneren.

For at dividere to brøker skal du gange den første brøk med den "omvendte" anden.

Betegnelse:

Af definitionen følger, at divisionen af brøker reduceres til multiplikation. For at vende en brøk, skal du bare bytte tæller og nævner. Derfor vil hele lektionen overveje hovedsageligt multiplikation.

Som følge af multiplikation kan en reduceret brøk opstå (og ofte opstår) - selvfølgelig skal den reduceres. Hvis fraktionen efter alle reduktionerne viste sig at være forkert, skulle hele delen skelnes i den. Men hvad der absolut ikke vil ske med multiplikation, er reduktion til en fællesnævner: ingen tværgående metoder, maksimale faktorer og mindste fælles multipla.

Per definition har vi:

Multiplikation af brøker med en heltalsdel og negative brøker

Hvis der er en heltalsdel i brøkerne, skal de konverteres til ukorrekte - og først derefter ganges i henhold til skemaerne skitseret ovenfor.

Hvis der er et minus i tælleren af en brøk, i nævneren eller foran den, kan det tages ud af multiplikationsgrænserne eller fjernes helt efter følgende regler:

Plus gange minus giver minus;
To negativer gør en bekræftende.

Indtil nu har man kun stødt på disse regler, når man adderer og trækker negative brøker, hvor det var nødvendigt for at slippe af med hele delen. For et produkt kan de generaliseres for at "brænde" flere minusser på én gang:

Vi krydser minusserne ud i par, indtil de helt forsvinder. I et ekstremt tilfælde kan et minus overleve - det, der ikke fandt en match;
Hvis der ikke er minusser tilbage, er operationen fuldført - du kan begynde at gange. Hvis det sidste minus ikke er overstreget, da det ikke fandt et par, tager vi det ud af multiplikationsgrænserne. Du får en negativ brøkdel.

En opgave. Find værdien af udtrykket:

Vi oversætter alle brøker til ukorrekte, og så tager vi minusserne uden for multiplikationsgrænserne. Det tilbageværende ganges efter de sædvanlige regler. Vi får:

Lad mig igen minde dig om, at minus, der kommer før en brøk med en fremhævet heltalsdel, refererer specifikt til hele brøken, og ikke kun til dens heltalsdel (dette gælder for de sidste to eksempler).

Vær også opmærksom på negative tal: når de ganges, er de omgivet af parenteser. Dette gøres for at adskille minusserne fra multiplikationstegnene og gøre hele notationen mere nøjagtig.

Reduktion af fraktioner i farten

Multiplikation er en meget besværlig operation. Tallene her er ret store, og for at forenkle opgaven kan du forsøge at reducere brøken endnu mere før multiplikation. Faktisk er tællere og nævnere af brøker almindelige faktorer, og derfor kan de reduceres ved at bruge den grundlæggende egenskab for en brøk. Tag et kig på eksemplerne:

En opgave. Find værdien af udtrykket:

Per definition har vi:

I alle eksempler er de tal, der er blevet reduceret, og hvad der er tilbage af dem markeret med rødt.

Bemærk venligst: i det første tilfælde blev multiplikatorerne reduceret fuldstændigt. Enheder forblev på deres plads, hvilket generelt kan udelades. I det andet eksempel var det ikke muligt at opnå en fuldstændig reduktion, men den samlede mængde af beregninger faldt alligevel.

Brug dog under ingen omstændigheder denne teknik, når du tilføjer og subtraherer brøker! Ja, nogle gange er der lignende tal, som du bare vil reducere. Se her:

Det kan du ikke!

Fejlen opstår på grund af, at når man tilføjer en brøk, optræder summen i tælleren af en brøk, og ikke produktet af tal. Derfor er det umuligt at anvende hovedegenskaben for en brøk, da denne egenskab specifikt handler om multiplikation af tal.

Der er simpelthen ingen anden grund til at reducere fraktioner, så den korrekte løsning på det forrige problem ser sådan ud:

Den rigtige beslutning:

Som du kan se, viste det rigtige svar sig ikke at være så smukt. Generelt skal du være forsigtig.

OMGANG ALLEREDE DISSE RIVE! 🙂

Multiplikation og division af brøker.

Opmærksomhed!
Der er yderligere
materiale i specialafsnit 555.
For dem, der er stærke "ikke særlig. »
Og for dem, der “meget jævn. "")

Denne operation er meget bedre end addition-subtraktion! For det er nemmere. Jeg minder dig om: for at gange en brøk med en brøk, skal du gange tællerne (dette vil være tælleren for resultatet) og nævnerne (dette vil være nævneren). Det er:

Alt er ekstremt enkelt. Og led venligst ikke efter en fællesnævner! Har ikke brug for det her...

For at dividere en brøk med en brøk, skal du vende sekund(dette er vigtigt!) brøk og gange dem, dvs.:

Hvis multiplikation eller division med heltal og brøker fanges, er det okay. Ligesom med addition laver vi en brøk af et helt tal med en enhed i nævneren - og går! For eksempel:

I gymnasiet skal du ofte beskæftige dig med tre-etagers (eller endda fire-etagers!) brøker. For eksempel:

Hvordan bringer man denne fraktion til en anstændig form? Ja, meget nemt! Brug division gennem to punkter:

Men glem ikke delingsrækkefølgen! I modsætning til multiplikation er dette meget vigtigt her! Vi vil selvfølgelig ikke forveksle 4:2 eller 2:4. Men i en tre-etagers brøkdel er det let at lave en fejl. Bemærk f.eks.:

I det første tilfælde (udtryk til venstre):

I det andet (udtryk til højre):

Mærker du forskellen? 4 og 1/9!

Hvad er rækkefølgen af division? Eller parentes, eller (som her) længden af vandrette streger. Udvikle et øje. Og hvis der ikke er nogen parenteser eller bindestreger, som:

divider-multiplicer derefter i rækkefølge, venstre mod højre!

Og endnu et meget simpelt og vigtigt trick. I handlinger med grader, vil det være nyttigt for dig! Lad os dividere enheden med en hvilken som helst brøk, for eksempel med 13/15:

Skuddet er vendt! Og det sker altid. Når man dividerer 1 med en hvilken som helst brøk, er resultatet den samme brøk, kun omvendt.

Det er alle handlingerne med brøker. Sagen er ret enkel, men giver mere end nok fejl. Noter dig praktiske råd, så bliver der færre af dem (fejl)!

1. Det vigtigste, når man arbejder med brøkudtryk, er nøjagtighed og opmærksomhed! Det er ikke almindelige ord, ikke gode ønsker! Dette er et alvorligt behov! Lav alle beregningerne på eksamen som en fuldgyldig opgave, med koncentration og klarhed. Det er bedre at skrive to ekstra linjer i en kladde end at rode, når du regner i dit hoved.

2. I eksempler med forskellige typer brøker - gå til almindelige brøker.

3. Vi reducerer alle fraktioner til stop.

4. Vi reducerer brøkudtryk på flere niveauer til almindelige udtryk ved hjælp af division gennem to punkter (vi følger rækkefølgen af division!).

Her er de opgaver, du skal udføre. Der gives svar efter alle opgaver. Brug materialerne til dette emne og praktiske råd. Estimer, hvor mange eksempler du kunne løse korrekt. Den første gang! Uden lommeregner! Og drag de rigtige konklusioner.

Husk det rigtige svar opnået fra anden (især tredje) gang - tæller ikke! Sådan er det barske liv.

Så, løse i eksamenstilstand ! Dette er i øvrigt forberedelse til eksamen. Vi løser et eksempel, vi tjekker, vi løser følgende. Vi besluttede alt - vi tjekkede igen fra den første til den sidste. Men kun efter se på svarene.

Leder efter svar, der matcher dine. Jeg skrev dem bevidst ned i et rod, væk fra fristelser, så at sige. Her er de, svarene, adskilt af et semikolon.

0; 17/22; 3/4; 2/5; 1; 25.

Og nu drager vi konklusioner. Hvis alt lykkedes - glad for dig! Elementære beregninger med brøker er ikke dit problem! Du kan gøre mere seriøse ting. Hvis ikke.

Så du har et af to problemer. Eller begge dele på én gang.) Mangel på viden og (eller) uopmærksomhed. Men. det løselig Problemer.

I Special Section 555 "Brøker" analyseres alle disse (og ikke kun!) eksempler. Med detaljerede forklaringer på hvad, hvorfor og hvordan. Sådan en analyse hjælper meget med manglende viden og færdigheder!

Ja, og på det andet problem er der noget der.) Ganske praktiske råd, hvordan man bliver mere opmærksom. Ja Ja! Råd der kan gælde hver.

Ud over viden og opmærksomhed er der behov for en vis automatisme for succes. Hvor kan man få det? Jeg hører et tungt suk... Ja, kun i praksis, ingen andre steder.

Du kan gå til webstedet 321start.ru til træning. Der, i "Prøv" muligheden, er der 10 eksempler, som alle kan bruge. Med øjeblikkelig verifikation. For registrerede brugere - 34 eksempler fra simple til svære. Det er kun for brøkdele.

Hvis du kan lide denne side.

Forresten har jeg et par flere interessante sider til dig.)

Her kan du øve dig i at løse eksempler og finde ud af dit niveau. Test med øjeblikkelig verifikation. Lær med interesse!

Og her kan du stifte bekendtskab med funktioner og afledte.

Regel 1

For at gange en brøk med et naturligt tal, skal du gange dens tæller med dette tal og lade nævneren være uændret.

Regel 2

For at gange en brøk med en brøk:

1. find produktet af tællere og produktet af nævnerne af disse brøker

2. Skriv det første produkt som tæller, og det andet som nævneren.

Regel 3

For at gange blandede tal skal du skrive dem som uægte brøker og derefter bruge reglen til at gange brøker.

Regel 4

For at dividere en brøk med en anden, skal du gange udbyttet med den gensidige divisor.

Eksempel 1

Beregn

Eksempel 2

Beregn

Eksempel 3

Beregn

Eksempel 4

Beregn

Matematik. Andre materialer

At hæve et tal til en rationel magt. (

At hæve et tal til en naturlig magt. (

Generaliseret intervalmetode til løsning af algebraiske uligheder (forfatter Kolchanov A.V.)

Metode til erstatning af faktorer til løsning af algebraiske uligheder (forfatter Kolchanov A.V.)

Tegn på delelighed (Lungu Alena)

Test dig selv om emnet 'Multiplikation og division af almindelige brøker'

Multiplikation af brøker

Vi vil overveje multiplikationen af almindelige brøker på flere mulige måder.

At gange en brøk med en brøk

Dette er det enkleste tilfælde, hvor du skal bruge følgende brøkmultiplikationsregler.

Til gange en brøk med en brøk, nødvendigt:

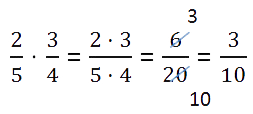
gange tælleren for den første brøk med tælleren for den anden brøk og skriv deres produkt ind i tælleren for den nye brøk;

gange nævneren af den første brøk med nævneren af den anden brøk og skriv deres produkt ind i nævneren af den nye brøk;

Før du gange tællere og nævnere, skal du kontrollere, om brøkerne kan reduceres. At reducere brøker i beregninger vil i høj grad lette dine beregninger.

At gange en brøk med et naturligt tal

Til brøk gange med et naturligt tal du skal gange brøkens tæller med dette tal og lade brøkens nævner være uændret.

Hvis resultatet af multiplikationen er en ukorrekt brøk, så glem ikke at gøre det til et blandet tal, det vil sige, vælg hele delen.

Multiplikation af blandede tal

For at gange blandede tal skal du først omdanne dem til uægte brøker og derefter gange efter reglen for at gange almindelige brøker.

En anden måde at gange en brøk med et naturligt tal

Nogle gange i beregninger er det mere bekvemt at bruge en anden metode til at gange en almindelig brøk med et tal.

For at gange en brøk med et naturligt tal skal du dividere brøkens nævner med dette tal og lade tælleren være den samme.

Som det fremgår af eksemplet, er det mere bekvemt at bruge denne version af reglen, hvis nævneren af brøken er delelig uden en rest med et naturligt tal.

Division af en brøk med et tal

Hvad er den hurtigste måde at dividere en brøk med et tal? Lad os analysere teorien, drage en konklusion og bruge eksempler til at se, hvordan divisionen af en brøk med et tal kan udføres efter en ny kort regel.

Normalt udføres divisionen af en brøk med et tal efter reglen om brøkdeling. Det første tal (brøken) ganges med det gensidige af det andet. Da det andet tal er et heltal, er dets gensidige en brøk, hvis tæller er lig med én, og nævneren er det givne tal. Skematisk ser det sådan ud at dividere en brøk med et naturligt tal:

Heraf konkluderer vi:

For at dividere en brøk med et tal skal du gange nævneren med det tal og lade tælleren være den samme. Reglen kan formuleres endnu mere kort:

Når du dividerer en brøk med et tal, går tallet til nævneren.

Divider en brøk med et tal:

For at dividere en brøk med et tal, omskriver vi tælleren uændret og gange nævneren med dette tal. Vi reducerer 6 og 3 med 3.

Når vi dividerer en brøk med et tal, omskriver vi tælleren og multiplicerer nævneren med det tal. Vi reducerer 16 og 24 med 8.

Når man dividerer en brøk med et tal, går tallet til nævneren, så vi lader tælleren være den samme og gange nævneren med divisor. Vi reducerer 21 og 35 med 7.

Multiplikation og division af brøker

Sidste gang lærte vi at lægge til og trække brøker fra (se lektionen "At tilføje og trække brøker fra"). Det sværeste øjeblik i disse handlinger var at bringe brøker til en fællesnævner.

For at gange to brøker skal du gange deres tællere og nævnere hver for sig. Det første tal vil være tælleren for den nye brøk, og det andet vil være nævneren.

For at dividere to brøker skal du gange den første brøk med den "omvendte" anden.

En opgave. Find værdien af udtrykket:

Per definition har vi:

Multiplikation af brøker med en heltalsdel og negative brøker

Hvis der er en heltalsdel i brøkerne, skal de konverteres til ukorrekte - og først derefter ganges i henhold til skemaerne skitseret ovenfor.

Hvis der er et minus i tælleren af en brøk, i nævneren eller foran den, kan det tages ud af multiplikationsgrænserne eller fjernes helt efter følgende regler:

Plus gange minus giver minus;
To negativer gør en bekræftende.

Vi krydser minusserne ud i par, indtil de helt forsvinder. I et ekstremt tilfælde kan et minus overleve - det, der ikke fandt en match;
Hvis der ikke er minusser tilbage, er operationen fuldført - du kan begynde at gange. Hvis det sidste minus ikke er overstreget, da det ikke fandt et par, tager vi det ud af multiplikationsgrænserne. Du får en negativ brøkdel.

Vi oversætter alle brøker til ukorrekte, og så tager vi minusserne uden for multiplikationsgrænserne. Det tilbageværende ganges efter de sædvanlige regler. Vi får:

Vær også opmærksom på negative tal: når de ganges, er de omgivet af parenteser. Dette gøres for at adskille minusserne fra multiplikationstegnene og gøre hele notationen mere nøjagtig.

Reduktion af fraktioner i farten

I alle eksempler er de tal, der er blevet reduceret, og hvad der er tilbage af dem markeret med rødt.

Brug dog under ingen omstændigheder denne teknik, når du tilføjer og subtraherer brøker! Ja, nogle gange er der lignende tal, som du bare vil reducere. Se her:

Det kan du ikke!

Der er simpelthen ingen anden grund til at reducere fraktioner, så den korrekte løsning på det forrige problem ser sådan ud:

Som du kan se, viste det rigtige svar sig ikke at være så smukt. Generelt skal du være forsigtig.

Inddeling af brøker.

Division af en brøk med et naturligt tal.

Eksempler på at dividere en brøk med et naturligt tal

Division af et naturligt tal med en brøk.

Eksempler på at dividere et naturligt tal med en brøk

Division af almindelige brøker.

Eksempler på division af almindelige brøker

Division af blandede tal.

konverter blandede fraktioner til ukorrekte;
gange den første brøk med den gensidige af den anden;
reducere den resulterende fraktion;
Hvis du får en uægte brøk, skal du konvertere den uægte brøk til en blandet.

Eksempler på at dividere blandede tal

1 1 2: 2 2 3 = 1 2 + 1 2: 2 3 + 2 3 = 3 2: 8 3 = 3 2 3 8 = 3 3 2 8 = 9 16

2 1 7: 3 5 = 2 7 + 1 7: 3 5 = 15 7: 3 5 = 15 7 5 3 = 15 5 7 3 = 5 5 7 = 25 7 = 7 3 + 4 7 = 3 4 7

Eventuelle obskøne kommentarer vil blive fjernet og deres forfattere sortlistet!

Velkommen til OnlineMSschool.
Mit navn er Dovzhik Mikhail Viktorovich. Jeg er ejer og forfatter af denne side, jeg har skrevet alt det teoretiske materiale, samt udviklet online øvelser og lommeregnere, som du kan bruge til at studere matematik.

Brøker. Multiplikation og division af brøker.

At gange en brøk med en brøk.

For at gange almindelige brøker er det nødvendigt at gange tælleren med tælleren (vi får produktets tæller) og nævneren med nævneren (vi får produktets nævner).

Brøk multiplikationsformel:

Før du fortsætter med multiplikationen af tællere og nævnere, er det nødvendigt at kontrollere muligheden for at reducere brøken. Hvis du formår at reducere brøken, så bliver det nemmere for dig at fortsætte med at lave beregninger.

Bemærk! Der er ingen grund til at lede efter en fællesnævner!!

Division af en almindelig brøk med en brøk.

Opdelingen af en almindelig brøk med en brøk er som følger: vend den anden brøk om (dvs. skift tæller og nævner flere steder) og derefter ganges brøkerne.

Formlen til at dividere almindelige brøker:

At gange en brøk med et naturligt tal.

Bemærk! Når man multiplicerer en brøk med et naturligt tal, ganges brøkens tæller med vores naturlige tal, og nævneren for brøken forbliver den samme. Hvis resultatet af produktet er en ukorrekt fraktion, skal du sørge for at vælge hele delen ved at omdanne den ukorrekte fraktion til en blandet.

Division af brøker, der involverer et naturligt tal.

Det er ikke så skræmmende, som det ser ud til. Som ved addition omregner vi et heltal til en brøk med en enhed i nævneren. For eksempel:

Multiplikation af blandede fraktioner.

Regler for at gange brøker (blandet):

konverter blandede fraktioner til ukorrekte;
gange tællere og nævnere af brøker;
vi reducerer fraktionen;
hvis vi får en uægte brøk, så konverterer vi den uægte brøk til en blandet.

Bemærk! For at gange en blandet brøk med en anden blandet brøk, skal du først bringe dem i form af uægte brøker og derefter gange i henhold til reglen for at gange almindelige brøker.

Den anden måde at gange en brøk med et naturligt tal.

Det er mere praktisk at bruge den anden metode til at gange en almindelig brøk med et tal.

Bemærk! For at gange en brøk med et naturligt tal, er det nødvendigt at dividere brøkens nævner med dette tal og lade tælleren være uændret.

Fra ovenstående eksempel er det klart, at denne mulighed er mere praktisk at bruge, når nævneren af en brøk divideres uden en rest med et naturligt tal.

Brøker på flere niveauer.

I gymnasiet findes ofte tre-etagers (eller flere) brøker. Eksempel:

For at bringe en sådan brøk til sin sædvanlige form bruges division gennem 2 punkter:

Bemærk! Når man deler brøker, er rækkefølgen af division meget vigtig. Vær forsigtig, det er nemt at blive forvirret her.

Bemærk, for eksempel:

Når man dividerer en med en hvilken som helst brøk, vil resultatet være den samme brøk, kun omvendt:

Praktiske tips til at gange og dividere brøker:

1. Det vigtigste i arbejdet med brøkudtryk er nøjagtighed og opmærksomhed. Foretag alle beregninger omhyggeligt og præcist, koncentreret og klart. Det er bedre at skrive et par ekstra linjer ned i en kladde end at blive forvirret i beregningerne i dit hoved.

2. I opgaver med forskellige typer brøker, gå til typen af almindelige brøker.

3. Vi reducerer alle fraktioner, indtil det ikke længere er muligt at reducere.

4. Vi bringer brøkudtryk på flere niveauer ind i almindelige udtryk ved hjælp af division gennem 2 punkter.

Under- og ikke op til- Omarbejdet sang "Forårstango" (Tiden kommer - fugle fra syd kommer) - musik. Valery Milyaev Jeg hørte forkert, jeg misforstod, jeg indhentede ikke, i den forstand, at jeg ikke gættede, jeg skrev alle verberne med ikke separat, jeg vidste ikke om præfikset nedo-. Det sker, […]
Siden blev ikke fundet Ved tredje slutbehandling blev der vedtaget en pakke af regeringsdokumenter, der sørger for oprettelse af særlige administrative regioner (SAR). På grund af udtræden af Den Europæiske Union vil Storbritannien ikke blive inkluderet i det europæiske momsområde og […]
Det fælles efterforskningsudvalg vil dukke op i efteråret Det fælles efterforskningsudvalg dukker op i efteråret. Efterforskningen af alle retshåndhævende myndigheder vil blive samlet under ét tag på det fjerde forsøg Allerede i efteråret 2014, ifølge Izvestia, præsident Vladimir Putin [ …]
Et algoritmepatent Sådan ser et algoritmepatent ud Hvordan et algoritmepatent bliver udarbejdet At udarbejde tekniske beskrivelser af metoder til lagring, behandling og transmission af signaler og/eller data specifikt til patenteringsformål er normalt ikke særlig vanskeligt, og […]
HVAD ER VIGTIGT AT VIDE OM DET NYE UDKAST TIL PENSIONER 12. december 1993 DEN RUSSISKE FØDERATIONS FORfatning (med forbehold for ændringer foretaget af Den Russiske Føderations love om ændringer til Den Russiske Føderations forfatning dateret 30. december 2008 N 6-6. FKZ, dateret 30. december 2008 N 7-FKZ, […]
Chastushkas om pensionering for en kvinde er seje for en dagens helt for en mand til en mands fødselsdag - i kor for en kvindes helt af dagen - dedikation til pensionister for kvinder er komisk Konkurrencer for pensionister vil være interessant Vært: Kære venner! Et øjebliks opmærksomhed! Sensation! Kun […]

Vi vil overveje multiplikationen af almindelige brøker på flere mulige måder.

At gange en brøk med en brøk

Dette er det enkleste tilfælde, hvor du skal bruge følgende brøkmultiplikationsregler.

Til gange en brøk med en brøk, nødvendigt:

gange tælleren for den første brøk med tælleren for den anden brøk og skriv deres produkt ind i tælleren for den nye brøk;
gange nævneren af den første brøk med nævneren af den anden brøk og skriv deres produkt ind i nævneren af den nye brøk;

Før du gange tællere og nævnere, skal du kontrollere, om brøkerne kan reduceres. At reducere brøker i beregninger vil i høj grad lette dine beregninger.

At gange en brøk med et naturligt tal

Til brøk gange med et naturligt tal du skal gange brøkens tæller med dette tal og lade brøkens nævner være uændret.

Hvis resultatet af multiplikationen er en ukorrekt brøk, så glem ikke at gøre det til et blandet tal, det vil sige, vælg hele delen.

Multiplikation af blandede tal

For at gange blandede tal skal du først omdanne dem til uægte brøker og derefter gange efter reglen for at gange almindelige brøker.

En anden måde at gange en brøk med et naturligt tal

Nogle gange i beregninger er det mere bekvemt at bruge en anden metode til at gange en almindelig brøk med et tal.

For at gange en brøk med et naturligt tal skal du dividere brøkens nævner med dette tal og lade tælleren være den samme.

Som det fremgår af eksemplet, er det mere bekvemt at bruge denne version af reglen, hvis nævneren af brøken er delelig uden en rest med et naturligt tal.

Handlinger med brøker

Tilføjelse af brøker med samme nævnere

Tilføjelse af brøker er af to typer:

Tilføjelse af brøker med samme nævnere
Tilføjelse af brøker med forskellige nævnere

Lad os starte med at tilføje brøker med de samme nævnere. Alt er enkelt her. For at tilføje brøker med de samme nævnere, skal du tilføje deres tællere og lade nævneren være uændret. Lad os f.eks. tilføje brøkerne og . Vi tilføjer tællere og lader nævneren være uændret:

Dette eksempel kan let forstås, hvis vi tænker på en pizza, der er opdelt i fire dele. Tilføjer du pizza til pizza, får du pizza:

Eksempel 2 Tilføj brøker og .

Tilføj igen tællere, og lad nævneren være uændret:

Svaret er en upassende brøk. Hvis slutningen af opgaven kommer, så er det sædvanligt at slippe af med ukorrekte fraktioner. For at slippe af med en ukorrekt fraktion skal du vælge hele delen i den. I vores tilfælde tildeles heltalsdelen let - to divideret med to er lig med en:

Dette eksempel kan let forstås, hvis vi tænker på en pizza, der er opdelt i to dele. Tilføjer du flere pizzaer til pizzaen, får du en hel pizza:

Eksempel 3. Tilføj brøker og .

Dette eksempel kan let forstås, hvis vi tænker på en pizza, der er opdelt i tre dele. Tilføjer du flere pizzaer til pizza, får du pizzaer:

Eksempel 4 Find værdien af et udtryk

Dette eksempel er løst på nøjagtig samme måde som de foregående. Tællerne skal tilføjes og nævneren forblive uændret:

Lad os prøve at skildre vores løsning ved hjælp af et billede. Tilføjer du pizzaer til en pizza og tilføjer flere pizzaer, får du 1 hel pizza og flere pizzaer.

Som du kan se, er det ikke svært at tilføje brøker med de samme nævnere. Det er nok at forstå følgende regler:

For at tilføje brøker med samme nævner, skal du tilføje deres tællere og lade nævneren være den samme;
Hvis svaret viste sig at være en ukorrekt brøkdel, skal du vælge hele delen i den.

Tilføjelse af brøker med forskellige nævnere

Nu vil vi lære at tilføje brøker med forskellige nævnere. Når du tilføjer brøker, skal nævnerne for disse brøker være de samme. Men de er ikke altid ens.

For eksempel kan brøker tilføjes, fordi de har de samme nævnere.

Men brøker kan ikke tilføjes på én gang, fordi disse brøker har forskellige nævnere. I sådanne tilfælde skal brøker reduceres til samme (fælles)nævner.

Der er flere måder at reducere brøker til den samme nævner. I dag vil vi kun overveje en af dem, da resten af metoderne kan virke komplicerede for en begynder.

Essensen af denne metode er, at der først søges efter det mindste fælles multiplum (LCM) af nævnerne i begge brøker. Derefter divideres LCM med nævneren af den første brøk, og den første yderligere faktor opnås. De gør det samme med den anden fraktion - NOC divideres med nævneren for den anden fraktion, og den anden yderligere faktor opnås.

Derefter ganges brøkernes tællere og nævnere med deres yderligere faktorer. Som et resultat af disse handlinger bliver brøker, der havde forskellige nævnere, til brøker, der har de samme nævnere. Og vi ved allerede, hvordan man tilføjer sådanne brøker.

Eksempel 1. Tilføj brøker og

Disse brøker har forskellige nævnere, så du skal bringe dem til den samme (fælles) nævner.

Først og fremmest finder vi det mindste fælles multiplum af nævnerne i begge brøker. Nævneren i den første brøk er tallet 3, og nævneren i den anden brøk er tallet 2. Det mindste fælles multiplum af disse tal er 6

LCM (2 og 3) = 6

Nu tilbage til brøker og . Først dividerer vi LCM med nævneren af den første brøk og får den første ekstra faktor. LCM er tallet 6, og nævneren i den første brøk er tallet 3. Divider 6 med 3, så får vi 2.

Det resulterende nummer 2 er den første yderligere faktor. Vi skriver det ned til den første brøk. For at gøre dette laver vi en lille skrå linje over brøken og skriver den fundne ekstra faktor ned over den:

Vi gør det samme med den anden brøk. Vi dividerer LCM med nævneren af den anden brøk og får den anden ekstra faktor. LCM er tallet 6, og nævneren i den anden brøk er tallet 2. Divider 6 med 2, så får vi 3.

Det resulterende nummer 3 er den anden yderligere faktor. Vi skriver det til den anden brøk. Igen laver vi en lille skrå linje over den anden brøk og skriver den fundne ekstra faktor over den:

Nu er vi klar til at tilføje. Det er tilbage at gange tællere og nævnere af brøker med deres yderligere faktorer:

Se nøje på, hvad vi er kommet til. Vi kom til den konklusion, at brøker, der havde forskellige nævnere, blev til brøker, der havde samme nævnere. Og vi ved allerede, hvordan man tilføjer sådanne brøker. Lad os fuldende dette eksempel til ende:

Således slutter eksemplet. For at tilføje viser det sig.

Lad os prøve at skildre vores løsning ved hjælp af et billede. Tilføjer du pizzaer til en pizza, får du en hel pizza og en anden sjettedel af en pizza:

Reduktion af brøker til samme (fælles)nævner kan også afbildes ved hjælp af et billede. Ved at bringe brøkerne og til en fællesnævner får vi brøkerne og . Disse to fraktioner vil være repræsenteret af de samme skiver af pizzaer. Den eneste forskel vil være, at de denne gang bliver delt i lige store andele (reduceret til samme nævner).

Den første tegning viser en brøk (fire stykker ud af seks), og det andet billede viser en brøk (tre stykker ud af seks). Ved at sætte disse stykker sammen får vi (syv stykker ud af seks). Denne brøk er forkert, så vi har fremhævet heltalsdelen i den. Resultatet blev (en hel pizza og en anden sjette pizza).

Bemærk, at vi har malet dette eksempel for meget detaljeret. På uddannelsesinstitutioner er det ikke sædvanligt at skrive så detaljeret. Du skal hurtigt kunne finde LCM for både nævnere og yderligere faktorer til dem, samt hurtigt gange de yderligere faktorer fundet af dine tællere og nævnere. Mens vi var i skolen, skulle vi skrive dette eksempel som følger:

Men der er også den anden side af medaljen. Hvis der ikke laves detaljerede noter på de første stadier af matematikstudiet, så spørgsmål af slagsen "Hvor kommer det tal fra?", "Hvorfor bliver brøker pludselig til helt andre brøker? «.

For at gøre det nemmere at tilføje brøker med forskellige nævnere kan du bruge følgende trinvise instruktioner:

Find LCM for nævnerne af brøker;
Divider LCM med nævneren for hver brøk og få en ekstra multiplikator for hver brøk;
Multiplicer tællere og nævnere af brøker med deres yderligere faktorer;
Tilføj brøker, der har de samme nævnere;
Hvis svaret viste sig at være en ukorrekt brøk, så vælg hele dens del;

Eksempel 2 Find værdien af et udtryk .

Lad os bruge diagrammet ovenfor.

Trin 1. Find LCM for nævnerne af brøker

Vi finder LCM for nævnerne af begge brøker. Nævnerne af brøkerne er tallene 2, 3 og 4. Du skal finde LCM for disse tal:

Trin 2. Divider LCM med nævneren for hver brøk og få en ekstra multiplikator for hver brøk

Divider LCM med nævneren af den første brøk. LCM er tallet 12, og nævneren for den første brøk er tallet 2. Divider 12 med 2, vi får 6. Vi fik den første ekstra faktor 6. Vi skriver den over den første brøk:

Nu dividerer vi LCM med nævneren af den anden brøk. LCM er tallet 12, og nævneren for den anden brøk er tallet 3. Divider 12 med 3, vi får 4. Vi fik den anden ekstra faktor 4. Vi skriver den over den anden brøk:

Nu dividerer vi LCM med nævneren af den tredje brøk. LCM er tallet 12, og nævneren for den tredje brøk er tallet 4. Divider 12 med 4, vi får 3. Vi fik den tredje ekstra faktor 3. Vi skriver den over den tredje brøk:

Trin 3. Gang tællere og nævnere af brøker med dine yderligere faktorer

Vi multiplicerer tællere og nævnere med vores yderligere faktorer:

Trin 4. Tilføj brøker, der har de samme nævnere

Vi kom til den konklusion, at brøker, der havde forskellige nævnere, blev til brøker, der har de samme (fælles)nævnere. Det er tilbage at tilføje disse fraktioner. Tilføj:

Tilføjelsen passede ikke på én linje, så vi flyttede det resterende udtryk til den næste linje. Dette er tilladt i matematik. Når et udtryk ikke passer på én linje, føres det over til næste linje, og det er nødvendigt at sætte et lighedstegn (=) i slutningen af den første linje og i begyndelsen af en ny linje. Lighedstegnet på den anden linje indikerer, at dette er en fortsættelse af det udtryk, der var på den første linje.

Trin 5. Hvis svaret viste sig at være en ukorrekt brøk, så vælg dens heltalsdel

Vores svar er en ukorrekt brøkdel. Vi skal fremhæve hele den del af det. Vi fremhæver:

Fik et svar

Subtraktion af brøker med samme nævnere

Der er to typer brøksubtraktion:

Subtraktion af brøker med samme nævnere
Subtraktion af brøker med forskellige nævnere

Lad os først lære, hvordan man trækker brøker med de samme nævnere. Alt er enkelt her. For at trække en anden fra en brøk, skal du trække tælleren for den anden brøk fra tælleren i den første brøk og lade nævneren være den samme.

Lad os f.eks. finde værdien af udtrykket . For at løse dette eksempel er det nødvendigt at trække tælleren for den anden brøk fra tælleren i den første brøk og lade nævneren være den samme. Lad os gøre det:

Dette eksempel kan let forstås, hvis vi tænker på en pizza, der er opdelt i fire dele. Hvis du skærer pizzaer fra en pizza, får du pizzaer:

Eksempel 2 Find værdien af udtrykket.

Igen, fra tælleren for den første brøk, trækker du tælleren fra den anden brøk, og lad nævneren være den samme:

Dette eksempel kan let forstås, hvis vi tænker på en pizza, der er opdelt i tre dele. Hvis du skærer pizzaer fra en pizza, får du pizzaer:

Eksempel 3 Find værdien af et udtryk

Dette eksempel er løst på nøjagtig samme måde som de foregående. Fra tælleren for den første brøk skal du trække tællerne for de resterende brøker fra:

Svaret er en upassende brøk. Hvis eksemplet er komplet, er det sædvanligt at slippe af med den ukorrekte fraktion. Lad os slippe af med den forkerte brøkdel i svaret. For at gøre dette skal du vælge hele dens del:

Som du kan se, er der ikke noget kompliceret i at trække brøker fra med de samme nævnere. Det er nok at forstå følgende regler:

For at trække en anden fra en brøk, skal du trække tælleren for den anden brøk fra tælleren i den første brøk og lade nævneren være den samme;

Hvis svaret viste sig at være en ukorrekt brøkdel, skal du vælge hele dens del.

Subtraktion af brøker med forskellige nævnere

For eksempel kan en brøk trækkes fra en brøk, da disse brøker har de samme nævnere. Men en brøk kan ikke trækkes fra en brøk, fordi disse brøker har forskellige nævnere. I sådanne tilfælde skal brøker reduceres til samme (fælles)nævner.

Fællesnævneren findes efter samme princip, som vi brugte ved addering af brøker med forskellige nævnere. Først og fremmest skal du finde LCM for nævnerne af begge brøker. Derefter divideres LCM med nævneren af den første brøk, og den første yderligere faktor opnås, som skrives over den første brøk. På samme måde divideres LCM med nævneren for den anden brøk, og der opnås en anden yderligere faktor, som skrives over den anden brøk.

Brøkerne ganges derefter med deres yderligere faktorer. Som et resultat af disse operationer bliver brøker, der havde forskellige nævnere, til brøker, der har de samme nævnere. Og vi ved allerede, hvordan man trækker sådanne brøker fra.

Eksempel 1 Find værdien af et udtryk:

Først finder vi LCM for nævnerne af begge brøker. Nævneren i den første brøk er tallet 3, og nævneren i den anden brøk er tallet 4. Det mindste fælles multiplum af disse tal er 12

LCM (3 og 4) = 12

Nu tilbage til brøker og

Lad os finde en ekstra faktor for den første brøk. For at gøre dette dividerer vi LCM med nævneren af den første brøk. LCM er tallet 12, og nævneren for den første brøk er tallet 3. Divider 12 med 3, vi får 4. Vi skriver de fire over den første brøk:

Vi gør det samme med den anden brøk. Vi dividerer LCM med nævneren af den anden brøk. LCM er tallet 12, og nævneren for den anden brøk er tallet 4. Divider 12 med 4, vi får 3. Vi skriver tredobbelt over den anden brøk:

Nu er vi alle klar til subtraktion. Det er tilbage at gange brøkerne med deres yderligere faktorer:

Vi kom til den konklusion, at brøker, der havde forskellige nævnere, blev til brøker, der havde samme nævnere. Og vi ved allerede, hvordan man trækker sådanne brøker fra. Lad os fuldende dette eksempel til ende:

Fik et svar

Lad os prøve at skildre vores løsning ved hjælp af et billede. Hvis du skærer pizzaer fra en pizza, får du pizzaer.

Dette er den detaljerede version af løsningen. Da vi var i skole, skulle vi løse dette eksempel på en kortere måde. En sådan løsning vil se sådan ud:

Reduktion af brøker og til en fællesnævner kan også afbildes ved hjælp af et billede. Ved at bringe disse brøker til en fællesnævner, får vi brøkerne og . Disse brøker vil være repræsenteret af de samme pizzaskiver, men denne gang vil de blive opdelt i de samme brøker (reduceret til samme nævner):

Den første tegning viser en brøk (otte stykker ud af tolv), og det andet billede viser en brøk (tre stykker ud af tolv). Ved at skære tre stykker af fra otte stykker får vi fem stykker ud af tolv. Brøken beskriver disse fem stykker.

Eksempel 2 Find værdien af et udtryk

Disse brøker har forskellige nævnere, så du skal først bringe dem til den samme (fælles) nævner.

Find LCM for nævnerne af disse brøker.

Brøkernes nævnere er tallene 10, 3 og 5. Det mindste fælles multiplum af disse tal er 30

LCM(10; 3; 5) = 30

Nu finder vi yderligere faktorer for hver brøkdel. For at gøre dette dividerer vi LCM med nævneren for hver brøk.

Lad os finde en ekstra faktor for den første brøk. LCM er tallet 30, og nævneren for den første brøk er tallet 10. Divider 30 med 10, vi får den første ekstra faktor 3. Vi skriver den over den første brøk:

Nu finder vi en ekstra faktor for den anden fraktion. Divider LCM med nævneren af den anden brøk. LCM er tallet 30, og nævneren for den anden brøk er tallet 3. Divider 30 med 3, vi får den anden ekstra faktor 10. Vi skriver den over den anden brøk:

Nu finder vi en ekstra faktor for den tredje fraktion. Divider LCM med nævneren af den tredje brøk. LCM er tallet 30, og nævneren for den tredje brøk er tallet 5. Divider 30 med 5, vi får den tredje ekstra faktor 6. Vi skriver den over den tredje brøk:

Nu er alt klar til subtraktion. Det er tilbage at gange brøkerne med deres yderligere faktorer:

Vi kom til den konklusion, at brøker, der havde forskellige nævnere, blev til brøker, der har de samme (fælles)nævnere. Og vi ved allerede, hvordan man trækker sådanne brøker fra. Lad os afslutte dette eksempel.

Fortsættelsen af eksemplet vil ikke passe på én linje, så vi flytter fortsættelsen til næste linje. Glem ikke lighedstegnet (=) på den nye linje:

Svaret viste sig at være en korrekt brøk, og alt ser ud til at passe os, men det er for besværligt og grimt. Vi bør gøre det enklere og mere æstetisk tiltalende. Hvad kan gøres? Du kan reducere denne brøkdel. Husk, at reduktionen af en brøk er divisionen af tælleren og nævneren med den største fælles divisor af tælleren og nævneren.

For at reducere en brøk korrekt skal du dividere dens tæller og nævner med den største fælles divisor (GCD) af tallene 20 og 30.

Forveksle ikke GCD med NOC. Den mest almindelige fejl mange begyndere begår. GCD er den største fælles divisor. Vi finder det til fraktionsreduktion.

Og LCM er det mindste fælles multiplum. Vi finder det for at bringe brøker til den samme (fælles)nævner.

Nu vil vi finde den største fælles divisor (gcd) af tallene 20 og 30.

Så vi finder GCD for tallene 20 og 30:

GCD (20 og 30) = 10

Nu vender vi tilbage til vores eksempel og dividerer brøkens tæller og nævner med 10:

Fik et godt svar

At gange en brøk med et tal

For at gange en brøk med et tal, skal du gange tælleren for den givne brøk med dette tal og lade nævneren være den samme.

Eksempel 1. Gang brøken med tallet 1.

Gang brøkens tæller med tallet 1

Indgangen kan forstås som at den tager halv 1 gang. Tager du fx pizza 1 gang, får du pizza

Fra multiplikationslovene ved vi, at hvis multiplikanten og multiplikatoren ombyttes, så vil produktet ikke ændre sig. Hvis udtrykket skrives som , så vil produktet stadig være lig med . Igen fungerer reglen for at gange et heltal og en brøk:

Denne post kan forstås som at tage halvdelen af enheden. For eksempel, hvis der er 1 hel pizza, og vi tager halvdelen af den, så vil vi have pizza:

Eksempel 2. Find værdien af et udtryk

Gang brøkens tæller med 4

Udtrykket kan forstås som at det tager to kvarter 4 gange. Tager du fx pizzaer 4 gange, får du to hele pizzaer.

Og hvis vi bytter multiplikanten og multiplikatoren på plads, får vi udtrykket. Det vil også være lig med 2. Dette udtryk kan forstås som at tage to pizzaer fra fire hele pizzaer:

Multiplikation af brøker

For at gange brøker skal du gange deres tællere og nævnere. Hvis svaret er en uægte brøk, skal du vælge hele delen i den.

Eksempel 1 Find værdien af udtrykket.

Fik et svar. Det er ønskeligt at reducere denne fraktion. Fraktionen kan reduceres med 2. Så vil den endelige opløsning have følgende form:

Udtrykket kan forstås som at tage en pizza fra en halv pizza. Lad os sige, at vi har en halv pizza:

Hvordan tager man to tredjedele fra denne halvdel? Først skal du dele denne halvdel i tre lige store dele:

Og tag to fra disse tre stykker:

Vi henter pizza. Husk hvordan en pizza ser ud opdelt i tre dele:

En skive fra denne pizza og de to skiver, vi tog, vil have samme dimensioner:

Vi taler med andre ord om samme pizzastørrelse. Derfor er værdien af udtrykket

Eksempel 2. Find værdien af et udtryk

Multiplicer tælleren for den første brøk med tælleren i den anden brøk og nævneren for den første brøk med nævneren i den anden brøk:

Svaret er en upassende brøk. Lad os tage en hel del af det:

Eksempel 3 Find værdien af et udtryk

Svaret viste sig at være en korrekt brøk, men det vil være godt, hvis det reduceres. For at reducere denne brøk skal den divideres med gcd for tælleren og nævneren. Så lad os finde GCD for tallene 105 og 450:

GCD for (105 og 150) er 15

Nu deler vi tælleren og nævneren af vores svar på GCD:

Repræsenterer et heltal som en brøk

Ethvert helt tal kan repræsenteres som en brøk. For eksempel kan tallet 5 repræsenteres som . Fra dette vil de fem ikke ændre sin betydning, da udtrykket betyder "tallet fem divideret med en", og dette, som du ved, er lig med fem:

Omvendte tal

Nu vil vi stifte bekendtskab med et meget interessant emne i matematik. Det kaldes "omvendte tal".

Definition. Vend til nummer -en er det tal, der ganges med -en giver en enhed.

Lad os erstatte i denne definition i stedet for en variabel -en nummer 5 og prøv at læse definitionen:

Vend til nummer 5 er det tal, der ganges med 5 giver en enhed.

Er det muligt at finde et tal, der, når det ganges med 5, giver et? Det viser sig, at du kan. Lad os repræsentere fem som en brøk:

Derefter ganges denne brøk med sig selv, bare skift tæller og nævner. Med andre ord, gange brøken med sig selv, kun inverteret:

Hvad bliver resultatet af dette? Hvis vi fortsætter med at løse dette eksempel, får vi et:

Det betyder, at det omvendte af tallet 5 er tallet, da når 5 ganges med én, opnås en.

Det gensidige kan også findes for ethvert andet heltal.

den gensidige af 3 er en brøkdel
den reciproke af 4 er en brøkdel

Du kan også finde den gensidige for enhver anden fraktion. For at gøre dette er det nok at vende det om.

Multiplikation og division af brøker.

Opmærksomhed!
Der er yderligere
materiale i specialafsnit 555.
For dem, der stærkt "ikke særlig..."
Og for dem, der "meget...")

For eksempel:

Alt er ekstremt enkelt. Og led venligst ikke efter en fællesnævner! Har ikke brug for det her...

For at dividere en brøk med en brøk, skal du vende sekund(dette er vigtigt!) brøk og gange dem, dvs.:

For eksempel:

Hvis multiplikation eller division med heltal og brøker fanges, er det okay. Ligesom med addition laver vi en brøk af et helt tal med en enhed i nævneren - og går! For eksempel:

I gymnasiet skal du ofte beskæftige dig med tre-etagers (eller endda fire-etagers!) brøker. For eksempel:

Hvordan bringer man denne fraktion til en anstændig form? Ja, meget nemt! Brug division gennem to punkter:

I det første tilfælde (udtryk til venstre):

I det andet (udtryk til højre):

Mærker du forskellen? 4 og 1/9!

Hvad er rækkefølgen af division? Eller parentes, eller (som her) længden af vandrette streger. Udvikle et øje. Og hvis der ikke er nogen parenteser eller bindestreger, som:

divider-multiplicer derefter i rækkefølge, venstre mod højre!

Og endnu et meget simpelt og vigtigt trick. I handlinger med grader, vil det være nyttigt for dig! Lad os dividere enheden med en hvilken som helst brøk, for eksempel med 13/15:

Skuddet er vendt! Og det sker altid. Når man dividerer 1 med en hvilken som helst brøk, er resultatet den samme brøk, kun omvendt.

Det er alle handlingerne med brøker. Sagen er ret enkel, men giver mere end nok fejl. Noter dig praktiske råd, så bliver der færre af dem (fejl)!

Praktiske tips:

2. I eksempler med forskellige typer brøker - gå til almindelige brøker.

3. Vi reducerer alle fraktioner til stop.

4. Vi reducerer brøkudtryk på flere niveauer til almindelige udtryk ved hjælp af division gennem to punkter (vi følger rækkefølgen af division!).

5. Vi deler enheden i en brøk i vores sind, blot ved at vende brøken om.

Husk det rigtige svar opnået fra anden (især tredje) gang - tæller ikke! Sådan er det barske liv.

Beregn:

Besluttede du dig?

Leder efter svar, der matcher dine. Jeg skrev dem specifikt ned i et rod, væk fra fristelsen, så at sige... Her er de svarene, skrevet ned med semikolon.

0; 17/22; 3/4; 2/5; 1; 25.

Og nu drager vi konklusioner. Hvis alt lykkedes - glad for dig! Elementære beregninger med brøker er ikke dit problem! Du kan gøre mere seriøse ting. Hvis ikke...

Så du har et af to problemer. Eller begge dele på én gang.) Mangel på viden og (eller) uopmærksomhed. Men dette løselig Problemer.

Hvis du kan lide denne side...

Forresten har jeg et par flere interessante sider til dig.)

Du kan øve dig i at løse eksempler og finde ud af dit niveau. Test med øjeblikkelig verifikation. Lær - med interesse!)

du kan stifte bekendtskab med funktioner og afledte.

) og nævneren ved nævneren (vi får produktets nævner).

Brøk multiplikationsformel:

For eksempel:

Før du fortsætter med multiplikationen af tællere og nævnere, er det nødvendigt at kontrollere muligheden for brøkreduktion. Hvis du formår at reducere brøken, så bliver det nemmere for dig at fortsætte med at lave beregninger.

Division af en almindelig brøk med en brøk.

Division af brøker, der involverer et naturligt tal.

Det er ikke så skræmmende, som det ser ud til. Som ved addition omregner vi et heltal til en brøk med en enhed i nævneren. For eksempel:

Multiplikation af blandede fraktioner.

Regler for at gange brøker (blandet):

konverter blandede fraktioner til ukorrekte;
gange tællere og nævnere af brøker;
vi reducerer fraktionen;
hvis vi får en uægte brøk, så konverterer vi den uægte brøk til en blandet.

Bemærk! For at gange en blandet brøk med en anden blandet brøk, skal du først bringe dem i form af uægte brøker og derefter gange i henhold til reglen for at gange almindelige brøker.

Den anden måde at gange en brøk med et naturligt tal.

Det er mere praktisk at bruge den anden metode til at gange en almindelig brøk med et tal.

Bemærk! For at gange en brøk med et naturligt tal, er det nødvendigt at dividere brøkens nævner med dette tal og lade tælleren være uændret.

Fra ovenstående eksempel er det klart, at denne mulighed er mere praktisk at bruge, når nævneren af en brøk divideres uden en rest med et naturligt tal.

Brøker på flere niveauer.

I gymnasiet findes ofte tre-etagers (eller flere) brøker. Eksempel:

For at bringe en sådan brøk til sin sædvanlige form bruges division gennem 2 punkter:

Bemærk! Når man deler brøker, er rækkefølgen af division meget vigtig. Vær forsigtig, det er nemt at blive forvirret her.

Bemærk, for eksempel:

Når man dividerer en med en hvilken som helst brøk, vil resultatet være den samme brøk, kun omvendt:

Praktiske tips til at gange og dividere brøker:

2. I opgaver med forskellige typer brøker - gå til typen af almindelige brøker.

3. Vi reducerer alle fraktioner, indtil det ikke længere er muligt at reducere.

4. Vi bringer brøkudtryk på flere niveauer ind i almindelige udtryk ved hjælp af division gennem 2 punkter.

5. Vi deler enheden i en brøk i vores sind, blot ved at vende brøken om.

Multiplikation af brøker med en heltalsdel og negative brøker

Reduktion af fraktioner i farten

Multiplikation og division af brøker.

Hvis du kan lide denne side.

At hæve et tal til en rationel magt. (

At hæve et tal til en naturlig magt. (

Generaliseret intervalmetode til løsning af algebraiske uligheder (forfatter Kolchanov A.V.)

Metode til erstatning af faktorer til løsning af algebraiske uligheder (forfatter Kolchanov A.V.)

Tegn på delelighed (Lungu Alena)

Multiplikation af brøker

At gange en brøk med en brøk

At gange en brøk med et naturligt tal

Multiplikation af blandede tal

En anden måde at gange en brøk med et naturligt tal

Division af en brøk med et tal

Multiplikation og division af brøker

Multiplikation af brøker med en heltalsdel og negative brøker

Reduktion af fraktioner i farten

Inddeling af brøker.

Division af en brøk med et naturligt tal.

Eksempler på at dividere en brøk med et naturligt tal

Division af et naturligt tal med en brøk.

Eksempler på at dividere et naturligt tal med en brøk

Division af almindelige brøker.

Eksempler på division af almindelige brøker

Division af blandede tal.

Eksempler på at dividere blandede tal

Brøker. Multiplikation og division af brøker.

At gange en brøk med en brøk.

Division af en almindelig brøk med en brøk.

At gange en brøk med et naturligt tal.

Division af brøker, der involverer et naturligt tal.

Multiplikation af blandede fraktioner.

Den anden måde at gange en brøk med et naturligt tal.

Brøker på flere niveauer.

At gange en brøk med en brøk

At gange en brøk med et naturligt tal

Multiplikation af blandede tal

En anden måde at gange en brøk med et naturligt tal

Handlinger med brøker

Tilføjelse af brøker med samme nævnere

Tilføjelse af brøker med forskellige nævnere

Subtraktion af brøker med samme nævnere

Subtraktion af brøker med forskellige nævnere

At gange en brøk med et tal

Multiplikation af brøker

Repræsenterer et heltal som en brøk

Omvendte tal

Multiplikation og division af brøker.

Hvis du kan lide denne side...

Division af en almindelig brøk med en brøk.

Division af brøker, der involverer et naturligt tal.

Multiplikation af blandede fraktioner.

Den anden måde at gange en brøk med et naturligt tal.

Brøker på flere niveauer.

Redaktørens valg