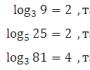परीक्षेच्या उदाहरणांवर लॉगरिदम. लॉगरिदम: उदाहरणे आणि उपाय

लॉगरिदमिक अभिव्यक्ती, उदाहरणे सोडवणे. या लेखात आपण लॉगरिदम सोडवण्याशी संबंधित समस्या पाहू. कार्ये अभिव्यक्तीचा अर्थ शोधण्याचा प्रश्न विचारतात. हे नोंद घ्यावे की लॉगरिथमची संकल्पना अनेक कार्यांमध्ये वापरली जाते आणि त्याचा अर्थ समजून घेणे अत्यंत आवश्यक आहे. युनिफाइड स्टेट परीक्षेसाठी, समीकरणे सोडवताना, लागू केलेल्या समस्यांमध्ये आणि फंक्शन्सच्या अभ्यासाशी संबंधित कामांमध्ये लॉगरिदम वापरला जातो.

लॉगॅरिथमचा अर्थ समजून घेण्यासाठी उदाहरणे देऊ:

मूलभूत लॉगरिदमिक ओळख:

लॉगरिदमचे गुणधर्म जे नेहमी लक्षात ठेवले पाहिजेत:

*उत्पादनाचा लॉगरिदम घटकांच्या लॉगरिदमच्या बेरजेइतका असतो.

* * *

*भागफलाचा (अपूर्णांक) लॉगरिदम हा घटकांच्या लॉगरिदममधील फरकाइतका असतो.

* * *

*घातांकाचा लॉगरिदम हा घातांकाच्या गुणाकार आणि त्याच्या पायाच्या लॉगरिदमच्या बरोबरीचा असतो.

* * *

*नवीन पायावर संक्रमण

* * *

अधिक गुणधर्म:

* * *

लॉगरिदमची गणना घातांकांच्या गुणधर्मांच्या वापराशी जवळून संबंधित आहे.

चला त्यापैकी काहींची यादी करूया:

या गुणधर्माचा सार असा आहे की जेव्हा अंश भाजकाकडे हस्तांतरित केला जातो आणि त्याउलट, घातांकाचे चिन्ह उलट बदलते. उदाहरणार्थ:

या मालमत्तेचा परिणाम:

* * *

पॉवरला पॉवर वाढवताना, बेस समान राहतो, परंतु घातांक गुणाकार केला जातो.

* * *

तुम्ही पाहिल्याप्रमाणे, लॉगरिथमची संकल्पना स्वतःच सोपी आहे. मुख्य गोष्ट अशी आहे की आपल्याला चांगल्या सरावाची आवश्यकता आहे, जे आपल्याला एक विशिष्ट कौशल्य देते. अर्थात, सूत्रांचे ज्ञान आवश्यक आहे. जर प्राथमिक लॉगरिदम रूपांतरित करण्याचे कौशल्य विकसित केले गेले नसेल, तर साधी कार्ये सोडवताना आपण सहजपणे चूक करू शकता.

सराव करा, प्रथम गणिताच्या अभ्यासक्रमातील सर्वात सोपी उदाहरणे सोडवा, नंतर अधिक जटिल उदाहरणांकडे जा. भविष्यात, मी निश्चितपणे "भयानक" लॉगरिदम कसे सोडवतात हे दर्शवेल; ते युनिफाइड स्टेट परीक्षेत दिसणार नाहीत, परंतु ते स्वारस्यपूर्ण आहेत, त्यांना चुकवू नका!

इतकंच! तुला शुभेच्छा!

विनम्र, अलेक्झांडर क्रुतित्स्कीख

P.S: तुम्ही मला सोशल नेटवर्क्सवरील साइटबद्दल सांगितल्यास मी आभारी राहीन.

तुमची गोपनीयता राखणे आमच्यासाठी महत्त्वाचे आहे. या कारणास्तव, आम्ही एक गोपनीयता धोरण विकसित केले आहे जे आम्ही तुमची माहिती कशी वापरतो आणि संचयित करतो याचे वर्णन करते. कृपया आमच्या गोपनीयता पद्धतींचे पुनरावलोकन करा आणि तुम्हाला काही प्रश्न असल्यास आम्हाला कळवा.

वैयक्तिक माहितीचे संकलन आणि वापर

वैयक्तिक माहिती डेटाचा संदर्भ देते ज्याचा वापर एखाद्या विशिष्ट व्यक्तीला ओळखण्यासाठी किंवा त्याच्याशी संपर्क साधण्यासाठी केला जाऊ शकतो.

तुम्ही आमच्याशी संपर्क साधता तेव्हा तुम्हाला तुमची वैयक्तिक माहिती देण्यास सांगितले जाऊ शकते.

खाली आम्ही एकत्रित केलेल्या वैयक्तिक माहितीच्या प्रकारांची आणि आम्ही अशी माहिती कशी वापरू शकतो याची काही उदाहरणे दिली आहेत.

आम्ही कोणती वैयक्तिक माहिती गोळा करतो:

• तुम्ही साइटवर अर्ज सबमिट करता तेव्हा, आम्ही तुमचे नाव, दूरध्वनी क्रमांक, ईमेल पत्ता इत्यादीसह विविध माहिती गोळा करू शकतो.

आम्ही तुमची वैयक्तिक माहिती कशी वापरतो:

• आम्ही संकलित केलेली वैयक्तिक माहिती आम्हाला अनन्य ऑफर, जाहिराती आणि इतर कार्यक्रम आणि आगामी कार्यक्रमांसह तुमच्याशी संपर्क साधण्याची अनुमती देते.
• वेळोवेळी, महत्त्वाच्या सूचना आणि संप्रेषणे पाठवण्यासाठी आम्ही तुमची वैयक्तिक माहिती वापरू शकतो.
• आम्ही प्रदान करत असल्या सेवा सुधारण्यासाठी आणि तुम्हाला आमच्या सेवांसंबंधी शिफारशी प्रदान करण्यासाठी ऑडिट, डेटा विश्लेषण आणि विविध संशोधन करण्यासाठी आम्ही अंतर्गत उद्देशांसाठी वैयक्तिक माहिती देखील वापरू शकतो.
• तुम्ही बक्षीस सोडत, स्पर्धा किंवा तत्सम जाहिरातींमध्ये भाग घेतल्यास, आम्ही अशा कार्यक्रमांचे व्यवस्थापन करण्यासाठी तुम्ही प्रदान केलेली माहिती वापरू शकतो.

तृतीय पक्षांना माहितीचे प्रकटीकरण

तुमच्याकडून मिळालेली माहिती आम्ही तृतीय पक्षांना उघड करत नाही.

अपवाद:

• आवश्यक असल्यास - कायद्यानुसार, न्यायालयीन प्रक्रियेनुसार, कायदेशीर कार्यवाहीमध्ये आणि/किंवा सार्वजनिक विनंत्या किंवा रशियन फेडरेशनच्या प्रदेशातील सरकारी अधिकाऱ्यांच्या विनंत्यांच्या आधारावर - तुमची वैयक्तिक माहिती उघड करणे. सुरक्षा, कायद्याची अंमलबजावणी किंवा इतर सार्वजनिक महत्त्वाच्या उद्देशांसाठी असे प्रकटीकरण आवश्यक किंवा योग्य आहे हे आम्ही निर्धारित केल्यास आम्ही तुमच्याबद्दलची माहिती देखील उघड करू शकतो.
• पुनर्रचना, विलीनीकरण किंवा विक्री झाल्यास, आम्ही संकलित केलेली वैयक्तिक माहिती लागू उत्तराधिकारी तृतीय पक्षाकडे हस्तांतरित करू शकतो.

वैयक्तिक माहितीचे संरक्षण

तुमच्या वैयक्तिक माहितीचे नुकसान, चोरी आणि गैरवापर, तसेच अनधिकृत प्रवेश, प्रकटीकरण, बदल आणि विनाश यापासून संरक्षण करण्यासाठी आम्ही - प्रशासकीय, तांत्रिक आणि भौतिक यासह - खबरदारी घेतो.

कंपनी स्तरावर तुमच्या गोपनीयतेचा आदर करणे

तुमची वैयक्तिक माहिती सुरक्षित असल्याची खात्री करण्यासाठी, आम्ही आमच्या कर्मचाऱ्यांना गोपनीयता आणि सुरक्षा मानके संप्रेषण करतो आणि गोपनीयता पद्धतींची काटेकोरपणे अंमलबजावणी करतो.

या व्हिडिओ ट्यूटोरियलमध्ये आम्ही एक गंभीर लॉगरिदमिक समीकरण सोडवण्याकडे लक्ष देऊ, ज्यामध्ये तुम्हाला फक्त मुळे शोधण्याची गरज नाही, तर दिलेल्या सेगमेंटवर असलेले ते देखील निवडणे आवश्यक आहे.

समस्या C1. समीकरण सोडवा. मध्यांतराशी संबंधित या समीकरणाची सर्व मुळे शोधा.

लॉगरिदमिक समीकरणांबद्दल एक टीप

तथापि, वर्षानुवर्षे असे विद्यार्थी माझ्याकडे येतात जे असे सोडवण्याचा प्रयत्न करतात, स्पष्टपणे, कठीण समीकरणे, परंतु त्याच वेळी ते समजू शकत नाहीत: त्यांनी अगदी कोठून सुरुवात करावी आणि लॉगरिदमकडे कसे जायचे? ही समस्या मजबूत, चांगली तयारी असलेल्या विद्यार्थ्यांमध्ये देखील उद्भवू शकते.

परिणामी, अनेकांना या विषयाची भीती वाटू लागते किंवा स्वतःला मूर्ख समजतात. तर, लक्षात ठेवा: जर तुम्ही असे समीकरण सोडवू शकत नसाल तर याचा अर्थ असा नाही की तुम्ही मूर्ख आहात. कारण, उदाहरणार्थ, तुम्ही हे समीकरण जवळजवळ तोंडी हाताळू शकता:

लॉग 2 x = 4

आणि जर तसे नसेल, तर तुम्ही हा मजकूर आता वाचत नसाल, कारण तुम्ही सोप्या आणि अधिक सांसारिक कामांमध्ये व्यस्त होता. अर्थात, आता कोणीतरी आक्षेप घेईल: "या सर्वात सोप्या समीकरणाचा आपल्या निरोगी रचनेशी काय संबंध आहे?" मी उत्तर देतो: कोणतेही लॉगरिदमिक समीकरण, ते कितीही क्लिष्ट असले तरीही, शेवटी या सर्वात सोप्या रचनांवर येते जे तोंडी सोडवता येते.

अर्थात, एखाद्याने जटिल लघुगणकीय समीकरणांमधून सोप्या समीकरणांकडे वळले पाहिजे, निवडून किंवा डफ वाजवून नाचून नव्हे, तर स्पष्ट, दीर्घ-परिभाषित नियमांनुसार, ज्याला म्हणतात - लॉगरिदमिक अभिव्यक्ती रूपांतरित करण्याचे नियम. ते जाणून घेतल्यास, तुम्ही गणितातील युनिफाइड स्टेट परीक्षेतील अगदी अत्याधुनिक समीकरणांनाही सहजपणे सामोरे जाऊ शकता.

आणि या नियमांबद्दल आपण आजच्या धड्यात बोलू. जा!

समस्या C1 मधील लॉगरिदमिक समीकरण सोडवणे

तर, आम्ही समीकरण सोडवतो:

सर्व प्रथम, जेव्हा लॉगरिदमिक समीकरणांचा विचार केला जातो तेव्हा आपल्याला मूलभूत युक्त्या आठवतात - म्हणजे लॉगरिदमिक समीकरणे सोडवण्याचा मूलभूत नियम. यात खालील गोष्टींचा समावेश आहे:

कॅनोनिकल फॉर्म प्रमेय. कोणतेही लॉगॅरिदमिक समीकरण, त्यात काय समाविष्ट आहे हे महत्त्वाचे नाही, कोणतेही लॉगरिदम असो, कोणताही आधार असो आणि त्यात काहीही असले तरीही, ते फॉर्मच्या समीकरणापर्यंत कमी करणे आवश्यक आहे:

log a f (x) = log a g (x)

जर आपण आपले समीकरण पाहिले तर आपल्याला दोन समस्या लगेच लक्षात येतात:

1. डावीकडे आमच्याकडे आहे दोन संख्यांची बेरीज, ज्यापैकी एक अजिबात लॉगरिदम नाही.
2. उजवीकडे एक लॉगरिथम आहे, परंतु त्याच्या पायथ्याशी मूळ आहे. आणि डावीकडील लॉगरिथम फक्त 2 आहे, म्हणजे. डावीकडे आणि उजवीकडे लॉगरिदमचे आधार वेगळे आहेत.

म्हणून, आम्ही समस्यांची ही यादी तयार केली आहे जी आमचे समीकरण त्यापासून वेगळे करतात प्रामाणिक समीकरण, ज्यामध्ये समाधान प्रक्रियेदरम्यान कोणतेही लॉगरिदमिक समीकरण कमी करणे आवश्यक आहे. अशा प्रकारे, या टप्प्यावर आपले समीकरण सोडवणे वर वर्णन केलेल्या दोन समस्या दूर करण्यासाठी खाली येते.

कोणतेही लॉगॅरिदमिक समीकरण तुम्ही त्याचे प्रमाणिक स्वरूप कमी केल्यास ते पटकन आणि सहज सोडवले जाऊ शकते.

लॉगरिदम आणि उत्पादनाच्या लॉगरिदमची बेरीज

चला क्रमाने पुढे जाऊया. प्रथम, डावीकडील रचना पाहू. दोन लॉगरिदमच्या बेरजेबद्दल आपण काय म्हणू शकतो? चला अद्भुत सूत्र लक्षात ठेवूया:

log a f (x) + log a g (x) = log a f (x) g (x)

परंतु हे लक्षात घेण्यासारखे आहे की आमच्या बाबतीत पहिली संज्ञा अजिबात लॉगरिथम नाही. याचा अर्थ असा की आपल्याला एकक ते बेस 2 ला लॉगॅरिथम म्हणून प्रस्तुत करणे आवश्यक आहे (तंतोतंत 2, कारण लॉगरिथम ते बेस 2 डावीकडे आहे). ते कसे करायचे? चला पुन्हा एकदा अद्भुत सूत्र लक्षात ठेवूया:

a = लॉग b b a

येथे तुम्हाला हे समजून घेणे आवश्यक आहे: जेव्हा आपण "कोणताही आधार b" म्हणतो, तेव्हा आपला अर्थ असा होतो की b अजूनही अनियंत्रित संख्या असू शकत नाही. जर आपण लॉगरिदममध्ये संख्या समाविष्ट केली तर निश्चित निर्बंध, म्हणजे: लॉगरिदमचा आधार 0 पेक्षा मोठा असणे आवश्यक आहे आणि 1 च्या बरोबरीचे नसावे. अन्यथा, लॉगरिदमला अर्थ नाही. चला हे लिहूया:

0 < b ≠ 1

आमच्या बाबतीत काय होते ते पाहूया:

1 = लॉग 2 2 1 = लॉग 2 2

आता ही वस्तुस्थिती लक्षात घेऊन आपले संपूर्ण समीकरण पुन्हा लिहू. आणि आम्ही ताबडतोब दुसरा नियम लागू करतो: लॉगरिदमची बेरीज वितर्कांच्या उत्पादनाच्या लॉगरिदमच्या समान असते. परिणामी आम्हाला मिळते:

आमचे एक नवीन समीकरण आहे. जसे आपण पाहतो, ते आपण ज्या प्रामाणिक समीकरणासाठी प्रयत्न करत आहोत त्याच्या अगदी जवळ आहे. पण एक समस्या आहे, आम्ही तो दुसरा मुद्दा म्हणून लिहिला आहे: आमचे लॉगरिदम, जे डावीकडे आणि उजवीकडे आहेत, भिन्न कारणे. चला पुढच्या पायरीवर जाऊया.

लॉगरिदममधून शक्ती वजा करण्याचे नियम

तर डावीकडील लॉगरिथमचा आधार फक्त 2 आहे आणि उजवीकडील लॉगरिदमला मूळ आहे. परंतु लॉगरिदमच्या वितर्कांचे आधार शक्तींपर्यंत वाढवता येतात हे लक्षात ठेवल्यास ही समस्या नाही. चला यापैकी एक नियम लिहू:

log a b n = n log a b

मानवी भाषेत अनुवादित: तुम्ही लॉगरिदमच्या बेसमधून पॉवर काढू शकता आणि गुणक म्हणून समोर ठेवू शकता. लॉगरिदममधून n संख्या "स्थलांतरित" झाली आणि समोर एक गुणांक बनला.

लॉगरिदमच्या पायावरून आपण शक्ती तितक्याच सहजतेने मिळवू शकतो. हे असे दिसेल:

दुसऱ्या शब्दांत, जर तुम्ही लॉगरिदमच्या युक्तिवादातून पदवी काढून टाकली तर, ही पदवी लॉगरिदमच्या आधी एक घटक म्हणून देखील लिहिली जाते, परंतु संख्या म्हणून नाही, तर परस्पर संख्या 1/k म्हणून.

तथापि, ते सर्व नाही! आपण ही दोन सूत्रे एकत्र करू शकतो आणि पुढील सूत्र घेऊन येऊ शकतो:

जेव्हा लॉगरिदमच्या बेस आणि आर्ग्युमेंट या दोन्हीमध्ये पॉवर दिसून येते, तेव्हा आम्ही वेळ वाचवू शकतो आणि बेस आणि आर्ग्युमेंट या दोन्ही मधून ताबडतोब पॉवर काढून गणिते सोपी करू शकतो. या प्रकरणात, युक्तिवादात काय होते (आमच्या बाबतीत, हे गुणांक n आहे) अंशात दिसून येईल. आणि पायावर पदवी काय होती, a k, भाजकाकडे जाईल.

आणि हीच सूत्रे आपण आता आपले लॉगरिदम समान बेसवर कमी करण्यासाठी वापरणार आहोत.

सर्व प्रथम, चला अधिक किंवा कमी सुंदर बेस निवडूया. साहजिकच, मुळापेक्षा बेसवर दोन सोबत काम करणे जास्त आनंददायी आहे. तर दुसरा लॉगरिदम बेस २ वर कमी करण्याचा प्रयत्न करूया. हा लॉगरिथम स्वतंत्रपणे लिहू:

आपण येथे काय करू शकतो? परिमेय घातांकासह शक्ती सूत्र आठवूया. दुसऱ्या शब्दांत, आपण परिमेय घातांकासह बळ म्हणून मुळे लिहू शकतो. आणि मग आपण तर्क आणि लॉगरिदमचा आधार या दोन्हीपैकी 1/2 ची शक्ती घेतो. आम्ही लॉगरिदमला तोंड देत असलेल्या अंश आणि भाजकातील गुणांकातील दोन कमी करतो:

शेवटी, नवीन गुणांक लक्षात घेऊन मूळ समीकरण पुन्हा लिहू:

लॉग 2 2(9x 2 + 5) = लॉग 2 (8x 4 + 14)

आम्ही कॅनोनिकल लॉगरिदमिक समीकरण प्राप्त केले आहे. डावीकडे आणि उजवीकडे दोन्हीकडे आपल्याकडे समान बेस 2 ला लॉगरिदम आहे. या लॉगरिदम व्यतिरिक्त, कोणतेही गुणांक नाहीत, डावीकडे किंवा उजवीकडे कोणतेही पद नाहीत.

परिणामी, आपण लॉगरिदमच्या चिन्हापासून मुक्त होऊ शकतो. अर्थात, व्याख्येचे डोमेन लक्षात घेऊन. परंतु आपण ते करण्यापूर्वी, आपण मागे जाऊ आणि अपूर्णांकांबद्दल थोडे स्पष्टीकरण करू.

अपूर्णांकाला अपूर्णांकाने विभाजित करणे: अतिरिक्त विचार

उजव्या लॉगरिदमसमोरील घटक कुठून येतात आणि कुठे जातात हे सर्वच विद्यार्थ्यांना समजत नाही. चला ते पुन्हा लिहू:

अपूर्णांक म्हणजे काय ते शोधूया. चला खाली लिहू:

आता आपण अपूर्णांकांना विभाजित करण्याचा नियम लक्षात ठेवूया: 1/2 ने भागण्यासाठी आपल्याला उलटा अपूर्णांकाने गुणाकार करणे आवश्यक आहे:

अर्थात, पुढील गणनेच्या सोयीसाठी, आपण 2/1 असे दोन लिहू शकतो - आणि हेच आपण समाधान प्रक्रियेतील दुसरे गुणांक म्हणून पाहतो.

मला आशा आहे की आता प्रत्येकाला दुसरा गुणांक कुठून येतो हे समजले असेल, म्हणून आपण थेट आपले प्रमाणिक लॉगरिदमिक समीकरण सोडवण्याकडे जाऊ या.

लॉगरिथम चिन्हापासून मुक्त होणे

मी तुम्हाला आठवण करून देतो की आता आपण लॉगरिदमपासून मुक्त होऊ शकतो आणि खालील अभिव्यक्ती सोडू शकतो:

2(9x 2 + 5) = 8x 4 + 14

चला डावीकडील कंस उघडू. आम्हाला मिळते:

18x 2 + 10 = 8x 4 + 14

चला सर्व काही डावीकडून उजवीकडे हलवू:

8x 4 + 14 − 18x 2 − 10 = 0

चला तत्सम आणू आणि मिळवा:

8x 4 − 18x 2 + 4 = 0

गुणांक सुलभ करण्यासाठी आपण या समीकरणाच्या दोन्ही बाजूंना 2 ने विभाजित करू शकतो आणि आपल्याला मिळते:

4x 4 − 9x 2 + 2 = 0

आमच्या आधी नेहमीचा आहे द्विचक्र समीकरण, आणि त्याची मुळे भेदभावाद्वारे सहजपणे मोजली जातात. तर, भेदभाव लिहूया:

D = 81 − 4 4 2 = 81 − 32 = 49

छान, भेदभाव करणारा "सुंदर" आहे, त्याचे मूळ 7 आहे. तेच आहे, आपण स्वतः X ची गणना करूया. परंतु या प्रकरणात, मुळे x नसून x 2 असतील, कारण आपल्याकडे द्विचौकीय समीकरण आहे. तर, आमचे पर्यायः

कृपया लक्षात ठेवा: आम्ही मुळे काढली, त्यामुळे दोन उत्तरे असतील, कारण... चौरस - सम कार्य. आणि जर आपण फक्त दोनचे मूळ लिहितो, तर आपण फक्त दुसरे मूळ गमावू.

आता आपण आपल्या द्विचक्र समीकरणाचे दुसरे मूळ लिहू:

पुन्हा, आपण आपल्या समीकरणाच्या दोन्ही बाजूंचे अंकगणित वर्गमूळ घेतो आणि दोन मुळे मिळवतो. तथापि, लक्षात ठेवा:

लॉगॅरिथमच्या वितर्कांना प्रमाणिक स्वरूपात समीकरण करणे पुरेसे नाही. व्याख्या डोमेन लक्षात ठेवा!

एकूण चार मुळे मिळाली. ते सर्व खरोखरच आपल्या मूळ समीकरणाचे निराकरण आहेत. एक नजर टाका: आमच्या मूळ लॉगरिदमिक समीकरणात, आत लॉगरिदम एकतर 9x 2 + 5 (हे कार्य नेहमी सकारात्मक असते) किंवा 8x 4 + 14 - जे नेहमी सकारात्मक असते. म्हणून, लॉगॅरिथमच्या व्याख्येचे डोमेन कोणत्याही परिस्थितीत समाधानी आहे, आपल्याला कोणतेही मूळ मिळाले तरीही याचा अर्थ असा आहे की सर्व चार मुळे आपल्या समीकरणाचे निराकरण आहेत.

छान, आता समस्येच्या दुसऱ्या भागाकडे जाऊया.

एका खंडावरील लॉगरिदमिक समीकरणाच्या मुळांची निवड

आपल्या चार मुळांमधून आपण त्या भागावर पडलेल्यांची निवड करतो [−1; ८/९]. आम्ही आमच्या मुळांकडे परतलो आणि आता आम्ही त्यांची निवड करू. सुरुवातीला, मी निर्देशांक अक्ष काढण्याचा आणि त्यावरील विभागाचे टोक चिन्हांकित करण्याचा सल्ला देतो:

दोन्ही बिंदू छायांकित केले जातील. त्या. समस्येच्या परिस्थितीनुसार, आम्हाला छायांकित विभागात स्वारस्य आहे. आता मुळे पाहू.

अतार्किक मुळे

चला तर्कहीन मुळांपासून सुरुवात करूया. लक्षात घ्या की ८/९< 9/9 = 1. С другой стороны, корень из двух явно больше единицы. Следовательно, наши корни будут находиться на отрезке в таком положении:

यावरून असे दिसून येते की दोनचे मूळ आपल्या आवडीच्या विभागात येत नाही. त्याचप्रमाणे, आपण नकारात्मक मुळासह प्राप्त करू: ते −1 पेक्षा कमी आहे, म्हणजेच ते आपल्या आवडीच्या विभागाच्या डावीकडे आहे.

तर्कशुद्ध मुळे

दोन मुळे शिल्लक आहेत: x = 1/2 आणि x = −1/2. चला लक्षात घ्या की विभागाचे डावे टोक (−1) ऋण आहे, आणि उजवे टोक (8/9) धनात्मक आहे. म्हणून, या टोकांच्या दरम्यान कुठेतरी 0 ही संख्या आहे. मूळ x = −1/2 −1 आणि 0 च्या दरम्यान असेल, म्हणजे. अंतिम उत्तरात समाप्त होईल. आपण रूट x = 1/2 सह असेच करतो. हे मूळ देखील विचाराधीन विभागावर आहे.

तुम्ही खात्री करू शकता की 8/9 1/2 पेक्षा मोठा आहे. चला या संख्या एकमेकांमधून वजा करूया:

आम्हाला अपूर्णांक 7/18 > 0 मिळाला, ज्याचा अर्थ 8/9 > 1/2 असा होतो.

समन्वय अक्षावर योग्य मुळे चिन्हांकित करू:

अंतिम उत्तर दोन मुळे असतील: 1/2 आणि −1/2.

अपरिमेय संख्यांची तुलना: एक सार्वत्रिक अल्गोरिदम

शेवटी, मी पुन्हा एकदा अपरिमेय संख्येकडे परत येऊ इच्छितो. त्यांचे उदाहरण वापरून, आता आपण गणितातील परिमेय आणि अपरिमेय प्रमाणांची तुलना कशी करायची ते पाहू. सुरुवातीला, त्यांच्यामध्ये अशी टिक आहे V - "अधिक" किंवा "कमी" चिन्ह, परंतु ते कोणत्या दिशेने निर्देशित केले आहे हे आम्हाला अद्याप माहित नाही. चला खाली लिहू:

आम्हाला कोणत्याही तुलना अल्गोरिदमची अजिबात गरज का आहे? वस्तुस्थिती अशी आहे की या समस्येमध्ये आम्ही खूप भाग्यवान होतो: भागाकार क्रमांक 1 सोडवण्याच्या प्रक्रियेत, ज्याबद्दल आम्ही निश्चितपणे म्हणू शकतो:

तथापि, तुम्हाला अशी संख्या लगेच दिसणार नाही. चला तर मग आपल्या संख्यांची थेट तुलना करण्याचा प्रयत्न करूया.

ते कसे केले जाते? आम्ही सामान्य असमानतेप्रमाणेच करतो:

1. प्रथम, आपल्याकडे कुठेतरी ऋण गुणांक असल्यास, आपण असमानतेच्या दोन्ही बाजूंना −1 ने गुणाकार करू. अर्थातच चिन्ह बदलणे. हा चेकमार्क V यात बदलेल - Λ.
2. परंतु आमच्या बाबतीत, दोन्ही बाजू आधीच सकारात्मक आहेत, त्यामुळे काहीही बदलण्याची गरज नाही. खरोखर गरज काय आहे दोन्ही बाजूंना चौरसमूलगामी लावतात.

जर, अपरिमेय संख्यांची तुलना करताना, विभक्त घटक त्वरित निवडणे शक्य नसेल, तर मी अशी तुलना "हेड-ऑन" करण्याची शिफारस करतो - त्याचे वर्णन सामान्य असमानता म्हणून करा.

ते सोडवताना, ते याप्रमाणे औपचारिक केले जाते:

आता हे सर्व तुलना करणे सोपे आहे. मुद्दा असा आहे की 64/81< 81/81 = 1 < 2. На основании той цепочки преобразований мы заключаем, что 64/81 < 2 и, следовательно, корень больше 8/9.

एवढेच, आम्हाला कठोर पुरावा मिळाला आहे की सर्व संख्या x क्रमांकाच्या रेषेवर अचूकपणे आणि नेमक्या त्या क्रमाने चिन्हांकित केल्या आहेत ज्यामध्ये त्या प्रत्यक्षात असाव्यात. या सोल्यूशनमध्ये कोणालाही दोष आढळणार नाही, म्हणून लक्षात ठेवा: जर तुम्हाला भागाकार संख्या लगेच दिसत नसेल (आमच्या बाबतीत ती 1 आहे), तर मोकळ्या मनाने वरील रचना लिहा, गुणाकार करा, त्याचे वर्ग करा - आणि शेवटी तुम्ही एक सुंदर असमानता मिळवा. या विषमतेवरून कोणती संख्या जास्त आणि कोणती कमी हे स्पष्ट होईल.

आमच्या समस्येकडे परत येताना, मी पुन्हा एकदा तुमचे लक्ष वेधून घेऊ इच्छितो की आम्ही आमचे समीकरण सोडवताना अगदी सुरुवातीला काय केले. उदाहरणार्थ: आम्ही आमचे मूळ लॉगरिदमिक समीकरण जवळून पाहिले आणि ते कमी करण्याचा प्रयत्न केला प्रामाणिकलॉगरिदमिक समीकरण. जिथे डावीकडे आणि उजवीकडे फक्त लॉगरिदम आहेत - कोणत्याही अतिरिक्त अटींशिवाय, समोर गुणांक इ. आम्हाला a किंवा b वर आधारित दोन लॉगरिदमची आवश्यकता नाही, परंतु दुसर्या लॉगरिदमच्या समान लॉगरिदमची आवश्यकता आहे.

याव्यतिरिक्त, लॉगरिदमचे बेस देखील समान असले पाहिजेत. शिवाय, जर समीकरण योग्यरित्या तयार केले असेल, तर प्राथमिक लॉगरिदमिक परिवर्तनांच्या मदतीने (लोगॅरिथमची बेरीज, एका संख्येचे लॉगरिदममध्ये रूपांतर इ.) आपण हे समीकरण प्रमाणानुसार कमी करू.

म्हणून, आतापासून, जेव्हा तुम्हाला लॉगरिदमिक समीकरण दिसेल जे सरळ सोडवता येत नाही, तेव्हा तुम्ही हरवून जाऊ नका किंवा उत्तर शोधण्याचा प्रयत्न करू नका. आपल्याला फक्त या चरणांचे अनुसरण करण्याची आवश्यकता आहे:

1. सर्व मुक्त घटकांना लॉगरिथममध्ये रूपांतरित करा;
2. नंतर हे लॉगरिदम जोडा;
3. परिणामी बांधकामात, सर्व लॉगरिदम समान बेसवर कमी करा.

परिणामी, तुम्हाला एक साधे समीकरण मिळेल जे इयत्ता 8-9 मटेरियलमधील प्राथमिक बीजगणित साधनांचा वापर करून सोडवले जाऊ शकते. सर्वसाधारणपणे, माझ्या वेबसाइटवर जा, लॉगरिदम सोडवण्याचा सराव करा, माझ्यासारखे लॉगरिदमिक समीकरण सोडवा, माझ्यापेक्षा चांगले सोडवा. आणि ते सर्व माझ्यासाठी आहे. पावेल बर्डोव्ह तुमच्यासोबत होता. पुन्हा भेटू!

लॉगरिदम म्हणजे काय?

लक्ष द्या!
अतिरिक्त आहेत
विशेष कलम 555 मधील साहित्य.
जे खूप "फार नाही..." आहेत त्यांच्यासाठी
आणि ज्यांना "खूप ...")

लॉगरिदम म्हणजे काय? लॉगरिदम कसे सोडवायचे? हे प्रश्न अनेक पदवीधरांना गोंधळात टाकतात. पारंपारिकपणे, लॉगरिदमचा विषय जटिल, अनाकलनीय आणि भितीदायक मानला जातो. विशेषत: लॉगरिदमसह समीकरणे.

हे अजिबात खरे नाही. एकदम! माझ्यावर विश्वास नाही? ठीक आहे. आता, फक्त 10-20 मिनिटांत तुम्ही:

1. तुम्हाला समजेल लॉगरिथम काय आहे.

2. घातांकीय समीकरणांचा संपूर्ण वर्ग सोडवायला शिका. आपण त्यांच्याबद्दल काहीही ऐकले नसले तरीही.

3. साध्या लॉगरिदमची गणना करायला शिका.

शिवाय, यासाठी तुम्हाला फक्त गुणाकार सारणी आणि संख्या घात कशी वाढवायची हे माहित असणे आवश्यक आहे...

मला वाटते की तुम्हाला शंका आहे... ठीक आहे, वेळ चिन्हांकित करा! जा!

प्रथम, हे समीकरण तुमच्या डोक्यात सोडवा:

जर तुम्हाला ही साइट आवडली असेल तर...

तसे, माझ्याकडे तुमच्यासाठी आणखी काही मनोरंजक साइट्स आहेत.)

तुम्ही उदाहरणे सोडवण्याचा सराव करू शकता आणि तुमची पातळी शोधू शकता. त्वरित पडताळणीसह चाचणी. चला जाणून घेऊ - स्वारस्याने!)

आपण फंक्शन्स आणि डेरिव्हेटिव्ह्जसह परिचित होऊ शकता.

तुम्हाला माहिती आहेच की, अभिव्यक्तींचा शक्तींसह गुणाकार करताना, त्यांचे घातांक नेहमी जोडतात (a b *a c = a b+c). हा गणिती नियम आर्किमिडीजने काढला आणि नंतरच्या काळात 8व्या शतकात विरासेन या गणितज्ञाने पूर्णांक घातांकांची तक्ता तयार केली. लॉगरिदमच्या पुढील शोधासाठी त्यांनीच काम केले. हे फंक्शन वापरण्याची उदाहरणे जवळपास सर्वत्र आढळू शकतात जिथे तुम्हाला साध्या बेरीज करून त्रासदायक गुणाकार सुलभ करणे आवश्यक आहे. तुम्ही हा लेख वाचण्यात 10 मिनिटे घालवल्यास, आम्ही तुम्हाला लॉगरिदम काय आहेत आणि त्यांच्यासह कसे कार्य करावे हे समजावून सांगू. सोप्या आणि सुलभ भाषेत.

गणितातील व्याख्या

लॉगॅरिथम ही खालील स्वरूपाची अभिव्यक्ती आहे: लॉग a b=c, म्हणजेच कोणत्याही नॉन-नकारात्मक संख्येचा (म्हणजे कोणताही सकारात्मक) "b" त्याच्या बेस "a" मधील लॉगरिथम "c" ची शक्ती मानली जाते. " ज्यावर शेवटी "b" मूल्य मिळविण्यासाठी आधार "a" वाढवणे आवश्यक आहे. उदाहरणे वापरून लॉगरिथमचे विश्लेषण करू या, एक अभिव्यक्ती लॉग आहे म्हणू 2 8. उत्तर कसे शोधायचे? हे अगदी सोपे आहे, तुम्हाला अशी पॉवर शोधावी लागेल की 2 ते आवश्यक पॉवरपर्यंत तुम्हाला 8 मिळतील. तुमच्या डोक्यात काही आकडेमोड केल्यावर, आम्हाला 3 क्रमांक मिळेल! आणि ते खरे आहे, कारण 2 ते 3 च्या घाताचे उत्तर 8 असे देते.

लॉगरिदमचे प्रकार

बऱ्याच विद्यार्थी आणि विद्यार्थ्यांसाठी, हा विषय क्लिष्ट आणि अनाकलनीय वाटतो, परंतु प्रत्यक्षात लॉगरिदम इतके भयानक नाहीत, मुख्य गोष्ट म्हणजे त्यांचे सामान्य अर्थ समजून घेणे आणि त्यांचे गुणधर्म आणि काही नियम लक्षात ठेवणे. लॉगरिदमिक अभिव्यक्तीचे तीन स्वतंत्र प्रकार आहेत:

1. नैसर्गिक लॉगॅरिथम ln a, जेथे आधार हा यूलर क्रमांक आहे (e = 2.7).
2. दशांश a, जेथे पाया 10 आहे.
3. बेस a>1 पर्यंत b कोणत्याही संख्येचा लॉगरिदम.

लॉगरिदमिक प्रमेयांचा वापर करून एकल लॉगॅरिथममध्ये सरलीकरण, घट आणि त्यानंतरच्या कपात यासह, त्यापैकी प्रत्येक मानक पद्धतीने सोडवला जातो. लॉगरिदमची योग्य मूल्ये प्राप्त करण्यासाठी, आपण त्यांचे गुणधर्म आणि त्यांचे निराकरण करताना क्रियांचा क्रम लक्षात ठेवावा.

नियम आणि काही निर्बंध

गणितामध्ये असे अनेक नियम-अवरोध आहेत जे स्वयंसिद्ध म्हणून स्वीकारले जातात, म्हणजेच ते चर्चेच्या अधीन नसतात आणि सत्य असतात. उदाहरणार्थ, संख्यांना शून्याने विभाजित करणे अशक्य आहे आणि ऋण संख्यांचे सम मूळ काढणे देखील अशक्य आहे. लॉगरिदमचे देखील त्यांचे स्वतःचे नियम आहेत, ज्याचे अनुसरण करून आपण लांब आणि क्षमता असलेल्या लॉगरिदमिक अभिव्यक्तीसह देखील कार्य करण्यास सहजपणे शिकू शकता:

• बेस "a" नेहमी शून्यापेक्षा मोठा असावा आणि 1 च्या बरोबरीचा नसावा, अन्यथा अभिव्यक्तीचा अर्थ गमवाल, कारण "1" आणि "0" कोणत्याही प्रमाणात त्यांच्या मूल्यांच्या समान असतात;
• जर a > 0, नंतर a b > 0, असे दिसून येते की "c" देखील शून्यापेक्षा जास्त असणे आवश्यक आहे.

लॉगरिदम कसे सोडवायचे?

उदाहरणार्थ, 10 x = 100 या समीकरणाचे उत्तर शोधण्याचे कार्य दिले आहे. हे खूप सोपे आहे, आपल्याला 100 प्राप्त होणारी संख्या दहा वाढवून घात निवडणे आवश्यक आहे. हे अर्थातच 10 2 = आहे. 100.

आता ही अभिव्यक्ती लॉगरिदमिक स्वरूपात दर्शवू. आम्हाला लॉग 10 100 = 2 मिळतो. लॉगरिदम सोडवताना, दिलेली संख्या मिळविण्यासाठी लॉगरिदमच्या बेसमध्ये प्रवेश करणे आवश्यक असलेली शक्ती शोधण्यासाठी सर्व क्रिया व्यावहारिकरित्या एकत्रित होतात.

अज्ञात पदवीचे मूल्य अचूकपणे निर्धारित करण्यासाठी, आपल्याला पदवीच्या सारणीसह कसे कार्य करावे हे शिकण्याची आवश्यकता आहे. हे असे दिसते:

तुम्ही बघू शकता, तुमच्याकडे तांत्रिक मन आणि गुणाकार सारणीचे ज्ञान असल्यास काही घातांकांचा अंतर्ज्ञानाने अंदाज लावला जाऊ शकतो. तथापि, मोठ्या मूल्यांसाठी आपल्याला पॉवर टेबलची आवश्यकता असेल. ज्यांना गणिताच्या गुंतागुंतीच्या विषयांबद्दल काहीच माहिती नाही अशांनाही याचा वापर करता येतो. डाव्या स्तंभात संख्या (बेस a) आहेत, संख्यांची वरची पंक्ती ही संख्या a वाढवलेली शक्ती c चे मूल्य आहे. छेदनबिंदूवर, सेलमध्ये संख्या मूल्ये असतात जी उत्तरे असतात (a c =b). उदाहरणार्थ, 10 क्रमांकाचा पहिला सेल घ्या आणि त्याचा वर्ग करा, आपल्याला 100 मूल्य मिळेल, जे आपल्या दोन पेशींच्या छेदनबिंदूवर सूचित केले आहे. सर्व काही इतके सोपे आणि सोपे आहे की अगदी खऱ्या मानवतावादीलाही समजेल!

समीकरणे आणि असमानता

असे दिसून आले की विशिष्ट परिस्थितींमध्ये घातांक हा लॉगरिथम आहे. म्हणून, कोणतीही गणितीय संख्यात्मक अभिव्यक्ती लॉगरिदमिक समानता म्हणून लिहिली जाऊ शकते. उदाहरणार्थ, 3 4 =81 हे 81 समान चार (लॉग 3 81 = 4) चा आधार 3 लॉगरिथम म्हणून लिहिता येईल. नकारात्मक शक्तींसाठी नियम समान आहेत: 2 -5 = 1/32 आपण लॉगरिदम म्हणून लिहू, आपल्याला लॉग 2 (1/32) = -5 मिळेल. गणितातील सर्वात आकर्षक विभागांपैकी एक म्हणजे “लोगॅरिथम” हा विषय. समीकरणांच्या गुणधर्मांचा अभ्यास केल्यावर लगेचच त्यांची उदाहरणे आणि उपाय आपण खाली पाहू. आता असमानता कशा दिसतात आणि त्यांना समीकरणांमधून कसे वेगळे करायचे ते पाहू.

खालील अभिव्यक्ती दिली आहे: लॉग 2 (x-1) > 3 - ही लॉगरिदमिक असमानता आहे, कारण अज्ञात मूल्य "x" लॉगरिदमिक चिन्हाखाली आहे. आणि अभिव्यक्तीमध्ये देखील दोन प्रमाणांची तुलना केली जाते: इच्छित संख्येचा बेस दोनचा लॉगरिदम क्रमांक तीनपेक्षा मोठा आहे.

लॉगरिदमिक समीकरणे आणि असमानता यांच्यातील सर्वात महत्त्वाचा फरक म्हणजे लॉगरिदमसह समीकरणे (उदाहरणार्थ, लॉगरिदम 2 x = √9) उत्तरात एक किंवा अधिक विशिष्ट संख्यात्मक मूल्ये दर्शवतात, तर असमानता सोडवताना, दोन्ही स्वीकार्य श्रेणी मूल्ये आणि बिंदू हे कार्य खंडित करून निर्धारित केले जातात. परिणामी, उत्तर हे समीकरणाच्या उत्तराप्रमाणे वैयक्तिक संख्यांचा साधा संच नसून सतत मालिका किंवा संख्यांचा संच आहे.

लॉगरिदम बद्दल मूलभूत प्रमेये

लॉगरिथमची मूल्ये शोधण्याची आदिम कार्ये सोडवताना, त्याचे गुणधर्म ज्ञात नसतील. तथापि, जेव्हा लॉगरिदमिक समीकरणे किंवा असमानता येतात, तेव्हा सर्व प्रथम, लॉगरिदमचे सर्व मूलभूत गुणधर्म स्पष्टपणे समजून घेणे आणि व्यवहारात लागू करणे आवश्यक आहे. आपण समीकरणांची उदाहरणे नंतर पाहू; प्रथम प्रत्येक गुणधर्म अधिक तपशीलाने पाहू.

1. मुख्य ओळख यासारखी दिसते: a logaB =B. हे फक्त तेव्हाच लागू होते जेव्हा a 0 पेक्षा मोठा असतो, एकाच्या बरोबरीचा नसतो आणि B शून्यापेक्षा मोठा असतो.
2. उत्पादनाचा लॉगरिथम खालील सूत्रामध्ये दर्शविला जाऊ शकतो: लॉग d (s 1 * s 2) = log d s 1 + log d s 2. या प्रकरणात, अनिवार्य अट आहे: d, s 1 आणि s 2 > 0; a≠1. तुम्ही उदाहरणे आणि सोल्यूशनसह या लॉगरिदमिक सूत्रासाठी पुरावा देऊ शकता. लॉग a s 1 = f 1 आणि log a s 2 = f 2, नंतर a f1 = s 1, a f2 = s 2. आम्हाला मिळते की s 1 * s 2 = a f1 *a f2 = a f1+f2 (चे गुणधर्म अंश ), आणि नंतर व्याख्येनुसार: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, जे सिद्ध करणे आवश्यक आहे.
3. भागाचे लॉगरिदम असे दिसते: log a (s 1/s 2) = log a s 1 - log a s 2.
4. सूत्राच्या स्वरुपातील प्रमेय खालील फॉर्म घेते: लॉग a q b n = n/q log a b.

या सूत्राला "लोगॅरिथमच्या अंशाची मालमत्ता" असे म्हणतात. हे सामान्य अंशांच्या गुणधर्मांसारखे आहे आणि हे आश्चर्यकारक नाही, कारण सर्व गणित नैसर्गिक पोस्ट्युलेट्सवर आधारित आहे. चला पुरावा पाहू.

लॉग a b = t करू द्या, ते t = b निघेल. जर आपण दोन्ही भागांना m पॉवर वर वाढवले: a tn = b n ;

पण a tn = (a q) nt/q = b n असल्याने, म्हणून a q b n = (n*t)/t लॉग करा, नंतर a q b n = n/q लॉग a b ला लॉग करा. प्रमेय सिद्ध झाले आहे.

समस्या आणि असमानतेची उदाहरणे

लॉगरिदमवरील समस्यांचे सर्वात सामान्य प्रकार म्हणजे समीकरणे आणि असमानतेची उदाहरणे. ते जवळजवळ सर्व समस्यांच्या पुस्तकांमध्ये आढळतात आणि ते गणिताच्या परीक्षांचा आवश्यक भाग देखील आहेत. विद्यापीठात प्रवेश करण्यासाठी किंवा गणितातील प्रवेश परीक्षा उत्तीर्ण करण्यासाठी, आपल्याला अशी कार्ये योग्यरित्या कशी सोडवायची हे माहित असणे आवश्यक आहे.

दुर्दैवाने, लॉगरिदमचे अज्ञात मूल्य सोडवण्यासाठी आणि निर्धारित करण्यासाठी कोणतीही एक योजना किंवा योजना नाही, परंतु प्रत्येक गणितीय असमानता किंवा लॉगरिदमिक समीकरणासाठी काही नियम लागू केले जाऊ शकतात. सर्व प्रथम, आपण अभिव्यक्ती सरलीकृत किंवा सामान्य स्वरूपात कमी केली जाऊ शकते की नाही हे शोधले पाहिजे. जर तुम्ही त्यांचे गुणधर्म योग्यरित्या वापरत असाल तर तुम्ही लांब लॉगरिदमिक अभिव्यक्ती सुलभ करू शकता. चला त्यांना लवकर ओळखू या.

लॉगरिदमिक समीकरणे सोडवताना, आपण कोणत्या प्रकारचे लॉगरिदम आहे हे निर्धारित केले पाहिजे: उदाहरणाच्या अभिव्यक्तीमध्ये नैसर्गिक लॉगरिथम किंवा दशांश असू शकतात.

येथे ln100, ln1026 उदाहरणे आहेत. त्यांचे समाधान या वस्तुस्थितीवर उकळते की त्यांना बेस 10 अनुक्रमे 100 आणि 1026 च्या बरोबरीची शक्ती निश्चित करणे आवश्यक आहे. नैसर्गिक लॉगरिदम सोडवण्यासाठी, तुम्हाला लॉगरिदमिक ओळख किंवा त्यांचे गुणधर्म लागू करणे आवश्यक आहे. विविध प्रकारच्या लॉगरिदमिक समस्या सोडवण्याची उदाहरणे पाहू.

लॉगरिदम सूत्र कसे वापरावे: उदाहरणे आणि उपायांसह

तर, लॉगरिदम बद्दल मूलभूत प्रमेय वापरण्याची उदाहरणे पाहू.

1. उत्पादनाच्या लॉगरिदमचा गुणधर्म अशा कार्यांमध्ये वापरला जाऊ शकतो जेथे b संख्याचे मोठ्या मूल्याचे सोप्या घटकांमध्ये विघटन करणे आवश्यक आहे. उदाहरणार्थ, लॉग 2 4 + लॉग 2 128 = लॉग 2 (4*128) = लॉग 2 512. उत्तर 9 आहे.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1.5 - जसे आपण पाहू शकता, लॉगरिदम पॉवरच्या चौथ्या गुणधर्माचा वापर करून, आम्ही एक जटिल आणि न सोडवता येणारी अभिव्यक्ती सोडवण्यात व्यवस्थापित केले. तुम्हाला फक्त बेस फॅक्टर करणे आवश्यक आहे आणि नंतर लॉगरिदमच्या चिन्हातून घातांक मूल्ये काढणे आवश्यक आहे.

युनिफाइड स्टेट परीक्षेतील असाइनमेंट

लॉगरिदम बहुतेकदा प्रवेश परीक्षांमध्ये आढळतात, विशेषत: युनिफाइड स्टेट परीक्षा (सर्व शालेय पदवीधरांसाठी राज्य परीक्षा) मध्ये अनेक लॉगरिदमिक समस्या. सामान्यतः, ही कार्ये केवळ भाग A (परीक्षेतील सर्वात सोपा चाचणी भाग) मध्येच नसतात तर भाग C (सर्वात जटिल आणि विपुल कार्ये) मध्ये देखील उपस्थित असतात. परीक्षेसाठी “नैसर्गिक लॉगरिदम” या विषयाचे अचूक आणि परिपूर्ण ज्ञान आवश्यक आहे.

युनिफाइड स्टेट परीक्षेच्या अधिकृत आवृत्त्यांमधून उदाहरणे आणि समस्यांचे निराकरण केले जाते. अशी कार्ये कशी सोडवली जातात ते पाहूया.

दिलेला लॉग 2 (2x-1) = 4. उपाय:
चला अभिव्यक्ती पुन्हा लिहू, थोडेसे लॉग 2 (2x-1) = 2 2 सोपे करून, लॉगरिदमच्या व्याख्येनुसार आपल्याला 2x-1 = 2 4 मिळेल, म्हणून 2x = 17; x = 8.5.

• सर्व लॉगरिदम समान बेसवर कमी करणे चांगले आहे जेणेकरून समाधान अवजड आणि गोंधळात टाकणार नाही.
• लॉगरिदम चिन्हाखालील सर्व अभिव्यक्ती सकारात्मक म्हणून दर्शविल्या जातात, म्हणून जेव्हा लॉगरिथम चिन्हाखाली असलेल्या अभिव्यक्तीचा घातांक आणि त्याचा आधार गुणक म्हणून काढला जातो, तेव्हा लॉगरिदम अंतर्गत उरलेली अभिव्यक्ती सकारात्मक असणे आवश्यक आहे.