රවුමක හරස්කඩ ප්රදේශය සඳහා සූත්රය. කව ප්රදේශය: සූත්රය
උපදෙස්
රවුමක දන්නා ප්රදේශයෙන් අරය සොයා ගැනීමට pi භාවිතා කරන්න. මෙම නියතය රවුමක විෂ්කම්භය සහ එහි මායිමේ දිග (රවුම) අතර අනුපාතය නියම කරයි. රවුමක පරිධිය යනු එහි ආධාරයෙන් ආවරණය කළ හැකි තලයේ උපරිම ප්රදේශය වන අතර විෂ්කම්භය අරය දෙකකට සමාන වේ, එබැවින් අරය ඇති ප්රදේශය ද හැකි අනුපාතයකින් එකිනෙකා සමඟ සහසම්බන්ධ වේ. Pi අනුව ප්රකාශ කළ හැක. මෙම නියතය (π) වෘත්තයේ වර්ගඵලය (S) සහ වර්ග අරය (r) ලෙස අර්ථ දැක්වේ. මින් පහත දැක්වෙන්නේ අරය Pi: r=√(S/π) අංකයෙන් ප්රදේශය බෙදීමේ ප්රමාණයේ වර්ගමූලය ලෙස ප්රකාශ කළ හැකි බවයි.
පුරාණ ලෝකයේ වඩාත්ම ප්රසිද්ධ පුස්තකාලය වන ඇලෙක්සැන්ඩ්රියාවේ පුස්තකාලයේ දිගු කලක් එරාස්ටෝෆෙන් ප්රධානියා විය. ඔහු අපේ ග්රහලෝකයේ ප්රමාණය ගණනය කළ කාරණයට අමතරව, ඔහු වැදගත් සොයාගැනීම් සහ සොයාගැනීම් ගණනාවක් සිදු කළේය. ප්රථමික සංඛ්යා නිර්ණය කිරීම සඳහා සරල ක්රමයක් සොයා ගන්නා ලදී, දැන් එය "Erastothenes' sieve" ලෙස හැඳින්වේ.
ඔහු "ලෝක සිතියමක්" ඇද, පුරාණ ග්රීකයන්ට එකල දන්නා ලෝකයේ සියලුම ප්රදේශ පෙන්වීය. සිතියම එහි කාලය සඳහා හොඳම එකක් ලෙස සැලකේ. ඔහු දේශාංශ සහ අක්ෂාංශ පද්ධතියක් සහ අධික වර්ෂ ඇතුළත් දින දර්ශනයක් නිර්මාණය කළේය. ආමිලරි ගෝලය සොයා ගන්නා ලදී, මුල් තාරකා විද්යාඥයින් විසින් අහසේ තරු වල පෙනෙන චලනය ප්රදර්ශනය කිරීමට සහ පුරෝකථනය කිරීමට භාවිතා කරන ලද යාන්ත්රික උපකරණයකි. ඔහු තරු 675 ක් ඇතුළත් තරු නාමාවලියක් ද සම්පාදනය කළේය.
මූලාශ්ර:
- ග්රීක විද්යාඥයෙකු වූ සයිරේන්හි එරතොස්තනීස් ලොව ප්රථම වරට පෘථිවියේ අරය ගණනය කළේය.
- Eratosthenes "පෘථිවි ගණනය" වට ප්රමාණය
- එරතොස්තනීස්
- මෙය පැතලි රූපයක් වන අතර එය මධ්යයේ සිට සමාන දුරින් පිහිටි ලක්ෂ්ය සමූහයකි. ඒවා සියල්ලම එකම දුරින් පිහිටා ඇති අතර රවුමක් සාදයි.
රවුමක කේන්ද්රය එහි වට ප්රමාණයේ ලක්ෂ්ය සමඟ සම්බන්ධ කරන රේඛා ඛණ්ඩයක් ලෙස හැඳින්වේ අරය. සෑම රවුමකම, සියලු අරය එකිනෙකට සමාන වේ. රවුමක ලක්ෂ්ය දෙකක් සම්බන්ධ කර කේන්ද්රය හරහා ගමන් කරන රේඛාවක් ලෙස හැඳින්වේ විෂ්කම්භය. වෘත්තයක ප්රදේශය සඳහා වන සූත්රය ගණනය කරනු ලබන්නේ ගණිතමය නියතයක් භාවිතා කරමිනි - අංකය π ..
මෙය සිත්ගන්නා සුළුය : pi අංකය. රවුමක වට ප්රමාණය එහි විෂ්කම්භයේ දිගට අනුපාතය වන අතර එය නියත අගයකි. 1737 දී L. Euler ගේ කාර්යයෙන් පසුව π = 3.1415926 අගය භාවිතා කරන ලදී.
රවුමක වර්ගඵලය නියත π භාවිතයෙන් ගණනය කළ හැක. සහ රවුමේ අරය. අරය අනුව රවුමක ප්රදේශය සඳහා වන සූත්රය මේ ආකාරයෙන් පෙනේ:
![]()
අරය භාවිතා කරමින් රවුමක වර්ගඵලය ගණනය කිරීමේ උදාහරණයක් සලකා බලන්න. R = 4 cm අරය සහිත කවයක් ලබා දෙන්න, අපි රූපයේ ප්රදේශය සොයා ගනිමු.
අපගේ රවුමේ ප්රදේශය වර්ග මීටර් 50.24 ට සමාන වේ. සෙමී.
සූත්රයක් තියෙනවා විෂ්කම්භය හරහා රවුමක ප්රදේශය. අවශ්ය පරාමිතීන් ගණනය කිරීම සඳහා ද එය බහුලව භාවිතා වේ. මෙම සූත්ර සොයා ගැනීමට භාවිතා කළ හැක.

විෂ්කම්භය හරහා රවුමක ප්රදේශය ගණනය කිරීමේ උදාහරණයක් සලකා බලන්න, එහි අරය දැන ගන්න. R = 4 cm අරයක් සහිත කවයක් ලබා දෙමු, පළමුව, ඔබ දන්නා පරිදි, අරය මෙන් දෙගුණයක් වන විෂ්කම්භය සොයා ගනිමු.
දැන් අපි ඉහත සූත්රය භාවිතා කරමින් රවුමක ප්රදේශය ගණනය කිරීමේ උදාහරණය සඳහා දත්ත භාවිතා කරමු:
ඔබට පෙනෙන පරිදි, එහි ප්රතිඵලයක් වශයෙන් පළමු ගණනය කිරීම්වලදී සමාන පිළිතුරක් අපට ලැබේ.
රවුමක ප්රදේශය ගණනය කිරීම සඳහා සම්මත සූත්ර පිළිබඳ දැනුම අනාගතයේදී පහසුවෙන් තීරණය කිරීමට උපකාරී වේ. අංශ ප්රදේශයසහ නැතිවූ ප්රමාණයන් සොයා ගැනීම පහසුය.
රවුමක ප්රදේශය සඳහා වන සූත්රය ගණනය කරනු ලබන්නේ නියත අගය වන π සහ රවුමේ අරයේ වර්ගඵලය හරහා බව අපි දැනටමත් දනිමු. අරය රවුමක පරිධිය අනුව ප්රකාශ කළ හැකි අතර වට ප්රමාණය අනුව රවුමක ප්රදේශය සඳහා සූත්රයේ ප්රකාශනය ආදේශ කරන්න:
දැන් අපි මෙම සමානාත්මතාවය රවුමක වර්ගඵලය ගණනය කිරීමේ සූත්රයට ආදේශ කර වට ප්රමාණය හරහා රවුමේ ප්රදේශය සොයා ගැනීමේ සූත්රය ලබා ගනිමු.

වට ප්රමාණය හරහා රවුමක ප්රදේශය ගණනය කිරීමේ උදාහරණයක් සලකා බලන්න. දිග l = 8 cm සහිත කවයක් ලබා දෙමු. ව්යුත්පන්න සූත්රයේ අගය ආදේශ කරමු: 
රවුමේ මුළු ප්රදේශය වර්ග මීටර් 5 ක් වනු ඇත. සෙමී.
චතුරස්රයක් වටා වට කර ඇති රවුමක ප්රදේශය

චතුරස්රයක් වටා වට කර ඇති රවුමක ප්රදේශය සොයා ගැනීම ඉතා පහසුය.
මේ සඳහා අවශ්ය වන්නේ චතුරස්රයේ පැත්ත සහ සරල සූත්ර පිළිබඳ දැනුම පමණි. චතුරස්රයේ විකර්ණය වටකුරු රවුමේ විකර්ණයට සමාන වේ. A පැත්ත දැන ගැනීම, එය පයිතගරස් ප්රමේයය භාවිතයෙන් සොයාගත හැකිය: මෙතැන් සිට.
විකර්ණය සොයාගත් පසු, අපට අරය ගණනය කළ හැකිය: .
ඉන්පසුව අපි චතුරස්රයක් වටා වට කර ඇති රවුමක ප්රදේශය සඳහා මූලික සූත්රය තුළට සියල්ල ආදේශ කරමු:
වෘත්තයක් යනු මධ්යයේ සිට එකම දුරින් ඇති බොහෝ ලක්ෂ්යවල දෘශ්ය එකතුවකි. එහි ප්රදේශය සොයා ගැනීමට, ඔබ අරය, විෂ්කම්භය, π අංකය සහ පරිධිය යනු කුමක්දැයි දැනගත යුතුය.
රවුමක ප්රදේශය ගණනය කිරීමට සම්බන්ධ ප්රමාණ
රවුමේ කේන්ද්රීය ලක්ෂ්යයෙන් සහ රවුමේ ඕනෑම ලක්ෂ්යයකින් සීමා වූ දුර මෙම ජ්යාමිතික රූපයේ අරය ලෙස හැඳින්වේ. එක් කවයක සියලුම අරයවල දිග සමාන වේ. කේන්ද්ර ලක්ෂ්යය හරහා ගමන් කරන රවුමේ ඕනෑම ලක්ෂ්ය 2ක් අතර රේඛා ඛණ්ඩය විෂ්කම්භය ලෙස හැඳින්වේ. විෂ්කම්භයේ දිග අරයේ දිග 2 න් ගුණ කළ විට සමාන වේ.
රවුමක වර්ගඵලය ගණනය කිරීම සඳහා, π අංකයේ අගය භාවිතා වේ. මෙම අගය රවුමේ විෂ්කම්භයේ දිගට පරිධියේ අනුපාතයට සමාන වන අතර නියත අගයක් ඇත. Π = 3.1415926. පරිධිය ගණනය කරනු ලබන්නේ L=2πR සූත්රය භාවිතා කරමිනි.
අරය භාවිතයෙන් රවුමක ප්රදේශය සොයන්න
එබැවින්, රවුමක වර්ගඵලය π අංකයේ ගුණිතයට සමාන වන අතර රවුමේ අරය 2 වන බලයට ඔසවා ඇත. උදාහරණයක් ලෙස, අපි රවුමේ අරයේ දිග සෙන්ටිමීටර 5 ට සමාන කරමු, එවිට S වෘත්තයේ වර්ගඵලය වර්ග මීටර් 3.14 * 5 ^ 2 = 78.5 ට සමාන වේ. සෙමී.


විෂ්කම්භය අනුව රවුම් ප්රදේශය
රවුමක ප්රදේශය ද රවුමේ විෂ්කම්භය දැන ගැනීමෙන් ගණනය කළ හැක. මෙම අවස්ථාවේදී, S = (π/4)*d^2, මෙහි d යනු රවුමේ විෂ්කම්භය වේ. අරය 5 cm වන උදාහරණයම ගනිමු.එවිට එහි විෂ්කම්භය 5*2=10 cm වේ.රවුමේ වර්ගඵලය S=3.14/4*10^2=78.5 sq.cm වේ. පළමු උදාහරණයේ ගණනය කිරීම් වල එකතුවට සමාන ප්රතිඵලය, අවස්ථා දෙකෙහිම ගණනය කිරීම් වල නිවැරදි බව තහවුරු කරයි.


වට ප්රමාණය අනුව රවුමක ප්රදේශය
රවුමක අරය වට ප්රමාණය හරහා නිරූපණය කරන්නේ නම්, එම සූත්රය මේ ආකාරයෙන් පෙනෙනු ඇත: R=(L/2)π. මෙම ප්රකාශනය රවුමක ප්රදේශය සඳහා සූත්රයට ආදේශ කරන්න, එහි ප්රතිඵලයක් ලෙස අපට S=(L^2)/4π ලැබේ. වට ප්රමාණය සෙන්ටිමීටර 10 ක් වන උදාහරණයක් සලකා බලන්න, එවිට රවුමේ වර්ගඵලය S = (10 ^ 2) / 4 * 3.14 = 7.96 වර්ග මීටර් වේ. සෙමී.
කොටා ඇති චතුරස්රයක පැත්තක දිග අනුව රවුමක ප්රදේශය
චතුරස්රයක් රවුමක කොටා ඇත්නම්, රවුමේ විෂ්කම්භයේ දිග චතුරස්රයේ විකර්ණයේ දිගට සමාන වේ. චතුරස්රයේ පැත්තේ ප්රමාණය දැන ගැනීමෙන්, ඔබට පහසුවෙන් රවුමේ විෂ්කම්භය සූත්රය මගින් සොයාගත හැකිය: d ^ 2 \u003d 2a ^ 2. වෙනත් වචන වලින් කිවහොත්, 2 හි බලයට විෂ්කම්භය චතුරස්රයේ පැත්තට 2 ගුණයක බලයට සමාන වේ.
රවුමක විෂ්කම්භයේ දිගේ අගය ගණනය කිරීමෙන් ඔබට එහි අරය ද සොයාගත හැකිය, ඉන්පසු රවුමක ප්රදේශය තීරණය කිරීම සඳහා සූත්ර වලින් එකක් භාවිතා කරන්න.
රවුමක අංශ ප්රදේශය
අංශයක් යනු අරය 2 කින් සහ ඒවා අතර චාපයකින් සීමා වූ රවුමක කොටසකි. එහි ප්රදේශය සොයා ගැනීම සඳහා, ඔබ අංශයේ කෝණය මැනිය යුතුය. ඊට පසු, භාගයක් රචනා කිරීම අවශ්ය වේ, එහි අංශයේ කෝණයේ අගය ඇති සංඛ්යාවේ සහ හරය තුළ - 360. අංශයේ ප්රදේශය ගණනය කිරීම සඳහා, අගය භාගය බෙදීමේ ප්රති result ලයක් ලෙස ලබාගත් ඉහත සූත්රවලින් එකක් භාවිතා කර ගණනය කරන ලද රවුමේ ප්රදේශයෙන් ගුණ කළ යුතුය.


කවයන් සඳහා වඩාත් ප්රවේශම් සහගත ප්රවේශයක් අවශ්ය වන අතර B5 කාර්යයන්හි බහුලව දක්නට නොලැබේ. ඒ අතරම, සාමාන්ය විසඳුම් යෝජනා ක්රමය බහුඅස්රවලට වඩා සරල ය (“ඛණ්ඩාංක ජාලයක බහුඅස්ර ප්රදේශ” පාඩම බලන්න).
එවැනි කාර්යයන් වලදී අවශ්ය වන්නේ R රවුමේ අරය සොයා ගැනීමයි. එවිට ඔබට S = πR 2 සූත්රය භාවිතා කර රවුමේ ප්රදේශය ගණනය කළ හැකිය. විසඳුම සඳහා R 2 සොයා ගැනීම ප්රමාණවත් බව මෙම සූත්රයෙන් ද අනුගමනය කරයි.
දක්වා ඇති අගයන් සොයා ගැනීම සඳහා, රවුමේ ජාලක රේඛාවල මංසන්ධියේ ඇති ලක්ෂ්යයක් දැක්වීම ප්රමාණවත් වේ. ඉන්පසු පයිතගරස් ප්රමේයය භාවිතා කරන්න. අරය ගණනය කිරීමේ නිශ්චිත උදාහරණ සලකා බලන්න:
කාර්යයක්. රූපයේ දැක්වෙන කව තුනේ අරය සොයන්න:
එක් එක් කවය තුළ අතිරේක ඉදිකිරීම් සිදු කරමු:
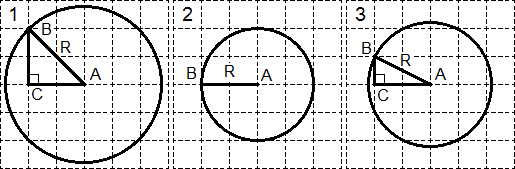
සෑම අවස්ථාවකම B ලක්ෂ්යය ජාල රේඛාවල මංසන්ධියේ වැතිරීමට රවුම මත තෝරා ගනු ලැබේ. 1 සහ 3 කව වල C ලක්ෂ්යය නිවැරදි ත්රිකෝණයකට රූපය සම්පූර්ණ කරයි. අරය සොයා ගැනීමට ඉතිරිව ඇත:
පළමු කවයේ ABC ත්රිකෝණය සලකා බලන්න. පයිතගරස් ප්රමේයය අනුව: R 2 \u003d AB 2 \u003d AC 2 + BC 2 \u003d 2 2 + 2 2 \u003d 8.
දෙවන කවය සඳහා, සියල්ල පැහැදිලිය: R = AB = 2.
තෙවන නඩුව පළමු එකට සමාන වේ. පයිතගරස් ප්රමේයය අනුව ABC ත්රිකෝණයෙන්: R 2 \u003d AB 2 \u003d AC 2 + BC 2 \u003d 1 2 + 2 2 \u003d 5.
දැන් අපි රවුමක අරය (හෝ අඩුම තරමින් එහි වර්ග) සොයා ගන්නේ කෙසේදැයි දනිමු. එබැවින්, අපට ප්රදේශය සොයාගත හැකිය. සමස්ත කවයම නොව අංශයක ප්රදේශය සොයා ගැනීමට අවශ්ය කාර්යයන් තිබේ. එවැනි අවස්ථාවන්හිදී, මෙම අංශයේ රවුමේ කොටස කුමක්දැයි සොයා ගැනීමට පහසු වන අතර, එමගින් ප්රදේශය සොයා ගන්න.
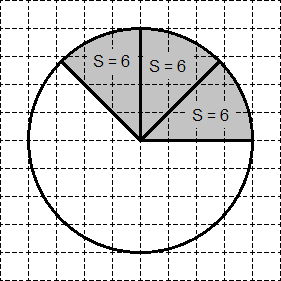
කාර්යයක්. සෙවන ලද අංශයේ S ප්රදේශය සොයා ගන්න. ඔබේ පිළිතුරේ S / π සඳහන් කරන්න.
පැහැදිලිවම, අංශය රවුමෙන් හතරෙන් එකකි. එබැවින්, රවුමේ S = 0.25 S.
රවුමේ S සොයා ගැනීමට එය ඉතිරිව ඇත - රවුමේ ප්රදේශය. මෙය සිදු කිරීම සඳහා, අපි අතිරේක ඉදිකිරීමක් සිදු කරන්නෙමු:
ABC ත්රිකෝණය ඍජු ත්රිකෝණයකි. පයිතගරස් ප්රමේයය අනුව, අපට ඇත්තේ: R 2 \u003d AB 2 \u003d AC 2 + BC 2 \u003d 2 2 + 2 2 \u003d 8.
දැන් අපි රවුමේ සහ අංශයේ ප්රදේශය සොයා ගනිමු: රවුමේ S = πR 2 = 8π; S = 0.25 S කවය = 2π.
අවසාන වශයෙන්, අපේක්ෂිත අගය S /π = 2 ට සමාන වේ.
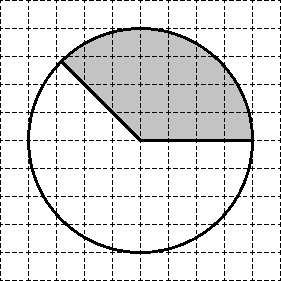
නොදන්නා අරය සහිත අංශ ප්රදේශය
මෙය සම්පූර්ණයෙන්ම නව ආකාරයේ කාර්යයකි, 2010-2011 දී එවැනි කිසිවක් නොතිබුණි. කොන්දේසිය අනුව, අපට යම් ප්රදේශයක කවයක් ලබා දී ඇත (එනම්, ප්රදේශය, අරය නොවේ!). එවිට, මෙම කවය තුළ, අංශයක් වෙන් කරනු ලැබේ, එහි ප්රදේශය සොයා ගැනීමට අවශ්ය වේ.
ශුභාරංචිය නම්, ගණිතයේ විභාගයේ ඇති චතුරස්රයේ ඇති සියලුම ගැටළු වලින් මෙම ගැටළු පහසුම වීමයි. මීට අමතරව, රවුම සහ අංශය සෑම විටම සම්බන්ධීකරණ ජාලය මත තබා ඇත. එමනිසා, එවැනි ගැටළු විසඳන්නේ කෙසේදැයි ඉගෙන ගැනීමට, පින්තූරය දෙස බලන්න:
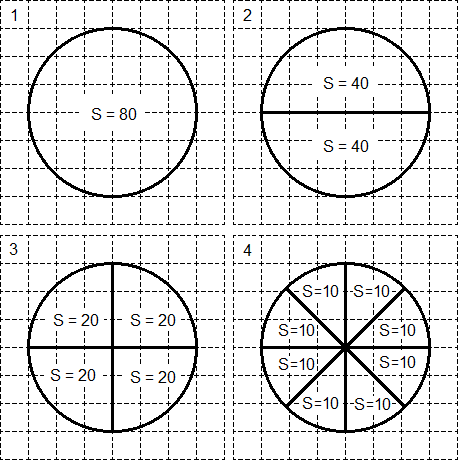
මුල් කවයට රවුමේ S ප්රදේශය = 80 ට ඉඩ දෙන්න. එවිට එය S = 40 බැගින් වූ ප්රදේශ දෙකකට බෙදිය හැකිය (පියවර 2 බලන්න). ඒ හා සමානව, මෙම සෑම "අර්ධ" අංශයක්ම නැවත අඩකට බෙදිය හැකිය - අපට S = 20 බැගින් වූ අංශ හතරක් ලැබේ (පියවර 3 බලන්න). අවසාන වශයෙන්, ඔබට මෙම එක් එක් අංශය තවත් දෙකකට බෙදිය හැකිය - අපට අංශ 8 ක් ලැබේ - "කුඩා කෑලි". මෙම එක් එක් "කුට්ටි" ප්රදේශය S = 10 වේ.
කරුණාකර සටහන් කර ගන්න: ගණිතයේ කිසිදු USE කාර්යයක කුඩා බෙදීමක් නොමැත! මේ අනුව, B-3 ගැටළුව විසඳීම සඳහා ඇල්ගොරිතම පහත පරිදි වේ:
- මුල් කවය අංශ 8 කට කපන්න - "කෑලි". ඒවායින් එක් එක් ප්රදේශය මුළු රවුමේ ප්රදේශයෙන් හරියටම 1/8 කි. උදාහරණයක් ලෙස, කොන්දේසිය අනුව රවුමට රවුමේ S ප්රදේශය = 240 තිබේ නම්, "පට්ටි" වල S = 240: 8 = 30;
- ඔබට සොයා ගැනීමට අවශ්ය ප්රදේශයේ මුල් අංශයට "ගැටිති" කීයක් ගැලපේදැයි සොයා බලන්න. උදාහරණයක් ලෙස, අපගේ අංශයේ 30 ක වපසරියක් සහිත "පට්ටි" 3 ක් අඩංගු නම්, අපේක්ෂිත අංශයේ ප්රදේශය S = 3 30 = 90 වේ. මෙය පිළිතුර වනු ඇත.
එච්චරයි! ගැටළුව ප්රායෝගිකව වාචිකව විසඳනු ලැබේ. ඔබට තවමත් යමක් තේරෙන්නේ නැත්නම්, පීසා එකක් මිල දී ගෙන එය කොටස් 8 කට කපා ගන්න. එවැනි සෑම කැබැල්ලක්ම එකම අංශයක් වනු ඇත - විශාල කැබලිවලට ඒකාබද්ධ කළ හැකි "කුට්ටිය".
දැන් අපි අත්හදා බැලීමේ විභාගයේ උදාහරණ දෙස බලමු:
කාර්යයක්. 40 ක වපසරියකින් යුත් කවයක් පිරික්සුම් කඩදාසි මත ඇඳ ඇත. සෙවන ලද රූපයේ ප්රදේශය සොයා ගන්න.
එබැවින්, රවුමේ ප්රදේශය 40. එය අංශ 8 කට බෙදන්න - එක් එක් ප්රදේශය S = 40: 5 = 8. අපට ලැබෙන්නේ:
නිසැකවම, සෙවන ලද අංශය හරියටම "කුඩා" අංශ දෙකකින් සමන්විත වේ. එබැවින්, එහි වර්ගඵලය 2 5 = 10. සම්පූර්ණ විසඳුම එයයි!
කාර්යයක්. 64 ක වපසරියකින් යුත් කවයක් පිරික්සුම් කඩදාසි මත ඇඳ ඇත. සෙවන ලද රූපයේ ප්රදේශය සොයා ගන්න.
නැවතත්, සම්පූර්ණ රවුම සමාන අංශ 8 කට බෙදන්න. නිසැකවම, ඔවුන්ගෙන් එක් ප්රදේශයක් සොයා ගැනීමට අවශ්ය වේ. එබැවින්, එහි ප්රදේශය S = 64: 8 = 8 වේ.
කාර්යයක්. 48 ක වපසරියකින් යුත් කවයක් පිරික්සුම් කඩදාසි මත ඇඳ ඇත. සෙවන ලද රූපයේ ප්රදේශය සොයා ගන්න.
නැවතත්, රවුම සමාන අංශ 8 කට බෙදන්න. ඒවායින් එක් එක් ප්රදේශය S = 48: 8 = 6 ට සමාන වේ. හරියටම අංශ තුනක් - "කුඩා" අපේක්ෂිත අංශයේ තබා ඇත (රූපය බලන්න). එබැවින්, අපේක්ෂිත අංශයේ ප්රදේශය 3 6 = 18 වේ.