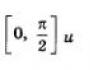Graf over funktionen y sin x. Funktionsgrafer

>>Matematik: Funktioner y = sin x, y = cos x, deres egenskaber og grafer

Funktioner y = sin x, y = cos x, deres egenskaber og grafer

I dette afsnit vil vi diskutere nogle egenskaber ved funktionerne y = sin x, y = cos x og konstruere deres grafer.

1. Funktion y = sin X.

Ovenfor har vi i § 20 formuleret en regel, der tillader, at hvert tal t kan forbindes med et cos t-tal, dvs. karakteriseret funktionen y = sin t. Lad os bemærke nogle af dens egenskaber.

Egenskaber for funktionen u = sin t.

Definitionsdomænet er mængden K af reelle tal.
Dette følger af, at ethvert tal 2 svarer til et punkt M(1) på talcirklen, som har en veldefineret ordinat; denne ordinat er cos t.

u = sin t er en ulige funktion.

Dette følger af, at der, som det blev bevist i § 19, for enhver t ligestillingen
Det betyder, at grafen for funktionen u = sin t, ligesom grafen for enhver ulige funktion, er symmetrisk med hensyn til oprindelsen i det rektangulære koordinatsystem tOi.

Funktionen u = sin t øges med intervallet
Dette følger af, at når et punkt bevæger sig langs den første fjerdedel af talcirklen, stiger ordinaten gradvist (fra 0 til 1 - se fig. 115), og når punktet bevæger sig langs den anden fjerdedel af talcirklen, vil den. ordinat falder gradvist (fra 1 til 0 - se fig. 116).

Funktionen u = sint er afgrænset både under og over. Dette følger af, at, som vi så i § 19, for enhver t gælder uligheden

(funktionen når denne værdi på et hvilket som helst tidspunkt i formen (funktionen når denne værdi på et hvilket som helst tidspunkt i formen
Ved hjælp af de opnåede egenskaber vil vi konstruere en graf over funktionen af ​​interesse for os. Men (opmærksomhed!) i stedet for u - sin t vil vi skrive y = sin x (vi er trods alt mere vant til at skrive y = f(x), og ikke u = f(t)). Det betyder, at vi bygger en graf i det sædvanlige xOy-koordinatsystem (og ikke tOy).

Lad os lave en tabel over værdierne af funktionen y - sin x:

Kommentar.

Lad os give en af ​​versionerne af oprindelsen af ​​udtrykket "sinus". På latin betyder sinus bøjning (buestreng).

Den konstruerede graf retfærdiggør til en vis grad denne terminologi.

Linjen, der fungerer som en graf for funktionen y = sin x, kaldes en sinusbølge. Den del af sinusoiden, der er vist i fig. 118 eller 119 kaldes en sinusbølge, og den del af sinusbølgen, der er vist i fig. 117, kaldes en halvbølge eller bue af en sinusbølge.

2. Funktion y = cos x.

Undersøgelsen af ​​funktionen y = cos x kunne udføres omtrent efter samme skema, som blev brugt ovenfor for funktionen y = sin x. Men vi vil vælge den vej, der fører til målet hurtigere. For det første vil vi bevise to formler, der er vigtige i sig selv (det vil du se i gymnasiet), men som for øjeblikket kun har en ekstra betydning for vores formål.

For enhver værdi af t er følgende ligheder gyldige:

Bevis. Lad tallet t svare til punktet M i den numeriske cirkel n, og tallet * + - punktet P (fig. 124; for nemheds skyld tog vi punktet M i første kvartal). Buerne AM og BP er lige store, og de retvinklede trekanter OKM og OLBP er tilsvarende lige store. Dette betyder O K = Ob, MK = Pb. Ud fra disse ligheder og fra placeringen af ​​trekanter OCM og OBP i koordinatsystemet drager vi to konklusioner:

1) ordinaten af ​​punktet P både i størrelse og fortegn falder sammen med abscissen af ​​punktet M; det betyder at

2) abscissen af ​​punktet P er lig i absolut værdi med ordinaten af ​​punktet M, men afviger i fortegn fra det; det betyder at

Tilnærmelsesvis samme ræsonnement føres i de tilfælde, hvor punkt M ikke hører til første kvartal.
Lad os bruge formlen (dette er formlen bevist ovenfor, men i stedet for variablen t bruger vi variablen x). Hvad giver denne formel os? Det giver os mulighed for at hævde, at funktionerne

er identiske, hvilket betyder, at deres grafer falder sammen.
Lad os plotte funktionen For at gøre dette, lad os gå videre til et hjælpekoordinatsystem med origo i et punkt (den stiplede linje er tegnet i fig. 125). Lad os binde funktionen y = sin x til det nye koordinatsystem - dette vil være grafen for funktionen (Fig. 125), dvs. graf for funktionen y - cos x. Den kaldes ligesom grafen for funktionen y = sin x en sinusbølge (hvilket er ret naturligt).

Egenskaber for funktionen y = cos x.

y = cos x er en lige funktion.

Byggestadierne er vist i fig. 126:

1) byg en graf af funktionen y = cos x (mere præcist en halvbølge);
2) ved at strække den konstruerede graf fra x-aksen med en faktor på 0,5 opnår vi en halvbølge af den nødvendige graf;
3) ved hjælp af den resulterende halvbølge konstruerer vi hele grafen for funktionen y = 0,5 cos x.

Fungerey = syndx

Grafen for funktionen er en sinusformet.

Den komplette ikke-gentagende del af en sinusbølge kaldes en sinusbølge.

En halv sinusbølge kaldes en halv sinusbølge (eller bue).

Funktionsegenskabery = syndx:

At tegne en funktion y= synd x Det er praktisk at bruge følgende skalaer:

På et ark papir med en firkant tager vi længden af ​​to firkanter som en segmentenhed.

På aksen x Lad os måle længden π. Samtidig præsenterer vi for nemheds skyld 3,14 i form af 3 - altså uden en brøkdel. Så på et ark papir i en celle vil π være 6 celler (tre gange 2 celler). Og hver celle vil modtage sit eget naturlige navn (fra den første til den sjette): π/6, π/3, π/2, 2π/3, 5π/6, π. Disse er betydningerne x.

På y-aksen markerer vi 1, som omfatter to celler.

Lad os oprette en tabel med funktionsværdier ved hjælp af vores værdier x:

Dernæst laver vi en tidsplan. Resultatet er en halvbølge, hvis højeste punkt er (π/2; 1). Dette er grafen for funktionen y= synd x på segmentet. Lad os tilføje en symmetrisk halvbølge til den konstruerede graf (symmetrisk i forhold til origo, dvs. på segmentet -π). Toppen af ​​denne halvbølge er under x-aksen med koordinater (-1; -1). Resultatet bliver en bølge. Dette er grafen for funktionen y= synd x på segmentet [-π; π].

Du kan fortsætte bølgen ved at konstruere den på segmentet [π; 3π], [π; 5π], [π; 7π], osv. På alle disse segmenter vil grafen for funktionen se ud som på segmentet [-π; π]. Du vil få en kontinuerlig bølget linje med identiske bølger.

Fungerey = cosx.

Grafen for en funktion er en sinusbølge (nogle gange kaldet en cosinusbølge).

Funktionsegenskabery = cosx:

Fungerey = mf(x).

Lad os tage den forrige funktion y=cos x. Som du allerede ved, er dens graf en sinusbølge. Hvis vi gange cosinus af denne funktion med et vist tal m, vil bølgen udvide sig fra aksen x(eller vil krympe, afhængig af værdien af ​​m).
Denne nye bølge vil være grafen for funktionen y = mf(x), hvor m er et hvilket som helst reelt tal.

Således er funktionen y = mf(x) den velkendte funktion y = f(x) ganget med m.

Hvism< 1, то синусоида сжимается к оси x ved koefficientenm. Hvism > 1, så strækkes sinusoiden fra aksenx ved koefficientenm.

Når du udfører strækning eller kompression, kan du først plotte kun en halv-bølge af en sinusbølge og derefter fuldføre hele grafen.

Fungerey = f(kx).

Hvis funktionen y =mf(x) fører til strækning af sinusoiden fra aksen x eller kompression mod aksen x, så fører funktionen y = f(kx) til strækning fra aksen y eller kompression mod aksen y.

Desuden er k et hvilket som helst reelt tal.

Ved 0< k< 1 синусоида растягивается от оси y ved koefficientenk. Hvisk > 1, så komprimeres sinusoiden mod akseny ved koefficientenk.

Når du tegner grafen for denne funktion, kan du først bygge en halvbølge af en sinusbølge og derefter bruge den til at færdiggøre hele grafen.

Fungerey = tgx.

Funktionsgraf y= tg x er en tangent.

Det er nok at konstruere en del af grafen i intervallet fra 0 til π/2, og så kan man symmetrisk fortsætte den i intervallet fra 0 til 3π/2.

Funktionsegenskabery = tgx:

Fungerey = ctgx

Funktionsgraf y=ctg x er også en tangentoid (det kaldes nogle gange en cotangentoid).

Funktionsegenskabery = ctgx:

Tilbage frem

Opmærksomhed! Forhåndsvisninger af dias er kun til informationsformål og repræsenterer muligvis ikke alle funktionerne i præsentationen. Hvis du er interesseret i dette arbejde, bedes du downloade den fulde version.

Jern ruster uden at finde nogen brug,
stående vand rådner eller fryser i kulden,
og en persons sind, der ikke finder nogen brug for sig selv, sygner hen.
Leonardo Da Vinci

Anvendte teknologier: problembaseret læring, kritisk tænkning, kommunikativ kommunikation.

Mål:

• Udvikling af kognitiv interesse for læring.
• At studere egenskaberne for funktionen y = sin x.
• Dannelse af praktiske færdigheder i at konstruere en graf over funktionen y = sin x ud fra det undersøgte teoretiske materiale.

Opgaver:

1. Brug det eksisterende potentiale for viden om egenskaberne ved funktionen y = sin x i specifikke situationer.

2. Anvende bevidst etablering af sammenhænge mellem analytiske og geometriske modeller af funktionen y = sin x.

Udvikle initiativ, en vis vilje og interesse for at finde en løsning; evnen til at træffe beslutninger, ikke stoppe der, og forsvare dit synspunkt.

At fremme kognitiv aktivitet hos eleverne, ansvarsfølelse, respekt for hinanden, gensidig forståelse, gensidig støtte og selvtillid; kommunikationskultur.

Under timerne

Scene 1. Opdatering af grundlæggende viden, motiverende indlæring af nyt materiale

"Gå ind i lektionen."

Der er skrevet 3 udtalelser på tavlen:

1. Den trigonometriske ligning sin t = a har altid løsninger.
2. Grafen for en ulige funktion kan konstrueres ved hjælp af en symmetritransformation om Oy-aksen.
3. En trigonometrisk funktion kan tegnes ved hjælp af en primær halvbølge.

Eleverne diskuterer i par: er udsagnene sande? (1 minut). Resultaterne af den indledende diskussion (ja, nej) indtastes derefter i tabellen i kolonnen "Før".

Læreren sætter mål og mål for lektionen.

2. Opdatering af viden (frontalt på en model af en trigonometrisk cirkel).

Vi har allerede stiftet bekendtskab med funktionen s = sin t.

1) Hvilke værdier kan variablen t tage. Hvad er omfanget af denne funktion?

2) I hvilket interval er værdierne af udtrykket sin t indeholdt? Find den største og mindste værdi af funktionen s = sin t.

3) Løs ligningen sin t = 0.

4) Hvad sker der med ordinaten af ​​et punkt, når det bevæger sig langs det første kvarter? (ordinaten stiger). Hvad sker der med ordinaten af ​​et punkt, når det bevæger sig i andet kvartal? (ordinaten falder gradvist). Hvordan hænger dette sammen med funktionens monotoni? (funktionen s = sin t stiger på segmentet og falder på segmentet ).

5) Lad os skrive funktionen s = sin t i formen y = sin x, der er kendt for os (vi vil konstruere den i det sædvanlige xOy-koordinatsystem) og kompilere en tabel med værdierne for denne funktion.

Etape 2. Perception, forståelse, primær konsolidering, ufrivillig memorering

Etape 4. Primær systematisering af viden og aktivitetsmetoder, deres overførsel og anvendelse i nye situationer

6. Nr. 10.18 (b,c)

Etape 5. Afsluttende kontrol, rettelse, vurdering og selvevaluering

7. Vi vender tilbage til udsagn (begyndelsen af ​​lektionen), diskuterer ved hjælp af egenskaberne for den trigonometriske funktion y = sin x, og udfylder kolonnen "Efter" i tabellen.

8. D/z: paragraf 10, nr. 10.7(a), 10.8(b), 10.11(b), 10.16(a)

For at bruge præsentationseksempler skal du oprette en Google-konto og logge ind på den: https://accounts.google.com

Slide billedtekster:

Funktioner y = sin x og y = cos x og deres grafer (medfølgende præsentation til lektionen) KORPUSOVA TATYANA SERGEEVNA matematiklærer MBOU LSOSH nr. 2 opkaldt efter. N.F.Struchenkova Bryansk-regionen.

DEFINITION Numeriske funktioner defineret af formlerne y = sin x og y = cos x kaldes henholdsvis sinus og cosinus. 10-11-2013 KORPUSOVA T.S.

Funktion y=sin x, graf og egenskaber. 10-11-2013 KORPUSOVA T.S.

Sinusbølge 1 - π/2 π 2 π 3 π x -3 π/2 - π 0 π/2 3 π/2 5 π/2 -1 11/10/2013 KORPUSOVA T.S.

y = sin(x+a) EKSEMPEL y 1 -1 π 2 π - π 11/10/2013 KORPUSOVA T.S.

y = sin x + a 1) y = sin x + 1; y 1 x - π 0 π 2 π x -1 x 2) y = sin x - 1 11/10/2013 KORPUSOVA T.S.

Plotning af grafer y=sin(x+m)+l y 1 - π 0 π 2 π 3 π x -1 11/10/2013 KORPUSOVA T.S.

Funktion y = cos x, dens egenskaber og graf. 10-11-2013 KORPUSOVA T.S.

y = cos x y 1 - π/2 π 2 π 3 π x - π 0 π/2 3 π/2 5 π/2 -1 Grafen for funktionen y= cos x blev opnået ved at flytte sinusoiden til venstre ved at π/2 11/10/2013 KORPUSOVA T.S.

Plotning af grafer y = cos (x+m)+l 1)y =- cos x; y 2 y x 0 x -1 2)y= cos (x- π/4)+2 11/10/2013 KORPUSOVA T.S.

Plotning af grafer y=k · sin x y 2,5 1 x -1 -2,5 11/10/2013 KORPUSOVA T.S.

Find perioden for trigonometriske funktioner Hvis y=f(x) er periodisk og har den mindste positive periode T₁, så er funktionen y=A· f(kx+b), hvor A, k og b er konstante, og k ≠ 0 , er også periodisk med en periode Eksempler : 11/10/2013 KORPUSOVA T.S. 1) y=sin 6 x +2, Т₁=2 π T₁=2 π

Plotning af grafer for periodiske funktioner 11/10/2013 KORPUSOVA T.S. y x 1 1 y x 1 1 1)T= 4 2)T= 4 Givet funktionen y= f(x) . Konstruer dens graf, hvis perioden er kendt. y x 1 1 3)T= 3

Tegn en graf over funktionen: y=2cos(2x- π/3)-0,5 og find definitionsdomænet og værdiområdet for funktionen 11/10/2013 KORPUSOVA T.S. y x 1 -1 π - π 2 π -2 π T= π

Lektion og oplæg om emnet: "Funktion y=sin(x). Definitioner og egenskaber"

Yderligere materialer
Kære brugere, glem ikke at efterlade dine kommentarer, anmeldelser, ønsker! Alt materiale er blevet kontrolleret af et antivirusprogram.

Manualer og simulatorer i Integral-onlinebutikken til klasse 10 fra 1C
Vi løser problemer inden for geometri. Interaktive byggeopgaver for 7-10 klassetrin
Softwaremiljø "1C: Mathematical Constructor 6.1"

Hvad vi vil studere:

• Egenskaber for funktionen Y=sin(X).
• Funktionsgraf.
• Hvordan man bygger en graf og dens skala.
• Eksempler.

Egenskaber for sinus. Y=sin(X)

Gutter, vi har allerede stiftet bekendtskab med trigonometriske funktioner af et numerisk argument. Kan du huske dem?

Lad os se nærmere på funktionen Y=sin(X)

Lad os nedskrive nogle egenskaber ved denne funktion:
1) Definitionsdomænet er mængden af ​​reelle tal.
2) Funktionen er ulige. Lad os huske definitionen af ​​en ulige funktion. En funktion kaldes ulige, hvis ligheden holder: y(-x)=-y(x). Som vi husker fra spøgelsesformlerne: sin(-x)=-sin(x). Definitionen er opfyldt, hvilket betyder Y=sin(X) er en ulige funktion.
3) Funktionen Y=sin(X) stiger på segmentet og falder på segmentet [π/2; π]. Når vi bevæger os langs den første fjerdedel (mod uret), øges ordinaten, og når vi bevæger os gennem den anden fjerdedel aftager den.

4) Funktionen Y=sin(X) er begrænset nedefra og ovenfra. Denne egenskab følger af, at
-1 ≤ sin(X) ≤ 1
5) Funktionens mindste værdi er -1 (ved x = - π/2+ πk). Funktionens største værdi er 1 (ved x = π/2+ πk).

Lad os bruge egenskaberne 1-5 til at plotte funktionen Y=sin(X). Vi vil bygge vores graf sekventielt ved at anvende vores egenskaber. Lad os begynde at bygge en graf på segmentet.

Der skal lægges særlig vægt på skalaen. På ordinataksen er det mere bekvemt at tage et enhedssegment svarende til 2 celler, og på abscisseaksen er det mere bekvemt at tage et enhedssegment (to celler) svarende til π/3 (se figur).

Plot sinusfunktionen x, y=sin(x)

Lad os beregne værdierne af funktionen på vores segment:

Lad os bygge en graf ved hjælp af vores point under hensyntagen til den tredje egenskab.

Konverteringstabel til spøgelsesformler

Lad os bruge den anden egenskab, som siger, at vores funktion er ulige, hvilket betyder, at den kan reflekteres symmetrisk i forhold til oprindelsen:

Vi ved, at sin(x+ 2π) = sin(x). Det betyder, at på intervallet [- π; π] grafen ser den samme ud som på segmentet [π; 3π] eller eller [-3π; - π] og så videre. Det eneste, vi skal gøre, er omhyggeligt at gentegne grafen i den foregående figur langs hele x-aksen.

Grafen for funktionen Y=sin(X) kaldes en sinusformet.

Lad os skrive et par egenskaber mere i henhold til den konstruerede graf:
6) Funktionen Y=sin(X) stiger på ethvert segment af formen: [- π/2+ 2πk; π/2+ 2πk], k er et heltal og falder på et hvilket som helst segment af formen: [π/2+ 2πk; 3π/2+ 2πk], k – heltal.
7) Funktion Y=sin(X) er en kontinuerlig funktion. Lad os se på grafen for funktionen og sikre os, at vores funktion ikke har nogen pauser, det betyder kontinuitet.
8) Område af værdier: segment [- 1; 1]. Dette er også tydeligt synligt på grafen for funktionen.
9) Funktion Y=sin(X) - periodisk funktion. Lad os se på grafen igen og se, at funktionen tager de samme værdier med bestemte intervaller.

Eksempler på problemer med sinus

1. Løs ligningen sin(x)= x-π

Løsning: Lad os bygge 2 grafer af funktionen: y=sin(x) og y=x-π (se figur).
Vores grafer skærer hinanden i et punkt A(π;0), dette er svaret: x = π

2. Tegn grafen for funktionen y=sin(π/6+x)-1

Løsning: Den ønskede graf opnås ved at flytte grafen for funktionen y=sin(x) π/6 enheder til venstre og 1 enhed ned.

Løsning: Lad os plotte funktionen og overveje vores segment [π/2; 5π/4].
Funktionens graf viser, at de største og mindste værdier opnås i enderne af segmentet, henholdsvis i punkterne π/2 og 5π/4.
Svar: sin(π/2) = 1 – den største værdi, sin(5π/4) = den mindste værdi.

Sinusproblemer til uafhængig løsning

• Løs ligningen: sin(x)= x+3π, sin(x)= x-5π
• Tegn grafen til funktionen y=sin(π/3+x)-2
• Tegn grafen til funktionen y=sin(-2π/3+x)+1
• Find den største og mindste værdi af funktionen y=sin(x) på segmentet
• Find den største og mindste værdi af funktionen y=sin(x) på intervallet [- π/3; 5π/6]