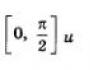Graf for funktionen sinx x. Funktionerne y=sin x og y=cos x og deres grafer præsentation for en algebra lektion (10. klasse) om emnet
Lektion og oplæg om emnet: "Funktion y=sin(x). Definitioner og egenskaber"
Yderligere materialer
Kære brugere, glem ikke at efterlade dine kommentarer, anmeldelser, ønsker! Alt materiale er blevet kontrolleret af et antivirusprogram.
Manualer og simulatorer i Integral-onlinebutikken til klasse 10 fra 1C
Vi løser problemer inden for geometri. Interaktive byggeopgaver for 7-10 klassetrin
Softwaremiljø "1C: Mathematical Constructor 6.1"
Hvad vi vil studere:
- Egenskaber for funktionen Y=sin(X).
- Funktionsgraf.
- Hvordan man bygger en graf og dens skala.
- Eksempler.
Egenskaber for sinus. Y=sin(X)
Gutter, vi har allerede stiftet bekendtskab med trigonometriske funktioner af et numerisk argument. Kan du huske dem?
Lad os se nærmere på funktionen Y=sin(X)
Lad os nedskrive nogle egenskaber ved denne funktion:
1) Definitionsdomænet er mængden af reelle tal.
2) Funktionen er ulige. Lad os huske definitionen af en ulige funktion. En funktion kaldes ulige, hvis ligheden holder: y(-x)=-y(x). Som vi husker fra spøgelsesformlerne: sin(-x)=-sin(x). Definitionen er opfyldt, hvilket betyder Y=sin(X) er en ulige funktion.
3) Funktionen Y=sin(X) stiger på segmentet og falder på segmentet [π/2; π]. Når vi bevæger os langs den første fjerdedel (mod uret), øges ordinaten, og når vi bevæger os gennem den anden fjerdedel aftager den.
4) Funktionen Y=sin(X) er begrænset nedefra og ovenfra. Denne egenskab følger af, at
-1 ≤ sin(X) ≤ 1
5) Funktionens mindste værdi er -1 (ved x = - π/2+ πk). Funktionens største værdi er 1 (ved x = π/2+ πk).
Lad os bruge egenskaberne 1-5 til at plotte funktionen Y=sin(X). Vi vil bygge vores graf sekventielt ved at anvende vores egenskaber. Lad os begynde at bygge en graf på segmentet.
Der skal lægges særlig vægt på skalaen. På ordinataksen er det mere bekvemt at tage et enhedssegment svarende til 2 celler, og på abscisseaksen er det mere bekvemt at tage et enhedssegment (to celler) svarende til π/3 (se figur).
_2.png)
Plot sinusfunktionen x, y=sin(x)
Lad os beregne værdierne af funktionen på vores segment:
_3.png)
Lad os bygge en graf ved hjælp af vores point under hensyntagen til den tredje egenskab.
_4.png)
Konverteringstabel til spøgelsesformler
Lad os bruge den anden egenskab, som siger, at vores funktion er ulige, hvilket betyder, at den kan reflekteres symmetrisk i forhold til oprindelsen:
_5.png)
Vi ved, at sin(x+ 2π) = sin(x). Det betyder, at på intervallet [- π; π] grafen ser den samme ud som på segmentet [π; 3π] eller eller [-3π; - π] og så videre. Det eneste, vi skal gøre, er omhyggeligt at gentegne grafen i den foregående figur langs hele x-aksen.
_6.png)
Grafen for funktionen Y=sin(X) kaldes en sinusformet.
Lad os skrive et par egenskaber mere i henhold til den konstruerede graf:
6) Funktionen Y=sin(X) stiger på ethvert segment af formen: [- π/2+ 2πk; π/2+ 2πk], k er et heltal og falder på et hvilket som helst segment af formen: [π/2+ 2πk; 3π/2+ 2πk], k – heltal.
7) Funktion Y=sin(X) er en kontinuerlig funktion. Lad os se på grafen for funktionen og sikre os, at vores funktion ikke har nogen pauser, det betyder kontinuitet.
8) Område af værdier: segment [- 1; 1]. Dette er også tydeligt synligt på grafen for funktionen.
9) Funktion Y=sin(X) - periodisk funktion. Lad os se på grafen igen og se, at funktionen tager de samme værdier med bestemte intervaller.
Eksempler på problemer med sinus
1. Løs ligningen sin(x)= x-π
Løsning: Lad os bygge 2 grafer af funktionen: y=sin(x) og y=x-π (se figur).
Vores grafer skærer hinanden i et punkt A(π;0), dette er svaret: x = π
_7.png)
2. Tegn grafen for funktionen y=sin(π/6+x)-1
Løsning: Den ønskede graf opnås ved at flytte grafen for funktionen y=sin(x) π/6 enheder til venstre og 1 enhed ned.
_8.png)
Løsning: Lad os plotte funktionen og overveje vores segment [π/2; 5π/4].
Funktionens graf viser, at de største og mindste værdier opnås i enderne af segmentet, henholdsvis i punkterne π/2 og 5π/4.
Svar: sin(π/2) = 1 – den største værdi, sin(5π/4) = den mindste værdi.
_9.png)
Sinusproblemer til uafhængig løsning
- Løs ligningen: sin(x)= x+3π, sin(x)= x-5π
- Tegn grafen til funktionen y=sin(π/3+x)-2
- Tegn grafen til funktionen y=sin(-2π/3+x)+1
- Find den største og mindste værdi af funktionen y=sin(x) på segmentet
- Find den største og mindste værdi af funktionen y=sin(x) på intervallet [- π/3; 5π/6]
Centreret i et punkt EN.
α
- vinkel udtrykt i radianer.
Definition
Sinus (sin α) er en trigonometrisk funktion afhængig af vinklen α mellem hypotenusen og benet i en retvinklet trekant, lig med forholdet mellem længden af det modsatte ben |BC| til længden af hypotenusen |AC|.
Cosinus (cos α) er en trigonometrisk funktion afhængig af vinklen α mellem hypotenusen og benet i en retvinklet trekant, lig med forholdet mellem længden af det tilstødende ben |AB| til længden af hypotenusen |AC|.
Accepterede notationer
;
;
.
;
;
.
Graf over sinusfunktionen, y = sin x
Graf over cosinusfunktionen, y = cos x

Egenskaber for sinus og cosinus
Periodicitet
Funktioner y = synd x og y = fordi x periodisk med punktum 2π.
Paritet
Sinusfunktionen er ulige. Cosinusfunktionen er jævn.
Definitionsdomæne og værdier, ekstrema, stigning, fald
Sinus- og cosinusfunktionerne er kontinuerte i deres definitionsdomæne, det vil sige for alle x (se bevis for kontinuitet). Deres hovedegenskaber er præsenteret i tabellen (n - heltal).
| y = synd x | y = fordi x | |
| Omfang og kontinuitet | - ∞ < x < + ∞ | - ∞ < x < + ∞ |
| Vifte af værdier | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Stigende | ||
| Aftagende | ||
| Maxima, y = 1 | ||
| Minima, y = - 1 | ||
| Nuller, y = 0 | ||
| Skæringspunkter med ordinataksen, x = 0 | y = 0 | y = 1 |
Grundlæggende formler
Summen af kvadrater af sinus og cosinus
Formler for sinus og cosinus fra sum og forskel
;
;
Formler for produktet af sinus og cosinus
Sum- og differensformler
Udtrykker sinus gennem cosinus
;
;
;
.
Udtrykker cosinus gennem sinus
;
;
;
.
Udtryk gennem tangent
; .
Hvornår har vi:
;
.
kl.:
;
.
Tabel over sinus og cosinus, tangenter og cotangenter
Denne tabel viser værdierne af sinus og cosinus for visse værdier af argumentet. 
Udtryk gennem komplekse variable
;
Eulers formel
Udtryk gennem hyperbolske funktioner
;
;
Derivater
; . Udledning af formler > > >
Afledte af n. orden:
{ -∞ <
x < +∞ }
Sekant, cosecant
Omvendte funktioner
De omvendte funktioner af sinus og cosinus er henholdsvis arcsinus og arccosinus.
Arcsine, arcsin
Arccosine, arccos
Referencer:
I. Bronstein, K.A. Semendyaev, Håndbog i matematik for ingeniører og universitetsstuderende, "Lan", 2009.
FUNKTIONSGRAFIK
Sinus funktion

- en masse R alle reelle tal.
Flere funktionsværdier— segment [-1; 1], dvs. sinus funktion - begrænset.
Ulige funktion: sin(−x)=−sin x for alle x ∈ R.
Funktionen er periodisk
sin(x+2π k) = sin x, hvor k ∈ Z for alle x ∈ R.
sin x = 0 for x = π·k, k ∈ Z.
sin x > 0(positiv) for alle x ∈ (2π·k , π+2π·k ), k ∈ Z.
synd x< 0 (negativ) for alle x ∈ (π+2π·k , 2π+2π·k ), k ∈ Z.
Cosinus funktion

Funktion Domæne- en masse R alle reelle tal.
Flere funktionsværdier— segment [-1; 1], dvs. cosinus funktion - begrænset.
Jævn funktion: cos(−x)=cos x for alle x ∈ R.
Funktionen er periodisk med den mindste positive periode 2π:
cos(x+2π k) = cos x, hvor k ∈ Z for alle x ∈ R.
| cos x = 0 på | |
| cos x > 0 for alle | |
| fordi x< 0 for alle | |
| Funktionen øges fra -1 til 1 i intervaller: | |
| Funktionen er aftagende fra -1 til 1 i intervaller: | |
| Den største værdi af funktionen sin x = 1 på punkter: | |
| Den mindste værdi af funktionen sin x = −1 på punkter: |
Tangent funktion

Flere funktionsværdier— hele tallinjen, dvs. tangent - funktion ubegrænset.
Ulige funktion: tg(−x)=−tg x
Grafen for funktionen er symmetrisk om OY-aksen.
Funktionen er periodisk med den mindste positive periode π, dvs. tg(x+π k) = tan x, k ∈ Z for alle x fra definitionsdomænet.
Cotangens funktion

Flere funktionsværdier— hele tallinjen, dvs. cotangens - funktion ubegrænset.
Ulige funktion: ctg(−x)=−ctg x for alle x fra definitionsdomænet.Grafen for funktionen er symmetrisk om OY-aksen.
Funktionen er periodisk med den mindste positive periode π, dvs. cotg(x+π k)=ctg x, k ∈ Z for alle x fra definitionsdomænet.
Arcsine funktion

Funktion Domæne— segment [-1; 1]
Flere funktionsværdier- segment -π /2 arcsin x π /2, dvs. arcsine - funktion begrænset.
Ulige funktion: arcsin(−x)=−arcsin x for alle x ∈ R.
Grafen for funktionen er symmetrisk om oprindelsen.
Gennem hele definitionsområdet.
Arc cosinus funktion

Funktion Domæne— segment [-1; 1]
Flere funktionsværdier— segment 0 arccos x π, dvs. arccosine - funktion begrænset.
Funktionen er stigende over hele definitionsområdet.
Arctangens funktion

Funktion Domæne- en masse R alle reelle tal.
Flere funktionsværdier— segment 0 π, dvs. arctangens - funktion begrænset.
Ulige funktion: arctg(−x)=−arctg x for alle x ∈ R.
Grafen for funktionen er symmetrisk om oprindelsen.
Funktionen er stigende over hele definitionsområdet.
Arc tangens funktion

Funktion Domæne- en masse R alle reelle tal.
Flere funktionsværdier— segment 0 π, dvs. arccotangens - funktion begrænset.
Funktionen er hverken lige eller ulige.
Funktionens graf er asymmetrisk hverken med hensyn til oprindelsen eller med hensyn til Oy-aksen.
Funktionen er aftagende over hele definitionsområdet.
I denne lektion vil vi se nærmere på funktionen y = sin x, dens grundlæggende egenskaber og graf. I begyndelsen af lektionen vil vi give definitionen af den trigonometriske funktion y = sin t på koordinatcirklen og betragte grafen for funktionen på cirklen og linjen. Lad os vise periodiciteten af denne funktion på grafen og overveje funktionens hovedegenskaber. I slutningen af lektionen vil vi løse flere simple problemer ved at bruge grafen for en funktion og dens egenskaber.
Emne: Trigonometriske funktioner
Lektion: Funktion y=sinx, dens grundlæggende egenskaber og graf
Når man overvejer en funktion, er det vigtigt at knytte hver argumentværdi til en enkelt funktionsværdi. Det her brevloven og kaldes en funktion.
Lad os definere korrespondanceloven for .
Ethvert reelt tal svarer til et enkelt punkt på enhedscirklen Et punkt har en enkelt ordinat, som kaldes tallets sinus (fig. 1).

![]()
Hver argumentværdi er knyttet til en enkelt funktionsværdi.
Indlysende egenskaber følger af definitionen af sinus.
Det viser figuren ![]() fordi er ordinaten af et punkt på enhedscirklen.
fordi er ordinaten af et punkt på enhedscirklen.
Overvej grafen for funktionen. Lad os huske den geometriske fortolkning af argumentet. Argumentet er den centrale vinkel, målt i radianer. Langs aksen vil vi plotte reelle tal eller vinkler i radianer, langs aksen de tilsvarende værdier af funktionen.
For eksempel svarer en vinkel på enhedscirklen til et punkt på grafen (fig. 2)

Vi har fået en graf over funktionen i området, men ved at kende sinusperioden kan vi afbilde funktionens graf over hele definitionsdomænet (fig. 3).

Funktionens hovedperiode er. Dette betyder, at grafen kan hentes på et segment og derefter fortsættes gennem hele definitionsdomænet.
Overvej funktionens egenskaber:
1) Definitionsomfang:
2) Værdiinterval: ![]()
3) Ulige funktion:
4) Mindste positive periode:
5) Koordinater for grafens skæringspunkter med abscisseaksen: ![]()
6) Koordinater for grafens skæringspunkt med ordinataksen:
7) Intervaller, hvor funktionen tager positive værdier:
8) Intervaller, hvor funktionen tager negative værdier:
9) Stigende intervaller:
10) Aftagende intervaller:
11) Minimum point: ![]()
12) Minimum funktioner:
13) Maksimalt antal point: ![]()
14) Maksimale funktioner:
Vi så på egenskaberne for funktionen og dens graf. Egenskaberne vil blive brugt gentagne gange ved løsning af problemer.
Bibliografi
1. Algebra og begyndelse af analyse, karakter 10 (i to dele). Lærebog for almene uddannelsesinstitutioner (profilniveau), red. A. G. Mordkovich. -M.: Mnemosyne, 2009.
2. Algebra og begyndelse af analyse, karakter 10 (i to dele). Problembog for uddannelsesinstitutioner (profilniveau), red. A. G. Mordkovich. -M.: Mnemosyne, 2007.
3. Vilenkin N.Ya., Ivashev-Musatov O.S., Shvartsburd S.I. Algebra og matematisk analyse for klasse 10 (lærebog for elever i skoler og klasser med dybdegående studier af matematik). - M.: Prosveshchenie, 1996.
4. Galitsky M.L., Moshkovich M.M., Shvartsburd S.I. Dybdegående undersøgelse af algebra og matematisk analyse.-M.: Education, 1997.
5. Samling af problemer i matematik for ansøgere til videregående uddannelsesinstitutioner (redigeret af M.I. Skanavi).- M.: Higher School, 1992.
6. Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebraisk simulator.-K.: A.S.K., 1997.
7. Sahakyan S.M., Goldman A.M., Denisov D.V. Problemer med algebra og analyseprincipper (en manual for studerende i klasse 10-11 på almene uddannelsesinstitutioner). - M.: Prosveshchenie, 2003.
8. Karp A.P. Samling af problemer om algebra og analyseprincipper: lærebog. godtgørelse for 10-11 klassetrin. med dybde studeret Matematik.-M.: Uddannelse, 2006.
Lektier
Algebra og begyndelse af analyse, karakter 10 (i to dele). Problembog for uddannelsesinstitutioner (profilniveau), red.
A. G. Mordkovich. -M.: Mnemosyne, 2007.
№№ 16.4, 16.5, 16.8.
Yderligere webressourcer
3. Uddannelsesportal til eksamensforberedelse ().
I denne lektion vil vi se nærmere på funktionen y = sin x, dens grundlæggende egenskaber og graf. I begyndelsen af lektionen vil vi give definitionen af den trigonometriske funktion y = sin t på koordinatcirklen og betragte grafen for funktionen på cirklen og linjen. Lad os vise periodiciteten af denne funktion på grafen og overveje funktionens hovedegenskaber. I slutningen af lektionen vil vi løse flere simple problemer ved at bruge grafen for en funktion og dens egenskaber.
Emne: Trigonometriske funktioner
Lektion: Funktion y=sinx, dens grundlæggende egenskaber og graf
Når man overvejer en funktion, er det vigtigt at knytte hver argumentværdi til en enkelt funktionsværdi. Det her brevloven og kaldes en funktion.
Lad os definere korrespondanceloven for .
Ethvert reelt tal svarer til et enkelt punkt på enhedscirklen Et punkt har en enkelt ordinat, som kaldes tallets sinus (fig. 1).

![]()
Hver argumentværdi er knyttet til en enkelt funktionsværdi.
Indlysende egenskaber følger af definitionen af sinus.
Det viser figuren ![]() fordi er ordinaten af et punkt på enhedscirklen.
fordi er ordinaten af et punkt på enhedscirklen.
Overvej grafen for funktionen. Lad os huske den geometriske fortolkning af argumentet. Argumentet er den centrale vinkel, målt i radianer. Langs aksen vil vi plotte reelle tal eller vinkler i radianer, langs aksen de tilsvarende værdier af funktionen.
For eksempel svarer en vinkel på enhedscirklen til et punkt på grafen (fig. 2)

Vi har fået en graf over funktionen i området, men ved at kende sinusperioden kan vi afbilde funktionens graf over hele definitionsdomænet (fig. 3).

Funktionens hovedperiode er. Dette betyder, at grafen kan hentes på et segment og derefter fortsættes gennem hele definitionsdomænet.
Overvej funktionens egenskaber:
1) Definitionsomfang:
2) Værdiinterval: ![]()
3) Ulige funktion:
4) Mindste positive periode:
5) Koordinater for grafens skæringspunkter med abscisseaksen: ![]()
6) Koordinater for grafens skæringspunkt med ordinataksen:
7) Intervaller, hvor funktionen tager positive værdier:
8) Intervaller, hvor funktionen tager negative værdier:
9) Stigende intervaller:
10) Aftagende intervaller:
11) Minimum point: ![]()
12) Minimum funktioner:
13) Maksimalt antal point: ![]()
14) Maksimale funktioner:
Vi så på egenskaberne for funktionen og dens graf. Egenskaberne vil blive brugt gentagne gange ved løsning af problemer.
Bibliografi
1. Algebra og begyndelse af analyse, karakter 10 (i to dele). Lærebog for almene uddannelsesinstitutioner (profilniveau), red. A. G. Mordkovich. -M.: Mnemosyne, 2009.
2. Algebra og begyndelse af analyse, karakter 10 (i to dele). Problembog for uddannelsesinstitutioner (profilniveau), red. A. G. Mordkovich. -M.: Mnemosyne, 2007.
3. Vilenkin N.Ya., Ivashev-Musatov O.S., Shvartsburd S.I. Algebra og matematisk analyse for klasse 10 (lærebog for elever i skoler og klasser med dybdegående studier af matematik). - M.: Prosveshchenie, 1996.
4. Galitsky M.L., Moshkovich M.M., Shvartsburd S.I. Dybdegående undersøgelse af algebra og matematisk analyse.-M.: Education, 1997.
5. Samling af problemer i matematik for ansøgere til videregående uddannelsesinstitutioner (redigeret af M.I. Skanavi).- M.: Higher School, 1992.
6. Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebraisk simulator.-K.: A.S.K., 1997.
7. Sahakyan S.M., Goldman A.M., Denisov D.V. Problemer med algebra og analyseprincipper (en manual for studerende i klasse 10-11 på almene uddannelsesinstitutioner). - M.: Prosveshchenie, 2003.
8. Karp A.P. Samling af problemer om algebra og analyseprincipper: lærebog. godtgørelse for 10-11 klassetrin. med dybde studeret Matematik.-M.: Uddannelse, 2006.
Lektier
Algebra og begyndelse af analyse, karakter 10 (i to dele). Problembog for uddannelsesinstitutioner (profilniveau), red.
A. G. Mordkovich. -M.: Mnemosyne, 2007.
№№ 16.4, 16.5, 16.8.
Yderligere webressourcer
3. Uddannelsesportal til eksamensforberedelse ().