Rektangulært koordinatsystem

For at definere begrebet koordinater af punkter, skal vi indtaste et koordinatsystem, hvor vi vil bestemme dets koordinater. Det samme punkt i forskellige koordinatsystemer kan have forskellige koordinater. Her vil vi betragte et rektangulært koordinatsystem i rummet.

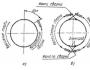
Tag et punkt $ O $ i rummet og indtast koordinaterne $ (0,0,0) $ for det. Lad os kalde det oprindelsen af ​​koordinatsystemet. Lad os gennem den tegne tre indbyrdes vinkelrette akser $ Ox $, $ Oy $ og $ Oz $, som i figur 1. Disse akser vil blive kaldt henholdsvis abscisse, ordinat og applikatakse. Det er kun tilbage at indtaste skalaen på akserne (enhedssegment) - det rektangulære koordinatsystem i rummet er klar (fig. 1)

Figur 1. Rektangulært koordinatsystem i rummet. Author24 - online udveksling af studenterpapirer

Punktkoordinater

Lad os nu analysere, hvordan koordinaterne for ethvert punkt bestemmes i et sådant system. Tag et vilkårligt punkt $ M $ (fig. 2).

Lad os konstruere et rektangulært parallelepipedum på koordinatakserne, så punkterne $ O $ og $ M $ er dets modsatte hjørner (fig. 3).

Figur 3. Konstruktion af et rektangulært parallelepipedum. Author24 - online udveksling af studenterpapirer

Så vil punktet $ M $ have koordinater $ (X, Y, Z) $, hvor $ X $ er værdien på den numeriske akse $ Ox $, $ Y $ er værdien på den numeriske akse $ Oy $, og $ Z $ er værdien på den numeriske akse $ Oz $.

Eksempel 1

Det er nødvendigt at finde en løsning på følgende problem: skriv koordinaterne for hjørnerne af parallelepipedet vist i figur 4.

Opløsning.

Punkt $ O $ er oprindelsen, derfor $ O = (0,0,0) $.

Punkterne $ Q $, $ N $ og $ R $ ligger på henholdsvis akserne $ Ox $, $ Oz $ og $ Oy $, hvilket betyder

$ Q = (2,0,0) $, $ N = (0,0,1.5) $, $ R = (0,2.5,0) $

Punkterne $ S $, $ L $ og $ M $ ligger i henholdsvis flyene $ Oxz $, $ Oxy $ og $ Oyz $, hvilket betyder

$ S = (2,0,1.5) $, $ L = (2,2.5,0) $, $ R = (0,2.5,1.5) $

Punkt $ P $ har koordinater $ P = (2,2.5,1.5) $

Vektorkoordinater med to punkter og formlen til at finde

For at finde ud af, hvordan man finder en vektor ved koordinaterne af to punkter, skal du overveje det koordinatsystem, vi introducerede tidligere. I den, fra punktet $ O $ i retning af $ Ox $-aksen, udskyder vi enhedsvektoren $ \ overline (i) $, i retning af $ Oy $-aksen - enhedsvektoren $ \ overline (j ) $, og enhedsvektoren $ \ overline (k) $ skal rettes langs $ Oz $-aksen.

For at introducere begrebet koordinater for en vektor introducerer vi følgende sætning (vi vil ikke overveje dets bevis her).

Sætning 1

En vilkårlig vektor i rummet kan udvides til hvilke som helst tre vektorer, der ikke ligger i samme plan, og koefficienterne i en sådan ekspansion vil blive entydigt bestemt.

Matematisk ser det sådan ud:

$ \ overline (δ) = m \ overline (α) + n \ overline (β) + l \ overline (γ) $

Da vektorerne $ \ overline (i) $, $ \ overline (j) $ og $ \ overline (k) $ er bygget på koordinatakserne i et rektangulært koordinatsystem, vil de naturligvis ikke tilhøre samme plan. Derfor kan enhver vektor $ \ overline (δ) $ i dette koordinatsystem, ved sætning 1, have følgende form

$ \ overline (δ) = m \ overline (i) + n \ overline (j) + l \ overline (k) $ (1)

hvor $ n, m, l∈R $.

Definition 1

De tre vektorer $ \ overline (i) $, $ \ overline (j) $ og $ \ overline (k) $ vil blive kaldt koordinatvektorer.

Definition 2

Koefficienterne foran vektorerne $ \ overline (i) $, $ \ overline (j) $ og $ \ overline (k) $ i ekspansion (1) vil blive kaldt koordinaterne for denne vektor i det givne koordinatsystem, dvs. er

$ \ overline (δ) = (m, n, l) $

Lineære operationer på vektorer

Sætning 2

Sumsætning: Koordinaterne for summen af ​​et vilkårligt antal vektorer bestemmes af summen af ​​deres respektive koordinater.

Bevis.

Vi vil bevise denne sætning for 2 vektorer. For 3 eller flere vektorer er beviset konstrueret på lignende måde. Lad $ \ overline (α) = (α_1, α_2, α_3) $, $ \ overline (β) = (β_1, β_2, β_3) $.

Disse vektorer kan skrives som følger

$ \ overline (α) = α_1 \ overline (i) + α_2 \ overline (j) + α_3 \ overline (k) $, $ \ overline (β) = β_1 \ overline (i) + β_2 \ overline (j) + β_3 \ overline (k) $

For at bruge koordinatmetoden skal du kende formlerne godt. Der er tre af dem:

Ved første øjekast ser det truende ud, men bare lidt øvelse og alt vil fungere fantastisk.

Opgave. Find cosinus for vinklen mellem vektorerne a = (4; 3; 0) og b = (0; 12; 5).

Opløsning. Da vektorernes koordinater er givet til os, erstatter vi dem i den første formel:

Opgave. Lav en ligning for planet, der går gennem punkterne M = (2; 0; 1), N = (0; 1; 1) og K = (2; 1; 0), hvis det er kendt, at det ikke passerer igennem oprindelsen.

Opløsning. Planens generelle ligning: Ax + By + Cz + D = 0, men da den ønskede plan ikke passerer gennem koordinaternes begyndelse - punktet (0; 0; 0) - så sætter vi D = 1. Da denne flyet passerer gennem punkterne M, N og K, så skulle koordinaterne for disse punkter gøre ligningen til den korrekte numeriske lighed.

Erstat i stedet for x-, y- og z-koordinater for punktet M = (2; 0; 1). Vi har:
A2 + B0 + C1 + 1 = 0 ⇒ 2A + C + 1 = 0;

Tilsvarende får vi for punkterne N = (0; 1; 1) og K = (2; 1; 0) ligningerne:
A 0 + B 1 + C 1 + 1 = 0 ⇒ B + C + 1 = 0;
A2 + B1 + C0 + 1 = 0 ⇒ 2A + B + 1 = 0;

Så vi har tre ligninger og tre ubekendte. Lad os sammensætte og løse ligningssystemet:

Vi fik, at flyets ligning har formen: - 0,25x - 0,5y - 0,5z + 1 = 0.

Opgave. Planen er givet ved ligningen 7x - 2y + 4z + 1 = 0. Find vektorens koordinater vinkelret på den givne plan.

Opløsning. Ved at bruge den tredje formel får vi n = (7; - 2; 4) - det er alt!

Beregning af vektorers koordinater

Men hvad nu hvis der ikke er vektorer i problemet - der er kun punkter, der ligger på lige linjer, og du skal beregne vinklen mellem disse lige linjer? Det er enkelt: Ved at kende punkternes koordinater - begyndelsen og slutningen af ​​vektoren - kan du beregne koordinaterne for selve vektoren.

For at finde koordinaterne for en vektor skal du trække koordinaterne for begyndelsen fra koordinaterne for dens ende.

Denne sætning fungerer på samme måde både på planet og i rummet. Udtrykket "træk koordinater fra" betyder, at et andet punkts x-koordinat trækkes fra x-koordinaten for et punkt, så skal det samme gøres med y- og z-koordinaterne. Her er nogle eksempler:

Opgave. Der er tre punkter i rummet, givet ved deres koordinater: A = (1; 6; 3), B = (3; - 1; 7) og C = (- 4; 3; - 2). Find koordinaterne for vektorerne AB, AC og BC.

Overvej en vektor AB: dens oprindelse er ved punkt A, og dens ende er ved punkt B. For at finde dens koordinater er det derfor nødvendigt at trække koordinaterne til punkt A fra koordinaterne til punkt B:
AB = (3 - 1; - 1 - 6; 7 - 3) = (2; - 7; 4).

På samme måde er begyndelsen af ​​vektoren AC stadig det samme punkt A, men slutningen er punkt C. Derfor har vi:
AC = (- 4 - 1; 3 - 6; - 2 - 3) = (- 5; - 3; - 5).

Til sidst, for at finde koordinaterne til vektoren BC, skal du trække koordinaterne for punkt B fra koordinaterne til punkt C:
BC = (- 4 - 3; 3 - (- 1); - 2 - 7) = (- 7; 4; - 9).

Svar: AB = (2; - 7; 4); AC = (-5; -3; -5); BC = (- 7; 4; - 9)

Vær opmærksom på beregningen af ​​koordinaterne for den sidste BC-vektor: mange mennesker laver fejl, når de arbejder med negative tal. Det drejer sig om variablen y: punkt B har y = - 1, og punkt C y = 3. Vi får præcis 3 - (- 1) = 4, og ikke 3 - 1, som mange tror. Lav ikke sådanne dumme fejl!

Beregning af retningsvektorer for rette linjer

Hvis du læser opgave C2 omhyggeligt, vil du blive overrasket over at opdage, at der ikke er nogen vektorer der. Der er kun lige linjer og planer.

Lad os starte med de lige linjer. Alt er enkelt her: på enhver lige linje er der mindst to forskellige punkter, og omvendt definerer alle to forskellige punkter en enkelt lige linje ...

Er der nogen, der forstår, hvad der står i det foregående afsnit? Jeg forstod det ikke selv, så jeg vil forklare det lettere: I opgave C2 er lige linjer altid givet af et par punkter. Hvis vi introducerer et koordinatsystem og betragter en vektor med en begyndelse og en ende i disse punkter, får vi den såkaldte retningsvektor for en ret linje:

Hvorfor er denne vektor nødvendig? Pointen er, at vinklen mellem to rette linjer er vinklen mellem deres retningsvektorer. Således går vi fra uforståelige lige linjer til specifikke vektorer, hvis koordinater er nemme at beregne. Hvor nemt er det? Tag et kig på eksempler:

Opgave. I terningen er ABCDA 1 B 1 C 1 D 1 tegnet linjerne AC og BD 1. Find koordinaterne for retningsvektorerne for disse linjer.

Da længden af ​​terningens kanter ikke er angivet i betingelsen, sætter vi AB = 1. Vi indfører et koordinatsystem med origo i punktet A og akserne x, y, z rettet langs linjerne AB, AD og AA 1, henholdsvis. Enhedssegmentet er lig med AB = 1.

Nu vil vi finde koordinaterne for retningsvektoren for linjen AC. Vi har brug for to punkter: A = (0; 0; 0) og C = (1; 1; 0). Herfra får vi koordinaterne til vektoren AC = (1 - 0; 1 - 0; 0 - 0) = (1; 1; 0) - dette er retningsvektoren.

Lad os nu beskæftige os med den lige linje BD 1. Den har også to punkter: B = (1; 0; 0) og D 1 = (0; 1; 1). Vi får retningsvektoren BD 1 = (0 - 1; 1 - 0; 1 - 0) = (- 1; 1; 1).

Svar: AC = (1; 1; 0); BD 1 = (- 1; 1; 1)

Opgave. I et regulært trekantet prisme ABCA 1 B 1 C 1, hvor alle kanter er lig med 1, tegnes linjerne AB 1 og AC 1. Find koordinaterne for retningsvektorerne for disse linjer.

Lad os introducere koordinatsystemet: oprindelsen er i punkt A, x-aksen falder sammen med AB, z-aksen falder sammen med AA 1, y-aksen danner OXY-planen med x-aksen, som falder sammen med ABC-planen .

Lad os først beskæftige os med den lige linje AB 1. Alt er enkelt her: vi har punkterne A = (0; 0; 0) og B 1 = (1; 0; 1). Vi får retningsvektoren AB 1 = (1 - 0; 0 - 0; 1 - 0) = (1; 0; 1).

Nu finder vi retningsvektoren for AC 1. Alligevel - den eneste forskel er, at punkt C 1 har irrationelle koordinater. Så A = (0; 0; 0), så vi har:

Svar: AB 1 = (1; 0; 1);

En lille, men meget vigtig bemærkning om det sidste eksempel. Hvis vektorens oprindelse falder sammen med oprindelsen, er beregningerne meget forenklet: vektorens koordinater er simpelthen lig med koordinaterne for enden. Desværre gælder dette kun for vektorer. For eksempel, når du arbejder med fly, komplicerer tilstedeværelsen af ​​oprindelsen på dem kun beregningerne.

Beregning af normalvektorer for planer

Normale vektorer er ikke vektorer, der gør eller klarer sig godt. Per definition er en normalvektor (normal) til et plan en vektor vinkelret på det plan.

Med andre ord er en normal en vektor vinkelret på enhver vektor i et givet plan. Du har helt sikkert opfyldt en sådan definition - men i stedet for vektorer talte vi om lige linjer. Men lige over blev det vist, at i opgave C2 kan du arbejde med ethvert bekvemt objekt - endda en lige linje, endda en vektor.

Lad mig igen minde dig om, at ethvert plan er defineret i rummet af ligningen Ax + By + Cz + D = 0, hvor A, B, C og D er nogle koefficienter. Uden tab af generalitet af løsningen kan vi antage D = 1, hvis planet ikke passerer gennem origo, eller D = 0, hvis det gør. Under alle omstændigheder er koordinaterne for normalvektoren til dette plan n = (A; B; C).

Så flyet kan også med succes erstattes af en vektor - den samme normal. Ethvert plan er defineret i rummet af tre punkter. Hvordan man finder flyets ligning (og derfor normalen), har vi allerede diskuteret i begyndelsen af ​​artiklen. Denne proces forårsager dog problemer for mange, så jeg vil give et par flere eksempler:

Opgave. Snit A 1 BC 1 er tegnet i terningen ABCDA 1 B 1 C 1 D 1. Find normalvektoren for dette snits plan, hvis origo er i punktet A, og x-, y- og z-akserne falder sammen med henholdsvis kanterne AB, AD og AA 1.

Da flyet ikke går gennem oprindelsen, ser dens ligning således ud: Ax + By + Cz + 1 = 0, dvs. koefficient D = 1. Da denne plan går gennem punkterne A 1, B og C 1, forvandler koordinaterne for disse punkter planets ligning til den korrekte numeriske lighed.

A 0 + B 0 + C 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = - 1;

Tilsvarende får vi for punkterne B = (1; 0; 0) og C 1 = (1; 1; 1) ligningerne:
A 1 + B 0 + C 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = - 1;
A 1 + B 1 + C 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Men vi kender allerede koefficienterne A = - 1 og C = - 1, så det er tilbage at finde koefficienten B:
B = - 1 - A - C = - 1 + 1 + 1 = 1.

Vi får flyets ligning: - A + B - C + 1 = 0, Derfor er koordinaterne for normalvektoren lig med n = (- 1; 1; - 1).

Opgave. Snit AA 1 C 1 C er tegnet i terningen ABCDA 1 B 1 C 1 D 1. Find normalvektoren for dette snits plan, hvis origo er i punkt A, og x-, y- og z-akserne falder sammen med kanter AB, AD og AA 1 hhv.

I dette tilfælde passerer planet gennem origo, så koefficienten D = 0, og planligningen ser således ud: Ax + By + Cz = 0. Da planet passerer gennem punkterne A1 og C, er koordinaterne for disse punkter vend planligningen til den korrekte numeriske lighed.

Erstat i stedet for x-, y- og z-koordinater for punktet A 1 = (0; 0; 1). Vi har:
A 0 + B 0 + C 1 = 0 ⇒ C = 0;

På samme måde får vi for punktet C = (1; 1; 0) ligningen:
A 1 + B 1 + C 0 = 0 ⇒ A + B = 0 ⇒ A = - B;

Vi sætter B = 1. Så er A = - B = - 1, og hele planens ligning har formen: - A + B = 0, Derfor er koordinaterne for normalvektoren lig med n = (- 1; 1; 0).

Generelt er det i ovenstående problemer nødvendigt at sammensætte et ligningssystem og løse det. Der vil være tre ligninger og tre variable, men i det andet tilfælde vil en af ​​dem være fri, dvs. tage vilkårlige værdier. Derfor har vi ret til at sætte B = 1 - uden at det berører løsningens almene karakter og svarets rigtighed.

Meget ofte i C2-problemet er det påkrævet at arbejde med punkter, der deler segmentet i to. Koordinaterne for sådanne punkter kan let beregnes, hvis koordinaterne for enderne af segmentet er kendt.

Så lad segmentet være defineret af dets ender - punkterne A = (x a; ya; z a) og B = (x b; y b; z b). Så kan koordinaterne for segmentets midtpunkt - vi betegner det med punktet H - findes ved formlen:

Med andre ord er koordinaterne for midtpunktet af et segment det aritmetiske middelværdi af koordinaterne for dets ender.

Opgave. Enhedsterningen ABCDA 1 B 1 C 1 D 1 placeres i koordinatsystemet, så x-, y- og z-akserne er rettet langs kanterne henholdsvis AB, AD og AA 1, og origo falder sammen med punktet A. Punkt K er midtpunktet af kanten A 1 B en . Find koordinaterne for dette punkt.

Da punkt K er midtpunktet af segmentet A 1 B 1, er dets koordinater lig med det aritmetiske middelværdi af endernes koordinater. Lad os nedskrive koordinaterne for enderne: A 1 = (0; 0; 1) og B 1 = (1; 0; 1). Lad os nu finde koordinaterne for punkt K:

Opgave. Enhedskuben ABCDA 1 B 1 C 1 D 1 placeres i koordinatsystemet, så x-, y- og z-akserne er rettet langs kanterne henholdsvis AB, AD og AA 1, og origo falder sammen med punkt A. Find koordinaterne til punktet L, hvor de skærer diagonalerne af kvadratet A 1 B 1 C 1 D 1.

Det er kendt fra planimetriforløbet, at skæringspunktet for diagonalerne i et kvadrat er lige langt fra alle dets hjørner. Især A1L = C1L, dvs. punkt L er midtpunktet af segment A 1 C 1. Men A 1 = (0; 0; 1), C 1 = (1; 1; 1), så vi har:

Svar: L = (0,5; 0,5; 1)

Lad os tilsidesætte enhedsvektorer fra oprindelsen, det vil sige vektorer, hvis længder er lig med én. Retningen af ​​vektoren i → skal falde sammen med O x-aksen, og retningen af ​​vektoren j → med O y-aksen.

Yandex.RTB R-A-339285-1 Definition 1

Vektorerne i → og j → kaldes koordinatvektorer.

Koordinatvektorer er ikke-kollineære. Derfor kan enhver vektor p → udvides i vektorer p → = x i → + y j →. Koefficienterne x og y er entydigt bestemt. Ekspansionskoefficienterne for vektoren p → i koordinatvektorer kaldes koordinaterne for vektoren p → i det givne koordinatsystem.

Vektorkoordinater er skrevet med krøllede klammeparenteser p → x; y. På figuren har vektoren OA → koordinaterne 2; 1, og vektoren b → har koordinaterne 3; - 2. Nulvektoren er repræsenteret som 0 → 0; 0.

Hvis vektorerne a → og b → er ens, så er y 1 = y 2. Vi skriver det sådan her: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j →, så x 1 = x 2, y 1 = y 2.

Således er koordinaterne for lige store vektorer henholdsvis ens.

Hvis koordinatpunktet ikke falder sammen med dets oprindelse af koordinatsystemet, så overvej problemet. Lad koordinaterne for start- og slutpunkterne A B → er angivet i det kartesiske koordinatsystem på O x y: A x a, y a, B x b, y b. Find koordinaterne for den givne vektor.

Lad os tegne en koordinatakse.

Fra vektoradditionsformlen har vi O A → + A B → = O B →, hvor O er oprindelsen. Det følger, at A B → = O B → - OA →.

OA → og O B → er radiusvektorerne for de givne punkter A og B, så punkternes koordinater har værdierne OA → = x a, ya, O B → = x b, y b.

Ved reglen for operationer på vektorer finder vi A B → = O B → - O A → = x b - x a, y b - y a.

At finde i tredimensionelt rum følger samme princip, kun for tre punkter.

For at finde koordinaterne for en vektor skal du finde forskellen mellem dens ende- og begyndelsespunkter.

Eksempel 1

Find koordinaterne OA → og A B → ved værdien af ​​koordinaterne for punkterne A (2, - 3), B (- 4, - 1).

Opløsning

Til at begynde med bestemmes radiusvektoren for punkt A. OA → = (2, - 3). For at finde A B → skal du trække værdien af ​​startpunkternes koordinater fra koordinaterne for slutpunkterne.

Vi får: A B → = (- 4 - 2, - 1 - (- 3)) = (- 6, 2).

Svar: OA → = (2, - 3), A B → = (- 6, - 2).

Eksempel 2

Et tredimensionelt rum med et punkt A = (3, 5, 7), A B → = (2, 0, - 2) er givet. Find koordinaterne for enden A B →.

Opløsning

Erstat koordinaterne for punkt A: A B → = (x b - 3, y b - 5, z b - 7).

Ved hypotese er det kendt, at A B → = (2, 0, - 2).

Det er kendt, at vektorernes lighed er sand, når koordinaterne er ens hhv. Lad os sammensætte et ligningssystem: x b - 3 = 2 y b - 5 = 0 z b - 7 = - 2

Det følger heraf, at koordinaterne for punktet B A B → er ens: x b = 5 y b = 5 z b = 5

Svar: B (5, 5, 5).

Hvis du bemærker en fejl i teksten, skal du vælge den og trykke på Ctrl + Enter

Første niveau

Koordinater og vektorer. Omfattende vejledning (2019)

I denne artikel vil vi begynde en diskussion af en "tryllestav", der vil give dig mulighed for at reducere mange geometriproblemer til simpel aritmetik. Denne "pind" kan gøre dit liv meget lettere, især i det tilfælde, hvor du føler dig usikker i konstruktionen af ​​rumlige figurer, sektioner osv. Alt dette kræver en vis fantasi og praktiske færdigheder. Metoden, som vi vil begynde at overveje her, vil give dig mulighed for næsten fuldstændig at abstrahere dig selv fra alle former for geometriske konstruktioner og ræsonnementer. Metoden kaldes "Koordinat metode"... I denne artikel vil vi overveje følgende spørgsmål:

1. Koordinat fly
2. Punkter og vektorer i planet
3. Konstruktion af en vektor ud fra to punkter
4. Vektorlængde (afstand mellem to punkter)
5. Midtpunktskoordinater
6. Punktprodukt af vektorer
7. Vinkel mellem to vektorer

Jeg tror, ​​du allerede har gættet, hvorfor koordinatmetoden hedder det? Det er rigtigt, at han modtog et sådant navn, da han ikke opererer med geometriske objekter, men med deres numeriske karakteristika (koordinater). Og selve transformationen, som giver os mulighed for at gå fra geometri til algebra, består i at indføre et koordinatsystem. Hvis den oprindelige figur var flad, så er koordinaterne todimensionelle, og hvis figuren er tredimensionelle, så er koordinaterne tredimensionelle. I denne artikel vil vi kun overveje det todimensionelle tilfælde. Og hovedmålet med artiklen er at lære dig, hvordan du bruger nogle grundlæggende teknikker i koordinatmetoden (de viser sig nogle gange at være nyttige til at løse problemer med planimetri i del B af eksamen). De næste to afsnit om dette emne er afsat til diskussion af metoder til løsning af problemer C2 (problemet med stereometri).

Hvor ville det være logisk at begynde at diskutere koordinatmetoden? Sandsynligvis ud fra begrebet et koordinatsystem. Husk da du først stødte på hende. Det forekommer mig, at man i 7. klasse, da man lærte om eksistensen af ​​en lineær funktion, f.eks. Lad mig minde dig om, at du byggede det punkt for punkt. Kan du huske? Du valgte et vilkårligt tal, erstattede det i formlen og beregnede på den måde. For eksempel hvis, så, hvis, så osv. Hvad fik du til sidst? Og du modtog point med koordinater: og. Derefter tegnede du et "kryds" (koordinatsystem), valgte en skala på det (hvor mange celler du vil have som et enhedssegment) og markerede på det de punkter, du modtog, som du derefter forbinder med en ret linje, den resulterende linje er grafen for funktionen.

Der er flere punkter her, som bør forklares dig lidt mere detaljeret:

1. Du vælger af bekvemmelighedsgrunde et enkelt segment, så det hele passer fint og kompakt ind i billedet.

2. Det antages, at aksen går fra venstre mod højre, og aksen går fra bund til top.

3. De skærer hinanden i rette vinkler, og punktet for deres skæringspunkt kaldes oprindelsen. Det er angivet med et bogstav.

4. Når du skriver koordinaterne for et punkt, for eksempel, til venstre i parentes er koordinaten for punktet langs aksen og til højre langs aksen. Især betyder det blot, at på det tidspunkt

5. For at indstille ethvert punkt på koordinataksen, skal du angive dets koordinater (2 tal)

6. For ethvert punkt på aksen,

7. For ethvert punkt på aksen,

8. Aksen kaldes abscisseaksen.

9. Aksen kaldes y-aksen.

Lad os nu tage det næste skridt med dig: Marker to punkter. Lad os forbinde disse to punkter med et segment. Og vi vil sætte pilen, som om vi tegnede et segment fra punkt til punkt: det vil sige, vi vil gøre vores segment rettet!

Husk, hvad kaldes en retningslinje ellers? Det er rigtigt, det kaldes en vektor!

Så hvis vi forbinder et punkt med et punkt, desuden vil begyndelsen være punkt A, og slutningen vil være punkt B, så får vi en vektor. Du lavede også denne dannelse i 8. klasse, husker du?

Det viser sig, at vektorer ligesom punkter kan betegnes med to tal: disse tal kaldes vektorens koordinater. Spørgsmålet er: tror du, det er nok for os at kende koordinaterne for begyndelsen og slutningen af ​​vektoren for at finde dens koordinater? Det viser sig, at ja! Og dette gøres meget enkelt:

Da punktet i vektoren er begyndelsen og a er slutningen, har vektoren således følgende koordinater:

For eksempel hvis, så er vektorens koordinater

Lad os nu gøre det modsatte, find vektorens koordinater. Hvad skal vi ændre for dette? Ja, du skal bytte begyndelsen og slutningen: nu vil begyndelsen af ​​vektoren være på punktet, og slutningen vil være på punktet. Derefter:

Se nærmere, hvordan er vektorer og? Deres eneste forskel er tegnene i koordinaterne. De er modsatte. Det er sædvanligt at skrive dette faktum sådan:

Nogle gange, hvis det ikke er specifikt specificeret, hvilket punkt der er begyndelsen af ​​vektoren, og hvilket er slutningen, så er vektorer ikke angivet med to store bogstaver, men med et lille bogstav, for eksempel: osv.

Nu lidt øve sig selv og find koordinaterne for følgende vektorer:

Undersøgelse:

Løs nu problemet lidt sværere:

Vektor med na-cha-lom på punktet har co-eller-di-na-ty. Nej-di-de abs-cis-su-punkter.

Alligevel er det ret prosaisk: Lad være koordinaterne til et punkt. Derefter

Jeg opgjorde systemet ved definition af, hvad koordinaterne for en vektor er. Så har punktet koordinater. Vi er interesserede i abscissen. Derefter

Svar:

Hvad kan du ellers gøre med vektorer? Ja, næsten alt er det samme som med almindelige tal (bortset fra at du ikke kan dividere, men du kan gange på to måder, hvoraf den ene vil diskutere her lidt senere)

1. Vektorer kan tilføjes til hinanden
2. Vektorer kan trækkes fra hinanden
3. Vektorer kan multipliceres (eller divideres) med et vilkårligt tal, der ikke er nul
4. Vektorer kan ganges med hinanden

Alle disse operationer har en meget klar geometrisk repræsentation. For eksempel, trekanten (eller parallelogram) reglen for addition og subtraktion:

Vektoren udvider eller trækker sig sammen eller ændrer retning, når den ganges eller divideres med et tal:

Men her vil vi være interesserede i spørgsmålet om, hvad der sker med koordinaterne.

1. Når vi adderer (fratrækker) to vektorer, adderer (fratrækker) vi deres koordinater element for element. Det er:

2. Når man multiplicerer (dividerer) en vektor med et tal, multipliceres (divideres) alle dens koordinater med dette tal:

For eksempel:

· Nej-di-te summen af ​​co-eller-di-nat vek-to-ra.

Lad os først finde koordinaterne for hver af vektorerne. De har begge samme oprindelse - oprindelsespunktet. Deres ender er anderledes. Derefter, . Lad os nu beregne koordinaterne for vektoren. Så er summen af ​​koordinaterne for den resulterende vektor.

Svar:

Løs nu selv følgende problem:

Find summen af ​​koordinaterne for en vektor

Vi tjekker:

Lad os nu overveje følgende problem: vi har to punkter på koordinatplanet. Hvordan finder man afstanden mellem dem? Lad det første punkt være, og det andet. Lad os betegne afstanden mellem dem igennem. Lad os lave følgende tegning for klarhedens skyld:

Hvad jeg har gjort? Jeg forbandt for det første punkterne, og også fra punktet tegnede jeg en linje parallel med aksen, og fra punktet tegnede jeg en linje parallel med aksen. Skærede de hinanden på et tidspunkt og dannede dermed en vidunderlig figur? Hvad er det bemærkelsesværdigt for? Ja, du og jeg ved næsten alt om en retvinklet trekant. Nå, Pythagoras sætning - helt sikkert. Det søgte segment er hypotenusen af ​​denne trekant, og segmenterne er benene. Hvad er koordinaterne for et punkt? Ja, de er lette at finde ud fra billedet: Da segmenterne er parallelle med akserne, og derfor er deres længder nemme at finde: hvis du angiver længderne af segmenterne, henholdsvis med, så

Lad os nu bruge Pythagoras sætning. Vi kender længden af ​​benene, vi finder hypotenusen:

Således er afstanden mellem to punkter roden af ​​summen af ​​kvadraterne af forskellene fra koordinaterne. Eller - afstanden mellem to punkter er længden af ​​den linje, der forbinder dem. Det er let at se, at afstanden mellem punkter er uafhængig af retning. Derefter:

Ud fra dette drager vi tre konklusioner:

Lad os øve os lidt i at beregne afstanden mellem to punkter:

For eksempel hvis, så er afstanden mellem og lig med

Eller lad os gå anderledes: find vektorens koordinater

Og find længden af ​​vektoren:

Som du kan se, det samme!

Træn nu selv lidt:

Opgave: find afstanden mellem de angivne punkter:

Vi tjekker:

Her er et par problemer mere for den samme formel, selvom de lyder lidt anderledes:

1. Nay-di-te kvadratrotte af længden af ​​århundrede-til-ra.

2. Nay-di-te kvadratisk rotte af længden af ​​århundrede-til-ra

Jeg tror, ​​du gjorde det nemt med dem? Vi tjekker:

1. Og dette er for opmærksomhed) Vi har allerede fundet koordinaterne for vektorerne og tidligere:. Så har vektoren koordinater. Kvadraten af ​​dens længde vil være:

2. Find vektorens koordinater

Så er kvadratet af dens længde

Intet kompliceret, vel? Simpel aritmetik, intet mere.

Følgende opgaver kan ikke kategoriseres entydigt, de er mere tilbøjelige til generel lærdom og evnen til at tegne enkle billeder.

1. Nay-di-te sinus af en vinkel on-off-cut, co-uni-nya-yu-shch-th punkt, med abscisse-aksen.

og

Hvad skal vi her? Du skal finde sinus for vinklen mellem og aksen. Og hvor ved vi, hvordan man leder efter en sinus? Til højre, i en retvinklet trekant. Så hvad skal vi gøre? Byg denne trekant!

Da koordinaterne for punktet er og, er segmentet ens, og segmentet. Vi skal finde vinklens sinus. Lad mig minde dig om, at sinus er forholdet mellem det modsatte ben og hypotenusen

Hvad er der tilbage for os at gøre? Find hypotenusen. Du kan gøre det på to måder: ved Pythagoras sætning (benene er kendt!) Eller ved formlen for afstanden mellem to punkter (faktisk det samme som den første måde!). Jeg vil gå den anden vej:

Svar:

Den næste opgave vil virke endnu lettere for dig. Hun - på koordinaterne af punktet.

Mål 2. Per-pen-di-kular sænkes fra punktet til abs-ciss-aksen. Nay-di-te abs-cis-su os-no-va-nia per-pen-di-ku-la-ra.

Lad os lave en tegning:

Basen af ​​den vinkelrette er det punkt, hvor den krydser abscisse-aksen (aksen), for mig er dette punktet. Figuren viser, at den har koordinater:. Vi er interesserede i abscissen - det vil sige "x"-komponenten. Det er ligeværdigt.

Svar: .

Mål 3. Under betingelserne i den foregående opgave, find summen af ​​afstandene fra et punkt til koordinatakserne.

Opgaven er generelt elementær, hvis du ved, hvad afstanden fra et punkt til akserne er. Du ved? Jeg håber, men jeg minder dig stadig om:

Så på mit billede, der ligger lidt højere, har jeg allerede tegnet en sådan vinkelret? Hvilken akse er det til? Til aksen. Og hvad er dens længde så lig? Det er ligeværdigt. Tegn nu selv vinkelret på aksen og find dens længde. Det bliver lige, ikke? Så er deres sum lig.

Svar: .

Opgave 4. I betingelserne for opgave 2, find ordinaten af ​​punktet symmetrisk med punktet i forhold til abscisseaksen.

Jeg tror, ​​du intuitivt forstår, hvad symmetri er? Mange genstande har det: mange bygninger, borde, flyvemaskiner, mange geometriske former: en kugle, cylinder, firkant, rombe osv. Groft sagt kan symmetri forstås som følger: en figur består af to (eller flere) identiske halvdele. Denne symmetri kaldes aksial. Hvad er så en akse? Dette er præcis den linje, langs hvilken en figur relativt set kan "skæres" i identiske halvdele (på dette billede er symmetriaksen en lige linje):

Lad os nu vende tilbage til vores problem. Vi ved, at vi leder efter et punkt, der er symmetrisk om aksen. Så er denne akse symmetriaksen. Det betyder, at vi skal markere et punkt, så aksen skærer segmentet i to lige store dele. Prøv selv at markere et sådant punkt. Sammenlign nu med min løsning:

Gjorde du det samme? Godt! På det fundne punkt er vi interesserede i ordinaten. Hun er ligeværdig

Svar:

Fortæl mig nu, efter at have tænkt over sekunder, hvad vil abscissen være af et punkt, der er symmetrisk til punkt A med hensyn til ordinaten? Hvad er dit svar? Rigtigt svar: .

Generelt kan reglen skrives sådan:

Et punkt, der er symmetrisk til et punkt i forhold til abscisseaksen, har koordinater:

Et punkt, der er symmetrisk med et punkt omkring ordinataksen, har koordinater:

Nå, nu er det fuldstændig skræmmende opgave: find koordinaterne for et punkt, der er symmetrisk med et punkt, i forhold til origo. Du tænker først selv, og ser så på min tegning!

Svar:

Nu parallelogram problem:

Opgave 5: Punkterne er ver-shi-na-mi paral-le-lo-gram-ma. Nej-di-te eller-di-na-tu point.

Du kan løse dette problem på to måder: logik og koordinatmetoden. Jeg vil først anvende koordinatmetoden, og derefter vil jeg fortælle dig, hvordan du kan beslutte andet.

Det er helt klart, at punktets abscisse er lig med. (den ligger på vinkelret tegnet fra et punkt til abscisseaksen). Vi skal finde ordinaten. Lad os udnytte det faktum, at vores figur er et parallelogram, hvilket betyder det. Find længden af ​​segmentet ved hjælp af formlen for afstanden mellem to punkter:

Vi sænker den vinkelrette, der forbinder punktet med aksen. Skæringspunktet vil være markeret med et bogstav.

Segmentlængden er. (find selve problemet, hvor vi diskuterede dette punkt), så finder vi længden af ​​segmentet ved Pythagoras sætning:

Længden af ​​linjen er nøjagtig den samme som dens ordinat.

Svar: .

En anden løsning (jeg giver lige et billede, der illustrerer det)

Løsningsfremskridt:

1. Opførsel

2. Find koordinaterne for punktet og længden

3. Bevis det.

En til segmentlængdeproblem:

Punkterne vises-la-are-sya ver-shi-na-mi tre-kul-ni-ka. Nay-di-te er længden af ​​dens midterlinje, paral-lel-noy.

Kan du huske, hvad midterlinjen i en trekant er? Så er denne opgave elementær for dig. Hvis du ikke husker det, så vil jeg minde dig om: midterlinjen i en trekant er den linje, der forbinder midtpunkterne på modsatte sider. Den er parallel med basen og lig med halvdelen af ​​den.

Basen er et linjestykke. Vi var nødt til at lede efter dens længde tidligere, den er ens. Så er længden af ​​midterlinjen halv og lige.

Svar: .

Kommentar: dette problem kan løses på en anden måde, som vi vender tilbage til lidt senere.

I mellemtiden er her et par opgaver til dig, øv dem, de er ret enkle, men de hjælper dig med at "få din hånd" ved hjælp af koordinatmetoden!

1. Punkterne er ver-shi-na-mi tra-petsii. Nay-di-te er længden af ​​dens midterlinje.

2. Prikker og are-la-is-sya ver-shi-na-mi pa-ra-le-lo-gram-ma. Nej-di-te eller-di-na-tu point.

3. Nay-di-te længde fra-cut, co-single-nya-yu-shch-go point og

4. Nay-di-te område af den smukke fi-gu-ry på co-or-di-nat-noy flyet.

5. Cirklen med centrum ved na-cha-le ko-or-di-nat passerer gennem punktet. Nej-di-te hendes ra-di-us.

6. Nai-di-te ra-di-us af cirklen, beskrevet-san-noy nær rect-coal-ni-ka, hjørnerne af ko-to-ro-go har en co-op -di-na -du med-dyrlæge-men

Løsninger:

1. Det er kendt, at midterlinjen i en trapez er lig med halvsummen af ​​dens baser. Grundlaget er ens, og basen er. Derefter

Svar:

2. Den nemmeste måde at løse dette problem på er at bemærke det (parallelografireglen). Beregn koordinaterne for vektorer og er ikke svært:. Når vektorer tilføjes, tilføjes koordinaterne. Derefter har koordinater. Punktet har også de samme koordinater, da vektorens oprindelse er punktet med koordinater. Vi er interesserede i ordinaten. Det er ligeværdigt.

Svar:

3. Vi handler umiddelbart efter formlen for afstanden mellem to punkter:

Svar:

4. Se på billedet og fortæl mig, mellem hvilke to figurer er det skraverede område "sandwich"? Det er klemt mellem to firkanter. Så er arealet af den krævede figur lig med arealet af den store firkant minus arealet af den lille. Siden af ​​den lille firkant er et linjestykke, der forbinder punkterne, og dets længde er

Så er arealet af den lille firkant

Vi gør det samme med en stor firkant: dens side er et segment, der forbinder punkterne, og dens længde er

Så er arealet af den store plads

Vi finder arealet af den nødvendige figur ved formlen:

Svar:

5. Hvis cirklen har oprindelsen af ​​koordinater som centrum og går gennem et punkt, så vil dens radius være nøjagtigt lig med længden af ​​segmentet (tegn et billede, og du vil forstå, hvorfor dette er indlysende). Lad os finde længden af ​​dette segment:

Svar:

6. Det er kendt, at radius af en cirkel omskrevet om et rektangel er lig med halvdelen af ​​dens diagonal. Lad os finde længden af ​​en af ​​de to diagonaler (i et rektangel er de trods alt lige store!)

Svar:

Nå, har du beskæftiget dig med alt? Det var ikke særlig svært at finde ud af det, vel? Reglen her er én - at kunne lave et visuelt billede og blot "læse" alle data fra det.

Vi har meget lidt tilbage. Der er bogstaveligt talt to punkter mere, som jeg gerne vil diskutere.

Lad os prøve at løse dette simple problem. Lad to point og få. Find koordinaterne for segmentets midtpunkt. Løsningen på dette problem er som følger: lad punktet være det ønskede midtpunkt, så har det koordinaterne:

Det er: koordinaterne for stykkets midtpunkt = det aritmetiske middelværdi af de tilsvarende koordinater for stykkets ender.

Denne regel er meget enkel og forårsager normalt ikke vanskeligheder for eleverne. Lad os se, hvilke opgaver og hvordan det bruges:

1. Nay-di-te eller-di-na-tu-re-di-us from-cut, co-uni-nya-yu-shch-go point og

2. Punkterne vises-la-are-sya ver-shi-na-mi-you-rekh-coal-no-ka. Nay-di-te eller-di-na-tu punkter af pe-re-se-ch-niya hans dia-go-na-lei.

3. Nej-di-de abs-cis-su center-tra af cirklen, beskrevet-san-noy nær kul-no-ka, hjørnerne af ko-to-ro-go har co-op-di- na-du med-dyrlæge-men.

Løsninger:

1. Det første problem er bare en klassiker. Vi handler med det samme for at bestemme midten af ​​segmentet. Den har koordinater. Ordinaten er.

Svar:

2. Det er let at se, at den givne firkant er et parallelogram (selv en rombe!). Det kan du selv bevise ved at beregne længderne af siderne og sammenligne dem med hinanden. Hvad ved jeg om et parallelogram? Dens diagonaler er halveret af skæringspunktet! Aha! Så hvad er skæringspunktet for diagonalerne? Dette er midten af ​​enhver af diagonalerne! Jeg vil især vælge diagonalen. Så har punktet koordinater Punktets ordinat er lig med.

Svar:

3.Hvad er midten af ​​cirklen omskrevet om rektanglet med? Det falder sammen med skæringspunktet mellem dets diagonaler. Hvad ved du om diagonalerne i et rektangel? De er lige store, og krydset er halveret. Opgaven blev reduceret til den forrige. Tag for eksempel diagonalen. Så hvis er midten af ​​den omskrevne cirkel, så er midten. Leder efter koordinater: Abscisse er ens.

Svar:

Øv dig nu lidt selv, jeg vil lige give svarene på hver opgave, så du kan teste dig selv.

1. Nai-di-te ra-di-us af cirklen, beskrevet-san-noy omkring trekanten, hjørnerne af co-to-ro-go har co-eller-di -no misters

2. Nai-di-te eller-di-na-tu center-tra af cirklen, beskriv-san-noy omkring trekanten-nik, hjørnerne af ko-to-ro-go har koordinater

3. How-to-ra-di-u-sa skal der være en cirkel med et centrum i punktet, så den ville røre abs-cissa-aksen?

4. Nay-di-te eller-di-na-tu punkter for gensåning af aksen og cut-off, co-uni-nya-yu-shch-go punkt og

Svar:

Lykkedes det? Jeg håber virkelig på det! Nu - det sidste skub. Vær særlig forsigtig nu. Det materiale, som jeg nu vil forklare, er direkte relateret ikke kun til simple problemer på koordinatmetoden fra B-delen, men forekommer også overalt i C2-problemet.

Hvilke af mine løfter har jeg ikke holdt endnu? Husk, hvilke operationer på vektorer jeg lovede at introducere, og hvilke jeg til sidst introducerede? Er jeg sikker på, at jeg ikke har glemt noget? Glemte! Glemte at forklare, hvad multiplikation af vektorer betyder.

Der er to måder at gange en vektor med en vektor. Afhængigt af den valgte metode vil vi få genstande af forskellig karakter:

Vektorproduktet er ret vanskeligt. Hvordan man gør det, og hvad det er til, vil vi diskutere med dig i den næste artikel. Og i denne vil vi fokusere på prikproduktet.

Der er allerede to måder, vi kan beregne det på:

Som du gættede, skulle resultatet være det samme! Så lad os først se på den første måde:

Prik produkt med hensyn til koordinater

Find: - almindelig prik produktnotation

Formlen for beregningen er som følger:

Det vil sige, at prikproduktet = summen af ​​produkterne af vektorernes koordinater!

Eksempel:

Nai di te

Opløsning:

Lad os finde koordinaterne for hver af vektorerne:

Vi beregner prikproduktet ved formlen:

Svar:

Se, absolut intet kompliceret!

Nå, prøv det nu selv:

Nay-di-te scalar-noe pro-iz-ve-de-de-vek-to-moat og

Klarede du dig? Måske har du bemærket en lille fangst? Lad os tjekke:

Koordinaterne for vektorerne er de samme som i forrige opgave! Svar: .

Ud over koordinaten er der en anden måde at beregne prikproduktet på, nemlig gennem længderne af vektorerne og cosinus af vinklen mellem dem:

Angiver vinklen mellem vektorer og.

Det vil sige, at prikproduktet er lig med produktet af vektorernes længder og cosinus af vinklen mellem dem.

Hvorfor har vi brug for denne anden formel, hvis vi har den første, som er meget enklere, i det mindste er der ingen cosinus i den. Og det er nødvendigt, så vi ud fra den første og anden formel kan udlede, hvordan vi finder vinklen mellem vektorer!

Lad Så husk formlen for længden af ​​vektoren!

Så hvis jeg erstatter disse data med prikproduktformlen, får jeg:

Men på en anden måde:

Så hvad fik du og jeg? Vi har nu en formel til at beregne vinklen mellem to vektorer! Nogle gange er det også skrevet sådan for kortheds skyld:

Det vil sige, at algoritmen til at beregne vinklen mellem vektorer er som følger:

1. Beregn prikproduktet i form af koordinater
2. Find længderne af vektorerne og gang dem
3. Divider resultatet af punkt 1 med resultatet af punkt 2

Lad os øve os med eksempler:

1. Nay-di-te er vinklen mellem århundrede-til-ra-mi og. Giv svaret i gra-du-sakh.

2. Under betingelserne i den foregående opgave, find cosinus mellem vektorerne

Lad os gøre dette: Jeg hjælper dig med at løse det første problem, og prøv at gøre det andet selv! Jeg er enig? Så lad os komme i gang!

1. Disse vektorer er vores gamle kendinge. Vi har allerede talt deres prik-produkt, og det var lige. Deres koordinater er:,. Så finder vi deres længder:

Så leder vi efter cosinus mellem vektorerne:

Hvad er cosinus af vinklen? Dette er hjørnet.

Svar:

Løs nu det andet problem selv, og så sammenligner vi! Jeg vil kun give dig en meget kort løsning:

2. har koordinater, har koordinater.

Lad være vinklen mellem vektorer og så

Svar:

Det skal bemærkes, at problemer direkte på vektorer og koordinatmetoden i del B af eksamensarbejdet er ret sjældne. Langt de fleste C2-problemer kan dog nemt løses ved at indføre et koordinatsystem. Så du kan betragte denne artikel som grundlaget, på grundlag af hvilket vi vil lave ret snedige konstruktioner, som vi skal bruge til at løse komplekse problemer.

KOORDINATER OG VEKTORER. GENNEMSNIT ROVEN

Du og jeg fortsætter med at studere koordinatmetoden. I den sidste del udledte vi en række vigtige formler, der giver dig mulighed for at:

1. Find vektorkoordinater
2. Find længden af ​​en vektor (alternativt: afstanden mellem to punkter)
3. Tilføj, subtraher vektorer. Gang dem med et reelt tal
4. Find midtpunktet af et linjestykke
5. Beregn prikprodukt af vektorer
6. Find vinklen mellem vektorer

Hele koordinatmetoden passer naturligvis ikke ind i disse 6 punkter. Det ligger i hjertet af sådan en videnskab som analytisk geometri, som du skal stifte bekendtskab med på universitetet. Jeg vil bare bygge et fundament, der giver dig mulighed for at løse problemer i en enkelt stat. eksamen. Vi fandt ud af opgaverne i del B i Nu er det tid til at flytte til et kvalitativt nyt niveau! Denne artikel vil blive afsat til metoden til at løse de problemer C2, hvor det ville være rimeligt at skifte til metoden med koordinater. Denne rationalitet er bestemt af, hvad der kræves for at finde i problemet, og hvilken figur der er givet. Så jeg ville bruge koordinatmetoden, hvis spørgsmålene er:

1. Find vinklen mellem to planer
2. Find vinklen mellem en linje og et plan
3. Find vinklen mellem to rette linjer
4. Find afstanden fra et punkt til et fly
5. Find afstanden fra et punkt til en lige linje
6. Find afstanden fra en lige linje til et fly
7. Find afstanden mellem to lige linjer

Hvis tallet i problemformuleringen er et omdrejningslegeme (kugle, cylinder, kegle ...)

Egnede former for koordinatmetoden er:

1. Rektangulær parallelepipedum
2. Pyramide (trekantet, firkantet, sekskantet)

Også efter min erfaring det er uhensigtsmæssigt at bruge koordinatmetoden til:

1. Finde tværsnitsarealerne
2. Beregning af kropsvolumen

Det skal dog straks bemærkes, at tre situationer "ugunstige" for koordinatmetoden er ret sjældne i praksis. I de fleste opgaver kan han blive din redningsmand, især hvis du ikke er særlig stærk i tredimensionelle konstruktioner (som nogle gange er ret indviklede).

Hvad er alle de tal, jeg har nævnt ovenfor? De er ikke længere flade, som for eksempel en firkant, trekant, cirkel, men tredimensionelle! Derfor skal vi ikke overveje et todimensionelt, men et tredimensionelt koordinatsystem. Den bygges ganske let: Ud over abscisse- og ordinatakserne vil vi introducere endnu en akse, applikataksen. Figuren viser skematisk deres relative position:

Alle af dem er indbyrdes vinkelrette, skærer hinanden på et punkt, som vi vil kalde oprindelsen. Abscisseaksen vil som før blive betegnet, ordinataksen - og den indtastede applikationsakse -.

Hvis hvert punkt på flyet tidligere var karakteriseret ved to tal - abscissen og ordinaten, så er hvert punkt i rummet allerede beskrevet med tre numre - abscissen, ordinaten, anvendelig. For eksempel:

Følgelig er punktets abscisse ens, ordinaten er og applikatet er det.

Nogle gange kaldes et punkts abscisse også for punktets projektion på abscisseaksen, ordinaten er punktets projektion på ordinataksen, og applikatet er projektionen af ​​punktet på applikationsaksen. Følgelig, hvis et punkt er specificeret, så et punkt med koordinater:

kaldes projektion af et punkt på et plan

kaldes projektion af et punkt på et plan

Et naturligt spørgsmål opstår: Er alle formler afledt for det todimensionelle tilfælde gyldige i rummet? Svaret er ja, de er fair og ser ens ud. For en lille detalje. Jeg tror, ​​du allerede har gættet til hvilken. Vi bliver nødt til at tilføje endnu et udtryk til alle formler, som er ansvarlig for den applikerede akse. Nemlig.

1. Hvis der gives to point:, så:

• Vektorkoordinater:
• Afstand mellem to punkter (eller vektorlængde)
• Midten af ​​segmentet har koordinater

2. Hvis to vektorer er givet: og, så:

• Deres punktprodukt er:
• Cosinus for vinklen mellem vektorer er:

Pladsen er dog ikke så enkel. Som du kan forestille dig, introducerer tilføjelsen af ​​endnu en koordinat en betydelig variation i spektret af figurer, der "lever" i dette rum. Og for yderligere fortælling er jeg nødt til at introducere nogle, groft sagt, "generalisering" af den lige linje. Denne "generalisering" er flyet. Hvad ved du om et fly? Prøv at besvare spørgsmålet, hvad er et fly? Det er meget svært at sige. Men vi har alle en intuitiv idé om, hvordan det ser ud:

Groft sagt er dette en slags endeløst "blad" gemt i rummet. "Uendelig" skal forstås, at planet strækker sig i alle retninger, det vil sige, at dets areal er lig med uendelig. Denne forklaring "på fingrene" giver dog ikke den mindste idé om flyets struktur. Og vi vil være interesserede i det.

Lad os huske et af geometriens grundlæggende aksiomer:

• en lige linje går gennem to forskellige punkter på planet, desuden kun ét:

Eller dets modstykke i rummet:

Selvfølgelig husker du, hvordan man udleder ligningen for en lige linje fra to givne punkter, det er slet ikke svært: hvis det første punkt har koordinater: og det andet, så vil ligningen for den rette linje være som følger:

Du gik igennem det her i 7. klasse. I rummet ser ligningen for en ret linje således ud: lad os have to punkter med koordinater: så har ligningen for en ret linje, der går gennem dem, formen:

For eksempel går en lige linje gennem punkterne:

Hvordan skal dette forstås? Det skal forstås som følger: et punkt ligger på en ret linje, hvis dets koordinater opfylder følgende system:

Vi vil ikke være særlig interesserede i linjens ligning, men vi skal være opmærksomme på det meget vigtige koncept for en linjes retningsvektor. - enhver ikke-nul vektor, der ligger på den givne linje eller parallelt med den.

For eksempel er begge vektorer retningsvektorer af en ret linje. Lad være et punkt, der ligger på en lige linje, og være dets retningsvektor. Så kan ligningen for den rette linje skrives på følgende form:

Endnu en gang vil jeg ikke være særlig interesseret i ligningen for en lige linje, men jeg har virkelig brug for, at du husker, hvad en retningsvektor er! Igen: det er ENHVER ikke-nul vektor, der ligger på en lige linje eller parallel med den.

Træk tilbage ligning af et plan i tre givne punkter er ikke længere så trivielt, og normalt behandles dette problem ikke i et gymnasieforløb. Men forgæves! Denne teknik er afgørende, når vi bruger koordinatmetoden til at løse komplekse problemer. Jeg går dog ud fra, at du er ivrig efter at lære noget nyt? Desuden vil du være i stand til at imponere din lærer på universitetet, når det viser sig, at du allerede ved hvordan med den metodik, der normalt studeres i løbet af analytisk geometri. Så lad os komme i gang.

Et plans ligning er ikke for forskellig fra ligningen for en lige linje på et plan, den har nemlig formen:

nogle tal (ikke alle lig nul), men variabler, for eksempel: osv. Som du kan se, er planens ligning ikke meget forskellig fra ligningen for en ret linje (lineær funktion). Men kan du huske, hvad du og jeg sagde? Vi sagde, at hvis vi har tre punkter, der ikke ligger på en lige linje, så kan flyets ligning rekonstrueres entydigt ud fra dem. Men hvordan? Jeg vil prøve at forklare dig.

Da planens ligning har formen:

Og punkterne hører til dette plan, så når vi erstatter koordinaterne for hvert punkt i planets ligning, skulle vi få den korrekte identitet:

Således bliver det nødvendigt at løse tre ligninger selv med ukendte! Dilemma! Det kan du dog altid gå ud fra (hertil skal du dividere med). Således får vi tre ligninger med tre ubekendte:

Vi vil dog ikke løse et sådant system, men skrive et mystisk udtryk, der følger af det:

Ligning for et plan, der passerer gennem tre givne punkter

\ [\ venstre | (\ begynder (array) (* (20) (c)) (x - (x_0)) & ((x_1) - (x_0)) & ((x_2) - (x_0)) \\ (y - (y_0) ) & ((y_1) - (y_0)) & ((y_2) - (y_0)) \\ (z - (z_0)) & ((z_1) - (z_0)) & ((z_2) - (z_0)) \ ende (array)) \ højre | = 0 \]

Hold op! Hvad er dette? Et meget usædvanligt modul! Det objekt, du ser foran dig, har dog intet at gøre med modulet. Dette objekt kaldes en tredjeordens determinant. Fra nu af, når du beskæftiger dig med metoden med koordinater på et plan, vil du meget ofte støde på de samme determinanter. Hvad er en tredjeordens determinant? Mærkeligt nok er dette kun et tal. Det er tilbage at forstå, hvilket specifikt tal vi vil sammenligne med determinanten.

Lad os først skrive tredjeordens determinant i en mere generel form:

Hvor er nogle tal. Desuden mener vi med det første indeks linjenummeret og med indekset - kolonnenummeret. For eksempel betyder det, at det givne tal er i skæringspunktet mellem den anden række og den tredje kolonne. Lad os stille det næste spørgsmål: hvordan skal vi præcist beregne en sådan determinant? Det vil sige, hvilket specifikt tal vil vi matche til det? For determinanten af ​​den tredje orden er der en heuristisk (visuel) regel for trekanten, den ser sådan ud:

1. Produktet af elementerne i hoveddiagonalen (fra øverste venstre hjørne til nederste højre) produktet af elementerne, der danner den første trekant "vinkelret" på hoveddiagonalens produkt af de elementer, der danner den anden trekant "vinkelret" på hoveddiagonalen diagonal
2. Produktet af elementerne i den sekundære diagonal (fra øverste højre hjørne til nederste venstre) produktet af elementerne, der danner den første trekant "vinkelret" på den sekundære diagonale produkt af de elementer, der danner den anden trekant "vinkelret" på den sekundære diagonal
3. Så er determinanten lig med forskellen mellem værdierne opnået ved trin og

Hvis vi skriver alt dette i tal, får vi følgende udtryk:

Ikke desto mindre behøver du ikke huske beregningsmetoden i denne form, det er nok bare at beholde trekanterne og selve ideen om, hvad der lægger op til hvad, og hvad der så trækkes fra hvad).

Lad os illustrere trekantmetoden med et eksempel:

1. Beregn determinanten:

Lad os finde ud af, hvad vi tilføjer, og hvad vi trækker fra:

Udtrykket, der kommer med et "plus":

Dette er hoveddiagonalen: produktet af elementerne er

Den første trekant, "vinkelret på hoveddiagonalen: produktet af elementerne er

Den anden trekant, "vinkelret på hoveddiagonalen: produktet af elementerne er

Tilføj tre tal:

Udtryk, der kommer med et "minus"

Dette er en sidediagonal: produktet af elementerne er

Den første trekant, "vinkelret på sidediagonalen: produktet af elementerne er

Anden trekant, "vinkelret på sidediagonalen: produktet af elementerne er

Tilføj tre tal:

Det eneste, der skal gøres, er at trække summen af ​​minusleddene fra summen af ​​plusleddene:

På denne måde

Som du kan se, er der intet kompliceret og overnaturligt i beregningen af ​​determinanter af tredje orden. Det er bare vigtigt at huske på trekanter og ikke lave regnefejl. Prøv nu at beregne det selv:

Vi tjekker:

1. Første trekant vinkelret på hoveddiagonalen:
2. Anden trekant vinkelret på hoveddiagonalen:
3. Summen af ​​udtryk med plus:
4. Første trekant vinkelret på sidediagonalen:
5. Anden trekant vinkelret på den sekundære diagonal:
6. Summen af ​​led med minus:
7. Summen af ​​led med plus minus summen af ​​led med minus:

Her er et par flere determinanter til dig, beregn deres værdier selv og sammenlign dem med svarene:

Svar:

Tja, faldt det hele sammen? Super, så kan du komme videre! Hvis der er vanskeligheder, så er mit råd dette: På internettet er der en masse programmer til beregning af determinanten online. Det eneste du skal bruge er at komme med din egen determinant, udregne den selv og derefter sammenligne den med, hvad programmet beregner. Og så videre, indtil resultaterne begynder at falde sammen. Jeg er sikker på, at dette øjeblik ikke lader vente på sig!

Lad os nu gå tilbage til den determinant, som jeg skrev ud, da jeg talte om ligningen for et fly, der passerer gennem tre givne punkter:

Alt du behøver er at beregne dens værdi direkte (ved hjælp af trekanter-metoden) og sætte resultatet til nul. Da de er variable, vil du naturligvis få nogle udtryk, der afhænger af dem. Det er dette udtryk, der vil være ligningen for planet, der passerer gennem tre givne punkter, der ikke ligger på én lige linje!

Lad os illustrere dette med et simpelt eksempel:

1. Konstruer ligningen for det plan, der passerer gennem punkterne

Lad os sammensætte determinanten for disse tre punkter:

Lad os forenkle:

Nu beregner vi det direkte ved reglen om trekanter:

\ [(\ venstre | (\ begynder (matrix) (* (20) (c)) (x + 3) & 2 & 6 \\ (y - 2) & 0 & 1 \\ (z + 1) & 5 & 0 \ ende (array)) \ højre | = \ venstre ((x + 3) \ højre) \ cdot 0 \ cdot 0 + 2 \ cdot 1 \ cdot \ venstre ((z + 1) \ højre) + \ venstre ((y - 2) \ højre) \ cdot 5 \ cdot 6 -) \]

Således har ligningen for planet, der passerer gennem punkterne, formen:

Prøv nu at løse et problem selv, og så vil vi diskutere det:

2. Find ligningen for det fly, der går gennem punkterne

Nå, lad os nu diskutere løsningen:

Vi sammensætter determinanten:

Og vi beregner dens værdi:

Så har planens ligning formen:

Eller, efter at have reduceret med, får vi:

Nu to opgaver til selvkontrol:

1. Konstruer ligningen for et plan, der går gennem tre punkter:

Svar:

Var det hele sammenfaldende? Igen, hvis der er visse vanskeligheder, så er mit råd dette: du tager tre punkter fra dit hoved (med en høj grad af sandsynlighed vil de ikke ligge på den samme lige linje), du bygger et fly langs dem. Og så tjekker du dig selv online. For eksempel på webstedet:

Men ved hjælp af determinanter vil vi ikke kun konstruere flyets ligning. Husk, at jeg fortalte dig, at det ikke kun er prikproduktet, der er defineret for vektorer. Der er også et vektorprodukt, såvel som et blandet produkt. Og hvis prikproduktet af to vektorer er et tal, så vil vektorproduktet af to vektorer være en vektor, og denne vektor vil være vinkelret på de givne:

Desuden vil dets modul være lig med arealet af parallelogrammet bygget på vektorerne og. Vi skal bruge denne vektor til at beregne afstanden fra et punkt til en ret linje. Hvordan kan vi beregne krydsproduktet af vektorer, og hvis deres koordinater er givet? Determinanten for den tredje orden kommer os til hjælp igen. Inden jeg går videre til algoritmen til beregning af vektorproduktet, skal jeg dog lave en lille lyrisk digression.

Denne digression vedrører basisvektorer.

De er vist skematisk i figuren:

Hvorfor tror du, de kaldes basic? Faktum er, at:

Eller på billedet:

Gyldigheden af ​​denne formel er indlysende, fordi:

Vektor produkt

Nu kan jeg begynde at introducere krydsproduktet:

Vektorproduktet af to vektorer er en vektor, der beregnes efter følgende regel:

Lad os nu give nogle eksempler på beregning af et krydsprodukt:

Eksempel 1: Find krydsproduktet af vektorer:

Løsning: Jeg komponerer en determinant:

Og jeg regner det ud:

Nu, fra notation i form af basisvektorer, vil jeg vende tilbage til den sædvanlige notation af en vektor:

På denne måde:

Prøv det nu.

Parat? Vi tjekker:

Og traditionelt to opgaver til kontrol:

1. Find krydsproduktet af følgende vektorer:
2. Find krydsproduktet af følgende vektorer:

Svar:

Blandet produkt af tre vektorer

Den sidste konstruktion, jeg har brug for, er et blandet produkt af tre vektorer. Det er ligesom et skalært tal et tal. Der er to måder at beregne det på. - gennem en determinant, - gennem et blandet produkt.

Lad os nemlig have tre vektorer:

Derefter kan det blandede produkt af tre vektorer, betegnet med, beregnes som:

1. - det vil sige, at det blandede produkt er prikproduktet af en vektor ved krydsproduktet af to andre vektorer

For eksempel er det blandede produkt af tre vektorer:

Prøv selv at beregne det gennem krydsproduktet og sørg for, at resultaterne stemmer overens!

Og igen - to eksempler på en uafhængig løsning:

Svar:

Koordinere systemvalg

Nå, nu har vi alt det nødvendige grundlag af viden til at løse komplekse stereometriske problemer i geometri. Men før jeg går direkte videre til eksemplerne og algoritmerne for deres løsning, tror jeg, at det vil være nyttigt at dvæle ved et andet spørgsmål: hvordan præcist vælge et koordinatsystem for en bestemt figur. Det er jo valget af den relative position af koordinatsystemet og figuren i rummet, der i sidste ende vil afgøre, hvor besværlige beregningerne bliver.

Lad mig minde dig om, at vi i dette afsnit ser på følgende former:

1. Rektangulær parallelepipedum
2. Lige prisme (trekantet, sekskantet ...)
3. Pyramide (trekantet, firkantet)
4. Tetraeder (samme som trekantet pyramide)

For en rektangulær kasse eller terning anbefaler jeg dig følgende konstruktion:

Det vil sige, jeg vil placere figuren "i hjørnet". Terningen og parallelepipediet er meget flotte former. For dem kan du altid nemt finde koordinaterne for dets hjørner. For eksempel, hvis (som vist på billedet)

så er koordinaterne for hjørnerne som følger:

Det behøver du selvfølgelig ikke huske, men det er ønskeligt at huske, hvordan man bedst placerer en terning eller et rektangulært parallelepipedum.

Lige prisme

Prismet er en mere skadelig figur. Den kan placeres i rummet på forskellige måder. Imidlertid forekommer følgende mulighed for mig at være den mest acceptable:

Trekantet prisme:

Det vil sige, at vi sætter en af ​​siderne af trekanten helt på aksen, og en af ​​hjørnerne falder sammen med oprindelsen.

Sekskantet prisme:

Det vil sige, at et af hjørnerne falder sammen med oprindelsen, og en af ​​siderne ligger på aksen.

Firkantet og sekskantet pyramide:

En situation, der ligner en terning: Juster de to sider af basen med koordinatakserne, juster en af ​​hjørnerne med oprindelsen. Den eneste lille vanskelighed vil være at beregne koordinaterne for punktet.

For en sekskantet pyramide - det samme som for et sekskantet prisme. Hovedopgaven vil igen være at finde toppunktets koordinater.

Tetrahedron (trekantet pyramide)

Situationen er meget lig den, jeg gav for et trekantet prisme: et toppunkt falder sammen med oprindelsen, den ene side ligger på koordinataksen.

Nå, nu er du og jeg endelig tæt på at komme i gang med at løse problemer. Ud fra det, jeg sagde i begyndelsen af ​​artiklen, kunne du drage følgende konklusion: De fleste C2-problemer er opdelt i 2 kategorier: hjørneproblemer og afstandsproblemer. Først vil vi overveje problemet med at finde en vinkel. De er til gengæld opdelt i følgende kategorier (i takt med at sværhedsgraden øges):

At finde hjørner

1. Find vinklen mellem to lige linjer
2. Finde vinklen mellem to planer

Lad os overveje disse opgaver sekventielt: start med at finde vinklen mellem to lige linjer. Nå, husk, har du og jeg ikke løst lignende eksempler før? Husk, vi havde allerede noget lignende ... Vi ledte efter en vinkel mellem to vektorer. Jeg vil minde dig om, hvis to vektorer er givet: og så er vinklen mellem dem fundet ud fra forholdet:

Nu har vi et mål - at finde vinklen mellem to lige linjer. Lad os vende tilbage til det "flade billede":

Hvor mange vinkler fik vi, når to lige linjer skærer hinanden? Lige så mange ting. Sandt nok er kun to af dem ikke ens, mens andre er lodrette i forhold til dem (og derfor falder sammen med dem). Så hvilken vinkel skal vi overveje vinklen mellem to rette linjer: eller? Her er reglen: vinklen mellem to rette linjer er altid ikke mere end grader... Det vil sige, at vi fra to vinkler altid vil vælge den vinkel med det mindste gradmål. Det vil sige, at på dette billede er vinklen mellem to rette linjer ens. For ikke at bøvle med at finde den mindste af to vinkler hver gang, foreslog snedige matematikere at bruge modulet. Vinklen mellem to rette linjer bestemmes således af formlen:

Du, som en opmærksom læser, burde have et spørgsmål: hvor får vi i virkeligheden netop disse tal, som vi skal bruge for at beregne cosinus af en vinkel? Svar: vi tager dem fra retningsvektorerne for de rette linjer! Algoritmen til at finde vinklen mellem to rette linjer er således som følger:

1. Vi anvender formel 1.

Eller mere detaljeret:

1. Vi leder efter koordinaterne for retningsvektoren for den første rette linje
2. Vi leder efter koordinaterne for retningsvektoren for den anden rette linje
3. Beregn modulet af deres prikprodukt
4. Vi leder efter længden af ​​den første vektor
5. Vi leder efter længden af ​​den anden vektor
6. Multiplicer resultaterne fra punkt 4 med resultaterne fra punkt 5
7. Divider resultatet af punkt 3 med resultatet af punkt 6. Vi får cosinus af vinklen mellem linjerne
8. Hvis dette resultat giver dig mulighed for at beregne vinklen nøjagtigt, skal du kigge efter den
9. Ellers skriver vi gennem den omvendte cosinus

Nå, nu er det tid til at gå videre til problemerne: Jeg vil demonstrere løsningen af ​​de to første i detaljer, jeg vil præsentere løsningen for en anden i en kort form, og for de sidste to problemer vil jeg kun give svar, du skal selv udføre alle beregninger for dem.

Opgaver:

1. I den korrekte tet-ra-ed-re, nej-di-de vinkel mellem dig-så-det tet-ra-ed-ra og med-di-a-noy bo-kovy ansigt.

2. I den højrehåndede seks-kul-noy pi-ra-mi-de er siderne af os-no-va-nia ens, og ribbenene er lige, find vinklen mellem de rette linjer og.

3. Længderne af alle kanterne af den korrekte fire-du-rekh-kul pi-ra-mi-dy er lig med hinanden. Nej-di-de vinkler mellem de lige linjer, og hvis fra-snit er du-med-det givet pi-ra-mi-dy, er punktet se-re-di-na hendes bo-ko-andre ribben

4. På kanten af ​​terningen fra-me-che-na punkt, så Nay-di-te er vinklen mellem rette linjer og

5. Punkt - se-re-di-på kanterne af terningen Nay-di-te vinkel mellem rette linjer og.

Det er ikke tilfældigt, at jeg har ordnet opgaverne i denne rækkefølge. Mens du endnu ikke har haft tid til at begynde at navigere i koordinatmetoden, vil jeg selv analysere de mest "problematiske" figurer, og jeg vil lade dig beskæftige dig med den enkleste terning! Efterhånden skal du lære at arbejde med alle figurerne, jeg vil øge kompleksiteten af ​​opgaverne fra emne til emne.

Lad os begynde at løse problemer:

1. Tegn et tetraeder, placer det i koordinatsystemet som jeg foreslog tidligere. Da tetraederet er regulært, er alle dets flader (inklusive basen) regelmæssige trekanter. Da vi ikke får opgivet længden af ​​siden, kan jeg tage det lige. Jeg tror, ​​du forstår, at vinklen ikke rigtig afhænger af, hvor meget vores tetraeder er "strakt" ?. Jeg vil også tegne højden og medianen i tetraederet. Undervejs vil jeg tegne dens base (det vil også være nyttigt for os).

Jeg skal finde vinklen mellem og. Hvad ved vi? Vi kender kun koordinaten for punktet. Det betyder, at vi også skal finde punkternes koordinater. Nu tænker vi: et punkt er skæringspunktet for trekantens højder (eller halveringslinjer eller medianer). Et punkt er et hævet punkt. Punktet er midten af ​​segmentet. Så skal vi endelig finde: koordinater af punkter:.

Lad os starte med det enkleste: punktkoordinater. Se på billedet: Det er tydeligt, at punktets anvendelse er lig med nul (punktet ligger på planet). Dens ordinat er (siden - medianen). Det er sværere at finde sin abscisse. Dette gøres dog nemt ud fra Pythagoras sætning: Overvej en trekant. Dens hypotenus er ens, og et af benene er lige. Så:

Endelig har vi:.

Lad os nu finde koordinaterne for punktet. Det er tydeligt, at dens anvendelse igen er lig med nul, og dens ordinat er den samme som for et punkt, dvs. Lad os finde dens abscisse. Dette gøres ganske trivielt, hvis du husker det højderne af en ligesidet trekant divideres med skæringspunktet i forhold tæller fra toppen. Da:, så er den nødvendige abscisse af punktet, lig med længden af ​​segmentet, lig med:. Således er koordinaterne for punktet ens:

Lad os finde koordinaterne for punktet. Det er klart, at dens abscisse og ordinat falder sammen med punktets abscisse og ordinat. Og ansøgningen er lig med længden af ​​segmentet. - dette er et af trekantens ben. Hypotenusen af ​​en trekant er et segment - et ben. Den søges ud fra de betragtninger, som jeg har fremhævet med fed skrift:

Punktet er midtpunktet af linjestykket. Så skal vi huske formlen for koordinaterne for segmentets midtpunkt:

Det er det, nu kan vi søge efter koordinaterne for retningsvektorerne:

Nå, alt er klar: vi erstatter alle data i formlen:

På denne måde

Svar:

Du skal ikke lade dig skræmme af sådanne "skræmmende" svar: For C2-problemer er dette en almindelig praksis. Jeg vil hellere blive overrasket over det "pæne" svar i denne del. Også, som du har bemærket, har jeg praktisk talt ikke ty til andet end Pythagoras sætning og egenskaben for højder af en ligesidet trekant. Det vil sige, for at løse det stereometriske problem brugte jeg det allermindste af stereometri. Gevinsten heri er delvist "slukket" ved ret besværlige beregninger. Men de er ret algoritmiske!

2. Lad os tegne en regulær sekskantet pyramide sammen med et koordinatsystem, samt dens base:

Vi skal finde vinklen mellem linjerne og. Således er vores opgave reduceret til at finde koordinaterne for punkter:. Vi finder koordinaterne for de sidste tre ud fra det lille billede, og vi finder koordinaten for toppunktet gennem punktets koordinat. Arbejd i løs vægt, men du skal starte det!

a) Koordinat: det er klart, at dets applikat og ordinat er lig med nul. Lad os finde abscissen. For at gøre dette skal du overveje en retvinklet trekant. Ak, i den kender vi kun hypotenusen, som er lig med. Vi vil forsøge at finde benet (for det er klart, at den fordoblede benlængde vil give os abscissen af ​​spidsen). Hvordan kan vi finde hende? Lad os huske, hvilken slags figur vi har i bunden af ​​pyramiden? Dette er en regulær sekskant. Hvad betyder det? Det betyder, at alle sider og alle vinkler er lige store. Jeg burde finde et sådant hjørne. Nogle ideer? Der er mange ideer, men der er en formel:

Summen af ​​vinklerne af en regulær n-gon er .

Således er summen af ​​vinklerne på en regulær sekskant lig med grader. Så er hver af vinklerne lig med:

Vi ser på billedet igen. Det er tydeligt, at segmentet er halveringslinjen af ​​vinklen. Så er vinklen lig med grader. Derefter:

Så hvor.

Den har således koordinater

b) Nu kan vi nemt finde koordinaten for punktet:.

c) Find punktets koordinater. Da dens abscisse falder sammen med længden af ​​segmentet, er den lig med. At finde ordinaten er heller ikke særlig svært: hvis vi forbinder punkterne og betegner skæringspunktet for den lige linje, f.eks. (Gør det selv nem konstruktion). Så Ordinaten af ​​punkt B er lig med summen af ​​længderne af segmenterne. Lad os se på trekanten igen. Derefter

Så siden Så har punktet koordinater

d) Nu finder vi punktets koordinater. Overvej et rektangel og bevis, at koordinaterne for punktet er:

e) Tilbage er at finde toppunktets koordinater. Det er klart, at dens abscisse og ordinat falder sammen med punktets abscisse og ordinat. Lad os finde applikatoren. Siden da. Overvej en retvinklet trekant. Ved erklæringen om problemet, sidekanten. Dette er hypotenusen i min trekant. Så er højden af ​​pyramiden benet.

Så har punktet koordinater:

Okay, jeg har koordinaterne for alle punkter af interesse for mig. Leder du efter koordinaterne for retningsvektorerne for rette linjer:

Vi leder efter vinklen mellem disse vektorer:

Svar:

Igen, ved at løse dette problem, brugte jeg ingen sofistikerede tricks, bortset fra formlen for summen af ​​vinklerne af en regulær n-gon, samt bestemmelse af cosinus og sinus i en retvinklet trekant.

3. Da vi igen ikke får længden af ​​ribbenene i pyramiden, vil jeg betragte dem som lig med én. Da ALLE kanter, og ikke kun de laterale, er ens med hinanden, så ligger der ved bunden af ​​pyramiden og mig en firkant, og sidekanterne er regelmæssige trekanter. Lad os tegne en sådan pyramide såvel som dens base på et plan, der markerer alle dataene i opgaveteksten:

Vi leder efter vinklen mellem og. Jeg vil lave meget korte beregninger, når jeg søger efter punkternes koordinater. Du bliver nødt til at "dechifrere" dem:

b) - midten af ​​segmentet. Dens koordinater:

c) Jeg vil finde længden af ​​segmentet ved Pythagoras sætning i en trekant. Jeg vil finde det i en trekant ved Pythagoras sætning.

Koordinater:

d) er segmentets midtpunkt. Dens koordinater er ens

e) Vektorkoordinater

f) Vektorkoordinater

g) Leder du efter en vinkel:

Terningen er den enkleste figur. Jeg er sikker på, at du kan finde ud af det på egen hånd. Svarene på opgave 4 og 5 er som følger:

Finde vinklen mellem en ret linje og et plan

Nå, tiden for simple opgaver er forbi! Nu bliver eksemplerne endnu mere komplicerede. For at finde vinklen mellem en ret linje og et plan, går vi frem som følger:

1. Ud fra tre punkter konstruerer vi planets ligning
   ,
   ved at bruge en tredjeordens determinant.
2. Vi leder efter koordinaterne for den rette linjes retningsvektor ved to punkter:
3. Vi anvender formlen til at beregne vinklen mellem en ret linje og en plan:

Som du kan se, ligner denne formel meget den, vi brugte til at finde vinklerne mellem to lige linjer. Strukturen i højre side er præcis den samme, og til venstre leder vi nu efter sinus, ikke cosinus, som før. Nå, en grim handling blev tilføjet - søgningen efter flyets ligning.

Lad os ikke udsætte løsning af eksempler:

1. Hoved-men-va-no-em direkte-vi-er-la-er-lige-men-fattig-slidt trekantet-kælenavn Du-så-at præmier-vi er lige. Nai di te vinkel mellem lige og flad

2. I rektangulær pa-ra-le-le-pi-pe-de fra West Nay-di-te-vinklen mellem ret linje og plan

3. I det korrekte sekskulsprisme er alle kanter ens. Nej-di-disse vinkel mellem lige linje og plan.

4. I den højrehåndede trekantede pi-ra-mi-de med os-no-va-ne-det kendes ribben Nay-di-te vinkel, ob-ra-zo-van flad-til-knogle os-no -va-nia og lige, pro-ho-dya-shi gennem se-re-di-us af ribbenene og

5. Længderne af alle ribberne i den korrekte fire-hjørne pyramide med spids er lig med hinanden. Nay-di-te er vinklen mellem en ret linje og et plan, hvis punktet er se-re-di-na bo-ko-th ribben pi-ra-mi-dy.

Igen vil jeg løse de to første problemer i detaljer, det tredje - kort, og de to sidste lader jeg dig løse på egen hånd. Derudover har du allerede beskæftiget dig med trekantede og firkantede pyramider, men ikke med prismer endnu.

Løsninger:

1. Lad os skildre prismet, såvel som dets base. Lad os kombinere det med koordinatsystemet og markere alle dataene i problemformuleringen:

Jeg undskylder for en vis manglende overholdelse af proportionerne, men for at løse problemet er dette faktisk ikke så vigtigt. Flyet er bare "bagvæggen" af mit prisme. Det er let nok at gætte, at ligningen for et sådant plan har formen:

Dette kan dog vises direkte:

Lad os vælge vilkårlige tre punkter på dette plan: for eksempel.

Lad os sammensætte flyets ligning:

En øvelse til dig: beregn selv denne determinant. Gjorde du det? Så har planligningen formen:

Eller simpelthen

På denne måde

For at løse eksemplet skal jeg finde koordinaterne for retningsvektoren for en ret linje. Da punktet er faldet sammen med origo, vil vektorens koordinater blot falde sammen med punktets koordinater For at gøre dette finder vi først punktets koordinater.

For at gøre dette skal du overveje en trekant. Lad os tegne højden (det er medianen og halveringslinjen) fra toppunktet. Siden er ordinaten af ​​punktet lig med. For at finde abscissen af ​​dette punkt, skal vi beregne længden af ​​segmentet. Ved Pythagoras sætning har vi:

Så har punktet koordinater:

Et punkt "hæves" med et punkt:

Så er vektorens koordinater:

Svar:

Som du kan se, er der ikke noget grundlæggende svært ved at løse sådanne problemer. Faktisk forenkler processen yderligere "ligeheden" af en form, såsom et prisme. Lad os nu gå videre til næste eksempel:

2. Tegn et parallelepipedum, tegn et plan og en lige linje i det, og tegn også separat dens nederste base:

Først finder vi flyets ligning: Koordinater for tre punkter, der ligger i det:

(de to første koordinater blev opnået på en indlysende måde, og du kan nemt finde den sidste koordinat fra billedet fra punktet). Så komponerer vi flyets ligning:

Vi beregner:

Vi leder efter retningsvektorens koordinater: Det er tydeligt, at dens koordinater falder sammen med punktets koordinater, er det ikke? Hvordan finder jeg koordinaterne? Dette er punktets koordinater, hævet langs applikationens akse med én! ... Så leder vi efter den ønskede vinkel:

Svar:

3. Tegn en regulær sekskantet pyramide, og tegn derefter et plan og en ret linje i den.

Her er selv at tegne et fly problematisk, for ikke at nævne løsningen af ​​dette problem, men koordinatmetoden er ligeglad! Det er i dens alsidighed, at dens største fordel ligger!

Flyet passerer gennem tre punkter:. Vi leder efter deres koordinater:

en) . Tegn selv koordinaterne for de sidste to punkter. Løsningen på problemet med en sekskantet pyramide vil være praktisk til dette!

2) Vi bygger flyets ligning:

Vi leder efter vektorens koordinater:. (se det trekantede pyramideproblem igen!)

3) Leder du efter en vinkel:

Svar:

Som du kan se, er der ikke noget overnaturligt svært i disse opgaver. Du skal bare være meget forsigtig med rødderne. Til de sidste to problemer vil jeg kun give svar:

Som du kan se, er teknikken til at løse problemer den samme overalt: Hovedopgaven er at finde koordinaterne for hjørnerne og erstatte dem i nogle formler. Det er tilbage for os at overveje endnu en klasse af problemer til beregning af vinkler, nemlig:

Beregning af vinkler mellem to planer

Løsningsalgoritmen vil være som følger:

1. Med tre punkter leder vi efter ligningen for det første plan:
2. For de tre andre punkter leder vi efter ligningen for det andet plan:
3. Vi anvender formlen:

Som du kan se, ligner formlen meget de to foregående, ved hjælp af hvilke vi søgte efter vinklerne mellem rette linjer og mellem en ret linje og et plan. Så det vil ikke være svært for dig at huske denne. Lad os gå direkte til analysen af ​​opgaver:

1. Et hundrede-ro-na af os-no-va-nia af det højrehåndede trekantede prisme er lig, og dia-go-nalen af ​​det store ansigt er lig. Nej-di-disse vinkler mellem planet og prismets plan.

2. I den korrekte fire-du-rekh-kul-noy pi-ra-mi-de, hvis kanter er lige store, skal du finde sinus for vinklen mellem planet og planet til-stu, pro-ho- dya-shchey gennem punktet per-pen-di-ku-lar-men lige.

3. I det korrekte fire-du-rekh-kulprisme er siderne af os-no-va-nia ens, og siderne er lige store. På kanten er der et punkt, så. Find vinklen mellem planet-til-sti-mi og

4. I det højre firhjørneprisme er siderne af os-no-va-nia ens, og sidekanterne ens. På kanten fra-mig-che-til punkt, så Nay-di-te er vinklen mellem plan-til-st-mi og.

5. I terningen nay-di-te ko-si-nus af vinklen mellem planet-ko-sti-mi og

Problemløsninger:

1. Jeg tegner et regulært (ved bunden - en ligesidet trekant) trekantet prisme og markerer på det de planer, der vises i problemformuleringen:

Vi skal finde ligningerne for to planer: Basens ligning er triviel: du kan sammensætte den tilsvarende determinant med tre punkter, men jeg vil sammensætte ligningen med det samme:

Nu vil vi finde ligningen Punkt har koordinater Punkt - Da er medianen og højden af ​​trekanten, er det let at finde i en trekant ved Pythagoras sætning. Så har punktet koordinater: Find anvendelsen af ​​punktet For at gøre dette skal du overveje en retvinklet trekant

Så får vi følgende koordinater: Tegn planens ligning.

Vi beregner vinklen mellem planerne:

Svar:

2. Lav en tegning:

Det sværeste er at forstå, hvad dette mystiske plan er, der passerer gennem et punkt vinkelret. Nå, det vigtigste er, hvad er det her? Det vigtigste er opmærksomhed! Faktisk er linjen vinkelret. Den lige linje er også vinkelret. Så vil flyet, der passerer gennem disse to lige linjer, være vinkelret på den lige linje, og i øvrigt passere gennem punktet. Dette fly går også gennem toppen af ​​pyramiden. Så det ønskede fly - Og flyet er allerede givet til os. Vi leder efter punkternes koordinater.

Find koordinaten for punktet gennem punktet. Ud fra den lille figur er det let at udlede, at punktets koordinater bliver som følger: Hvad er der nu tilbage at finde for at finde koordinaterne til toppen af ​​pyramiden? Du skal også beregne dens højde. Dette gøres ved hjælp af den samme Pythagoras sætning: Bevis først det (trivielt fra små trekanter, der danner en firkant ved bunden). Da vi efter betingelse har:

Nu er alt klar: koordinaterne for toppunktet:

Vi sammensætter flyets ligning:

Du er allerede speciel i at beregne determinanter. Du kan nemt få:

Eller også (hvis vi gange begge dele med roden af ​​to)

Nu finder vi flyets ligning:

(Du har ikke glemt, hvordan vi får flyets ligning, vel? Hvis du ikke forstår, hvor denne minus ene kom fra, så gå tilbage til definitionen af ​​flyets ligning! Det er bare det, før det viste sig, at oprindelsen af ​​koordinater tilhørte mit fly!)

Vi beregner determinanten:

(Du kan se, at flyets ligning falder sammen med ligningen for den rette linje, der går gennem punkterne og! Tænk hvorfor!)

Nu beregner vi vinklen:

Vi skal finde sinus:

Svar:

3. Et vanskeligt spørgsmål: hvad tror du er et rektangulært prisme? Det er bare et parallelepipedum, du kender godt! Lav en tegning med det samme! Det er endda muligt ikke at afbilde basen separat, der er ringe fordel af det her:

Flyet, som vi bemærkede tidligere, er skrevet i form af en ligning:

Nu laver vi flyet

Vi sammensætter straks flyets ligning:

Leder efter en vinkel:

Nu svarene på de sidste to problemer:

Nå, nu er det tid til at tage en pause, for du og jeg er fantastiske og har gjort et godt stykke arbejde!

Koordinater og vektorer. Avanceret niveau

I denne artikel vil vi diskutere med dig en anden klasse af problemer, der kan løses ved hjælp af koordinatmetoden: afstandsproblemer. Du og jeg vil nemlig overveje følgende tilfælde:

1. Beregning af afstanden mellem krydsede linjer.

Jeg har bestilt disse opgaver, efterhånden som deres kompleksitet øges. Det viser sig at være det nemmeste at finde afstand fra punkt til plan, og det sværeste er at finde afstand mellem krydsende linjer... Selvom, selvfølgelig, intet er umuligt! Lad os ikke udsætte og straks gå videre til overvejelsen af ​​den første klasse af problemer:

Beregning af afstanden fra et punkt til et fly

Hvad har vi brug for for at løse dette problem?

1. Punktkoordinater

Så så snart vi får alle de nødvendige data, anvender vi formlen:

Du burde allerede vide, hvordan vi konstruerer flyets ligning ud fra de tidligere problemer, som jeg diskuterede i sidste del. Lad os gå i gang med opgaverne med det samme. Skemaet er som følger: 1, 2, jeg hjælper dig med at løse, og i nogle detaljer, 3, 4 - kun svaret, du træffer selv beslutningen og sammenligner. Lad os begynde!

Opgaver:

1. Givet en terning. Længden af ​​kanten af ​​terningen er. Nej-di-te distance-i-ni fra se-re-di-us fra-cut til flad-til-sti

2. Givet den rigtige-vil-naya fire-du-rekh-kul-naya pi-ra-mi-da Bo-kovoe kanten af ​​side-ro-on af os-no-va-nia er lige. Nay-di-te distance-i-nie fra punkt til plan-til-sti hvor - se-re-di-na ribben.

3. I den højrehåndede trekantede pi-ra-mi-de med os-no-va-no er bo-kov-kanten lig, og side-ro-na er-no-va- er lig med. Nay-di-te distance-i-nye fra toppen til flyet.

4. I et regulært sekskulsprisme er alle kanter ens. Nej-di-te distance-i-nye fra punkt til plan.

Løsninger:

1. Tegn en terning med enhedskanter, byg et segment og en plan, mærk midten af ​​segmentet med bogstavet

.

Lad os først starte med en nem en: find koordinaterne for et punkt. Siden da (husk koordinaterne for segmentets midtpunkt!)

Nu komponerer vi flyets ligning med tre punkter

\ [\ venstre | (\ start (array) (* (20) (c)) x & 0 & 1 \\ y & 1 & 0 \\ z & 1 & 1 \ end (array)) \ højre | = 0 \]

Nu kan jeg begynde at lede efter afstand:

2. Start igen med tegningen, hvorpå vi markerer alle data!

For pyramiden ville det være nyttigt at tegne dens base separat.

Selv det faktum, at jeg tegner som en kylling med en pote, forhindrer os ikke i nemt at løse dette problem!

Nu er det nemt at finde koordinaterne for et punkt

Siden koordinaterne for punktet, altså

2. Da koordinaterne for punkt a er midtpunktet af segmentet, så

Vi kan også finde koordinaterne for yderligere to punkter på planet uden problemer. Vi sammensætter flyets ligning og forenkler den:

\ [\ venstre | (\ venstre | (\ begynder (array) (* (20) (c)) x & 1 & (\ frac (3) (2)) \\ y & 0 & (\ frac (3) (2)) \ \ z & 0 & (\ frac ( (\ sqrt 3)) (2)) \ end (array)) \ højre |) \ højre | = 0 \]

Da punktet har koordinater:, så beregner vi afstanden:

Svar (meget sjældent!):

Nå, fandt ud af det? Det forekommer mig, at alt her er lige så teknisk som i de eksempler, vi overvejede med dig i den foregående del. Så jeg er sikker på, at hvis du mestrer det materiale, så vil det ikke være svært for dig at løse de resterende to problemer. Jeg vil lige give svarene:

Beregning af afstanden fra en lige linje til et plan

Faktisk er der ikke noget nyt her. Hvordan kan en linje og et plan placeres i forhold til hinanden? De har alle mulighederne: skærer hinanden, eller en lige linje er parallel med planet. Hvad tror du er afstanden fra en ret linje til det plan, som denne rette linje skærer? Det forekommer mig, at det her er klart, at en sådan afstand er lig med nul. En uinteressant sag.

Det andet tilfælde er mere vanskeligt: ​​her er afstanden allerede nul. Men da linjen er parallel med planet, så er hvert punkt på linjen lige langt fra dette plan:

På denne måde:

Og det betyder, at min opgave er blevet reduceret til den forrige: vi leder efter koordinaterne for ethvert punkt på en lige linje, vi leder efter planens ligning, vi beregner afstanden fra et punkt til planet. Faktisk er sådanne opgaver yderst sjældne i eksamen. Det lykkedes mig kun at finde ét problem, og dataene i det var sådan, at koordinatmetoden ikke var særlig anvendelig til det!

Lad os nu gå videre til en anden, meget vigtigere klasse af problemer:

Beregning af afstanden af ​​et punkt til en ret linje

Hvad har vi brug for?

1. Koordinater for det punkt, hvorfra vi leder efter afstanden:

2. Koordinater for ethvert punkt, der ligger på en lige linje

3. Koordinater for retningsvektoren for en ret linje

Hvilken formel bruger vi?

Hvad betyder nævneren for en given brøk for dig, så det burde være klart: dette er længden af ​​den rettede vektor af en ret linje. Der er en meget vanskelig tæller her! Udtrykket betyder modulet (længden) af vektorproduktet af vektorer og Hvordan man beregner krydsproduktet, studerede vi i den foregående del af arbejdet. Opdater din viden, de vil være meget nyttige for os nu!

Algoritmen til løsning af problemer vil således være som følger:

1. Vi leder efter koordinaterne for det punkt, hvorfra vi leder efter afstanden:

2. Vi leder efter koordinaterne for ethvert punkt på den lige linje, som vi leder efter afstanden til:

3. Byg en vektor

4. Byg retningsvektoren for den rette linje

5. Beregn krydsproduktet

6. Vi leder efter længden af ​​den resulterende vektor:

7. Beregn afstanden:

Vi har meget arbejde, og eksemplerne bliver ret komplekse! Så fokuser nu hele din opmærksomhed!

1. Dana er en højre-vil-naya trekantet pi-ra-mi-da med en top. Et hundrede-ro-na os-no-va-nia pi-ra-mi-dy er lige, du-så-det er lige. Nej-di-dem afstand fra se-re-di-ny af bo-ko-th kant til den lige linje, hvor punkterne og er se-re-di-ny af ribbenene og så-fra-vet -men.

2. Længderne af ribbenene og den rektangulære pa-ral-le-le-pi-pe-da er henholdsvis lige store og Nay-di-dem afstand fra top til lige

3. I det korrekte sekskulsprisme er alle kanterne på en sværm lige store afstande fra et punkt til en ret linje

Løsninger:

1. Vi laver en pæn tegning, hvorpå vi markerer alle data:

Vi har en masse arbejde med dig! Først vil jeg gerne beskrive med ord, hvad vi vil lede efter og i hvilken rækkefølge:

1. Koordinater af punkter og

2. Punktkoordinater

3. Koordinater af punkter og

4. Koordinater af vektorer og

5. Deres krydsprodukt

6. Længden af ​​vektoren

7. Længden af ​​vektorproduktet

8. Afstand fra til

Nå, vi har meget arbejde at gøre! Vi går i gang og smøger ærmerne op!

1. For at finde koordinaterne til pyramidens højde skal vi kende koordinaterne for punktet. Dets anvendelse er lig med nul, og ordinaten er lig med Abscissen, er den lig med længden af ​​segmentet. er højden af ​​en ligesidet trekant, er den delt i forhold, regnet fra toppen, fremover. Til sidst fik vi koordinaterne:

Punktkoordinater

2. - midten af ​​segmentet

3. - midten af ​​segmentet

Midtpunktet af segmentet

4.Koordinater

Vektorkoordinater

5. Vi beregner krydsproduktet:

6. Vektorens længde: den nemmeste måde er at erstatte, at segmentet er trekantens midterlinje, hvilket betyder, at det er lig med halvdelen af ​​grundfladen. Så det.

7. Vi overvejer længden af ​​vektorproduktet:

8. Til sidst finder vi afstanden:

Pyha, det er det! Helt ærligt ville løsningen på dette problem ved hjælp af traditionelle metoder (gennem konstruktioner) være meget hurtigere. Men her har jeg reduceret alt til en færdiglavet algoritme! Jeg tror, ​​at løsningsalgoritmen er klar for dig? Derfor vil jeg bede dig om at løse de resterende to problemer på egen hånd. Lad os sammenligne svarene?

Igen, jeg gentager: det er nemmere (hurtigere) at løse disse problemer gennem konstruktioner, og ikke at ty til koordinatmetoden. Jeg har demonstreret denne løsning kun for at vise dig en universel metode, der giver dig mulighed for at "intet fuldføre".

Overvej endelig den sidste klasse af problemer:

Beregning af afstanden mellem krydsede linjer

Her vil problemløsningsalgoritmen ligne den forrige. Hvad vi har:

3. Alle vektorforbindelsespunkter på den første og anden rette linie:

Hvordan finder vi afstanden mellem rette linjer?

Formlen er som følger:

Tælleren er modulet af det blandede produkt (vi introducerede det i forrige del), og nævneren er den samme som i den foregående formel (modulet for vektorproduktet af retningsvektorerne for de rette linjer, afstanden mellem hvilke vi leder efter).

Det vil jeg minde dig om

derefter formlen for afstanden kan omskrives som:

En slags determinant divideret med en determinant! Selvom jeg for at være ærlig ikke har tid til vittigheder her! Denne formel er faktisk meget besværlig og fører til ret komplicerede beregninger. Hvis jeg var dig, ville jeg kun bruge det som en sidste udvej!

Lad os prøve at løse flere problemer ved hjælp af ovenstående metode:

1. I det rigtige trekantede prisme er alle kanter ens, find afstanden mellem de rette linjer og.

2. Givet et højrehåndet trekantet prisme er alle kanterne af os-no-va-tionen af ​​en sværm lige store ribben og se-re-di-brønd ribben yav-la-et-sya square-ra-tom. Nay-di-te distance-i-nie mellem straight-we-mi og

Jeg bestemmer det første, og ud fra det bestemmer du det andet!

1. Tegn et prisme og marker de rette linjer og

Punkt C-koordinater: derefter

Punktkoordinater

Vektorkoordinater

Punktkoordinater

Vektorkoordinater

Vektorkoordinater

\ [\ venstre ((B, \ overhøjre pil (A (A_1))) \ overhøjre pil (B (C_1))) \ højre) = \ venstre | (\ start (array) (* (20) (l)) (\ start (array) (* (20) (c)) 0 & 1 & 0 \ end (array)) \\ (\ start (array) ( * (20) (c)) 0 & 0 & 1 \ end (array)) \\ (\ start (array) (* (20) (c)) (\ frac ((\ sqrt 3)) (2)) & (- \ frac (1) (2)) & 1 \ end (array)) \ end (array)) \ højre | = \ frac ((\ sqrt 3)) (2) \]

Vi betragter krydsproduktet mellem vektorer og

\ [\ overhøjre pil (A (A_1)) \ cdot \ overhøjre pil (B (C_1)) = \ venstre | \ start (array) (l) \ start (array) (* (20) (c)) (\ overhøjre pil i) & (\ overhøjre pil j) & (\ overhøjre pil k) \ ende (array) \\\ begynde (array) ) (* (20) (c)) 0 & 0 & 1 \ end (array) \\\ start (array) (* (20) (c)) (\ frac ((\ sqrt 3)) (2)) & (- \ frac (1) (2)) & 1 \ end (array) \ end (array) \ højre | - \ frac ((\ sqrt 3)) (2) \ overhøjre pil k + \ frac (1) (2) \ overhøjre pil i \]

Nu beregner vi dens længde:

Svar:

Prøv nu at fuldføre den anden opgave omhyggeligt. Svaret på det bliver:.

Koordinater og vektorer. Kort beskrivelse og grundlæggende formler

En vektor er et rettet linjestykke. - begyndelsen af ​​vektoren, - slutningen af ​​vektoren.
Vektoren er betegnet med eller.

Absolut værdi vektor - længden af ​​det segment, der repræsenterer vektoren. Det er angivet som.

Vektorkoordinater:

,
hvor er enderne af vektoren \ displaystyle a.

Summen af ​​vektorer:.

Produkt af vektorer:

Punktprodukt af vektorer:

Rektangulært koordinatsystem

For at definere begrebet koordinater af punkter, skal vi indtaste et koordinatsystem, hvor vi vil bestemme dets koordinater. Det samme punkt i forskellige koordinatsystemer kan have forskellige koordinater. Her vil vi betragte et rektangulært koordinatsystem i rummet.

Tag et punkt $ O $ i rummet og indtast koordinaterne $ (0,0,0) $ for det. Lad os kalde det oprindelsen af ​​koordinatsystemet. Lad os gennem den tegne tre indbyrdes vinkelrette akser $ Ox $, $ Oy $ og $ Oz $, som i figur 1. Disse akser vil blive kaldt henholdsvis abscisse, ordinat og applikatakse. Det er kun tilbage at indtaste skalaen på akserne (enhedssegment) - det rektangulære koordinatsystem i rummet er klar (fig. 1)

Figur 1. Rektangulært koordinatsystem i rummet. Author24 - online udveksling af studenterpapirer

Punktkoordinater

Lad os nu analysere, hvordan koordinaterne for ethvert punkt bestemmes i et sådant system. Tag et vilkårligt punkt $ M $ (fig. 2).

Lad os konstruere et rektangulært parallelepipedum på koordinatakserne, så punkterne $ O $ og $ M $ er dets modsatte hjørner (fig. 3).

Figur 3. Konstruktion af et rektangulært parallelepipedum. Author24 - online udveksling af studenterpapirer

Så vil punktet $ M $ have koordinater $ (X, Y, Z) $, hvor $ X $ er værdien på den numeriske akse $ Ox $, $ Y $ er værdien på den numeriske akse $ Oy $, og $ Z $ er værdien på den numeriske akse $ Oz $.

Eksempel 1

Det er nødvendigt at finde en løsning på følgende problem: skriv koordinaterne for hjørnerne af parallelepipedet vist i figur 4.

Opløsning.

Punkt $ O $ er oprindelsen, derfor $ O = (0,0,0) $.

Punkterne $ Q $, $ N $ og $ R $ ligger på henholdsvis akserne $ Ox $, $ Oz $ og $ Oy $, hvilket betyder

$ Q = (2,0,0) $, $ N = (0,0,1.5) $, $ R = (0,2.5,0) $

Punkterne $ S $, $ L $ og $ M $ ligger i henholdsvis flyene $ Oxz $, $ Oxy $ og $ Oyz $, hvilket betyder

$ S = (2,0,1.5) $, $ L = (2,2.5,0) $, $ R = (0,2.5,1.5) $

Punkt $ P $ har koordinater $ P = (2,2.5,1.5) $

Vektorkoordinater med to punkter og formlen til at finde

For at finde ud af, hvordan man finder en vektor ved koordinaterne af to punkter, skal du overveje det koordinatsystem, vi introducerede tidligere. I den, fra punktet $ O $ i retning af $ Ox $-aksen, udskyder vi enhedsvektoren $ \ overline (i) $, i retning af $ Oy $-aksen - enhedsvektoren $ \ overline (j ) $, og enhedsvektoren $ \ overline (k) $ skal rettes langs $ Oz $-aksen.

For at introducere begrebet koordinater for en vektor introducerer vi følgende sætning (vi vil ikke overveje dets bevis her).

Sætning 1

En vilkårlig vektor i rummet kan udvides til hvilke som helst tre vektorer, der ikke ligger i samme plan, og koefficienterne i en sådan ekspansion vil blive entydigt bestemt.

Matematisk ser det sådan ud:

$ \ overline (δ) = m \ overline (α) + n \ overline (β) + l \ overline (γ) $

Da vektorerne $ \ overline (i) $, $ \ overline (j) $ og $ \ overline (k) $ er bygget på koordinatakserne i et rektangulært koordinatsystem, vil de naturligvis ikke tilhøre samme plan. Derfor kan enhver vektor $ \ overline (δ) $ i dette koordinatsystem, ved sætning 1, have følgende form

$ \ overline (δ) = m \ overline (i) + n \ overline (j) + l \ overline (k) $ (1)

hvor $ n, m, l∈R $.

Definition 1

De tre vektorer $ \ overline (i) $, $ \ overline (j) $ og $ \ overline (k) $ vil blive kaldt koordinatvektorer.

Definition 2

Koefficienterne foran vektorerne $ \ overline (i) $, $ \ overline (j) $ og $ \ overline (k) $ i ekspansion (1) vil blive kaldt koordinaterne for denne vektor i det givne koordinatsystem, dvs. er

$ \ overline (δ) = (m, n, l) $

Lineære operationer på vektorer

Sætning 2

Sumsætning: Koordinaterne for summen af ​​et vilkårligt antal vektorer bestemmes af summen af ​​deres respektive koordinater.

Bevis.

Vi vil bevise denne sætning for 2 vektorer. For 3 eller flere vektorer er beviset konstrueret på lignende måde. Lad $ \ overline (α) = (α_1, α_2, α_3) $, $ \ overline (β) = (β_1, β_2, β_3) $.

Disse vektorer kan skrives som følger

$ \ overline (α) = α_1 \ overline (i) + α_2 \ overline (j) + α_3 \ overline (k) $, $ \ overline (β) = β_1 \ overline (i) + β_2 \ overline (j) + β_3 \ overline (k) $