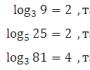Logaritmit tenttiesimerkeissä. Logaritmit: esimerkkejä ja ratkaisuja

Logaritmiset lausekkeet, ratkaisuesimerkit. Tässä artikkelissa tarkastellaan logaritmien ratkaisemiseen liittyviä ongelmia. Tehtävissä kysytään ilmaisun merkityksen löytämistä. On huomattava, että logaritmin käsitettä käytetään monissa tehtävissä ja sen merkityksen ymmärtäminen on erittäin tärkeää. Unified State Examissa logaritmia käytetään yhtälöiden ratkaisemisessa, sovellettavissa tehtävissä sekä funktioiden tutkimiseen liittyvissä tehtävissä.

Antakaamme esimerkkejä logaritmin merkityksen ymmärtämiseksi:

Logaritmisen perusidentiteetti:

Logaritmien ominaisuudet, jotka tulee aina muistaa:

*Tulostuksen logaritmi on yhtä suuri kuin tekijöiden logaritmien summa.

* * *

*Osamäärän (murto-osan) logaritmi on yhtä suuri kuin tekijöiden logaritmien välinen erotus.

* * *

* Eksponentin logaritmi on yhtä suuri kuin eksponentin ja sen kantaluvun logaritmi.

* * *

*Siirtyminen uudelle perustalle

* * *

Lisää kiinteistöjä:

* * *

Logaritmien laskenta liittyy läheisesti eksponenttiominaisuuksien käyttöön.

Listataanpa joitain niistä:

Tämän ominaisuuden ydin on, että kun osoittaja siirretään nimittäjään ja päinvastoin, eksponentin etumerkki muuttuu päinvastaiseksi. Esimerkiksi:

Seuraus tästä omaisuudesta:

* * *

Kun potenssi nostetaan potenssiksi, kanta pysyy samana, mutta eksponentit kerrotaan.

* * *

Kuten olet nähnyt, logaritmin käsite itsessään on yksinkertainen. Tärkeintä on, että tarvitset hyvää harjoitusta, joka antaa sinulle tietyn taidon. Tietysti kaavojen tuntemus vaaditaan. Jos alkeislogaritmien muuntamisen taitoa ei ole kehitetty, niin yksinkertaisia ​​tehtäviä ratkaistaessa voit helposti tehdä virheen.

Harjoittele, ratkaise ensin matematiikan kurssin yksinkertaisimmat esimerkit ja siirry sitten monimutkaisempiin. Tulevaisuudessa näytän ehdottomasti, kuinka "pelottavia" logaritmeja ratkaistaan; ne eivät näy Unified State -kokeessa, mutta ne ovat mielenkiintoisia, älä missaa niitä!

Siinä kaikki! Onnea sinulle!

Ystävällisin terveisin Alexander Krutitskikh

P.S: Olisin kiitollinen, jos kertoisit minulle sivustosta sosiaalisessa mediassa.

Yksityisyytesi säilyttäminen on meille tärkeää. Tästä syystä olemme kehittäneet tietosuojakäytännön, joka kuvaa kuinka käytämme ja säilytämme tietojasi. Tutustu tietosuojakäytäntöihimme ja kerro meille, jos sinulla on kysyttävää.

Henkilötietojen kerääminen ja käyttö

Henkilötiedoilla tarkoitetaan tietoja, joiden avulla voidaan tunnistaa tietty henkilö tai ottaa häneen yhteyttä.

Sinua voidaan pyytää antamaan henkilötietosi milloin tahansa, kun otat meihin yhteyttä.

Alla on esimerkkejä siitä, minkä tyyppisistä henkilötiedoista saatamme kerätä ja kuinka voimme käyttää tällaisia ​​tietoja.

Mitä henkilötietoja keräämme:

• Kun lähetät hakemuksen sivustolla, voimme kerätä erilaisia ​​tietoja, kuten nimesi, puhelinnumerosi, sähköpostiosoitteesi jne.

Kuinka käytämme henkilötietojasi:

• Keräämiemme henkilötietojen avulla voimme ottaa sinuun yhteyttä ainutlaatuisten tarjousten, kampanjoiden ja muiden tapahtumien ja tulevien tapahtumien yhteydessä.
• Ajoittain voimme käyttää henkilötietojasi tärkeiden ilmoitusten ja viestien lähettämiseen.
• Saatamme myös käyttää henkilötietoja sisäisiin tarkoituksiin, kuten auditointiin, data-analyysiin ja erilaisiin tutkimuksiin parantaaksemme tarjoamiamme palveluita ja tarjotaksemme sinulle palveluitamme koskevia suosituksia.
• Jos osallistut arvontaan, kilpailuun tai vastaavaan promootioon, voimme käyttää antamiasi tietoja tällaisten ohjelmien hallinnointiin.

Tietojen luovuttaminen kolmansille osapuolille

Emme luovuta sinulta saatuja tietoja kolmansille osapuolille.

Poikkeukset:

• Tarvittaessa - lain, oikeudellisen menettelyn, oikeudellisen menettelyn mukaisesti ja/tai Venäjän federaation alueella olevien julkisten pyyntöjen tai viranomaisten pyyntöjen perusteella - paljastaa henkilötietosi. Saatamme myös paljastaa tietoja sinusta, jos katsomme, että tällainen paljastaminen on tarpeellista tai tarkoituksenmukaista turvallisuus-, lainvalvonta- tai muihin yleisiin tarkoituksiin liittyvistä syistä.
• Uudelleenjärjestelyn, sulautumisen tai myynnin yhteydessä voimme siirtää keräämämme henkilötiedot sovellettavalle seuraajalle kolmannelle osapuolelle.

Henkilötietojen suojaaminen

Ryhdymme varotoimiin - mukaan lukien hallinnolliset, tekniset ja fyysiset - henkilötietojesi suojaamiseksi katoamiselta, varkaudelta ja väärinkäytöltä sekä luvattomalta käytöltä, paljastamiselta, muuttamiselta ja tuhoutumiselta.

Yksityisyytesi kunnioittaminen yritystasolla

Varmistaaksemme, että henkilötietosi ovat turvassa, välitämme tietosuoja- ja turvallisuusstandardit työntekijöillemme ja noudatamme tiukasti tietosuojakäytäntöjä.

Tässä video-opetusohjelmassa tarkastellaan melko vakavan logaritmisen yhtälön ratkaisemista, jossa sinun ei tarvitse vain löytää juuria, vaan myös valita ne, jotka sijaitsevat tietyllä segmentillä.

Ongelma C1. Ratkaise yhtälö. Etsi kaikki tämän yhtälön juuret, jotka kuuluvat väliin.

Huomautus logaritmisista yhtälöistä

Kuitenkin vuodesta toiseen luokseni tulee opiskelijoita, jotka yrittävät ratkaista tällaisia, suoraan sanottuna, vaikeita yhtälöitä, mutta samalla he eivät voi ymmärtää: mistä heidän pitäisi edes aloittaa ja miten lähestyä logaritmeja? Tämä ongelma voi syntyä jopa vahvojen, hyvin valmistautuneiden opiskelijoiden keskuudessa.

Tämän seurauksena monet alkavat pelätä tätä aihetta tai jopa pitävät itseään tyhminä. Joten muista: jos et pysty ratkaisemaan tällaista yhtälöä, tämä ei tarkoita ollenkaan, että olet tyhmä. Koska esimerkiksi voit käsitellä tätä yhtälöä melkein sanallisesti:

log 2 x = 4

Ja jos näin ei ole, et lukisi tätä tekstiä nyt, koska olit kiireinen yksinkertaisempien ja arkipäiväisempien tehtävien parissa. Tietysti joku nyt vastustaa: "Mitä tekemistä tällä yksinkertaisimmalla yhtälöllä on terveen rakenteemme kanssa?" Vastaan: mikä tahansa logaritminen yhtälö, olipa se kuinka monimutkainen tahansa, johtaa lopulta näihin yksinkertaisimpiin rakenteisiin, jotka voidaan ratkaista suullisesti.

Tietysti monimutkaisista logaritmisista yhtälöistä yksinkertaisempiin on siirryttävä ei valinnan tai tamburiinin kanssa tanssimisen kautta, vaan selkeiden, pitkään määriteltyjen sääntöjen mukaan, joita kutsutaan - säännöt logaritmisen lausekkeiden muuntamiseen. Kun tiedät ne, voit helposti käsitellä jopa kaikkein kehittyneimmät yhtälöt matematiikan yhtenäisessä valtionkokeessa.

Ja juuri näistä säännöistä puhumme tämän päivän oppitunnilla. Mennä!

Logaritmisen yhtälön ratkaiseminen tehtävässä C1

Joten ratkaisemme yhtälön:

Ensinnäkin, kun on kyse logaritmisista yhtälöistä, muistamme perustaktiikat - niin sanotusti logaritmisen yhtälöiden ratkaisemisen perussäännön. Se koostuu seuraavista:

Kanonisen muodon lause. Mikä tahansa logaritminen yhtälö, riippumatta siitä, mitä se sisältää, mitä logaritmeja, mitä kantaa tahansa ja mitä se sisältää, on välttämättä pelkistettävä muodon yhtälöksi:

log a f (x) = log a g (x)

Jos katsomme yhtälöämme, huomaamme heti kaksi ongelmaa:

1. Meillä on vasemmalla kahden luvun summa, joista yksi ei ole ollenkaan logaritmi.
2. Oikealla on melkoinen logaritmi, mutta sen juuressa on juuri. Ja logaritmi vasemmalla on yksinkertaisesti 2, ts. Vasemman ja oikeanpuoleisten logaritmien perusteet ovat erilaiset.

Joten, olemme koonneet tämän luettelon ongelmista, jotka erottavat yhtälömme siitä kanoninen yhtälö, johon mikä tahansa logaritminen yhtälö on vähennettävä ratkaisuprosessin aikana. Siten yhtälömme ratkaiseminen tässä vaiheessa merkitsee kahden yllä kuvatun ongelman poistamista.

Mikä tahansa logaritminen yhtälö voidaan ratkaista nopeasti ja helposti, jos pelkistät sen kanoniseen muotoonsa.

Logaritmien summa ja tulon logaritmi

Jatketaan järjestyksessä. Katsotaanpa ensin vasemmalla olevaa rakennetta. Mitä voimme sanoa kahden logaritmin summasta? Muistakaamme upea kaava:

log a f (x) + log a g (x) = log a f (x) g (x)

Mutta on syytä harkita, että meidän tapauksessamme ensimmäinen termi ei ole logaritmi ollenkaan. Tämä tarkoittaa, että meidän on esitettävä yksikkö logaritmina kantaan 2 (täsmälleen 2, koska logaritmi kantaan 2 on vasemmalla). Kuinka tehdä se? Muistakaamme jälleen upea kaava:

a = log b b a

Tässä sinun on ymmärrettävä: kun sanomme "Mikä tahansa kanta b", tarkoitamme, että b ei silti voi olla mielivaltainen luku. Jos lisäämme luvun logaritmiin, varma rajoituksia, nimittäin: logaritmin kantaluvun on oltava suurempi kuin 0 eikä se saa olla yhtä suuri kuin 1. Muuten logaritmissa ei yksinkertaisesti ole järkeä. Kirjoitetaan tämä muistiin:

0 < b ≠ 1

Katsotaanpa mitä meidän tapauksessamme tapahtuu:

1 = log 2 2 1 = log 2 2

Nyt kirjoitetaan koko yhtälömme uudelleen ottaen tämä tosiasia huomioon. Ja sovellamme heti toista sääntöä: logaritmien summa on yhtä suuri kuin argumenttien tulon logaritmi. Tuloksena saamme:

Meillä on uusi yhtälö. Kuten näemme, se on jo paljon lähempänä kanonista yhtälöä, johon pyrimme. Mutta on yksi ongelma, kirjoitimme sen ylös toiseksi pisteeksi: logaritmimme, jotka ovat vasemmalla ja oikealla, eri syistä. Siirrytään seuraavaan vaiheeseen.

Säännöt potenssien vähentämiseksi logaritmista

Joten vasemmanpuoleisen logaritmin kanta on vain 2 ja oikeanpuoleisen logaritmin juuri on tyvessä. Mutta tämä ei ole ongelma, jos muistamme, että logaritmin argumenttien perusteet voidaan nostaa potenssiin. Kirjataan yksi näistä säännöistä:

log a b n = n log a b

Ihmiskielelle käännettynä: voit ottaa logaritmin kantasta tehon ja laittaa sen eteen kertoimeksi. Luku n "siirtyi" logaritmista ulospäin ja muuttui kertoimeksi edessä.

Voimme yhtä helposti johtaa tehon logaritmin kantasta. Se näyttää tältä:

Toisin sanoen, jos poistat logaritmin argumentista asteen, tämä aste kirjoitetaan myös tekijäksi ennen logaritmia, mutta ei numerona, vaan käänteislukuna 1/k.

Siinä ei kuitenkaan vielä kaikki! Voimme yhdistää nämä kaksi kaavaa ja saada seuraavan kaavan:

Kun potenssi esiintyy sekä logaritmin kanta- että argumentissa, voimme säästää aikaa ja yksinkertaistaa laskelmia ottamalla potenssit välittömästi pois sekä kanta- että argumentista. Tässä tapauksessa se, mikä oli argumentissa (meidän tapauksessamme tämä on kerroin n), näkyy osoittajassa. Ja mikä oli kannan aste, a k, menee nimittäjään.

Ja juuri näitä kaavoja käytämme nyt pienentääksemme logaritmimme samaan kantaan.

Ensinnäkin valitaan enemmän tai vähemmän kaunis pohja. On selvää, että on paljon miellyttävämpää työskennellä kahdella tyvessä kuin juurella. Yritetään siis pienentää toinen logaritmi kantaan 2. Kirjoitetaan tämä logaritmi erikseen:

Mitä voimme tehdä täällä? Muistakaamme potenssikaava rationaalisen eksponentin kanssa. Toisin sanoen juuret voidaan kirjoittaa potenssina, jolla on rationaalinen eksponentti. Ja sitten otetaan 1/2 potenssi pois sekä argumentista että logaritmin kannasta. Vähennämme kertoimien kahdet logaritmia vastapäätä osoittajassa ja nimittäjässä:

Lopuksi kirjoitetaan uudelleen alkuperäinen yhtälö ottaen huomioon uudet kertoimet:

log 2 2 (9 x 2 + 5) = log 2 (8 x 4 + 14)

Olemme saaneet kanonisen logaritmisen yhtälön. Sekä vasemmalla että oikealla on logaritmi samaan kantaan 2. Näiden logaritmien lisäksi ei ole kertoimia, ei termejä ei vasemmalla eikä oikealla.

Näin ollen voimme päästä eroon logaritmin merkistä. Tietysti ottaen huomioon määritelmäalueen. Mutta ennen kuin teemme sen, palataanpa takaisin ja tehdään pieni selvennys murtoluvuista.

Murtoluvun jakaminen murtoluvulla: Muita huomioita

Kaikki opiskelijat eivät ymmärrä, mistä oikean logaritmin edessä olevat tekijät tulevat ja minne ne menevät. Kirjoitetaan se uudestaan ​​ylös:

Selvitetään mikä murto-osa on. kirjoitetaan:

Muistetaan nyt murto-osien jakamissääntö: jakaaksesi 1/2, sinun on kerrottava käänteisellä murtoluvulla:

Tietenkin lisälaskutoimitusten helpottamiseksi voimme kirjoittaa kaksi arvoksi 2/1 - ja tämä on se, mitä havaitsemme ratkaisuprosessin toisena kertoimena.

Toivon, että nyt kaikki ymmärtävät, mistä toinen kerroin tulee, joten siirrytään suoraan kanonisen logaritmisen yhtälömme ratkaisemiseen.

Logaritmimerkistä eroon pääseminen

Haluan muistuttaa, että nyt voimme päästä eroon logaritmeista ja jättää seuraavan lausekkeen:

2(9x2 + 5) = 8x4 + 14

Avataan vasemmalla olevat kiinnikkeet. Saamme:

18x 2 + 10 = 8x 4 + 14

Siirretään kaikki vasemmalta puolelta oikealle:

8x 4 + 14 - 18x 2 - 10 = 0

Otetaan samanlaiset ja hankitaan:

8x 4 − 18x 2 + 4 = 0

Voimme jakaa tämän yhtälön molemmat puolet kahdella kertoimien yksinkertaistamiseksi, ja saamme:

4x 4 − 9x 2 + 2 = 0

Edessämme on tavallista bikvadraattinen yhtälö, ja sen juuret on helppo laskea diskriminantin avulla. Joten kirjoitetaan diskriminantti ylös:

D = 81 − 4 4 2 = 81 − 32 = 49

Hienoa, erottelija on "kaunis", sen juuri on 7. Siinä se, lasketaan X:t itse. Mutta tässä tapauksessa juuret eivät ole x, vaan x 2, koska meillä on kaksikvadraattinen yhtälö. Eli vaihtoehtomme:

Huomaa: poimimme juuret, joten vastauksia on kaksi, koska... neliö - tasainen toiminto. Ja jos kirjoitamme vain kahden juuren, menetämme yksinkertaisesti toisen juuren.

Nyt kirjoitamme kaksikvadraattisen yhtälömme toisen juuren:

Otamme jälleen yhtälön molempien puolten aritmeettisen neliöjuuren ja saamme kaksi juuria. Muista kuitenkin:

Ei riitä, että logaritmien argumentit yksinkertaisesti rinnastetaan kanoniseen muotoon. Muista määritelmän alue!

Kaiken kaikkiaan meillä on neljä juuria. Ne kaikki ovat todellakin ratkaisuja alkuperäiseen yhtälöimme. Katso: alkuperäisessä logaritmisessa yhtälössämme logaritmit ovat joko 9x 2 + 5 (tämä funktio on aina positiivinen) tai 8x 4 + 14 - mikä on myös aina positiivinen. Siksi logaritmien määritelmäalue täyttyy joka tapauksessa riippumatta siitä, minkä juuren saamme, mikä tarkoittaa, että kaikki neljä juuria ovat ratkaisuja yhtälöimme.

Hienoa, siirrytään nyt ongelman toiseen osaan.

Logaritmisen yhtälön juurien valinta segmentillä

Valitsemme neljästä juuristamme ne, jotka sijaitsevat segmentillä [−1; 8/9]. Palaamme juurillemme, ja nyt teemme heidän valinnan. Aluksi suosittelen piirtämään koordinaattiakselin ja merkitsemään segmentin päät siihen:

Molemmat kohdat varjostetaan. Nuo. Ongelman ehtojen mukaan olemme kiinnostuneita varjostetusta segmentistä. Katsotaan nyt juuria.

Irrationaaliset juuret

Aloitetaan irrationaalisista juurista. Huomaa, että 8.9< 9/9 = 1. С другой стороны, корень из двух явно больше единицы. Следовательно, наши корни будут находиться на отрезке в таком положении:

Tästä seuraa, että kahden juuri ei kuulu meitä kiinnostavaan segmenttiin. Vastaavasti saamme negatiivisen juuren kanssa: se on pienempi kuin −1, eli se sijaitsee meitä kiinnostavan segmentin vasemmalla puolella.

Rationaaliset juuret

Jäljellä on kaksi juuria: x = 1/2 ja x = −1/2. Huomaa, että segmentin vasen pää (−1) on negatiivinen ja oikea pää (8/9) on positiivinen. Siksi jossain näiden päiden välissä on luku 0. Juuri x = −1/2 on välillä −1 ja 0, ts. päätyy lopulliseen vastaukseen. Teemme samoin juurella x = 1/2. Tämä juuri on myös tarkasteltavalla segmentillä.

Voit varmistaa, että 8/9 on suurempi kuin 1/2. Vähennetään nämä luvut toisistaan:

Saimme murto-osan 7/18 > 0, mikä määritelmän mukaan tarkoittaa, että 8/9 > 1/2.

Merkitään koordinaattiakselille sopivat juuret:

Lopullinen vastaus on kaksi juuria: 1/2 ja −1/2.

Irrationaalisten lukujen vertailu: universaali algoritmi

Lopuksi haluaisin palata vielä kerran irrationaalisiin lukuihin. Heidän esimerkkinsä avulla tarkastelemme nyt, kuinka rationaalisia ja irrationaalisia suureita verrataan matematiikassa. Aluksi niiden välillä on sellainen rasti V - "enemmän" tai "vähemmän" -merkki, mutta emme vielä tiedä mihin suuntaan se on suunnattu. kirjoitetaan:

Miksi ylipäänsä tarvitsemme vertailualgoritmeja? Tosiasia on, että tässä ongelmassa olimme erittäin onnekkaita: jakonumero 1 syntyi ratkaisuprosessissa, josta voimme ehdottomasti sanoa:

Et kuitenkaan aina näe tällaista numeroa heti. Yritetään siis verrata lukujamme suoraan.

Miten se on tehty? Teemme samoin kuin tavallisten epäyhtälöiden kanssa:

1. Ensinnäkin, jos meillä olisi negatiiviset kertoimet jossain, kertoisimme epäyhtälön molemmat puolet −1:llä. Tietysti merkin vaihtaminen. Tämä valintamerkki V muuttuisi tähän - Λ.
2. Mutta meidän tapauksessamme molemmat osapuolet ovat jo positiivisia, joten mitään ei tarvitse muuttaa. Se, mitä todella tarvitaan, on neliön molemmin puolin päästä eroon radikaalista.

Jos irrationaalisia lukuja verrattaessa ei ole mahdollista valita välittömästi erottelevaa elementtiä, suosittelen tällaisen vertailun suorittamista "päässä" - kuvaamalla sitä tavallisena epäyhtälönä.

Kun se ratkaistaan, se muotoillaan seuraavasti:

Nyt kaikkea on helppo verrata. Pointti on, että 64/81< 81/81 = 1 < 2. На основании той цепочки преобразований мы заключаем, что 64/81 < 2 и, следовательно, корень больше 8/9.

Siinä se, olemme saaneet tiukan todisteen siitä, että kaikki numerot on merkitty numeroriville x oikein ja täsmälleen siinä järjestyksessä, jossa niiden pitäisi olla. Kukaan ei löydä vikaa tästä ratkaisusta, joten muista: jos et heti näe jakolukua (meidän tapauksessamme se on 1), kirjoita vapaasti yllä oleva konstruktio, kerro, neliöi se - ja lopulta saada kaunis epätasa-arvo. Tästä epätasa-arvosta selviää kumpi luku on suurempi ja mikä pienempi.

Palatakseni ongelmaamme, haluaisin vielä kerran kiinnittää huomionne siihen, mitä teimme aivan alussa, kun ratkaisimme yhtälömme. Nimittäin: tarkastelimme tarkasti alkuperäistä logaritmista yhtälöämme ja yritimme pelkistää sen kanoninen logaritminen yhtälö. Missä on vain logaritmit vasemmalla ja oikealla - ilman lisätermejä, kertoimia edessä jne. Emme tarvitse kahta logaritmia a:n tai b:n perusteella, vaan logaritmin, joka on yhtä suuri kuin toinen logaritmi.

Lisäksi logaritmien kantalukujen tulee olla yhtä suuret. Lisäksi, jos yhtälö on muodostettu oikein, niin elementaaristen logaritmien muunnosten (logaritmien summa, luvun muuntaminen logaritmiksi jne.) avulla vähennämme tämän yhtälön kanoniseksi.

Tästä lähtien, kun näet logaritmisen yhtälön, jota ei voida ratkaista heti, sinun ei pitäisi eksyä tai yrittää selvittää vastausta. Sinun tarvitsee vain noudattaa näitä ohjeita:

1. Muunna kaikki vapaat elementit logaritmeiksi;
2. Lisää sitten nämä logaritmit;
3. Vähennä tuloksena olevassa konstruktiossa kaikki logaritmit samaan kantaan.

Tuloksena saat yksinkertaisen yhtälön, joka voidaan ratkaista alkebraalgebran työkaluilla luokkien 8-9 materiaaleista. Yleensä mene verkkosivustolleni, harjoittele logaritmien ratkaisemista, ratkaise logaritmiset yhtälöt kuten minä, ratkaise ne paremmin kuin minä. Ja siinä kaikki minulle. Pavel Berdov oli kanssasi. Nähdään taas!

Mikä on logaritmi?

Huomio!
On olemassa ylimääräisiä
materiaalit erityisosastossa 555.
Niille, jotka ovat erittäin "ei kovin..."
Ja niille, jotka "erittäin...")

Mikä on logaritmi? Kuinka ratkaista logaritmit? Nämä kysymykset hämmentävät monia valmistuneita. Perinteisesti logaritmien aihetta pidetään monimutkaisena, käsittämättömänä ja pelottavana. Erityisesti yhtälöt logaritmeilla.

Tämä ei todellakaan ole totta. Ehdottomasti! Etkö usko minua? Hieno. Nyt vain 10–20 minuutissa:

1. Ymmärrät mikä on logaritmi.

2. Opi ratkaisemaan koko luokka eksponentiaaliyhtälöitä. Vaikka et ole kuullut niistä mitään.

3. Opi laskemaan yksinkertaisia ​​logaritmeja.

Lisäksi tätä varten sinun tarvitsee vain tietää kertotaulukko ja kuinka nostaa luku potenssiin...

Minusta tuntuu, että sinulla on epäilyksiä... No, okei, merkitse aika! Mennä!

Ratkaise ensin tämä yhtälö päässäsi:

Jos pidät tästä sivustosta...

Muuten, minulla on sinulle pari muuta mielenkiintoista sivustoa.)

Voit harjoitella esimerkkien ratkaisemista ja selvittää tasosi. Testaus välittömällä vahvistuksella. Opitaan - mielenkiinnolla!)

Voit tutustua funktioihin ja johdannaisiin.

Kuten tiedät, kun lausekkeita kerrotaan potenssien kanssa, niiden eksponentit laskevat aina yhteen (a b *a c = a b+c). Tämän matemaattisen lain johti Arkhimedes, ja myöhemmin, 800-luvulla, matemaatikko Virasen loi kokonaislukueksponenttien taulukon. Juuri he palvelivat logaritmien edelleen löytämistä. Esimerkkejä tämän toiminnon käytöstä löytyy melkein kaikkialta, missä sinun täytyy yksinkertaistaa hankalaa kertolaskua yksinkertaisella yhteenlaskolla. Jos käytät 10 minuuttia tämän artikkelin lukemiseen, selitämme sinulle, mitä logaritmit ovat ja miten niitä käytetään. Yksinkertaisella ja ymmärrettävällä kielellä.

Määritelmä matematiikassa

Logaritmi on seuraavan muodon lauseke: log a b=c, eli minkä tahansa ei-negatiivisen luvun (eli minkä tahansa positiivisen) logaritmi "b" kantaansa "a" katsotaan potenssiksi "c". ", johon kantaa "a" on nostettava, jotta lopulta saadaan arvo "b". Analysoidaan logaritmia esimerkein, oletetaan, että on lauseke log 2 8. Miten löytää vastaus? Se on hyvin yksinkertaista, sinun täytyy löytää teho, joka on sellainen, että 2:sta vaadittuun tehoon saat 8. Kun olet tehnyt joitain laskelmia päässäsi, saamme luvun 3! Ja se on totta, koska 2 3:n potenssiin antaa vastauksen 8.

Logaritmien tyypit

Monille oppilaille ja opiskelijoille tämä aihe näyttää monimutkaiselta ja käsittämättömältä, mutta itse asiassa logaritmit eivät ole niin pelottavia, tärkeintä on ymmärtää niiden yleinen merkitys ja muistaa niiden ominaisuudet ja jotkut säännöt. Logaritmisia lausekkeita on kolme eri tyyppiä:

1. Luonnollinen logaritmi ln a, jossa kanta on Eulerin luku (e = 2,7).
2. Desimaali a, jossa kantaluku on 10.
3. Minkä tahansa luvun b logaritmi kantaan a>1.

Jokainen niistä ratkaistaan ​​tavallisella tavalla, mukaan lukien yksinkertaistaminen, pelkistys ja myöhempi pelkistys yhdeksi logaritmiksi logaritmisilla teoreemoilla. Saadaksesi oikeat logaritmien arvot, sinun tulee muistaa niiden ominaisuudet ja toimintojen järjestys niitä ratkaiseessasi.

Säännöt ja joitain rajoituksia

Matematiikassa on useita sääntöjä-rajoituksia, jotka hyväksytään aksioomina, eli niistä ei keskustella ja ne ovat totuuksia. Esimerkiksi on mahdotonta jakaa lukuja nollalla, ja on myös mahdotonta erottaa negatiivisten lukujen parillinen juuri. Logaritmeilla on myös omat sääntönsä, joita noudattamalla voit helposti oppia työskentelemään pitkien ja tilavien logaritmien lausekkeiden kanssa:

• Kanta "a" on aina suurempi kuin nolla, eikä yhtä suuri kuin 1, muuten lauseke menettää merkityksensä, koska "1" ja "0" missä tahansa määrin ovat aina yhtä suuria kuin niiden arvot;
• jos a > 0, niin a b >0, käy ilmi, että myös c:n on oltava suurempi kuin nolla.

Kuinka ratkaista logaritmit?

Tehtävänä on esimerkiksi löytää vastaus yhtälöön 10 x = 100. Tämä on erittäin helppoa, sinun on valittava potenssi nostamalla lukua kymmenen, johon saamme 100. Tämä on tietysti 10 2 = 100.

Esitetään nyt tämä lauseke logaritmisessa muodossa. Saamme log 10 100 = 2. Logaritmeja ratkaistaessa kaikki toiminnot käytännössä konvergoivat löytääkseen potenssin, johon on syötettävä logaritmin kanta tietyn luvun saamiseksi.

Tuntemattoman asteen arvon määrittämiseksi tarkasti sinun on opittava työskentelemään astetaulukon kanssa. Se näyttää tältä:

Kuten näet, jotkut eksponentit voidaan arvata intuitiivisesti, jos sinulla on tekninen mieli ja tietoa kertotaulukosta. Suuremmille arvoille tarvitset kuitenkin tehotaulukon. Sitä voivat käyttää myös ne, jotka eivät tiedä yhtään mitään monimutkaisista matemaattisista aiheista. Vasemmassa sarakkeessa on numeroita (kanta a), ylimmällä rivillä on potenssin c arvo, johon luku a korotetaan. Leikkauskohdassa solut sisältävät numeroarvot, jotka ovat vastaus (a c =b). Otetaan esimerkiksi aivan ensimmäinen solu numerolla 10 ja neliötetään se, saamme arvon 100, joka on merkitty kahden solumme leikkauspisteeseen. Kaikki on niin yksinkertaista ja helppoa, että jopa todellisin humanisti ymmärtää!

Yhtälöt ja epäyhtälöt

Osoittautuu, että tietyissä olosuhteissa eksponentti on logaritmi. Siksi mikä tahansa matemaattinen numeerinen lauseke voidaan kirjoittaa logaritmisena yhtälönä. Esimerkiksi 3 4 =81 voidaan kirjoittaa 81:n kanta-3 logaritmiksi, joka on yhtä suuri kuin neljä (log 3 81 = 4). Negatiivisten potenssien säännöt ovat samat: 2 -5 = 1/32 kirjoitetaan se logaritmina, saadaan log 2 (1/32) = -5. Yksi kiehtovimmista matematiikan osista on "logaritmien" aihe. Katsomme alla esimerkkejä ja ratkaisuja yhtälöistä heti niiden ominaisuuksien tutkimisen jälkeen. Katsotaanpa nyt, miltä epäyhtälöt näyttävät ja miten ne voidaan erottaa yhtälöistä.

Seuraava lauseke annetaan: log 2 (x-1) > 3 - se on logaritminen epäyhtälö, koska tuntematon arvo “x” on logaritmisen merkin alla. Ja myös lausekkeessa verrataan kahta suuruutta: halutun luvun logaritmi kahdelle on suurempi kuin luku kolme.

Tärkein ero logaritmien yhtälöiden ja epäyhtälöiden välillä on se, että yhtälöt, joissa on logaritmi (esim. logaritmi 2 x = √9) sisältävät yhden tai useamman tietyn numeerisen arvon vastauksessa, kun taas epäyhtälöä ratkaistaessa molemmat hyväksyttävien arvojen alue. arvot ja pisteet määritetään rikkoen tämän funktion. Tämän seurauksena vastaus ei ole yksinkertainen joukko yksittäisiä lukuja, kuten yhtälön vastauksessa, vaan jatkuva sarja tai numerosarja.

Peruslauseita logaritmeista

Ratkaistaessa primitiivisiä tehtäviä logaritmin arvojen löytämiseksi, sen ominaisuuksia ei ehkä tunneta. Logaritmisista yhtälöistä tai epäyhtälöistä tulee kuitenkin ennen kaikkea ymmärtää ja soveltaa käytännössä kaikki logaritmien perusominaisuudet. Katsomme esimerkkejä yhtälöistä myöhemmin; tarkastellaan ensin jokaista ominaisuutta yksityiskohtaisemmin.

1. Pääidentiteetti näyttää tältä: a logaB =B. Sitä sovelletaan vain, kun a on suurempi kuin 0, ei yhtä kuin yksi ja B on suurempi kuin nolla.
2. Tuloksen logaritmi voidaan esittää seuraavalla kaavalla: log d (s 1 * s 2) = log d s 1 + log d s 2. Tässä tapauksessa pakollinen ehto on: d, s 1 ja s 2 > 0; a≠1. Voit todistaa tämän logaritmisen kaavan esimerkeineen ja ratkaisuineen. Olkoon log a s 1 = f 1 ja log a s 2 = f 2, sitten a f1 = s 1, a f2 = s 2. Saadaan, että s 1 * s 2 = a f1 *a f2 = a f1+f2 (ominaisuudet astetta ), ja sitten määritelmän mukaan: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, mikä oli todistettava.
3. Osamäärän logaritmi näyttää tältä: log a (s 1/s 2) = log a s 1 - log a s 2.
4. Kaavan muodossa oleva lause saa seuraavan muodon: log a q b n = n/q log a b.

Tätä kaavaa kutsutaan "logaritmiasteen ominaisuudeksi". Se muistuttaa tavallisten asteiden ominaisuuksia, eikä se ole yllättävää, koska kaikki matematiikka perustuu luonnollisiin postulaatteihin. Katsotaanpa todistetta.

Olkoon log a b = t, niin saadaan a t =b. Jos nostetaan molemmat osat potenssiin m: a tn = b n ;

mutta koska a tn = (a q) nt/q = b n, log a q b n = (n*t)/t, sitten log a q b n = n/q log a b. Lause on todistettu.

Esimerkkejä ongelmista ja eriarvoisuudesta

Yleisimmät logaritmien ongelmatyypit ovat esimerkkejä yhtälöistä ja epäyhtälöistä. Ne löytyvät lähes kaikista ongelmakirjoista, ja ne ovat myös pakollinen osa matematiikan kokeita. Jos haluat päästä yliopistoon tai läpäistä matematiikan pääsykokeita, sinun on tiedettävä, kuinka ratkaista tällaiset tehtävät oikein.

Valitettavasti ei ole olemassa yhtä suunnitelmaa tai kaaviota logaritmin tuntemattoman arvon ratkaisemiseksi ja määrittämiseksi, mutta jokaiseen matemaattiseen epäyhtälöön tai logaritmiseen yhtälöön voidaan soveltaa tiettyjä sääntöjä. Ensinnäkin sinun tulee selvittää, voidaanko lauseke yksinkertaistaa tai pelkistää yleiseen muotoon. Voit yksinkertaistaa pitkiä logaritmisia lausekkeita, jos käytät niiden ominaisuuksia oikein. Tutustutaan heihin nopeasti.

Ratkaistaessamme logaritmisia yhtälöitä on määritettävä, minkä tyyppinen logaritmi meillä on: esimerkkilauseke voi sisältää luonnollisen logaritmin tai desimaalilogaritmin.

Tässä on esimerkkejä ln100, ln1026. Heidän ratkaisunsa tiivistyy siihen tosiasiaan, että heidän on määritettävä teho, jolla kanta 10 on vastaavasti 100 ja 1026. Luonnollisten logaritmien ratkaisemiseksi sinun on käytettävä logaritmisia identiteettejä tai niiden ominaisuuksia. Katsotaanpa esimerkkejä erityyppisten logaritmien ongelmien ratkaisemisesta.

Logaritmikaavojen käyttäminen: Esimerkkejä ja ratkaisuja

Katsotaanpa siis esimerkkejä logaritmien peruslauseiden käytöstä.

1. Tuloksen logaritmin ominaisuutta voidaan käyttää tehtävissä, joissa on tarpeen jakaa suuri luvun b arvo yksinkertaisempiin tekijöihin. Esimerkiksi log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Vastaus on 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - kuten näette, logaritmin potenssin neljättä ominaisuutta käyttämällä onnistuimme ratkaisemaan näennäisesti monimutkaisen ja ratkaisemattoman lausekkeen. Sinun tarvitsee vain ottaa kantaa huomioon ja sitten ottaa eksponenttiarvot pois logaritmin etumerkistä.

Tehtävät yhtenäisestä valtionkokeesta

Logaritmeja löytyy usein pääsykokeista, erityisesti monia logaritmisongelmia Unified State Examissa (valtiokoe kaikille valmistuneille). Tyypillisesti nämä tehtävät eivät ole vain osassa A (kokeen helpoin testiosa), vaan myös osassa C (monimutkaisimmat ja laajimmat tehtävät). Tentti vaatii tarkan ja täydellisen tuntemuksen aiheesta "Luonnolliset logaritmit".

Esimerkit ja ratkaisut ongelmiin on otettu Unified State Exam -testin virallisista versioista. Katsotaan kuinka tällaiset tehtävät ratkaistaan.

Annettu log 2 (2x-1) = 4. Ratkaisu:
kirjoitetaan lauseke uudelleen yksinkertaistaen sitä hieman log 2 (2x-1) = 2 2, logaritmin määritelmällä saadaan, että 2x-1 = 2 4, siis 2x = 17; x = 8,5.

• On parasta vähentää kaikki logaritmit samaan kantaan, jotta ratkaisu ei ole hankala ja hämmentävä.
• Kaikki logaritmimerkin alla olevat lausekkeet ilmoitetaan positiivisina, joten kun logaritmimerkin alla olevan lausekkeen eksponentti ja sen kanta otetaan pois kertoimesta, logaritmin alle jäävän lausekkeen tulee olla positiivinen.