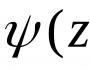ഹോർണർ സർക്യൂട്ട് നിർവചനം. ഉയർന്ന ഗണിതത്തിലെ സമവാക്യങ്ങൾ ബഹുപദങ്ങളുടെ യുക്തിസഹമായ വേരുകൾ

സ്ലൈഡ് 3

ഹോർണർ വില്യംസ് ജോർജ്ജ് (1786-22.9.1837) - ഇംഗ്ലീഷ് ഗണിതശാസ്ത്രജ്ഞൻ. ബ്രിസ്റ്റോളിൽ ജനിച്ചു. അവൻ അവിടെ പഠിക്കുകയും ജോലി ചെയ്യുകയും ചെയ്തു, തുടർന്ന് ബാത്തിലെ സ്കൂളുകളിൽ. ബീജഗണിതത്തെക്കുറിച്ചുള്ള അടിസ്ഥാന കൃതികൾ. 1819-ൽ ഒരു പോളിനോമിയലിന്റെ യഥാർത്ഥ വേരുകളുടെ ഏകദേശ കണക്കുകൂട്ടലിനായി ഒരു രീതി പ്രസിദ്ധീകരിച്ചു, അതിനെ ഇപ്പോൾ റുഫിനി-ഹോർണർ രീതി എന്ന് വിളിക്കുന്നു (ഈ രീതി ചൈനക്കാർക്ക് 13-ആം നൂറ്റാണ്ടിൽ അറിയാമായിരുന്നു). ഹോർണറിന് ശേഷം.

സ്ലൈഡ് 4

ഹോർണർ സ്കീം

nth ഡിഗ്രിയുടെ ഒരു പോളിനോമിയലിനെ ഒരു ലീനിയർ ബൈനോമിയൽ കൊണ്ട് ഹരിക്കുന്നതിനുള്ള ഒരു രീതി - a, അപൂർണ്ണമായ ഘടകത്തിന്റെയും ശേഷിക്കുന്നതിന്റെയും ഗുണകങ്ങൾ വിഭജിക്കപ്പെടുന്ന പോളിനോമിയലിന്റെ ഗുണകങ്ങളുമായി സൂത്രവാക്യങ്ങളുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു എന്ന വസ്തുതയെ അടിസ്ഥാനമാക്കി:

സ്ലൈഡ് 5

ഹോർണറുടെ സ്കീം അനുസരിച്ച് കണക്കുകൂട്ടലുകൾ പട്ടികയിൽ സ്ഥാപിച്ചിരിക്കുന്നു:

ഉദാഹരണം 1. ഭാഗിക ഘടകം x3-x2+3x - 13 ഉം ബാക്കി 42=f(-3) ഉം ആണ്.

സ്ലൈഡ് 6

ഈ രീതിയുടെ പ്രധാന നേട്ടം നൊട്ടേഷന്റെ ഒതുക്കവും ഒരു പോളിനോമിയലിനെ ഒരു ദ്വിപദമായി വേഗത്തിൽ വിഭജിക്കാനുള്ള കഴിവുമാണ്. വാസ്തവത്തിൽ, ഗ്രൂപ്പിംഗ് രീതി റെക്കോർഡുചെയ്യുന്നതിനുള്ള മറ്റൊരു രൂപമാണ് ഹോർണറുടെ സ്കീം, എന്നിരുന്നാലും, രണ്ടാമത്തേതിൽ നിന്ന് വ്യത്യസ്തമായി, ഇത് പൂർണ്ണമായും ദൃശ്യമല്ല. ഉത്തരം (ഘടകവൽക്കരണം) ഇവിടെ തന്നെ ലഭിക്കുന്നു, അത് നേടുന്ന പ്രക്രിയ ഞങ്ങൾ കാണുന്നില്ല. ഞങ്ങൾ ഹോർണറുടെ സ്കീമിന്റെ കർശനമായ സാധൂകരണത്തിൽ ഏർപ്പെടില്ല, അത് എങ്ങനെ പ്രവർത്തിക്കുന്നുവെന്ന് മാത്രം കാണിക്കും.

സ്ലൈഡ് 7

ഉദാഹരണം 2.

P(x)=x4-6x3+7x-392 എന്ന ബഹുപദം x-7 കൊണ്ട് ഹരിക്കാവുന്നതാണെന്ന് നമുക്ക് തെളിയിക്കാം, കൂടാതെ വിഭജനത്തിന്റെ ഘടകം കണ്ടെത്താം. പരിഹാരം. ഹോർണറുടെ സ്കീം ഉപയോഗിച്ച്, നമ്മൾ P(7) കണ്ടെത്തുന്നു: ഇവിടെ നിന്ന് നമുക്ക് P(7)=0 ലഭിക്കും, അതായത്. ഒരു ബഹുപദത്തെ x-7 കൊണ്ട് ഹരിക്കുമ്പോൾ ബാക്കിയുള്ളത് പൂജ്യത്തിന് തുല്യമാണ്, അതിനാൽ, P(x) എന്നത് (x-7) ഗുണിതമാണ്. P(x) ന്റെ ഘടകഭാഗം (x-7) കൊണ്ട് ഹരിക്കുന്നു, അതിനാൽ P(x)=(x-7)(x3+x2+7x+56).

സ്ലൈഡ് 8

പോളിനോമിയൽ x3 - 5x2 - 2x + 16 ഫാക്ടർ ചെയ്യുക.

ഈ ബഹുപദത്തിന് പൂർണ്ണസംഖ്യ ഗുണകങ്ങൾ ഉണ്ട്. ഒരു പൂർണ്ണസംഖ്യ ഈ പോളിനോമിയലിന്റെ മൂലമാണെങ്കിൽ, അത് 16 എന്ന സംഖ്യയുടെ ഒരു ഹരിച്ചാണ്. അതിനാൽ, നൽകിയിരിക്കുന്ന പോളിനോമിയലിന് പൂർണ്ണസംഖ്യ വേരുകളുണ്ടെങ്കിൽ, ഇവ ±1 സംഖ്യകൾ മാത്രമായിരിക്കും; ± 2; ± 4; ± 8; ±16. നേരിട്ടുള്ള സ്ഥിരീകരണത്തിലൂടെ, സംഖ്യ 2 ഈ പോളിനോമിയലിന്റെ റൂട്ട് ആണെന്ന് ഞങ്ങൾക്ക് ബോധ്യമുണ്ട്, അതായത്, x3 – 5x2 – 2x + 16 = (x – 2)Q(x), ഇവിടെ Q(x) രണ്ടാം ഡിഗ്രിയുടെ ഒരു ബഹുപദമാണ്.

സ്ലൈഡ് 9

തത്ഫലമായുണ്ടാകുന്ന സംഖ്യകൾ 1, −3, -8 എന്നത് പോളിനോമിയലിന്റെ ഗുണകങ്ങളാണ്, ഇത് യഥാർത്ഥ പോളിനോമിയലിനെ x – 2 കൊണ്ട് ഹരിച്ചാൽ ലഭിക്കുന്നു. ഇതിനർത്ഥം വിഭജനത്തിന്റെ ഫലം: 1 x2 + (–3)x + ( –8) = x2 – 3x – 8. ഡിവിഷൻ ഫലമായുണ്ടാകുന്ന ഒരു പോളിനോമിയലിന്റെ ഡിഗ്രി എല്ലായ്പ്പോഴും ഒറിജിനൽ ഡിഗ്രിയേക്കാൾ 1 കുറവാണ്. അതിനാൽ: x3 – 5x2 – 2x + 16 = (x – 2)(x2 – 3x – 8).

തുടങ്ങിയവ. ഒരു പൊതു വിദ്യാഭ്യാസ സ്വഭാവമുള്ളതും ഉന്നത ഗണിതശാസ്ത്രത്തിന്റെ മുഴുവൻ കോഴ്‌സും പഠിക്കുന്നതിന് വലിയ പ്രാധാന്യമുള്ളതുമാണ്. ഇന്ന് നമ്മൾ "സ്കൂൾ" സമവാക്യങ്ങൾ ആവർത്തിക്കും, പക്ഷേ "സ്കൂൾ" മാത്രമല്ല - വിവിധ വിഷ്മത് പ്രശ്നങ്ങളിൽ എല്ലായിടത്തും കാണപ്പെടുന്നവ. പതിവുപോലെ, കഥ പ്രയോഗിക്കുന്ന രീതിയിൽ പറയും, അതായത്. ഞാൻ നിർവചനങ്ങളിലും വർഗ്ഗീകരണങ്ങളിലും ശ്രദ്ധ കേന്ദ്രീകരിക്കില്ല, പക്ഷേ അത് പരിഹരിക്കുന്നതിനുള്ള എന്റെ വ്യക്തിപരമായ അനുഭവം നിങ്ങളുമായി പങ്കിടും. വിവരങ്ങൾ പ്രാഥമികമായി തുടക്കക്കാർക്കായി ഉദ്ദേശിച്ചുള്ളതാണ്, എന്നാൽ കൂടുതൽ വിപുലമായ വായനക്കാർ തങ്ങൾക്കായി രസകരമായ നിരവധി പോയിന്റുകൾ കണ്ടെത്തും. തീർച്ചയായും ഹൈസ്കൂളിനപ്പുറം പോകുന്ന പുതിയ മെറ്റീരിയലുകൾ ഉണ്ടാകും.

അതിനാൽ സമവാക്യം…. പലരും ഈ വാക്ക് ഒരു നടുക്കത്തോടെ ഓർക്കുന്നു. വേരുകളുള്ള "സങ്കീർണമായ" സമവാക്യങ്ങൾ എന്തൊക്കെയാണ്... ... അവയെക്കുറിച്ച് മറക്കുക! കാരണം ഈ ഇനത്തിന്റെ ഏറ്റവും നിരുപദ്രവകരമായ "പ്രതിനിധികളെ" നിങ്ങൾ കണ്ടുമുട്ടും. അല്ലെങ്കിൽ ഡസൻ കണക്കിന് പരിഹാര രീതികളുള്ള വിരസമായ ത്രികോണമിതി സമവാക്യങ്ങൾ. സത്യം പറഞ്ഞാൽ എനിക്ക് അവരെ ഇഷ്ടമായിരുന്നില്ല... പരിഭ്രാന്തി വേണ്ട! - പിന്നെ മിക്കവാറും "ഡാൻഡെലിയോൺസ്" 1-2 ഘട്ടങ്ങളിൽ വ്യക്തമായ ഒരു പരിഹാരവുമായി നിങ്ങളെ കാത്തിരിക്കുന്നു. "ബർഡോക്ക്" തീർച്ചയായും പറ്റിപ്പിടിക്കുന്നുണ്ടെങ്കിലും, നിങ്ങൾ ഇവിടെ വസ്തുനിഷ്ഠമായിരിക്കണം.

വിചിത്രമെന്നു പറയട്ടെ, ഉയർന്ന ഗണിതശാസ്ത്രത്തിൽ വളരെ പ്രാകൃതമായ സമവാക്യങ്ങൾ കൈകാര്യം ചെയ്യുന്നത് വളരെ സാധാരണമാണ്. രേഖീയമായസമവാക്യങ്ങൾ

ഈ സമവാക്യം പരിഹരിക്കുക എന്നതിന്റെ അർത്ഥമെന്താണ്? ഇതിനർത്ഥം "x" (റൂട്ട്) യുടെ അത്തരം മൂല്യം കണ്ടെത്തുക, അത് യഥാർത്ഥ സമത്വത്തിലേക്ക് മാറ്റുന്നു. അടയാളം മാറ്റിക്കൊണ്ട് നമുക്ക് "മൂന്ന്" വലതുവശത്തേക്ക് എറിയാം:

വലതുവശത്തേക്ക് "രണ്ട്" ഇടുക (അല്ലെങ്കിൽ, ഒരേ കാര്യം - രണ്ട് വശങ്ങളും കൊണ്ട് ഗുണിക്കുക) :

പരിശോധിക്കുന്നതിന്, നേടിയ ട്രോഫി യഥാർത്ഥ സമവാക്യത്തിലേക്ക് മാറ്റിസ്ഥാപിക്കാം:

ശരിയായ സമത്വം ലഭിക്കുന്നു, അതായത് കണ്ടെത്തിയ മൂല്യം തീർച്ചയായും ഈ സമവാക്യത്തിന്റെ റൂട്ട് ആണ്. അല്ലെങ്കിൽ, അവർ പറയുന്നതുപോലെ, ഈ സമവാക്യം തൃപ്തിപ്പെടുത്തുന്നു.

റൂട്ട് ഒരു ദശാംശ ഭിന്നസംഖ്യയായും എഴുതാമെന്നത് ശ്രദ്ധിക്കുക:
ഈ മോശം ശൈലിയിൽ പറ്റിനിൽക്കാതിരിക്കാൻ ശ്രമിക്കുക! ഞാൻ കാരണം ഒന്നിലധികം തവണ ആവർത്തിച്ചു, പ്രത്യേകിച്ചും, ആദ്യ പാഠത്തിൽ തന്നെ ഉയർന്ന ബീജഗണിതം.

വഴിയിൽ, സമവാക്യം "അറബിയിൽ" പരിഹരിക്കാനും കഴിയും:

ഈ റെക്കോർഡിംഗ് പൂർണ്ണമായും നിയമപരമാണ് എന്നതാണ് ഏറ്റവും രസകരമായ കാര്യം! എന്നാൽ നിങ്ങൾ ഒരു അധ്യാപകനല്ലെങ്കിൽ, ഇത് ചെയ്യാതിരിക്കുന്നതാണ് നല്ലത്, കാരണം മൗലികത ഇവിടെ ശിക്ഷാർഹമാണ് =)

ഇപ്പോൾ കുറച്ച്

ഗ്രാഫിക്കൽ പരിഹാര രീതി

സമവാക്യത്തിന് രൂപമുണ്ട്, അതിന്റെ റൂട്ട് ആണ് "എക്സ്" കോർഡിനേറ്റ് കവല പോയിന്റുകൾ ലീനിയർ ഫംഗ്ഷൻ ഗ്രാഫ്ഒരു ലീനിയർ ഫംഗ്‌ഷന്റെ ഗ്രാഫ് ഉപയോഗിച്ച് (x അക്ഷം):

ഉദാഹരണം വളരെ പ്രാഥമികമാണെന്ന് തോന്നുന്നു, ഇവിടെ കൂടുതൽ വിശകലനം ചെയ്യാൻ ഒന്നുമില്ല, പക്ഷേ അതിൽ നിന്ന് ഒരു അപ്രതീക്ഷിത സൂക്ഷ്മത കൂടി "ഞെക്കിപ്പിടിക്കാൻ" കഴിയും: നമുക്ക് അതേ സമവാക്യം രൂപത്തിൽ അവതരിപ്പിച്ച് ഫംഗ്ഷനുകളുടെ ഗ്രാഫുകൾ നിർമ്മിക്കാം:

അതിൽ, ദയവായി രണ്ട് ആശയങ്ങളും ആശയക്കുഴപ്പത്തിലാക്കരുത്: ഒരു സമവാക്യം ഒരു സമവാക്യമാണ്, കൂടാതെ പ്രവർത്തനം- ഇതൊരു ചടങ്ങാണ്! പ്രവർത്തനങ്ങൾ സഹായം മാത്രംസമവാക്യത്തിന്റെ വേരുകൾ കണ്ടെത്തുക. അവയിൽ രണ്ടോ മൂന്നോ നാലോ അല്ലെങ്കിൽ അനന്തമായി പലതും ഉണ്ടാകാം. ഈ അർത്ഥത്തിൽ ഏറ്റവും അടുത്ത ഉദാഹരണം അറിയപ്പെടുന്നതാണ് ക്വാഡ്രാറ്റിക് സമവാക്യം, ഒരു പ്രത്യേക ഖണ്ഡിക ലഭിച്ച പരിഹാര അൽഗോരിതം "ചൂടുള്ള" സ്കൂൾ ഫോർമുലകൾ. ഇത് യാദൃശ്ചികമല്ല! നിങ്ങൾക്ക് ഒരു ക്വാഡ്രാറ്റിക് സമവാക്യം പരിഹരിച്ച് അറിയാൻ കഴിയുമെങ്കിൽ പൈത്തഗോറസ് സിദ്ധാന്തം, അപ്പോൾ ഒരാൾ പറഞ്ഞേക്കാം, "ഉയർന്ന ഗണിതത്തിന്റെ പകുതി ഇതിനകം നിങ്ങളുടെ പോക്കറ്റിൽ ഉണ്ട്" =) അതിശയോക്തി, തീർച്ചയായും, എന്നാൽ സത്യത്തിൽ നിന്ന് വളരെ അകലെയല്ല!

അതിനാൽ, നമുക്ക് മടിയനാകാതെ ചില ക്വാഡ്രാറ്റിക് സമവാക്യങ്ങൾ ഉപയോഗിച്ച് പരിഹരിക്കാം സ്റ്റാൻഡേർഡ് അൽഗോരിതം:

, അതായത് സമവാക്യത്തിന് രണ്ട് വ്യത്യസ്തതകളുണ്ട് സാധുവായറൂട്ട്:

കണ്ടെത്തിയ രണ്ട് മൂല്യങ്ങളും യഥാർത്ഥത്തിൽ ഈ സമവാക്യത്തെ തൃപ്തിപ്പെടുത്തുന്നുവെന്ന് പരിശോധിക്കുന്നത് എളുപ്പമാണ്:

നിങ്ങൾ പെട്ടെന്ന് സൊല്യൂഷൻ അൽഗോരിതം മറന്നു പോയാൽ, കൈയ്യിൽ മാർഗങ്ങൾ/സഹായം ഇല്ലെങ്കിൽ എന്തുചെയ്യും? ഈ സാഹചര്യം ഉണ്ടാകാം, ഉദാഹരണത്തിന്, ഒരു ടെസ്റ്റ് അല്ലെങ്കിൽ പരീക്ഷ സമയത്ത്. ഞങ്ങൾ ഗ്രാഫിക്കൽ രീതി ഉപയോഗിക്കുന്നു! കൂടാതെ രണ്ട് വഴികളുണ്ട്: നിങ്ങൾക്ക് കഴിയും പോയിന്റ് ബൈ പോയിന്റ് നിർമ്മിക്കുകപരവലയം , അതുവഴി അത് അച്ചുതണ്ടിനെ എവിടെയാണ് വിഭജിക്കുന്നതെന്ന് കണ്ടെത്തുന്നു (അത് കടക്കുകയാണെങ്കിൽ). എന്നാൽ കൂടുതൽ തന്ത്രപരമായി എന്തെങ്കിലും ചെയ്യുന്നതാണ് നല്ലത്: സമവാക്യം രൂപത്തിൽ സങ്കൽപ്പിക്കുക, ലളിതമായ പ്രവർത്തനങ്ങളുടെ ഗ്രാഫുകൾ വരയ്ക്കുക - കൂടാതെ "എക്സ്" കോർഡിനേറ്റുകൾഅവയുടെ വിഭജന പോയിന്റുകൾ വ്യക്തമായി കാണാം!


നേർരേഖ പരവലയത്തെ സ്പർശിക്കുന്നതായി മാറുകയാണെങ്കിൽ, സമവാക്യത്തിന് രണ്ട് ഏകീകൃത (ഒന്നിലധികം) വേരുകൾ ഉണ്ട്. നേർരേഖ പരവലയത്തെ വിഭജിക്കുന്നില്ലെന്ന് തെളിഞ്ഞാൽ, യഥാർത്ഥ വേരുകൾ ഇല്ല.

ഇത് ചെയ്യുന്നതിന്, തീർച്ചയായും, നിങ്ങൾക്ക് നിർമ്മിക്കാൻ കഴിയണം പ്രാഥമിക പ്രവർത്തനങ്ങളുടെ ഗ്രാഫുകൾ, എന്നാൽ മറുവശത്ത്, ഒരു സ്കൂൾ കുട്ടിക്ക് പോലും ഈ കഴിവുകൾ ചെയ്യാൻ കഴിയും.

വീണ്ടും - ഒരു സമവാക്യം ഒരു സമവാക്യമാണ്, കൂടാതെ ഫംഗ്ഷനുകൾ ഫംഗ്ഷനുകളാണ് വെറുതെ സഹായിച്ചുസമവാക്യം പരിഹരിക്കുക!

ഇവിടെ, വഴിയിൽ, ഒരു കാര്യം കൂടി ഓർക്കുന്നത് ഉചിതമായിരിക്കും: ഒരു സമവാക്യത്തിന്റെ എല്ലാ ഗുണകങ്ങളും പൂജ്യമല്ലാത്ത ഒരു സംഖ്യ കൊണ്ട് ഗുണിച്ചാൽ, അതിന്റെ വേരുകൾ മാറില്ല.

അതിനാൽ, ഉദാഹരണത്തിന്, സമവാക്യം ഒരേ വേരുകളുണ്ട്. ലളിതമായ ഒരു "തെളിവ്" എന്ന നിലയിൽ, ഞാൻ ബ്രാക്കറ്റുകളിൽ നിന്ന് സ്ഥിരമായത് എടുക്കും:
ഞാൻ അത് വേദനയില്ലാതെ നീക്കം ചെയ്യും (ഞാൻ രണ്ട് ഭാഗങ്ങളെയും "മൈനസ് രണ്ട്" കൊണ്ട് ഹരിക്കും):

പക്ഷേ!ഞങ്ങൾ ഫംഗ്ഷൻ പരിഗണിക്കുകയാണെങ്കിൽ , അപ്പോൾ നിങ്ങൾക്ക് ഇവിടെ സ്ഥിരമായത് ഒഴിവാക്കാൻ കഴിയില്ല! ഗുണിതം ബ്രാക്കറ്റുകളിൽ നിന്ന് പുറത്തെടുക്കാൻ മാത്രമേ അനുവദനീയമായിട്ടുള്ളൂ: .

പലരും ഗ്രാഫിക്കൽ സൊല്യൂഷൻ രീതിയെ കുറച്ചുകാണുന്നു, അത് "മാന്യമല്ലാത്തത്" ആയി കണക്കാക്കുന്നു, ചിലർ ഈ സാധ്യതയെക്കുറിച്ച് പൂർണ്ണമായും മറക്കുന്നു. ഇത് അടിസ്ഥാനപരമായി തെറ്റാണ്, കാരണം ഗ്രാഫുകൾ പ്ലോട്ട് ചെയ്യുന്നത് ചിലപ്പോൾ സാഹചര്യം സംരക്ഷിക്കുന്നു!

മറ്റൊരു ഉദാഹരണം: ഏറ്റവും ലളിതമായ ത്രികോണമിതി സമവാക്യത്തിന്റെ വേരുകൾ നിങ്ങൾ ഓർക്കുന്നില്ലെന്ന് കരുതുക: . പൊതു സൂത്രവാക്യം സ്കൂൾ പാഠപുസ്തകങ്ങളിലാണ്, പ്രാഥമിക ഗണിതത്തെക്കുറിച്ചുള്ള എല്ലാ റഫറൻസ് പുസ്തകങ്ങളിലും, പക്ഷേ അവ നിങ്ങൾക്ക് ലഭ്യമല്ല. എന്നിരുന്നാലും, സമവാക്യം പരിഹരിക്കുന്നത് നിർണായകമാണ് (അല്ലെങ്കിൽ "രണ്ട്"). ഒരു എക്സിറ്റ് ഉണ്ട്! - പ്രവർത്തനങ്ങളുടെ ഗ്രാഫുകൾ നിർമ്മിക്കുക:


അതിനുശേഷം ഞങ്ങൾ അവരുടെ കവല പോയിന്റുകളുടെ "X" കോർഡിനേറ്റുകൾ ശാന്തമായി എഴുതുന്നു:

അനന്തമായി ധാരാളം വേരുകൾ ഉണ്ട്, ബീജഗണിതത്തിൽ അവയുടെ ഘനീഭവിച്ച നൊട്ടേഷൻ അംഗീകരിക്കപ്പെടുന്നു:
, എവിടെ ( – പൂർണ്ണസംഖ്യകളുടെ കൂട്ടം) .

കൂടാതെ, "പോകാതെ", ഒരു വേരിയബിൾ ഉപയോഗിച്ച് അസമത്വങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ഗ്രാഫിക്കൽ രീതിയെക്കുറിച്ചുള്ള കുറച്ച് വാക്കുകൾ. തത്വം ഒന്നുതന്നെയാണ്. അതിനാൽ, ഉദാഹരണത്തിന്, അസമത്വത്തിനുള്ള പരിഹാരം ഏതെങ്കിലും "x" ആണ്, കാരണം sinusoid ഏതാണ്ട് പൂർണ്ണമായും നേർരേഖയ്ക്ക് കീഴിലാണ്. സിനുസോയിഡിന്റെ കഷണങ്ങൾ നേർരേഖയ്ക്ക് മുകളിൽ കർശനമായി കിടക്കുന്ന ഇടവേളകളുടെ കൂട്ടമാണ് അസമത്വത്തിനുള്ള പരിഹാരം. (x-അക്ഷം):

അല്ലെങ്കിൽ, ചുരുക്കത്തിൽ:

എന്നാൽ അസമത്വത്തിന് നിരവധി പരിഹാരങ്ങൾ ഇതാ: ശൂന്യം, സൈനസോയിഡിന്റെ ഒരു ബിന്ദുവും നേർരേഖയ്ക്ക് മുകളിലല്ല എന്നതിനാൽ.

നിങ്ങൾക്ക് മനസ്സിലാകാത്ത എന്തെങ്കിലും ഉണ്ടോ? എന്ന പാഠഭാഗങ്ങൾ അടിയന്തിരമായി പഠിക്കുക സെറ്റുകൾഒപ്പം ഫംഗ്ഷൻ ഗ്രാഫുകൾ!

നമുക്ക് ചൂടാക്കാം:

വ്യായാമം 1

ഇനിപ്പറയുന്ന ത്രികോണമിതി സമവാക്യങ്ങൾ ഗ്രാഫിക്കായി പരിഹരിക്കുക:

പാഠത്തിന്റെ അവസാനം ഉത്തരങ്ങൾ

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, കൃത്യമായ ശാസ്ത്രം പഠിക്കാൻ സൂത്രവാക്യങ്ങളും റഫറൻസ് പുസ്തകങ്ങളും ആവശ്യമില്ല! മാത്രമല്ല, ഇത് അടിസ്ഥാനപരമായി വികലമായ ഒരു സമീപനമാണ്.

പാഠത്തിന്റെ തുടക്കത്തിൽ തന്നെ ഞാൻ നിങ്ങൾക്ക് ഉറപ്പുനൽകിയതുപോലെ, ഉയർന്ന ഗണിതശാസ്ത്രത്തിന്റെ ഒരു സ്റ്റാൻഡേർഡ് കോഴ്സിലെ സങ്കീർണ്ണമായ ത്രികോണമിതി സമവാക്യങ്ങൾ വളരെ അപൂർവമായി മാത്രമേ പരിഹരിക്കപ്പെടൂ. എല്ലാ സങ്കീർണ്ണതയും, ഒരു ചട്ടം പോലെ, സമവാക്യങ്ങളിൽ അവസാനിക്കുന്നു, ഇതിന്റെ പരിഹാരം ഏറ്റവും ലളിതമായ സമവാക്യങ്ങളിൽ നിന്ന് ഉത്ഭവിക്കുന്ന വേരുകളുടെ രണ്ട് ഗ്രൂപ്പുകളാണ്. . രണ്ടാമത്തേത് പരിഹരിക്കുന്നതിനെക്കുറിച്ച് വളരെയധികം വിഷമിക്കേണ്ട - ഒരു പുസ്തകത്തിൽ നോക്കുക അല്ലെങ്കിൽ ഇന്റർനെറ്റിൽ കണ്ടെത്തുക =)

ഗ്രാഫിക്കൽ സൊല്യൂഷൻ രീതി വളരെ നിസ്സാരമായ സന്ദർഭങ്ങളിലും സഹായിക്കും. ഉദാഹരണത്തിന്, ഇനിപ്പറയുന്ന "റാഗ്ടാഗ്" സമവാക്യം പരിഗണിക്കുക:

അതിന്റെ പരിഹാരത്തിനുള്ള സാധ്യതകൾ നോക്കുന്നു... ഒന്നും പോലെ കാണുന്നില്ല, എന്നാൽ രൂപത്തിലുള്ള സമവാക്യം നിങ്ങൾ സങ്കൽപ്പിക്കേണ്ടതുണ്ട്, നിർമ്മിക്കുക ഫംഗ്ഷൻ ഗ്രാഫുകൾഎല്ലാം അവിശ്വസനീയമാംവിധം ലളിതമായി മാറും. എന്നതിനെക്കുറിച്ചുള്ള ലേഖനത്തിന്റെ മധ്യത്തിൽ ഒരു ഡ്രോയിംഗ് ഉണ്ട് അനന്തമായ പ്രവർത്തനങ്ങൾ (അടുത്ത ടാബിൽ തുറക്കും).

ഒരേ ഗ്രാഫിക്കൽ രീതി ഉപയോഗിച്ച്, സമവാക്യത്തിന് ഇതിനകം രണ്ട് വേരുകളുണ്ട്, അവയിലൊന്ന് പൂജ്യത്തിന് തുല്യമാണെന്നും മറ്റൊന്ന്, പ്രത്യക്ഷമായും, യുക്തിരഹിതമായവിഭാഗത്തിൽ പെടുന്നു. ഈ റൂട്ട് ഏകദേശം കണക്കാക്കാം, ഉദാഹരണത്തിന്, ടാൻജെന്റ് രീതി. വഴിയിൽ, ചില പ്രശ്നങ്ങളിൽ, നിങ്ങൾ വേരുകൾ കണ്ടെത്തേണ്ടതില്ല, പക്ഷേ കണ്ടെത്തുക അവ നിലവിലുണ്ടോ?. ഇവിടെയും ഒരു ഡ്രോയിംഗ് സഹായിക്കും - ഗ്രാഫുകൾ വിഭജിക്കുന്നില്ലെങ്കിൽ, വേരുകളൊന്നുമില്ല.

പൂർണ്ണസംഖ്യ ഗുണകങ്ങളുള്ള ബഹുപദങ്ങളുടെ യുക്തിസഹമായ വേരുകൾ.
ഹോർണർ സ്കീം

ഇപ്പോൾ നിങ്ങളുടെ നോട്ടം മധ്യകാലഘട്ടത്തിലേക്ക് തിരിയാനും ക്ലാസിക്കൽ ബീജഗണിതത്തിന്റെ അതുല്യമായ അന്തരീക്ഷം അനുഭവിക്കാനും ഞാൻ നിങ്ങളെ ക്ഷണിക്കുന്നു. മെറ്റീരിയലിനെ നന്നായി മനസ്സിലാക്കാൻ, നിങ്ങൾ അൽപ്പമെങ്കിലും വായിക്കാൻ ഞാൻ ശുപാർശ ചെയ്യുന്നു സങ്കീർണ്ണ സംഖ്യകൾ.

അവരാണ് ഏറ്റവും മികച്ചത്. ബഹുപദങ്ങൾ.

ഫോമിന്റെ ഏറ്റവും സാധാരണമായ ബഹുപദങ്ങളായിരിക്കും ഞങ്ങളുടെ താൽപ്പര്യത്തിന്റെ ലക്ഷ്യം മുഴുവൻഗുണകങ്ങൾ ഒരു സ്വാഭാവിക സംഖ്യ എന്ന് വിളിക്കുന്നു ബഹുപദത്തിന്റെ ബിരുദം, നമ്പർ - ഉയർന്ന ഡിഗ്രിയുടെ ഗുണകം (അല്ലെങ്കിൽ ഏറ്റവും ഉയർന്ന ഗുണകം), കൂടാതെ ഗുണകം ആണ് സ്വതന്ത്ര അംഗം.

ഈ ബഹുപദത്തെ ഞാൻ ചുരുക്കമായി സൂചിപ്പിക്കും.

ഒരു ബഹുപദത്തിന്റെ വേരുകൾസമവാക്യത്തിന്റെ വേരുകൾ വിളിക്കുക

എനിക്ക് ഇരുമ്പ് യുക്തി ഇഷ്ടമാണ് =)

ഉദാഹരണങ്ങൾക്ക്, ലേഖനത്തിന്റെ തുടക്കത്തിൽ തന്നെ പോകുക:

1, 2 ഡിഗ്രികളുടെ പോളിനോമിയലുകളുടെ വേരുകൾ കണ്ടെത്തുന്നതിൽ പ്രശ്‌നങ്ങളൊന്നുമില്ല, എന്നാൽ നിങ്ങൾ വർദ്ധിപ്പിക്കുമ്പോൾ ഈ ടാസ്ക് കൂടുതൽ കൂടുതൽ ബുദ്ധിമുട്ടാണ്. മറുവശത്ത്, എല്ലാം കൂടുതൽ രസകരമാണ്! പാഠത്തിന്റെ രണ്ടാം ഭാഗം നീക്കിവയ്ക്കുന്നത് ഇതാണ്.

ആദ്യം, അക്ഷരാർത്ഥത്തിൽ സിദ്ധാന്തത്തിന്റെ പകുതി സ്ക്രീനിൽ:

1) അനന്തരഫലം അനുസരിച്ച് ബീജഗണിതത്തിന്റെ അടിസ്ഥാന സിദ്ധാന്തം, ഡിഗ്രി പോളിനോമിയലിന് കൃത്യമായി ഉണ്ട് സങ്കീർണ്ണമായവേരുകൾ. ചില വേരുകൾ (അല്ലെങ്കിൽ എല്ലാം പോലും) പ്രത്യേകിച്ച് ആയിരിക്കാം സാധുവായ. മാത്രമല്ല, യഥാർത്ഥ വേരുകൾക്കിടയിൽ സമാനമായ (ഒന്നിലധികം) വേരുകൾ ഉണ്ടാകാം (കുറഞ്ഞത് രണ്ട്, പരമാവധി കഷണങ്ങൾ).

ചില സങ്കീർണ്ണ സംഖ്യകൾ ഒരു ബഹുപദത്തിന്റെ മൂലമാണെങ്കിൽ സംയോജിപ്പിക്കുകഅതിന്റെ സംഖ്യയും ഈ ബഹുപദത്തിന്റെ മൂലമാണ് (സംയോജിത സങ്കീർണ്ണ വേരുകൾക്ക് ഒരു രൂപമുണ്ട്).

ഏറ്റവും ലളിതമായ ഉദാഹരണം ഒരു ക്വാഡ്രാറ്റിക് സമവാക്യമാണ്, അത് ആദ്യമായി 8-ൽ നേരിട്ടു (ഇഷ്ടം)ക്ലാസ്സ്, വിഷയത്തിൽ ഞങ്ങൾ ഒടുവിൽ "പൂർത്തിയാക്കി" സങ്കീർണ്ണ സംഖ്യകൾ. ഞാൻ നിങ്ങളെ ഓർമ്മിപ്പിക്കട്ടെ: ഒരു ക്വാഡ്രാറ്റിക് സമവാക്യത്തിന് ഒന്നുകിൽ രണ്ട് വ്യത്യസ്ത യഥാർത്ഥ വേരുകളുണ്ട്, അല്ലെങ്കിൽ ഒന്നിലധികം വേരുകൾ അല്ലെങ്കിൽ സങ്കീർണ്ണമായ വേരുകൾ സംയോജിപ്പിക്കുക.

2) നിന്ന് ബെസൗട്ടിന്റെ സിദ്ധാന്തംഒരു സംഖ്യ ഒരു സമവാക്യത്തിന്റെ മൂലമാണെങ്കിൽ, അനുബന്ധ ബഹുപദം ഫാക്‌ടറൈസ് ചെയ്യാവുന്നതാണ്:
, ഡിഗ്രിയുടെ ഒരു ബഹുപദം എവിടെയാണ്.

വീണ്ടും, നമ്മുടെ പഴയ ഉദാഹരണം: സമവാക്യത്തിന്റെ റൂട്ട് ആയതിനാൽ . അതിനുശേഷം, അറിയപ്പെടുന്ന "സ്കൂൾ" വിപുലീകരണം നേടുന്നത് ബുദ്ധിമുട്ടുള്ള കാര്യമല്ല.

Bezout ന്റെ സിദ്ധാന്തത്തിന്റെ അനന്തരഫലത്തിന് വലിയ പ്രായോഗിക മൂല്യമുണ്ട്: 3rd ഡിഗ്രിയുടെ ഒരു സമവാക്യത്തിന്റെ റൂട്ട് നമുക്ക് അറിയാമെങ്കിൽ, നമുക്ക് അതിനെ രൂപത്തിൽ പ്രതിനിധീകരിക്കാം. ക്വാഡ്രാറ്റിക് സമവാക്യത്തിൽ നിന്ന് അവശേഷിക്കുന്ന വേരുകൾ കണ്ടെത്തുന്നത് എളുപ്പമാണ്. 4-ആം ഡിഗ്രിയുടെ ഒരു സമവാക്യത്തിന്റെ റൂട്ട് നമുക്ക് അറിയാമെങ്കിൽ, ഇടത് വശം ഒരു ഉൽപ്പന്നത്തിലേക്ക് വികസിപ്പിക്കാൻ കഴിയും.

കൂടാതെ ഇവിടെ രണ്ട് ചോദ്യങ്ങളുണ്ട്:

ചോദ്യം ഒന്ന്. ഈ റൂട്ട് എങ്ങനെ കണ്ടെത്താം? ഒന്നാമതായി, നമുക്ക് അതിന്റെ സ്വഭാവം നിർവചിക്കാം: ഉയർന്ന ഗണിതശാസ്ത്രത്തിലെ പല പ്രശ്നങ്ങളിലും അത് കണ്ടെത്തേണ്ടത് ആവശ്യമാണ് യുക്തിസഹമായ, പ്രത്യേകിച്ച് മുഴുവൻബഹുപദങ്ങളുടെ വേരുകൾ, ഇക്കാര്യത്തിൽ, ഇനി നമുക്ക് അവയിൽ താൽപ്പര്യമുണ്ടാകും. ...അവർ വളരെ നല്ലവരാണ്, വളരെ മൃദുലമാണ്, നിങ്ങൾ അവരെ കണ്ടെത്താൻ ആഗ്രഹിക്കുന്നു! =)

ആദ്യം മനസ്സിൽ വരുന്നത് തിരഞ്ഞെടുക്കൽ രീതിയാണ്. ഉദാഹരണത്തിന്, സമവാക്യം പരിഗണിക്കുക. ഇവിടെ പിടിക്കുന്നത് സ്വതന്ത്ര പദത്തിലാണ് - അത് പൂജ്യത്തിന് തുല്യമാണെങ്കിൽ, എല്ലാം ശരിയാകും - ഞങ്ങൾ ബ്രാക്കറ്റുകളിൽ നിന്ന് “x” എടുക്കുകയും വേരുകൾ തന്നെ ഉപരിതലത്തിലേക്ക് “വീഴുകയും” ചെയ്യുന്നു:

എന്നാൽ ഞങ്ങളുടെ സ്വതന്ത്ര പദം "മൂന്ന്" എന്നതിന് തുല്യമാണ്, അതിനാൽ ഞങ്ങൾ "റൂട്ട്" എന്ന് അവകാശപ്പെടുന്ന സമവാക്യത്തിലേക്ക് വിവിധ സംഖ്യകൾ മാറ്റിസ്ഥാപിക്കാൻ തുടങ്ങുന്നു. ഒന്നാമതായി, ഏക മൂല്യങ്ങളുടെ പകരക്കാരൻ സ്വയം നിർദ്ദേശിക്കുന്നു. നമുക്ക് പകരം വയ്ക്കാം:

ലഭിച്ചു തെറ്റായസമത്വം, അതിനാൽ, യൂണിറ്റ് "യോഗ്യമല്ല." ശരി, നമുക്ക് പകരം വയ്ക്കാം:

ലഭിച്ചു സത്യംസമത്വം! അതായത്, ഈ സമവാക്യത്തിന്റെ മൂലമാണ് മൂല്യം.

മൂന്നാം ഡിഗ്രിയുടെ ഒരു ബഹുപദത്തിന്റെ വേരുകൾ കണ്ടെത്തുന്നതിന്, ഒരു വിശകലന രീതിയുണ്ട് (കാർഡാനോ ഫോർമുലകൾ എന്ന് വിളിക്കപ്പെടുന്നവ), എന്നാൽ ഇപ്പോൾ ഞങ്ങൾക്ക് അൽപ്പം വ്യത്യസ്തമായ ഒരു ജോലിയിൽ താൽപ്പര്യമുണ്ട്.

- നമ്മുടെ ബഹുപദത്തിന്റെ മൂലമായതിനാൽ, പോളിനോമിയലിനെ രൂപത്തിൽ പ്രതിനിധീകരിക്കാനും ഉത്ഭവിക്കാനും കഴിയും രണ്ടാമത്തെ ചോദ്യം: ഒരു "ഇളയ സഹോദരനെ" എങ്ങനെ കണ്ടെത്താം?

ഏറ്റവും ലളിതമായ ബീജഗണിത പരിഗണനകൾ ഇത് ചെയ്യുന്നതിന് നമ്മൾ വിഭജിക്കണമെന്ന് നിർദ്ദേശിക്കുന്നു. ഒരു പോളിനോമിയലിനെ ഒരു പോളിനോമിയൽ കൊണ്ട് എങ്ങനെ ഹരിക്കാം? സാധാരണ സംഖ്യകളെ വിഭജിക്കുന്ന അതേ സ്കൂൾ രീതി - "നിര"! പാഠത്തിന്റെ ആദ്യ ഉദാഹരണങ്ങളിൽ ഞാൻ ഈ രീതി വിശദമായി ചർച്ച ചെയ്തു. സങ്കീർണ്ണമായ പരിധികൾ, ഇപ്പോൾ നമ്മൾ മറ്റൊരു രീതി നോക്കും, അതിനെ വിളിക്കുന്നു ഹോർണർ സ്കീം.

ആദ്യം നമ്മൾ "ഏറ്റവും ഉയർന്ന" ബഹുപദം എഴുതുന്നു എല്ലാവരോടും കൂടെ , പൂജ്യം ഗുണകങ്ങൾ ഉൾപ്പെടെ:
, അതിനുശേഷം ഞങ്ങൾ ഈ ഗുണകങ്ങൾ (കർശനമായി ക്രമത്തിൽ) പട്ടികയുടെ മുകളിലെ വരിയിലേക്ക് നൽകുന്നു:

ഞങ്ങൾ ഇടതുവശത്ത് റൂട്ട് എഴുതുന്നു:

"ചുവപ്പ്" നമ്പർ ആണെങ്കിൽ ഹോർണറുടെ സ്കീമും പ്രവർത്തിക്കുമെന്ന് ഞാൻ ഉടൻ റിസർവേഷൻ ചെയ്യും അല്ലബഹുപദത്തിന്റെ മൂലമാണ്. എന്നിരുന്നാലും, കാര്യങ്ങൾ തിരക്കുകൂട്ടരുത്.

മുകളിൽ നിന്ന് ഞങ്ങൾ മുൻനിര ഗുണകം നീക്കംചെയ്യുന്നു:

താഴത്തെ സെല്ലുകൾ പൂരിപ്പിക്കുന്ന പ്രക്രിയ എംബ്രോയ്ഡറിയെ ഒരു പരിധിവരെ അനുസ്മരിപ്പിക്കുന്നു, അവിടെ "മൈനസ് വൺ" എന്നത് തുടർന്നുള്ള ഘട്ടങ്ങളിൽ വ്യാപിക്കുന്ന ഒരുതരം "സൂചി" ആണ്. ഞങ്ങൾ "വഹിച്ച" സംഖ്യയെ (-1) കൊണ്ട് ഗുണിക്കുകയും മുകളിലെ സെല്ലിൽ നിന്ന് ഉൽപ്പന്നത്തിലേക്ക് നമ്പർ ചേർക്കുകയും ചെയ്യുന്നു:

ഞങ്ങൾ കണ്ടെത്തിയ മൂല്യത്തെ "ചുവന്ന സൂചി" കൊണ്ട് ഗുണിക്കുകയും ഉൽപ്പന്നത്തിലേക്ക് ഇനിപ്പറയുന്ന സമവാക്യ ഗുണകം ചേർക്കുകയും ചെയ്യുന്നു:

ഒടുവിൽ, തത്ഫലമായുണ്ടാകുന്ന മൂല്യം വീണ്ടും "സൂചി", മുകളിലെ ഗുണകം എന്നിവ ഉപയോഗിച്ച് "പ്രോസസ്സ്" ചെയ്യുന്നു:

അവസാന സെല്ലിലെ പൂജ്യം പോളിനോമിയലിനെ വിഭജിച്ചിരിക്കുന്നുവെന്ന് നമ്മോട് പറയുന്നു ഒരു തുമ്പും ഇല്ലാതെ (അത് ആയിരിക്കണം), വിപുലീകരണ ഗുണകങ്ങൾ പട്ടികയുടെ താഴത്തെ വരിയിൽ നിന്ന് നേരിട്ട് "നീക്കംചെയ്യപ്പെടും":

അങ്ങനെ, ഞങ്ങൾ സമവാക്യത്തിൽ നിന്ന് തുല്യമായ ഒരു സമവാക്യത്തിലേക്ക് നീങ്ങി, ശേഷിക്കുന്ന രണ്ട് വേരുകൾ ഉപയോഗിച്ച് എല്ലാം വ്യക്തമാണ് (ഈ സാഹചര്യത്തിൽ നമുക്ക് സങ്കീർണ്ണമായ വേരുകൾ ലഭിക്കുന്നു).

സമവാക്യം ഗ്രാഫിക്കായി പരിഹരിക്കാനും കഴിയും: പ്ലോട്ട് "മിന്നൽ" ഗ്രാഫ് x-അക്ഷം കടക്കുന്നുവെന്ന് കാണുക () ബിന്ദുവില് . അല്ലെങ്കിൽ അതേ "തന്ത്രപരമായ" തന്ത്രം - ഞങ്ങൾ ഫോമിൽ സമവാക്യം മാറ്റിയെഴുതുകയും പ്രാഥമിക ഗ്രാഫുകൾ വരയ്ക്കുകയും അവയുടെ വിഭജന പോയിന്റിന്റെ "X" കോർഡിനേറ്റ് കണ്ടെത്തുകയും ചെയ്യുന്നു.

വഴിയിൽ, 3 ഡിഗ്രിയിലെ ഏതെങ്കിലും ഫംഗ്ഷൻ-പോളിനോമിയലിന്റെ ഗ്രാഫ് ഒരു തവണയെങ്കിലും അക്ഷത്തെ വിഭജിക്കുന്നു, അതിനർത്ഥം അനുബന്ധ സമവാക്യം ഇത്രയെങ്കിലുംഒന്ന് സാധുവായറൂട്ട്. ഈ വസ്‌തുത വിചിത്രമായ ഡിഗ്രിയുടെ ഏതൊരു പോളിനോമിയൽ ഫംഗ്‌ഷനിലും ശരിയാണ്.

ഇവിടെയും ഞാൻ താമസിക്കാൻ ആഗ്രഹിക്കുന്നു പ്രധാനപ്പെട്ട പോയിന്റ്പദാവലിയുമായി ബന്ധപ്പെട്ടത്: ബഹുപദംഒപ്പം ബഹുപദ പ്രവർത്തനം – അത് ഒരേ കാര്യമല്ല! എന്നാൽ പ്രായോഗികമായി അവർ പലപ്പോഴും സംസാരിക്കുന്നു, ഉദാഹരണത്തിന്, "ഒരു ബഹുപദത്തിന്റെ ഗ്രാഫ്" കുറിച്ച്, തീർച്ചയായും, അശ്രദ്ധയാണ്.

എന്നിരുന്നാലും, നമുക്ക് ഹോർണറുടെ സ്കീമിലേക്ക് മടങ്ങാം. ഞാൻ അടുത്തിടെ സൂചിപ്പിച്ചതുപോലെ, ഈ സ്കീം മറ്റ് നമ്പറുകൾക്കായി പ്രവർത്തിക്കുന്നു, പക്ഷേ നമ്പർ ആണെങ്കിൽ അല്ലസമവാക്യത്തിന്റെ റൂട്ട് ആണ്, അപ്പോൾ പൂജ്യമല്ലാത്ത ഒരു കൂട്ടിച്ചേർക്കൽ (ബാക്കിയുള്ളത്) ഞങ്ങളുടെ ഫോർമുലയിൽ ദൃശ്യമാകും:

ഹോർണറുടെ സ്കീം അനുസരിച്ച് നമുക്ക് "വിജയിക്കാത്ത" മൂല്യം "റൺ" ചെയ്യാം. ഈ സാഹചര്യത്തിൽ, ഒരേ പട്ടിക ഉപയോഗിക്കുന്നത് സൗകര്യപ്രദമാണ് - ഇടതുവശത്ത് ഒരു പുതിയ "സൂചി" എഴുതുക, മുകളിൽ നിന്ന് മുൻനിര ഗുണകം നീക്കുക (ഇടത് പച്ച അമ്പടയാളം), ഞങ്ങൾ പോകുന്നു:

പരിശോധിക്കാൻ, നമുക്ക് ബ്രാക്കറ്റുകൾ തുറന്ന് സമാനമായ പദങ്ങൾ അവതരിപ്പിക്കാം:
, ശരി.

ബാക്കിയുള്ളത് ("ആറ്") എന്നതിലെ പോളിനോമിയലിന്റെ മൂല്യമാണെന്ന് കാണാൻ എളുപ്പമാണ്. വാസ്തവത്തിൽ - ഇത് എങ്ങനെയുള്ളതാണ്:
, അതിലും മനോഹരം - ഇതുപോലെ:

മേൽപ്പറഞ്ഞ കണക്കുകൂട്ടലുകളിൽ നിന്ന്, ഹോർണറുടെ സ്കീം പോളിനോമിയലിനെ ഫാക്ടർ ചെയ്യാൻ മാത്രമല്ല, റൂട്ടിന്റെ "നാഗരിക" തിരഞ്ഞെടുപ്പ് നടത്താനും അനുവദിക്കുന്നു എന്ന് മനസ്സിലാക്കാൻ എളുപ്പമാണ്. ഒരു ചെറിയ ടാസ്ക് ഉപയോഗിച്ച് കണക്കുകൂട്ടൽ അൽഗോരിതം സ്വയം ഏകീകരിക്കാൻ ഞാൻ നിർദ്ദേശിക്കുന്നു:

ടാസ്ക് 2

ഹോർണറുടെ സ്കീം ഉപയോഗിച്ച്, സമവാക്യത്തിന്റെ പൂർണ്ണസംഖ്യ റൂട്ട് കണ്ടെത്തുകയും അനുബന്ധ പോളിനോമിയലിന്റെ ഘടകം കണ്ടെത്തുകയും ചെയ്യുക

മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, അവസാന നിരയിൽ ഒരു പൂജ്യം ശേഷിക്കുന്നത് വരെ നിങ്ങൾ 1, –1, 2, –2, ... – അക്കങ്ങൾ തുടർച്ചയായി പരിശോധിക്കേണ്ടതുണ്ട്. ഈ വരിയുടെ "സൂചി" പോളിനോമിയലിന്റെ റൂട്ട് ആണെന്ന് ഇതിനർത്ഥം

ഒരൊറ്റ പട്ടികയിൽ കണക്കുകൂട്ടലുകൾ ക്രമീകരിക്കുന്നത് സൗകര്യപ്രദമാണ്. പാഠത്തിന്റെ അവസാനം വിശദമായ പരിഹാരവും ഉത്തരവും.

താരതമ്യേന ലളിതമായ സന്ദർഭങ്ങളിൽ വേരുകൾ തിരഞ്ഞെടുക്കുന്ന രീതി നല്ലതാണ്, എന്നാൽ ബഹുപദത്തിന്റെ ഗുണകങ്ങളും കൂടാതെ/അല്ലെങ്കിൽ ഡിഗ്രിയും വലുതാണെങ്കിൽ, പ്രക്രിയയ്ക്ക് വളരെയധികം സമയമെടുത്തേക്കാം. അല്ലെങ്കിൽ അതേ ലിസ്റ്റിൽ 1, –1, 2, –2 എന്നിവയിൽ നിന്ന് ചില മൂല്യങ്ങൾ ഉണ്ടായിരിക്കാം, പരിഗണിക്കുന്നതിൽ അർത്ഥമില്ലേ? കൂടാതെ, വേരുകൾ ഫ്രാക്ഷണൽ ആയി മാറിയേക്കാം, ഇത് പൂർണ്ണമായും അശാസ്ത്രീയമായ പോക്കിംഗിലേക്ക് നയിക്കും.

ഭാഗ്യവശാൽ, യുക്തിസഹമായ വേരുകൾക്കായുള്ള "കാൻഡിഡേറ്റ്" മൂല്യങ്ങൾക്കായുള്ള തിരയൽ ഗണ്യമായി കുറയ്ക്കാൻ കഴിയുന്ന രണ്ട് ശക്തമായ സിദ്ധാന്തങ്ങളുണ്ട്:

സിദ്ധാന്തം 1നമുക്ക് പരിഗണിക്കാം അപ്രസക്തമായഅംശം, എവിടെ. സംഖ്യയാണ് സമവാക്യത്തിന്റെ മൂലമെങ്കിൽ, സ്വതന്ത്ര പദത്തെ വിഭജിക്കുകയും മുൻനിര ഗുണകത്തെ ഹരിക്കുകയും ചെയ്യുന്നു.

പ്രത്യേകിച്ച്, ലീഡിംഗ് കോഫിഫിഷ്യന്റ് ആണെങ്കിൽ, ഈ യുക്തിസഹമായ റൂട്ട് ഒരു പൂർണ്ണസംഖ്യയാണ്:

ഈ രുചികരമായ വിശദാംശങ്ങൾ ഉപയോഗിച്ച് ഞങ്ങൾ സിദ്ധാന്തം ചൂഷണം ചെയ്യാൻ തുടങ്ങുന്നു:

നമുക്ക് സമവാക്യത്തിലേക്ക് മടങ്ങാം. അതിന്റെ ലീഡിംഗ് കോഫിഫിഷ്യന്റ് ആയതിനാൽ, സാങ്കൽപ്പിക യുക്തിസഹമായ വേരുകൾ പ്രത്യേകമായി പൂർണ്ണസംഖ്യയാകാം, കൂടാതെ സ്വതന്ത്ര പദം അവശിഷ്ടങ്ങളില്ലാതെ ഈ വേരുകളായി വിഭജിക്കേണ്ടതാണ്. കൂടാതെ "മൂന്ന്" എന്നത് 1, -1, 3, -3 എന്നിങ്ങനെ വിഭജിക്കാം. അതായത്, ഞങ്ങൾക്ക് 4 "റൂട്ട് കാൻഡിഡേറ്റുകൾ" മാത്രമേയുള്ളൂ. കൂടാതെ, അനുസരിച്ച് സിദ്ധാന്തം 1, മറ്റ് യുക്തിസഹ സംഖ്യകൾ തത്വത്തിലെ ഈ സമവാക്യത്തിന്റെ വേരുകളാകാൻ കഴിയില്ല.

സമവാക്യത്തിൽ കുറച്ചുകൂടി "മത്സരാർത്ഥികൾ" ഉണ്ട്: സ്വതന്ത്ര പദം 1, -1, 2, - 2, 4, -4 എന്നിങ്ങനെ തിരിച്ചിരിക്കുന്നു.

1, –1 അക്കങ്ങൾ സാധ്യമായ വേരുകളുടെ പട്ടികയുടെ "റെഗുലർ" ആണെന്ന് ദയവായി ശ്രദ്ധിക്കുക (സിദ്ധാന്തത്തിന്റെ വ്യക്തമായ അനന്തരഫലം)മുൻഗണനാ പരിശോധനയ്ക്കുള്ള മികച്ച ചോയിസും.

നമുക്ക് കൂടുതൽ അർത്ഥവത്തായ ഉദാഹരണങ്ങളിലേക്ക് പോകാം:

പ്രശ്നം 3

പരിഹാരം: ലീഡിംഗ് കോഫിഫിഷ്യന്റ് ആയതിനാൽ, സാങ്കൽപ്പിക യുക്തിസഹമായ വേരുകൾക്ക് പൂർണ്ണസംഖ്യ മാത്രമേ ഉണ്ടാകൂ, അവ നിർബന്ധമായും സ്വതന്ത്ര പദത്തിന്റെ ഹരിച്ചുകളായിരിക്കണം. "മൈനസ് ഫോർട്ടി" ഇനിപ്പറയുന്ന ജോഡി സംഖ്യകളായി തിരിച്ചിരിക്കുന്നു:
- ആകെ 16 "സ്ഥാനാർത്ഥികൾ".

ഇവിടെ പ്രലോഭിപ്പിക്കുന്ന ഒരു ചിന്ത ഉടനടി പ്രത്യക്ഷപ്പെടുന്നു: എല്ലാ നെഗറ്റീവ് അല്ലെങ്കിൽ എല്ലാ പോസിറ്റീവ് വേരുകളും കളയാൻ കഴിയുമോ? ചില സന്ദർഭങ്ങളിൽ ഇത് സാധ്യമാണ്! ഞാൻ രണ്ട് അടയാളങ്ങൾ രൂപപ്പെടുത്തും:

1) എങ്കിൽ എല്ലാംപോളിനോമിയലിന്റെ ഗുണകങ്ങൾ നോൺ-നെഗറ്റീവ് ആണെങ്കിൽ, അതിന് പോസിറ്റീവ് വേരുകൾ ഉണ്ടാകില്ല. നിർഭാഗ്യവശാൽ, ഇത് ഞങ്ങളുടെ കാര്യമല്ല (ഇപ്പോൾ, നമുക്ക് ഒരു സമവാക്യം നൽകിയിട്ടുണ്ടെങ്കിൽ - അതെ, പോളിനോമിയലിന്റെ ഏതെങ്കിലും മൂല്യം മാറ്റിസ്ഥാപിക്കുമ്പോൾ, പോളിനോമിയലിന്റെ മൂല്യം കർശനമായി പോസിറ്റീവ് ആണ്, അതായത് എല്ലാ പോസിറ്റീവ് സംഖ്യകളും (കൂടാതെ യുക്തിരഹിതമായവയും)സമവാക്യത്തിന്റെ വേരുകളാകാൻ കഴിയില്ല.

2) ഒറ്റ ശക്തികൾക്കുള്ള ഗുണകങ്ങൾ നോൺ-നെഗറ്റീവ് ആണെങ്കിൽ, എല്ലാ ഇരട്ട ശക്തികൾക്കും (സ്വതന്ത്ര അംഗം ഉൾപ്പെടെ)നെഗറ്റീവ് ആണെങ്കിൽ, പോളിനോമിയലിന് നെഗറ്റീവ് വേരുകൾ ഉണ്ടാകില്ല. ഇതാണ് ഞങ്ങളുടെ കേസ്! അൽപ്പം അടുത്ത് നോക്കുമ്പോൾ, ഏതെങ്കിലും നെഗറ്റീവ് "എക്സ്" സമവാക്യത്തിലേക്ക് മാറ്റിസ്ഥാപിക്കുമ്പോൾ, ഇടത് വശം കർശനമായി നെഗറ്റീവ് ആയിരിക്കും, അതായത് നെഗറ്റീവ് വേരുകൾ അപ്രത്യക്ഷമാകും.

അതിനാൽ, ഗവേഷണത്തിനായി 8 സംഖ്യകൾ അവശേഷിക്കുന്നു:

ഹോർണറുടെ സ്കീം അനുസരിച്ച് ഞങ്ങൾ അവയെ തുടർച്ചയായി "ചാർജ്" ചെയ്യുന്നു. നിങ്ങൾ ഇതിനകം മാനസിക കണക്കുകൂട്ടലുകൾ നേടിയിട്ടുണ്ടെന്ന് ഞാൻ പ്രതീക്ഷിക്കുന്നു:

"രണ്ട്" പരീക്ഷിക്കുമ്പോൾ ഭാഗ്യം ഞങ്ങളെ കാത്തിരുന്നു. അതിനാൽ, പരിഗണനയിലുള്ള സമവാക്യത്തിന്റെ റൂട്ട് ആണ്, കൂടാതെ

സമവാക്യം പഠിക്കാൻ അവശേഷിക്കുന്നു . വിവേചനക്കാരൻ വഴി ഇത് ചെയ്യാൻ എളുപ്പമാണ്, എന്നാൽ അതേ സ്കീം ഉപയോഗിച്ച് ഞാൻ ഒരു സൂചക പരിശോധന നടത്തും. ഒന്നാമതായി, സ്വതന്ത്ര പദം 20 ന് തുല്യമാണെന്ന് നമുക്ക് ശ്രദ്ധിക്കാം, അതായത് സിദ്ധാന്തം 1സാധ്യമായ വേരുകളുടെ പട്ടികയിൽ നിന്ന് 8 ഉം 40 ഉം അക്കങ്ങൾ പുറത്തുവരുന്നു, ഇത് ഗവേഷണത്തിനുള്ള മൂല്യങ്ങൾ അവശേഷിപ്പിക്കുന്നു (ഹോർണറുടെ സ്കീം അനുസരിച്ച് ഒരാൾ ഒഴിവാക്കപ്പെട്ടു).

പുതിയ പട്ടികയുടെ മുകളിലെ വരിയിൽ ഞങ്ങൾ ട്രൈനോമിയലിന്റെ ഗുണകങ്ങൾ എഴുതുന്നു ഞങ്ങൾ ഒരേ "രണ്ട്" ഉപയോഗിച്ച് പരിശോധിക്കാൻ തുടങ്ങുന്നു. എന്തുകൊണ്ട്? വേരുകൾ ഗുണിതങ്ങളാകാം എന്നതിനാൽ, ദയവായി: - ഈ സമവാക്യത്തിന് 10 സമാന വേരുകളുണ്ട്. എന്നാൽ നാം ശ്രദ്ധ തിരിക്കരുത്:

ഇവിടെ, തീർച്ചയായും, വേരുകൾ യുക്തിസഹമാണെന്ന് അറിഞ്ഞുകൊണ്ട് ഞാൻ കുറച്ച് കിടക്കുകയായിരുന്നു. എല്ലാത്തിനുമുപരി, അവ യുക്തിരഹിതമോ സങ്കീർണ്ണമോ ആണെങ്കിൽ, ശേഷിക്കുന്ന എല്ലാ നമ്പറുകളുടെയും ഒരു പരാജയപ്പെട്ട പരിശോധനയെ ഞാൻ അഭിമുഖീകരിക്കും. അതിനാൽ, പ്രായോഗികമായി, വിവേചനക്കാരാൽ നയിക്കപ്പെടുക.

ഉത്തരം: യുക്തിസഹമായ വേരുകൾ: 2, 4, 5

ഞങ്ങൾ വിശകലനം ചെയ്ത പ്രശ്നത്തിൽ, ഞങ്ങൾ ഭാഗ്യവാനായിരുന്നു, കാരണം: എ) നെഗറ്റീവ് മൂല്യങ്ങൾ ഉടനടി വീണു, ബി) ഞങ്ങൾ റൂട്ട് വളരെ വേഗത്തിൽ കണ്ടെത്തി (സൈദ്ധാന്തികമായി ഞങ്ങൾക്ക് മുഴുവൻ പട്ടികയും പരിശോധിക്കാം).

എന്നാൽ വാസ്തവത്തിൽ സ്ഥിതി വളരെ മോശമാണ്. "ദി ലാസ്റ്റ് ഹീറോ" എന്ന ആവേശകരമായ ഗെയിം കാണാൻ ഞാൻ നിങ്ങളെ ക്ഷണിക്കുന്നു:

പ്രശ്നം 4

സമവാക്യത്തിന്റെ യുക്തിസഹമായ വേരുകൾ കണ്ടെത്തുക

പരിഹാരം: വഴി സിദ്ധാന്തം 1സാങ്കൽപ്പിക യുക്തിസഹമായ വേരുകളുടെ സംഖ്യകൾ വ്യവസ്ഥയെ തൃപ്തിപ്പെടുത്തണം (“പന്ത്രണ്ടിനെ എൽ കൊണ്ട് ഹരിക്കുന്നു” എന്ന് നമ്മൾ വായിക്കുന്നു), കൂടാതെ ഡിനോമിനേറ്ററുകൾ വ്യവസ്ഥയുമായി പൊരുത്തപ്പെടുന്നു. ഇതിനെ അടിസ്ഥാനമാക്കി, നമുക്ക് രണ്ട് ലിസ്റ്റുകൾ ലഭിക്കും:

"ലിസ്റ്റ് el":
കൂടാതെ "ലിസ്‌റ്റ് ഉം": (ഭാഗ്യവശാൽ, ഇവിടെയുള്ള അക്കങ്ങൾ സ്വാഭാവികമാണ്).

ഇനി സാധ്യമായ എല്ലാ വേരുകളുടെയും ഒരു ലിസ്റ്റ് ഉണ്ടാക്കാം. ആദ്യം, നമ്മൾ "എൽ ലിസ്റ്റ്" ആയി വിഭജിക്കുന്നു. അതേ നമ്പറുകൾ തന്നെ ലഭിക്കുമെന്ന് തികച്ചും വ്യക്തമാണ്. സൗകര്യാർത്ഥം, നമുക്ക് അവയെ ഒരു പട്ടികയിൽ ഇടാം:

നിരവധി ഭിന്നസംഖ്യകൾ കുറച്ചു, അതിന്റെ ഫലമായി ഇതിനകം "ഹീറോ ലിസ്റ്റിൽ" ഉള്ള മൂല്യങ്ങൾ. ഞങ്ങൾ "നവാഗതരെ" മാത്രം ചേർക്കുന്നു:

അതുപോലെ, ഞങ്ങൾ ഒരേ "ലിസ്റ്റിനെ" വിഭജിക്കുന്നു:

ഒടുവിൽ ഓൺ

അങ്ങനെ, ഞങ്ങളുടെ ഗെയിമിൽ പങ്കെടുക്കുന്നവരുടെ ടീം പൂർത്തിയായി:


നിർഭാഗ്യവശാൽ, ഈ പ്രശ്നത്തിലെ ബഹുപദം "പോസിറ്റീവ്" അല്ലെങ്കിൽ "നെഗറ്റീവ്" മാനദണ്ഡം പാലിക്കുന്നില്ല, അതിനാൽ നമുക്ക് മുകളിലോ താഴെയോ നിര നിരസിക്കാൻ കഴിയില്ല. എല്ലാ നമ്പറുകളും ഉപയോഗിച്ച് നിങ്ങൾ പ്രവർത്തിക്കേണ്ടതുണ്ട്.

നിനക്ക് എങ്ങനെയിരിക്കുന്നു? വരൂ, നിങ്ങളുടെ തല ഉയർത്തുക - ആലങ്കാരികമായി "കൊലയാളി സിദ്ധാന്തം" എന്ന് വിളിക്കാവുന്ന മറ്റൊരു സിദ്ധാന്തമുണ്ട്. ...“സ്ഥാനാർത്ഥികൾ”, തീർച്ചയായും =)

എന്നാൽ ആദ്യം നിങ്ങൾ ഹോർണറുടെ ഡയഗ്രാമിലൂടെ ഒന്ന് സ്ക്രോൾ ചെയ്യേണ്ടതുണ്ട് മുഴുവൻസംഖ്യകൾ. പരമ്പരാഗതമായി, നമുക്ക് ഒരെണ്ണം എടുക്കാം. മുകളിലെ വരിയിൽ ഞങ്ങൾ പോളിനോമിയലിന്റെ ഗുണകങ്ങൾ എഴുതുന്നു, എല്ലാം പതിവുപോലെ:

നാല് വ്യക്തമായും പൂജ്യമല്ലാത്തതിനാൽ, മൂല്യം ചോദ്യം ചെയ്യപ്പെടുന്ന ബഹുപദത്തിന്റെ മൂലമല്ല. എന്നാൽ അവൾ ഞങ്ങളെ വളരെയധികം സഹായിക്കും.

സിദ്ധാന്തം 2ചിലർക്കാണെങ്കിൽ പൊതുവായിപോളിനോമിയലിന്റെ മൂല്യം പൂജ്യമല്ല: , തുടർന്ന് അതിന്റെ യുക്തിസഹമായ വേരുകൾ (അവർ ആണെങ്കിൽ)വ്യവസ്ഥ തൃപ്തിപ്പെടുത്തുക

ഞങ്ങളുടെ കാര്യത്തിൽ, അതിനാൽ സാധ്യമായ എല്ലാ വേരുകളും അവസ്ഥയെ തൃപ്തിപ്പെടുത്തണം (നമുക്ക് ഇതിനെ കണ്ടീഷൻ നമ്പർ 1 എന്ന് വിളിക്കാം). ഈ നാലുപേരും പല "സ്ഥാനാർത്ഥികളുടെയും" "കൊലയാളി" ആയിരിക്കും. ഒരു പ്രകടനമെന്ന നിലയിൽ, ഞാൻ കുറച്ച് പരിശോധനകൾ നോക്കാം:

നമുക്ക് "സ്ഥാനാർത്ഥി" പരിശോധിക്കാം. ഇത് ചെയ്യുന്നതിന്, നമുക്ക് അതിനെ ഒരു ഭിന്നസംഖ്യയുടെ രൂപത്തിൽ കൃത്രിമമായി പ്രതിനിധീകരിക്കാം, അതിൽ നിന്ന് അത് വ്യക്തമായി കാണാം . ടെസ്റ്റ് വ്യത്യാസം നമുക്ക് കണക്കാക്കാം: . നാലിനെ "മൈനസ് രണ്ട്" കൊണ്ട് ഹരിച്ചിരിക്കുന്നു: , സാധ്യമായ റൂട്ട് പരീക്ഷയിൽ വിജയിച്ചു എന്നാണ്.

മൂല്യം പരിശോധിക്കാം. ഇവിടെ ടെസ്റ്റ് വ്യത്യാസം ഇതാണ്: . തീർച്ചയായും, അതിനാൽ രണ്ടാമത്തെ "വിഷയവും" പട്ടികയിൽ തുടരുന്നു.

"പ്രൊഫഷണൽ മാത്തമാറ്റിക്സ് ട്യൂട്ടർ" എന്ന വെബ്സൈറ്റ് അധ്യാപനത്തെക്കുറിച്ചുള്ള രീതിശാസ്ത്ര ലേഖനങ്ങളുടെ പരമ്പര തുടരുന്നു. സ്കൂൾ പാഠ്യപദ്ധതിയിലെ ഏറ്റവും സങ്കീർണ്ണവും പ്രശ്നകരവുമായ വിഷയങ്ങൾ ഉപയോഗിച്ച് എന്റെ ജോലിയുടെ രീതികളുടെ വിവരണങ്ങൾ ഞാൻ പ്രസിദ്ധീകരിക്കുന്നു. റെഗുലർ പ്രോഗ്രാമിലും മാത്തമാറ്റിക്സ് ക്ലാസുകളുടെ പ്രോഗ്രാമിലും 8-11 ഗ്രേഡുകളിലെ വിദ്യാർത്ഥികളുമായി പ്രവർത്തിക്കുന്ന ഗണിതശാസ്ത്രത്തിലെ അധ്യാപകർക്കും അധ്യാപകർക്കും ഈ മെറ്റീരിയൽ ഉപയോഗപ്രദമാകും.

ഒരു ഗണിത അദ്ധ്യാപകന് എല്ലായ്പ്പോഴും പാഠപുസ്തകത്തിൽ മോശമായി അവതരിപ്പിച്ചിരിക്കുന്ന കാര്യങ്ങൾ വിശദീകരിക്കാൻ കഴിയില്ല. നിർഭാഗ്യവശാൽ, അത്തരം വിഷയങ്ങൾ കൂടുതൽ കൂടുതൽ ആയിത്തീരുന്നു, കൂടാതെ മാനുവലുകളുടെ രചയിതാക്കളെ പിന്തുടരുന്ന അവതരണ പിശകുകൾ കൂട്ടത്തോടെ നിർമ്മിക്കപ്പെടുന്നു. തുടക്കക്കാരായ മാത്ത് ട്യൂട്ടർമാർക്കും പാർട്ട് ടൈം ട്യൂട്ടർമാർക്കും (അധ്യാപകർ വിദ്യാർത്ഥികളും യൂണിവേഴ്സിറ്റി ട്യൂട്ടർമാരുമാണ്) മാത്രമല്ല, പരിചയസമ്പന്നരായ അധ്യാപകർ, പ്രൊഫഷണൽ ട്യൂട്ടർമാർ, പരിചയവും യോഗ്യതയും ഉള്ള അധ്യാപകർ എന്നിവർക്കും ഇത് ബാധകമാണ്. എല്ലാ ഗണിതശാസ്ത്ര അധ്യാപകർക്കും സ്കൂൾ പാഠപുസ്തകങ്ങളിലെ പരുക്കൻ അറ്റങ്ങൾ സമർത്ഥമായി തിരുത്താനുള്ള കഴിവില്ല. ഈ തിരുത്തലുകൾ (അല്ലെങ്കിൽ കൂട്ടിച്ചേർക്കലുകൾ) ആവശ്യമാണെന്ന് എല്ലാവരും മനസ്സിലാക്കുന്നില്ല. കുട്ടികളുടെ ഗുണപരമായ ധാരണയ്ക്കായി മെറ്റീരിയൽ പൊരുത്തപ്പെടുത്തുന്നതിൽ കുറച്ച് കുട്ടികൾ ഉൾപ്പെടുന്നു. ദൗർഭാഗ്യവശാൽ, ഗണിതശാസ്ത്ര അദ്ധ്യാപകരും മെത്തഡോളജിസ്റ്റുകളും പ്രസിദ്ധീകരണങ്ങളുടെ രചയിതാക്കളും ചേർന്ന് പാഠപുസ്തകത്തിലെ ഓരോ അക്ഷരങ്ങളും കൂട്ടമായി ചർച്ച ചെയ്യുന്ന കാലം കടന്നുപോയി. മുമ്പ്, സ്കൂളുകളിൽ ഒരു പാഠപുസ്തകം പുറത്തിറക്കുന്നതിന് മുമ്പ്, പഠന ഫലങ്ങളെക്കുറിച്ചുള്ള ഗൗരവമായ വിശകലനങ്ങളും പഠനങ്ങളും നടത്തിയിരുന്നു. ശക്തമായ ഗണിതശാസ്ത്ര ക്ലാസുകളുടെ നിലവാരത്തിലേക്ക് അവയെ ക്രമീകരിച്ചുകൊണ്ട് പാഠപുസ്തകങ്ങൾ സാർവത്രികമാക്കാൻ ശ്രമിക്കുന്ന അമച്വർമാരുടെ സമയം അതിക്രമിച്ചിരിക്കുന്നു.

വിവരങ്ങളുടെ അളവ് വർദ്ധിപ്പിക്കുന്നതിനുള്ള ഓട്ടം അതിന്റെ സ്വാംശീകരണത്തിന്റെ ഗുണനിലവാരം കുറയുന്നതിലേക്ക് നയിക്കുന്നു, അതിന്റെ ഫലമായി ഗണിതശാസ്ത്രത്തിലെ യഥാർത്ഥ അറിവിന്റെ നിലവാരം കുറയുന്നു. എന്നാൽ ഇതൊന്നും ആരും ശ്രദ്ധിക്കാറില്ല. ഞങ്ങളുടെ കുട്ടികൾ ഇതിനകം എട്ടാം ക്ലാസിൽ, ഇൻസ്റ്റിറ്റ്യൂട്ടിൽ പഠിച്ച കാര്യങ്ങൾ പഠിക്കാൻ നിർബന്ധിതരാകുന്നു: പ്രോബബിലിറ്റി തിയറി, ഉയർന്ന ഡിഗ്രി സമവാക്യങ്ങൾ പരിഹരിക്കൽ എന്നിവയും മറ്റെന്തെങ്കിലും. ഒരു കുട്ടിയുടെ പൂർണ്ണമായ ധാരണയ്‌ക്കായി പുസ്‌തകങ്ങളിലെ മെറ്റീരിയലുകളുടെ പൊരുത്തപ്പെടുത്തൽ ആഗ്രഹിക്കുന്നത് വളരെയധികം അവശേഷിക്കുന്നു, ഒരു ഗണിത അധ്യാപകൻ ഇത് എങ്ങനെയെങ്കിലും കൈകാര്യം ചെയ്യാൻ നിർബന്ധിതനാകുന്നു.

മുതിർന്നവർക്കുള്ള ഗണിതശാസ്ത്രത്തിൽ "ബെസൗട്ടിന്റെ സിദ്ധാന്തവും ഹോർണറുടെ സ്കീമും" എന്ന് അറിയപ്പെടുന്ന "ഒരു പോളിനോമിയലിനെ ഒരു പോളിനോമിയലിനെ ഒരു കോണിലൂടെ ഹരിക്കൽ" പോലുള്ള ഒരു നിർദ്ദിഷ്ട വിഷയം പഠിപ്പിക്കുന്നതിനുള്ള രീതിശാസ്ത്രത്തെക്കുറിച്ച് നമുക്ക് സംസാരിക്കാം. കുറച്ച് വർഷങ്ങൾക്ക് മുമ്പ്, ഒരു ഗണിത അദ്ധ്യാപകനെ ചോദ്യം അത്ര ബുദ്ധിമുട്ടുള്ളതായിരുന്നില്ല, കാരണം അത് പ്രധാന സ്കൂൾ പാഠ്യപദ്ധതിയുടെ ഭാഗമല്ലായിരുന്നു. ഇപ്പോൾ ടെലിയാക്കോവ്സ്കി എഡിറ്റുചെയ്ത പാഠപുസ്തകത്തിന്റെ ബഹുമാനപ്പെട്ട രചയിതാക്കൾ, എന്റെ അഭിപ്രായത്തിൽ, ഏറ്റവും മികച്ച പാഠപുസ്തകത്തിന്റെ ഏറ്റവും പുതിയ പതിപ്പിൽ മാറ്റങ്ങൾ വരുത്തി, അത് പൂർണ്ണമായും നശിപ്പിച്ച ശേഷം, ട്യൂട്ടർക്ക് അനാവശ്യമായ ആശങ്കകൾ മാത്രം നൽകി. ഗണിതശാസ്ത്ര പദവി ഇല്ലാത്ത സ്കൂളുകളിലെയും ക്ലാസുകളിലെയും അധ്യാപകർ, രചയിതാക്കളുടെ പുതുമകളിൽ ശ്രദ്ധ കേന്ദ്രീകരിച്ച്, അവരുടെ പാഠങ്ങളിൽ അധിക ഖണ്ഡികകൾ ഉൾപ്പെടുത്താൻ തുടങ്ങി, കൂടാതെ അന്വേഷണാത്മക കുട്ടികൾ അവരുടെ ഗണിത പാഠപുസ്തകത്തിന്റെ മനോഹരമായ പേജുകൾ നോക്കുന്നത് കൂടുതലായി ചോദിക്കുന്നു. അദ്ധ്യാപകൻ: "എന്താണ് ഈ കോണിലൂടെയുള്ള വിഭജനം? നമ്മൾ ഇതിലൂടെ പോകുമോ? ഒരു മൂല എങ്ങനെ പങ്കിടാം? അത്തരം നേരിട്ടുള്ള ചോദ്യങ്ങളിൽ നിന്ന് ഇനി മറച്ചുവെക്കാനില്ല. ട്യൂട്ടർ കുട്ടിയോട് എന്തെങ്കിലും പറയേണ്ടിവരും.

പക്ഷേ? പാഠപുസ്തകങ്ങളിൽ സമർത്ഥമായി അവതരിപ്പിച്ചിരുന്നെങ്കിൽ ആ വിഷയവുമായി ബന്ധപ്പെട്ട് പ്രവർത്തിക്കുന്ന രീതി ഞാൻ വിവരിക്കുമായിരുന്നില്ല. എല്ലാം നമ്മോടൊപ്പം എങ്ങനെ പോകുന്നു? പാഠപുസ്തകങ്ങൾ അച്ചടിച്ച് വിൽക്കണം. ഇതിനായി അവ പതിവായി അപ്‌ഡേറ്റ് ചെയ്യേണ്ടതുണ്ട്. അറിവും നൈപുണ്യവുമില്ലാതെ ശൂന്യമായ തലയുമായി കുട്ടികൾ അവരുടെ അടുത്തേക്ക് വരുന്നുവെന്ന് സർവകലാശാലാ അധ്യാപകർ പരാതിപ്പെടുമോ? ഗണിതശാസ്ത്ര പരിജ്ഞാനത്തിനുള്ള ആവശ്യകതകൾ വർദ്ധിക്കുന്നുണ്ടോ? കൊള്ളാം! നമുക്ക് ചില വ്യായാമങ്ങൾ നീക്കം ചെയ്യാം, പകരം മറ്റ് പ്രോഗ്രാമുകളിൽ പഠിച്ച വിഷയങ്ങൾ ചേർക്കുക. എന്തുകൊണ്ടാണ് നമ്മുടെ പാഠപുസ്തകം മോശമായത്? ഞങ്ങൾ ചില അധിക അധ്യായങ്ങൾ ഉൾപ്പെടുത്തും. ഒരു മൂലയെ വിഭജിക്കുന്ന നിയമം സ്കൂൾ കുട്ടികൾക്ക് അറിയില്ലേ? ഇതാണ് അടിസ്ഥാന ഗണിതശാസ്ത്രം. "കൂടുതൽ അറിയാൻ ആഗ്രഹിക്കുന്നവർക്ക്" എന്ന തലക്കെട്ടിൽ ഈ ഖണ്ഡിക ഓപ്ഷണൽ ആക്കണം. ഇതിനെതിരെ അധ്യാപകർ? എന്തുകൊണ്ടാണ് ഞങ്ങൾ ട്യൂട്ടർമാരെ പൊതുവെ ശ്രദ്ധിക്കുന്നത്? മെത്തഡോളജിസ്റ്റുകളും സ്കൂൾ അധ്യാപകരും എതിരാണോ? ഞങ്ങൾ മെറ്റീരിയലിനെ സങ്കീർണ്ണമാക്കില്ല, മാത്രമല്ല അതിന്റെ ഏറ്റവും ലളിതമായ ഭാഗം പരിഗണിക്കുകയും ചെയ്യും.

അത് ഇവിടെ തുടങ്ങുന്നു. വിഷയത്തിന്റെ ലാളിത്യവും അതിന്റെ സ്വാംശീകരണത്തിന്റെ ഗുണനിലവാരവും, ഒന്നാമതായി, അതിന്റെ യുക്തി മനസ്സിലാക്കുന്നതിലാണ്, അല്ലാതെ, പാഠപുസ്തക രചയിതാക്കളുടെ നിർദ്ദേശങ്ങൾക്കനുസൃതമായി, പരസ്പരം വ്യക്തമായി ബന്ധമില്ലാത്ത ഒരു നിശ്ചിത പ്രവർത്തനങ്ങൾ നടത്തുന്നതിൽ അല്ല. . അല്ലെങ്കിൽ, വിദ്യാർത്ഥിയുടെ തലയിൽ മൂടൽമഞ്ഞ് ഉണ്ടാകും. രചയിതാക്കൾ താരതമ്യേന ശക്തരായ വിദ്യാർത്ഥികളെ ലക്ഷ്യമിടുന്നുവെങ്കിൽ (എന്നാൽ ഒരു സാധാരണ പ്രോഗ്രാമിൽ പഠിക്കുന്നു), നിങ്ങൾ വിഷയം ഒരു കമാൻഡ് ഫോമിൽ അവതരിപ്പിക്കരുത്. പാഠപുസ്തകത്തിൽ നമ്മൾ എന്താണ് കാണുന്നത്? കുട്ടികളേ, ഈ നിയമം അനുസരിച്ച് നമ്മൾ വിഭജിക്കണം. കോണിന്റെ കീഴിൽ ബഹുപദം നേടുക. അങ്ങനെ, യഥാർത്ഥ ബഹുപദം ഫാക്‌ടറൈസ് ചെയ്യപ്പെടും. എന്നിരുന്നാലും, കോണിന് കീഴിലുള്ള പദങ്ങൾ കൃത്യമായി ഈ രീതിയിൽ തിരഞ്ഞെടുത്തത് എന്തുകൊണ്ടാണെന്ന് മനസിലാക്കാൻ വ്യക്തമല്ല, എന്തുകൊണ്ടാണ് അവ മൂലയ്ക്ക് മുകളിലുള്ള പോളിനോമിയൽ കൊണ്ട് ഗുണിക്കുകയും തുടർന്ന് നിലവിലുള്ള ശേഷിപ്പിൽ നിന്ന് കുറയ്ക്കുകയും ചെയ്യേണ്ടത്. ഏറ്റവും പ്രധാനമായി, തിരഞ്ഞെടുത്ത മോണോമിയലുകൾ ആത്യന്തികമായി ചേർക്കേണ്ടത് എന്തുകൊണ്ടാണെന്നും തത്ഫലമായുണ്ടാകുന്ന ബ്രാക്കറ്റുകൾ യഥാർത്ഥ ബഹുപദത്തിന്റെ വികാസമാകുന്നത് എന്തുകൊണ്ടാണെന്നും വ്യക്തമല്ല. പ്രഗത്ഭരായ ഏതൊരു ഗണിതശാസ്ത്രജ്ഞനും പാഠപുസ്തകത്തിൽ നൽകിയിരിക്കുന്ന വിശദീകരണങ്ങൾക്ക് മേൽ ധീരമായ ചോദ്യചിഹ്നം ഇടും.

പാഠപുസ്തകത്തിൽ പറഞ്ഞിരിക്കുന്നതെല്ലാം പ്രായോഗികമായി വിദ്യാർത്ഥിക്ക് വ്യക്തമാക്കുന്ന പ്രശ്നത്തിനുള്ള എന്റെ പരിഹാരം ഞാൻ ട്യൂട്ടർമാരുടെയും ഗണിതശാസ്ത്ര അധ്യാപകരുടെയും ശ്രദ്ധയിൽപ്പെടുത്തുന്നു. വാസ്തവത്തിൽ, ഞങ്ങൾ ബെസൗട്ടിന്റെ സിദ്ധാന്തം തെളിയിക്കും: a എന്ന സംഖ്യ ഒരു ബഹുപദത്തിന്റെ മൂലമാണെങ്കിൽ, ഈ ബഹുപദത്തെ ഘടകങ്ങളായി വിഘടിപ്പിക്കാം, അവയിലൊന്ന് x-a ആണ്, രണ്ടാമത്തേത് യഥാർത്ഥത്തിൽ നിന്ന് മൂന്ന് വഴികളിലൊന്നിൽ ലഭിക്കും: രൂപാന്തരങ്ങളിലൂടെ ഒരു രേഖീയ ഘടകം വേർതിരിക്കുന്നതിലൂടെ, ഒരു മൂലയാൽ ഹരിച്ചുകൊണ്ട് അല്ലെങ്കിൽ ഹോർണറുടെ സ്കീം വഴി. ഈ ഫോർമുലേഷൻ ഉപയോഗിച്ചാണ് ഒരു ഗണിത അധ്യാപകന് പ്രവർത്തിക്കുന്നത് എളുപ്പമാകുന്നത്.

എന്താണ് അധ്യാപന രീതിശാസ്ത്രം? ഒന്നാമതായി, ഗണിതശാസ്ത്രപരമായ നിഗമനങ്ങൾ വരച്ചതിന്റെ അടിസ്ഥാനത്തിൽ വിശദീകരണങ്ങളുടെയും ഉദാഹരണങ്ങളുടെയും ക്രമത്തിൽ ഇത് വ്യക്തമായ ക്രമമാണ്. ഈ വിഷയം ഒരു അപവാദമല്ല. ഒരു ഗണിതശാസ്ത്ര അധ്യാപകന് കുട്ടിയെ ബെസൗട്ടിന്റെ സിദ്ധാന്തം പരിചയപ്പെടുത്തുന്നത് വളരെ പ്രധാനമാണ് ഒരു മൂല കൊണ്ട് ഹരിക്കുന്നതിന് മുമ്പ്. ഇത് വളരെ പ്രധാനപെട്ടതാണ്! ഒരു പ്രത്യേക ഉദാഹരണം ഉപയോഗിച്ച് മനസ്സിലാക്കുന്നത് നല്ലതാണ്. തിരഞ്ഞെടുത്ത റൂട്ട് ഉപയോഗിച്ച് കുറച്ച് പോളിനോമിയൽ എടുത്ത്, ഏഴാം ക്ലാസ് മുതൽ സ്കൂൾ കുട്ടികൾക്ക് പരിചിതമായ ഐഡന്റിറ്റി ട്രാൻസ്ഫോർമേഷൻ രീതി ഉപയോഗിച്ച് അതിനെ ഘടകങ്ങളാക്കി മാറ്റുന്നതിനുള്ള സാങ്കേതികത കാണിക്കാം. ഒരു ഗണിത അധ്യാപകനിൽ നിന്നുള്ള ഉചിതമായ വിശദീകരണങ്ങളും ഊന്നലും നുറുങ്ങുകളും ഉപയോഗിച്ച്, പൊതുവായ ഗണിതശാസ്ത്ര കണക്കുകൂട്ടലുകളോ അനിയന്ത്രിതമായ ഗുണകങ്ങളോ ഡിഗ്രികളോ ഇല്ലാതെ മെറ്റീരിയൽ കൈമാറുന്നത് തികച്ചും സാദ്ധ്യമാണ്.

ഒരു ഗണിത അധ്യാപകനുള്ള പ്രധാന ഉപദേശം- തുടക്കം മുതൽ അവസാനം വരെ നിർദ്ദേശങ്ങൾ പാലിക്കുക, ഈ ക്രമം മാറ്റരുത്.

അതിനാൽ, നമുക്ക് ഒരു ബഹുപദം ഉണ്ടെന്ന് പറയാം. സംഖ്യ 1-ന് പകരം അതിന്റെ X-ന് പകരം വയ്ക്കുകയാണെങ്കിൽ, പോളിനോമിയലിന്റെ മൂല്യം പൂജ്യത്തിന് തുല്യമായിരിക്കും. അതുകൊണ്ട് x=1 അതിന്റെ റൂട്ട് ആണ്. നമുക്ക് അതിനെ രണ്ട് പദങ്ങളായി വിഘടിപ്പിക്കാൻ ശ്രമിക്കാം, അതിലൂടെ അവയിലൊന്ന് ഒരു രേഖീയ പദപ്രയോഗത്തിന്റെയും ചില മോണോമിയലിന്റെയും ഉൽപ്പന്നമാണ്, രണ്ടാമത്തേതിന് ഒരു ഡിഗ്രി കുറവാണ്. അതായത്, നമുക്ക് അതിനെ രൂപത്തിൽ പ്രതിനിധീകരിക്കാം

റെഡ് ഫീൽഡിനായി ഞങ്ങൾ മോണോമിയൽ തിരഞ്ഞെടുക്കുന്നു, അതുവഴി ലീഡിംഗ് പദത്താൽ ഗുണിക്കുമ്പോൾ, അത് യഥാർത്ഥ പോളിനോമിയലിന്റെ ലീഡിംഗ് പദവുമായി പൂർണ്ണമായും യോജിക്കുന്നു. വിദ്യാർത്ഥി ഏറ്റവും ദുർബലനല്ലെങ്കിൽ, ഗണിത അദ്ധ്യാപകനോട് ആവശ്യമായ പദപ്രയോഗം പറയാൻ അയാൾ തികച്ചും പ്രാപ്തനാണ്: . അത് ചുവന്ന ഫീൽഡിലേക്ക് തിരുകാനും അവ തുറക്കുമ്പോൾ എന്ത് സംഭവിക്കുമെന്ന് കാണിക്കാനും ട്യൂട്ടറോട് ഉടൻ ആവശ്യപ്പെടണം. ഈ വെർച്വൽ താൽക്കാലിക പോളിനോമിയൽ അമ്പടയാളങ്ങൾക്ക് കീഴിൽ (ചെറിയ ഫോട്ടോയ്ക്ക് കീഴിൽ) ഒപ്പിടുന്നതാണ് നല്ലത്, ഇത് കുറച്ച് നിറത്തിൽ ഹൈലൈറ്റ് ചെയ്യുന്നു, ഉദാഹരണത്തിന്, നീല. ചുവന്ന ഫീൽഡിനായി ഒരു പദം തിരഞ്ഞെടുക്കാൻ ഇത് നിങ്ങളെ സഹായിക്കും, തിരഞ്ഞെടുക്കലിന്റെ ശേഷിക്കുന്ന ഭാഗം. ഈ ശേഷിപ്പ് കുറയ്ക്കുന്നതിലൂടെ കണ്ടെത്താനാകുമെന്ന് ഇവിടെ ചൂണ്ടിക്കാണിക്കാൻ ഞാൻ അധ്യാപകരെ ഉപദേശിക്കുന്നു. ഈ പ്രവർത്തനം നടത്തുമ്പോൾ നമുക്ക് ലഭിക്കുന്നത്:

ഈ സമത്വത്തിലേക്ക് ഒരെണ്ണം മാറ്റിസ്ഥാപിക്കുന്നതിലൂടെ, അതിന്റെ ഇടതുവശത്ത് (1 യഥാർത്ഥ ബഹുപദത്തിന്റെ മൂലമായതിനാൽ) പൂജ്യം ലഭിക്കുമെന്ന് ഉറപ്പുനൽകുന്നു എന്ന വസ്തുതയിലേക്ക് ഗണിത അദ്ധ്യാപകൻ വിദ്യാർത്ഥിയുടെ ശ്രദ്ധ ആകർഷിക്കണം, കൂടാതെ വലതുവശത്ത്, ഞങ്ങൾ ആദ്യ ടേമിനെ പൂജ്യമാക്കുകയും ചെയ്യും. ഇതിനർത്ഥം, ഒരു സ്ഥിരീകരണവുമില്ലാതെ, "പച്ച അവശിഷ്ടത്തിന്റെ" മൂലമാണ് ഒന്ന് എന്ന് നമുക്ക് പറയാൻ കഴിയും.

ഒറിജിനൽ പോളിനോമിയലിൽ നിന്ന് അതേ രേഖീയ ഘടകത്തെ വേർതിരിച്ച് നമുക്ക് അതേ രീതിയിൽ കൈകാര്യം ചെയ്യാം. ഗണിത അധ്യാപകൻ വിദ്യാർത്ഥിയുടെ മുന്നിൽ രണ്ട് ഫ്രെയിമുകൾ വരച്ച് ഇടത്തുനിന്ന് വലത്തോട്ട് പൂരിപ്പിക്കാൻ ആവശ്യപ്പെടുന്നു.

വിദ്യാർത്ഥി അദ്ധ്യാപകനായി ചുവന്ന ഫീൽഡിനായി ഒരു മോണോമിയൽ തിരഞ്ഞെടുക്കുന്നു, അതുവഴി ലീനിയർ എക്‌സ്‌പ്രഷന്റെ ലീഡിംഗ് പദത്താൽ ഗുണിക്കുമ്പോൾ, അത് വികസിക്കുന്ന പോളിനോമിയലിന്റെ മുൻനിര പദം നൽകുന്നു. ഞങ്ങൾ അത് ഫ്രെയിമിലേക്ക് ഘടിപ്പിക്കുന്നു, ഉടനടി ബ്രാക്കറ്റ് തുറന്ന് മടക്കിയതിൽ നിന്ന് കുറയ്ക്കേണ്ട എക്സ്പ്രഷൻ നീലയിൽ ഹൈലൈറ്റ് ചെയ്യുക. ഈ ഓപ്പറേഷൻ നടത്തുമ്പോൾ നമുക്ക് ലഭിക്കും

ഒടുവിൽ, അവസാനത്തെ ശേഷിക്കുന്ന കാര്യത്തിലും അങ്ങനെ തന്നെ ചെയ്യുന്നു

ഞങ്ങൾക്ക് അത് ഒടുവിൽ ലഭിക്കും

ഇപ്പോൾ നമുക്ക് എക്സ്പ്രഷൻ ബ്രാക്കറ്റിൽ നിന്ന് പുറത്തെടുക്കാം, യഥാർത്ഥ പോളിനോമിയലിന്റെ വിഘടനം ഘടകങ്ങളായി നമുക്ക് കാണാം, അതിലൊന്ന് "തിരഞ്ഞെടുത്ത റൂട്ട് x മൈനസ്" ആണ്.

അവസാനത്തെ "പച്ച അവശിഷ്ടം" ആകസ്മികമായി ആവശ്യമായ ഘടകങ്ങളിലേക്ക് വിഘടിപ്പിച്ചുവെന്ന് വിദ്യാർത്ഥി ചിന്തിക്കാതിരിക്കാൻ, ഗണിതശാസ്ത്ര അധ്യാപകൻ എല്ലാ പച്ച അവശിഷ്ടങ്ങളുടെയും ഒരു പ്രധാന സ്വത്ത് ചൂണ്ടിക്കാണിക്കണം - അവയിൽ ഓരോന്നിനും 1 ന്റെ റൂട്ട് ഉണ്ട്. ഡിഗ്രി മുതൽ ഈ അവശിഷ്ടങ്ങൾ കുറയുന്നു, പിന്നീട് നമുക്ക് എത്ര പോളിനോമിയൽ നൽകിയാലും ഇനീഷ്യലിന്റെ ഏത് ഡിഗ്രിയായാലും, താമസിയാതെ അല്ലെങ്കിൽ പിന്നീട് നമുക്ക് റൂട്ട് 1 ഉള്ള ഒരു രേഖീയ “പച്ച അവശിഷ്ടം” ലഭിക്കും, അതിനാൽ അത് ഒരു നിശ്ചിത ഉൽപ്പന്നത്തിലേക്ക് വിഘടിപ്പിക്കും. സംഖ്യയും ഒരു പദപ്രയോഗവും.

അത്തരം തയ്യാറെടുപ്പ് ജോലികൾക്ക് ശേഷം, ഒരു കോണിൽ വിഭജിക്കുമ്പോൾ എന്താണ് സംഭവിക്കുന്നതെന്ന് വിദ്യാർത്ഥിയോട് വിശദീകരിക്കാൻ ഒരു ഗണിതശാസ്ത്ര അധ്യാപകന് ബുദ്ധിമുട്ടുണ്ടാകില്ല. ഇത് ഒരേ പ്രക്രിയയാണ്, ചെറുതും കൂടുതൽ ഒതുക്കമുള്ളതുമായ രൂപത്തിൽ, തുല്യ ചിഹ്നങ്ങളില്ലാതെ, അതേ ഹൈലൈറ്റ് ചെയ്ത പദങ്ങൾ വീണ്ടും എഴുതാതെ. ലീനിയർ ഫാക്ടർ വേർതിരിച്ചെടുത്ത പോളിനോമിയൽ മൂലയുടെ ഇടതുവശത്ത് എഴുതിയിരിക്കുന്നു, തിരഞ്ഞെടുത്ത ചുവന്ന മോണോമിയലുകൾ ഒരു കോണിൽ ശേഖരിക്കുന്നു (അവ എന്തിനാണ് കൂട്ടിച്ചേർക്കേണ്ടതെന്ന് ഇപ്പോൾ വ്യക്തമാകും), “നീല പോളിനോമിയലുകൾ”, “ചുവപ്പ് ” എന്നവയെ x-1 കൊണ്ട് ഗുണിക്കണം, തുടർന്ന് സംഖ്യകളുടെ സാധാരണ വിഭജനത്തിൽ ഒരു നിരയിലേക്ക് ഇത് എങ്ങനെ ചെയ്യപ്പെടുന്നു എന്ന് തിരഞ്ഞെടുത്തതിൽ നിന്ന് കുറയ്ക്കണം (മുമ്പ് പഠിച്ചതിന്റെ ഒരു സാമ്യം ഇവിടെയുണ്ട്). തത്ഫലമായുണ്ടാകുന്ന "പച്ച അവശിഷ്ടങ്ങൾ" പുതിയ ഒറ്റപ്പെടലിനും "റെഡ് മോണോമിയലുകൾ" തിരഞ്ഞെടുക്കുന്നതിനും വിധേയമാണ്. പൂജ്യം "ഗ്രീൻ ബാലൻസ്" ലഭിക്കുന്നതുവരെ അങ്ങനെ. കോണിന് മുകളിലും താഴെയുമുള്ള ലിഖിത ബഹുപദങ്ങളുടെ കൂടുതൽ വിധി വിദ്യാർത്ഥി മനസ്സിലാക്കുന്നു എന്നതാണ് ഏറ്റവും പ്രധാനപ്പെട്ട കാര്യം. വ്യക്തമായും, ഇവ ബ്രാക്കറ്റുകളാണ്, അവയുടെ ഉൽപ്പന്നം യഥാർത്ഥ ബഹുപദത്തിന് തുല്യമാണ്.

ഗണിതശാസ്ത്ര അധ്യാപകന്റെ ജോലിയുടെ അടുത്ത ഘട്ടം ബെസൗട്ടിന്റെ സിദ്ധാന്തത്തിന്റെ രൂപീകരണമാണ്. വാസ്തവത്തിൽ, അദ്ധ്യാപകന്റെ ഈ സമീപനത്തിലൂടെ അതിന്റെ രൂപീകരണം വ്യക്തമാകും: a എന്ന സംഖ്യ ഒരു ബഹുപദത്തിന്റെ മൂലമാണെങ്കിൽ, അതിനെ ഫാക്‌ടറൈസ് ചെയ്യാം, അതിലൊന്ന് , മറ്റൊന്ന് യഥാർത്ഥത്തിൽ നിന്ന് മൂന്ന് വഴികളിൽ ഒന്നിൽ നിന്ന് ലഭിക്കും. :

• നേരിട്ടുള്ള വിഘടനം (ഗ്രൂപ്പിംഗ് രീതിക്ക് സമാനമാണ്)
• ഒരു കോണിൽ ഹരിക്കൽ (ഒരു നിരയിൽ)
• ഹോർണർ സർക്യൂട്ട് വഴി

എല്ലാ ഗണിതശാസ്ത്ര അദ്ധ്യാപകരും അവരുടെ വിദ്യാർത്ഥികൾക്ക് ഹോർണർ ഡയഗ്രം കാണിക്കുന്നില്ലെന്നും എല്ലാ സ്കൂൾ അധ്യാപകരും (ഭാഗ്യവശാൽ ട്യൂട്ടർമാർക്ക് തന്നെ) പാഠങ്ങൾക്കിടയിൽ വിഷയത്തിലേക്ക് ആഴത്തിൽ പോകുന്നില്ലെന്നും പറയണം. എന്നിരുന്നാലും, ഒരു ഗണിത ക്ലാസ് വിദ്യാർത്ഥിക്ക്, നീണ്ട വിഭജനത്തിൽ നിർത്താൻ ഞാൻ ഒരു കാരണവും കാണുന്നില്ല. മാത്രമല്ല, ഏറ്റവും സൗകര്യപ്രദവും വേഗംവിഘടിപ്പിക്കൽ സാങ്കേതികത കൃത്യമായി ഹോർണറുടെ സ്കീമിനെ അടിസ്ഥാനമാക്കിയുള്ളതാണ്. ഒരു കുട്ടിക്ക് അത് എവിടെ നിന്നാണ് വരുന്നതെന്ന് വിശദീകരിക്കാൻ, പച്ച അവശിഷ്ടങ്ങളിൽ ഉയർന്ന ഗുണകങ്ങളുടെ രൂപം ഒരു കോണിലൂടെ വിഭജിക്കുന്നതിന്റെ ഉദാഹരണം ഉപയോഗിച്ച് കണ്ടെത്തുന്നത് മതിയാകും. പ്രാരംഭ പോളിനോമിയലിന്റെ ലീഡിംഗ് കോഫിഫിഷ്യന്റ് ആദ്യത്തെ "റെഡ് മോണോമിയലിന്റെ" കോഫിഫിഷ്യന്റിലേക്കും നിലവിലുള്ള അപ്പർ പോളിനോമിയലിന്റെ രണ്ടാമത്തെ കോഫിഫിഷ്യന്റിലേക്കും കൊണ്ടുപോകുന്നുവെന്ന് വ്യക്തമാകും. കുറച്ചിരിക്കുന്നു"റെഡ് മോണോമിയലിന്റെ" നിലവിലെ ഗുണകത്തെ ഗുണിച്ചതിന്റെ ഫലം. അതുകൊണ്ട് അത് സാധ്യമാണ് ചേർക്കുകകൊണ്ട് ഗുണിച്ചതിന്റെ ഫലം. ഗുണകങ്ങളുള്ള പ്രവർത്തനങ്ങളുടെ പ്രത്യേകതകളിൽ വിദ്യാർത്ഥിയുടെ ശ്രദ്ധ കേന്ദ്രീകരിച്ച ശേഷം, വേരിയബിളുകൾ സ്വയം രേഖപ്പെടുത്താതെ ഈ പ്രവർത്തനങ്ങൾ സാധാരണയായി എങ്ങനെ ചെയ്യുന്നുവെന്ന് ഒരു ഗണിത അധ്യാപകന് കാണിക്കാൻ കഴിയും. ഇത് ചെയ്യുന്നതിന്, ഇനിപ്പറയുന്ന പട്ടികയിൽ മുൻ‌ഗണനയുടെ ക്രമത്തിൽ യഥാർത്ഥ പോളിനോമിയലിന്റെ റൂട്ടും ഗുണകങ്ങളും നൽകുന്നത് സൗകര്യപ്രദമാണ്:

ഒരു പോളിനോമിയലിൽ ഏതെങ്കിലും ബിരുദം ഇല്ലെങ്കിൽ, അതിന്റെ പൂജ്യം ഗുണകം പട്ടികയിലേക്ക് നിർബന്ധിതമാക്കും. "ചുവന്ന പോളിനോമിയലുകളുടെ" ഗുണകങ്ങൾ "ഹുക്ക്" റൂൾ അനുസരിച്ച് താഴത്തെ വരിയിൽ എഴുതിയിരിക്കുന്നു:

റൂട്ട് അവസാനത്തെ റെഡ് കോഫിഫിഷ്യന്റ് കൊണ്ട് ഗുണിച്ചു, മുകളിലെ വരിയിലെ അടുത്ത കോഫിഫിഷ്യന്റിലേക്ക് ചേർത്തു, ഫലം താഴെയുള്ള വരിയിലേക്ക് എഴുതുന്നു. അവസാന നിരയിൽ, അവസാനത്തെ "ഗ്രീൻ ബാക്കി" യുടെ ഉയർന്ന ഗുണകം ലഭിക്കുമെന്ന് നമുക്ക് ഉറപ്പുനൽകുന്നു, അതായത് പൂജ്യം. പ്രക്രിയ പൂർത്തിയാക്കിയ ശേഷം, അക്കങ്ങൾ പൊരുത്തപ്പെടുന്ന റൂട്ടിനും പൂജ്യം ശേഷിക്കും ഇടയിൽ സാൻഡ്‌വിച്ച് ചെയ്‌തുരണ്ടാമത്തെ (രേഖീയമല്ലാത്ത) ഘടകത്തിന്റെ ഗുണകങ്ങളായി മാറുന്നു.

a എന്ന റൂട്ട് താഴത്തെ വരിയുടെ അവസാനം ഒരു പൂജ്യം നൽകുന്നതിനാൽ, ഒരു പോളിനോമിയലിന്റെ റൂട്ടിന്റെ ശീർഷകത്തിനായി അക്കങ്ങൾ പരിശോധിക്കാൻ ഹോർണറുടെ സ്കീം ഉപയോഗിക്കാം. ഒരു യുക്തിസഹമായ റൂട്ട് തിരഞ്ഞെടുക്കുന്നതിൽ ഒരു പ്രത്യേക സിദ്ധാന്തമാണെങ്കിൽ. അതിന്റെ സഹായത്തോടെ ലഭിച്ച ഈ ശീർഷകത്തിനായുള്ള എല്ലാ കാൻഡിഡേറ്റുകളും ഇടതുവശത്ത് നിന്ന് ഹോർണറുടെ ഡയഗ്രാമിലേക്ക് ലളിതമായി ചേർത്തിരിക്കുന്നു. നമുക്ക് പൂജ്യം ലഭിച്ചാലുടൻ, പരീക്ഷിച്ച സംഖ്യ ഒരു റൂട്ടായിരിക്കും, അതേ സമയം യഥാർത്ഥ പോളിനോമിയലിന്റെ ഫാക്റ്ററൈസേഷന്റെ ഗുണകങ്ങൾ അതിന്റെ വരിയിൽ നമുക്ക് ലഭിക്കും. വളരെ സുഖകരമായി.

ഉപസംഹാരമായി, ഹോർണറുടെ സ്കീം കൃത്യമായി അവതരിപ്പിക്കുന്നതിനും വിഷയം പ്രായോഗികമായി ഏകീകരിക്കുന്നതിനും, ഒരു ഗണിതശാസ്ത്ര അദ്ധ്യാപകന് തന്റെ പക്കൽ മതിയായ മണിക്കൂർ ഉണ്ടായിരിക്കണം എന്നത് ഞാൻ ശ്രദ്ധിക്കാൻ ആഗ്രഹിക്കുന്നു. "ആഴ്ചയിൽ ഒരിക്കൽ" ഭരണകൂടവുമായി പ്രവർത്തിക്കുന്ന ഒരു അധ്യാപകൻ കോർണർ ഡിവിഷനിൽ ഏർപ്പെടരുത്. ഗണിതശാസ്ത്രത്തിലെ ഏകീകൃത സംസ്ഥാന പരീക്ഷയിലും ഗണിതത്തിലെ സ്റ്റേറ്റ് അക്കാദമി ഓഫ് മാത്തമാറ്റിക്‌സിലും, ആദ്യ ഭാഗത്തിൽ അത്തരം മാർഗ്ഗങ്ങളിലൂടെ പരിഹരിക്കാൻ കഴിയുന്ന മൂന്നാം ഡിഗ്രിയുടെ ഒരു സമവാക്യം നിങ്ങൾക്ക് എപ്പോഴെങ്കിലും നേരിടാൻ സാധ്യതയില്ല. മോസ്കോ സ്റ്റേറ്റ് യൂണിവേഴ്സിറ്റിയിൽ ഒരു ഗണിതശാസ്ത്ര പരീക്ഷയ്ക്ക് ഒരു ട്യൂട്ടർ ഒരു കുട്ടിയെ തയ്യാറാക്കുകയാണെങ്കിൽ, വിഷയം പഠിക്കുന്നത് നിർബന്ധമാണ്. യൂണിവേഴ്സിറ്റി അധ്യാപകർ, ഏകീകൃത സംസ്ഥാന പരീക്ഷയുടെ കംപൈലർമാരിൽ നിന്ന് വ്യത്യസ്തമായി, ഒരു അപേക്ഷകന്റെ അറിവിന്റെ ആഴം പരിശോധിക്കാൻ ശരിക്കും ഇഷ്ടപ്പെടുന്നു.

കോൾപാക്കോവ് അലക്സാണ്ടർ നിക്കോളാവിച്ച്, മാത്തമാറ്റിക്സ് ട്യൂട്ടർ മോസ്കോ, സ്ട്രോഗിനോ

ഹോർണറുടെ സ്കീം - ഒരു ബഹുപദത്തെ വിഭജിക്കുന്ന രീതി

$$P_n(x)=\sum\പരിധി_(i=0)^(n)a_(i)x^(n-i)=a_(0)x^(n)+a_(1)x^(n-1 )+a_(2)x^(n-2)+\ldots+a_(n-1)x+a_n$$

$x-a$ എന്ന ദ്വിപദത്തിൽ. നിങ്ങൾ ഒരു പട്ടികയുമായി പ്രവർത്തിക്കേണ്ടതുണ്ട്, അതിന്റെ ആദ്യ വരിയിൽ തന്നിരിക്കുന്ന പോളിനോമിയലിന്റെ ഗുണകങ്ങൾ അടങ്ങിയിരിക്കുന്നു. രണ്ടാമത്തെ വരിയുടെ ആദ്യ ഘടകം $a$ എന്ന സംഖ്യയായിരിക്കും, $x-a$ എന്ന ദ്വിപദത്തിൽ നിന്ന് എടുത്തതാണ്:

nth ഡിഗ്രിയുടെ ഒരു പോളിനോമിയലിനെ $x-a$ എന്ന ബൈനോമിയൽ കൊണ്ട് ഹരിച്ചതിന് ശേഷം, യഥാർത്ഥ ഡിഗ്രിയേക്കാൾ ഒന്ന് കുറവുള്ള ഒരു ബഹുപദം നമുക്ക് ലഭിക്കും, അതായത്. $n-1$ തുല്യമാണ്. ഹോർണർ സ്‌കീമിന്റെ നേരിട്ടുള്ള പ്രയോഗം ഉദാഹരണങ്ങൾ സഹിതം പ്രകടിപ്പിക്കാൻ എളുപ്പമാണ്.

ഉദാഹരണം നമ്പർ 1

ഹോർണറുടെ സ്കീം ഉപയോഗിച്ച് $5x^4+5x^3+x^2-11$ കൊണ്ട് $x-1$ കൊണ്ട് ഹരിക്കുക.

നമുക്ക് രണ്ട് വരികളുടെ ഒരു പട്ടിക ഉണ്ടാക്കാം: ആദ്യ വരിയിൽ $ x$ എന്ന വേരിയബിളിന്റെ പവറിന്റെ അവരോഹണ ക്രമത്തിൽ ക്രമീകരിച്ചിരിക്കുന്ന $5x^4+5x^3+x^2-11$ എന്ന ബഹുപദത്തിന്റെ ഗുണകങ്ങൾ ഞങ്ങൾ എഴുതുന്നു. ഈ പോളിനോമിയലിൽ ഒന്നാം ഡിഗ്രി വരെ $x$ അടങ്ങിയിട്ടില്ല എന്നത് ശ്രദ്ധിക്കുക, അതായത്. ആദ്യ പവറിലേക്കുള്ള $x$ ന്റെ ഗുണകം 0 ആണ്. നമ്മൾ $x-1$ കൊണ്ട് ഹരിക്കുന്നതിനാൽ, രണ്ടാമത്തെ വരിയിൽ ഒന്ന് എഴുതുന്നു:

രണ്ടാമത്തെ വരിയിലെ ശൂന്യമായ കളങ്ങൾ പൂരിപ്പിക്കാൻ തുടങ്ങാം. രണ്ടാമത്തെ വരിയുടെ രണ്ടാമത്തെ സെല്ലിൽ ഞങ്ങൾ $5$ എന്ന സംഖ്യ എഴുതുന്നു, ആദ്യ വരിയുടെ അനുബന്ധ സെല്ലിൽ നിന്ന് അത് നീക്കുക:

ഈ തത്വമനുസരിച്ച് അടുത്ത സെൽ പൂരിപ്പിക്കാം: $1\cdot 5+5=10$:

രണ്ടാമത്തെ വരിയിലെ നാലാമത്തെ സെല്ലും ഇതേ രീതിയിൽ പൂരിപ്പിക്കാം: $1\cdot 10+1=11$:

അഞ്ചാമത്തെ സെല്ലിന് നമുക്ക് ലഭിക്കുന്നത്: $1\cdot 11+0=11$:

ഒടുവിൽ, അവസാനത്തെ, ആറാമത്തെ സെല്ലിനായി, നമുക്കുള്ളത്: $1\cdot 11+(-11)=0$:

പ്രശ്നം പരിഹരിച്ചു, ഉത്തരം എഴുതുക മാത്രമാണ് അവശേഷിക്കുന്നത്:

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, രണ്ടാമത്തെ വരിയിൽ സ്ഥിതി ചെയ്യുന്ന സംഖ്യകൾ (ഒന്നിനും പൂജ്യത്തിനും ഇടയിൽ) $5x^4+5x^3+x^2-11$ $x-1$ കൊണ്ട് ഹരിച്ചാൽ ലഭിക്കുന്ന ബഹുപദത്തിന്റെ ഗുണകങ്ങളാണ്. സ്വാഭാവികമായും, യഥാർത്ഥ ബഹുപദമായ $5x^4+5x^3+x^2-11$ നാലിന് തുല്യമായതിനാൽ, ഫലമായുണ്ടാകുന്ന $5x^3+10x^2+11x+11$ എന്ന ബഹുപദത്തിന്റെ ബിരുദം ഒന്നാണ്. കുറവ്, അതായത്. മൂന്ന് തുല്യമാണ്. $5x^4+5x^3+x^2-11$ എന്ന ബഹുപദത്തെ $x-1$ കൊണ്ട് ഹരിക്കുമ്പോൾ രണ്ടാമത്തെ വരിയിലെ (പൂജ്യം) അവസാനത്തെ സംഖ്യ അർത്ഥമാക്കുന്നു. ഞങ്ങളുടെ കാര്യത്തിൽ, ബാക്കിയുള്ളത് പൂജ്യമാണ്, അതായത്. ബഹുപദങ്ങൾ തുല്യമായി വിഭജിക്കപ്പെടുന്നു. ഈ ഫലത്തെ ഇനിപ്പറയുന്ന രീതിയിൽ ചിത്രീകരിക്കാം: $x=1$ ന് $5x^4+5x^3+x^2-11$ എന്ന ബഹുപദത്തിന്റെ മൂല്യം പൂജ്യത്തിന് തുല്യമാണ്.

നിഗമനം ഈ രൂപത്തിലും രൂപപ്പെടുത്താം: $5x^4+5x^3+x^2-11$ എന്ന പോളിനോമിയലിന്റെ മൂല്യം $x=1$-ൽ പൂജ്യത്തിന് തുല്യമായതിനാൽ, ഏകത്വം എന്നത് ബഹുപദത്തിന്റെ മൂലമാണ്. $5x^4+5x^3+ x^2-11$.

ഉദാഹരണം നമ്പർ 2

ഹോർണറുടെ സ്കീം ഉപയോഗിച്ച് $x^4+3x^3+4x^2-5x-47$ എന്ന ബഹുപദത്തെ $x+3$ കൊണ്ട് ഹരിക്കുക.

$x+3$ എന്ന പദപ്രയോഗം $x-(-3)$ എന്ന രൂപത്തിൽ അവതരിപ്പിക്കണമെന്ന് നമുക്ക് ഉടനടി വ്യവസ്ഥ ചെയ്യാം. ഹോർണറുടെ സ്കീമിൽ കൃത്യമായി $-3$ ഉൾപ്പെടുന്നു. യഥാർത്ഥ പോളിനോമിയലിന്റെ ഡിഗ്രി $x^4+3x^3+4x^2-5x-47$ നാലിന് തുല്യമായതിനാൽ, വിഭജനത്തിന്റെ ഫലമായി നമുക്ക് മൂന്നാം ഡിഗ്രിയുടെ ഒരു ബഹുപദം ലഭിക്കും:

ഫലം അർത്ഥമാക്കുന്നത്

$$x^4+3x^3+4x^2-5x-47=(x+3)(x^3+0\cdot x^2 +4x-17)+4=(x+3)(x^ 3+4x-17)+4$$

ഈ സാഹചര്യത്തിൽ, $x^4+3x^3+4x^2-5x-47$ കൊണ്ട് $x+3$ കൊണ്ട് ഹരിക്കുമ്പോൾ ബാക്കിയുള്ളത് $4$ ആണ്. അല്ലെങ്കിൽ, അതേ കാര്യം, $x=-3$ എന്നതിനുള്ള ബഹുപദമായ $x^4+3x^3+4x^2-5x-47$ മൂല്യം $4$-ന് തുല്യമാണ്. വഴിയിൽ, തന്നിരിക്കുന്ന ബഹുപദത്തിലേക്ക് നേരിട്ട് $x=-3$ പകരം വയ്ക്കുന്നതിലൂടെ ഇത് രണ്ടുതവണ പരിശോധിക്കുന്നത് എളുപ്പമാണ്:

$$x^4+3x^3+4x^2-5x-47=(-3)^4+3 \cdot (-3)^3-5 \cdot (-3)-47=4.$$

ആ. ഒരു വേരിയബിളിന്റെ തന്നിരിക്കുന്ന മൂല്യത്തിന് ഒരു പോളിനോമിയലിന്റെ മൂല്യം കണ്ടെത്തണമെങ്കിൽ ഹോർണറുടെ സ്കീം ഉപയോഗിക്കാം. ഒരു പോളിനോമിയലിന്റെ എല്ലാ വേരുകളും കണ്ടെത്തുക എന്നതാണ് ഞങ്ങളുടെ ലക്ഷ്യമെങ്കിൽ, ഉദാഹരണം നമ്പർ 3 ൽ ചർച്ച ചെയ്തതുപോലെ, എല്ലാ വേരുകളും തീർന്നുപോകുന്നതുവരെ ഹോർണറുടെ സ്കീം തുടർച്ചയായി നിരവധി തവണ പ്രയോഗിക്കാൻ കഴിയും.

ഉദാഹരണം നമ്പർ 3

Horner's സ്കീം ഉപയോഗിച്ച് $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ പോളിനോമിയലിന്റെ എല്ലാ പൂർണ്ണസംഖ്യ വേരുകളും കണ്ടെത്തുക.

ചോദ്യം ചെയ്യപ്പെടുന്ന പോളിനോമിയലിന്റെ ഗുണകങ്ങൾ പൂർണ്ണസംഖ്യകളാണ്, കൂടാതെ വേരിയബിളിന്റെ (അതായത് $x^6$) ഉയർന്ന ശക്തിയുടെ ഗുണകം ഒന്നിന് തുല്യമാണ്. ഈ സാഹചര്യത്തിൽ, സ്വതന്ത്ര പദത്തിന്റെ വിഭജനങ്ങൾക്കിടയിൽ ബഹുപദത്തിന്റെ പൂർണ്ണസംഖ്യ വേരുകൾ അന്വേഷിക്കണം, അതായത്. 45 എന്ന സംഖ്യയുടെ വിഭജനങ്ങൾക്കിടയിൽ. നൽകിയിരിക്കുന്ന ഒരു ബഹുപദത്തിന്, അത്തരം വേരുകൾ സംഖ്യകൾ $45 ആകാം; \; 15; \; 9; \; 5; \; 3; \; 1$, $-45; \; -15; \; -9; \; -5; \; -3; \; -1$. നമുക്ക് പരിശോധിക്കാം, ഉദാഹരണത്തിന്, $1$:

നിങ്ങൾക്ക് കാണാനാകുന്നതുപോലെ, $x=1$ ഉള്ള ബഹുപദമായ $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ മൂല്യം $192$-ന് തുല്യമാണ് (അവസാന സംഖ്യ രണ്ടാമത്തെ വരിയിൽ), കൂടാതെ $0 $ അല്ല, അതിനാൽ ഏകത്വം ഈ ബഹുപദത്തിന്റെ മൂലമല്ല. ഒരെണ്ണത്തിനായുള്ള പരിശോധന പരാജയപ്പെട്ടതിനാൽ, നമുക്ക് $x=-1$ മൂല്യം പരിശോധിക്കാം. ഇതിനായി ഞങ്ങൾ ഒരു പുതിയ പട്ടിക സൃഷ്ടിക്കില്ല, പക്ഷേ പട്ടിക ഉപയോഗിക്കുന്നത് തുടരും. നമ്പർ 1, അതിലേക്ക് ഒരു പുതിയ (മൂന്നാം) വരി ചേർക്കുന്നു. $1$ ന്റെ മൂല്യം പരിശോധിച്ച രണ്ടാമത്തെ വരി ചുവപ്പ് നിറത്തിൽ ഹൈലൈറ്റ് ചെയ്യപ്പെടും, അത് തുടർന്നുള്ള ചർച്ചകളിൽ ഉപയോഗിക്കില്ല.

നിങ്ങൾക്ക് തീർച്ചയായും, പട്ടിക വീണ്ടും എഴുതാം, പക്ഷേ ഇത് സ്വമേധയാ പൂരിപ്പിക്കുന്നതിന് ധാരാളം സമയമെടുക്കും. മാത്രമല്ല, സ്ഥിരീകരണം പരാജയപ്പെടുന്ന നിരവധി നമ്പറുകൾ ഉണ്ടാകാം, ഓരോ തവണയും ഒരു പുതിയ പട്ടിക എഴുതുന്നത് ബുദ്ധിമുട്ടാണ്. "കടലാസിൽ" കണക്കാക്കുമ്പോൾ, ചുവന്ന വരകൾ ലളിതമായി മറികടക്കാൻ കഴിയും.

അതിനാൽ, $x=-1$ എന്നതിൽ $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ എന്ന ബഹുപദത്തിന്റെ മൂല്യം പൂജ്യത്തിന് തുല്യമാണ്, അതായത്. $-1$ എന്ന സംഖ്യയാണ് ഈ ബഹുപദത്തിന്റെ റൂട്ട്. $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ എന്ന ബഹുപദത്തെ $x-(-1)=x+1$ കൊണ്ട് ഹരിച്ചാൽ നമുക്ക് $x എന്ന ബഹുപദം ലഭിക്കും ^5+x ^4-22x^3+2x^2+69x+45$, ഇവയുടെ ഗുണകങ്ങൾ പട്ടികയുടെ മൂന്നാം നിരയിൽ നിന്ന് എടുത്തതാണ്. നമ്പർ 2 (ഉദാഹരണം നമ്പർ 1 കാണുക). കണക്കുകൂട്ടലുകളുടെ ഫലം ഈ ഫോമിലും അവതരിപ്പിക്കാം:

\begin(സമവാക്യം)x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)(x^5+x^4-22x^3+2x^2 +69x+45)\ അവസാനം(സമവാക്യം)

നമുക്ക് പൂർണ്ണസംഖ്യ വേരുകൾക്കായുള്ള തിരയൽ തുടരാം. ഇപ്പോൾ നമ്മൾ $x^5+x^4-22x^3+2x^2+69x+45$ എന്ന ബഹുപദത്തിന്റെ വേരുകൾ നോക്കേണ്ടതുണ്ട്. വീണ്ടും, ഈ ബഹുപദത്തിന്റെ പൂർണ്ണസംഖ്യ വേരുകൾ അതിന്റെ സ്വതന്ത്ര പദമായ $45$ എന്ന സംഖ്യകളുടെ വിഭജനങ്ങൾക്കിടയിൽ തിരയുന്നു. $-1$ നമ്പർ വീണ്ടും പരിശോധിക്കാൻ ശ്രമിക്കാം. ഞങ്ങൾ ഒരു പുതിയ പട്ടിക സൃഷ്ടിക്കില്ല, എന്നാൽ മുമ്പത്തെ പട്ടിക ഉപയോഗിക്കുന്നത് തുടരും. നമ്പർ 2, അതായത്. ഇതിലേക്ക് ഒരു വരി കൂടി ചേർക്കാം:

അതിനാൽ, $x^5+x^4-22x^3+2x^2+69x+45$ എന്ന ബഹുപദത്തിന്റെ മൂലമാണ് $-1$ എന്ന സംഖ്യ. ഈ ഫലം ഇങ്ങനെ എഴുതാം:

\begin(സമവാക്യം)x^5+x^4-22x^3+2x^2+69x+45=(x+1)(x^4-22x^2+24x+45) \ അവസാനം(സമവാക്യം)

തുല്യത (2) കണക്കിലെടുക്കുമ്പോൾ, സമത്വം (1) ഇനിപ്പറയുന്ന രൂപത്തിൽ മാറ്റിയെഴുതാം:

\ആരംഭിക്കുക(സമവാക്യം)\ആരംഭിക്കുക(വിന്യസിച്ചു) & x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)(x^5+x^4-22x ^2+2x^2+69x+45)=\\ & =(x+1)(x+1)(x^4-22x^2+24x+45)=(x+1)^2(x^ 4-22x^2+24x+45)\അവസാനം(വിന്യസിച്ചു)\അവസാനം(സമവാക്യം)

ഇപ്പോൾ നമ്മൾ $x^4-22x^2+24x+45$ എന്ന ബഹുപദത്തിന്റെ വേരുകൾ അന്വേഷിക്കേണ്ടതുണ്ട് - സ്വാഭാവികമായും, അതിന്റെ സ്വതന്ത്ര പദത്തിന്റെ ($45$ സംഖ്യകൾ) ഹരിച്ചുള്ളവയിൽ. നമുക്ക് $-1$ നമ്പർ വീണ്ടും പരിശോധിക്കാം:

$x^4-22x^2+24x+45$ എന്ന ബഹുപദത്തിന്റെ മൂലമാണ് $-1$ എന്ന സംഖ്യ. ഈ ഫലം ഇങ്ങനെ എഴുതാം:

\begin(സമവാക്യം)x^4-22x^2+24x+45=(x+1)(x^3-x^2-21x+45) \ അവസാനം(സമവാക്യം)

തുല്യത (4) കണക്കിലെടുത്ത്, ഞങ്ങൾ സമത്വം (3) ഇനിപ്പറയുന്ന രൂപത്തിൽ മാറ്റിയെഴുതുന്നു:

\ആരംഭിക്കുക(സമവാക്യം)\ആരംഭിക്കുക(വിന്യസിച്ചു) & x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)^2(x^4-22x^3 +24x+45)= \\ & =(x+1)^2(x+1)(x^3-x^2-21x+45)=(x+1)^3(x^3-x^ 2-21x+45)\അവസാനം(വിന്യസിച്ചു)\അവസാനം(സമവാക്യം)

ഇപ്പോൾ നമ്മൾ $x^3-x^2-21x+45$ എന്ന ബഹുപദത്തിന്റെ വേരുകൾ തിരയുകയാണ്. നമുക്ക് $-1$ നമ്പർ വീണ്ടും പരിശോധിക്കാം:

പരിശോധന പരാജയത്തിൽ അവസാനിച്ചു. ആറാമത്തെ വരി ചുവപ്പിൽ ഹൈലൈറ്റ് ചെയ്ത് മറ്റൊരു നമ്പർ പരിശോധിക്കാൻ ശ്രമിക്കാം, ഉദാഹരണത്തിന്, നമ്പർ $3$:

ബാക്കിയുള്ളത് പൂജ്യമാണ്, അതിനാൽ $3$ എന്ന സംഖ്യയാണ് ചോദ്യം ചെയ്യപ്പെടുന്ന പോളിനോമിയലിന്റെ റൂട്ട്. അതിനാൽ, $x^3-x^2-21x+45=(x-3)(x^2+2x-15)$. ഇനി സമത്വം (5) ഇങ്ങനെ മാറ്റിയെഴുതാം.

തിരികെ മുന്നോട്ട്

ശ്രദ്ധ! സ്ലൈഡ് പ്രിവ്യൂകൾ വിവര ആവശ്യങ്ങൾക്ക് മാത്രമുള്ളതാണ്, അവ അവതരണത്തിന്റെ എല്ലാ സവിശേഷതകളെയും പ്രതിനിധീകരിക്കണമെന്നില്ല. നിങ്ങൾക്ക് ഈ ജോലിയിൽ താൽപ്പര്യമുണ്ടെങ്കിൽ, ദയവായി പൂർണ്ണ പതിപ്പ് ഡൗൺലോഡ് ചെയ്യുക.

പാഠ തരം: പ്രാഥമിക അറിവ് മാസ്റ്റേഴ്സ് ചെയ്യുന്നതിനും ഏകീകരിക്കുന്നതിനുമുള്ള ഒരു പാഠം.

പാഠത്തിന്റെ ഉദ്ദേശ്യം:

• ഒരു പോളിനോമിയലിന്റെ വേരുകൾ എന്ന ആശയം വിദ്യാർത്ഥികളെ പരിചയപ്പെടുത്തുകയും അവ എങ്ങനെ കണ്ടെത്താമെന്ന് പഠിപ്പിക്കുകയും ചെയ്യുക. ഒരു ബഹുപദത്തെ ശക്തികളാൽ വികസിപ്പിക്കുന്നതിനും ഒരു ബഹുപദത്തെ ബൈനോമിയൽ കൊണ്ട് ഹരിക്കുന്നതിനുമായി ഹോർണറുടെ സ്കീം ഉപയോഗിക്കുന്നതിനുള്ള കഴിവുകൾ മെച്ചപ്പെടുത്തുക.
• ഹോർണറുടെ ഡയഗ്രം ഉപയോഗിച്ച് ഒരു സമവാക്യത്തിന്റെ വേരുകൾ കണ്ടെത്താൻ പഠിക്കുക.
• അമൂർത്തമായ ചിന്ത വികസിപ്പിക്കുക.
• ഒരു കമ്പ്യൂട്ടിംഗ് സംസ്കാരം വളർത്തിയെടുക്കുക.
• ഇന്റർ ഡിസിപ്ലിനറി കണക്ഷനുകളുടെ വികസനം.

ക്ലാസുകൾക്കിടയിൽ

1. സംഘടനാ നിമിഷം.

പാഠത്തിന്റെ വിഷയം അറിയിക്കുക, ലക്ഷ്യങ്ങൾ രൂപപ്പെടുത്തുക.

2. ഗൃഹപാഠം പരിശോധിക്കുന്നു.

3. പുതിയ മെറ്റീരിയൽ പഠിക്കുന്നു.

Fn(x) അനുവദിക്കുക = a n x n +a n-1 x n-1 +...+ a 1 x +a 0 - n ഡിഗ്രിയുടെ x ന്റെ ബഹുപദം, ഇവിടെ a 0 , a 1 ,...,a n എന്നിവയ്ക്ക് സംഖ്യകൾ നൽകിയിരിക്കുന്നു, കൂടാതെ a 0 എന്നത് 0 ന് തുല്യമല്ല. , അപ്പോൾ ഘടകഭാഗം (അപൂർണ്ണമായ ഘടകം) n-1 ഡിഗ്രിയുടെ ബഹുപദമായ Q ​​n-1 (x) ആണ്, ശേഷിക്കുന്ന R ഒരു സംഖ്യയാണ്, തുല്യത ശരിയാണ് F n (x)=(x-a) Q n-1 (x) +R.ബഹുപദമായ F n (x) R=0 ന്റെ കാര്യത്തിൽ മാത്രമേ ബൈനോമിയൽ (x-a) കൊണ്ട് ഹരിക്കാനാകൂ.

ബെസൗട്ടിന്റെ സിദ്ധാന്തം: F n (x) എന്ന ബഹുപദത്തെ ബൈനോമിയൽ (x-a) കൊണ്ട് ഹരിക്കുമ്പോൾ ബാക്കിയുള്ള R എന്നത് x=a എന്ന പോളിനോമിയൽ F n (x) മൂല്യത്തിന് തുല്യമാണ്, അതായത്. R=Pn(a).

ഒരു ചെറിയ ചരിത്രം. പ്രകടമായ ലാളിത്യവും വ്യക്തതയും ഉണ്ടായിരുന്നിട്ടും, ബെസൗട്ടിന്റെ സിദ്ധാന്തം ബഹുപദ സിദ്ധാന്തത്തിന്റെ അടിസ്ഥാന സിദ്ധാന്തങ്ങളിലൊന്നാണ്. ഈ സിദ്ധാന്തം പോളിനോമിയലുകളുടെ ബീജഗണിത ഗുണങ്ങളെ അവയുടെ പ്രവർത്തന ഗുണങ്ങളുമായി (ബഹുനോമിയലുകളെ പൂർണ്ണസംഖ്യകളായി കണക്കാക്കാൻ അനുവദിക്കുന്ന) ബന്ധപ്പെടുത്തുന്നു. ഉയർന്ന ഡിഗ്രി സമവാക്യങ്ങൾ പരിഹരിക്കാനുള്ള ഒരു മാർഗ്ഗം സമവാക്യത്തിന്റെ ഇടതുവശത്തുള്ള ബഹുപദത്തെ ഫാക്ടർ ചെയ്യുക എന്നതാണ്. പോളിനോമിയലിന്റെ ഗുണകങ്ങളുടെ കണക്കുകൂട്ടലും ബാക്കിയുള്ളവയും ഹോർണർ സ്കീം എന്ന പട്ടികയുടെ രൂപത്തിൽ എഴുതിയിരിക്കുന്നു.

ബഹുപദങ്ങളെ വിഭജിക്കുന്നതിനുള്ള ഒരു അൽഗോരിതം ആണ് ഹോർണേഴ്‌സ് സ്കീം, ഘടകഭാഗം ഒരു ദ്വിപദത്തിന് തുല്യമായിരിക്കുമ്പോൾ പ്രത്യേക കേസിനായി എഴുതിയതാണ് x–a.

ഹോർണർ വില്യം ജോർജ്ജ് (1786 - 1837), ഇംഗ്ലീഷ് ഗണിതശാസ്ത്രജ്ഞൻ. പ്രധാന ഗവേഷണം ബീജഗണിത സമവാക്യങ്ങളുടെ സിദ്ധാന്തത്തെക്കുറിച്ചാണ്. ഏതെങ്കിലും ഡിഗ്രിയുടെ സമവാക്യങ്ങളുടെ ഏകദേശ പരിഹാരത്തിനായി ഒരു രീതി വികസിപ്പിച്ചെടുത്തു. 1819-ൽ അദ്ദേഹം ബീജഗണിതത്തിന് ഒരു പോളിനോമിയലിനെ ബൈനോമിയൽ x - a (ഹോർണർ സ്കീം) കൊണ്ട് ഹരിക്കുന്നതിനുള്ള ഒരു പ്രധാന രീതി അവതരിപ്പിച്ചു.

ഹോർണറുടെ സ്കീമിന്റെ പൊതുവായ സൂത്രവാക്യത്തിന്റെ വ്യുൽപ്പന്നം.

ഒരു പോളിനോമിയൽ f(x) നെ ബാക്കിയുള്ള ഒരു ബൈനോമിയൽ കൊണ്ട് ഹരിക്കുക (x-c) എന്നതിനർത്ഥം ഒരു ബഹുപദം q(x) കണ്ടെത്തുകയും f(x)=(x-c)q(x)+r എന്ന സംഖ്യ r കണ്ടെത്തുക എന്നാണ്.

നമുക്ക് ഈ സമത്വം വിശദമായി എഴുതാം:

f 0 x n + f 1 x n-1 + f 2 x n-2 + ...+f n-1 x + f n =(x-c) (q 0 x n-1 + q 1 x n-2 + q 2 x n-3 +...+ q n-2 x + q n-1)+r

നമുക്ക് ഗുണകങ്ങളെ ഒരേ ഡിഗ്രിയിൽ തുല്യമാക്കാം:

xn:	f 0 = q 0	=> q 0 = f 0
xn-1:	f 1 = q 1 - c q 0	=> q 1 = f 1 + c q 0
xn-2:	f 2 = q 2 - c q 1	=> q 2 = f 2 + c q 1
...		...
x0:	f n = q n - c q n-1	=> q n = f n + c q n-1.

ഒരു ഉദാഹരണം ഉപയോഗിച്ച് ഹോർണറുടെ സർക്യൂട്ടിന്റെ പ്രദർശനം.

വ്യായാമം 1.ഹോർണറുടെ സ്കീം ഉപയോഗിച്ച്, നമ്മൾ പോളിനോമിയൽ f(x) = x 3 - 5x 2 + 8 ബാക്കിയുള്ള ബൈനോമിയൽ x-2 കൊണ്ട് ഹരിക്കുന്നു.

f(x) = x 3 - 5x 2 + 8 =(x-2)(x 2 -3x-6)-4, ഇവിടെ g(x)= (x 2 -3x-6), r = -4 ശേഷിക്കുന്നു.

ഒരു ദ്വിപദത്തിന്റെ ശക്തികളിൽ ഒരു ബഹുപദത്തിന്റെ വികാസം.

ഹോർണറുടെ സ്കീം ഉപയോഗിച്ച്, ബൈനോമിയലിന്റെ (x+2) ശക്തികളിൽ f(x)=x 3 +3x 2 -2x+4 എന്ന ബഹുപദം ഞങ്ങൾ വികസിപ്പിക്കുന്നു.

തൽഫലമായി, നമുക്ക് f(x) = x 3 +3x 2 -2x+4 = (x+2)(x 2 +x-4)+12 = (x+2)((x-1) വിപുലീകരണം ലഭിക്കും. )(x+ 2)-2)+12 = (((1*(x+2)-3)(x+2)-2)(x+2))+12 = (x+2) 3 -3( x+2 ) 2 -2(x+2)+12

മൂന്നാമത്തേയും നാലാമത്തേയും ഉയർന്ന ഡിഗ്രികളുടേയും സമവാക്യങ്ങൾ പരിഹരിക്കുമ്പോൾ, പോളിനോമിയലിനെ ഒരു ബൈനോമിയൽ x-a ആയി വികസിപ്പിക്കാൻ സൗകര്യപ്രദമാകുമ്പോൾ ഹോർണറുടെ സ്കീം പലപ്പോഴും ഉപയോഗിക്കാറുണ്ട്. നമ്പർ എവിളിച്ചു ബഹുപദത്തിന്റെ റൂട്ട് F n (x) = f 0 x n + f 1 x n-1 + f 2 x n-2 + ...+f n-1 x + f n, ആണെങ്കിൽ x=a F n (x) എന്ന ബഹുപദത്തിന്റെ മൂല്യം പൂജ്യത്തിന് തുല്യമാണ്: F n (a)=0, അതായത്. ബഹുപദം ബൈനോമിയൽ x-a കൊണ്ട് ഹരിച്ചാൽ.

ഉദാഹരണത്തിന്, F 3 (2)=0 എന്നതിനാൽ, F 3 (x)=3x 3 -2x-20 എന്ന ബഹുപദത്തിന്റെ മൂലമാണ് നമ്പർ 2. അതിന്റെ അർത്ഥം. ഈ ബഹുപദത്തിന്റെ ഫാക്‌ടറൈസേഷനിൽ x-2 എന്ന ഘടകം അടങ്ങിയിരിക്കുന്നു.

F 3 (x)=3x 3 -2x-20=(x-2)(3x 2 +6x+10).

ഏതെങ്കിലും ബഹുപദമായ F n(x) ഡിഗ്രി എൻ 1-ന് ഇനി ഉണ്ടാകില്ല എൻയഥാർത്ഥ വേരുകൾ.

പൂർണ്ണസംഖ്യ ഗുണകങ്ങളുള്ള ഒരു സമവാക്യത്തിന്റെ ഏതെങ്കിലും പൂർണ്ണസംഖ്യ റൂട്ട് അതിന്റെ സ്വതന്ത്ര പദത്തിന്റെ വിഭജനമാണ്.

ഒരു സമവാക്യത്തിന്റെ ലീഡിംഗ് കോഫിഫിഷ്യന്റ് 1 ആണെങ്കിൽ, സമവാക്യത്തിന്റെ എല്ലാ യുക്തിസഹമായ വേരുകളും നിലവിലുണ്ടെങ്കിൽ അവ പൂർണ്ണസംഖ്യകളാണ്.

പഠിച്ച മെറ്റീരിയലിന്റെ ഏകീകരണം.

പുതിയ മെറ്റീരിയൽ ഏകീകരിക്കുന്നതിന്, പാഠപുസ്തകം 2.41, 2.42 (പേജ് 65) എന്നിവയിൽ നിന്നുള്ള സംഖ്യകൾ പൂർത്തിയാക്കാൻ വിദ്യാർത്ഥികളെ ക്ഷണിക്കുന്നു.

(2 വിദ്യാർത്ഥികൾ ബോർഡിൽ പരിഹരിക്കുന്നു, ബാക്കിയുള്ളവർ തീരുമാനിച്ചുകഴിഞ്ഞാൽ, ബോർഡിലെ ഉത്തരങ്ങൾക്കൊപ്പം നോട്ട്ബുക്കിലെ അസൈൻമെന്റുകൾ പരിശോധിക്കുക).

സംഗ്രഹിക്കുന്നു.

ഹോർണർ സ്കീമിന്റെ ഘടനയും പ്രവർത്തന തത്വവും മനസ്സിലാക്കിയ ശേഷം, പൂർണ്ണസംഖ്യകളെ ദശാംശ സംഖ്യ സിസ്റ്റത്തിൽ നിന്ന് ബൈനറി സിസ്റ്റത്തിലേക്കും തിരിച്ചും പരിവർത്തനം ചെയ്യുന്ന പ്രശ്നം പരിഗണിക്കുമ്പോൾ, കമ്പ്യൂട്ടർ സയൻസ് പാഠങ്ങളിലും ഇത് ഉപയോഗിക്കാം. ഒരു നമ്പർ സിസ്റ്റത്തിൽ നിന്ന് മറ്റൊന്നിലേക്ക് മാറ്റുന്നതിനുള്ള അടിസ്ഥാനം ഇനിപ്പറയുന്ന പൊതു സിദ്ധാന്തമാണ്

സിദ്ധാന്തം.ഒരു പൂർണ്ണ സംഖ്യ പരിവർത്തനം ചെയ്യാൻ Apനിന്ന് പി-ary നമ്പർ സിസ്റ്റം മുതൽ അടിസ്ഥാന നമ്പർ സിസ്റ്റം വരെ ഡിആവശ്യമായ Apബാക്കിയുള്ളവയെ സംഖ്യകൊണ്ട് തുടർച്ചയായി ഹരിക്കുക ഡി, അതേ എഴുതിയിരിക്കുന്നു പിതത്ഫലമായുണ്ടാകുന്ന ഘടകഭാഗം പൂജ്യത്തിന് തുല്യമാകുന്നതുവരെ -ary സിസ്റ്റം. ഡിവിഷനിൽ നിന്ന് ബാക്കിയുള്ളവ ആയിരിക്കും ഡി- സംഖ്യാ അക്കങ്ങൾ പരസ്യം, ഏറ്റവും ചെറിയ വിഭാഗം മുതൽ ഏറ്റവും മുതിർന്നവർ വരെ. എല്ലാ പ്രവർത്തനങ്ങളും നടത്തണം പി-ary നമ്പർ സിസ്റ്റം. ഒരു വ്യക്തിക്ക്, ഈ നിയമം എപ്പോൾ മാത്രം സൗകര്യപ്രദമാണ് പി= 10, അതായത്. വിവർത്തനം ചെയ്യുമ്പോൾ നിന്ന്ദശാംശ വ്യവസ്ഥ. കമ്പ്യൂട്ടറിനെ സംബന്ധിച്ചിടത്തോളം, നേരെമറിച്ച്, ബൈനറി സിസ്റ്റത്തിൽ കണക്കുകൂട്ടലുകൾ നടത്തുന്നത് "കൂടുതൽ സൗകര്യപ്രദമാണ്". അതിനാൽ, "2 മുതൽ 10 വരെ" പരിവർത്തനം ചെയ്യാൻ, ബൈനറി സിസ്റ്റത്തിൽ പത്തിനെ തുടർച്ചയായി വിഭജനം ഉപയോഗിക്കുന്നു, കൂടാതെ "10 മുതൽ 2" എന്നത് പത്തിന്റെ ശക്തികളുടെ കൂട്ടിച്ചേർക്കലാണ്. “10 ഇൻ 2” നടപടിക്രമത്തിന്റെ കണക്കുകൂട്ടലുകൾ ഒപ്റ്റിമൈസ് ചെയ്യുന്നതിന്, കമ്പ്യൂട്ടർ ഹോർണറുടെ സാമ്പത്തിക കമ്പ്യൂട്ടിംഗ് സ്കീം ഉപയോഗിക്കുന്നു.

ഹോം വർക്ക്. രണ്ട് ജോലികൾ പൂർത്തിയാക്കാൻ നിർദ്ദേശിക്കുന്നു.

1st. ഹോർണറുടെ സ്കീം ഉപയോഗിച്ച്, പോളിനോമിയൽ f(x)=2x 5 -x 4 -3x 3 +x-3 ബൈനോമിയൽ (x-3) കൊണ്ട് ഹരിക്കുക.

രണ്ടാമത്തേത്. f(x)=x 4 -2x 3 +2x 2 -x-6 എന്ന പോളിനോമിയലിന്റെ പൂർണ്ണസംഖ്യ വേരുകൾ കണ്ടെത്തുക. (പൂർണ്ണസംഖ്യ ഗുണകങ്ങളുള്ള ഒരു സമവാക്യത്തിന്റെ ഏതെങ്കിലും പൂർണ്ണസംഖ്യ റൂട്ട് അതിന്റെ സ്വതന്ത്ര പദത്തിന്റെ വിഭജനമാണെന്ന് കണക്കിലെടുക്കുമ്പോൾ)

സാഹിത്യം.

1. കുറോഷ് എ.ജി. "ഉയർന്ന ആൾജിബ്രയുടെ കോഴ്സ്."
2. നിക്കോൾസ്കി എസ്.എം., പൊട്ടപോവ് എം.കെ. ഗ്രേഡ് 10 "ആൾജിബ്രയും ഗണിതശാസ്ത്ര വിശകലനത്തിന്റെ തുടക്കവും."
3. http://inf.1september.ru/article.php?ID=200600907.