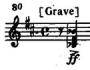Nilai mutlak bagi nombor a Adalah jarak dari asal ke titik A(a).

Untuk memahami definisi ini, ganti pemboleh ubah a sebarang nombor, contohnya 3 dan cuba baca lagi:

Nilai mutlak sesuatu nombor 3 Adakah jarak dari asal ke titik A(3 ).

Menjadi jelas bahawa modul tidak lebih dari jarak biasa. Mari cuba lihat jarak dari asal ke titik A ( 3 )

Jarak dari tempat asal ke titik A ( 3 ) sama dengan 3 (tiga unit atau tiga langkah).

Modulus nombor ditunjukkan oleh dua garis menegak, contohnya:

Modulus nombor 3 dilambangkan sebagai berikut: | 3 |

Modulus nombor 4 dilambangkan seperti berikut: | 4 |

Modulus nombor 5 dilambangkan seperti berikut: | 5 |

Kami mencari modulus nombor 3 dan mendapati ia adalah 3. Oleh itu, kami menulis:

Ia berbunyi seperti: "Modulus nombor tiga adalah tiga"

Sekarang mari kita cuba mencari modulus nombor -3. Sekali lagi, kembali ke definisi dan gantikan nombor -3 ke dalamnya. Hanya bukannya titik A gunakan titik baru B... Titik A kita telah pun menggunakan dalam contoh pertama.

Nombor modulo - 3 adalah jarak dari asal ke titik B(—3 ).

Jarak dari satu titik ke titik yang lain tidak boleh negatif. Oleh itu, modulus sebarang nombor negatif, menjadi jarak, juga tidak akan negatif. Modulus nombor -3 akan menjadi nombor 3. Jarak dari asal ke titik B (-3) juga tiga unit:

Ia berbunyi seperti: "Modulus nombor tolak tiga adalah tiga"

Nilai mutlak nombor 0 adalah 0, kerana titik dengan koordinat 0 bertepatan dengan asal, iaitu jarak dari tempat asal ke titik O (0) sama dengan sifar:

"Modulus sifar adalah sifar"

Kami membuat kesimpulan:

• Modulus nombor tidak boleh negatif;
• Untuk nombor positif dan sifar, modulus sama dengan nombor itu sendiri, dan untuk nombor negatif, nombor bertentangan;
• Nombor bertentangan mempunyai modul yang sama.

Nombor bertentangan

Nombor yang hanya berbeza dalam tanda disebut bertentangan... Contohnya, nombor −2 dan 2 bertentangan. Mereka hanya berbeza tanda. Angka −2 memiliki tanda tolak, dan 2 memiliki tanda tambah, tetapi kami tidak melihatnya, kerana, seperti yang kami katakan sebelumnya, menurut tradisi mereka tidak menulis tambah.

Lebih banyak contoh nombor bertentangan:

Nombor bertentangan mempunyai modul yang sama. Contohnya, cari modul untuk −2 dan 2

Angka itu menunjukkan bahawa jarak dari titik asal ke titik A (−2) dan B (2) sama dengan dua langkah.

Adakah anda suka pelajaran?
Sertailah kumpulan Vkontakte baru kami dan mula menerima pemberitahuan mengenai pelajaran baru

Kami tidak memilih matematik profesionnya, dan dia memilih kami.

Ahli matematik Rusia Yu.I. Manin

Persamaan dengan modulus

Masalah matematik sekolah yang paling sukar untuk diselesaikan ialah persamaan yang mengandungi pemboleh ubah di bawah tanda modulus. Untuk berjaya menyelesaikan persamaan tersebut, anda perlu mengetahui definisi dan sifat asas modul. Secara semula jadi, pelajar harus mempunyai kemahiran untuk menyelesaikan persamaan jenis ini.

Konsep dan sifat asas

Modulus (nilai mutlak) nombor nyata dilambangkan dan ditakrifkan sebagai berikut:

Sifat mudah modul termasuk nisbah berikut:

Catatan, bahawa dua sifat terakhir adalah sah untuk sebarang tahap genap.

Selain itu, jika, di mana, maka

Sifat modul yang lebih kompleks, yang dapat digunakan dengan berkesan untuk menyelesaikan persamaan dengan modul, dirumuskan melalui teorema berikut:

Teorem 1.Untuk sebarang fungsi analitik dan ketaksamaan itu benar

Teorem 2. Persamaan sama dengan ketaksamaan.

Teorem 3. Kesaksamaan sama dengan ketidaksamaan.

Mari kita pertimbangkan contoh tipikal untuk menyelesaikan masalah pada topik "Persamaan, mengandungi pemboleh ubah di bawah tanda modul ".

Menyelesaikan persamaan dengan modulus

Kaedah yang paling biasa dalam matematik sekolah untuk menyelesaikan persamaan dengan modul adalah kaedah, berdasarkan pengembangan modul. Kaedah ini serba boleh, namun, secara umum, aplikasinya dapat menghasilkan pengiraan yang sangat membebankan. Sehubungan dengan itu, pelajar harus peka dengan yang lain, kaedah dan teknik yang lebih berkesan untuk menyelesaikan persamaan tersebut. Khususnya, anda perlu mempunyai kemahiran dalam menerapkan teorema, diberikan dalam artikel ini.

Contoh 1. Selesaikan persamaan. (1)

Penyelesaian. Persamaan (1) akan diselesaikan dengan kaedah "klasik" - kaedah memperluas modul. Untuk melakukan ini, kami membahagikan paksi nombor mata dan secara berkala dan mempertimbangkan tiga kes.

1. Jika, maka,,, dan persamaan (1) dalam bentuk. Oleh itu ia mengikuti. Oleh itu, di sini, nilai yang dijumpai bukanlah punca persamaan (1).

2. Jika, maka dari persamaan (1) kita memperoleh atau.

Sejak itu punca persamaan (1).

3. Jika, maka persamaan (1) mengambil bentuk atau. Perhatikan bahawa.

Jawapan: , .

Semasa menyelesaikan persamaan berikutnya dengan modul, kita akan menggunakan sifat modul secara aktif untuk meningkatkan kecekapan menyelesaikan persamaan tersebut.

Contoh 2. Selesaikan persamaan.

Penyelesaian. Sejak dan, maka persamaan membayangkan... Sehubungan itu ,,, dan persamaannya mengambil bentuk... Daripada ini kita dapat... Tetapi, oleh itu, persamaan asal tidak mempunyai akar.

Jawapan: tiada akar.

Contoh 3. Selesaikan persamaan.

Penyelesaian. Sejak itu. Sekiranya, maka, dan persamaannya mengambil bentuk.

Dari sini kita dapat.

Contoh 4. Selesaikan persamaan.

Penyelesaian.Kami menulis semula persamaan dalam bentuk yang setara. (2)

Persamaan yang terhasil tergolong dalam persamaan jenis.

Dengan mengambil kira Teorem 2, boleh dikatakan bahawa persamaan (2) adalah bersamaan dengan ketaksamaan. Dari sini kita dapat.

Jawapan:.

Contoh 5. Selesaikan persamaan.

Penyelesaian. Persamaan ini mempunyai bentuk... Sebab itu, menurut Teorem 3, di sini kita mempunyai ketaksamaan atau.

Contoh 6. Selesaikan persamaan.

Penyelesaian. Sepatutnya begitu. kerana , maka persamaan yang diberikan mengambil bentuk persamaan kuadratik, (3)

di mana ... Oleh kerana persamaan (3) mempunyai satu punca positif dan kemudian ... Oleh itu, kami memperoleh dua punca persamaan asal: dan .

Contoh 7. Selesaikan persamaan. (4)

Penyelesaian. Sejak persamaanadalah bersamaan dengan gabungan dua persamaan: dan, maka, ketika menyelesaikan persamaan (4), perlu mempertimbangkan dua kes.

1. Sekiranya, maka atau.

Dari sini kita dapat, dan.

2. Jika, maka atau.

Sejak itu.

Jawapan: , , , .

Contoh 8.Selesaikan persamaan . (5)

Penyelesaian. Sejak dan, kemudian. Dari ini dan dari Persamaan (5) ia mengikuti bahawa dan, iaitu di sini kita mempunyai sistem persamaan

Walau bagaimanapun, sistem persamaan ini tidak konsisten.

Jawapan: tiada akar.

Contoh 9. Selesaikan persamaan. (6)

Penyelesaian. Sekiranya kita menunjukkan, maka dan daripada persamaan (6) kita perolehi

Atau. (7)

Oleh kerana persamaan (7) mempunyai bentuk, persamaan ini setara dengan ketaksamaan. Dari sini kita dapat. Sejak, kemudian atau.

Jawapan:.

Contoh 10.Selesaikan persamaan. (8)

Penyelesaian.Menurut Teorem 1, kita boleh menulis

(9)

Dengan mengambil kira persamaan (8), kami menyimpulkan bahawa kedua-dua ketaksamaan (9) berubah menjadi persamaan, iaitu sistem persamaan memegang

Walau bagaimanapun, oleh Teorem 3, sistem persamaan di atas setara dengan sistem ketaksamaan

(10)

Menyelesaikan sistem ketaksamaan (10), kami memperoleh. Oleh kerana sistem ketaksamaan (10) adalah bersamaan dengan persamaan (8), persamaan asal mempunyai punca tunggal.

Jawapan:.

Contoh 11. Selesaikan persamaan. (11)

Penyelesaian. Biarkan dan, kemudian persamaan berlaku dari persamaan (11).

Oleh itu ia mengikuti dan. Oleh itu, di sini kita mempunyai sistem ketidaksamaan

Penyelesaian sistem ketaksamaan ini adalah dan .

Jawapan: , .

Contoh 12.Selesaikan persamaan. (12)

Penyelesaian. Persamaan (12) akan diselesaikan dengan kaedah pengembangan modul secara berurutan. Untuk melakukan ini, pertimbangkan beberapa kes.

1. Sekiranya, maka.

1.1. Jika, maka dan,.

1.2. Sekiranya, maka. Tetapi, oleh itu, dalam kes ini, persamaan (12) tidak mempunyai punca.

2. Sekiranya, maka.

2.1. Jika, maka dan,.

2.2. Jika, maka dan.

Jawapan:,,,,.

Contoh 13.Selesaikan persamaan. (13)

Penyelesaian. Oleh kerana persamaan sebelah kiri (13) tidak negatif, maka dan. Dalam hal ini, dan persamaan (13)

mengambil bentuk atau.

Telah diketahui bahawa persamaan adalah bersamaan dengan gabungan dua persamaan dan, memutuskan mana yang kita dapat,. Kerana, maka persamaan (13) mempunyai satu punca.

Jawapan:.

Contoh 14. Selesaikan sistem persamaan (14)

Penyelesaian. Sejak dan, kemudian dan. Oleh itu, dari sistem persamaan (14) kita memperoleh empat sistem persamaan:

Punca-punca sistem persamaan di atas ialah punca-punca sistem persamaan (14).

Jawapan: ,,,,,,.

Contoh 15. Selesaikan sistem persamaan (15)

Penyelesaian. Sejak itu. Dalam hal ini, dari sistem persamaan (15), kita memperoleh dua sistem persamaan

Punca-punca sistem persamaan pertama ialah dan, dan daripada sistem persamaan kedua kita perolehi dan.

Jawapan: , , , .

Contoh 16. Selesaikan sistem persamaan (16)

Penyelesaian. Daripada persamaan pertama sistem (16) ia mengikuti bahawa.

Sejak itu ... Pertimbangkan persamaan kedua sistem. Sejauh mana, kemudian, dan persamaannya mengambil bentuk, atau.

Jika anda menggantikan nilaike dalam persamaan pertama sistem (16), kemudian, atau.

Jawapan: , .

Untuk kajian yang lebih mendalam mengenai kaedah penyelesaian masalah, berkaitan dengan menyelesaikan persamaan, mengandungi pemboleh ubah di bawah tanda modul, anda boleh mengesyorkan tutorial daripada senarai bacaan yang disyorkan.

1. Pengumpulan masalah dalam matematik untuk pemohon ke kolej teknikal / Ed. M.I. Skanavi. - M .: Damai dan Pendidikan, 2013 .-- 608 p.

2. Suprun V.P. Matematik untuk pelajar sekolah menengah: masalah peningkatan kerumitan. - M .: CD "Librokom" / URSS, 2017 .-- 200 p.

3. Suprun V.P. Matematik untuk pelajar sekolah menengah: kaedah penyelesaian masalah bukan standard. - M .: CD "Librokom" / URSS, 2017 .-- 296 p.

Masih ada soalan?

Untuk mendapatkan bantuan daripada tutor - daftar.

laman web, dengan penyalinan penuh atau sebahagian dari bahan, pautan ke sumber diperlukan.

Salah satu topik yang paling sukar bagi pelajar adalah menyelesaikan persamaan yang mengandungi pemboleh ubah di bawah tanda modulus. Mari kita fikirkan sebagai permulaan, dengan apa ini berkaitan? Mengapa, sebagai contoh, persamaan kuadratik adalah klik seperti kacang untuk kebanyakan kanak-kanak, dan dengan konsep yang jauh daripada rumit sebagai modul, ia mempunyai banyak masalah?

Pada pendapat saya, semua kesukaran ini berkaitan dengan kurangnya peraturan yang digubal dengan jelas untuk menyelesaikan persamaan dengan modulus. Jadi, menyelesaikan persamaan kuadratik, pelajar tahu pasti bahawa dia perlu terlebih dahulu menggunakan formula diskriminasi, dan kemudian formula untuk punca-punca persamaan kuadratik. Tetapi bagaimana jika terdapat modul dalam persamaan? Kami akan cuba menerangkan dengan jelas rancangan tindakan yang diperlukan untuk kes tersebut apabila persamaan mengandungi yang tidak diketahui di bawah tanda modulus. Berikut adalah beberapa contoh untuk setiap kes.

Tetapi pertama, mari kita ingat definisi modul... Jadi, modulus nombor itu a nombor ini sendiri dipanggil jika a tidak negatif dan -a sekiranya bilangannya a kurang daripada sifar. Anda boleh menulisnya seperti ini:

| a | = a jika a ≥ 0 dan | a | = -a jika a< 0

Bercakap tentang pengertian geometri modul, harus diingat bahawa setiap nombor nyata sepadan dengan titik tertentu pada paksi angka - k menyelaras. Jadi, nilai modulus atau mutlak suatu nombor adalah jarak dari titik ini ke asal paksi berangka. Jarak selalu dinyatakan sebagai nombor positif. Oleh itu, nilai mutlak bagi sebarang nombor negatif adalah nombor positif. Ngomong-ngomong, walaupun pada tahap ini, ramai pelajar mula keliru. Sebarang nombor boleh ada di modul, tetapi hasil penggunaan modul selalu merupakan angka positif.

Sekarang mari kita pergi secara langsung untuk menyelesaikan persamaan.

1. Pertimbangkan persamaan bentuk | x | = c, di mana c adalah nombor nyata. Persamaan ini boleh diselesaikan menggunakan definisi modulus.

Kami membahagikan semua nombor nyata kepada tiga kumpulan: mereka yang lebih besar daripada sifar, mereka yang kurang dari sifar, dan kumpulan ketiga adalah nombor 0. Mari tulis penyelesaiannya dalam bentuk rajah:

(± c jika c> 0

Sekiranya | x | = c, maka x = (0, jika c = 0

(tiada akar jika dengan< 0

1) | x | = 5, kerana 5> 0, maka x = ± 5;

2) | x | = -5, kerana -5< 0, то уравнение не имеет корней;

3) | x | = 0, maka x = 0.

2. Persamaan bentuk | f (x) | = b, di mana b> 0. Untuk menyelesaikan persamaan ini, adalah perlu untuk menghilangkan modulus. Kami melakukannya seperti ini: f (x) = b atau f (x) = -b. Sekarang adalah perlu untuk menyelesaikan setiap persamaan yang diperoleh secara berasingan. Sekiranya dalam persamaan asal b< 0, решений не будет.

1) | x + 2 | = 4, kerana 4> 0, kemudian

x + 2 = 4 atau x + 2 = -4

2) | x 2 - 5 | = 11, kerana 11> 0, kemudian

x 2 - 5 = 11 atau x 2 - 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 tiada akar

3) | x 2 - 5x | = -8, kerana -selapan< 0, то уравнение не имеет корней.

3. Persamaan bentuk | f (x) | = g (x). Dalam arti modulus, persamaan seperti itu akan mempunyai penyelesaian jika sebelah kanannya lebih besar daripada atau sama dengan sifar, iaitu. g (x) ≥ 0. Maka kita akan mempunyai:

f (x) = g (x) atau f (x) = -g (x).

1) | 2x - 1 | = 5x - 10. Persamaan ini akan berakar jika 5x - 10 ≥ 0. Dengan inilah penyelesaian persamaan tersebut bermula.

1.O.D.Z. 5x - 10 ≥ 0

2. Penyelesaian:

2x - 1 = 5x - 10 atau 2x - 1 = - (5x - 10)

3. Kita satukan ODZ. dan penyelesaiannya, kami mendapat:

Punca x = 11/7 tidak sesuai mengikut O.D.Z., ia kurang daripada 2, dan x = 3 memenuhi syarat ini.

Jawapan: x = 3

2) | x - 1 | = 1 - x 2.

1.O.D.Z. 1 - x 2 ≥ 0. Kami menyelesaikan ketaksamaan ini dengan kaedah selang:

(1 - x) (1 + x) ≥ 0

2. Penyelesaian:

x - 1 = 1 - x 2 atau x - 1 = - (1 - x 2)

x 2 + x - 2 = 0 x 2 - x = 0

x = -2 atau x = 1 x = 0 atau x = 1

3. Kami menggabungkan penyelesaian dan ODZ:

Hanya akar x = 1 dan x = 0 yang sesuai.

Jawapan: x = 0, x = 1.

4. Persamaan bentuk | f (x) | = | g (x) |. Persamaan sedemikian adalah bersamaan dengan dua persamaan berikut f (x) = g (x) atau f (x) = -g (x).

1) | x 2 - 5x + 7 | = | 2x - 5 |. Persamaan ini bersamaan dengan dua perkara berikut:

x 2 - 5x + 7 = 2x - 5 atau x 2 - 5x +7 = -2x + 5

x 2 - 7x + 12 = 0 x 2 - 3x + 2 = 0

x = 3 atau x = 4 x = 2 atau x = 1

Jawapan: x = 1, x = 2, x = 3, x = 4.

5. Persamaan Diselesaikan dengan Kaedah Penggantian (Perubahan Pembolehubah). Kaedah penyelesaian ini paling mudah dijelaskan dengan contoh tertentu. Oleh itu, biarkan persamaan kuadratik dengan modulus diberikan:

x 2 - 6 | x | + 5 = 0. Dengan sifat modul x 2 = | x | 2, sehingga persamaan dapat ditulis semula seperti berikut:

| x | 2 - 6 | x | + 5 = 0. Mari kita ganti | x | = t ≥ 0, maka kita akan mempunyai:

t 2 - 6t + 5 = 0. Menyelesaikan persamaan ini, kita mendapat t = 1 atau t = 5. Mari kita kembali ke penggantian:

| x | = 1 atau | x | = 5

x = ± 1 x = ± 5

Jawapan: x = -5, x = -1, x = 1, x = 5.

Mari kita ambil contoh lain:

x 2 + | x | - 2 = 0. Dengan sifat modul x 2 = | x | 2, oleh itu

| x | 2 + | x | - 2 = 0. Mari kita gantikan | x | = t ≥ 0, kemudian:

t 2 + t - 2 = 0. Untuk menyelesaikan persamaan ini, kita memperoleh t = -2 atau t = 1. Mari kita kembali ke penggantian:

| x | = -2 atau | x | = 1

Tiada akar x = ± 1

Jawapan: x = -1, x = 1.

6. Jenis persamaan lain ialah persamaan dengan modulus "kompleks". Persamaan ini merangkumi persamaan yang mempunyai "modul dalam modul". Persamaan seperti ini boleh diselesaikan menggunakan sifat modul.

1) | 3 - | x || = 4. Kami akan meneruskan cara yang sama seperti pada persamaan jenis kedua. Kerana 4> 0, maka kita mendapat dua persamaan:

3 - | x | = 4 atau 3 - | x | = -4.

Sekarang kita menyatakan dalam setiap persamaan modulus x, kemudian | x | = -1 atau | x | = 7.

Kami menyelesaikan setiap persamaan yang diperoleh. Tidak ada akar dalam persamaan pertama, kerana -1< 0, а во втором x = ±7.

Jawapannya ialah x = -7, x = 7.

2) | 3 + | x + 1 || = 5. Kami menyelesaikan persamaan ini dengan cara yang sama:

3 + | x + 1 | = 5 atau 3 + | x + 1 | = -5

| x + 1 | = 2 | x + 1 | = -8

x + 1 = 2 atau x + 1 = -2. Tiada akar.

Jawapan: x = -3, x = 1.

Terdapat juga kaedah universal untuk menyelesaikan persamaan dengan modulus. Ini adalah kaedah jarak. Tetapi kita akan mempertimbangkannya kemudian.

laman blog, dengan penyalinan penuh atau sebahagian dari bahan, diperlukan pautan ke sumbernya.

Kalkulator matematik dalam talian ini akan membantu anda menyelesaikan persamaan atau ketaksamaan dengan moduli... Program untuk penyelesaian persamaan dan ketaksamaan dengan moduli tidak hanya memberi jawapan kepada masalah, ia memberi penyelesaian terperinci dengan penjelasan, iaitu memaparkan proses memperoleh hasilnya.

Program ini boleh berguna untuk pelajar senior sekolah menengah sebagai persediaan untuk ujian dan peperiksaan, semasa menyemak pengetahuan sebelum peperiksaan, untuk ibu bapa mengawal penyelesaian banyak masalah dalam matematik dan algebra. Atau mungkin terlalu mahal untuk anda mengupah tutor atau membeli buku teks baru? Atau adakah anda hanya mahu menyelesaikan kerja rumah matematik atau aljabar anda secepat mungkin? Dalam kes ini, anda juga boleh menggunakan program kami dengan penyelesaian terperinci.

Dengan cara ini, anda boleh menjalankan pengajaran anda sendiri dan / atau mengajar adik-adik lelaki atau perempuan anda, manakala tahap pendidikan dalam bidang masalah yang diselesaikan meningkat.

Masukkan Persamaan atau Ketidaksamaan dengan Modul

Didapati bahawa beberapa skrip yang diperlukan untuk menyelesaikan masalah ini tidak dimuat, dan program mungkin tidak berfungsi.
Mungkin anda telah mengaktifkan AdBlock.
Dalam kes ini, nonaktifkan dan muat semula halaman.

Kerana Terdapat ramai orang yang ingin menyelesaikan masalah, permintaan anda beratur.
Selepas beberapa saat, penyelesaiannya akan muncul di bawah.
Sila tunggu sek ...

Jika awak menyedari ralat dalam penyelesaiannya, maka anda boleh menulis mengenai perkara ini dalam Borang Maklum Balas.
Jangan lupa nyatakan tugas yang mana anda tentukan dan apa masukkan di ladang.

Permainan, teka-teki, emulator kami:

Sedikit teori.

Persamaan dan Ketaksamaan dengan Modul

Dalam kursus algebra di sekolah asas, anda mungkin menghadapi persamaan dan ketaksamaan yang paling mudah dengan modul. Untuk menyelesaikannya, anda boleh menggunakan kaedah geometri berdasarkan fakta bahawa \ (| xa | \) ialah jarak pada garis nombor antara titik x dan a: \ (| xa | = \ rho (x; \; a ) \). Contohnya, untuk menyelesaikan persamaan \ (| x-3 | = 2 \), anda perlu mencari titik pada garis nombor yang berada pada jarak 2 dari titik 3. Terdapat dua titik seperti itu: \ (x_1 = 1 \) dan \ (x_2 = 5 \) ...

Menyelesaikan ketaksamaan \ (| 2x + 7 |

Tetapi cara utama untuk menyelesaikan persamaan dan ketidaksamaan dengan modul dikaitkan dengan apa yang disebut "pengembangan modul mengikut definisi":
jika \ (a \ geq 0 \), maka \ (| a | = a \);
jika \ (a Sebagai peraturan, persamaan (ketaksamaan) dengan moduli diturunkan menjadi satu set persamaan (ketaksamaan) yang tidak mengandungi tanda modulus.

Sebagai tambahan kepada definisi yang ditentukan, pernyataan berikut digunakan:
1) Jika \ (c> 0 \), maka persamaan \ (| f (x) | = c \) bersamaan dengan satu set persamaan: \ (\ kiri [\ begin (array) (l) f (x ) = c \\ f (x) = - c \ end (susunan) \ kanan. \)
2) Jika \ (c> 0 \), maka ketaksamaan \ (| f (x) | 3) Jika \ (c \ geq 0 \), maka ketaksamaan \ (| f (x) |> c \) adalah bersamaan dengan set ketaksamaan : \ (\ kiri [\ mula (tatasusunan) (l) f (x) c \ hujung (tatasusunan) \ kanan. \)
4) Sekiranya kedua-dua sisi ketaksamaan \ (f (x) CONTOH 1. Selesaikan persamaan \ (x ^ 2 +2 | x-1 | -6 = 0 \).

Sekiranya \ (x-1 \ geq 0 \), maka \ (| x-1 | = x-1 \) dan persamaan yang diberikan mengambil bentuk
\ (x ^ 2 +2 (x-1) -6 = 0 \ Anak panah kanan x ^ 2 + 2x -8 = 0 \).
Sekiranya \ (x-1 \ (x ^ 2 -2 (x-1) -6 = 0 \ Garis kanan x ^ 2 -2x -4 = 0 \).
Oleh itu, persamaan yang diberikan harus dipertimbangkan secara berasingan dalam setiap dua kes yang ditunjukkan.
1) Biarkan \ (x-1 \ geq 0 \), iaitu \ (x \ geq 1 \). Dari persamaan \ (x ^ 2 + 2x -8 = 0 \) kita dapati \ (x_1 = 2, \; x_2 = -4 \). Syarat \ (x \ geq 1 \) dipenuhi hanya dengan nilai \ (x_1 = 2 \).
2) Mari \ (x-1 Jawapan: \ (2; \; \; 1- \ sqrt (5) \)

CONTOH 2. Selesaikan persamaan \ (| x ^ 2-6x + 7 | = \ frac (5x-9) (3) \).

Cara pertama(pengembangan modul mengikut definisi).
Berhujah seperti dalam contoh 1, kami membuat kesimpulan bahawa persamaan yang diberikan mesti dipertimbangkan secara berasingan jika dua syarat dipenuhi: \ (x ^ 2-6x + 7 \ geq 0 \) atau \ (x ^ 2-6x + 7

1) Jika \ (x ^ 2-6x + 7 \ geq 0 \), maka \ (| x ^ 2-6x + 7 | = x ^ 2-6x + 7 \) dan persamaan yang diberikan mengambil bentuk \ (x ^ 2 -6x + 7 = \ frac (5x-9) (3) \ Anak panah kanan 3x ^ 2-23x + 30 = 0 \). Setelah menyelesaikan persamaan kuadratik ini, kita mendapat: \ (x_1 = 6, \; x_2 = \ frac (5) (3) \).
Mari kita ketahui sama ada nilai \ (x_1 = 6 \) memenuhi syarat \ (x ^ 2-6x + 7 \ geq 0 \). Untuk melakukan ini, kita menggantikan nilai yang ditentukan menjadi ketaksamaan segi empat sama. Kami mendapat: \ (6 ^ 2-6 \ cdot 6 + 7 \ geq 0 \), i.e. \ (7 \ geq 0 \) adalah ketaksamaan yang sebenarnya. Oleh itu, \ (x_1 = 6 \) adalah punca persamaan yang diberikan.
Marilah kita mengetahui sama ada nilai \ (x_2 = \ frac (5) (3) \) memenuhi syarat \ (x ^ 2-6x + 7 \ geq 0 \). Untuk melakukan ini, kami menggantikan nilai yang ditentukan ke dalam ketaksamaan kuasa dua. Kami mendapat: \ (\ kiri (\ frac (5) (3) \ kanan) ^ 2 - \ frac (5) (3) \ cdot 6 + 7 \ geq 0 \), iaitu \ (\ frac (25) (9) -3 \ geq 0 \) - ketaksamaan yang salah. Oleh itu, \ (x_2 = \ frac (5) (3) \) bukan punca persamaan yang diberikan.

2) Jika \ (x ^ 2-6x + 7 Nilai \ (x_3 = 3 \) memenuhi syarat \ (x ^ 2-6x + 7 Nilai \ (x_4 = \ frac (4) (3) \) tidak memuaskan keadaan \ (x ^ 2-6x + 7 Jadi, persamaan yang diberikan mempunyai dua punca: \ (x = 6, \; x = 3 \).

Cara kedua. Jika persamaan \ (| f (x) | = h (x) \) diberikan, maka untuk \ (h (x) \ (\ kiri [\ mulakan (tatasusunan) (l) x ^ 2-6x + 7 = \ frac (5x-9) (3) \\ x ^ 2-6x + 7 = - \ frac (5x-9) (3) \ akhir (susunan) \ kanan. \)
Kedua-dua persamaan ini diselesaikan di atas (dengan cara pertama untuk menyelesaikan persamaan yang diberikan), akarnya adalah seperti berikut: \ (6, \; \ frac (5) (3), \; 3, \; \ frac (4 ) (3) \). Keadaan \ (\ frac (5x-9) (3) \ geq 0 \) daripada empat nilai ini hanya dipenuhi oleh dua: 6 dan 3. Oleh itu, persamaan yang diberikan mempunyai dua punca: \ (x = 6, \; x = 3 \).

cara ketiga(grafik).
1) Mari plot fungsi \ (y = | x ^ 2-6x + 7 | \). Pertama, bina parabola \ (y = x ^ 2-6x + 7 \). Kami mempunyai \ (x ^ 2-6x + 7 = (x-3) ^ 2-2 \). Grafik fungsi \ (y = (x-3) ^ 2-2 \) dapat diperoleh dari grafik fungsi \ (y = x ^ 2 \) dengan menggesernya dengan 3 unit skala ke kanan (bersama paksi x) dan dengan 2 unit skala ke bawah ( pada paksi-y). Garis lurus x = 3 adalah paksi parabola yang kami minati. Adalah mudah untuk mengambil titik (3; -2) - bucu parabola, titik (0; 7) dan titik (6; 7) simetri kepadanya berbanding dengan paksi parabola sebagai titik kawalan untuk plot yang lebih tepat bagi graf.
Untuk memetakan grafik fungsi \ (y = | x ^ 2-6x + 7 | \), anda perlu meninggalkan bahagian parabola yang tidak berubah yang tidak terletak di bawah paksi-x, dan mencerminkan bahagian parabola yang terletak di bawah paksi-x mengenai paksi-x.
2) Mari bina graf bagi fungsi linear \ (y = \ frac (5x-9) (3) \). Lebih mudah untuk mengambil titik (0; –3) dan (3; 2) sebagai titik kawalan.

Adalah penting bahawa titik x = 1,8 persilangan garis lurus dengan paksi absis terletak di sebelah kanan titik kiri persilangan parabola dengan paksi absis - ini ialah titik \ (x = 3 - \ sqrt (2) \) (sejak \ (3- \ sqrt (2) 3) Dilihat oleh gambar, grafik bersilang pada dua titik - A (3; 2) dan B (6; 7) Menggantikan abses dari titik-titik ini x = 3 dan x = 6 dalam persamaan yang diberikan, kami memastikan bahawa untuk kedua-dua nilai yang lain memberikan persamaan angka yang betul, yang bermaksud bahawa hipotesis kami telah disahkan - persamaan mempunyai dua punca: x = 3 dan x = 6. Jawapan: 3; 6.

Komen... Kaedah grafik, untuk semua rahmatnya, sangat tidak boleh dipercayai. Dalam contoh yang dipertimbangkan, ia hanya berfungsi kerana punca persamaannya adalah bilangan bulat.

CONTOH 3. Selesaikan persamaan \ (| 2x-4 | + | x + 3 | = 8 \)

Cara pertama
Ungkapan 2x - 4 menjadi 0 pada titik x = 2, dan ungkapan x + 3 pada titik x = –3. Dua titik ini membahagi garis nombor menjadi tiga selang: \ (x

Pertimbangkan rentang pertama: \ ((- \ infty; \; -3) \).
Jika x Pertimbangkan selang kedua: \ ([- 3; \; 2) \).
Sekiranya \ (- 3 \ leq x Pertimbangkan selang ketiga: \ ()