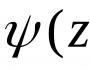Hvad kaldes nuller af en funktion? Reglen for funktion nuller
Argument værdier z hvorpå f(z) går til nul kaldet. nulpunkt, dvs. Hvis f(-en) = 0, så et - nulpunkt.
Def. Prik EN hedder nul ordenn
, hvis
FKP kan repræsenteres i formularen f(z) = , hvor 
analytisk funktion og 
0.
I dette tilfælde, i Taylor-seriens udvidelse af funktionen (43), den første n koefficienter er nul
=
=
Etc. Bestem rækkefølgen af nul for 
og (1 -cos z) kl z
=
0
=
=
nul 1. orden
1 - cos z
=
=
nul 2. orden
Def. Prik z
=
hedder peger på det uendelige Og nul funktioner f(z), hvis f(
) = 0. En sådan funktion kan udvides til en række i negative potenser z
: f(z)
=
. Hvis
først n
koefficienter er lig med nul, så kommer vi frem til nul orden n
på et punkt i det uendelige: f(z)
= z
-
n
.
Isolerede entalspunkter er opdelt i: a) aftagelige entalspunkter; b) ordenspolern; V) i det væsentlige enkeltstående punkter.
Prik EN hedder aftagelig singular spids funktioner f(z) hvis kl z 
-en
lim f(z)
= med - endeligt nummer .
Prik EN hedder ordensordenn
(n
1) funktioner f(z), hvis den omvendte funktion 
=
1/
f(z) har nul orden n på punktet EN. En sådan funktion kan altid repræsenteres som f(z)
=
, Hvor 
- analytisk funktion og 
.
Prik EN hedder i bund og grund en særlig pointe funktioner f(z), hvis kl z 
-en
lim f(z) eksisterer ikke.
Laurent-serien
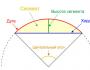
Lad os overveje tilfældet med en ringkonvergensregion r < | z 0 – -en| < R centreret i et punkt EN til funktion f(z). Lad os introducere to nye cirkler L 1 (r) Og L 2 (R) nær ringens grænser med et punkt z 0 mellem dem. Lad os lave et snit af ringen, forbinde cirklerne langs snittets kanter, gå videre til et enkelt forbundet område og ind
Cauchy-integralformel (39) får vi to integraler over variablen z
f(z 0)
=
+
,
(42)
hvor integrationen går i modsatte retninger.
For det integrale over L 1 betingelse er opfyldt | z 0 – -en | > | z – -en |, og for integralet over L 2 omvendt tilstand | z 0 – -en | < | z – -en |. Derfor er faktoren 1/( z – z 0) udvide til serie (a) i integralet over L 2 og i serie (b) i integralet over L 1 . Som et resultat opnår vi udvidelsen f(z) i ringområdet i Laurent-serien ved positive og negative kræfter ( z 0 – -en)
f(z 0)
=
EN n
(z 0 -en) n
(43)
Hvor EN n
=
=
;EN -n
=
Udvidelse af positive kræfter (z 0 - A) hedder den rigtige del Laurent-serien (Taylor-serien), og ekspansion i negative kræfter kaldes. hoveddel Laurent-serien.
Hvis inde i cirklen L 1 er der ingen entalspunkter, og funktionen er analytisk, så i (44) er det første integral lig med nul ved Cauchys sætning, og kun den korrekte del er tilbage i udvidelsen af funktionen. Negative potenser i ekspansion (45) vises kun, når analyticitet er krænket inden for den indre cirkel og tjener til at beskrive funktionen nær isolerede entalspunkter.
At konstruere Laurent-serien (45) til f(z) kan du beregne udvidelseskoefficienter ved hjælp af en generel formel eller bruge udvidelser af elementære funktioner inkluderet i f(z).
Antal udtryk ( n) af hoveddelen af Laurent-serien afhænger af typen af ental punkt: aftagelig singular spids
(n
=
0)
; i det væsentlige enestående punkt
(n 
);
poln- wow rækkefølge(n
-
endeligt nummer).
og for f(z)
=
prik z
= 0 aftageligt ental punkt, fordi der er ingen hoveddel. f(z)
=
(z
-
) = 1 -
b) For f(z)
=
prik z
= 0 -
1. ordens stang
f(z)
=
(z
-
) =
-
c) For f(z) = e 1 / z prik z = 0 - i det væsentlige enestående punkt
f(z)
=
e 1 /
z =
Hvis f(z) er analytisk i domænet D med undtagelse af m isolerede enkeltpunkter 
og | z 1 |
< |z 2 |
< . . . < |z m| , så når man udvider funktionen i potenser z hele flyet er opdelt i m+ 1 ring | z jeg |
< | z
| < | z jeg+ 1 | og Laurent-serien har et forskelligt udseende for hver ring. Når man udvider i beføjelser ( z
–
z jeg
) konvergensområdet for Laurent-serien er cirklen | z
–
z jeg
| < r, Hvor r
– afstand til nærmeste entalspunkt.
Etc. Lad os udvide funktionen f(z)
=
i Laurent-serien i magter z og ( z
-
1).
Løsning. Lad os repræsentere funktionen i formen f(z)
= - z 2
. Vi bruger formlen for summen af en geometrisk progression 
. I cirklen |z|< 1 ряд сходится и f(z)
= - z 2
(1 + z
+ z 2
+ z 3
+ z 4
+ . . .) = - z 2
- z 3
- z 4 - . . . , dvs. nedbrydningen indeholder kun korrekt En del. Lad os gå til det ydre område af cirklen |z| > 1. Lad os repræsentere funktionen i formen 
, hvor 1/| z|
< 1, и получим разложение f(z)
= z
=z
+ 1 +
Fordi udvidelse af en funktion i potenser ( z
-
1) ligner f(z)
= (z
-
1) -1
+ 2 + (z
-
1) for alle 
1.
Etc. Udvid funktionen til en Laurent-serie f(z)
=
:
a) i grader z i en cirkel | z|
< 1; b)
по степеням z
ring 1<
|z|
< 3 ; c)
по степеням (z
–
2). Løsning. Lad os dekomponere funktionen i simple brøker
=
=
+
=
.
Ud fra forholdene z
=1
EN
= -1/2 , z
=3
B
= ½.
EN) f(z)
=
½ [ 
]
= ½ [ 
-(1/3)
], med | z|<
1.
b) f(z)
= - ½ [ 
+
]
= -
(
), ved 1< |z|
< 3.
Med) f(z)
=
½ [ 
]= -
½
[ 
]
=
=
- ½
= -
, med |2 - z|
< 1
Det er en cirkel med radius 1 centreret ved z = 2 .
I nogle tilfælde kan potensrækker reduceres til et sæt geometriske progressioner, og efter dette er det let at bestemme området for deres konvergens.
Etc. Undersøg konvergensen af serien
.
. . +
+
+
+
1
+ ()
+ ()
2
+ ()
3
+ . . .
Løsning. Dette er summen af to geometriske progressioner med q 1
=
, q 2 = () . Af betingelserne for deres konvergens følger det 
< 1 ,
< 1 или |z|
> 1 , |z|
< 2 , т.е. область сходимости ряда кольцо
1 < |z|
< 2 .
Funktion nuller er argumentværdierne, hvor funktionen er lig med nul.
For at finde nullerne i funktionen givet af formlen y=f(x), skal du løse ligningen f(x)=0.
Hvis ligningen ikke har nogen rødder, har funktionen ingen nuller.
Eksempler.
1) Find nullerne for den lineære funktion y=3x+15.
For at finde funktionens nuller løses ligningen 3x+15=0.
Således er nulpunktet for funktionen y=3x+15 x= -5.
Svar: x= -5.
2) Find nullerne for den kvadratiske funktion f(x)=x²-7x+12.
For at finde funktionens nuller skal du løse andengradsligningen
Dens rødder x1=3 og x2=4 er nuller for denne funktion.
Svar: x=3; x=4.
Instruktioner
1. En funktions nul er værdien af argumentet x, hvor værdien af funktionen er lig med nul. Imidlertid kan kun de argumenter, der er inden for rammerne af definitionen af den undersøgte funktion, være nuller. Det vil sige, at der er mange værdier, hvor funktionen f(x) er nyttig. 2. Skriv den givne funktion ned og lig den med nul, sig f(x) = 2x?+5x+2 = 0. Løs den resulterende ligning og find dens reelle rødder. Rødderne af en andengradsligning beregnes med støtte til at finde diskriminanten. 2x?+5x+2 = 0;D = b?-4ac = 5a-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0,5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. Således opnås i dette tilfælde to rødder af andengradsligningen, svarende til argumenter for startfunktionen f(x). 3. Kontroller alle detekterede x-værdier for at tilhøre definitionsdomænet for den givne funktion. Find ud af OOF, for at gøre dette skal du kontrollere det indledende udtryk for tilstedeværelsen af lige rødder af formen?f (x), for tilstedeværelsen af brøker i funktionen med et argument i nævneren, for tilstedeværelsen af logaritmisk eller trigonometrisk udtryk. 4. Når du betragter en funktion med et udtryk under en rod af en lige grad, skal du tage som definitionsdomæne alle argumenterne x, hvis værdier ikke gør det radikale udtryk til et negativt tal (tværtimod gør funktionen det ikke giver mening). Kontroller, om funktionens detekterede nuller falder inden for et bestemt interval af acceptable x-værdier. 5. Nævneren af brøken kan ikke gå til nul; udeluk derfor de argumenter x, der fører til et sådant resultat. For logaritmiske størrelser skal kun de værdier af argumentet tages i betragtning, for hvilke selve udtrykket er større end nul. Nuller af funktionen, der gør det sublogaritmiske udtryk til nul eller et negativt tal, skal kasseres fra det endelige resultat. Bemærk! Når man finder rødderne til en ligning, kan der forekomme ekstra rødder. Dette er nemt at kontrollere: indsæt blot den resulterende værdi af argumentet i funktionen og sørg for, om funktionen bliver nul. Nyttige råd Af og til kommer en funktion ikke til udtryk på en åbenlys måde gennem sin argumentation, så er det let at vide, hvad denne funktion er. Et eksempel på dette er ligningen for en cirkel.
Funktion nuller Abscisseværdien, hvor værdien af funktionen er lig med nul, kaldes.
Hvis en funktion er givet ved dens ligning, så vil funktionens nuller være løsningerne til ligningen. Hvis der er givet en graf for en funktion, så er funktionens nuller de værdier, hvor grafen skærer x-aksen.
Indhold:
En funktions nul er værdien af x, hvor værdien af funktionen er nul. Typisk finder man nullerne for en funktion ved at løse en polynomialligning, såsom x 2 + 4x +3 = 0. Her er flere måder at finde en funktions nuller på.
Trin
1 Faktorisering
- 1
Skriv ligningen, så den ligner x 2 + 5x + 4. Start med et højere ordensled (såsom x 2) og arbejd derefter ned til et frit led (en konstant uden en variabel; et tal). Sæt lighedstegn mellem det resulterende udtryk med 0.
- Polynomier (ligninger) skrevet korrekt:
- x 2 + 5x + 6 = 0
- x 2 - 2x – 3 = 0
- Polynomier (ligninger) skrevet forkert:
- 5x + 6 = -x 2
- x 2 = 2x + 3
- Polynomier (ligninger) skrevet korrekt:
- 2
-en", "b", "c".
Dette vil forenkle faktoriseringsproblemet. Skriv ligningen i dette format: -en x 2 ± b x ± c = 0. Find nu -en, b, c fra ligningen givet til dig. Her er nogle eksempler:
- x 2 + 5x + 6 = 0
- -en
- b = 5
- c = 6
- x 2 - 2x – 3 = 0
- -en= 1 (der er ingen koefficient før "x", så koefficient = 1)
- b = -2
- c = -3
- x 2 + 5x + 6 = 0
- 3
Skriv alle par af koefficientfaktorer ned" Med".
Et par faktorer af et givet tal er to tal, der, når de ganges, giver det tal. Vær særlig opmærksom på negative tal. To negative tal giver et positivt tal, når de ganges. Rækkefølgen af multiplikationen er ligegyldig ("1 x 4" er det samme som "4 x 1").
- Ligning: x 2 + 5x + 6 = 0
- Multiplikatorpar 6, eller c:
- 1 x 6 = 6
- -1 x -6 = 6
- 2 x 3 = 6
- -2 x -3 = 6
- 4
Find et par faktorer, hvis sum er " b" .
Se på betydningen b og find hvilke af parrene, når de summeres, der vil give dette tal.
- b = 5
- Et multiplikatorpar, hvis sum er 5, er 2 og 3
- 2 + 3 = 5
- 5
Ud fra dette par af faktorer, lav 2 binomialer og kombiner dem til et binomial. Et binomial er produktet af binomialer af formen (x ± tal) (x ± tal). Hvordan ved du, hvilket tegn (plus eller minus) du skal vælge? Se bare på tallenes fortegn fra et par faktorer: et positivt tal er et plustegn, et negativt tal er et minustegn. Her er et par faktorer, som vi lavede binomialet med:
- (x + 2)(x + 3) = 0
- 6
Løs hvert binomium ved at flytte det ukendte til den anden side af ligningen. Sæt lighedstegn mellem hvert binomium med 0: (x + 2) = 0 og (x + 3) = 0, og løs derefter ligningen:
- (x + 2) = 0; x = -2
- (x + 3) = 0; x = -3
- 7 Dette er funktionens nuller.
2 Løsning af en andengradsligning
- 1 Den andengradsligning ser således ud:
- 2 Angiv koefficienterne i din ligning med " -en", "b", "c". Dette vil forenkle problemet med at løse ligningen. Skriv ligningen i dette format: -en x 2 ± b x ± c = 0.
- 3 Find nu -en, b, c fra ligningen givet til dig.
- 4
Løs ligningen. For at løse en andengradsligning skal du kende formlen til løsning af en sådan ligning. Alt andet er bare substitution og beregning.
- En anden mulighed for at løse en andengradsligning er et perfekt kvadrat. Nogle mennesker anser denne metode for enklere end at løse med formel.
- 5 Resultatet af at løse en andengradsligning ved hjælp af formlen vil være "nullerne" af den funktion, du leder efter. Formlen giver svaret i form af to tal, som er løsningen (nullerne) af denne funktion.
3 Graf over en andengradsligning
- 1 Tegn en graf af funktionen. Funktionen skrives som x 2 + 8x + 12 = 0.
- 2 Find x-skæringspunkterne. Disse to punkter vil være funktionens nuller.
- 3 Brug grafen som en måde at kontrollere, ikke som en måde at løse en ligning på. Hvis du plotter for at vise en funktions nuller, skal du bruge dette til at dobbelttjekke dine resultater.
- Du kan kontrollere dine beregninger ved at erstatte de fundne løsninger i den indledende ligning. Hvis ligningen er lig nul, så er løsningerne korrekte.
Den matematiske repræsentation af en funktion viser tydeligt, hvordan en størrelse fuldstændig bestemmer værdien af en anden størrelse. Traditionelt betragtes numeriske funktioner, der tildeler et nummer til et andet. En funktions nul er normalt værdien af argumentet, hvor funktionen bliver nul.
Instruktioner
1. For at detektere en funktions nuller skal du sætte lighedstegn mellem dens højre side og nul og løse den resulterende ligning. Lad os forestille os, at du får en funktion f(x)=x-5.
2. For at finde denne funktions nuller, lad os tage og sidestille dens højre side med nul: x-5=0.
3. Efter at have løst denne ligning, finder vi, at x=5 og denne værdi af argumentet vil være nul for funktionen. Det vil sige, at når argumentværdien er 5, bliver funktionen f(x) nul.
Under udsigten funktioner i matematik forstår vi sammenhængen mellem elementerne i mængder. For at sige det mere korrekt er dette en "lov", ifølge hvilken hele elementet i et sæt (kaldet definitionsdomænet) er forbundet med et bestemt element i et andet sæt (kaldet værdidomænet).
Du får brug for
- Kendskab til algebra og matematisk gennemgang.
Instruktioner
1. Værdier funktioner Dette er et bestemt område, hvorfra en funktion kan tage værdier. Lad os sige rækkevidden af værdier funktioner f(x)=|x| fra 0 til uendelig. For at opdage betyder funktioner på et bestemt tidspunkt skal du erstatte argumentet funktioner dets numeriske ækvivalent, vil det resulterende tal være betyder m funktioner. Lad funktionen f(x)=|x| – 10 + 4x. Lad os finde ud af det betyder funktioner ved punkt x=-2. Lad os erstatte x med tallet -2: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16. Det er betyder funktioner ved punkt -2 er lig med -16.
Bemærk!
Før du leder efter værdien af en funktion på et punkt, skal du sikre dig, at den er inden for funktionens domæne.
Nyttige råd
En lignende metode gør det muligt at opdage betydningen af funktionen af flere argumenter. Forskellen er, at du i stedet for ét tal skal erstatte flere - alt efter antallet af argumenter for funktionen.
Funktionen repræsenterer den etablerede forbindelse mellem variablen y og variablen x. Desuden svarer alle værdierne af x, kaldet argumentet, til den ekstraordinære værdi af y - funktionen. I grafisk form er en funktion afbildet på et kartesisk koordinatsystem i form af en graf. Skæringspunkterne for grafen med abscisseaksen, hvorpå argumenterne x er plottet, kaldes funktionen nuller. At finde acceptable nuller er en af opgaverne med at finde en given funktion. I dette tilfælde tages der hensyn til alle tilladte værdier af den uafhængige variabel x, der danner definitionsdomænet for funktionen (DOF).
Instruktioner
1. En funktions nul er værdien af argumentet x, hvor værdien af funktionen er lig med nul. Imidlertid kan kun de argumenter, der er inden for rammerne af definitionen af den undersøgte funktion, være nuller. Det vil sige, at der er mange værdier, hvor funktionen f(x) er nyttig.
2. Skriv den givne funktion ned og lig den med nul, sig f(x) = 2x?+5x+2 = 0. Løs den resulterende ligning og find dens reelle rødder. Rødderne af en andengradsligning beregnes med støtte til at finde diskriminanten. 2x?+5x+2 = 0;D = b?-4ac = 5a-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0,5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. Således opnås i dette tilfælde to rødder af andengradsligningen, svarende til argumenter for startfunktionen f(x).
3. Kontroller alle detekterede x-værdier for at tilhøre definitionsdomænet for den givne funktion. Find ud af OOF, for at gøre dette skal du kontrollere det indledende udtryk for tilstedeværelsen af lige rødder af formen?f (x), for tilstedeværelsen af brøker i funktionen med et argument i nævneren, for tilstedeværelsen af logaritmisk eller trigonometrisk udtryk.
4. Når du betragter en funktion med et udtryk under en rod af en lige grad, skal du tage som definitionsdomæne alle argumenterne x, hvis værdier ikke gør det radikale udtryk til et negativt tal (tværtimod gør funktionen det ikke giver mening). Kontroller, om funktionens detekterede nuller falder inden for et bestemt interval af acceptable x-værdier.
5. Nævneren af brøken kan ikke gå til nul; udeluk derfor de argumenter x, der fører til et sådant resultat. For logaritmiske størrelser skal kun de værdier af argumentet tages i betragtning, for hvilke selve udtrykket er større end nul. Nuller af funktionen, der gør det sublogaritmiske udtryk til nul eller et negativt tal, skal kasseres fra det endelige resultat.
Bemærk!
Når man finder rødderne til en ligning, kan der forekomme ekstra rødder. Dette er nemt at kontrollere: indsæt blot den resulterende værdi af argumentet i funktionen og sørg for, om funktionen bliver nul.
Nyttige råd
Af og til kommer en funktion ikke til udtryk på en åbenlys måde gennem sin argumentation, så er det let at vide, hvad denne funktion er. Et eksempel på dette er ligningen for en cirkel.
I hvilken den tager værdien nul. For eksempel for en funktion givet af formlen
Er nul fordi
.En funktions nuller kaldes også funktionens rødder.
Konceptet med nuller af en funktion kan overvejes for alle funktioner, hvis værdiområde indeholder nul eller nulelementet i den tilsvarende algebraiske struktur.
For en funktion af en reel variabel er nuller de værdier, hvor funktionens graf skærer x-aksen.
At finde en funktions nuller kræver ofte brug af numeriske metoder (f.eks. Newtons metode, gradientmetoder).
Et af de uløste matematiske problemer er at finde nullerne i Riemann zeta-funktionen.
Roden til et polynomium
se også
Litteratur
Wikimedia Foundation. 2010.
Se, hvad "Function Zero" er i andre ordbøger:
Punktet hvor en given funktion f(z) forsvinder; således, N. f. f (z) er det samme som rødderne af ligningen f (z) = 0. For eksempel er punkterne 0, π, π, 2π, 2π,... nulpunkter for funktionen sinz. Nullpunkter for en analytisk funktion (Se Analytisk... ...
Nul funktion, nul funktion... Retskrivningsordbog-opslagsbog
Dette udtryk har andre betydninger, se Nul. Indholdet af denne artikel skal flyttes til artiklen "Funktion Null". Du kan hjælpe projektet ved at kombinere artikler. Hvis det er nødvendigt at diskutere gennemførligheden af sammenlægning, udskift denne ... Wikipedia
Eller C-streng (fra navnet på C-sproget) eller ASCIZ-streng (fra navnet på assembler-direktivet.asciz) en metode til at repræsentere strenge i programmeringssprog, hvor der, i stedet for at introducere en speciel strengtype, et array af tegn bruges, og til sidst ... ... Wikipedia
I kvantefeltteorien er det accepterede (jargon) navn for egenskaben ved at forsvinde renormaliseringsfaktoren for koblingskonstanten, hvor g0 er den nøgne koblingskonstant fra interaktionen Lagrangian, fysisk. koblingskonstant klædt ud som interaktion. Ligestilling Z... Fysisk encyklopædi
Nul mutation n-allel- Nul mutation, n. allel * nulmutation, n. allel * nulmutation eller n. allel eller tavs a. en mutation, der fører til fuldstændigt tab af funktion i den DNA-sekvens, hvori den opstod... Genetik. encyklopædisk ordbog
Udsagnet i sandsynlighedsteorien om, at enhver hændelse (den såkaldte restbegivenhed), hvis forekomst kun bestemmes af vilkårligt fjerne elementer i en sekvens af uafhængige tilfældige hændelser eller tilfældige variabler, har... ... Matematisk encyklopædi
1) Et tal, der har den egenskab, at ethvert (reelt eller komplekst) tal ikke ændres, når det føjes til det. Betegnes med symbolet 0. Produktet af ethvert tal med N. er lig med N.: Hvis produktet af to tal er lig N., så er en af faktorerne ... Matematisk encyklopædi
Funktioner defineret af relationer mellem uafhængige variable, der ikke er løst i forhold til sidstnævnte; disse relationer er en af måderne at specificere en funktion på. For eksempel definerer relationen x2 + y2 1 = 0 N.f. ... Store sovjetiske encyklopædi
Mættet af disse og kun de punkter, hvor i intet naboskab af den generaliserede funktion forsvinder. Den generaliserede funktion af forsvinder i det åbne sæt, hvis for alle. Ved at bruge enhedsudvidelsen er det vist, at hvis en generaliseret funktion ... Matematisk encyklopædi
