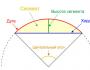
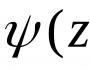Hvordan finder man nullerne for en funktion i en brøk. Sådan finder du nuller for en funktion

Funktion nuller er argumentværdierne, hvor funktionen er lig med nul.

For at finde nullerne i funktionen givet af formlen y=f(x), skal du løse ligningen f(x)=0.

Hvis ligningen ikke har nogen rødder, har funktionen ingen nuller.

Eksempler.

1) Find nullerne for den lineære funktion y=3x+15.

For at finde funktionens nuller løses ligningen 3x+15=0.

Således er nulpunktet for funktionen y=3x+15 x= -5.

Svar: x= -5.

2) Find nullerne for den kvadratiske funktion f(x)=x²-7x+12.

For at finde funktionens nuller skal du løse andengradsligningen

Dens rødder x1=3 og x2=4 er nuller for denne funktion.

Svar: x=3; x=4.

Instruktioner

1. En funktions nul er værdien af ​​argumentet x, hvor værdien af ​​funktionen er lig med nul. Imidlertid kan kun de argumenter, der er inden for rammerne af definitionen af ​​den undersøgte funktion, være nuller. Det vil sige, at der er mange værdier, hvor funktionen f(x) er nyttig. 2. Skriv den givne funktion ned og lig den med nul, sig f(x) = 2x?+5x+2 = 0. Løs den resulterende ligning og find dens reelle rødder. Rødderne af en andengradsligning beregnes med støtte til at finde diskriminanten. 2x?+5x+2 = 0;D = b?-4ac = 5a-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0,5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. Således opnås i dette tilfælde to rødder af andengradsligningen, svarende til argumenter for startfunktionen f(x). 3. Kontroller alle detekterede x-værdier for at tilhøre definitionsdomænet for den givne funktion. Find ud af OOF, for at gøre dette skal du kontrollere det indledende udtryk for tilstedeværelsen af ​​lige rødder af formen?f (x), for tilstedeværelsen af ​​brøker i funktionen med et argument i nævneren, for tilstedeværelsen af ​​logaritmisk eller trigonometrisk udtryk. 4. Når du betragter en funktion med et udtryk under en rod af en lige grad, skal du tage som definitionsdomæne alle argumenterne x, hvis værdier ikke gør det radikale udtryk til et negativt tal (tværtimod gør funktionen det ikke giver mening). Kontroller, om funktionens detekterede nuller falder inden for et bestemt interval af acceptable x-værdier. 5. Nævneren af ​​brøken kan ikke gå til nul; udeluk derfor de argumenter x, der fører til et sådant resultat. For logaritmiske størrelser skal kun de værdier af argumentet tages i betragtning, for hvilke selve udtrykket er større end nul. Nuller af funktionen, der gør det sublogaritmiske udtryk til nul eller et negativt tal, skal kasseres fra det endelige resultat. Bemærk! Når man finder rødderne til en ligning, kan der forekomme ekstra rødder. Dette er nemt at kontrollere: indsæt blot den resulterende værdi af argumentet i funktionen og sørg for, om funktionen bliver nul. Nyttige råd Af og til kommer en funktion ikke til udtryk på en åbenlys måde gennem sin argumentation, så er det let at vide, hvad denne funktion er. Et eksempel på dette er ligningen for en cirkel.

Funktion nuller Abscisseværdien, hvor værdien af ​​funktionen er lig med nul, kaldes.

Hvis en funktion er givet ved dens ligning, så vil funktionens nuller være løsningerne til ligningen. Hvis der er givet en graf for en funktion, så er funktionens nuller de værdier, hvor grafen skærer x-aksen.

Fungere er et af de vigtigste matematiske begreber. Funktion - variabel afhængighed på fra variabel x, hvis hver værdi x matcher en enkelt værdi på. Variabel x kaldet den uafhængige variabel eller argument. Variabel på kaldet den afhængige variabel. Alle værdier af den uafhængige variabel (variabel x) danner funktionens definitionsdomæne. Alle værdier, som den afhængige variabel tager (variabel y), danner rækken af ​​værdier for funktionen.

Funktionsgraf kald sættet af alle punkter i koordinatplanet, hvis abscisser er lig med værdierne af argumentet, og ordinaterne er lig med de tilsvarende værdier af funktionen, det vil sige værdierne af variable plottes langs abscisseaksen x, og værdierne af variablen er plottet langs ordinataksen y. For at tegne en funktion skal du kende funktionens egenskaber. Funktionens vigtigste egenskaber vil blive diskuteret nedenfor!

For at bygge en graf af en funktion, anbefaler vi at bruge vores program - Graffunktioner online. Hvis du har spørgsmål, mens du studerer materialet på denne side, kan du altid stille dem på vores forum. Også på forummet vil de hjælpe dig med at løse problemer i matematik, kemi, geometri, sandsynlighedsteori og mange andre fag!

Grundlæggende egenskaber ved funktioner.

1) Funktionsdomæne og funktionsområde.

Domænet for en funktion er sættet af alle gyldige gyldige argumentværdier x(variabel x), for hvilken funktionen y = f(x) fast besluttet.
Rækkevidden af ​​en funktion er mængden af ​​alle reelle værdier y, som funktionen accepterer.

I elementær matematik studeres funktioner kun på mængden af ​​reelle tal.

2) Funktionsnuller.

Funktion nul er værdien af ​​argumentet, hvor værdien af ​​funktionen er lig med nul.

3) Intervaller af konstant fortegn for en funktion.

Intervaller med konstant fortegn for en funktion er sæt af argumentværdier, hvor funktionsværdierne kun er positive eller kun negative.

4) Monotonicitet af funktionen.

En stigende funktion (i et bestemt interval) er en funktion, hvor en større værdi af argumentet fra dette interval svarer til en større værdi af funktionen.

En faldende funktion (i et bestemt interval) er en funktion, hvor en større værdi af argumentet fra dette interval svarer til en mindre værdi af funktionen.

5) Lige (ulige) funktion.

En lige funktion er en funktion, hvis definitionsdomæne er symmetrisk med hensyn til oprindelsen og for evt x fra definitionsdomænet ligheden f(-x) = f(x). Grafen for en lige funktion er symmetrisk omkring ordinaten.

En ulige funktion er en funktion, hvis definitionsdomæne er symmetrisk med hensyn til oprindelsen og for evt. x fra definitionsdomænet er ligheden sand f(-x) = - f(x). Grafen for en ulige funktion er symmetrisk om oprindelsen.

6) Begrænsede og ubegrænsede funktioner.

En funktion kaldes bundet, hvis der er et positivt tal M, således at |f(x)| ≤ M for alle værdier af x. Hvis et sådant nummer ikke findes, så er funktionen ubegrænset.

7) Funktionens periodicitet.

En funktion f(x) er periodisk, hvis der er et ikke-nul tal T, således at for enhver x f(x+T) = f(x). Dette mindste tal kaldes funktionens periode. Alle trigonometriske funktioner er periodiske. (Trigonometriske formler).

Efter at have studeret disse egenskaber for en funktion, kan du nemt udforske funktionen, og ved at bruge funktionens egenskaber kan du bygge en graf over funktionen. Se også på materialet om sandhedstabel, multiplikationstabel, periodisk tabel, afledt tabel og tabel over integraler.

Funktion nuller

Hvad er funktionsnuller? Hvordan bestemmer man nullerne for en funktion analytisk og grafisk?

Funktion nuller- disse er argumentværdierne, hvor funktionen er lig med nul.

For at finde nullerne i funktionen givet af formlen y=f(x), skal du løse ligningen f(x)=0.

Hvis ligningen ikke har nogen rødder, har funktionen ingen nuller.

1) Find nullerne for den lineære funktion y=3x+15.

For at finde funktionens nuller løses ligningen 3x+15 =0.

Funktionens nulpunkt er således y=3x+15 - x= -5.

2) Find nullerne for den kvadratiske funktion f(x)=x²-7x+12.

For at finde funktionens nuller skal du løse andengradsligningen

Dens rødder x1=3 og x2=4 er nuller for denne funktion.

3) Find funktionens nuller

En brøk giver mening, hvis nævneren ikke er nul. Derfor x²-1≠0, x² ≠ 1, x ≠±1. Det vil sige definitionsdomænet for en given funktion (DO)

Af rødderne af ligningen x²+5x+4=0 x1=-1 x2=-4 er kun x=-4 inkluderet i definitionsdomænet.

For at finde nulpunkterne for en funktion givet grafisk, skal du finde skæringspunkterne for funktionsgrafen med abscisseaksen.

Hvis grafen ikke skærer Ox-aksen, har funktionen ingen nuller.

funktionen, hvis graf er vist på figuren, har fire nuller -

I algebra opstår problemet med at finde en funktions nuller både som en selvstændig opgave og ved løsning af andre problemer, for eksempel ved undersøgelse af en funktion, løsning af uligheder osv.

www.algebraclass.ru

Reglen for funktion nuller

Grundlæggende begreber og egenskaber ved funktioner

Herske (lov om) korrespondance. Monotonisk funktion .

Begrænsede og ubegrænsede funktioner. Kontinuerlig og

diskontinuerlige funktioner . Lige og ulige funktioner.

Periodisk funktion. Funktionens periode.

Funktion nuller . Asymptote .

Definitionsdomænet og rækken af ​​værdier for en funktion. I elementær matematik studeres funktioner kun på mængden af ​​reelle tal R . Det betyder, at funktionsargumentet kun kan tage de reelle værdier, som funktionen er defineret for, dvs. den accepterer også kun reelle værdier. En masse x alle gyldige gyldige argumentværdier x, hvortil funktionen y = f (x) er defineret, kaldet funktionens domæne. En masse Y alle reelle værdier y, som funktionen accepterer, kaldes funktionsområde. Nu kan vi give en mere præcis definition af funktionen: Herske (lov) om korrespondance mellem sæt x Og Y , efter hvilken for hvert element fra sættet x du kan finde ét og kun ét element fra sættet Y, kaldes en funktion .

Af denne definition følger det, at en funktion betragtes som defineret, hvis:

— definitionsdomænet for funktionen er specificeret x ;

— funktionsområdet er angivet Y ;

— korrespondancereglen (loven) er kendt, og sådan at for hver

argumentværdi, kan der kun findes én funktionsværdi.

Dette krav om funktionens unikke karakter er obligatorisk.

Monotonisk funktion. Hvis for to værdier af argumentet x 1 og x 2 i betingelsen x 2 > x 1 følger f (x 2) > f (x 1), derefter funktionen f (x) Hedder stigende; hvis for nogen x 1 og x 2 i betingelsen x 2 > x 1 følger f (x 2)

Funktionen vist i fig. 3 er begrænset, men ikke monoton. Funktionen i fig. 4 er lige det modsatte, monoton, men ubegrænset. (Forklar dette venligst!).

Kontinuerlige og diskontinuerlige funktioner. Fungere y = f (x) Hedder sammenhængende på punktet x = -en, hvis:

1) funktionen er defineret hvornår x = -en, dvs. f (-en) eksisterer;

2) findes begrænset grænse lim f (x) ;

Hvis mindst en af ​​disse betingelser ikke er opfyldt, kaldes funktionen eksplosiv på punktet x = -en .

Hvis funktionen er kontinuerlig under alle sammen punkter i dets definitionsdomæne, så hedder det kontinuerlig funktion.

Lige og ulige funktioner. Hvis for nogen x fra definitionsdomænet for funktionen gælder følgende: f (— x) = f (x), så kaldes funktionen også selvom; hvis det sker: f (— x) = — f (x), så kaldes funktionen ulige. Graf over en lige funktion symmetrisk om Y-aksen(Fig. 5), en graf over en ulige funktion Sim metrisk med hensyn til oprindelsen(Fig. 6).

Periodisk funktion. Fungere f (x) — periodisk, hvis sådan noget eksisterer ikke-nul nummer T hvorfor nogen x fra definitionsdomænet for funktionen gælder følgende: f (x + T) = f (x). Det her mindst nummeret ringes op funktionsperiode. Alle trigonometriske funktioner er periodiske.

Eksempel 1. Bevis den synd x har en periode på 2.

Løsning: Vi ved, at synd ( x+ 2 n) = synd x, Hvor n= 0, ± 1, ± 2, …

Derfor tilføjes 2 n ikke til sinusargumentet

ændrer dens værdi e. Er der et andet nummer med dette

Lad os lade som om P– sådan et tal, dvs. lighed:

gyldig for enhver værdi x. Men så har det

sted og kl x= / 2, dvs.

synd(/2 + P) = synd / 2 = 1.

Men ifølge reduktionsformlen synd (/ 2 + P) = cos P. Derefter

af de to sidste ligheder følger, at cos P= 1, men vi

vi ved, at dette kun er sandt, når P = 2 n. Siden den mindste

ikke-nul tal fra 2 n er 2, så dette tal

og der er en periode synd x. Det kan bevises på samme måde, at 2

er også en periode for cos x .

Bevis, at funktionerne tan x og barneseng x har menstruation.

Eksempel 2. Hvilket tal er perioden for funktionen sin 2 x ?

Løsning: Overvej synd 2 x= synd (2 x+ 2 n) = synd [ 2 ( x + n) ] .

Det ser vi tilføje n til argumentationen x, ændres ikke

funktionsværdi. Mindste ikke-nul tal

fra n er , så dette er perioden synd 2 x .

Funktion nuller. Argumentværdien, hvor funktionen er lig med 0, kaldes nul ( root) funktion. En funktion kan have flere nuller. For eksempel funktionen y = x (x + 1) (x- 3) har tre nuller: x = 0, x = — 1, x= 3. Geometrisk null funktion – dette er abscissen af ​​funktionsgrafens skæringspunkt med aksen x .

Figur 7 viser en graf over en funktion med nuller: x = -en , x = b Og x = c .

Asymptote. Hvis grafen for en funktion uendeligt nærmer sig en bestemt linje, når den bevæger sig væk fra origo, så kaldes denne linje asymptote.

Emne 6. "Intervalmetode."

Hvis f (x) f (x 0) for x x 0, kaldes funktionen f (x). kontinuerlig ved punkt x 0.

Hvis en funktion er kontinuert på hvert punkt i et eller andet interval I, kaldes den kontinuerlig i intervallet I (intervallet I kaldes kontinuitetsinterval for funktionen). Grafen for en funktion på dette interval er en kontinuerlig linje, som de siger kan "trækkes uden at løfte blyanten fra papiret."

Ejendom af kontinuerlige funktioner.

Hvis funktionen f på intervallet (a ; b) er kontinuert og ikke forsvinder, så bevarer den et konstant fortegn på dette interval.

En metode til at løse uligheder med én variabel, intervalmetoden, er baseret på denne egenskab. Lad funktionen f(x) være kontinuert på intervallet I og forsvinde ved et endeligt antal punkter i dette interval. Ved egenskaben for kontinuerte funktioner deler disse punkter I i intervaller, i hvilke den kontinuerte funktion f(x) c hver bevarer et konstant fortegn. For at bestemme dette tegn er det nok at beregne værdien af ​​funktionen f(x) på et hvilket som helst punkt fra hvert sådant interval. Ud fra dette får vi følgende algoritme til løsning af uligheder ved hjælp af intervalmetoden.

Intervalmetode for uligheder i formen

Interval metode. Gennemsnitligt niveau.

Vil du teste din styrke og finde ud af resultatet af, hvor klar du er til Unified State-eksamenen eller Unified State-eksamenen?

Lineær funktion

En funktion af formen kaldes lineær. Lad os tage en funktion som eksempel. Den er positiv ved 3″> og negativ ved. Prikken er nulpunktet for funktionen (). Lad os vise tegnene for denne funktion på talaksen:

Vi siger, at "funktionen skifter fortegn, når den passerer gennem punktet".

Det kan ses, at funktionens fortegn svarer til funktionsgrafens position: Hvis grafen er over aksen, er tegnet " ", hvis det er under " ".

Hvis vi generaliserer den resulterende regel til en vilkårlig lineær funktion, får vi følgende algoritme:

Kvadratisk funktion

Jeg håber, du husker, hvordan man løser kvadratiske uligheder? Hvis ikke, så læs emnet "Kvadratiske uligheder." Lad mig minde dig om den generelle form for en kvadratisk funktion: .

Lad os nu huske, hvilke tegn den kvadratiske funktion tager. Dens graf er en parabel, og funktionen tager tegnet " " for dem, hvor parablen er over aksen, og " " - hvis parablen er under aksen:

Hvis en funktion har nuller (værdier ved hvilke), skærer parablen aksen i to punkter - rødderne af den tilsvarende andengradsligning. Således er aksen opdelt i tre intervaller, og funktionens fortegn skifter skiftevis, når den passerer gennem hver rod.

Er det muligt på en eller anden måde at bestemme tegnene uden at tegne en parabel hver gang?

Husk, at et kvadratisk trinomium kan faktoriseres:

Lad os markere rødderne på aksen:

Vi husker, at tegnet for en funktion kun kan ændre sig, når det passerer gennem roden. Lad os bruge denne kendsgerning: for hvert af de tre intervaller, som aksen er opdelt i med rødder, er det nok at bestemme tegnet for funktionen på kun et vilkårligt valgt punkt: ved de resterende punkter i intervallet vil tegnet være det samme .

I vores eksempel: ved 3″> er begge udtryk i parentes positive (erstat f.eks.: 0″>). Vi sætter et " "-tegn på aksen:

Nå, når (for eksempel erstatning) begge parenteser er negative, hvilket betyder, at produktet er positivt:

Det er, hvad det er interval metode: ved at kende tegnene på faktorerne på hvert interval, bestemmer vi tegnet for hele produktet.

Lad os også overveje tilfælde, hvor funktionen ikke har nogen nuller eller kun én.

Hvis de ikke er der, så er der ingen rødder. Det betyder, at der ikke vil være nogen "passering gennem roden". Det betyder, at funktionen kun tager ét fortegn på hele tallinjen. Det kan let bestemmes ved at erstatte det med en funktion.

Hvis der kun er én rod, rører parablen aksen, så funktionens fortegn ændres ikke, når den passerer gennem roden. Hvilken regel kan vi finde på i sådanne situationer?

Hvis du faktoriserer en sådan funktion, får du to identiske faktorer:

Og ethvert kvadratisk udtryk er ikke-negativt! Derfor ændres funktionens fortegn ikke. I sådanne tilfælde vil vi fremhæve roden, når vi passerer gennem hvilken tegnet ikke ændrer sig, ved at cirkle den med en firkant:

Vi vil kalde en sådan rod multipler.

Intervalmetode i uligheder

Nu kan enhver kvadratisk ulighed løses uden at tegne en parabel. Det er nok bare at placere fortegnene for den kvadratiske funktion på aksen og vælge intervaller afhængigt af tegnet på uligheden. For eksempel:

Lad os måle rødderne på aksen og placere tegnene:

Vi har brug for den del af aksen med tegnet " "; da uligheden ikke er streng, er selve rødderne også inkluderet i løsningen:

Overvej nu en rationel ulighed - en ulighed, hvis begge sider er rationelle udtryk (se "Rationelle ligninger").

Eksempel:

Alle faktorer undtagen én er "lineære" her, det vil sige, at de kun indeholder en variabel i første potens. Vi har brug for sådanne lineære faktorer for at anvende intervalmetoden - tegnet ændres, når det passerer gennem deres rødder. Men multiplikatoren har slet ingen rødder. Det betyder, at det altid er positivt (tjek selv dette), og påvirker derfor ikke tegnet på hele uligheden. Det betyder, at vi kan dividere venstre og højre side af uligheden med den, og dermed slippe af med den:

Nu er alt det samme, som det var med kvadratiske uligheder: vi bestemmer på hvilke punkter hver af faktorerne bliver nul, markerer disse punkter på aksen og arrangerer tegnene. Jeg vil gerne henlede din opmærksomhed på en meget vigtig kendsgerning:

I tilfælde af et lige tal gør vi det samme som før: vi cirkler punktet med en firkant og ændrer ikke tegnet, når vi passerer gennem roden. Men i tilfælde af et ulige tal, gælder denne regel ikke: tegnet vil stadig ændre sig, når det passerer gennem roden. Derfor gør vi ikke noget yderligere med sådan en rod, som om det ikke var et multiplum. Ovenstående regler gælder for alle lige og ulige potenser.

Hvad skal vi skrive i svaret?

Hvis vekslen af ​​tegn overtrædes, skal du være meget forsigtig, for hvis uligheden ikke er streng, bør svaret bl.a. alle skraverede punkter. Men nogle af dem står ofte fra hinanden, det vil sige, at de ikke er inkluderet i det skraverede område. I dette tilfælde tilføjer vi dem til svaret som isolerede punkter (i krøllede seler):

Eksempler (bestem selv):

Svar:

1. Hvis det blandt faktorerne er enkelt, er det en rod, fordi det kan repræsenteres som.
   .

2. Lad os finde funktionens nuller.

f(x) ved x .

Besvar f(x) ved x .

2) x2 >-4x-5;

x 2 +4x +5>0;

Lad f(x)=x 2 +4x +5, så lad os finde sådanne x, for hvilke f(x)>0,

D=-4 Ingen nuller.

4. Ulighedssystemer. Uligheder og ulighedssystemer med to variable

1) Sættet af løsninger til et system af uligheder er skæringspunktet mellem sæt af løsninger til de uligheder, der er inkluderet i det.

2) Mængden af ​​løsninger til uligheden f(x;y)>0 kan afbildes grafisk på koordinatplanet. Typisk deler linjen defineret af ligningen f(x;y) = 0 planet i 2 dele, hvoraf den ene er løsningen på uligheden. For at bestemme hvilken del, skal du erstatte koordinaterne for et vilkårligt punkt M(x0;y0), der ikke ligger på linjen f(x;y)=0 i uligheden. Hvis f(x0;y0) > 0, så er løsningen til uligheden den del af planet, der indeholder punktet M0. hvis f(x0;y0)<0, то другая часть плоскости.

3) Sættet af løsninger til et system af uligheder er skæringspunktet mellem sæt af løsninger til de uligheder der er inkluderet i det. Lad for eksempel få et system af uligheder:

.

For den første ulighed er løsningssættet en cirkel med radius 2 og centreret ved origo, og for den anden er det et halvt plan placeret over den rette linje 2x+3y=0. Sættet af løsninger af dette system er skæringspunktet mellem disse sæt, dvs. halvcirkel.

4) Eksempel. Løs ulighedssystemet:

Løsningen på den 1. ulighed er mængden, den 2. er mængden (2;7) og den tredje er mængden.

Skæringspunktet mellem disse mængder er intervallet (2;3], som er mængden af ​​løsninger til systemet af uligheder.

5. Løsning af rationelle uligheder ved hjælp af intervalmetoden

Metoden til intervaller er baseret på følgende egenskab for binomialet (x-a): punktet x = α deler talaksen i to dele - til højre for punktet α binomialet (x-α)>0, og til venstre for punktet α (x-α)<0.

Lad det være nødvendigt at løse uligheden (x-α 1)(x-α 2)...(x-α n)>0, hvor α 1, α 2 ...α n-1, α n er fikserede tal, blandt hvilke der ikke er lig, og sådan at α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 ved brug af intervalmetoden fortsæt som følger: tallene α 1, α 2 ...α n-1, α n er plottet på den numeriske akse; i intervallet til højre for den største af dem, dvs. tal α n, sæt et plustegn, i intervallet efter det fra højre mod venstre indsæt et minustegn, så et plustegn, så et minustegn osv. Så vil mængden af ​​alle løsninger til uligheden (x-α 1)(x‑α 2)...(x-α n)>0 være foreningen af ​​alle intervaller, hvori plustegnet er placeret, og mængden af løsninger til uligheden (x-α 1 )(x-α 2)...(x-α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».

1) Løsning af rationelle uligheder (dvs. uligheder i formen P(x) Q(x) hvor er polynomier) er baseret på følgende egenskab for en kontinuert funktion: hvis en kontinuert funktion forsvinder i punkterne x1 og x2 (x1; x2) og ikke har andre rødder mellem disse punkter, så i intervaller (x1; x2) beholder funktionen sit fortegn.

For at finde intervaller med konstant fortegn for funktionen y=f(x) på tallinjen skal du derfor markere alle de punkter, hvor funktionen f(x) forsvinder eller lider af en diskontinuitet. Disse punkter opdeler tallinjen i flere intervaller, inden for hver af dem er funktionen f(x) kontinuert og ikke forsvinder, dvs. gemmer skiltet. For at bestemme dette tegn er det nok at finde tegnet for funktionen på et hvilket som helst punkt i tallinjens betragtede interval.

2) For at bestemme intervaller af konstant fortegn for en rationel funktion, dvs. For at løse en rationel ulighed markerer vi på tallinjen rødderne af tælleren og rødderne til nævneren, som også er rødderne og brudpunkterne til den rationelle funktion.

Løsning af uligheder ved hjælp af intervalmetoden

3. < 20.

Løsning. Rækken af ​​acceptable værdier bestemmes af systemet af uligheder:

For funktionen f(x) = – 20. Find f(x):

hvoraf x = 29 og x = 13.

f(30) = – 20 = 0,3 > 0,

f(5) = – 1 – 20 = – 10< 0.

Svar: . Grundlæggende metoder til løsning af rationelle ligninger. 1) Den enkleste: løses ved de sædvanlige forenklinger - reduktion til en fællesnævner, reduktion af lignende udtryk, og så videre. Kvadratiske ligninger ax2 + bx + c = 0 løses ved...

X ændres på intervallet (0,1), og falder på intervallet = ½ [
-(1/3)
], med | z|< 1.

b) f(z) = - ½ [
+
] = - (
), ved 1< |z| < 3.

Med) f(z) = ½ [
]= - ½ [
] =

= - ½ = -
, med |2 - z| < 1

Det er en cirkel med radius 1 centreret ved z = 2 .

I nogle tilfælde kan potensrækker reduceres til et sæt geometriske progressioner, og efter dette er det let at bestemme området for deres konvergens.

Etc. Undersøg konvergensen af ​​serien

. . . + + + + 1 + () + () 2 + () 3 + . . .

Løsning. Dette er summen af ​​to geometriske progressioner med q 1 = , q 2 = () . Af betingelserne for deres konvergens følger det < 1 , < 1 или |z| > 1 , |z| < 2 , т.е. область сходимости ряда кольцо 1 < |z| < 2 .