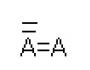Ֆրակտալներ. Կոխի կորը Ֆրակտալ բազմությունների ստացման ընթացակարգեր
Կոխի կորի երեք օրինակները, որոնք կառուցված են (իրենց կետերը դեպի դուրս) կանոնավոր եռանկյունու կողմերի վրա, կազմում են անսահման երկարությամբ փակ կոր, որը կոչվում է. Քոչի ձյան փաթիլը.
Այս ցուցանիշը գիտնականների կողմից ուսումնասիրված առաջին ֆրակտալներից է: Այն գալիս է երեք օրինակից Կոխի կորը, որն առաջին անգամ հայտնվեց շվեդ մաթեմատիկոս Հելգե ֆոն Կոխի աշխատության մեջ 1904 թվականին։ Այս կորը հորինվել է որպես շարունակական գծի օրինակ, որը չի կարող շոշափելի լինել որևէ կետի: Այս հատկությամբ գծերը հայտնի էին նախկինում (Կարլ Վայերշտրասը կառուցել է իր օրինակը դեռևս 1872 թվականին), բայց Կոխի կորը ուշագրավ է իր ձևավորման պարզությամբ: Պատահական չէ, որ նրա հոդվածը կոչվում է «Առանց շոշափողների շարունակական կորի մասին, որն առաջանում է տարրական երկրաչափությունից»։
Գծանկարը և անիմացիան հիանալի կերպով ցույց են տալիս, թե ինչպես է Քոչի կորը կառուցվում քայլ առ քայլ: Առաջին կրկնությունը պարզապես սկզբնական հատվածն է: Այնուհետև այն բաժանում են երեք հավասար մասերի, կենտրոնականը լրացնում են՝ ձևավորելով կանոնավոր եռանկյունի և հետո դուրս շպրտվում։ Արդյունքը երկրորդ կրկնությունն է՝ չորս հատվածից բաղկացած կոտրված գիծ: Նրանցից յուրաքանչյուրի նկատմամբ կիրառվում է նույն գործողությունը, և ստացվում է շինարարության չորրորդ քայլը։ Շարունակելով նույն ոգով, դուք կարող եք ավելի ու ավելի շատ նոր գծեր ստանալ (բոլորը կլինեն կոտրված գծեր): Իսկ այն, ինչ տեղի է ունենում սահմանի մեջ (սա արդեն երևակայական օբյեկտ կլինի) կոչվում է Կոխի կոր։
Կոխի կորի հիմնական հատկությունները1. Այն շարունակական է, բայց ոչ մի տեղ տարբերակելի։ Կոպիտ ասած՝ հենց դրա համար է այն հորինվել՝ որպես այս տեսակի մաթեմատիկական «ֆրիքսների» օրինակ։
2. Ունի անսահման երկարություն։ Թող սկզբնական հատվածի երկարությունը հավասար լինի 1-ի: Շինարարության յուրաքանչյուր քայլում մենք փոխարինում ենք գիծը կազմող հատվածներից յուրաքանչյուրը կոտրված գծով, որը 4/3 անգամ ավելի է: Սա նշանակում է, որ ամբողջ կոտրված գծի երկարությունը յուրաքանչյուր քայլում բազմապատկվում է 4/3-ով՝ թվով գծի երկարությունը։ nհավասար է (4/3) n-1. Հետևաբար, սահմանային գիծը այլընտրանք չունի, քան անսահման երկար լինելը:

3. Կոխի ձյան փաթիլը սահմանափակում է վերջավոր տարածքը։ Եվ դա չնայած այն բանին, որ նրա պարագիծն անսահման է։ Այս հատկությունը կարող է պարադոքսալ թվալ, բայց դա ակնհայտ է. ձյան փաթիլն ամբողջությամբ տեղավորվում է շրջանագծի մեջ, ուստի դրա տարածքն ակնհայտորեն սահմանափակ է: Տարածքը կարելի է հաշվարկել, և դրա համար ձեզ նույնիսկ հատուկ գիտելիքներ պետք չեն. դպրոցում դասավանդվում են եռանկյան մակերեսի և երկրաչափական առաջընթացի գումարի բանաձևեր: Հետաքրքրվողների համար հաշվարկը տրված է ստորև՝ մանրատառով:
Թող սկզբնական կանոնավոր եռանկյան կողմը հավասար լինի ա. Այնուհետև նրա տարածքն է. Նախ կողմը 1 է, իսկ մակերեսը՝ . Ի՞նչ է տեղի ունենում, երբ կրկնությունը մեծանում է: Կարելի է ենթադրել, որ փոքր հավասարակողմ եռանկյունները կցված են գոյություն ունեցող բազմանկյունին: Առաջին անգամ դրանք ընդամենը 3-ն են, իսկ հաջորդ անգամ՝ 4 անգամ ավելի, քան նախորդը։ Այսինքն՝ վրա nփուլը կավարտվի Tn= 3 4 n- 1 եռանկյուն: Նրանցից յուրաքանչյուրի կողմի երկարությունը նախորդ քայլով ավարտված եռանկյան կողմի մեկ երրորդն է։ Այսպիսով, այն հավասար է (1/3) n. Տարածքները համաչափ են կողմերի քառակուսիներին, ուստի յուրաքանչյուր եռանկյան մակերեսը հավասար է ![]() . Մեծ արժեքների համար nԻ դեպ, սա շատ քիչ է։ Այս եռանկյունների ընդհանուր ներդրումը ձյան փաթիլի տարածքում է Tn · Ս ն= 3/4 · (4/9) n · Ս 0 . Հետևաբար հետո n-քայլ, գործչի մակերեսը հավասար կլինի գումարին Ս 0 + Տ 1 · Ս 1 + Տ 2 · Ս 2 + ... +TnՍ n =
. Մեծ արժեքների համար nԻ դեպ, սա շատ քիչ է։ Այս եռանկյունների ընդհանուր ներդրումը ձյան փաթիլի տարածքում է Tn · Ս ն= 3/4 · (4/9) n · Ս 0 . Հետևաբար հետո n-քայլ, գործչի մակերեսը հավասար կլինի գումարին Ս 0 + Տ 1 · Ս 1 + Տ 2 · Ս 2 + ... +TnՍ n = ![]() . Ձյան փաթիլ է ստացվում անսահման թվով քայլերից հետո, որը համապատասխանում է n→ ∞. Արդյունքն անսահման գումար է, բայց սա նվազող երկրաչափական պրոգրեսիայի գումարն է, դրա համար կա մի բանաձև.
. Ձյան փաթիլ է ստացվում անսահման թվով քայլերից հետո, որը համապատասխանում է n→ ∞. Արդյունքն անսահման գումար է, բայց սա նվազող երկրաչափական պրոգրեսիայի գումարն է, դրա համար կա մի բանաձև. ![]() . Ձյան փաթիլի տարածքն է.
. Ձյան փաթիլի տարածքն է.
4. Ֆրակտալ չափումը հավասար է log4/log3 = log 3 4 ≈ 1,261859... . Ճշգրիտ հաշվարկը կպահանջի զգալի ջանքեր և մանրամասն բացատրություններ, ուստի այստեղ ավելի շուտ ֆրակտալ չափման սահմանման օրինակ է: Իշխանության օրենքի բանաձեւից Ն(δ ) ~ (1/δ )Դ, Որտեղ Ն- հատվող քառակուսիների քանակը, δ - նրանց չափը, և Դչափն է, մենք դա ստանում ենք Դ= մատյան 1/ δ Ն. Այս հավասարությունը ճշմարիտ է մինչև հաստատունի ավելացումը (նույնը բոլորի համար δ ) Նկարները ցույց են տալիս Կոխի կորի կառուցման հինգերորդ կրկնությունը, որի հետ հատվող ցանցային քառակուսիները կանաչ ստվերում են: Բնօրինակ հատվածի երկարությունը 1 է, ուստի վերին նկարում քառակուսիների կողմի երկարությունը 1/9 է։ 12 քառակուսի ստվերված է, log 9 12 ≈ 1.130929... . Դեռևս շատ նման չէ 1.261859-ին... . Եկեք նայենք հետագա: Միջին նկարում քառակուսիները կիսով չափ են, դրանց չափը՝ 1/18, ստվերավորված 30. log 18 30 ≈ 1,176733... . Արդեն ավելի լավ։ Ներքևում քառակուսիները դեռ կիսով չափ մեծ են, 72 կտոր արդեն ներկված է: log 72 30 ≈ 1.193426... . Նույնիսկ ավելի մոտ: Այնուհետև դուք պետք է մեծացնեք կրկնությունների թիվը և միևնույն ժամանակ կրճատեք քառակուսիները, այնուհետև Կոխի կորի չափման «էմպիրիկ» արժեքը անշեղորեն կմոտենա լոգին 3 4, իսկ սահմանում այն ամբողջությամբ կհամընկնի:

Կոխի ձյան փաթիլը «ընդհակառակը» ստացվում է, եթե սկզբնական հավասարակողմ եռանկյան ներսում կառուցենք կոխի կորեր:

Cesaro գծեր. Հավասարակողմ եռանկյունների փոխարեն օգտագործվում են 60°-ից 90° հիմքի անկյուն ունեցող հավասարաչափ եռանկյուններ։ Նկարում անկյունը 88° է։

Քառակուսի տարբերակ. Այստեղ հրապարակներն ավարտված են։
|
Ձյան փաթիլ Քոչ
կտավ (
եզրագիծը՝ 1px գծիկ սև;
}
var cos = 0.5,
sin = Math.sqrt(3) / 2,
deg = Math.PI / 180;
canv, ctx;
ֆունկցիա rebro(n, len) (
ctx.save(); // Պահպանել ընթացիկ փոխակերպումը
եթե (n == 0) ( // Ոչ ռեկուրսիվ դեպք - գիծ քաշեք
ctx.lineTo(len, 0);
}
ուրիշ (
ctx.scale (1/3, 1/3); // Մեծացնել 3 անգամ
ռեբրո (n-1, len); //RECUURSION եզրին
ctx.rotate (60 * deg);
ռեբրո (n-1, len);
ctx.rotate (-120 * deg);
ռեբրո (n-1, len);
ctx.rotate (60 * deg);
ռեբրո (n-1, len);
}
ctx.restore(); // Վերականգնել վերափոխումը
ctx.translate(len, 0); // գնալ ծայրի ծայրին
}
drawKochSnowflake ֆունկցիան (x, y, len, n) (
x = x - len / 2;
y = y + len / 2 * Math.sqrt(3)/3;
ctx.save();
ctx.beginPath();
ctx.translate (x, y);
ctx.moveTo (0, 0);
rebro(n, len); ctx.rotate (-120 * deg); //RECUUUURSION-ն արդեն եռանկյուն է
rebro(n, len); ctx.rotate (-120 * deg);
rebro(n, len); ctx.closePath();
ctx.strokeStyle = "#000";
ctx.stroke();
ctx.restore();
}
ֆունկցիա clearcanvas())( // մաքրել կտավը
ctx.save();
ctx.beginPath();
// Կտավը մաքրելիս օգտագործեք ինքնության մատրիցը
ctx.setTransform(1, 0, 0, 1, 0, 0);
ctx.clearRect(0, 0, canvas1.width, canvas1.height);
// Վերականգնել փոխակերպումը
ctx.restore();
}
գործառույթը run() (
canv = document.getElementById("canvas1");
ctx = canv.getContext ("2d");
var numberiter = document.getElementById("քանակ").արժեք;
drawKochSnowflake (canv.width/2, canv.height/2, 380, numberiter);
Ctx.stroke(); //արտադրություն
}
Կոխի ձյան փաթիլ - օրինակ
Բոստոնում անսովոր տաք ձմեռ էր, բայց մենք դեռ սպասում էինք առաջին ձյան տեղումներին։ Դիտելով, թե ինչպես է ձյունը ընկնում պատուհանից, ես մտածեցի ձյան փաթիլների մասին և թե ինչպես են դրանց կառուցվածքը մաթեմատիկորեն նկարագրելը: Այնուամենայնիվ, կա մեկ հատուկ տեսակի ձյան փաթիլ, որը հայտնի է որպես Կոխի ձյան փաթիլ, որը կարելի է համեմատաբար պարզ նկարագրել: Այսօր մենք կանդրադառնանք, թե ինչպես կարելի է դրա ձևը կառուցել՝ օգտագործելով COMSOL Multiphysics Application Builder-ը:
Կոխի ձյան փաթիլի պատրաստումըԻնչպես արդեն նշեցինք մեր բլոգում, ֆրակտալները կարող են օգտագործվել . Ձյան փաթիլ Քոչֆրակտալ է, որը հատկանշական է նրանով, որ այն կառուցելու համար կա շատ պարզ կրկնվող գործընթաց.
Այս ընթացակարգը պատկերված է ստորև բերված նկարում ձյան փաթիլ նկարելու առաջին չորս կրկնությունների համար:
Կոխի ձյան փաթիլի առաջին չորս կրկնությունները: Image by Wxs - Սեփական աշխատանք: Լիցենզավորված է CC BY-SA 3.0-ով, Wikimedia Commons-ի միջոցով:
Կոխի ձյան փաթիլների երկրաչափության կառուցումՔանի որ մենք հիմա գիտենք, թե որ ալգորիթմն օգտագործել, եկեք տեսնենք, թե ինչպես կարելի է ստեղծել նման կառուցվածք՝ օգտագործելով COMSOL Multiphysics Application Builder-ը: Մենք կբացենք նոր ֆայլ և կստեղծենք 2D օբյեկտ երկրաչափական մասհանգույցում Համաշխարհային սահմանումներ. Այս օբյեկտի համար մենք սահմանելու ենք հինգ մուտքային պարամետր՝ հավասարակողմ եռանկյան կողմի երկարությունը; X- Եվ y- հիմքի միջնակետի կոորդինատները. և նորմալ վեկտորի բաղադրիչները, որոնք ուղղված են հիմքի կեսից դեպի հակառակ գագաթը, ինչպես ցույց է տրված ստորև բերված նկարներում:

Հինգ պարամետր օգտագործվում է հավասարակողմ եռանկյան չափը, դիրքը և կողմնորոշումը սահմանելու համար:

Երկրաչափական մասի մուտքային պարամետրերի կարգավորում:  Հավասարակողմ եռանկյունի կառուցման համար օգտագործվում է բազմանկյուն պարզունակ:
Հավասարակողմ եռանկյունի կառուցման համար օգտագործվում է բազմանկյուն պարզունակ:

Օբյեկտը կարող է պտտվել ստորին եզրի կենտրոնի շուրջը:

Օբյեկտը կարող է տեղափոխվել ծագման համեմատ:
Այժմ, երբ մենք սահմանել ենք երկրաչափական մասը, այն օգտագործում ենք մեկ անգամ բաժնում Երկրաչափություն. Այս մեկ եռանկյունը համարժեք է Koch ձյան փաթիլի զրոյական կրկնությանը, և այժմ եկեք օգտագործենք Application Builder-ը ավելի բարդ ձյան փաթիլներ ստեղծելու համար:
Հավելվածի միջերեսի նշագրում հավելվածների ստեղծման մեջՀավելվածն ունի շատ պարզ օգտատիրոջ միջերես: Այն պարունակում է միայն երկու բաղադրիչ, որոնց հետ օգտագործողը կարող է փոխազդել. Slider (Slider)(նշված է որպես 1 ստորև նկարում), որով կարող եք սահմանել ձյան փաթիլ ստեղծելու համար անհրաժեշտ կրկնությունների քանակը, և Կոճակ(պիտակ 2), որի վրա սեղմելով ստեղծվում և ցուցադրվում է ստացված երկրաչափությունը: Այնտեղ կան նաեւ Տեքստի մակագրություն(պիտակ 3) և Տվյալների ցուցադրում (ցուցադրում):(պիտակ 4), որոնք ցույց են տալիս նշված կրկնությունների քանակը, ինչպես նաև պատուհանը Գծապատկերներ(պիտակ 5), որը ցույց է տալիս վերջնական երկրաչափությունը:

Դիմումը ունի մեկ միասնական ձև հինգ բաղադրիչով:
Հավելվածն ունի երկու Սահմանումներ, որոնցից մեկը սահմանում է Iterations կոչվող ամբողջ թիվ, որը կանխադրված է զրոյի, բայց կարող է փոփոխվել օգտագործողի կողմից։ Սահմանված է նաև կրկնակիների 1D զանգված, որը կոչվում է Կենտրոն: Զանգվածի մեկ տարրն ունի 0,5 արժեք, որն օգտագործվում է յուրաքանչյուր եզրի կենտրոնական կետը գտնելու համար։ Այս արժեքը երբեք չի փոխվում:

Կարգավորումներ երկու սահմանումների համար:
UI-ի Slider բաղադրիչը վերահսկում է ամբողջ թվի արժեքը, Iterations պարամետրը: Ստորև ներկայացված սքրինշոթը ցույց է տալիս «Slider»-ի կարգավորումները և արժեքները, որոնք սահմանված են որպես ամբողջ թվեր 0-ից 5-ի միջակայքում: Նույն աղբյուրը (ինչպես սահիչը) ընտրված է նաև բաղադրիչի համար: Տվյալների ցուցադրումհավելվածի էկրանին նշված կրկնությունների քանակը ցուցադրելու համար: Մենք պոտենցիալ օգտագործողին սահմանափակում ենք հինգ կրկնություններով, քանի որ օգտագործվող ալգորիթմը ոչ օպտիմալ է և ոչ այնքան արդյունավետ, բայց բավական պարզ է իրականացնելու և ցուցադրելու համար:

«Slider» բաղադրիչի կարգավորումներ:
Հաջորդը, եկեք նայենք մեր կոճակի կարգավորումներին, որոնք ներկայացված են ստորև ներկայացված սքրինշոթում: Երբ կոճակը սեղմվում է, երկու հրաման է կատարվում: Նախ կանչվում է CreateSnowFlake մեթոդը: Դրանից հետո ստացված երկրաչափությունը ցուցադրվում է գրաֆիկական պատուհանում:

Կոճակի կարգավորումներ:
Այժմ մենք նայեցինք մեր հավելվածի ինտերֆեյսին և կարող ենք տեսնել, որ ցանկացած ձյան փաթիլի երկրաչափություն ստեղծելը պետք է տեղի ունենա կոչվող մեթոդի միջոցով: Եկեք նայենք այս մեթոդի կոդը՝ ձախ կողմում ավելացված տողերի համարակալմամբ և կարմիրով ընդգծված տողերի հաստատուններով.
1 model.geom("geom1" ).feature().clear(); 2 model.geom("geom1" ).create("pi1", "PartInstance"); 3 model.geom("geom1" ).run("fin"); 4 համար (int iter = 1; iter «geom1» ).getNEdges()+1; 6 UnionList = «pi» + iter; 7 համար (int edge = 1; եզր «geom1» ).getNEdges(); edge++) ( 8 String newPartInstance = «pi» + iter + edge; 9 model.geom(«geom1» ).create(newPartInstance, «PartInstance» ).set(«part» , «part1»); 10 with(model. geom("geom1").հատկանիշ(newPartInstance)); 11 setEntry("inputexpr", "Length", toString(Math.pow(1.0/3.0, iter))); 12 setEntry("inputexpr", "px", model.geom("geom1").edgeX(եզր, կենտրոն)); 13 setEntry("inputexpr", "py" , model.geom("geom1").edgeX(եզր, կենտրոն)); 14 setEntry("inputexpr" " , "nx" , model.geom("geom1" ).edgeNormal(եզր, Կենտրոն)); 15 setEntry("inputexpr" , "ny" , model.geom("geom1" ).edgeNormal(եզր, Կենտրոն)) ; 16 endwith(); 17 UnionList = newPartInstance; 18) 19 model.geom("geom1" ).create("pi" +(iter+1), "Union" ).selection("input" ).set(UnionList ); 20 model.geom("geom1" ).feature("pi" +(iter+1)).set("intbnd", "off"); 21 model.geom("geom1" ).run("fin"); 22)
Եկեք տող առ տող անցնենք ծածկագրի միջով՝ հասկանալու համար, թե յուրաքանչյուր տող ինչ գործառույթ է կատարում.
Այսպիսով, մենք լուսաբանել ենք մեր դիմումի բոլոր ասպեկտներն ու տարրերը: Եկեք նայենք արդյունքներին:

Մեր պարզ հավելվածը Կոխի ձյան փաթիլը կառուցելու համար:
Մենք կարող ենք ընդլայնել մեր հավելվածը՝ երկրաչափություն գրելու ֆայլի վրա, կամ նույնիսկ ուղղակիորեն կատարել լրացուցիչ վերլուծություններ: Օրինակ, մենք կարող ենք նախագծել ֆրակտալ ալեհավաք: Եթե դուք հետաքրքրված եք ալեհավաքի դիզայնով, ստուգեք մեր օրինակը կամ նույնիսկ զրոյից կազմեք դրա դասավորությունը:
Փորձեք ինքներդԵթե ցանկանում եք ինքներդ ստեղծել այս հավելվածը, բայց դեռ չեք ավարտել Application Builder-ը, կարող եք օգտակար գտնել հետևյալ ռեսուրսները.
- Ներբեռնեք ուղեցույցը Ներածություն հավելվածների մշակման միջավայրին անգլերեն լեզվով
- Դիտեք այս տեսանյութերը և սովորեք, թե ինչպես օգտագործել
- Կարդացեք այս թեմաները՝ ծանոթանալու, թե ինչպես են օգտագործվում սիմուլյացիոն հավելվածները
Այս նյութը լուսաբանելուց հետո կտեսնեք, թե ինչպես կարելի է հավելվածի ֆունկցիոնալությունը ընդլայնել՝ ձյան փաթիլի չափը փոխելու, ստեղծված երկրաչափությունը արտահանելու, տարածքի և պարագծի գնահատման և շատ ավելին:
Ինչպիսի՞ հավելված կցանկանայիք ստեղծել COMSOL Multiphysics-ում: օգնության համար.
Ֆրակտալ ձյան փաթիլը՝ ամենահայտնի և առեղծվածային երկրաչափական առարկաներից մեկը, նկարագրել է Հելգա ֆոն Կոխը մեր դարասկզբին։ Ավանդույթի համաձայն՝ մեր գրականության մեջ այն կոչվում է Քոչի ձյան փաթիլ։ Սա շատ «կծու» երկրաչափական պատկեր է, որը փոխաբերաբար կարելի է դիտել որպես Դավթի աստղի բազմիցս ինքն իրեն «բազմապատկվելու» արդյունք: Նրա վեց հիմնական ճառագայթները ծածկված են անսահման թվով մեծ և փոքր «ասեղներով» գագաթներով։ Ձյան փաթիլի ուրվագծի յուրաքանչյուր մանրադիտակային հատված նման է պատիճում գտնվող երկու ոլոռի, իսկ մեծ ճառագայթն իր հերթին պարունակում է նույն մանրադիտակային բեկորների անսահման քանակություն:
1994 թվականին Վառնայում մաթեմատիկական մոդելավորման մեթոդիկայի վերաբերյալ միջազգային սիմպոզիումի ժամանակ ես հանդիպեցի բուլղար հեղինակների աշխատանքին, ովքեր նկարագրեցին իրենց փորձը՝ օգտագործելով Կոխի ձյան փաթիլները և այլ նմանատիպ առարկաներ ավագ դպրոցի դասերին՝ լուսաբանելու տարածության բաժանելիության և տարածության խնդիրը: Զենոնի փիլիսոփայական ապորիաները։ Բացի այդ, կրթական տեսանկյունից, իմ կարծիքով, շատ հետաքրքիր է կանոնավոր ֆրակտալ երկրաչափական կառուցվածքների կառուցման բուն սկզբունքը՝ հիմնական տարրի ռեկուրսիվ բազմապատկման սկզբունքը։ Իզուր չէ, որ բնությունը «սիրում է» ֆրակտալ ձևերը։ Սա բացատրվում է հենց նրանով, որ դրանք ստացվում են պարզ վերարտադրման և որոշակի տարրական շինանյութի չափը փոխելով։ Ինչպես գիտեք, բնությունը չի հեղեղվում տարբեր պատճառներով և, հնարավորության դեպքում, բավարարվում է ամենապարզ ալգորիթմական լուծումներով: Ուշադիր նայեք տերևների ուրվագծերին, և շատ դեպքերում դուք հստակ կապ կգտնեք կոխական ձյան փաթիլի ուրվագծի ձևի հետ:
Ֆրակտալ երկրաչափական կառույցների պատկերացումը հնարավոր է միայն համակարգչի օգնությամբ։ Արդեն շատ դժվար է ձեռքով երրորդ կարգի վերևում Կոխի ձյան փաթիլ կառուցելը, բայց դուք իսկապես ուզում եք նայել դեպի անսահմանություն: Հետեւաբար, ինչու չփորձել մշակել համապատասխան համակարգչային ծրագիր։ RuNet-ում կարող եք գտնել առաջարկություններ՝ եռանկյուններից Կոխի ձյան փաթիլ կառուցելու համար: Այս ալգորիթմի արդյունքը կարծես հատվող գծերի խառնաշփոթ է: Ավելի հետաքրքիր է այս ցուցանիշը համատեղել «կտորներից»: Կոխի ձյան փաթիլի ուրվագիծը բաղկացած է հավասար երկարությամբ հատվածներից, որոնք թեքված են 0°, 60° և 120° հորիզոնական x առանցքի նկատմամբ: Եթե դրանք նշանակենք համապատասխանաբար 1, 2 և 3, ապա ցանկացած կարգի ձյան փաթիլը բաղկացած կլինի հաջորդական եռյակներից՝ 1, 2, 3, 1, 2, 3, 1, 2, 3... և այլն։ Այս երեք տեսակներից յուրաքանչյուրը։ հատվածները կարող են կցվել նախորդին մեկ կամ մյուս ծայրով: Այս հանգամանքը հաշվի առնելով՝ կարելի է ենթադրել, որ ձյան փաթիլի ուրվագիծը բաղկացած է վեց տեսակի հատվածներից։ Նշենք դրանք 0, 1, 2, 3, 4, 5: Այսպիսով, մենք հնարավորություն ենք ստանում կոդավորել ցանկացած կարգի ուրվագիծ՝ օգտագործելով 6 նիշ (տե՛ս նկարը):
Ավելի բարձր կարգի ձյան փաթիլ ստացվում է ավելի ցածր կարգի նախորդից՝ յուրաքանչյուր եզրը փոխարինելով չորսով, որոնք կապված են ծալված ափերի նման (_/\_): Եզրային տիպը 0 փոխարինվում է չորս եզրերով 0, 5, 1, 0 և այլն՝ ըստ աղյուսակի.
| 0 | 0 1 5 0 |
| 1 | 1 2 0 1 |
| 2 | 2 3 1 2 |
| 3 | 3 4 2 3 |
| 4 | 4 5 3 4 |
| 5 | 5 0 4 5 |
Պարզ հավասարակողմ եռանկյունին կարելի է պատկերացնել որպես զրոյական կարգի կոխական ձյան փաթիլ: Նկարագրված կոդավորման համակարգում այն համապատասխանում է 0, 4, 2 մուտքին: Մնացած ամեն ինչ կարելի է ձեռք բերել նկարագրված փոխարինումներով: Ես այստեղ չեմ տրամադրի ընթացակարգի կոդը և դրանով իսկ կզրկեմ ձեզ սեփական ծրագիրը մշակելու հաճույքից: Այն գրելիս ամենևին էլ պարտադիր չէ օգտագործել բացահայտ ռեկուրսիվ զանգ։ Այն կարող է փոխարինվել սովորական ցիկլով։ Աշխատանքի ընթացքում դուք ևս մեկ առիթ կունենաք մտածելու ռեկուրսիայի և դրա դերի մասին մեզ շրջապատող աշխարհի քվազի-ֆրակտալ ձևերի ձևավորման և ուղու վերջում (եթե, իհարկե, շատ ծույլ չեք. դրա միջով մինչև վերջ անցնելու համար) դուք կկարողանաք հիանալ ֆրակտալ ձյան փաթիլի ուրվագծերի բարդ ձևով, ինչպես նաև վերջապես նայել անսահմանության դեմքին:
Թեմա՝ Ֆրակտալներ.
1. Ներածություն. Համառոտ պատմական նախադրյալներ ֆրակտալների վերաբերյալ. 2. Ֆրակտալները բնության մեջ երկրաչափության տարրեր են:
3. Բնության մեջ ֆրակտալ հատկություն ունեցող առարկաներ: 4. «Ֆրակտալներ» տերմինաբանության սահմանումը:
5.Ֆրակտալների դասեր.
6.Ֆրակտալ պրոցեսների նկարագրություն. 7. Ֆրակտալ հավաքածուների ստացման ընթացակարգեր.
8.1 Կոտրված Կոխա (ստանալու կարգ):
8.2 Koch Snowflake (Koch Fractal):
8.3 Menger սպունգեր.
9. Ֆրակտալների օգտագործման օրինակներ.
Ներածություն. Համառոտ պատմական նախադրյալներ ֆրակտալների վերաբերյալ.Ֆրակտալները դիսկրետ մաթեմատիկայի երիտասարդ ճյուղ են:
1904 թվականին շվեդ Կոխը առաջ բերեց շարունակական կոր, որը ոչ մի տեղ չունի շոշափող՝ Կոխի կորը:
1918 թվականին ֆրանսիացի Ջուլիան նկարագրել է ֆրակտալների մի ամբողջ ընտանիք։
1938 թվականին Պիեռ Լևին հրապարակեց «Հարվածային և տարածական կորեր և մակերեսներ, որոնք բաղկացած են ամբողջին նման մասերից» հոդվածը։
1982 թվականին Բենուա Մանդելբրոտը հրատարակեց «Բնության ֆրակտալ երկրաչափությունը» գիրքը։
Պարզ կոնստրուկցիաների և բանաձևերի միջոցով ստեղծվում են պատկերներ։ Հայտնվեց «Ֆրակտալ նկարչություն».
1993 թվականից World Scientific-ը հրատարակում է «Fractals» ամսագիրը։
Ֆրակտալները բնության մեջ երկրաչափության տարրեր են։Ֆրակտալները այնպիսի առարկաներ նկարագրելու միջոց են, ինչպիսիք են լեռնաշղթաների մոդելները, խորդուբորդ ափամերձ գծերը, բազմաթիվ մազանոթների և անոթների շրջանառության համակարգերը, ծառերի պսակները, կասկադային ջրվեժները, ապակու վրա ցրտաշունչ նախշերը:
Կամ սրանք՝ պտերի տերեւ, ամպեր, բիծ։
Նման օբյեկտների պատկերները կարելի է ներկայացնել ֆրակտալ գրաֆիկայի միջոցով:
Բնության մեջ ֆրակտալ հատկություններ ունեցող առարկաներ:CoralsStarfish and UrchinsSea Shells
Ծաղիկներ և բույսեր (բրոկկոլի, կաղամբ) Մրգեր (արքայախնձոր)
Ծառերի և բույսերի տերևների պսակներ Մարդկանց և կենդանիների շրջանառության համակարգ և բրոնխներ Անկենդան բնության մեջ.
Աշխարհագրական օբյեկտների (երկրներ, մարզեր, քաղաքներ) սահմաններ Ափամերձ լեռնաշղթաներ Ձյան փաթիլներ Ամպեր Կայծակ
Ապակու վրա ձևավորված նախշեր Բյուրեղներ Ստալակտիտներ, ստալագմիտներ, հելիկտիտներ:
«Ֆրակտալներ» տերմինաբանության սահմանումը.Ֆրակտալները երկրաչափական ձևեր են, որոնք բավարարում են հետևյալ հատկություններից մեկին կամ մի քանիսին.
Այն ունի բարդ ոչ տրիվիալ կառուցվածք ցանկացած խոշորացումով (բոլոր մասշտաբներով), այն (մոտավորապես) ինքնին նման է:
Այն ունի կոտորակային Hausdorff (ֆրակտալ) չափ կամ գերազանցում է տոպոլոգիականը; Կարող է կառուցվել ռեկուրսիվ ընթացակարգերով:
Կանոնավոր թվերի համար, ինչպիսիք են շրջանը, էլիպսը կամ հարթ ֆունկցիայի գրաֆիկը, շատ մեծ մասշտաբով փոքր հատվածը նման է ուղիղ գծի հատվածին: Ֆրակտալի համար սանդղակի մեծացումը չի հանգեցնում կառուցվածքի պարզեցման, բոլոր մասշտաբների համար մենք կտեսնենք հավասարապես բարդ նկարներ:
Ֆրակտալ դասերՖրակտալը ամբողջին նման մասերից (ենթակառուցվածքներից) կազմված կառուցվածք է։
Որոշ ֆրակտալներ, որպես բնության տարրեր, կարելի է դասակարգել որպես երկրաչափական (կառուցողական) ֆրակտալներ։
Մնացածը կարելի է դասակարգել որպես դինամիկ ֆրակտալներ (հանրահաշվական):

Սա ֆրակտալ կորեր ստանալու պարզ ռեկուրսիվ ընթացակարգ է. նշեք կամայական կոտրված գիծ՝ վերջավոր թվով հղումներով՝ գեներատոր: Հաջորդը, գեներատորի յուրաքանչյուր հատվածը փոխարինվում է դրանում: Այնուհետև դրա մեջ գտնվող յուրաքանչյուր հատվածը կրկին փոխարինվում է գեներատորով և այդպես անվերջ:
Ցուցադրված է. միավոր հատվածի բաժանումը 3 մասի (ա), քառակուսի մակերեսը 9 մասի (բ), միավոր խորանարդը 27 մասի (գ) և 64 մասի (դ): Մասերի թիվը n է, մասշտաբի գործակիցը k է, իսկ տարածության չափը՝ d։ Մենք ունենք հետևյալ հարաբերությունները՝ n = kd,
եթե n = 3, k = 3, ապա d = 1; եթե n = 9, k = 3, ապա d = 2; եթե n = 27, k = 3, ապա d = 3:
եթե n = 4, k = 4, ապա d = 1; եթե n = 16, k = 4, ապա d = 2; եթե n = 64, k = 4, ապա d = 3: Տարածության չափն արտահայտվում է ամբողջ թվերով. d = 1, 2, 3; n = 64-ի համար d-ի արժեքն է

Ցուցադրված է Կոխի պոլիգիծ կառուցելու հինգ քայլ՝ միավորի երկարության հատված (a), որը բաժանված է երեք մասի (k = 3), չորս մասից (n = 4) - կոտրված գիծ (b); յուրաքանչյուր ուղիղ հատված բաժանված է երեք մասի (k2 = 9) և 16 մասից (n2 = 16) - կոտրված գիծ (c); ընթացակարգը կրկնվում է k3 = 27 և n3 = 64 - կոտրված գիծ (g); k5 = 243 և n5 = 1024 համար - կոտրված գիծ (e):
Չափս
Սա կոտորակային կամ ֆրակտալ հարթություն է:
Կոխի պոլիգիծը, որն առաջարկվել է Հելգ ֆոն Կոխի կողմից 1904 թվականին, գործում է որպես ֆրակտալ, որը հարմար է ափամերձ գծի կոշտությունը մոդելավորելու համար: Մանդելբրոտը ափամերձ գծի կառուցման ալգորիթմի մեջ մտցրեց պատահականության տարր, որը, սակայն, չազդեց ափի երկարության վերաբերյալ հիմնական եզրակացության վրա: Քանի որ սահմանը
Ափի երկարությունը հակված է անսահմանության՝ ափի անվերջանալի խորդուբորդության պատճառով:
Ափամերձ գիծը հարթելու կարգը, երբ ավելի մանրամասն սանդղակից տեղափոխվում է ավելի քիչ մանրամասն, այսինքն.

Որպես շինարարության հիմք կարող եք վերցնել ոչ թե միավորի երկարության հատվածներ, այլ հավասարակողմ եռանկյուն, որի յուրաքանչյուր կողմում կարող եք երկարացնել անկանոնությունները բազմապատկելու կարգը։ Այս դեպքում մենք ստանում ենք կոխական ձյան փաթիլ (նկ.) և երեք տեսակի. միայն ներսում (ներս); պատահականորեն կամ արտաքին կամ ներս (դ) և (ե): Ինչպես կարող եք սահմանել Կոխի ֆրակտալի կառուցման կարգը:
Բրինձ. Ձյան փաթիլ Քոչ
Նկ. ցուցադրվում են երկու վեկտորային դիագրամներ. Սլաքների վերևում գտնվող թվերը հավանաբար հարց կառաջացնեն՝ ի՞նչ են դրանք նշանակում: Վեկտոր 0-ը համընկնում է աբսցիսային առանցքի դրական ուղղության հետ, քանի որ նրա փուլային գործակիցը exp (i2πl/6) l = 0-ում պահպանում է իր ուղղությունը: Վեկտոր 1-ը պտտվում է 0 վեկտորի նկատմամբ 2π/6 անկյան տակ, երբ l= 1: Վեկտոր 5-ն ունի փուլային գործակից exp (i2π5/6), l = 5: Վերջին վեկտորն ունի նույն փուլային գործակիցը, ինչ առաջինը ( լ = 0): Ամբողջ թվերը l բնութագրում են միավոր վեկտորի ֆազային գործոնի անկյունը:
Առաջին քայլը (նկ.) սահմանում է ռեկուրսիվ ընթացակարգ բոլոր հետագա քայլերի և, մասնավորապես, երկրորդ քայլի համար (նկ.): Ինչպե՞ս ֆ1 = (0 1 5 0) թվերի բազմությունից անցնել φ2 = (0 1 5 0 1 2 0 1 5 0 4 5 0 1 5 0): Պատասխան՝ ուղղակի մատրիցային բազմապատկման միջոցով, երբ մեկ մատրիցի յուրաքանչյուր տարր բազմապատկվում է սկզբնական մատրիցով: Քանի որ այս դեպքում գործ ունենք միաչափ զանգվածի հետ, այսինքն. Քանի որ մատրիցները վեկտորներ են, մի մատրից-վեկտորի յուրաքանչյուր տարր բազմապատկվում է մեկ այլ մատրից-վեկտորի բոլոր տարրերով: Բացի այդ, φ1 մատրից-վեկտորի տարրերը բաղկացած են exp (i2πl/6) էքսպոնենցիալ ֆունկցիաներից, հետևաբար, 10-ը h թիվը բազմապատկելիս անհրաժեշտ կլինի ավելացնել ըստ mod (6), այլ ոչ թե բազմապատկել։
Կոխի ձյան փաթիլի երկրաչափական ձևն այսպիսի տեսք ունի

Ինչպես նկարել կոխական ձյան փաթիլ

Եվ կա նաև Կոխի բուրգը

Ինչպես նկարել կոխական ձյան փաթիլ, կարող եք ավելի մանրամասն տեղեկանալ ստորև ներկայացված տեսանյութից: Ինչ-որ մեկը կարող է հասկանալ, ես հրաժարվեցի:
Նախ, եկեք նայենք այս կոխական ձյան փաթիլին: Ստորև բերված դիագրամը լավագույնս ցույց կտա մեզ:

Այսինքն՝ տվյալ ձյան փաթիլը նկարելու համար անհրաժեշտ է օգտագործել առանձին երկրաչափական ձևեր, որոնք կազմում են այս երկրաչափական ֆրակտալը։

Մեր գծագրի հիմքը հավասարակողմ եռանկյունն է: Յուրաքանչյուր կողմը բաժանված է երեք հատվածի, որոնցից կառուցված են հաջորդ՝ ավելի փոքր, հավասարակողմ եռանկյունները։ Նույն գործողությունը կատարվում է ստացված եռանկյունների հետ մի քանի անգամ։
Կոխի ձյան փաթիլը գիտնականների կողմից ուսումնասիրված առաջին ֆրակտալներից է։ Ձյան փաթիլ է ստացվել Կոխի կորի երեք օրինակից, այս հայտնագործության մասին տեղեկությունը հայտնվել է 1904 թվականին շվեդ մաթեմատիկոս Հելգե ֆոն Կոխի հոդվածում։ Ըստ էության, կորը հորինվել է որպես շարունակական գծի օրինակ, որին շոշափող գիծ չի կարելի գծել որևէ կետում: Կոխի կորը պարզ է իր ձևավորման մեջ:
Օրինակ՝ Քոչի ձյան փաթիլի նկարի ֆոտոնկար՝ քայլ առ քայլ նկարչությամբ։

Այս դիագրամում դուք կարող եք մանրամասնորեն ուսումնասիրել այն գծերը, որոնք հետագայում կստեղծեն կոխական ձյան փաթիլ:
Եվ սա նոր ձյան փաթիլի մեկնաբանություն է, որը հիմնված է Քոչի ձյան փաթիլի վրա:

Նախքան հասկանալը, թե ինչպես կարելի է նկարել կոխական ձյան փաթիլ, դուք պետք է որոշեք, թե ինչ է դա:
Այսպիսով, կոխական ձյան փաթիլը երկրաչափական պատկեր է՝ ֆրակտալ:
Կոխի ձյան փաթիլի ամբողջական սահմանումը տրված է ստորև նկարում։