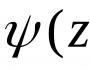Bir kəsrdə funksiyanın sıfırlarını necə tapmaq olar. Bir funksiyanın sıfırlarını necə tapmaq olar

Funksiya sıfırları funksiyanın sıfıra bərabər olduğu arqument dəyərləridir.

y=f(x) düsturu ilə verilmiş funksiyanın sıfırlarını tapmaq üçün f(x)=0 tənliyini həll etmək lazımdır.

Tənliyin kökləri yoxdursa, funksiyanın sıfırları yoxdur.

Nümunələr.

1) y=3x+15 xətti funksiyasının sıfırlarını tapın.

Funksiyanın sıfırlarını tapmaq üçün 3x+15=0 tənliyini həll edin.

Beləliklə, y=3x+15 funksiyasının sıfırı x= -5-dir.

Cavab: x= -5.

2) f(x)=x²-7x+12 kvadrat funksiyasının sıfırlarını tapın.

Funksiyanın sıfırlarını tapmaq üçün kvadrat tənliyi həll edin

Onun x1=3 və x2=4 kökləri bu funksiyanın sıfırlarıdır.

Cavab: x=3; x=4.

Təlimatlar

1. Funksiyanın sıfırı, funksiyanın dəyərinin sıfıra bərabər olduğu x arqumentinin qiymətidir. Bununla belə, yalnız tədqiq olunan funksiyanın tərifinin əhatə dairəsinə daxil olan arqumentlər sıfır ola bilər. Yəni f(x) funksiyasının faydalı olduğu bir çox dəyər var. 2. Verilmiş funksiyanı yazın və onu sıfıra bərabərləşdirin, deyək f(x) = 2x?+5x+2 = 0. Alınan tənliyi həll edin və onun həqiqi köklərini tapın. Kvadrat tənliyin kökləri diskriminantın tapılması dəstəyi ilə hesablanır. 2x?+5x+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0.5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. Beləliklə, bu halda kvadrat tənliyin iki kökü alınır f(x) başlanğıc funksiyasının arqumentləri. 3. Bütün aşkar edilmiş x dəyərlərini verilmiş funksiyanın təyini sahəsinə aid olub olmadığını yoxlayın. OOF-u tapın, bunun üçün ilkin ifadəni?f (x) formasının cüt köklərinin olub-olmaması, məxrəcdə arqumentlə funksiyada kəsrlərin olub-olmaması, loqarifmik və ya triqonometriklərin olub-olmaması üçün yoxlayın. ifadələri. 4. Cüt dərəcənin kökü altında ifadəsi olan funksiyanı nəzərdən keçirərkən, tərif sahəsi kimi dəyərləri radikal ifadəni mənfi ədədə çevirməyən bütün x arqumentlərini götürün (əksinə, funksiya yerinə yetirir. mənası yoxdur). Funksiyanın aşkar edilmiş sıfırlarının məqbul x dəyərlərinin müəyyən diapazonuna daxil olub-olmadığını yoxlayın. 5. Kəsrin məxrəci sıfıra gedə bilməz, buna görə də belə nəticəyə səbəb olan x arqumentlərini istisna edin. Loqarifmik kəmiyyətlər üçün yalnız ifadənin özü sıfırdan böyük olan arqumentin dəyərləri nəzərə alınmalıdır. Subloqarifmik ifadəni sıfıra və ya mənfi ədədə çevirən funksiyanın sıfırları yekun nəticədən atılmalıdır. Qeyd! Tənliyin köklərini taparkən əlavə köklər görünə bilər. Bunu yoxlamaq asandır: sadəcə olaraq arqumentin nəticə dəyərini funksiyaya əvəz edin və funksiyanın sıfıra çevrildiyinə əmin olun. Faydalı məsləhət Bəzən funksiya öz arqumenti vasitəsilə aşkar şəkildə ifadə olunmur, onda bu funksiyanın nə olduğunu bilmək asandır. Buna misal olaraq dairənin tənliyini göstərmək olar.

Funksiya sıfırları Funksiyanın qiymətinin sıfıra bərabər olduğu absis dəyəri deyilir.

Əgər funksiya onun tənliyi ilə verilirsə, onda funksiyanın sıfırları tənliyin həlli olacaqdır. Əgər funksiyanın qrafiki verilmişdirsə, onda funksiyanın sıfırları qrafikin x oxunu kəsdiyi qiymətlərdir.

Funksiyaən mühüm riyazi anlayışlardan biridir. Funksiya - dəyişən asılılıq saat dəyişəndən x, əgər hər bir dəyər X tək dəyərə uyğun gəlir saat. Dəyişən X müstəqil dəyişən və ya arqument adlanır. Dəyişən saat asılı dəyişən adlanır. Müstəqil dəyişənin bütün dəyərləri (dəyişən x) funksiyanın təyini oblastını təşkil edir. Asılı dəyişənin qəbul etdiyi bütün dəyərlər (dəyişən y), funksiyanın qiymət diapazonunu təşkil edir.

Funksiya qrafiki absisləri arqumentin qiymətlərinə, ordinatları isə funksiyanın müvafiq qiymətlərinə bərabər olan koordinat müstəvisinin bütün nöqtələrinin çoxluğuna, yəni Dəyişən absis oxu boyunca çəkilir x, və dəyişənin dəyərləri ordinat oxu boyunca çəkilir y. Bir funksiyanın qrafikini çəkmək üçün funksiyanın xassələrini bilmək lazımdır. Funksiyanın əsas xüsusiyyətləri aşağıda müzakirə olunacaq!

Funksiya qrafikini qurmaq üçün proqramımızdan istifadə etməyi məsləhət görürük - Qrafik funksiyaları online. Bu səhifədəki materialı öyrənərkən hər hansı bir sualınız olarsa, onları həmişə forumumuzda verə bilərsiniz. Həmçinin forumda onlar sizə riyaziyyat, kimya, həndəsə, ehtimal nəzəriyyəsi və bir çox başqa mövzularda problemləri həll etməyə kömək edəcəklər!

Funksiyaların əsas xassələri.

1) Funksiya sahəsi və funksiya diapazonu.

Funksiya sahəsi bütün etibarlı arqument dəyərlərinin məcmusudur x(dəyişən x), bunun üçün funksiya y = f(x) müəyyən edilmişdir.
Funksiya diapazonu bütün real dəyərlərin məcmusudur y, funksiyanın qəbul etdiyi.

İbtidai riyaziyyatda funksiyalar yalnız həqiqi ədədlər çoxluğunda öyrənilir.

2) Funksiya sıfırları.

Sıfır funksiyası, funksiyanın dəyərinin sıfıra bərabər olduğu arqumentin qiymətidir.

3) Funksiyanın sabit işarəsinin intervalları.

Bir funksiyanın sabit işarəsinin intervalları, funksiya dəyərləri yalnız müsbət və ya yalnız mənfi olan arqument dəyərlərinin dəstləridir.

4) funksiyanın monotonluğu.

Artan funksiya (müəyyən intervalda) bu intervaldan arqumentin daha böyük qiymətinin funksiyanın daha böyük dəyərinə uyğun gələn funksiyadır.

Azalan funksiya (müəyyən intervalda) bu intervaldan arqumentin daha böyük dəyərinin funksiyanın daha kiçik dəyərinə uyğun gələn funksiyadır.

5) Cüt (tək) funksiyası.

Cüt funksiya hər hansı bir mənşəyə və hər hansı bir funksiyaya görə təyinetmə sahəsi simmetrik olan funksiyadır X tərif sahəsindən bərabərlik f(-x) = f(x). Cüt funksiyanın qrafiki ordinata görə simmetrikdir.

Tək funksiya hər hansı bir mənşəyə və hər hansı bir funksiyaya görə təyinetmə sahəsi simmetrik olan funksiyadır X tərif sahəsindən bərabərlik doğrudur f(-x) = - f(x). Tək funksiyanın qrafiki mənşəyə görə simmetrikdir.

6) Məhdud və qeyri-məhdud funksiyalar.

|f(x)| kimi müsbət M ədədi varsa, funksiya məhdud adlanır Bütün x dəyərləri üçün ≤ M. Əgər belə bir nömrə yoxdursa, funksiya qeyri-məhduddur.

7) funksiyanın dövriliyi.

Hər hansı x f(x+T) = f(x) üçün sıfırdan fərqli T ədədi varsa f(x) funksiyası dövri xarakter daşıyır. Bu ən kiçik ədədə funksiyanın dövrü deyilir. Bütün triqonometrik funksiyalar dövri xarakter daşıyır. (Triqonometrik düsturlar).

Funksiyanın bu xassələrini öyrəndikdən sonra siz funksiyanı asanlıqla tədqiq edə və funksiyanın xassələrindən istifadə edərək funksiyanın qrafikini qura bilərsiniz. Həmçinin həqiqət cədvəli, vurma cədvəli, dövri cədvəl, törəmələr cədvəli və inteqral cədvəli haqqında materiala baxın.

Funksiya sıfırları

Funksiya sıfırları nədir? Funksiyanın sıfırlarını analitik və qrafik olaraq necə təyin etmək olar?

Funksiya sıfırları- bunlar funksiyanın sıfıra bərabər olduğu arqument dəyərləridir.

y=f(x) düsturu ilə verilmiş funksiyanın sıfırlarını tapmaq üçün f(x)=0 tənliyini həll etmək lazımdır.

Tənliyin kökləri yoxdursa, funksiyanın sıfırları yoxdur.

1) y=3x+15 xətti funksiyasının sıfırlarını tapın.

Funksiyanın sıfırlarını tapmaq üçün 3x+15 =0 tənliyini həll edin.

Beləliklə, funksiyanın sıfırı y=3x+15 - x= -5-dir.

2) f(x)=x²-7x+12 kvadrat funksiyasının sıfırlarını tapın.

Funksiyanın sıfırlarını tapmaq üçün kvadrat tənliyi həll edin

Onun x1=3 və x2=4 kökləri bu funksiyanın sıfırlarıdır.

3) funksiyanın sıfırlarını tapın

Məxrəc sıfırdan fərqli olduqda kəsr məna kəsb edir. Deməli, x²-1≠0, x² ≠ 1, x ≠±1. Yəni verilmiş funksiyanın tərif sahəsi (DO)

x²+5x+4=0 x1=-1 x2=-4 tənliyinin köklərindən yalnız x=-4 tərif dairəsinə daxil edilmişdir.

Qrafik olaraq verilmiş funksiyanın sıfırlarını tapmaq üçün funksiya qrafikinin absis oxu ilə kəsişmə nöqtələrini tapmaq lazımdır.

Qrafik Ox oxunu kəsmirsə, funksiyanın sıfırları yoxdur.

qrafiki şəkildə göstərilən funksiyanın dörd sıfırı var -

Cəbrdə funksiyanın sıfırlarının tapılması məsələsi həm müstəqil tapşırıq kimi, həm də digər məsələlərin həlli zamanı, məsələn, funksiyanı öyrənərkən, bərabərsizlikləri həll edərkən və s.

www.algebraclass.ru

Funksiya sıfırları qaydası

Funksiyaların əsas anlayışları və xassələri

Qayda (qanun) yazışma. Monoton funksiya .

Məhdud və qeyri-məhdud funksiyalar. Davamlı və

fasiləsiz funksiyalar . Cüt və tək funksiyalar.

Periodik funksiya. Funksiya müddəti.

Funksiya sıfırları . Asimptot .

Tərif sahəsi və funksiyanın dəyər diapazonu. İbtidai riyaziyyatda funksiyalar yalnız həqiqi ədədlər çoxluğunda öyrənilir R . Bu o deməkdir ki, funksiya arqumenti yalnız funksiyanın təyin olunduğu real dəyərləri qəbul edə bilər, yəni. həm də yalnız real dəyərləri qəbul edir. Bir dəstə X bütün etibarlı arqument dəyərləri x, bunun üçün funksiya y = f (x) müəyyən edilir, çağırılır funksiyanın domeni. Bir dəstə Y bütün real dəyərlər y funksiyanın qəbul etdiyi , adlanır funksiya diapazonu. İndi funksiyanın daha dəqiq tərifini verə bilərik: qayda çoxluqlar arasında uyğunluq (qanun). X Və Y , buna görə dəstdən hər bir element üçün X dəstdən yalnız bir element tapa bilərsiniz Y, funksiya adlanır .

Bu tərifdən belə çıxır ki, funksiya müəyyən edilmiş hesab olunur, əgər:

— funksiyanın təyini sahəsi müəyyən edilir X ;

— funksiya diapazonu müəyyən edilir Y ;

— yazışma qaydası (qanunu) məlumdur və hər biri üçün

arqument dəyəri, yalnız bir funksiya dəyəri tapıla bilər.

Funksiyanın unikallığının bu tələbi məcburidir.

Monoton funksiya. Arqumentin hər hansı iki dəyəri üçün x 1 və x vəziyyətin 2 x 2 > x 1 izləyir f (x 2) > f (x 1), sonra funksiya f (x) adlanır artır; əgər varsa x 1 və x vəziyyətin 2 x 2 > x 1 izləyir f (x 2)

Şəkil 3-də göstərilən funksiya məhduddur, lakin monoton deyil. Şəkil 4-dəki funksiya tam əksidir, monotondur, lakin qeyri-məhduddur. (Zəhmət olmasa bunu izah edin!).

Davamlı və fasiləsiz funksiyalar. Funksiya y = f (x) adlanır davamlı nöqtədə x = a, Əgər:

1) funksiya nə zaman müəyyən edilir x = a, yəni. f (a) mövcuddur;

2) mövcuddur sonlu limit lim f (x) ;

Bu şərtlərdən ən azı biri yerinə yetirilmirsə, funksiya çağırılır partlayıcı nöqtədə x = a .

Əgər funksiya müddətində fasiləsizdirsə hər kəs onun tərif dairəsinin nöqtələri, sonra çağırılır davamlı funksiya.

Cüt və tək funksiyalar. Əgər üçün hər hansı x funksiyanın tərif sahəsindən aşağıdakılar yerinə yetirilir: f (— x) = f (x), onda funksiya çağırılır hətta; baş verərsə: f (— x) = — f (x), onda funksiya çağırılır qəribə. Cüt funksiyanın qrafiki Y oxuna görə simmetrikdir(Şəkil 5), tək funksiyanın qrafiki Sim mənşəyə görə metrik(Şəkil 6).

Periodik funksiya. Funksiya f (x) — dövri, əgər belə bir şey varsa sıfırdan fərqli nömrə T nə üçün hər hansı x funksiyanın tərif sahəsindən aşağıdakılar yerinə yetirilir: f (x + T) = f (x). Bu ən azı nömrə çağırılır funksiyanın müddəti. Bütün triqonometrik funksiyalar dövri xarakter daşıyır.

Misal 1. Bu günahı sübut et x 2 dövrə malikdir.

Həll yolu: Biz bilirik ki, günah ( x+ 2 n) = günah x, Harada n= 0, ± 1, ± 2, …

Buna görə əlavə 2 n sinus arqumentinə deyil

dəyərini dəyişir e. Bununla başqa nömrə varmı

Belə iddia edək P– belə bir nömrə, yəni. bərabərlik:

istənilən dəyər üçün etibarlıdır x. Amma sonra var

yer və at x= / 2, yəni.

günah(/2 + P) = günah / 2 = 1.

Lakin azalma düsturuna görə günah (/ 2 + P) = cos P. Sonra

son iki bərabərlikdən belə çıxır ki, cos P= 1, amma biz

bunun yalnız o zaman doğru olduğunu bilirik P = 2 n. Ən kiçikdən

2-dən sıfırdan fərqli rəqəm n 2-dir, onda bu rəqəm

və bir müddət günah var x. Oxşar şəkildə sübut etmək olar ki, 2

cos üçün də bir dövrdür x .

Tan funksiyalarının olduğunu sübut edin x və çarpayı x dövrü var.

Misal 2. sin 2 funksiyasının dövrü hansı ədəddir x ?

Həll yolu: 2-ci günahı nəzərdən keçirin x= günah (2 x+ 2 n) = günah [ 2 ( x + n) ] .

Əlavə etdiyini görürük n arqumentə x, dəyişmir

funksiya dəyəri. Sıfırdan fərqli ən kiçik ədəd

-dan n dir, buna görə də bu, sin 2 dövrüdür x .

Funksiya sıfırları. Funksiyanın 0-a bərabər olduğu arqument dəyəri çağırılır sıfır ( kök) funksiyası. Funksiyada çoxlu sıfırlar ola bilər. Məsələn, funksiya y = x (x + 1) (x- 3) üç sıfır var: x = 0, x = — 1, x= 3. Həndəsi null funksiyası – bu funksiya qrafikinin oxu ilə kəsişmə nöqtəsinin absisidir X .

Şəkil 7-də sıfırları olan funksiyanın qrafiki göstərilir: x = a , x = b Və x = c .

Asimptot. Əgər funksiyanın qrafiki başlanğıcdan uzaqlaşdıqca qeyri-müəyyən bir xəttə yaxınlaşırsa, bu xətt adlanır. asimptot.

Mövzu 6. “İnterval metodu.”

Əgər x x 0 üçün f (x) f (x 0) olarsa, f (x) funksiyası çağırılır x 0 nöqtəsində davamlıdır.

Əgər funksiya hansısa I intervalının hər nöqtəsində fasiləsizdirsə, o zaman çağırılır intervalda davamlıdır I (interval I adlanır funksiyanın davamlılıq intervalı). Bu intervalda funksiyanın qrafiki davamlı bir xəttdir və onların dediyinə görə, “kağızdan qələmi qaldırmadan çəkilə bilər”.

Davamlı funksiyaların xassəsi.

Əgər (a ; b) intervalında f funksiyası fasiləsizdirsə və itmirsə, bu intervalda sabit işarəni saxlayır.

Bu xassə əsasında bir dəyişənli bərabərsizliklərin həlli metodu, interval üsulu dayanır. f(x) funksiyası I intervalında kəsilməz olsun və bu intervalda sonlu sayda nöqtədə yox olsun. Davamlı funksiyaların xassəsinə görə, bu nöqtələr I-ni intervallara bölür, onların hər birində f(x) c fasiləsiz funksiyası sabit işarəni saxlayır. Bu işarəni müəyyən etmək üçün hər bir belə intervaldan istənilən bir nöqtədə f(x) funksiyasının qiymətini hesablamaq kifayətdir. Buna əsaslanaraq bərabərsizliklərin interval üsulu ilə həlli üçün aşağıdakı alqoritmi əldə edirik.

Formanın bərabərsizlikləri üçün interval üsulu

İnterval üsulu. Orta səviyyə.

Gücünüzü sınamaq və Vahid Dövlət İmtahanı və ya Vahid Dövlət İmtahanına nə qədər hazır olduğunuzun nəticəsini öyrənmək istəyirsiniz?

Xətti funksiya

Formanın bir funksiyası xətti adlanır. Nümunə olaraq bir funksiya götürək. 3″>-də müsbət və mənfidir. Nöqtə () funksiyasının sıfırıdır. Bu funksiyanın işarələrini ədəd oxunda göstərək:

Biz deyirik ki, “nöqtədən keçəndə funksiya işarəsini dəyişir”.

Görünür ki, funksiyanın işarələri funksiya qrafikinin mövqeyinə uyğundur: qrafik oxun üstündədirsə, işarəsi “ ”, aşağıda “ ” olarsa.

Nəticə qaydasını ixtiyari xətti funksiyaya ümumiləşdirsək, aşağıdakı alqoritmi əldə edirik:

Kvadrat funksiya

Ümid edirəm kvadrat bərabərsizlikləri necə həll edəcəyinizi xatırlayırsınız? Yoxdursa, “Kvadrat bərabərsizliklər” mövzusunu oxuyun. Kvadrat funksiyanın ümumi formasını xatırlatdım: .

İndi kvadrat funksiyanın hansı işarələri aldığını xatırlayaq. Onun qrafiki paraboladır və funksiya parabola oxun üstündə olanlar üçün " " işarəsini alır və " " - əgər parabola oxun altındadırsa:

Əgər funksiyanın sıfırları (dəyərləri) varsa, parabola oxu iki nöqtədə - müvafiq kvadrat tənliyin köklərində kəsir. Beləliklə, ox üç intervala bölünür və hər bir kökdən keçərkən funksiyanın işarələri növbə ilə dəyişir.

Hər dəfə parabola çəkmədən işarələri müəyyən etmək olarmı?

Xatırladaq ki, kvadrat trinomial faktorlara bölünə bilər:

Oxda kökləri qeyd edək:

Xatırlayırıq ki, funksiyanın işarəsi yalnız kökdən keçərkən dəyişə bilər. Gəlin bu faktdan istifadə edək: oxun köklərə bölündüyü üç intervalın hər biri üçün funksiyanın işarəsini yalnız bir ixtiyari seçilmiş nöqtədə müəyyən etmək kifayətdir: intervalın qalan nöqtələrində işarə eyni olacaq. .

Bizim nümunəmizdə: 3″>-də mötərizədə olan hər iki ifadə müsbətdir (əvəz edin, məsələn: 0″>). Oxa “ ” işarəsi qoyuruq:

Yaxşı, (məsələn, əvəz edən) hər iki mötərizə mənfi olduqda, məhsul müsbətdir:

Bu budur interval üsulu: hər bir interval üzrə amillərin əlamətlərini bilməklə bütün məhsulun işarəsini təyin edirik.

Funksiyada sıfırın olmadığı və ya yalnız birinin olduğu halları da nəzərdən keçirək.

Əgər onlar yoxdursa, deməli, kök yoxdur. Bu o deməkdir ki, “kökdən keçmək” olmayacaq. Bu o deməkdir ki, funksiya bütün say xəttində yalnız bir işarə qəbul edir. Onu funksiyaya əvəz etməklə asanlıqla müəyyən edilə bilər.

Yalnız bir kök varsa, parabola oxa toxunur, buna görə də kökdən keçərkən funksiyanın işarəsi dəyişmir. Belə hallar üçün hansı qayda ilə çıxış edə bilərik?

Belə bir funksiyanı hesablasanız, iki eyni amil alırsınız:

Və istənilən kvadrat ifadə mənfi deyil! Buna görə də funksiyanın işarəsi dəyişmir. Belə hallarda, işarənin dəyişmədiyi kökü keçərkən kvadratla dövrə vuraraq vurğulayacağıq:

Biz belə bir kök adlandıracağıq qatlar.

Bərabərsizliklərdə interval üsulu

İndi istənilən kvadrat bərabərsizliyi parabola çəkmədən həll etmək olar. Kvadrat funksiyanın işarələrini ox üzərində yerləşdirmək və bərabərsizliyin işarəsindən asılı olaraq intervalları seçmək kifayətdir. Misal üçün:

Oxa kökləri ölçüb işarələri yerləşdirək:

Bizə "" işarəsi olan oxun hissəsi lazımdır; bərabərsizlik ciddi olmadığı üçün köklərin özləri də həllə daxildir:

İndi rasional bərabərsizliyi - hər iki tərəfi rasional ifadələr olan bərabərsizliyi nəzərdən keçirək (bax: "Rasional tənliklər").

Misal:

Birindən başqa bütün amillər burada “xətti”dir, yəni onların tərkibində yalnız birinci dərəcəyə dəyişən var. İnterval metodunu tətbiq etmək üçün bizə belə xətti amillər lazımdır - onların köklərindən keçərkən işarə dəyişir. Lakin çarpanın heç bir kökü yoxdur. Bu o deməkdir ki, həmişə müsbətdir (bunu özünüz yoxlayın) və buna görə də bütün bərabərsizliyin işarəsinə təsir göstərmir. Bu o deməkdir ki, bərabərsizliyin sol və sağ tərəflərini ona görə bölə bilərik və bununla da ondan qurtula bilərik:

İndi hər şey kvadrat bərabərsizliklərdə olduğu kimidir: amillərin hər birinin hansı nöqtələrdə sıfıra çevrildiyini müəyyənləşdiririk, bu nöqtələri oxda qeyd edirik və işarələri düzürük. Çox vacib bir fakta diqqətinizi çəkmək istərdim:

Cüt ədəd olduqda, biz əvvəlki kimi edirik: nöqtəni kvadratla dövrələyirik və kökdən keçərkən işarəni dəyişmirik. Ancaq tək ədəd olduqda, bu qayda tətbiq edilmir: kökdən keçərkən işarə hələ də dəyişəcəkdir. Buna görə də, belə bir köklə əlavə bir şey etmirik, sanki çox deyil. Yuxarıdakı qaydalar bütün cüt və tək güclərə aiddir.

Cavabda nə yazmalıyıq?

İşarələrin növbələşməsi pozulursa, çox diqqətli olmalısınız, çünki bərabərsizlik ciddi deyilsə, cavab daxil edilməlidir. bütün kölgəli nöqtələr. Ancaq bəziləri tez-tez bir-birindən ayrılır, yəni kölgəli sahəyə daxil edilmir. Bu halda onları cavaba təcrid olunmuş nöqtələr kimi əlavə edirik (buruq mötərizələrdə):

Nümunələr (özünüz qərar verin):

Cavablar:

1. Əgər amillər arasında sadədirsə, o, kökdür, çünki o, kimi təmsil oluna bilər.
   .

2. Funksiyanın sıfırlarını tapaq.

f(x) x-də .

x-də f(x) cavabını verin .

2) x 2 >-4x-5;

x 2 +4x +5>0;

f(x)=x 2 +4x +5 olsun, onda belə x tapaq ki, f(x)>0,

D=-4 Sıfır yoxdur.

4. Bərabərsizliklər sistemləri. İki dəyişənli bərabərsizliklər və bərabərsizliklər sistemləri

1) Bərabərsizliklər sisteminin həllər çoxluğu ona daxil olan bərabərsizliklərin həllər çoxluqlarının kəsişməsidir.

2) f(x;y)>0 bərabərsizliyinin həllər çoxluğunu koordinat müstəvisində qrafik şəkildə təsvir etmək olar. Tipik olaraq, f(x;y) = 0 tənliyi ilə müəyyən edilən xətt müstəvini 2 hissəyə bölür, bunlardan biri bərabərsizliyin həllidir. Hansı hissəni təyin etmək üçün f(x;y)=0 xəttində olmayan ixtiyari M(x0;y0) nöqtəsinin koordinatlarını bərabərsizliyə əvəz etmək lazımdır. Əgər f(x0;y0) > 0 olarsa, onda bərabərsizliyin həlli müstəvinin M0 nöqtəsini ehtiva edən hissəsidir. əgər f(x0;y0)<0, то другая часть плоскости.

3) Bərabərsizliklər sisteminin həllər çoxluğu ona daxil olan bərabərsizliklərin həllər çoxluqlarının kəsişməsidir. Məsələn, bərabərsizliklər sistemi verilsin:

.

Birinci bərabərsizlik üçün həllər çoxluğu radiusu 2 olan və mərkəzi başlanğıcda yerləşən çevrə, ikincisi üçün isə 2x+3y=0 düz xəttinin üstündə yerləşən yarımmüstəvidir. Bu sistemin həllər toplusu bu çoxluqların kəsişməsidir, yəni. yarımdairə.

4) Nümunə. Bərabərsizliklər sistemini həll edin:

1-ci bərabərsizliyin həlli çoxluq, 2-ci çoxluq (2;7) və üçüncü çoxluqdur.

Bu çoxluqların kəsişməsi bərabərsizliklər sisteminin həllər çoxluğu olan (2;3] intervalıdır.

5. Rasional bərabərsizliklərin interval üsulu ilə həlli

Intervallar metodu binomialın (x-a) aşağıdakı xassəsinə əsaslanır: x = α nöqtəsi ədəd oxunu iki hissəyə bölür - α nöqtəsinin sağında binomial (x-α)>0 və α nöqtəsinin solunda (x-α)<0.

(x-α 1)(x-α 2)...(x-α n)>0 bərabərsizliyini həll etmək lazım gəlsin, burada α 1, α 2 ...α n-1, α n sabitdir. Aralarında bərabərləri olmayan və α 1 olan ədədlər< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 interval metodundan istifadə edərək aşağıdakı kimi hərəkət edin: ədədi oxda α 1, α 2 ...α n-1, α n rəqəmləri çəkilir; onlardan ən böyüyünün sağındakı intervalda, yəni. α n rəqəmləri, artı işarəsi qoyun, ondan sonra sağdan sola doğru olan intervalda mənfi işarə, sonra artı işarəsi, sonra mənfi işarə və s. Onda (x-α 1)(x-α 2)...(x-α n)>0 bərabərsizliyinin bütün həllər çoxluğu artı işarəsinin qoyulduğu bütün intervalların birliyi və çoxluğu olacaqdır. bərabərsizliyin həlli (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».

1) Rasional bərabərsizliklərin (yəni formanın bərabərsizliklərinin) həlli P(x) Q(x) burada çoxhədlərdir) fasiləsiz funksiyanın aşağıdakı xassəsinə əsaslanır: əgər fasiləsiz funksiya x1 və x2 (x1; x2) nöqtələrində yox olursa və bu nöqtələr arasında başqa kök yoxdursa, onda intervallarda (x1; x2) funksiya öz işarəsini saxlayır.

Buna görə də say xəttində y=f(x) funksiyasının sabit işarəli intervallarını tapmaq üçün f(x) funksiyasının itdiyi və ya kəsildiyi bütün nöqtələri qeyd edin. Bu nöqtələr say xəttini bir neçə intervala bölür, onların hər birinin daxilində f(x) funksiyası davamlıdır və itmir, yəni. işarəni saxlayır. Bu işarəni təyin etmək üçün ədəd xəttinin nəzərdən keçirilən intervalının istənilən nöqtəsində funksiyanın işarəsini tapmaq kifayətdir.

2) Rasional funksiyanın sabit işarəsinin intervallarını təyin etmək üçün, yəni. Rasional bərabərsizliyi həll etmək üçün say xəttində payın köklərini və məxrəcin köklərini qeyd edirik ki, onlar da rasional funksiyanın kökləri və kəsilmə nöqtələridir.

İnterval üsulu ilə bərabərsizliklərin həlli

3. < 20.

Həll. Məqbul dəyərlər diapazonu bərabərsizliklər sistemi ilə müəyyən edilir:

f(x) = funksiyası üçün – 20. f(x)-i tapın:

buradan x = 29 və x = 13.

f(30) = – 20 = 0,3 > 0,

f(5) = – 1 – 20 = – 10< 0.

Cavab: . Rasional tənliklərin həllinin əsas üsulları. 1) Ən sadə: adi sadələşdirmələrlə həll olunur - ortaq məxrəcə endirmə, oxşar terminlərin ixtisarı və s. ax2 + bx + c = 0 kvadrat tənlikləri... həll edir.

X intervalında (0,1) dəyişir və = ½ [ intervalında azalır
-(1/3)
], ilə | z|< 1.

b) f(z) = - ½ [
+
] = - (
), 1-də< |z| < 3.

ilə) f(z) = ½ [
]= - ½ [
] =

= - ½ = -
, ilə |2 - z| < 1

Bu, radiusu 1 olan bir dairədir z = 2 .

Bəzi hallarda güc sıraları həndəsi irəliləyişlər toplusuna endirilə bilər və bundan sonra onların yaxınlaşma bölgəsini təyin etmək asandır.

və s. Seriyanın yaxınlaşmasını araşdırın

. . . + + + + 1 + () + () 2 + () 3 + . . .

Həll. Bu, iki həndəsi irəliləyişin cəmidir q 1 = , q 2 = () . Onların yaxınlaşma şərtlərindən belə çıxır < 1 , < 1 или |z| > 1 , |z| < 2 , т.е. область сходимости ряда кольцо 1 < |z| < 2 .