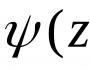Horner dövrəsinin tərifi. Ali riyaziyyatda tənliklər.Çoxhədlilərin rasional kökləri

Slayd 3

Horner Williams George (1786-22.9.1837) - ingilis riyaziyyatçısı. Bristolda anadan olub. Orada oxuyub işlədi, sonra Hamamdakı məktəblərdə. Cəbr üzrə əsas işlər. 1819-cu ildə polinomun həqiqi köklərinin təxmini hesablanması metodunu nəşr etdirmişdir ki, bu üsul hazırda Ruffini-Horner metodu adlanır (bu üsul hələ XIII əsrdə çinlilərə məlum idi) Çoxhədlinin x-a binomuna bölünməsi sxemi adlanır. Hornerdən sonra.

Slayd 4

HORNER SXEMİ

Natamam hissənin və qalığın əmsallarının bölünən çoxhədlinin əmsalları ilə və düsturlarla əlaqələndirilməsinə əsaslanan n-ci dərəcəli çoxhədli xətti binomiala - a bölünməsi üsulu:

Slayd 5

Horner sxeminə görə hesablamalar cədvəldə yerləşdirilmişdir:

Misal 1. Bölün Qismən hissə x3-x2+3x - 13, qalanı isə 42=f(-3) təşkil edir.

Slayd 6

Bu metodun əsas üstünlüyü qeydin yığcamlığı və çoxhədlini tez bir zamanda binomiala bölmək qabiliyyətidir. Əslində, Hornerin sxemi qruplaşdırma metodunu qeyd etməyin başqa bir formasıdır, baxmayaraq ki, sonuncudan fərqli olaraq, tamamilə qeyri-vizualdır. Cavab (faktorizasiya) burada öz-özünə alınır və biz onun alınma prosesini görmürük. Biz Hornerin sxeminin ciddi əsaslandırılması ilə məşğul olmayacağıq, ancaq onun necə işlədiyini göstərəcəyik.

Slayd 7

Misal 2.

P(x)=x4-6x3+7x-392 çoxhədlisinin x-7-yə bölündüyünü sübut edək və bölmənin bölünməsini tapaq. Həll. Horner sxemindən istifadə edərək P(7) tapırıq: Buradan P(7)=0 alırıq, yəni. çoxhədli x-7-yə bölündükdə qalıq sıfıra bərabərdir və buna görə də P(x) çoxhədli (x-7) çoxhədlidir.Bundan başqa, cədvəlin ikinci cərgəsindəki ədədlər əmsallardır. P(x) əmsalı (x-7) bölünür, buna görə də P(x)=(x-7)(x3+x2+7x+56).

Slayd 8

x3 – 5x2 – 2x + 16 çoxhədlini çarpanlayın.

Bu çoxhədli tam əmsallara malikdir. Əgər bu çoxhəddin kökü tam ədəddirsə, o, 16 ədədinin bölənidir. Beləliklə, verilmiş çoxhədlinin tam kökləri varsa, onda bunlar yalnız ±1 ədədləri ola bilər; ±2; ±4; ±8; ±16. Birbaşa yoxlama ilə biz əmin olduq ki, 2 rəqəmi bu çoxhədlinin köküdür, yəni x3 – 5x2 – 2x + 16 = (x – 2)Q(x), burada Q(x) ikinci dərəcəli çoxhəddir.

Slayd 9

Əldə edilən 1, −3, −8 ədədləri çoxhədlinin əmsallarıdır ki, bu da ilkin çoxhədlinin x – 2-yə bölünməsi ilə alınır. Bu o deməkdir ki, bölmənin nəticəsi: 1 x2 + (–3)x + ( –8) = x2 – 3x – 8. Bölünmə nəticəsində yaranan çoxhədlinin dərəcəsi həmişə ilkin dərəcəsindən 1 azdır. Beləliklə: x3 – 5x2 – 2x + 16 = (x – 2)(x2 – 3x – 8).

və s. ümumi təhsil xarakteri daşıyır və ali riyaziyyatın BÜTÜN kursunu öyrənmək üçün böyük əhəmiyyət kəsb edir. Bu gün biz "məktəb" tənliklərini təkrarlayacağıq, ancaq "məktəb" tənliklərini deyil - müxtəlif vyshmat problemlərində hər yerdə tapılanları. Həmişə olduğu kimi, hekayə tətbiqi şəkildə izah ediləcək, yəni. Mən təriflərə və təsnifatlara diqqət yetirməyəcəyəm, ancaq onun həlli ilə bağlı şəxsi təcrübəmi sizinlə bölüşəcəyəm. Məlumat ilk növbədə yeni başlayanlar üçün nəzərdə tutulub, lakin daha qabaqcıl oxucular da özləri üçün bir çox maraqlı məqamlar tapacaqlar. Və təbii ki, orta məktəbdən kənara çıxan yeni material olacaq.

Beləliklə, tənlik .... Çoxları bu sözü titrəyərək xatırlayır. Kökləri olan “mürəkkəb” tənliklər nələrdir... ...onları unut! Çünki o zaman bu növün ən zərərsiz “nümayəndələri” ilə qarşılaşacaqsınız. Yaxud onlarla həll üsulu ilə darıxdırıcı triqonometrik tənliklər. Düzünü desəm, mən onları çox sevmirdim... Təlaşlanmayın! – sonra 1-2 addımda aşkar həlli ilə sizi əsasən “dandelionlar” gözləyir. Baxmayaraq ki, "burdock" mütləq yapışır, burada obyektiv olmaq lazımdır.

Qəribədir ki, ali riyaziyyatda çox primitiv tənliklərlə məşğul olmaq daha çox yayılmışdır xətti tənliklər

Bu tənliyi həll etmək nə deməkdir? Bu, onu həqiqi bərabərliyə çevirən “x” (kök) BELƏ dəyərini tapmaq deməkdir. İşarə dəyişikliyi ilə "üç"ü sağa ataq:

və "iki" ni sağ tərəfə buraxın (və ya eyni şey - hər iki tərəfi çarpın) :

Yoxlamaq üçün gəlin qazanılmış kuboku orijinal tənliklə əvəz edək:

Düzgün bərabərlik əldə edilir, yəni tapılan dəyər həqiqətən də bu tənliyin köküdür. Yaxud da necə deyərlər, bu bərabərliyi ödəyir.

Nəzərə alın ki, kök onluq kəsr kimi də yazıla bilər:
Və bu pis üsluba sadiq qalmamağa çalışın! Səbəbini bir dəfədən çox təkrarladım, xüsusən də ilk dərsdə ali cəbr.

Yeri gəlmişkən, tənliyi “ərəb dilində” də həll etmək olar:

Ən maraqlısı isə odur ki, bu qeyd tamamilə qanunidir! Ancaq müəllim deyilsinizsə, bunu etməmək daha yaxşıdır, çünki burada orijinallıq cəzalandırılır =)

Və indi bir az

qrafik həll üsulu

Tənliyin forması və kökü var "X" koordinatı kəsişmə nöqtələri xətti funksiya qrafiki xətti funksiyanın qrafiki ilə (x oxu):

Belə görünür ki, misal o qədər elementardır ki, burada təhlil etmək üçün başqa heç nə yoxdur, lakin ondan daha bir gözlənilməz nüansı “sıxmaq” olar: gəlin eyni tənliyi formada təqdim edək və funksiyaların qrafiklərini quraq:

Orada, xahiş edirəm iki anlayışı qarışdırmayın: tənlik tənlikdir və funksiyası- bu bir funksiyadır! Funksiyalar yalnız kömək tənliyin köklərini tapın. Bunlardan iki, üç, dörd, hətta sonsuz sayda ola bilər. Bu mənada ən yaxın nümunə hamıya məlumdur kvadrat tənlik, həlli alqoritmi ayrı bir paraqraf aldı "isti" məktəb düsturları. Və bu təsadüf deyil! Kvadrat tənliyi həll edə bilsəniz və bilsəniz Pifaqor teoremi, onda biri deyə bilər ki, “ali riyaziyyatın yarısı artıq sizin cibinizdədir” =) Əlbəttə, şişirdilmiş, lakin həqiqətdən o qədər də uzaq deyil!

Buna görə də tənbəl olmayaq və bəzi kvadrat tənliyi istifadə edərək həll edək standart alqoritm:

, bu o deməkdir ki, tənliyin iki fərqli var etibarlıdır kök:

Tapılan hər iki dəyərin faktiki olaraq bu tənliyi təmin etdiyini yoxlamaq asandır:

Birdən həll alqoritmini unutmusunuzsa və əlinizdə heç bir vasitə/kömək əlləri yoxdursa nə etməli? Bu vəziyyət, məsələn, sınaq və ya imtahan zamanı yarana bilər. Qrafik metoddan istifadə edirik! Və iki yol var: edə bilərsiniz nöqtə-nöqtə qurmaq parabola , bununla da oxun harada kəsişdiyini tapmaq (ümumiyyətlə keçərsə). Ancaq daha hiyləgər bir şey etmək daha yaxşıdır: tənliyi formada təsəvvür edin, daha sadə funksiyaların qrafiklərini çəkin - və "X" koordinatları onların kəsişmə nöqtələri aydın görünür!


Düz xəttin parabolaya toxunduğu ortaya çıxarsa, tənliyin iki uyğun (çoxlu) kökü var. Düz xəttin parabolanı kəsmədiyi ortaya çıxarsa, onda həqiqi köklər yoxdur.

Bunun üçün təbii ki, qurmağı bacarmaq lazımdır elementar funksiyaların qrafikləri, lakin digər tərəfdən, hətta məktəbli bu bacarıqları edə bilər.

Və yenə də - tənlik tənlikdir, funksiyalar isə funksiyalardır yalnız kömək etdi tənliyi həll edin!

Və burada, yeri gəlmişkən, bir şeyi də xatırlamaq yerinə düşərdi: Əgər tənliyin bütün əmsalları sıfırdan fərqli bir ədədə vurularsa, onda onun kökləri dəyişməyəcək.

Beləliklə, məsələn, tənlik eyni köklərə malikdir. Sadə bir “sübut” olaraq sabiti mötərizədən çıxaracağam:
və mən onu ağrısız çıxaracağam (Hər iki hissəni “mənfi ikiyə” böləcəyəm):

AMMA! Funksiyanı nəzərə alsaq , onda burada sabitdən xilas ola bilməzsiniz! Yalnız çarpanın mötərizədən çıxarılmasına icazə verilir: .

Bir çox insanlar qrafik həll metodunu "ləyaqətsiz" bir şey hesab edərək düzgün qiymətləndirmir, bəziləri isə bu ehtimalı tamamilə unudurlar. Və bu, kökündən yanlışdır, çünki qrafiklərin tərtib edilməsi bəzən vəziyyəti xilas edir!

Başqa bir misal: tutaq ki, siz ən sadə triqonometrik tənliyin köklərini xatırlamırsınız: . Ümumi düstur məktəb dərsliklərində, ibtidai riyaziyyat üzrə bütün istinad kitablarında var, lakin onlar sizin üçün mövcud deyil. Bununla belə, tənliyin həlli vacibdir (aka "iki"). Çıxış var! – funksiyaların qrafiklərinin qurulması:


bundan sonra onların kəsişmə nöqtələrinin "X" koordinatlarını sakitcə yazırıq:

Sonsuz bir çox kök var və cəbrdə onların sıxlaşdırılmış qeydləri qəbul edilir:
, Harada ( – tam ədədlər dəsti) .

Və "uzaqlaşmadan" bir dəyişən ilə bərabərsizliklərin həllinin qrafik üsulu haqqında bir neçə söz. Prinsip eynidir. Beləliklə, məsələn, bərabərsizliyin həlli istənilən “x” dir, çünki Sinusoid demək olar ki, tamamilə düz xəttin altındadır. Bərabərsizliyin həlli sinusoidin hissələrinin düz xəttin üstündə yerləşdiyi intervallar toplusudur. (x oxu):

və ya qısaca:

Ancaq burada bərabərsizliyin bir çox həlli var: boş, sinusoidin heç bir nöqtəsi düz xəttin üstündə olmadığı üçün.

Anlamadığınız bir şey varmı? Təcili olaraq dərsləri öyrənin dəstləri Və funksiya qrafikləri!

Gəlin istiləşək:

Məşq 1

Aşağıdakı triqonometrik tənlikləri qrafik şəkildə həll edin:

Dərsin sonunda cavablar

Gördüyünüz kimi, dəqiq elmləri öyrənmək üçün düsturları və istinad kitablarını sıxışdırmaq heç də lazım deyil! Üstəlik, bu, kökündən qüsurlu bir yanaşmadır.

Dərsin əvvəlində sizi əmin etdiyim kimi, ali riyaziyyatın standart kursunda mürəkkəb triqonometrik tənliklər çox nadir hallarda həll edilməlidir. Bütün mürəkkəblik, bir qayda olaraq, kimi tənliklərlə başa çatır ki, onların həlli ən sadə tənliklərdən və ən sadə tənliklərdən yaranan iki kök qrupudur. . Sonuncunu həll etmək üçün çox narahat olmayın - kitaba baxın və ya İnternetdə tapın =)

Qrafik həll üsulu daha az əhəmiyyətsiz hallarda da kömək edə bilər. Məsələn, aşağıdakı "ragtag" tənliyini nəzərdən keçirək:

Onun həlli perspektivləri görünür... heç nəyə bənzəmir, ancaq tənliyi formada təsəvvür etmək, qurmaq lazımdır. funksiya qrafikləri və hər şey inanılmaz dərəcədə sadə olacaq. Haqqında məqalənin ortasında bir rəsm var sonsuz kiçik funksiyalar (növbəti tabda açılacaq).

Eyni qrafik metoddan istifadə edərək, tənliyin artıq iki kökü olduğunu və onlardan birinin sıfıra bərabər olduğunu, digərinin isə yəqin ki, irrasional və seqmentinə aiddir. Bu kök təxminən hesablana bilər, məsələn, tangens üsulu. Yeri gəlmişkən, bəzi problemlərdə elə olur ki, kökləri tapmaq lazım deyil, tapmaq lazımdır onlar ümumiyyətlə mövcuddurmu?. Və burada da bir rəsm kömək edə bilər - əgər qrafiklər kəsişmirsə, onda heç bir kök yoxdur.

Tam əmsallı çoxhədlilərin rasional kökləri.
Horner sxemi

İndi isə mən sizi baxışlarınızı Orta əsrlərə çevirməyə və klassik cəbrin unikal atmosferini hiss etməyə dəvət edirəm. Materialı daha yaxşı başa düşmək üçün sizə bir az da olsa oxumağı məsləhət görürəm mürəkkəb ədədlər.

Onlar ən yaxşısıdır. Polinomlar.

Bizim maraq obyektimiz formanın ən çox yayılmış polinomları olacaq bütövəmsallar Natural ədəd deyilir polinom dərəcəsi, sayı – ən yüksək dərəcə əmsalı (və ya ən yüksək əmsal), və əmsalıdır pulsuz üzv.

Bu çoxhədli qısaca ilə işarə edəcəyəm.

Çoxhədlinin kökləri tənliyin köklərini adlandırın

Mən dəmir məntiqi sevirəm =)

Nümunələr üçün məqalənin ən əvvəlinə keçin:

1-ci və 2-ci dərəcəli çoxhədlilərin köklərini tapmaqda heç bir problem yoxdur, lakin siz artırdıqca bu tapşırıq getdikcə çətinləşir. Digər tərəfdən, hər şey daha maraqlı olsa da! Və dərsin ikinci hissəsi məhz buna həsr olunacaq.

Birincisi, nəzəriyyənin ekranının yarısı:

1) Nəticəyə görə cəbrin əsas teoremi, dərəcə çoxhədli tam olaraq var kompleks kökləri. Bəzi köklər (və ya hətta hamısı) xüsusilə ola bilər etibarlıdır. Üstəlik, həqiqi köklər arasında eyni (çoxlu) köklər ola bilər (minimum iki, maksimum ədəd).

Əgər hansısa kompleks ədəd çoxhədlinin köküdürsə, onda qoşma onun sayı da mütləq bu çoxhədlinin köküdür (birləşən kompleks köklər formaya malikdir).

Ən sadə nümunə, ilk dəfə 8-də rast gəlinən kvadrat tənlikdir (kimi) sinif və nəhayət mövzunu “bitirdik” mürəkkəb ədədlər. Xatırladım: kvadrat tənliyin ya iki fərqli həqiqi kökü, ya çox kökü, ya da birləşmiş mürəkkəb kökləri var.

2) Kimdən Bezout teoremi Buradan belə nəticə çıxır ki, əgər ədəd tənliyin köküdürsə, onda müvafiq çoxhədli faktorlara bölünə bilər:
, burada dərəcə çoxhədlidir.

Yenə də köhnə nümunəmiz: tənliyin kökü olduğundan, onda . Bundan sonra məşhur "məktəb" genişlənməsini əldə etmək çətin deyil.

Bezout teoreminin nəticəsi böyük praktik əhəmiyyətə malikdir: əgər biz 3-cü dərəcəli tənliyin kökünü biliriksə, onda onu formada təqdim edə bilərik. və kvadrat tənlikdən qalan kökləri tapmaq asandır. Əgər 4-cü dərəcəli tənliyin kökünü biliriksə, onda sol tərəfi məhsula genişləndirmək olar və s.

Və burada iki sual var:

Sual bir. Bu kökü necə tapmaq olar? Əvvəlcə onun mahiyyətini müəyyən edək: ali riyaziyyatın bir çox məsələlərində onu tapmaq lazımdır rasional, xüsusilə bütövçoxhədlilərin kökləri və bu baxımdan, bizi əsasən onlarla maraqlandıracağıq.... ...o qədər yaxşı, o qədər tüklüdürlər ki, sadəcə onları tapmaq istəyirsən! =)

Ağla gələn ilk şey seçim üsuludur. Məsələn, tənliyi nəzərdən keçirək. Burada tutma sərbəst termindədir - sıfıra bərabər olsaydı, hər şey yaxşı olardı - mötərizədə "x" çıxarırıq və köklərin özləri səthə "düşür":

Amma bizim sərbəst terminimiz “üç”ə bərabərdir və buna görə də “kök” olduğunu iddia edən tənliyə müxtəlif ədədləri əvəz etməyə başlayırıq. Hər şeydən əvvəl, vahid dəyərlərin dəyişdirilməsi özünü təklif edir. Əvəz edək:

Qəbul edildi səhv bərabərlik, beləliklə, vahid "uyğun gəlmədi". Yaxşı, tamam, əvəz edək:

Qəbul edildi doğru bərabərlik! Yəni dəyər bu tənliyin köküdür.

3-cü dərəcəli çoxhədlinin köklərini tapmaq üçün analitik üsul var (Kardano düsturları adlanır), amma indi bizi bir az fərqli vəzifə maraqlandırır.

- çoxhədlimizin kökü olduğundan çoxhədli formada göstərilə bilər və yaranır İkinci sual: "kiçik qardaşı" necə tapmaq olar?

Ən sadə cəbri mülahizələr onu göstərir ki, bunu etmək üçün -ə bölmək lazımdır. Çoxhədli çoxhədliyə necə bölmək olar? Adi ədədləri bölən eyni məktəb üsulu - "sütun"! Bu metodu dərsin ilk nümunələrində ətraflı müzakirə etdim. Kompleks Limitlər, və indi adlanan başqa bir üsula baxacağıq Horner sxemi.

Əvvəlcə "ən yüksək" çoxhədli yazırıq hamı ilə , o cümlədən sıfır əmsallar:
, bundan sonra bu əmsalları (ciddi qaydada) cədvəlin yuxarı cərgəsinə daxil edirik:

Kökü sola yazırıq:

Dərhal qeyd edəcəyəm ki, "qırmızı" nömrə varsa, Hornerin sxemi də işləyir yoxçoxhədlinin köküdür. Bununla belə, hər şeyi tələsməyək.

Yuxarıdan aparıcı əmsalı çıxarırıq:

Aşağı hüceyrələrin doldurulması prosesi bir qədər tikməni xatırladır, burada "mənfi bir" sonrakı addımlara nüfuz edən bir növ "iynə" dir. “Daşınan” rəqəmi (–1)-ə vururuq və yuxarıdakı xanadakı rəqəmi məhsula əlavə edirik:

Tapılan dəyəri "qırmızı iynə" ilə çarpırıq və məhsula aşağıdakı tənlik əmsalını əlavə edirik:

Və nəhayət, nəticədə alınan dəyər yenidən "iynə" və yuxarı əmsal ilə "emal edilir":

Sonuncu xanadakı sıfır çoxhədlinin bölündüyünü bildirir izsiz (olduğu kimi), genişlənmə əmsalları birbaşa cədvəlin alt sətirindən "çıxarılır":

Beləliklə, biz tənlikdən ekvivalent tənliyə keçdik və qalan iki köklə hər şey aydındır. (bu halda biz birləşmiş kompleks kökləri alırıq).

Tənlik, yeri gəlmişkən, qrafik olaraq da həll edilə bilər: süjet "ildırım" və qrafikin x oxunu kəsdiyinə baxın () nöqtədə. Və ya eyni "hiyləgər" hiylə - tənliyi formada yenidən yazırıq, elementar qrafiklər çəkirik və onların kəsişmə nöqtəsinin "X" koordinatını tapırıq.

Yeri gəlmişkən, 3-cü dərəcəli hər hansı bir funksiya-polinomun qrafiki oxu ən azı bir dəfə kəsir, yəni müvafiq tənlik ən azı bir etibarlıdır kök. Bu fakt hər hansı tək dərəcəli çoxhədli funksiya üçün doğrudur.

Və burada da üzərində dayanmaq istərdim mühüm məqam terminologiyaya aiddir: çoxhədli Və polinom funksiyası – eyni şey deyil! Ancaq praktikada tez-tez, məsələn, "polinomun qrafiki" haqqında danışırlar, bu, əlbəttə ki, səhlənkarlıqdır.

Bununla belə, Hornerin sxeminə qayıdaq. Bu yaxınlarda qeyd etdiyim kimi, bu sxem digər nömrələr üçün işləyir, lakin əgər nömrə yox tənliyin köküdür, onda düsturumuzda sıfırdan fərqli əlavə (qalıq) görünür:

Hornerin sxeminə uyğun olaraq "uğursuz" dəyəri "çalışdıraq". Bu vəziyyətdə eyni cədvəldən istifadə etmək rahatdır - solda yeni bir "iynə" yazın, aparıcı əmsalı yuxarıdan hərəkət etdirin. (sol yaşıl ox), və gedirik:

Yoxlamaq üçün mötərizələri açıb oxşar şərtləri təqdim edək:
, TAMAM.

Qalığın (“altı”) çoxhədlinin tam dəyəri olduğunu görmək asandır. Və əslində - bu necədir:
, və daha da gözəl - bu kimi:

Yuxarıdakı hesablamalardan anlamaq asandır ki, Horner sxemi təkcə çoxhədli faktorlara deyil, həm də kökün "sivil" seçimini həyata keçirməyə imkan verir. Hesablama alqoritmini kiçik bir tapşırıqla özünüz birləşdirməyi təklif edirəm:

Tapşırıq 2

Horner sxemindən istifadə edərək, tənliyin tam kökünü tapın və uyğun çoxhədlini çarpazlayın.

Başqa sözlə, burada sonuncu sütunda sıfır qalıq “çəkilənə” qədər ardıcıl olaraq 1, –1, 2, –2, ... – rəqəmlərini yoxlamaq lazımdır. Bu o demək olacaq ki, bu xəttin “iynəsi” çoxhədlinin köküdür

Hesablamaları vahid cədvəldə təşkil etmək rahatdır. Dərsin sonunda ətraflı həll və cavab.

Köklərin seçilməsi üsulu nisbətən sadə hallar üçün yaxşıdır, lakin polinomun əmsalları və/yaxud dərəcəsi böyükdürsə, onda proses uzun müddət çəkə bilər. Və ya bəlkə eyni siyahıdan bəzi dəyərlər var 1, –1, 2, –2 və nəzərə almağın mənası yoxdur? Bundan əlavə, köklər fraksiya ola bilər ki, bu da tamamilə qeyri-elmi pokingə səbəb olacaqdır.

Xoşbəxtlikdən, rasional köklər üçün "namizəd" dəyərlərin axtarışını əhəmiyyətli dərəcədə azalda bilən iki güclü teorem var:

Teorem 1 Gəlin nəzərdən keçirək azalmaz kəsr, harada. Əgər ədəd tənliyin köküdürsə, sərbəst müddət bölünür və aparıcı əmsal bölünür.

Xüsusilə, əgər aparıcı əmsal olarsa, bu rasional kök tam ədəddir:

Və teoremi yalnız bu dadlı detalla istifadə etməyə başlayırıq:

Gəlin tənliyə qayıdaq. Onun aparıcı əmsalı olduğu üçün hipotetik rasional köklər yalnız tam ədəd ola bilər və sərbəst termin mütləq bu köklərə qalıqsız bölünməlidir. Və "üç" yalnız 1, -1, 3 və -3-ə bölünə bilər. Yəni bizim cəmi 4 “kök namizədimiz” var. Və, görə Teorem 1, digər rasional ədədlər PRİNSİPLƏ bu tənliyin kökləri ola bilməz.

Tənlikdə bir az daha “iddiaçılar” var: sərbəst termin 1, –1, 2, – 2, 4 və –4-ə bölünür.

Nəzərə alın ki, 1, –1 rəqəmləri mümkün köklər siyahısının “müntəzəmləridir” (teoremin aşkar nəticəsi) və prioritet test üçün ən yaxşı seçimdir.

Daha mənalı nümunələrə keçək:

Problem 3

Həll: aparıcı əmsal olduğu üçün hipotetik rasional köklər yalnız tam ədəd ola bilər və onlar mütləq sərbəst terminin bölənləri olmalıdırlar. "Mənfi qırx" aşağıdakı nömrə cütlərinə bölünür:
– cəmi 16 “namizəd”.

Və burada dərhal cazibədar bir fikir yaranır: bütün mənfi və ya bütün müsbət kökləri silmək mümkündürmü? Bəzi hallarda bu mümkündür! Mən iki işarəni tərtib edəcəyəm:

1) Əgər HamısıÇoxhədlinin əmsalları mənfi deyilsə, onun müsbət kökləri ola bilməz. Təəssüf ki, bu bizim vəziyyətimiz deyil (İndi, əgər bizə bir tənlik verilmişdirsə - onda bəli, çoxhədlinin hər hansı bir qiymətini əvəz edərkən, çoxhədlinin qiyməti tamamilə müsbətdir, yəni bütün müsbət ədədlər (və məntiqsiz olanlar da) tənliyin kökləri ola bilməz.

2) Tək dərəcələr üçün əmsallar mənfi deyilsə və bütün cüt dərəcələr üçün (pulsuz üzv daxil olmaqla) mənfi olarsa, çoxhədlinin mənfi kökləri ola bilməz. Bu bizim işimizdir! Bir az yaxından baxdıqda görə bilərsiniz ki, tənliyə hər hansı mənfi “X” əvəz edərkən sol tərəf ciddi şəkildə mənfi olacaq, yəni mənfi köklər yox olur.

Beləliklə, araşdırma üçün 8 nömrə qalıb:

Hornerin sxeminə uyğun olaraq onları ardıcıl olaraq “yükləyirik”. Ümid edirəm ki, siz artıq zehni hesablamaları mənimsəmisiniz:

"İki" ni sınaqdan keçirərkən şans bizi gözləyirdi. Beləliklə, baxılan tənliyin köküdür və

Tənliyi öyrənmək qalır . Bunu diskriminant vasitəsilə etmək asandır, lakin mən eyni sxemdən istifadə edərək göstərici testi keçirəcəyəm. Əvvəlcə qeyd edək ki, sərbəst termin 20-yə bərabərdir, yəni Teorem 1 8 və 40 rəqəmləri tədqiqat üçün dəyərləri tərk edərək mümkün köklər siyahısından çıxır (biri Hornerin sxeminə görə aradan qaldırıldı).

Yeni cədvəlin yuxarı cərgəsinə trinomialın əmsallarını yazırıq və Eyni "iki" ilə yoxlamağa başlayırıq. Niyə? Köklər çoxlu ola bildiyi üçün lütfən: - bu tənliyin 10 eyni kökü var. Ancaq diqqətimizi yayındırmayaq:

Burada isə təbii ki, köklərin rasional olduğunu bilə-bilə bir az yalan danışırdım. Axı, əgər onlar irrasional və ya mürəkkəb olsaydılar, qalan bütün nömrələrin uğursuz yoxlanışı ilə üzləşərdim. Buna görə də, praktikada diskriminant tərəfindən rəhbər olun.

Cavab verin: rasional köklər: 2, 4, 5

Təhlil etdiyimiz problemdə şanslı idik, çünki: a) mənfi dəyərlər dərhal düşdü və b) kökü çox tez tapdıq (və nəzəri olaraq bütün siyahını yoxlaya bildik).

Amma reallıqda vəziyyət daha pisdir. Sizi “Son Qəhrəman” adlı maraqlı oyuna baxmağa dəvət edirəm:

Problem 4

Tənliyin rasional köklərini tapın

Həll: By Teorem 1 hipotetik rasional köklərin sayları şərti ödəməlidir (biz "on iki el ilə bölünür" oxuyuruq), məxrəclər isə şərtə uyğundur. Buna əsaslanaraq iki siyahı alırıq:

"list el":
və "siyahı um": (xoşbəxtlikdən buradakı rəqəmlər təbiidir).

İndi bütün mümkün köklərin siyahısını tərtib edək. Əvvəlcə "el siyahısı" nı bölürük. Eyni rəqəmlərin alınacağı tamamilə aydındır. Rahatlıq üçün onları cədvəldə yerləşdirək:

Bir çox fraksiya azaldıldı, nəticədə artıq "qəhrəman siyahısında" olan dəyərlər yarandı. Biz yalnız "yenilər" əlavə edirik:

Eynilə, eyni “siyahı”nı aşağıdakılara bölürük:

və nəhayət

Beləliklə, oyunumuzun iştirakçılarının komandası tamamlandı:


Təəssüf ki, bu məsələdəki çoxhədli "müsbət" və ya "mənfi" kriteriyaya cavab vermir və buna görə də yuxarı və ya aşağı cərgədən imtina edə bilmərik. Bütün nömrələrlə işləməli olacaqsınız.

Özünü necə hiss edirsən? Buyurun, başınızı qaldırın – məcazi mənada “qatil teoremi” adlandırıla bilən başqa bir teorem var... ..."namizədlər", əlbəttə =)

Ancaq əvvəlcə Hornerin diaqramını ən azı biri üçün sürüşdürməlisiniz bütün nömrələri. Ənənəvi olaraq birini götürək. Üst sətirdə polinomun əmsallarını yazırıq və hər şey həmişəki kimidir:

Dörd aydın sıfır olmadığından, qiymət sözügedən polinomun kökü deyil. Amma o, bizə çox kömək edəcək.

Teorem 2 Bəziləri üçünsə ümumiyyətlə polinomun qiyməti sıfırdan fərqlidir: , onda onun rasional kökləri (əgər onlar varsa)şərti təmin etmək

Bizim vəziyyətimizdə və buna görə də bütün mümkün köklər şərti təmin etməlidir (gəlin buna Şərt №1 deyək). Bu dördlük bir çox “namizədlərin” “qatili” olacaq. Nümayiş olaraq bir neçə yoxlamaya baxacağam:

Gəlin “namizədi” yoxlayaq. Bunun üçün onu süni şəkildə kəsr şəklində təqdim edək ki, ondan aydın görünür ki, . Test fərqini hesablayaq: . Dörd "mənfi iki" ilə bölünür: , yəni mümkün kök testdən keçdi.

Dəyəri yoxlayaq. Burada test fərqi belədir: . Təbii ki, ikinci “mövzu” da siyahıda qalır.

“Peşəkar Riyaziyyat Tərbiyəçisi” saytı tədrislə bağlı metodik məqalələr silsiləsini davam etdirir. Məktəb kurikulumunun ən mürəkkəb və problemli mövzuları ilə işim üsullarının təsvirlərini dərc edirəm. Bu material həm adi proqramda, həm də riyaziyyat dərsləri proqramında 8-11-ci sinif şagirdləri ilə işləyən riyaziyyat müəllimləri və repetitorları üçün faydalı olacaqdır.

Riyaziyyat müəllimi həmişə dərslikdə zəif təqdim olunan materialı izah edə bilmir. Təəssüf ki, belə mövzular getdikcə çoxalır və dərsliklərin müəlliflərini izləyən təqdimat xətaları kütləvi şəkildə edilir. Bu, təkcə yeni başlayan riyaziyyat müəllimlərinə və qiyabi repetitorlara (tyutorlar tələbələr və universitet müəllimləridir) deyil, həm də təcrübəli müəllimlərə, peşəkar repetitorlara, təcrübə və ixtisasa malik repetitorlara aiddir. Bütün riyaziyyat müəllimləri məktəb dərsliklərindəki kobud kənarları bacarıqla düzəltmək qabiliyyətinə malik deyillər. Bu düzəlişlərin (və ya əlavələrin) zəruri olduğunu hər kəs də başa düşmür. Materialın uşaqlar tərəfindən keyfiyyətcə qavranılmasına uyğunlaşdırılmasında az sayda uşaq iştirak edir. Təəssüflər olsun ki, vaxt keçdi ki, riyaziyyat müəllimləri metodistlər və nəşrlərin müəllifləri ilə birlikdə dərsliyin hər hərfini kütləvi şəkildə müzakirə edirdilər. Əvvəllər dərslik məktəblərə buraxılmazdan əvvəl təlim nəticələri ilə bağlı ciddi təhlillər, araşdırmalar aparılırdı. Dərslikləri güclü riyaziyyat dərslərinin standartlarına uyğunlaşdıraraq universal hala gətirməyə çalışan həvəskarların vaxtı çatıb.

İnformasiyanın həcmini artırmaq yarışı yalnız onun mənimsənilməsinin keyfiyyətinin azalmasına və nəticədə riyaziyyatda real bilik səviyyəsinin aşağı düşməsinə səbəb olur. Amma heç kim buna əhəmiyyət vermir. Uşaqlarımız isə artıq 8-ci sinifdə institutda oxuduqlarımızı öyrənməyə məcburdurlar: ehtimal nəzəriyyəsi, yüksək dərəcəli tənliklərin həlli və başqa bir şey. Kitablardakı materialın uşağın tam qavrayışı üçün uyğunlaşdırılması çox şey arzulayır və riyaziyyat müəllimi bununla birtəhər məşğul olmağa məcbur olur.

Yetkinlər üçün riyaziyyatda daha çox “Bezout teoremi və Horner sxemi” kimi tanınan “polinomun çoxhədli ilə küncə bölünməsi” kimi xüsusi bir mövzunun tədrisi metodologiyasından danışaq. Cəmi bir neçə il əvvəl bu sual riyaziyyat müəllimi üçün o qədər də aktual deyildi, çünki bu, əsas məktəb kurikulumun bir hissəsi deyildi. İndi Telyakovskinin redaktoru olduğu dərsliyin hörmətli müəllifləri, fikrimcə, ən yaxşı dərsliyin son nəşrinə dəyişikliklər edib, onu tamamilə korlayıb, sadəcə olaraq repetitorun üzərinə lazımsız qayğılar əlavə ediblər. Riyaziyyat statusuna malik olmayan məktəb və sinif müəllimləri müəlliflərin yeniliklərinə diqqət yetirərək dərslərinə daha tez-tez əlavə abzaslar daxil etməyə başladılar, maraqlanan uşaqlar isə riyaziyyat dərsliyinin gözəl səhifələrinə baxaraq getdikcə daha çox müəllimlərdən soruşurlar. tərbiyəçi: “Bu künc bölgüsü nədir? Biz bunun öhdəsindən gələcəyikmi? Bir küncü necə bölüşmək olar? Artıq bu cür birbaşa suallardan gizlətmək yoxdur. Tərbiyəçi uşağa nəsə deməli olacaq.

Amma kimi? Dərsliklərdə səriştəli təqdim olunsaydı, yəqin ki, mövzu ilə işləmə metodunu təsvir etməzdim. Bizdə hər şey necə gedir? Dərslikləri çap edib satmaq lazımdır. Və bunun üçün onlar mütəmadi olaraq yenilənməlidirlər. Universitet müəllimləri uşaqların onlara başıboş, bilik və bacarıqsız gəlməsindən şikayətlənirlər? Riyazi biliyə tələblər artırmı? Əla! Bəzi məşqləri çıxaraq və yerinə başqa proqramlarda öyrənilən mövzuları daxil edək. Niyə bizim dərslik daha pisdir? Biz bəzi əlavə fəsilləri daxil edəcəyik. Məktəblilər künc ayırma qaydasını bilmirlər? Bu əsas riyaziyyatdır. Bu paraqraf “daha ​​çox bilmək istəyənlər üçün” başlığı ilə isteğe bağlı olmalıdır. Repetitorlar buna qarşı? Niyə biz ümumiyyətlə repetitorlarla maraqlanırıq? Metodistlər, məktəb müəllimləri də bunun əleyhinədir? Materialı çətinləşdirməyəcəyik və onun ən sadə hissəsini nəzərdən keçirəcəyik.

Və burada başlayır. Mövzunun sadəliyi və mənimsənilmə keyfiyyəti, ilk növbədə, dərslik müəlliflərinin göstərişlərinə uyğun olaraq, bir-biri ilə aydın əlaqəsi olmayan müəyyən əməliyyatlar toplusunu yerinə yetirməkdə deyil, onun məntiqini başa düşməkdədir. . Əks halda, tələbənin başında duman olacaq. Müəlliflər nisbətən güclü tələbələri hədəfləyirsə (lakin adi proqramda oxuyurlar), onda siz mövzunu komanda şəklində təqdim etməməlisiniz. Dərslikdə nə görürük? Uşaqlar, bu qaydaya görə bölmək lazımdır. Bucağın altındakı polinomu alın. Beləliklə, orijinal çoxhədli faktorlara bölünəcəkdir. Bununla belə, küncün altındakı şərtlərin niyə məhz bu şəkildə seçildiyini, nə üçün onları küncün üstündəki çoxhədli ilə vurmalı və sonra cari qalıqdan çıxarmaq lazım olduğunu başa düşmək aydın deyil. Və ən əsası, seçilmiş monomialların nə üçün sonda əlavə edilməli olduğu və ortaya çıxan mötərizələrin nə üçün orijinal polinomun genişlənməsi olacağı aydın deyil. İstənilən səriştəli riyaziyyatçı dərslikdə verilmiş izahatların üzərinə qalın sual işarəsi qoyacaqdır.

Dərslikdə deyilənlərin hamısını praktiki olaraq şagirdə aydın edən problemin həllini repetitorların və riyaziyyat müəllimlərinin nəzərinə çatdırıram. Əslində, biz Bezout teoremini sübut edəcəyik: əgər a sayı çoxhədlinin köküdürsə, onda bu çoxhədli amillərdən biri x-a, ikincisi isə ilkindən üç üsuldan birində alına bilən amillərə parçalana bilər: transformasiyalar vasitəsilə xətti faktoru təcrid etməklə, küncə bölmək və ya Horner sxemi ilə. Məhz bu formula ilə riyaziyyat müəlliminin işləməsi daha asan olacaq.

Tədris metodologiyası nədir? Əvvəla, bu, riyazi nəticələrin çıxarıldığı izahat və nümunələr ardıcıllığında aydın bir sıradır. Bu mövzu da istisna deyil. Riyaziyyat müəllimi üçün uşağı Bezout teoremi ilə tanış etmək çox vacibdir künclə bölmədən əvvəl. Bu çox vacibdir! Müəyyən bir nümunə ilə başa düşmək daha yaxşıdır. Seçilmiş kökü olan bəzi çoxhədli götürək və 7-ci sinifdən məktəblilərə tanış olan şəxsiyyətin çevrilməsi metodundan istifadə edərək onun faktorlara bölünməsi texnikasını göstərək. Riyaziyyat müəlliminin müvafiq izahatları, vurğuları və məsləhətləri ilə materialı heç bir ümumi riyazi hesablamalar, ixtiyari əmsallar və səlahiyyətlər olmadan çatdırmaq olduqca mümkündür.

Riyaziyyat müəllimi üçün vacib məsləhət- təlimatları əvvəldən axıra qədər izləyin və bu ardıcıllığı dəyişməyin.

Beləliklə, tutaq ki, bir çoxhədlimiz var. Əgər onun X əvəzinə 1 rəqəmini əvəz etsək, çoxhədlinin qiyməti sıfıra bərabər olacaqdır. Buna görə də x=1 onun köküdür. Gəlin onu iki şərtə parçalamağa çalışaq ki, onlardan biri xətti ifadənin və bəzi monomialın hasili olsun, ikincisi isə -dən bir dərəcə kiçik olsun. Yəni onu formada təmsil edək

Qırmızı sahə üçün monomial seçirik ki, aparıcı terminə vurulduqda o, ilkin çoxhədlinin aparıcı üzvü ilə tamamilə üst-üstə düşsün. Əgər şagird zəif deyilsə, o zaman riyaziyyat müəlliminə tələb olunan ifadəni demək iqtidarında olacaq: . Dərhal repetitordan onu qırmızı sahəyə daxil etməsi və açıldıqda nə olacağını göstərməsi xahiş edilməlidir. Bu virtual müvəqqəti polinomu oxların altında (kiçik fotoşəkilin altında) imzalamaq, onu bəzi rənglərlə, məsələn, mavi ilə vurğulamaq yaxşıdır. Bu, qırmızı sahə üçün seçimin qalan hissəsi adlanan termini seçməyə kömək edəcək. Repetitorlara burada qeyd etməyi məsləhət görərdim ki, bu qalığı çıxma ilə tapmaq olar. Bu əməliyyatı yerinə yetirərkən əldə edirik:

Riyaziyyat müəllimi şagirdin diqqətini ona yönəltməlidir ki, bu bərabərliyə birini əvəz etməklə onun sol tərəfində sıfır alacağımıza zəmanət verilir (çünki 1 ilkin çoxhədlinin köküdür), sağ tərəfdə isə, açıq-aydın, biz ilk müddəti də sıfırlayacaq. Bu o deməkdir ki, heç bir yoxlama olmadan birinin “yaşıl qalıq”ın kökü olduğunu söyləyə bilərik.

Gəlin onunla eyni xətti amili təcrid edərək, ilkin çoxhədli ilə etdiyimiz kimi məşğul olaq. Riyaziyyat müəllimi şagirdin qarşısında iki çərçivə çəkir və onlardan soldan sağa doldurmağı xahiş edir.

Tələbə repetitor üçün qırmızı sahə üçün monomial seçir ki, xətti ifadənin baş həddi ilə vurulduqda genişlənən çoxhədmin baş həddi olsun. Onu çərçivəyə yerləşdiririk, dərhal mötərizəni açırıq və qatlanan ifadədən çıxarılmalı olan ifadəni mavi rənglə vurğulayırıq. Bu əməliyyatı yerinə yetirərək alırıq

Və nəhayət, sonuncu qalıq ilə də eyni şeyi edirik

nəhayət alacağıq

İndi gəlin ifadəni mötərizədən çıxaraq və biz ilkin çoxhədlinin amillərə parçalanmasını görəcəyik, bunlardan biri “x minus seçilmiş kök”dür.

Tələbənin sonuncu “yaşıl qalığın” təsadüfən tələb olunan amillərə parçalandığını düşünməməsi üçün riyaziyyat müəllimi bütün yaşıl qalıqların mühüm xüsusiyyətini qeyd etməlidir – onların hər birinin kökü 1-dir. bu qalıqlar azalır, onda bizə nə qədər çoxhədli verilsə də, başlanğıcın hansı dərəcədə olmasından asılı olmayaraq, gec-tez kök 1 olan xətti “yaşıl qalıq” alacağıq və buna görə də o, mütləq müəyyən bir çoxhəcminin hasilinə parçalanacaq. rəqəm və ifadə.

Belə hazırlıq işlərindən sonra riyaziyyat müəllimi üçün küncə böləndə nə baş verdiyini şagirdə izah etmək çətin olmayacaq. Bu eyni prosesdir, yalnız daha qısa və daha yığcam formada, bərabər işarələr olmadan və eyni vurğulanmış şərtləri yenidən yazmadan. Xətti amilin çıxarıldığı çoxhədli küncün soluna yazılır, seçilmiş qırmızı monomiyallar bucaq altında toplanır (indi onların nə üçün toplanması aydın olur), “mavi polinomlar”, “qırmızı ” olanlar x-1-ə vurulmalı və sonra nömrələrin sütuna adi bölünməsində bunun necə edildiyini indi seçilmişdən çıxarmaq lazımdır (burada əvvəllər öyrənilənlərlə bənzətmə var). Nəticədə yaranan "yaşıl qalıqlar" yeni izolyasiyaya və "qırmızı monomialların" seçilməsinə məruz qalır. Və s. sıfır "yaşıl balans" əldə edənə qədər. Ən əsası odur ki, şagird bucağın üstündə və altında yazılan çoxhədlilərin sonrakı taleyini başa düşsün. Aydındır ki, bunlar məhsulu orijinal polinomuna bərabər olan mötərizələrdir.

Riyaziyyat müəlliminin işinin növbəti mərhələsi Bezout teoreminin formalaşdırılmasıdır. Əslində, repetitorun bu yanaşması ilə onun tərtibi göz qabağındadır: a rəqəmi çoxhədlinin köküdürsə, onu faktorlara ayırmaq olar, onlardan biri , digəri isə üç üsuldan birində orijinaldan alınır. :

• birbaşa parçalanma (qruplaşdırma metodunun analoqu)
• küncə bölmək (sütun içində)
• Horner dövrəsi vasitəsilə

Qeyd etmək lazımdır ki, heç də heç də bütün riyaziyyat müəllimləri şagirdlərə horner diaqramını göstərmir və bütün məktəb müəllimləri (xoşbəxtlikdən repetitorların özləri üçün) dərs zamanı mövzuya o qədər də dərindən girmirlər. Bununla belə, riyaziyyat sinif şagirdi üçün uzun bölgüdə dayanmaq üçün heç bir səbəb görmürəm. Üstəlik, ən rahat və sürətli Parçalanma texnikası tam olaraq Horner sxeminə əsaslanır. Uşağa bunun haradan gəldiyini izah etmək üçün yaşıl qalıqlarda daha yüksək əmsalların görünməsini küncə bölmə nümunəsindən istifadə edərək izləmək kifayətdir. Aydın olur ki, ilkin polinomun aparıcı əmsalı birinci “qırmızı monomial” əmsalına, daha sonra isə cari yuxarı polinomun ikinci əmsalına aparılır. çıxılır“qırmızı monomial”ın cari əmsalının çarpılmasının nəticəsi. Buna görə də mümkündür əlavə edin ilə vurulmasının nəticəsi. Şagirdin diqqətini əmsallı hərəkətlərin xüsusiyyətlərinə yönəltdikdən sonra riyaziyyat müəllimi dəyişənlərin özlərini qeyd etmədən bu hərəkətlərin adətən necə yerinə yetirildiyini göstərə bilər. Bunun üçün ilkin çoxhədlinin kökünü və əmsallarını aşağıdakı cədvələ üstünlük sırasına daxil etmək rahatdır:

Polinomda hər hansı bir dərəcə yoxdursa, onun sıfır əmsalı cədvələ məcbur edilir. “Qırmızı polinomların” əmsalları “qarmaq” qaydasına uyğun olaraq alt sətirdə növbə ilə yazılır:

Kök sonuncu qırmızı əmsala vurulur, yuxarı sətirdə növbəti əmsala əlavə edilir və nəticə aşağı sətirə yazılır. Son sütunda sonuncu "yaşıl qalığın", yəni sıfırın ən yüksək əmsalını alacağımıza zəmanət verilir. Proses başa çatdıqdan sonra nömrələr uyğun kök və sıfır qalıq arasında sıxışdırılır ikinci (qeyri-xətti) amilin əmsalları olur.

A kökü alt xəttin sonunda sıfır verdiyindən, Horner sxemindən çoxhədlinin kökünün başlığı üçün rəqəmləri yoxlamaq üçün istifadə edilə bilər. Rasional kökün seçilməsi ilə bağlı xüsusi teorem varsa. Onun köməyi ilə əldə edilən bu titul üçün bütün namizədlər sadəcə növbə ilə soldan Horner diaqramına daxil edilir. Sıfır əldə edən kimi yoxlanılan ədəd kök olacaq və eyni zamanda onun xətti üzrə ilkin çoxhədlinin faktorlara bölünməsi əmsallarını alacağıq. Çox rahat.

Sonda qeyd etmək istərdim ki, Hornerin sxemini düzgün təqdim etmək, eləcə də mövzunu praktiki şəkildə möhkəmləndirmək üçün riyaziyyat müəlliminin sərəncamında kifayət qədər saatlar olmalıdır. “Həftədə bir dəfə” rejimi ilə işləyən repetitor künc bölgüsü ilə məşğul olmamalıdır. Riyaziyyat üzrə Vahid Dövlət İmtahanında və Dövlət Riyaziyyat Akademiyasında, çətin ki, birinci hissədə bu cür vasitələrlə həll oluna bilən üçüncü dərəcəli tənliklə rastlaşasınız. Bir repetitor uşağı Moskva Dövlət Universitetində riyaziyyat imtahanına hazırlayırsa, mövzunun öyrənilməsi məcburi olur. Universitet müəllimləri, Vahid Dövlət İmtahanının tərtibatçılarından fərqli olaraq, həqiqətən abituriyentin bilik dərinliyini yoxlamağı sevirlər.

Kolpakov Alexander Nikolaevich, riyaziyyat müəllimi, Moskva, Strogino

Horner sxemi - polinomun bölünmə üsulu

$$P_n(x)=\sum\limits_(i=0)^(n)a_(i)x^(n-i)=a_(0)x^(n)+a_(1)x^(n-1) )+a_(2)x^(n-2)+\ldots+a_(n-1)x+a_n$$

$x-a$ binomunda. Birinci cərgə verilmiş polinomun əmsallarını ehtiva edən cədvəllə işləməli olacaqsınız. İkinci sətrin birinci elementi $x-a$ binomialından götürülən $a$ rəqəmi olacaq:

n-ci dərəcəli çoxhədlini $x-a$ binomuna böldükdən sonra dərəcəsi orijinaldan bir az olan çoxhədli alırıq, yəni. $n-1$-a bərabərdir. Horner sxeminin birbaşa tətbiqi nümunələrlə nümayiş etdirmək üçün ən asandır.

Nümunə № 1

Horner sxemindən istifadə edərək $5x^4+5x^3+x^2-11$-ı $x-1$-a bölün.

İki sətirdən ibarət cədvəl tərtib edək: birinci sətirdə $5x^4+5x^3+x^2-11$ çoxhədlisinin $x$ dəyişəninin dərəcələrinin azalma ardıcıllığı ilə düzülmüş əmsallarını yazırıq. Qeyd edək ki, bu çoxhədli birinci dərəcədə $x$ ehtiva etmir, yəni. $x$-ın birinci gücə əmsalı 0-dır. Biz $x-1$-a böldükdən sonra ikinci sətirə birini yazırıq:

İkinci sətirdəki boş xanaları doldurmağa başlayaq. İkinci sətrin ikinci xanasına $5$ rəqəmini yazırıq, sadəcə onu birinci sətrin müvafiq xanasından köçürürük:

Növbəti xananı bu prinsipə uyğun dolduraq: $1\cdot 5+5=10$:

İkinci sətrin dördüncü xanasını eyni şəkildə dolduraq: $1\cdot 10+1=11$:

Beşinci xana üçün alırıq: $1\cdot 11+0=11$:

Və nəhayət, sonuncu, altıncı xana üçün bizdə: $1\cdot 11+(-11)=0$:

Problem həll olundu, cavabı yazmaq qalır:

Göründüyü kimi, ikinci sətirdə (bir ilə sıfır arasında) yerləşən ədədlər $5x^4+5x^3+x^2-11$-nı $x-1$-a böldükdən sonra alınan polinomun əmsallarıdır. Təbii ki, ilkin $5x^4+5x^3+x^2-11$ çoxhədlinin dərəcəsi dördə bərabər olduğundan, nəticədə $5x^3+10x^2+11x+11$ çoxhədlinin dərəcəsi birdir. daha az, yəni. üçə bərabərdir. İkinci sətirdəki sonuncu ədəd (sıfır) $5x^4+5x^3+x^2-11$ polinomunu $x-1$-a bölərkən qalığı bildirir. Bizim vəziyyətimizdə qalıq sıfırdır, yəni. çoxhədlilər bərabər bölünür. Bu nəticəni də aşağıdakı kimi xarakterizə etmək olar: $x=1$ üçün $5x^4+5x^3+x^2-11$ polinomunun qiyməti sıfıra bərabərdir.

Nəticəni bu formada da tərtib etmək olar: $5x^4+5x^3+x^2-11$ polinomunun $x=1$-da qiyməti sıfıra bərabər olduğundan, çoxhədlinin kökü birlikdir. $5x^4+5x^3+ x^2-11$.

Nümunə № 2

$x^4+3x^3+4x^2-5x-47$ polinomunu Horner sxemindən istifadə edərək $x+3$-a bölün.

Dərhal şərt edək ki, $x+3$ ifadəsi $x-(-3)$ şəklində təqdim edilməlidir. Hornerin sxemi tam olaraq $-3$ təşkil edəcək. İlkin $x^4+3x^3+4x^2-5x-47$ çoxhədlinin dərəcəsi dördə bərabər olduğundan, bölmə nəticəsində üçüncü dərəcəli çoxhədli əldə edirik:

Nəticə o deməkdir ki

$$x^4+3x^3+4x^2-5x-47=(x+3)(x^3+0\cdot x^2 +4x-17)+4=(x+3)(x^ 3+4x-17)+4$$

Bu vəziyyətdə, $x^4+3x^3+4x^2-5x-47$-nı $x+3$-a böldükdə qalıq $4$ olur. Və ya eynidir, $x=-3$ üçün $x^4+3x^3+4x^2-5x-47$ polinomunun qiyməti $4$-a bərabərdir. Yeri gəlmişkən, $x=-3$-ı verilmiş polinomda birbaşa əvəz etməklə bunu ikiqat yoxlamaq asandır:

$$x^4+3x^3+4x^2-5x-47=(-3)^4+3 \cdot (-3)^3-5 \cdot (-3)-47=4.$$

Bunlar. Dəyişənin verilmiş qiyməti üçün çoxhədlinin qiymətini tapmaq lazımdırsa, Horner sxemindən istifadə etmək olar. Əgər bizim məqsədimiz çoxhədlinin bütün köklərini tapmaqdırsa, onda Horner sxemi 3 nömrəli misalda müzakirə edildiyi kimi, bütün kökləri tükənənə qədər ardıcıl olaraq bir neçə dəfə tətbiq oluna bilər.

Nümunə № 3

Horner sxemindən istifadə edərək $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ polinomunun bütün tam köklərini tapın.

Sözügedən polinomun əmsalları tam ədədlərdir və dəyişənin ən yüksək gücünün əmsalı (yəni $x^6$) birə bərabərdir. Bu halda polinomun tam kökləri sərbəst terminin bölənləri arasında axtarılmalıdır, yəni. 45 ədədinin bölənləri arasında. Verilmiş çoxhədli üçün belə köklər $45 ədədləri ola bilər; \; 15; \; 9; \; 5; \; 3; \; 1$ və -45$; \; -15; \; -9; \; -5; \; -3; \; -1$. Məsələn, $1$ rəqəmini yoxlayaq:

Gördüyünüz kimi, $x=1$ olan $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ polinomunun qiyməti $192$-a bərabərdir (son rəqəm ikinci sətirdə) və $0 $ deyil, ona görə də birlik bu çoxhədlinin kökü deyil. Birinin yoxlanması uğursuz olduğundan, $x=-1$ dəyərini yoxlayaq. Bunun üçün yeni cədvəl yaratmayacağıq, lakin cədvəldən istifadə etməyə davam edəcəyik. №1, ona yeni (üçüncü) sətir əlavə etməklə. $1$ dəyərinin yoxlanıldığı ikinci sətir qırmızı rənglə vurğulanacaq və sonrakı müzakirələrdə istifadə edilməyəcək.

Əlbəttə ki, sadəcə cədvəli yenidən yaza bilərsiniz, lakin onu əl ilə doldurmaq çox vaxt aparacaq. Üstəlik, yoxlanılması uğursuz olan bir neçə nömrə ola bilər və hər dəfə yeni cədvəl yazmaq çətindir. "Kağız üzərində" hesablayarkən qırmızı xətlər sadəcə olaraq kəsilə bilər.

Deməli, $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ polinomunun $x=-1$-da qiyməti sıfıra bərabərdir, yəni. $-1$ ədədi bu polinomun köküdür. $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ polinomunu $x-(-1)=x+1$ binomuna böldükdən sonra $x polinomunu alırıq. ^5+x ^4-22x^3+2x^2+69x+45$, əmsalları cədvəlin üçüncü sətirindən götürülür. № 2 (1 nömrəli nümunəyə bax). Hesablamaların nəticəsi də bu formada təqdim edilə bilər:

\begin(tənlik)x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)(x^5+x^4-22x^3+2x^2 +69x+45)\son(tənlik)

Tam köklərin axtarışına davam edək. İndi $x^5+x^4-22x^3+2x^2+69x+45$ polinomunun köklərini axtarmalıyıq. Yenə də bu çoxhədlinin tam kökləri onun sərbəst müddətinin bölənləri, $45$ ədədləri arasında axtarılır. Gəlin $-1$ rəqəmini yenidən yoxlamağa çalışaq. Yeni cədvəl yaratmayacağıq, lakin əvvəlki cədvəldən istifadə etməyə davam edəcəyik. 2 nömrəli, yəni. Gəlin ona daha bir sətir əlavə edək:

Deməli, $-1$ ədədi $x^5+x^4-22x^3+2x^2+69x+45$ polinomunun köküdür. Bu nəticəni belə yazmaq olar:

\begin(tənlik)x^5+x^4-22x^3+2x^2+69x+45=(x+1)(x^4-22x^2+24x+45) \end(tənlik)

Bərabərliyi (2) nəzərə alaraq bərabərlik (1) aşağıdakı formada yenidən yazıla bilər:

\begin(tənlik)\begin(düzləşdirilmiş) & x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)(x^5+x^4-22x) ^2+2x^2+69x+45)=\\ & =(x+1)(x+1)(x^4-22x^2+24x+45)=(x+1)^2(x^ 4-22x^2+24x+45)\end(düzləşdirilmiş)\end(tənlik)

İndi $x^4-22x^2+24x+45$ polinomunun köklərini axtarmalıyıq - təbii olaraq, onun sərbəst termininin (rəqəmləri $45$) bölənləri arasında. $-1$ rəqəmini yenidən yoxlayaq:

$-1$ ədədi $x^4-22x^2+24x+45$ polinomunun köküdür. Bu nəticəni belə yazmaq olar:

\begin(tənlik)x^4-22x^2+24x+45=(x+1)(x^3-x^2-21x+45) \end(tənlik)

Bərabərliyi (4) nəzərə alaraq bərabərliyi (3) aşağıdakı formada yenidən yazırıq:

\begin(tənlik)\begin(aligned) & x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)^2(x^4-22x^3) +24x+45)= \\ & =(x+1)^2(x+1)(x^3-x^2-21x+45)=(x+1)^3(x^3-x^ 2-21x+45)\end(düzləşdirilmiş)\end(tənlik)

İndi biz $x^3-x^2-21x+45$ polinomunun köklərini axtarırıq. $-1$ rəqəmini yenidən yoxlayaq:

Yoxlama uğursuzluqla başa çatıb. Altıncı sətri qırmızı rənglə vurğulayaq və başqa bir rəqəmi, məsələn, $3$ rəqəmini yoxlamağa çalışaq:

Qalan sıfırdır, ona görə də $3$ rəqəmi sözügedən polinomun köküdür. Beləliklə, $x^3-x^2-21x+45=(x-3)(x^2+2x-15)$. İndi bərabərliyi (5) aşağıdakı kimi yenidən yazmaq olar.

Geri irəli

Diqqət! Slayd önizləmələri yalnız məlumat məqsədi daşıyır və təqdimatın bütün xüsusiyyətlərini əks etdirməyə bilər. Bu işlə maraqlanırsınızsa, tam versiyanı yükləyin.

Dərs növü: İbtidai biliklərin mənimsənilməsi və möhkəmləndirilməsi dərsi.

Dərsin məqsədi:

• Şagirdləri çoxhədlinin kökləri anlayışı ilə tanış etmək və onları tapmağı öyrətmək. Çoxhədlini güclərlə genişləndirmək və çoxhədlini binomiala bölmək üçün Horner sxemindən istifadə bacarıqlarını təkmilləşdirin.
• Horner diaqramından istifadə edərək tənliyin köklərini tapmağı öyrənin.
• Mücərrəd düşüncəni inkişaf etdirin.
• Hesablama mədəniyyətini inkişaf etdirin.
• Fənlərarası əlaqələrin inkişafı.

Dərslər zamanı

1. Təşkilati məqam.

Dərsin mövzusunu xəbərdar edin, məqsədləri formalaşdırın.

2. Ev tapşırığını yoxlamaq.

3. Yeni materialın öyrənilməsi.

Qoy Fn(x) = a n x n +a n-1 x n-1 +...+ a 1 x +a 0 - n dərəcəli x üçün çoxhədli, burada a 0 , a 1 ,...,a n ədədləri verilir və a 0 0-a bərabər deyil. Əgər F n (x) çoxhədli qalığa x-a binomuna bölünürsə , onda bölmə (natamam hissə) n-1 dərəcə Q n-1 (x) polinomudur, qalan R ədəddir və bərabərlik doğrudur. F n (x)=(x-a) Q n-1 (x) +R. F n (x) çoxhədli yalnız R=0 olduqda binomuna (x-a) bölünür.

Bezout teoremi: F n (x) çoxhədlinin binomuna (x-a) bölünməsindən R qalığı F n (x) çoxhədlinin x=a-dakı qiymətinə bərabərdir, yəni. R=Pn(a).

Bir az tarix. Bezout teoremi zahiri sadəliyinə və aşkarlığına baxmayaraq, çoxhədlilər nəzəriyyəsinin əsas teoremlərindən biridir. Bu teorem çoxhədlilərin cəbri xassələrini (polinomlara tam ədədlər kimi baxmağa imkan verir) onların funksional xassələri ilə (polinomlara funksiya kimi baxmağa imkan verir) əlaqələndirir. Daha yüksək dərəcəli tənlikləri həll etməyin yollarından biri tənliyin sol tərəfindəki çoxhədli faktorlarla müəyyən etməkdir. Çoxhədlinin və qalığın əmsallarının hesablanması Horner sxemi adlanan cədvəl şəklində yazılır.

Horner sxemi çoxhədlilərin bölünməsi alqoritmidir, bölmənin binomiala bərabər olduğu xüsusi hal üçün yazılmışdır. x–a.

Horner William George (1786 - 1837), ingilis riyaziyyatçısı. Əsas tədqiqat cəbri tənliklər nəzəriyyəsinə aiddir. İstənilən dərəcəli tənliklərin təxmini həlli metodunu işləyib hazırlayıb. 1819-cu ildə o, çoxhədlinin x - a binomuna bölünməsi cəbri üçün vacib bir üsul təqdim etdi (Horner sxemi).

Horner sxemi üçün ümumi düsturun çıxarılması.

f(x) çoxhədlini qalıqla (x-c) binomuna bölmək q(x) çoxhədli və r ədədini tapmaq deməkdir ki, f(x)=(x-c)q(x)+r

Bu bərabərliyi ətraflı yazaq:

f 0 x n + f 1 x n-1 + f 2 x n-2 + ...+f n-1 x + f n =(x-c) (q 0 x n-1 + q 1 x n-2 + q 2) x n-3 +...+ q n-2 x + q n-1)+r

Eyni dərəcələrdə əmsalları bərabərləşdirək:

xn:	f 0 = q 0	=> q 0 = f 0
xn-1:	f 1 = q 1 - c q 0	=> q 1 = f 1 + c q 0
xn-2:	f 2 = q 2 - c q 1	=> q 2 = f 2 + c q 1
...		...
x0:	f n = q n - c q n-1	=> q n = f n + c q n-1.

Nümunədən istifadə edərək Horner dövrəsinin nümayişi.

Məşq 1. Horner sxemindən istifadə edərək, f(x) = x 3 - 5x 2 + 8 polinomunu qalığı ilə x-2 binomuna bölürük.

f(x) = x 3 - 5x 2 + 8 =(x-2)(x 2 -3x-6)-4, burada g(x)= (x 2 -3x-6), r = -4 qalıq.

Çoxhədlinin binomun səlahiyyətlərində genişlənməsi.

Horner sxemindən istifadə edərək f(x)=x 3 +3x 2 -2x+4 polinomunu (x+2) dərəcələrində genişləndiririk.

Nəticədə f(x) = x 3 +3x 2 -2x+4 = (x+2)(x 2 +x-4)+12 = (x+2)((x-1) genişlənməsini əldə etməliyik. )(x+ 2)-2)+12 = (((1*(x+2)-3)(x+2)-2)(x+2))+12 = (x+2) 3 -3( x+2 ) 2 -2(x+2)+12

Horner sxemi tez-tez üçüncü, dördüncü və daha yüksək dərəcəli tənliklərin həlli zamanı, polinomu x-a binomuna genişləndirmək əlverişli olduqda istifadə olunur. Nömrə açağırdı polinomun kökü F n (x) = f 0 x n + f 1 x n-1 + f 2 x n-2 + ...+f n-1 x + f n, əgər at x=açoxhədli F n (x) qiyməti sıfıra bərabərdir: F n (a)=0, yəni. çoxhədli x-a binomuna bölünürsə.

Məsələn, 2 rəqəmi F 3 (x)=3x 3 -2x-20 çoxhədlinin köküdür, çünki F 3 (2)=0. deməkdir. Bu polinomun faktorlara ayrılması x-2 faktorunu ehtiva edir.

F 3 (x)=3x 3 -2x-20=(x-2)(3x 2 +6x+10).

Hər hansı çoxhədli F n(x) dərəcə n 1 daha ola bilməz nəsl köklər.

Tam əmsallı tənliyin istənilən tam kökü onun sərbəst müddətinin bölənidir.

Əgər tənliyin aparıcı əmsalı 1-dirsə, onda tənliyin bütün rasional kökləri, əgər varsa, tam ədədlərdir.

Öyrənilən materialın konsolidasiyası.

Yeni materialı möhkəmləndirmək üçün tələbələrə dərslikdən 2.41 və 2.42 (səh. 65) nömrələrini tamamlamaq təklif olunur.

(2 şagird lövhədə həll edir, qalanları qərar verərək dəftərdəki tapşırıqları lövhədəki cavablarla yoxlayır).

Xülasə.

Horner sxeminin strukturunu və iş prinsipini başa düşərək, tam ədədlərin onluq say sistemindən ikilik sistemə və əksinə çevrilməsi məsələsinə baxıldıqda ondan informatika dərslərində də istifadə oluna bilər. Bir say sistemindən digərinə keçidin əsasını aşağıdakı ümumi teorem təşkil edir

Teorem. Tam ədədi çevirmək üçün Ap-dan səh-ar say sistemindən əsas say sisteminə d zəruri Ap ardıcıl olaraq qalanı ədədə bölün d, eyni şəkildə yazılmışdır səh-ar sistemi, nəticədə alınan hissə sıfıra bərabər olana qədər. Bölmədən qalanlar olacaq d- ədədi rəqəmlər Elan, ən gənc kateqoriyadan başlayaraq ən yaşlı kateqoriyaya qədər. Bütün tədbirlər həyata keçirilməlidir səh-ar say sistemi. Bir şəxs üçün bu qayda yalnız o zaman əlverişlidir səh= 10, yəni. tərcümə edərkən -dan onluq sistemi. Kompüterə gəldikdə isə, əksinə, onun ikili sistemdə hesablamalar aparması “daha ​​rahatdır”. Buna görə də, "2-dən 10-a" çevirmək üçün ikilik sistemdə ona ardıcıl bölmədən istifadə olunur və "10-dan 2" onluğun gücünün əlavə edilməsidir. “10-da 2” prosedurunun hesablamalarını optimallaşdırmaq üçün kompüter Hornerin qənaətcil hesablama sxemindən istifadə edir.

Ev tapşırığı. İki tapşırığın yerinə yetirilməsi təklif olunur.

1-ci Horner sxemindən istifadə edərək f(x)=2x 5 -x 4 -3x 3 +x-3 çoxhədlisini binomuna (x-3) bölün.

2-ci. f(x)=x 4 -2x 3 +2x 2 -x-6 çoxhədlinin tam köklərini tapın.(tam əmsallı tənliyin istənilən tam kökünün onun sərbəst üzvünə bölən olduğunu nəzərə alsaq)

Ədəbiyyat.

1. Kurosh A.G. “Ali Cəbr Kursu.”
2. Nikolski S.M., Potapov M.K. və başqaları 10-cu sinif “Cəbr və riyazi analizin başlanğıcları”.
3. http://inf.1september.ru/article.php?ID=200600907.