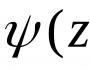अपूर्णांकातील फंक्शनचे शून्य कसे शोधायचे. फंक्शनचे शून्य कसे शोधायचे

कार्य शून्यही वितर्क मूल्ये आहेत ज्यावर फंक्शन शून्याच्या बरोबरीचे आहे.

y=f(x) सूत्राने दिलेल्या फंक्शनचे शून्य शोधण्यासाठी, तुम्हाला f(x)=0 हे समीकरण सोडवावे लागेल.

समीकरणाला मुळे नसल्यास, फंक्शनला शून्य नसते.

उदाहरणे.

1) y=3x+15 रेखीय कार्याचे शून्य शोधा.

फंक्शनचे शून्य शोधण्यासाठी, 3x+15=0 हे समीकरण सोडवा.

अशा प्रकारे, y=3x+15 फंक्शनचे शून्य x= -5 आहे.

उत्तर: x= -5.

2) चतुर्भुज फंक्शन f(x)=x²-7x+12 चे शून्य शोधा.

फंक्शनचे शून्य शोधण्यासाठी, चतुर्भुज समीकरण सोडवा

त्याची मुळे x1=3 आणि x2=4 या फंक्शनचे शून्य आहेत.

उत्तर: x=3; x=4.

सूचना

1. फंक्शनचे शून्य हे वितर्क x चे मूल्य असते ज्यावर फंक्शनचे मूल्य शून्य असते. तथापि, अभ्यासाधीन फंक्शनच्या व्याख्येच्या कक्षेत असलेले केवळ तेच वितर्क शून्य असू शकतात. म्हणजेच, अनेक मूल्ये आहेत ज्यासाठी फंक्शन f(x) उपयुक्त आहे. 2. दिलेले फंक्शन लिहा आणि त्याचे शून्याशी समीकरण करा, म्हणा f(x) = 2x?+5x+2 = 0. परिणामी समीकरण सोडवा आणि त्याची खरी मुळे शोधा. भेदभाव शोधण्यासाठी समर्थनासह चतुर्भुज समीकरणाची मुळे मोजली जातात. 2x?+5x+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0.5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. अशाप्रकारे, या प्रकरणात, चतुर्भुज समीकरणाची दोन मुळे मिळतील. प्रारंभिक कार्य f(x) चे वितर्क. 3. दिलेल्या फंक्शनच्या परिभाषेच्या डोमेनशी संबंधित सर्व शोधलेली x मूल्ये तपासा. OOF शोधा, हे करण्यासाठी, फॉर्म?f (x) च्या सम मुळांच्या उपस्थितीसाठी प्रारंभिक अभिव्यक्ती तपासा, फंक्शनमधील अपूर्णांकांच्या उपस्थितीसाठी, भाजकातील युक्तिवादासह, लॉगरिदमिक किंवा त्रिकोणमितीच्या उपस्थितीसाठी. अभिव्यक्ती 4. सम डिग्रीच्या मुळाखाली अभिव्यक्ती असलेल्या फंक्शनचा विचार करताना, व्याख्येचे क्षेत्र म्हणून सर्व वितर्क x घ्या, ज्याची मूल्ये मूलगामी अभिव्यक्तीला नकारात्मक संख्येमध्ये बदलत नाहीत (त्याउलट, फंक्शन असे करते. अर्थ नाही). फंक्शनचे आढळलेले शून्य स्वीकार्य x मूल्यांच्या विशिष्ट श्रेणीमध्ये येतात का ते तपासा. 5. अपूर्णांकाचा भाजक शून्यावर जाऊ शकत नाही; म्हणून, अशा परिणामाकडे नेणारे वितर्क x वगळा. लॉगरिदमिक परिमाणांसाठी, केवळ वितर्काची ती मूल्ये विचारात घेतली पाहिजे ज्यासाठी अभिव्यक्ती शून्यापेक्षा मोठी आहे. उपलोगॅरिदमिक अभिव्यक्ती शून्य किंवा ऋण संख्येमध्ये बदलणाऱ्या फंक्शनचे शून्य अंतिम परिणामातून टाकून दिले पाहिजेत. लक्षात ठेवा!समीकरणाची मुळे शोधताना, अतिरिक्त मुळे दिसू शकतात. हे तपासणे सोपे आहे: फंक्शनमध्ये वितर्काचे परिणामी मूल्य बदला आणि फंक्शन शून्यावर वळते की नाही याची खात्री करा. उपयुक्त सल्लाकधीकधी एखादे फंक्शन त्याच्या युक्तिवादाद्वारे स्पष्टपणे व्यक्त केले जात नाही, तर हे कार्य काय आहे हे जाणून घेणे सोपे आहे. याचे उदाहरण म्हणजे वर्तुळाचे समीकरण.

कार्य शून्य abscissa मूल्य ज्यावर फंक्शनचे मूल्य शून्य असते त्याला म्हणतात.

जर एखादे फंक्शन त्याच्या समीकरणाने दिले असेल, तर फंक्शनचे शून्य हे समीकरणाचे निराकरण असेल. जर फंक्शनचा आलेख दिला असेल, तर फंक्शनचे शून्य ही मूल्ये आहेत ज्यावर आलेख x-अक्षाला छेदतो.

कार्यही सर्वात महत्वाची गणिती संकल्पना आहे. कार्य - परिवर्तनशील अवलंबित्व येथेव्हेरिएबल पासून x, प्रत्येक मूल्य असल्यास एक्सएका मूल्याशी जुळते येथे. चल एक्सस्वतंत्र चल किंवा युक्तिवाद म्हणतात. चल येथेअवलंबून व्हेरिएबल म्हणतात. स्वतंत्र व्हेरिएबलची सर्व मूल्ये (व्हेरिएबल x) फंक्शनच्या व्याख्येचे डोमेन तयार करा. अवलंबून व्हेरिएबल घेते सर्व मूल्ये (व्हेरिएबल y), फंक्शनच्या मूल्यांची श्रेणी तयार करा.

कार्य आलेखकोऑर्डिनेट प्लेनच्या सर्व बिंदूंचा संच कॉल करा, ज्याचे abscissas वितर्काच्या मूल्यांच्या समान आहेत आणि ordinates फंक्शनच्या संबंधित मूल्यांच्या समान आहेत, म्हणजे, ची मूल्ये व्हेरिएबल abscissa अक्षावर प्लॉट केलेले आहेत x, आणि व्हेरिएबलची मूल्ये ऑर्डिनेट अक्षाच्या बाजूने प्लॉट केली जातात y. फंक्शनचा आलेख काढण्यासाठी, आपल्याला फंक्शनचे गुणधर्म माहित असणे आवश्यक आहे. फंक्शनच्या मुख्य गुणधर्मांची खाली चर्चा केली जाईल!

फंक्शनचा आलेख तयार करण्यासाठी, आम्ही आमचा प्रोग्राम - ग्राफिंग फंक्शन्स ऑनलाइन वापरण्याची शिफारस करतो. या पृष्ठावरील सामग्रीचा अभ्यास करताना आपल्याला काही प्रश्न असल्यास, आपण ते नेहमी आमच्या फोरमवर विचारू शकता. तसेच फोरमवर ते तुम्हाला गणित, रसायनशास्त्र, भूमिती, संभाव्यता सिद्धांत आणि इतर अनेक विषयांमधील समस्या सोडवण्यास मदत करतील!

फंक्शन्सचे मूलभूत गुणधर्म.

1) फंक्शन डोमेन आणि फंक्शन रेंज.

फंक्शनचे डोमेन हे सर्व वैध वैध वितर्क मूल्यांचा संच आहे x(चल x), ज्यासाठी कार्य y = f(x)निर्धारित
फंक्शनची श्रेणी सर्व वास्तविक मूल्यांचा संच आहे y, जे फंक्शन स्वीकारते.

प्राथमिक गणितामध्ये, फंक्शन्सचा अभ्यास केवळ वास्तविक संख्यांच्या सेटवर केला जातो.

2) कार्य शून्य.

फंक्शन शून्य हे वितर्काचे मूल्य आहे ज्यावर फंक्शनचे मूल्य शून्याच्या बरोबरीचे आहे.

3) फंक्शनच्या स्थिर चिन्हाचे अंतराल.

फंक्शनच्या स्थिर चिन्हाचे अंतराल हे वितर्क मूल्यांचे संच असतात ज्यावर फंक्शन मूल्ये केवळ सकारात्मक किंवा फक्त नकारात्मक असतात.

4) फंक्शनची मोनोटोनिसिटी.

वाढणारे फंक्शन (विशिष्ट अंतराल) हे असे फंक्शन असते ज्यामध्ये या मध्यांतरातील वितर्काचे मोठे मूल्य फंक्शनच्या मोठ्या मूल्याशी संबंधित असते.

कमी होत जाणारे फंक्शन (विशिष्ट अंतरालमध्ये) हे असे फंक्शन असते ज्यामध्ये या मध्यांतरातील वितर्काचे मोठे मूल्य फंक्शनच्या लहान मूल्याशी संबंधित असते.

5) सम (विषम) कार्य.

सम फंक्शन हे एक फंक्शन आहे ज्याचे परिभाषेचे डोमेन मूळ आणि कोणत्याही बाबतीत सममितीय आहे एक्सव्याख्या क्षेत्रातून समानता f(-x) = f(x). सम फंक्शनचा आलेख ऑर्डिनेटबद्दल सममितीय असतो.

विषम फंक्शन हे एक फंक्शन आहे ज्याचे परिभाषेचे डोमेन मूळ आणि कोणत्याही बाबतीत सममितीय आहे एक्सव्याख्येच्या क्षेत्रातून समानता सत्य आहे f(-x) = - f(x). विषम कार्याचा आलेख उत्पत्तीबद्दल सममितीय असतो.

6) मर्यादित आणि अमर्यादित कार्ये.

जर |f(x)| अशी सकारात्मक संख्या M असेल तर फंक्शनला बाउंडेड म्हणतात x च्या सर्व मूल्यांसाठी ≤ M. जर अशी संख्या अस्तित्वात नसेल, तर फंक्शन अमर्यादित आहे.

7) कार्याचा कालावधी.

कोणत्याही x f(x+T) = f(x) साठी शून्य संख्या T असल्यास फंक्शन f(x) नियतकालिक आहे. या सर्वात लहान संख्येला कार्याचा कालावधी म्हणतात. सर्व त्रिकोणमितीय कार्ये नियतकालिक असतात. (त्रिकोणमितीय सूत्र).

फंक्शनच्या या गुणधर्मांचा अभ्यास केल्यावर, तुम्ही फंक्शन सहजपणे एक्सप्लोर करू शकता आणि फंक्शनच्या गुणधर्मांचा वापर करून, तुम्ही फंक्शनचा आलेख तयार करू शकता. सत्य सारणी, गुणाकार सारणी, नियतकालिक सारणी, व्युत्पन्न सारणी आणि अविभाज्य सारणी बद्दलची सामग्री देखील पहा.

कार्य शून्य

फंक्शन शून्य म्हणजे काय? विश्लेषणात्मक आणि ग्राफिक पद्धतीने फंक्शनचे शून्य कसे ठरवायचे?

कार्य शून्य- ही वितर्क मूल्ये आहेत ज्यावर फंक्शन शून्याच्या बरोबरीचे आहे.

y=f(x) सूत्राने दिलेल्या फंक्शनचे शून्य शोधण्यासाठी, तुम्हाला f(x)=0 हे समीकरण सोडवावे लागेल.

समीकरणाला मुळे नसल्यास, फंक्शनला शून्य नसते.

1) y=3x+15 रेखीय कार्याचे शून्य शोधा.

फंक्शनचे शून्य शोधण्यासाठी, 3x+15 =0 हे समीकरण सोडवा.

अशा प्रकारे, फंक्शनचे शून्य y=3x+15 - x= -5 आहे.

2) चतुर्भुज फंक्शन f(x)=x²-7x+12 चे शून्य शोधा.

फंक्शनचे शून्य शोधण्यासाठी, चतुर्भुज समीकरण सोडवा

त्याची मुळे x1=3 आणि x2=4 या फंक्शनचे शून्य आहेत.

3) फंक्शनचे शून्य शोधा

जर भाजक शून्य नसलेला असेल तर अपूर्णांकाचा अर्थ होतो. म्हणून, x²-1≠0, x² ≠ 1, x ≠±1. म्हणजेच, दिलेल्या फंक्शनच्या व्याख्येचे डोमेन (DO)

x²+5x+4=0 x1=-1 x2=-4 या समीकरणाच्या मुळांपैकी फक्त x=-4 हे व्याख्येच्या क्षेत्रामध्ये समाविष्ट केले आहे.

ग्राफिक पद्धतीने दिलेल्या फंक्शनचे शून्य शोधण्यासाठी, तुम्हाला अॅब्सिसा अक्षासह फंक्शन आलेखाचे छेदनबिंदू शोधणे आवश्यक आहे.

आलेख ऑक्स-अक्षाला छेदत नसल्यास, फंक्शनमध्ये शून्य नसते.

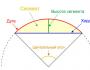
ज्या फंक्शनचा आलेख आकृतीमध्ये दाखवला आहे त्यात चार शून्य आहेत -

बीजगणितामध्ये, फंक्शनचे शून्य शोधण्याची समस्या स्वतंत्र कार्य म्हणून आणि इतर समस्या सोडवताना उद्भवते, उदाहरणार्थ, फंक्शनचा अभ्यास करताना, असमानता सोडवणे इ.

www.algebraclass.ru

कार्य शून्य नियम

मूलभूत संकल्पना आणि फंक्शन्सचे गुणधर्म

नियम (कायदा) पत्रव्यवहार. मोनोटोनिक फंक्शन .

मर्यादित आणि अमर्यादित कार्ये. सतत आणि

खंडित कार्ये . सम आणि विषम कार्ये.

नियतकालिक कार्य. कार्याचा कालावधी.

कार्य शून्य . विषमता .

परिभाषाचे डोमेन आणि फंक्शनच्या मूल्यांची श्रेणी. प्राथमिक गणितामध्ये, फंक्शन्सचा अभ्यास केवळ वास्तविक संख्यांच्या सेटवर केला जातो आर . याचा अर्थ असा की फंक्शन आर्ग्युमेंट फक्त ती वास्तविक मूल्ये घेऊ शकते ज्यासाठी फंक्शन परिभाषित केले आहे, उदा. ते केवळ वास्तविक मूल्ये देखील स्वीकारते. चा गठ्ठा, चा गुच्छ, चा घड एक्स सर्व वैध वैध युक्तिवाद मूल्ये x, ज्यासाठी कार्य y = f (x) परिभाषित केले जाते, म्हणतात फंक्शनचे डोमेन. चा गठ्ठा, चा गुच्छ, चा घड वाय सर्व वास्तविक मूल्ये y, जे फंक्शन स्वीकारते, त्याला म्हणतात कार्य श्रेणी. आता आपण फंक्शनची अधिक अचूक व्याख्या देऊ शकतो: नियम (कायदा) संचांमधील पत्रव्यवहार एक्सआणि वाय , त्यानुसार सेटमधील प्रत्येक घटकासाठी एक्सतुम्ही सेटमधून एक आणि फक्त एक घटक शोधू शकता वाय, याला फंक्शन म्हणतात .

या व्याख्येवरून असे दिसून येते की फंक्शन परिभाषित मानले जाते जर:

- फंक्शनच्या परिभाषाचे डोमेन निर्दिष्ट केले आहे एक्स ;

- कार्य श्रेणी निर्दिष्ट केली आहे वाय ;

- पत्रव्यवहाराचा नियम (कायदा) ज्ञात आहे आणि प्रत्येकासाठी

वितर्क मूल्य, फक्त एक फंक्शन मूल्य आढळू शकते.

फंक्शनच्या विशिष्टतेची ही आवश्यकता अनिवार्य आहे.

मोनोटोनिक फंक्शन. जर वादाच्या कोणत्याही दोन मूल्यांसाठी x 1 आणि xअट 2 x 2 > x 1 अनुसरण करतो f (x 2) > f (x 1), नंतर फंक्शन f (x) असे म्हणतात वाढत आहे; जर कोणत्याहीसाठी x 1 आणि xअट 2 x 2 > x 1 अनुसरण करतो f (x 2)

अंजीर 3 मध्ये दर्शविलेले कार्य मर्यादित आहे, परंतु मोनोटोनिक नाही. अंजीर 4 मधील फंक्शन अगदी उलट, मोनोटोनिक, परंतु अमर्यादित आहे. (कृपया हे समजावून सांगा!).

सतत आणि खंडित कार्ये. कार्य y = f (x) असे म्हणतात सतत बिंदूवर x = a, तर:

1) फंक्शन जेव्हा परिभाषित केले जाते x = a, म्हणजे f (a) अस्तित्वात;

2) अस्तित्वात आहे मर्यादितमर्यादा मर्यादा f (x) ;

यापैकी किमान एक अटी पूर्ण न झाल्यास, फंक्शन म्हणतात स्फोटकबिंदूवर x = a .

दरम्यान फंक्शन सतत चालू असल्यास प्रत्येकजण त्याच्या व्याख्येच्या क्षेत्राचे मुद्दे, नंतर म्हणतात सतत कार्य.

सम आणि विषम कार्ये. साठी असल्यास कोणतेही xफंक्शनच्या व्याख्येच्या डोमेनमधून खालील गोष्टी आहेत: f (— x) = f (x), नंतर फंक्शन म्हणतात अगदी; असे झाल्यास: f (— x) = — f (x), नंतर फंक्शन म्हणतात विषम. सम कार्याचा आलेख Y अक्षाबद्दल सममितीय(चित्र 5), विषम कार्याचा आलेख सिम मूळच्या संदर्भात मेट्रिक(चित्र 6).

नियतकालिक कार्य. कार्य f (x) — नियतकालिक, अशी एखादी गोष्ट अस्तित्वात असल्यास शून्य नसलेलेसंख्या टकशासाठी कोणतेही xफंक्शनच्या व्याख्येच्या डोमेनमधून खालील गोष्टी आहेत: f (x + ट) = f (x). या किमाननंबरला कॉल केला जातो कार्य कालावधी. सर्व त्रिकोणमितीय कार्ये नियतकालिक असतात.

उदाहरण १. ते पाप सिद्ध करा x 2 चा कालावधी आहे.

उपाय: आम्हाला माहित आहे की पाप ( x+ 2 n) = पाप x, कुठे n= 0, ± 1, ± 2, …

म्हणून, जोडणे 2 nसाइन युक्तिवादासाठी नाही

त्याचे मूल्य बदलते e. यासोबत दुसरा नंबर आहे का?

चला ते ढोंग करूया पी- अशी संख्या, म्हणजे समानता:

कोणत्याही मूल्यासाठी वैध x. पण नंतर आहे

ठिकाणी आणि येथे x= / 2, i.e.

पाप (/2 + पी) = पाप / 2 = 1.

पण घट सूत्रानुसार पाप (/ 2 + पी) = cos पी. मग

शेवटच्या दोन समानतेपासून ते कॉसचे अनुसरण करते पी= 1, पण आम्ही

हे तेव्हाच खरे आहे हे आपल्याला माहीत आहे पी = 2 n. सर्वात लहान असल्याने

2 पासून शून्य नसलेली संख्या n 2 आहे, नंतर ही संख्या

आणि एक कालावधी पाप आहे x. हे त्याच प्रकारे सिद्ध केले जाऊ शकते की 2

cos साठी देखील कालावधी आहे x .

सिद्ध करा की कार्ये तन xआणि खाट xकालावधी आहे.

उदाहरण 2. फंक्शन sin 2 चा कालावधी कोणती संख्या आहे x ?

उपाय: पाप 2 चा विचार करा x= पाप (2 x+ 2 n) = पाप [ २ ( x + n) ] .

त्यात भर पडताना दिसत आहे nयुक्तिवाद करण्यासाठी x, बदलत नाही

कार्य मूल्य. सर्वात लहान शून्य नसलेली संख्या

पासून nआहे, म्हणून हा कालावधी पाप 2 आहे x .

कार्य शून्य. ज्या आर्ग्युमेंट व्हॅल्यूवर फंक्शन 0 च्या बरोबरीचे असते त्याला म्हणतात शून्य ( रूट) फंक्शन. फंक्शनमध्ये अनेक शून्य असू शकतात. उदाहरणार्थ, फंक्शन y = x (x + 1) (x- 3) मध्ये तीन शून्य आहेत: x = 0, x = — 1, x= 3. भौमितिकदृष्ट्या शून्य कार्य – हे अक्षासह फंक्शन आलेखाच्या छेदनबिंदूच्या बिंदूचे abscissa आहे एक्स .

आकृती 7 शून्यासह फंक्शनचा आलेख दाखवते: x = a , x = bआणि x = c .

विषमता. जर एखाद्या फंक्शनचा आलेख एखाद्या विशिष्ट रेषेपर्यंत अनिश्चित काळासाठी उगमस्थानापासून दूर जात असेल, तर या रेषेला म्हणतात. लक्षणे.

विषय 6. "मध्यांतर पद्धत."

जर x x 0 साठी f (x) f (x 0) असेल तर फंक्शन f (x) म्हणतात बिंदू x 0 वर सतत.

जर फंक्शन काही अंतराल I च्या प्रत्येक बिंदूवर सतत असेल तर त्याला म्हणतात मध्यांतरावर सततमी (मला मध्यांतर म्हणतात फंक्शनचे सातत्य अंतराल). या मध्यांतरावरील फंक्शनचा आलेख एक सतत रेषा आहे, जी ते म्हणतात की "पेन्सिल कागदावरुन न उचलता काढता येते."

सतत फंक्शन्सचा गुणधर्म.

जर मध्यांतरावर (a ; b) फंक्शन f सतत असेल आणि नाहीसे होत नसेल, तर ते या मध्यांतरावर एक स्थिर चिन्ह टिकवून ठेवते.

एका व्हेरिएबलसह असमानता सोडवण्याची पद्धत, मध्यांतर पद्धत, या गुणधर्मावर आधारित आहे. फंक्शन f(x) हे मध्यांतर I वर सतत असू द्या आणि या मध्यांतरातील मर्यादित बिंदूंवर अदृश्य होऊ द्या. सतत फंक्शन्सच्या गुणधर्मानुसार, हे बिंदू I ला मध्यांतरांमध्ये विभाजित करतात, ज्यातील प्रत्येक फंक्शन f(x) c एक स्थिर चिन्ह ठेवते. हे चिन्ह निश्चित करण्यासाठी, अशा प्रत्येक मध्यांतरातून कोणत्याही एका बिंदूवर f(x) फंक्शनच्या मूल्याची गणना करणे पुरेसे आहे. यावर आधारित, आम्ही मध्यांतर पद्धत वापरून असमानता सोडवण्यासाठी खालील अल्गोरिदम प्राप्त करतो.

फॉर्मच्या असमानतेसाठी मध्यांतर पद्धत

मध्यांतर पद्धत. सरासरी पातळी.

तुम्हाला तुमची ताकद तपासायची आहे आणि तुम्ही युनिफाइड स्टेट परीक्षा किंवा युनिफाइड स्टेट परीक्षेसाठी किती तयार आहात याचा निकाल शोधू इच्छिता?

रेखीय कार्य

फॉर्मच्या फंक्शनला रेखीय म्हणतात. उदाहरण म्हणून फंक्शन घेऊ. ते 3″> वर सकारात्मक आणि नकारात्मक आहे. बिंदू हे फंक्शन () चे शून्य आहे. संख्या अक्षावर या फंक्शनची चिन्हे दाखवू.

आपण म्हणतो की “बिंदूमधून जाताना फंक्शन चिन्ह बदलते”.

हे पाहिले जाऊ शकते की फंक्शनची चिन्हे फंक्शन आलेखाच्या स्थितीशी संबंधित आहेत: जर आलेख अक्षाच्या वर असेल तर चिन्ह “” असेल, जर ते खाली असेल तर “”.

जर आपण परिणामी नियम एका अनियंत्रित रेखीय फंक्शनमध्ये सामान्यीकृत केले तर आपल्याला खालील अल्गोरिदम मिळेल:

चतुर्भुज कार्य

मला आशा आहे की तुम्हाला आठवत असेल की चतुर्भुज असमानता कशी सोडवायची? नसल्यास, “चतुर्भुज असमानता” हा विषय वाचा. मी तुम्हाला चतुर्भुज फंक्शनच्या सामान्य स्वरूपाची आठवण करून देतो: .

आता चतुर्भुज फंक्शन कोणती चिन्हे घेते ते लक्षात ठेवू. त्याचा आलेख पॅराबोला आहे, आणि फंक्शन ज्यामध्ये पॅराबोला अक्षाच्या वर असेल त्यांच्यासाठी " " चिन्ह घेते आणि " " - जर पॅराबोला अक्षाच्या खाली असेल तर:

जर फंक्शनमध्ये शून्य (ज्याची मूल्ये) असतील तर, पॅराबोला अक्ष दोन बिंदूंवर छेदतो - संबंधित द्विघात समीकरणाची मुळे. अशा प्रकारे, अक्ष तीन मध्यांतरांमध्ये विभागला जातो आणि प्रत्येक रूटमधून जाताना कार्याची चिन्हे वैकल्पिकरित्या बदलतात.

प्रत्येक वेळी पॅराबोला न काढता कसे तरी चिन्हे निश्चित करणे शक्य आहे का?

लक्षात ठेवा की चौरस त्रिपदी घटकबद्ध केली जाऊ शकते:

चला अक्षावर मुळे चिन्हांकित करूया:

आम्ही लक्षात ठेवतो की फंक्शनचे चिन्ह केवळ रूटमधून जात असताना बदलू शकते. चला या वस्तुस्थितीचा उपयोग करूया: अक्ष मुळांद्वारे विभाजित केलेल्या तीन मध्यांतरांपैकी प्रत्येकासाठी, केवळ एका अनियंत्रितपणे निवडलेल्या बिंदूवर फंक्शनचे चिन्ह निश्चित करणे पुरेसे आहे: मध्यांतराच्या उर्वरित बिंदूंवर चिन्ह समान असेल. .

आमच्या उदाहरणात: 3″> येथे कंसातील दोन्ही अभिव्यक्ती सकारात्मक आहेत (पर्यायी, उदाहरणार्थ: 0″>). आम्ही अक्षावर "" चिन्ह ठेवतो:

ठीक आहे, जेव्हा (पर्यायी, उदाहरणार्थ), दोन्ही कंस नकारात्मक असतात, याचा अर्थ उत्पादन सकारात्मक आहे:

तेच आहे मध्यांतर पद्धत: प्रत्येक मध्यांतरावरील घटकांची चिन्हे जाणून घेऊन, आम्ही संपूर्ण उत्पादनाचे चिन्ह निश्चित करतो.

फंक्शनमध्ये शून्य किंवा फक्त एक नसलेल्या प्रकरणांचा देखील विचार करूया.

जर ते नसतील तर मुळे नाहीत. याचा अर्थ असा की "मूळातून जाणे" होणार नाही. याचा अर्थ फंक्शन संपूर्ण संख्या रेषेवर फक्त एक चिन्ह घेते. फंक्शनमध्ये बदलून ते सहजपणे निर्धारित केले जाऊ शकते.

जर एकच मूळ असेल तर पॅराबोला अक्षाला स्पर्श करतो, त्यामुळे रूटमधून जाताना फंक्शनचे चिन्ह बदलत नाही. अशा परिस्थितींसाठी आपण कोणता नियम आणू शकतो?

जर तुम्ही अशा फंक्शनचे घटक केले तर तुम्हाला दोन समान घटक मिळतील:

आणि कोणतीही चौरस अभिव्यक्ती गैर-नकारात्मक असते! त्यामुळे फंक्शनचे चिन्ह बदलत नाही. अशा प्रकरणांमध्ये, आम्ही रूट हायलाइट करू, ज्यामधून जात असताना, चिन्ह बदलत नाही, त्यास चौरसाने प्रदक्षिणा घालून:

अशाला आपण मूळ म्हणू गुणाकार.

असमानता मध्ये मध्यांतर पद्धत

आता कोणतीही चतुर्भुज असमानता पॅराबोला न काढता सोडवता येते. केवळ अक्षावर चतुर्भुज कार्याची चिन्हे ठेवणे आणि असमानतेच्या चिन्हावर अवलंबून मध्यांतरे निवडणे पुरेसे आहे. उदाहरणार्थ:

चला अक्षावर मुळे मोजू आणि चिन्हे ठेवा:

आम्हाला " " चिन्हासह अक्षाचा भाग हवा आहे; असमानता कठोर नसल्यामुळे, मुळे देखील सोल्यूशनमध्ये समाविष्ट आहेत:

आता तर्कसंगत असमानतेचा विचार करा - एक असमानता, ज्याच्या दोन्ही बाजू तर्कसंगत अभिव्यक्ती आहेत (पहा "तर्कसंगत समीकरणे").

उदाहरण:

एक वगळता सर्व घटक येथे "रेषीय" आहेत, म्हणजे, त्यांच्यामध्ये फक्त पहिल्या पॉवरसाठी एक व्हेरिएबल आहे. मध्यांतर पद्धत लागू करण्यासाठी आम्हाला अशा रेखीय घटकांची आवश्यकता आहे - त्यांच्या मुळांमधून जात असताना चिन्ह बदलते. परंतु गुणकांना मुळीच मुळीच नाही. याचा अर्थ असा की ते नेहमीच सकारात्मक असते (हे स्वतःसाठी तपासा), आणि म्हणून संपूर्ण असमानतेच्या चिन्हावर परिणाम होत नाही. याचा अर्थ असा की आपण असमानतेच्या डाव्या आणि उजव्या बाजूंना विभाजित करू शकतो आणि अशा प्रकारे त्यातून मुक्त होऊ शकतो:

आता सर्व काही चतुर्भुज असमानतेप्रमाणेच आहे: प्रत्येक घटक कोणत्या बिंदूंवर शून्य होतो हे आम्ही ठरवतो, हे बिंदू अक्षावर चिन्हांकित करा आणि चिन्हे व्यवस्थित करा. मी एका अतिशय महत्त्वाच्या वस्तुस्थितीकडे तुमचे लक्ष वेधू इच्छितो:

सम संख्येच्या बाबतीत, आम्ही पूर्वीप्रमाणेच करतो: आम्ही चौकोनासह बिंदूवर वर्तुळ करतो आणि रूटमधून जाताना चिन्ह बदलत नाही. परंतु विषम संख्येच्या बाबतीत, हा नियम लागू होत नाही: रूटमधून जात असताना चिन्ह अजूनही बदलेल. म्हणून, आम्ही अशा रूटसह अतिरिक्त काहीही करत नाही, जसे की ते एक बहुविध नव्हते. वरील नियम सर्व सम आणि विषम शक्तींना लागू होतात.

उत्तरात काय लिहावे?

जर चिन्हांच्या बदलाचे उल्लंघन केले गेले असेल तर, आपण खूप सावधगिरी बाळगणे आवश्यक आहे, कारण असमानता कठोर नसल्यास, उत्तरामध्ये हे समाविष्ट केले पाहिजे सर्व छायांकित बिंदू. परंतु त्यापैकी काही अनेकदा वेगळे उभे राहतात, म्हणजेच ते छायांकित क्षेत्रामध्ये समाविष्ट केलेले नाहीत. या प्रकरणात, आम्ही त्यांना उत्तरामध्ये पृथक बिंदू (कुरळे ब्रेसेसमध्ये) म्हणून जोडतो:

उदाहरणे (स्वतःसाठी ठरवा):

उत्तरे:

1. जर घटकांपैकी ते सोपे असेल, तर ते मूळ आहे, कारण ते म्हणून प्रस्तुत केले जाऊ शकते.
   .

2. फंक्शनचे शून्य शोधू.

f(x) येथे x .

x वर f(x) उत्तर द्या .

2) x 2 >-4x-5;

x 2 +4x +5>0;

चला f(x)=x 2 +4x +5 मग असे x शोधू ज्यासाठी f(x)>0,

D=-4 शून्य नाही.

4. असमानता प्रणाली. दोन चलांसह असमानता आणि असमानता प्रणाली

1) असमानतेच्या प्रणालीवरील उपायांचा संच म्हणजे त्यात समाविष्ट असलेल्या असमानतेच्या उपायांच्या संचाचा छेदनबिंदू.

2) असमानता f(x;y)>0 च्या उपायांचा संच समन्वय समतलावर ग्राफिकरित्या चित्रित केला जाऊ शकतो. सामान्यतः, समीकरण f(x;y) = 0 द्वारे परिभाषित केलेली रेखा विमानाला 2 भागांमध्ये विभाजित करते, त्यापैकी एक असमानतेचे समाधान आहे. कोणता भाग निर्धारित करण्‍यासाठी, असमानतेमध्ये f(x;y)=0 या रेषेवर नसलेल्या अनियंत्रित बिंदू M(x0;y0) चे निर्देशांक बदलणे आवश्यक आहे. जर f(x0;y0) > 0 असेल, तर असमानतेचे समाधान म्हणजे विमानाचा भाग ज्यामध्ये M0 बिंदू आहे. जर f(x0;y0)<0, то другая часть плоскости.

3) असमानतेच्या प्रणालीवरील उपायांचा संच हा त्यात समाविष्ट असलेल्या असमानतेच्या उपायांच्या संचाचा छेदनबिंदू आहे. उदाहरणार्थ, असमानतेची प्रणाली द्या:

.

पहिल्या असमानतेसाठी, सोल्यूशन्सचा संच त्रिज्या 2 चे वर्तुळ आहे आणि उत्पत्तीच्या केंद्रस्थानी आहे आणि दुसऱ्यासाठी, ते 2x+3y=0 सरळ रेषेच्या वर स्थित अर्ध-विमान आहे. या प्रणालीच्या सोल्यूशनचा संच या संचांचा छेदनबिंदू आहे, म्हणजे. अर्धवर्तुळ

4) उदाहरण. असमानता प्रणाली सोडवा:

पहिल्या असमानतेचे समाधान म्हणजे संच, दुसरा संच (2;7) आणि तिसरा संच आहे.

या संचांचा छेदनबिंदू म्हणजे मध्यांतर (2;3], जो असमानतेच्या प्रणालीवरील उपायांचा संच आहे.

5. मध्यांतर पद्धती वापरून तर्कसंगत असमानता सोडवणे

मध्यांतरांची पद्धत द्विपदी (x-a) च्या खालील गुणधर्मावर आधारित आहे: बिंदू x = α संख्या अक्ष दोन भागांमध्ये विभाजित करतो - बिंदूच्या उजवीकडे α द्विपदी (x-α)>0, आणि बिंदूच्या डावीकडे α (x-α)<0.

असमानता सोडवणे आवश्यक आहे (x-α 1)(x-α 2)...(x-α n)>0, जेथे α 1, α 2 ...α n-1, α n निश्चित केले आहेत संख्या, ज्यामध्ये कोणतेही समान नाहीत आणि जसे की α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 मध्यांतर पद्धत वापरून पुढीलप्रमाणे पुढे जा: α 1, α 2 ...α n-1, α n संख्यात्मक अक्षावर प्लॉट केले आहेत; त्यातील सर्वात मोठ्याच्या उजवीकडे मध्यांतरात, म्हणजे. संख्या α n, एक अधिक चिन्ह ठेवा, मध्यांतरात उजवीकडून डावीकडे वजा चिन्ह, नंतर अधिक चिन्ह, नंतर वजा चिन्ह इ. नंतर असमानतेच्या सर्व उपायांचा संच (x-α 1)(x‑α 2)...(x-α n)>0 हा सर्व मध्यांतरांचा संघ असेल ज्यामध्ये अधिक चिन्ह ठेवले आहे आणि संच असमानतेचे उपाय (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».

1) तर्कसंगत असमानता सोडवणे (म्हणजे स्वरूपातील असमानता P(x) Q(x) जेथे बहुपदी आहेत) सतत फंक्शनच्या खालील गुणधर्मावर आधारित आहे: जर सतत फंक्शन x1 आणि x2 (x1; x2) बिंदूंवर नाहीसे झाले आणि या बिंदूंमध्ये दुसरे कोणतेही मूळ नसेल, तर अंतराल (x1; x2) फंक्शन त्याचे चिन्ह राखून ठेवते.

म्हणून, संख्या रेषेवरील फंक्शन y=f(x) च्या स्थिर चिन्हाचे मध्यांतर शोधण्यासाठी, फंक्शन f(x) ज्या बिंदूवर नाहीसे होते किंवा खंडित होते ते सर्व बिंदू चिन्हांकित करा. हे बिंदू संख्यारेषेला अनेक मध्यांतरांमध्ये विभाजित करतात, ज्यापैकी प्रत्येकामध्ये फंक्शन f(x) सतत आहे आणि नाहीसे होत नाही, म्हणजे. चिन्ह जतन करते. हे चिन्ह निश्चित करण्यासाठी, संख्या रेषेच्या विचारात घेतलेल्या मध्यांतराच्या कोणत्याही बिंदूवर फंक्शनचे चिन्ह शोधणे पुरेसे आहे.

2) तर्कसंगत कार्याच्या स्थिर चिन्हाचे अंतराल निर्धारित करण्यासाठी, उदा. परिमेय असमानतेचे निराकरण करण्यासाठी, आम्ही संख्या रेषेवर अंशाची मुळे आणि भाजकाची मुळे चिन्हांकित करतो, जे परिमेय कार्याची मुळे आणि ब्रेकपॉइंट देखील आहेत.

मध्यांतर पद्धत वापरून असमानता सोडवणे

3. < 20.

उपाय. स्वीकार्य मूल्यांची श्रेणी असमानतेच्या प्रणालीद्वारे निर्धारित केली जाते:

फंक्शन f(x) = साठी – २०. f(x) शोधा:

जेथून x = 29 आणि x = 13.

f(30) = – 20 = 0.3 > 0,

f(5) = – 1 – 20 = – 10< 0.

उत्तर:. तर्कसंगत समीकरणे सोडवण्यासाठी मूलभूत पद्धती. 1) सर्वात सोपा: नेहमीच्या सरलीकरणाद्वारे सोडवलेले - सामान्य भाजक कमी करणे, समान संज्ञा कमी करणे इ. द्विघात समीकरण ax2 + bx + c = 0 द्वारे सोडवले जातात...

मध्यांतरावर X बदलतो (0,1], आणि मध्यांतरावर कमी होतो = ½ [
-(1/3)
], सह | z|< 1.

ब) f(z) = - ½ [
+
] = - (
), 1 वाजता< |z| < 3.

सह) f(z) = ½ [
]= - ½ [
] =

= - ½ = -
, सह |2 - z| < 1

हे त्रिज्या 1 चे मध्यभागी असलेले वर्तुळ आहे z = 2 .

काही प्रकरणांमध्ये, पॉवर मालिका भौमितिक प्रगतीच्या संचापर्यंत कमी केली जाऊ शकते आणि त्यानंतर त्यांच्या अभिसरणाचा प्रदेश निश्चित करणे सोपे आहे.

इ. मालिकेच्या अभिसरणाची चौकशी करा

. . . + + + + 1 + () + () 2 + () 3 + . . .

उपाय. ही दोन भौमितिक प्रगतींची बेरीज आहे q 1 = , q२ = () . त्यांच्या अभिसरणाच्या स्थितीवरून ते खालीलप्रमाणे आहे < 1 , < 1 или |z| > 1 , |z| < 2 , т.е. область сходимости ряда кольцо 1 < |z| < 2 .