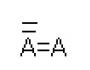Fractals. Koch curve Taratibu za kupata seti za fractal
Nakala tatu za curve ya Koch, iliyojengwa (na alama zake nje) kwenye pande za pembetatu ya kawaida, huunda mkunjo uliofungwa wa urefu usio na kikomo unaoitwa. Snowflake ya Koch.
Takwimu hii ni moja ya fractals ya kwanza iliyochunguzwa na wanasayansi. Inatoka kwa nakala tatu Koch curve, ambayo ilionekana kwa mara ya kwanza kwenye karatasi na mwanahisabati wa Uswidi Helge von Koch mnamo 1904. Mviringo huu ulivumbuliwa kama mfano wa mstari endelevu ambao hauwezi kulegea kwa uhakika wowote. Mistari iliyo na mali hii ilijulikana hapo awali (Karl Weierstrass aliunda mfano wake nyuma mnamo 1872), lakini curve ya Koch ni ya kushangaza kwa unyenyekevu wa muundo wake. Sio bahati mbaya kwamba nakala yake inaitwa "Kwenye mkunjo unaoendelea bila tanjiti, ambayo hutokana na jiometri ya msingi."
Mchoro na uhuishaji unaonyesha kikamilifu jinsi curve ya Koch inavyoundwa hatua kwa hatua. marudio ya kwanza ni sehemu ya awali tu. Kisha imegawanywa katika sehemu tatu sawa, moja ya kati imekamilika ili kuunda pembetatu ya kawaida na kisha kutupwa nje. Matokeo ni iteration ya pili - mstari uliovunjika unaojumuisha sehemu nne. Operesheni hiyo inatumika kwa kila mmoja wao, na hatua ya nne ya ujenzi hupatikana. Kuendelea kwa roho ile ile, unaweza kupata mistari mpya zaidi na zaidi (yote yatavunjwa mistari). Na kile kinachotokea katika kikomo (hii itakuwa tayari kuwa kitu cha kufikiria) inaitwa curve ya Koch.
Tabia za msingi za Curve ya Koch1. Ni endelevu, lakini hakuna mahali pa kutofautisha. Kwa kusema, hii ndio sababu iligunduliwa - kama mfano wa aina hii ya "freaks" za hesabu.
2. Ina urefu usio na kikomo. Hebu urefu wa sehemu ya awali iwe sawa na 1. Katika kila hatua ya ujenzi, tunabadilisha kila sehemu zinazounda mstari na mstari uliovunjika, ambao ni mara 4/3 zaidi. Hii inamaanisha kuwa urefu wa mstari mzima uliovunjika unazidishwa na 4/3 kwa kila hatua: urefu wa mstari na nambari. n sawa na (4/3) n-1 . Kwa hivyo, mstari wa kikomo hauna chaguo lakini kuwa mrefu sana.

3. Snowflake ya Koch hupunguza eneo la mwisho. Na hii licha ya ukweli kwamba mzunguko wake hauna mwisho. Mali hii inaweza kuonekana kuwa ya kushangaza, lakini ni dhahiri - theluji ya theluji inafaa kabisa kwenye mduara, kwa hivyo eneo lake ni wazi kabisa. Eneo linaweza kuhesabiwa, na hauitaji hata ujuzi maalum kwa hili - kanuni za eneo la pembetatu na jumla ya maendeleo ya kijiometri hufundishwa shuleni. Kwa wale wanaopenda, hesabu imeorodheshwa hapa chini kwa maandishi mazuri.
Acha upande wa pembetatu ya kawaida ya asili iwe sawa na a. Kisha eneo lake ni. Kwanza upande ni 1 na eneo ni:. Ni nini hufanyika wakati marudio yanapoongezeka? Tunaweza kudhani kuwa pembetatu ndogo za usawa zimeunganishwa kwenye poligoni iliyopo. Mara ya kwanza kuna 3 tu kati yao, na kila wakati ujao kuna mara 4 zaidi kuliko ya awali. Hiyo ni, juu n hatua ya th itakamilika Tn= 3 4 n-1 pembetatu. Urefu wa upande wa kila mmoja wao ni theluthi moja ya upande wa pembetatu iliyokamilishwa katika hatua ya awali. Kwa hivyo ni sawa na (1/3) n. Maeneo ni sawia na mraba wa pande, hivyo eneo la kila pembetatu ni ![]() . Kwa maadili makubwa n Kwa njia, hii ni kidogo sana. Mchango wa jumla wa pembetatu hizi kwa eneo la theluji ni Tn · S n= 3/4 · (4/9) n · S 0 . Kwa hivyo baada ya n-hatua, eneo la takwimu litakuwa sawa na jumla S 0 + T 1 · S 1 + T 2 · S 2 + ... +Tn S n =
. Kwa maadili makubwa n Kwa njia, hii ni kidogo sana. Mchango wa jumla wa pembetatu hizi kwa eneo la theluji ni Tn · S n= 3/4 · (4/9) n · S 0 . Kwa hivyo baada ya n-hatua, eneo la takwimu litakuwa sawa na jumla S 0 + T 1 · S 1 + T 2 · S 2 + ... +Tn S n = ![]() . Kitambaa cha theluji kinapatikana baada ya idadi isiyo na kipimo ya hatua, ambayo inalingana na n→ ∞. Matokeo yake ni jumla isiyo na kikomo, lakini hii ni jumla ya kupungua kwa maendeleo ya kijiometri; kuna fomula yake:
. Kitambaa cha theluji kinapatikana baada ya idadi isiyo na kipimo ya hatua, ambayo inalingana na n→ ∞. Matokeo yake ni jumla isiyo na kikomo, lakini hii ni jumla ya kupungua kwa maendeleo ya kijiometri; kuna fomula yake: ![]() . Eneo la theluji ni.
. Eneo la theluji ni.
4. Kipimo cha Fractal ni sawa na log4/log3 = logi 3 4 ≈ 1.261859... . Hesabu sahihi itahitaji juhudi kubwa na maelezo ya kina, kwa hivyo hapa kuna kielelezo cha ufafanuzi wa mwelekeo wa fractal. Kutoka kwa fomula ya sheria ya nguvu N(δ ) ~ (1/δ )D, Wapi N- idadi ya viwanja vya kuingiliana, δ - ukubwa wao, na D ni mwelekeo, tunapata hiyo D= logi 1/ δ N. Usawa huu ni kweli hadi nyongeza ya mara kwa mara (sawa kwa wote δ ) Takwimu zinaonyesha marudio ya tano ya ujenzi wa curve ya Koch; miraba ya gridi inayoingiliana nayo ni ya kijani iliyotiwa kivuli. Urefu wa sehemu ya awali ni 1, hivyo katika takwimu ya juu urefu wa upande wa mraba ni 1/9. Mraba 12 ni kivuli, logi 9 12 ≈ 1.130929... . Haifanani sana na 1.261859 bado... . Hebu tuangalie zaidi. Katika picha ya kati, mraba ni ukubwa wa nusu, ukubwa wao ni 1/18, kivuli 30. logi 18 30 ≈ 1.176733... . Tayari bora. Hapa chini, miraba bado ni nusu kubwa; vipande 72 tayari vimepakwa rangi. logi 72 30 ≈ 1.193426... . Hata karibu zaidi. Kisha unahitaji kuongeza nambari ya iteration na wakati huo huo kupunguza mraba, basi thamani ya "empirical" ya mwelekeo wa curve ya Koch itakaribia kwa kasi logi 3 4, na kwa kikomo itafanana kabisa.

Kitambaa cha theluji cha Koch "kinyume chake" kinapatikana ikiwa tutaunda curves za Koch ndani ya pembetatu ya asili ya usawa.

mistari ya Cesaro. Badala ya pembetatu za usawa, pembetatu za isosceles na angle ya msingi kutoka 60 ° hadi 90 ° hutumiwa. Katika takwimu, angle ni 88 °.

Chaguo la mraba. Hapa viwanja vimekamilika.
|
Snowflake Koch
turubai(
mpaka: 1px iliyopigwa nyeusi;
}
var cos = 0.5,
dhambi = Math.sqrt(3) / 2,
deg = Math.PI / 180;
canv, ctx;
kazi rebro(n, len) (
ctx.save(); // Hifadhi mabadiliko ya sasa
ikiwa (n == 0) ( // Kesi isiyo ya kujirudia - chora mstari
ctx.lineTo(len, 0);
}
mwingine (
ctx.scale(1 / 3, 1 / 3); // Kuza nje kwa mara 3
rebro(n-1, len); //RECUURSION ukingoni
ctx.rotate (60 * deg);
rebro(n-1, len);
ctx.rotate(-120 * deg);
rebro(n-1, len);
ctx.rotate (60 * deg);
rebro(n-1, len);
}
ctx.rejesha (); // Rejesha mabadiliko
ctx.translate(len, 0); // kwenda mwisho wa makali
}
kitendakazi kuchoraKochSnowflake(x, y, len, n) (
x = x - len / 2;
y = y + len / 2 * Math.sqrt(3)/3;
ctx.save();
ctx.beginPath();
ctx.tafsiri(x, y);
ctx.moveTo(0, 0);
rebro(n, len); ctx.rotate(-120 * deg); //RECUUUURSION tayari ni pembetatu
rebro(n, len); ctx.rotate(-120 * deg);
rebro(n, len); ctx.closePath();
ctx.strokeStyle = "#000";
ctx.stroke();
ctx.rejesha ();
}
fanya kazi clearcanvas())( //safisha turubai
ctx.save();
ctx.beginPath();
// Tumia matrix ya utambulisho wakati wa kusafisha turubai
ctx.setTransform(1, 0, 0, 1, 0, 0);
ctx.clearRect(0, 0, canvas1.width, canvas1.height);
// Rejesha ubadilishaji
ctx.rejesha ();
}
kazi run() (
canv = document.getElementById("canvas1");
ctx = canv.getContext("2d");
var numberiter = document.getElementById("qty").thamani;
drawKochSnowflake(canv.width/2, canv.height/2, 380, numberiter);
Ctx.stroke(); // utoaji
}
Snowflake ya Koch - mfano
Ilikuwa majira ya baridi kali isivyo kawaida huko Boston, lakini bado tulingoja theluji inyeshe kwa mara ya kwanza. Kuangalia theluji ikianguka kupitia dirisha, nilifikiria juu ya theluji na jinsi muundo wao sio rahisi kuelezea kihesabu. Hata hivyo kuna aina moja maalum ya theluji, inayojulikana kama theluji ya Koch, ambayo inaweza kuelezewa kwa urahisi. Leo tutaangalia jinsi umbo lake linaweza kujengwa kwa kutumia Kijenzi cha Maombi ya Multifizikia ya COMSOL.
Uundaji wa theluji ya KochKama tulivyokwisha sema kwenye blogi yetu, fractals inaweza kutumika katika . Snowflake Koch ni fractal, ambayo inajulikana kwa kuwa kuna mchakato rahisi sana wa kuijenga:
Utaratibu huu unaonyeshwa kwenye takwimu hapa chini kwa marudio manne ya kwanza ya kuchora kitambaa cha theluji.
Marudio manne ya kwanza ya theluji ya Koch. Picha na Wxs - Kazi yako mwenyewe. Imepewa leseni chini ya CC BY-SA 3.0, kupitia Wikimedia Commons.
Ujenzi wa jiometri ya theluji ya KochKwa kuwa sasa tunajua ni algorithm gani ya kutumia, hebu tuangalie jinsi ya kuunda muundo kama huo kwa kutumia Kijenzi cha Maombi ya Multifizikia ya COMSOL. Tutafungua faili mpya na kuunda kipengee cha P2 sehemu ya jiometri kwenye nodi Ufafanuzi wa kimataifa. Kwa kitu hiki, tutaweka vigezo vitano vya pembejeo: urefu wa upande wa pembetatu ya equilateral; X- Na y- kuratibu za katikati ya msingi; na vipengele vya vekta ya kawaida iliyoelekezwa kutoka katikati ya msingi hadi vertex kinyume, kama inavyoonyeshwa kwenye takwimu hapa chini.

Vigezo vitano vinavyotumika kuweka ukubwa, nafasi na uelekeo wa pembetatu iliyo sawa.

Kuweka vigezo vya pembejeo vya sehemu ya kijiometri.  Nyuma ya poligoni hutumiwa kuunda pembetatu iliyo sawa.
Nyuma ya poligoni hutumiwa kuunda pembetatu iliyo sawa.

Kitu kinaweza kuzunguka katikati ya makali ya chini.

Kitu kinaweza kusongezwa kulingana na asili.
Sasa kwa kuwa tumefafanua sehemu ya kijiometri, tunaitumia mara moja katika sehemu hiyo Jiometri. Pembetatu hii ni sawa na marudio ya sufuri ya theluji ya Koch, na sasa hebu tutumie Kiunda Programu kuunda vipande vya theluji ngumu zaidi.
Alama ya UI ya Programu katika Kiunda ProgramuProgramu ina kiolesura rahisi sana cha mtumiaji. Ina vipengele viwili tu ambavyo mtumiaji anaweza kuingiliana navyo: Kitelezi (Kitelezi)(iliyowekwa alama kama 1 kwenye takwimu hapa chini), ambayo unaweza kuweka idadi ya marudio yanayohitajika kuunda theluji, na Kitufe(lebo 2), kwa kubofya ambayo jiometri inayotokana imeundwa na kuonyeshwa. Wapo pia Uandishi wa maandishi(lebo 3) na Onyesha (Onyesho) la data(lebo 4), ambayo inaonyesha idadi ya marudio maalum, pamoja na dirisha Chati(lebo 5), ambayo inaonyesha jiometri ya mwisho.

Maombi yana fomu moja yenye vipengele vitano.
maombi ina mbili Ufafanuzi, moja ambayo inafafanua thamani kamili inayoitwa Iterations, ambayo hubadilika kuwa sifuri lakini inaweza kubadilishwa na mtumiaji. Safu ya 1D ya maradufu inayoitwa Center pia imefafanuliwa. Kipengele kimoja katika safu kina thamani ya 0.5, ambayo hutumiwa kupata sehemu ya katikati ya kila makali. Thamani hii haibadilika kamwe.

Mipangilio ya Fasili mbili.
Sehemu ya Kitelezi katika kiolesura hudhibiti thamani ya kigezo kamili, cha Marudio. Picha ya skrini iliyo hapa chini inaonyesha mipangilio ya "Kitelezi" na thamani, ambazo zimewekwa kama nambari kamili katika masafa kati ya 0 na 5. Chanzo sawa (kama cha kitelezi) pia kimechaguliwa kwa kipengele. Onyesho la Data kuonyesha idadi ya marudio maalum kwenye skrini ya programu. Tunawekea kikomo mtumiaji anayewezekana kwa marudio matano kwa sababu kanuni iliyotumika ni ndogo na haifanyi kazi vizuri sana, lakini ni rahisi vya kutosha kutekeleza na kuonyesha.

Mipangilio ya sehemu ya "Slider".
Ifuatayo, hebu tuangalie mipangilio ya kifungo chetu, kilichoonyeshwa kwenye skrini hapa chini. Wakati kifungo kinaposisitizwa, amri mbili zinatekelezwa. Kwanza, njia ya CreateSnowFlake inaitwa. Jiometri inayotokana inaonyeshwa kwenye dirisha la michoro.

Mipangilio ya kitufe.
Sasa tumeangalia kiolesura cha mtumiaji wa programu yetu na tunaweza kuona kwamba uundaji wa jiometri yoyote ya theluji lazima ifanyike kupitia njia inayoitwa. Wacha tuangalie nambari ya njia hii, na nambari za mstari zimeongezwa upande wa kushoto na viunga vya kamba vilivyoangaziwa kwa nyekundu:
1 model.geom("geom1" ).kipengele().clear(); 2 model.geom("geom1" ).unda("pi1" , "PartInstance" ); 3 model.geom("geom1" ).run("fin" ); 4 kwa (int iter = 1; iter "geom1" ).getNEdges()+1; 6 UnionList = "pi" + iter; 7 kwa (int edge = 1; makali "geom1").getNEdges(); edge++) ( 8 String newPartInstance = "pi" + iter + edge; 9 model.geom("geom1" ).create(newPartInstance, "PartInstance" ).set("part" , "part1" ); 10 with(model. geom("geom1" ).kipengele(newPartInstance)); 11 setEntry("inputexpr" , "Length" , toString(Math.pow(1.0/3.0, iter))); 12 setEntry("inputexpr" , "px" , model.geom("geom1" ).edgeX(edge, Center)); 13 setEntry("inputexpr" , "py" , model.geom("geom1").edgeX(edge, Center)); 14 setEntry("inputexpr " , "nx" , model.geom("geom1" ).edgeNormal(edge, Center)); 15 setEntry("inputexpr" , "ny" , model.geom("geom1").edgeNormal(edge, Center)) ; 16 endwith(); 17 UnionList = newPartInstance; 18 ) 19 model.geom("geom1" ).create("pi" +(iter+1), "Union" ).selection("input" ).set(UnionList ); 20 model.geom("geom1" ).kipengele("pi" +(iter+1)).set("intbnd" , "off" ); 21 model.geom("geom1" ).run("fin" ); 22)
Wacha tupitie mstari wa nambari kwa mstari ili kuelewa ni kazi gani kila mstari hufanya:
Kwa hivyo, tumeshughulikia vipengele na vipengele vyote vya maombi yetu. Hebu tuangalie matokeo!

Programu yetu rahisi ya kuunda theluji ya Koch.
Tunaweza kupanua maombi yetu ya kuandika jiometri kwenye faili, au hata kufanya uchanganuzi wa ziada moja kwa moja. Kwa mfano, tunaweza kuunda antenna ya fractal. Ikiwa una nia ya kubuni ya antenna, angalia mfano wetu, au hata ufanye mpangilio wake kutoka mwanzo.
Jaribu mwenyeweIkiwa ungependa kuunda programu hii mwenyewe, lakini bado hujakamilisha Kijenzi cha Maombi, unaweza kupata nyenzo zifuatazo zitakusaidia:
- Pakua mwongozo Utangulizi wa Mazingira ya Ukuzaji wa Maombi kwa Kiingereza
- Tazama video hizi na ujifunze jinsi ya kutumia
- Soma mada hizi ili kufahamiana na jinsi programu za uigaji zinavyotumika
Ukishashughulikia nyenzo hii, utaona jinsi utendakazi wa programu unavyoweza kupanuliwa ili kubadilisha ukubwa wa chembe ya theluji, kutuma jiometri iliyoundwa, eneo la makadirio na mzunguko, na mengi zaidi.
Ni aina gani ya programu ungependa kuunda katika Multifizikia ya COMSOL? kwa msaada.
Theluji ya theluji ya fractal, mojawapo ya vitu maarufu na vya ajabu vya kijiometri, ilielezwa na Helga von Koch mwanzoni mwa karne yetu. Kulingana na mila, katika fasihi zetu inaitwa theluji ya Koch. Hiki ni kielelezo cha kijiometri "kicho" sana, ambacho kinaweza kuonekana kisitiari kama matokeo ya Nyota ya Daudi "kuzidishwa" yenyewe mara kwa mara. Miale yake sita kuu imefunikwa na idadi isiyo na kikomo ya wima kubwa na ndogo za "sindano". Kila kipande kidogo sana cha mtaro wa kitambaa cha theluji ni kama mbaazi mbili kwenye ganda, na boriti kubwa, kwa upande wake, ina idadi isiyo na kikomo ya vipande sawa vya hadubini.
Katika kongamano la kimataifa juu ya mbinu ya modeli ya hesabu huko Varna mnamo 1994, nilikutana na kazi ya waandishi wa Kibulgaria ambao walielezea uzoefu wao wa kutumia theluji za Koch na vitu vingine sawa katika masomo ya shule ya upili ili kuonyesha shida ya mgawanyiko wa nafasi na vitu vingine vinavyofanana. aporia za kifalsafa za Zeno. Kwa kuongeza, kutoka kwa mtazamo wa elimu, kwa maoni yangu, kanuni yenyewe ya kujenga miundo ya kijiometri ya fractal inavutia sana - kanuni ya kuzidisha mara kwa mara ya kipengele cha msingi. Sio bure kwamba asili "inapenda" fomu za fractal. Hii inafafanuliwa kwa usahihi na ukweli kwamba hupatikana kwa uzazi rahisi na kubadilisha saizi ya jengo fulani la msingi. Kama unavyojua, asili haifuki kwa sababu mbalimbali na, inapowezekana, hufanya na ufumbuzi rahisi zaidi wa algorithmic. Angalia kwa karibu mtaro wa majani, na katika hali nyingi utapata uhusiano wazi na sura ya contour ya theluji ya Koch.
Taswira ya miundo ya kijiometri ya fractal inawezekana tu kwa msaada wa kompyuta. Tayari ni ngumu sana kuunda kitambaa cha theluji cha Koch juu ya mpangilio wa tatu kwa mikono, lakini kwa kweli unataka kuangalia ndani ya infinity! Kwa hiyo, kwa nini usijaribu kuendeleza programu inayofaa ya kompyuta. Katika RuNet unaweza kupata mapendekezo ya kujenga theluji ya Koch kutoka kwa pembetatu. Matokeo ya algoriti hii inaonekana kama msururu wa mistari inayokatiza. Inavutia zaidi kuchanganya takwimu hii kutoka kwa "vipande". Mtaro wa theluji ya Koch una sehemu za urefu sawa na 0 °, 60 °, na 120 ° kwa heshima na mhimili wa x mlalo. Ikiwa tunaashiria 1, 2 na 3 kwa mtiririko huo, basi theluji ya utaratibu wowote itakuwa na triplets mfululizo - 1, 2, 3, 1, 2, 3, 1, 2, 3 ... nk Kila moja ya aina hizi tatu. ya sehemu inaweza kushikamana na moja uliopita kwa moja au mwisho mwingine. Kwa kuzingatia hali hii, tunaweza kudhani kuwa contour ya theluji ina sehemu ya aina sita. Hebu tuwaashiria 0, 1, 2, 3, 4, 5. Kwa hivyo, tunapata fursa ya kusimba contour ya utaratibu wowote kwa kutumia tarakimu 6 (angalia takwimu).
Kitambaa cha theluji cha hali ya juu hupatikana kutoka kwa mtangulizi wa mpangilio wa chini kwa kubadilisha kila ukingo na nne, zilizounganishwa kama viganja vilivyokunjwa (_/\_). Aina ya makali 0 inabadilishwa na kingo nne 0, 5, 1, 0 na kadhalika kulingana na jedwali:
| 0 | 0 1 5 0 |
| 1 | 1 2 0 1 |
| 2 | 2 3 1 2 |
| 3 | 3 4 2 3 |
| 4 | 4 5 3 4 |
| 5 | 5 0 4 5 |
Pembetatu rahisi ya usawa inaweza kuzingatiwa kama theluji ya Koch isiyo na mpangilio. Katika mfumo wa encoding ulioelezwa, inafanana na kuingia 0, 4, 2. Kila kitu kingine kinaweza kupatikana kwa uingizwaji ulioelezwa. Sitatoa nambari ya utaratibu hapa na kwa hivyo kukunyima raha ya kuunda programu yako mwenyewe. Wakati wa kuiandika, sio lazima hata kidogo kutumia simu ya wazi ya kujirudia. Inaweza kubadilishwa na mzunguko wa kawaida. Katika mchakato wa kazi, utakuwa na sababu nyingine ya kufikiria juu ya kujirudia na jukumu lake katika malezi ya aina za ulimwengu unaotuzunguka, na mwisho wa njia (ikiwa, kwa kweli, wewe sio mvivu sana. kuipitia hadi mwisho) utaweza kupendeza muundo mgumu wa mtaro wa theluji ya theluji iliyovunjika, na pia uangalie mwishowe katika uso wa infinity.
Mada: Fractals.
1. Utangulizi. Asili fupi ya kihistoria juu ya fractal. 2. Fractals ni vipengele vya jiometri katika asili.
3. Vitu vyenye mali ya fractal katika asili. 4. Ufafanuzi wa istilahi "fractals".
5.Makundi ya fractals.
6.Maelezo ya michakato ya fractal. 7.Taratibu za kupata seti za fractal.
8.1 Kokha iliyovunjika (utaratibu wa kupata).
8.2 Koch Snowflake (Koch Fractal).
8.3 Sponge za Menger.
9. Mifano ya kutumia fractals.
Utangulizi. Asili fupi ya kihistoria juu ya fractal.Fractals ni tawi changa la hisabati tupu.
Mnamo 1904, Koch ya Uswidi ilikuja na curve inayoendelea ambayo haina tangent popote - curve ya Koch.
Mnamo 1918, Mfaransa Julia alielezea familia nzima ya fractals.
Mnamo 1938, Pierre Levy alichapisha makala "Ndege na mikondo ya anga na nyuso zenye sehemu zinazofanana na zima."
Mnamo 1982, Benoit Mandelbrot alichapisha kitabu "The Fractal Geometry of Nature."
Kutumia miundo rahisi na fomula, picha zinaundwa. "Uchoraji wa Fractal" ulionekana.
Tangu 1993, World Scientific imechapisha jarida "Fractals".
Fractals ni vipengele vya jiometri katika asili.Fractals ni njia ya kuelezea vitu kama mifano ya safu za milima, ukanda wa pwani wenye miamba, mifumo ya mzunguko wa mishipa na vyombo vingi, taji za miti, maporomoko ya maji, mifumo ya barafu kwenye glasi.
Au hizi: jani la fern, mawingu, blot.
Picha za vitu vile zinaweza kuwakilishwa kwa kutumia graphics fractal.
Vitu vilivyo na mali ya fractal katika asili.CoralsStarfish na UrchinsSea Shells
Maua na mimea (broccoli, kabichi) Matunda (mananasi)
Taji za miti na majani ya mimea Mfumo wa mzunguko na bronchi ya watu na wanyama Katika asili isiyo hai:
Mipaka ya vitu vya kijiografia (nchi, mikoa, miji) Mipaka ya Milima ya Milima ya Snowflakes Mawingu Umeme
Sampuli zinazoundwa kwenye kioo Fuwele Stalactites, stalagmites, helictites.
Ufafanuzi wa istilahi "fractals".Fractals ni maumbo ya kijiometri ambayo yanakidhi moja au zaidi ya sifa zifuatazo:
Ina muundo changamano usio wa kawaida katika ukuzaji wowote (kwenye mizani yote); Inafanana (takriban) yenyewe.
Ina kipimo cha sehemu ya Hausdorff (fractal) au inazidi ile ya topolojia; Inaweza kujengwa kwa taratibu za kujirudia.
Kwa takwimu za kawaida kama vile duara, duaradufu, au grafu ya kazi laini, kipande kidogo kwa kiwango kikubwa sana ni sawa na kipande cha mstari wa moja kwa moja. Kwa fractal, kuongeza kiwango haileti kurahisisha muundo; kwa mizani yote tutaona picha ngumu sawa.
Madarasa ya FractalFractal ni muundo unaojumuisha sehemu (substructures) zinazofanana na zima.
Baadhi ya vipande, kama vipengele vya asili, vinaweza kuainishwa kama fracti za kijiometri (za kujenga).
Zilizosalia zinaweza kuainishwa kama fractals zinazobadilika (algebraic).

Huu ni utaratibu rahisi wa kujirudia wa kupata curves fractal: taja mstari uliovunjika kiholela na idadi ndogo ya viungo - jenereta. Ifuatayo, kila sehemu ya jenereta inabadilishwa ndani yake. Kisha kila sehemu ndani yake inabadilishwa tena na jenereta, na kadhalika ad infinitum.
Imeonyeshwa: mgawanyiko wa sehemu ya kitengo katika sehemu 3 (a), eneo la mraba la kitengo katika sehemu 9 (b), mchemraba wa kitengo katika sehemu 27 (c) na sehemu 64 (d). Idadi ya sehemu ni n, kipengele cha kuongeza ni k, na ukubwa wa nafasi ni d. Tuna mahusiano yafuatayo: n = kd,
ikiwa n = 3, k = 3, basi d = 1; ikiwa n = 9, k = 3, basi d = 2; ikiwa n = 27, k = 3, basi d = 3.
ikiwa n = 4, k = 4, basi d = 1; ikiwa n = 16, k = 4, basi d = 2; ikiwa n = 64, k = 4, basi d = 3. Kipimo cha nafasi kinaonyeshwa kwa integers: d = 1, 2, 3; kwa n = 64, thamani ya d ni

Hatua tano za kujenga polyline ya Koch zinaonyeshwa: sehemu ya urefu wa kitengo (a), imegawanywa katika sehemu tatu (k = 3), kutoka sehemu nne (n = 4) - mstari uliovunjika (b); kila sehemu ya moja kwa moja imegawanywa katika sehemu tatu (k2 = 9) na sehemu 16 (n2 = 16) - mstari uliovunjika (c); utaratibu unarudiwa kwa k3 = 27 na n3 = 64 - mstari uliovunjika (g); kwa k5 = 243 na n5 = 1024 - mstari uliovunjika (e).
Dimension
Hii ni mwelekeo wa sehemu au fractal.
Laini ya polyline ya Koch, iliyopendekezwa na Helg von Koch mnamo 1904, inafanya kazi kama fractal ambayo inafaa kwa mfano wa ukali wa ukanda wa pwani. Mandelbrot alianzisha kipengele cha nasibu katika algorithm ya ujenzi wa ukanda wa pwani, ambayo, hata hivyo, haikuathiri hitimisho kuu kuhusu urefu wa ukanda wa pwani. Kwa sababu kikomo
Urefu wa ukanda wa pwani huelekea kutokuwa na mwisho kwa sababu ya ukali usio na mwisho wa pwani.
Utaratibu wa kulainisha ukanda wa pwani wakati wa kusonga kutoka kwa kiwango cha kina zaidi hadi kwa kina kidogo, i.e.

Kama msingi wa ujenzi, huwezi kuchukua sehemu za urefu wa kitengo, lakini pembetatu ya usawa, kwa kila upande ambao unaweza kupanua utaratibu wa kuzidisha makosa. Katika kesi hii, tunapata theluji ya theluji ya Koch (Mchoro.), Na ya aina tatu: pembetatu mpya zilizoundwa zinaelekezwa tu nje kutoka kwa pembetatu iliyopita (a) na (b); ndani tu (ndani); nasibu ama nje au ndani (d) na (e). Unawezaje kuweka utaratibu wa kujenga Koch fractal.
Mchele. Snowflake Koch
Katika Mtini. michoro mbili za vector zinaonyeshwa; Nambari zilizo juu ya mishale labda zitainua swali: zinamaanisha nini? Vector 0 inafanana na mwelekeo mzuri wa mhimili wa abscissa, kwa kuwa kipengele chake cha awamu exp (i2πl/6) saa l = 0 huhifadhi mwelekeo wake. Vekta 1 inazungushwa kuhusiana na vekta 0 kwa pembe ya 2π/6, wakati l = 1. Vekta 5 ina exp ya kipengele cha awamu (i2π5/6), l = 5. Vekta ya mwisho ina kipengele cha awamu sawa na cha kwanza ( l = 0). Nambari l zinaonyesha angle ya kipengele cha awamu ya vector ya kitengo.
Hatua ya kwanza (Mchoro.) Inabainisha utaratibu wa kujirudia kwa hatua zote zinazofuata na, hasa, kwa hatua ya pili (Mchoro.). Jinsi ya kwenda kutoka kwa seti ya nambari φ1 = (0 1 5 0) hadi φ2 = (0 1 5 0 1 2 0 1 5 0 4 5 0 1 5 0)? Jibu: kupitia kuzidisha kwa tumbo moja kwa moja, wakati kila kipengele cha matrix moja kinazidishwa na matrix ya asili. Kwa kuwa katika kesi hii tunashughulika na safu moja-dimensional, i.e. Kwa kuwa matrices ni vekta, kila kipengele cha matrix-vector moja huzidishwa na vipengele vyote vya vector nyingine ya matrix. Kwa kuongeza, vipengele vya matrix-vector φ1 vinajumuisha kazi za kielelezo exp (i2πl/6), kwa hiyo, 10 wakati wa kuzidisha nambari h itakuwa muhimu kuongeza kulingana na mod (6), na si kuzidisha.
Sura ya kijiometri ya theluji ya Koch inaonekana kama hii

Jinsi ya kuteka theluji ya Koch

Na pia kuna piramidi ya Koch

Unaweza kujua kwa undani zaidi jinsi ya kuteka theluji ya Koch kutoka kwenye video hapa chini. Mtu anaweza kuelewa, niliacha.
Kwanza, hebu tuangalie theluji hii ya Koch. Mchoro hapa chini utatuonyesha vyema zaidi.

Hiyo ni, kuteka theluji iliyotolewa, unahitaji kutumia maumbo ya kijiometri ya mtu binafsi, ambayo hufanya fractal hii ya kijiometri.

Msingi wa kuchora yetu ni pembetatu ya usawa. Kila upande umegawanywa katika makundi matatu, ambayo pembetatu inayofuata, ndogo, equilateral hujengwa. Operesheni hiyo hiyo inafanywa na pembetatu zinazosababisha mara kadhaa.
Kitambaa cha theluji cha Koch ni mojawapo ya vipande vya kwanza vilivyochunguzwa na wanasayansi. Kitambaa cha theluji kinapatikana kutoka kwa nakala tatu za Curve ya Koch, habari juu ya ugunduzi huu ilionekana mnamo 1904 katika nakala ya mtaalam wa hesabu wa Uswidi Helge von Koch. Kimsingi, mkunjo ulivumbuliwa kama mfano wa mstari unaoendelea ambapo mstari wa tanjiti hauwezi kuchorwa wakati wowote. Curve ya Koch ni rahisi katika muundo wake.
Mfano, mchoro wa picha ya picha ya theluji ya Koch na kuchora hatua kwa hatua.

Katika mchoro huu unaweza kuchunguza kwa undani mistari ambayo baadaye itafanya theluji ya Koch.
Na hii ni tafsiri ya theluji mpya kulingana na theluji ya Koch.

Kabla ya kuelewa jinsi ya kuteka theluji ya Koch, unahitaji kuamua ni nini.
Kwa hivyo, theluji ya theluji ya Koch ni picha ya kijiometri - fractal.
Ufafanuzi kamili wa theluji ya Koch hutolewa kwenye picha hapa chini.