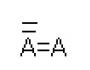Fractal. Koch curve Mga pamamaraan para sa pagkuha ng mga fractal set
Tatlong kopya ng Koch curve, na itinayo (na may mga puntos na palabas) sa mga gilid ng isang regular na tatsulok, ay bumubuo ng isang saradong kurba ng walang katapusang haba na tinatawag Ang snowflake ni Koch.
Ang figure na ito ay isa sa mga unang fractal na pinag-aralan ng mga siyentipiko. Galing ito sa tatlong kopya Kurba ng Koch, na unang lumabas sa isang papel ng Swedish mathematician na si Helge von Koch noong 1904. Ang kurba na ito ay naimbento bilang isang halimbawa ng isang tuloy-tuloy na linya na hindi maaaring maging tangent sa anumang punto. Ang mga linya na may ganitong ari-arian ay kilala noon (itinayo ni Karl Weierstrass ang kanyang halimbawa noong 1872), ngunit ang Koch curve ay kapansin-pansin para sa pagiging simple ng disenyo nito. Ito ay hindi nagkataon na ang kanyang artikulo ay tinatawag na "Sa isang tuluy-tuloy na kurba na walang tangents, na nagmumula sa elementarya na geometry."
Ang pagguhit at animation ay perpektong nagpapakita kung paano binuo ang Koch curve nang hakbang-hakbang. Ang unang pag-ulit ay simpleng paunang segment. Pagkatapos ito ay nahahati sa tatlong pantay na bahagi, ang gitnang isa ay nakumpleto upang bumuo ng isang regular na tatsulok at pagkatapos ay itinapon. Ang resulta ay ang pangalawang pag-ulit - isang putol na linya na binubuo ng apat na mga segment. Ang parehong operasyon ay inilalapat sa bawat isa sa kanila, at ang ika-apat na hakbang ng konstruksiyon ay nakuha. Ang pagpapatuloy sa parehong diwa, maaari kang makakuha ng higit pa at higit pang mga bagong linya (lahat ng mga ito ay magiging mga putol na linya). At kung ano ang mangyayari sa limitasyon (ito ay magiging isang haka-haka na bagay) ay tinatawag na Koch curve.
Mga pangunahing katangian ng Koch curve1. Ito ay tuluy-tuloy, ngunit wala saanman naiba. Sa halos pagsasalita, ito mismo ang dahilan kung bakit ito naimbento - bilang isang halimbawa ng ganitong uri ng mathematical na "freaks".
2. May walang katapusang haba. Hayaang ang haba ng orihinal na segment ay katumbas ng 1. Sa bawat hakbang ng konstruksiyon, pinapalitan namin ng putol na linya ang bawat isa sa mga segment na bumubuo sa linya, na 4/3 beses na mas mahaba. Nangangahulugan ito na ang haba ng buong putol na linya ay pinarami ng 4/3 sa bawat hakbang: ang haba ng linya na may numero n katumbas ng (4/3) n-1 . Samakatuwid, ang linya ng limitasyon ay walang mapagpipilian kundi maging walang hanggan ang haba.

3. Nililimitahan ng snowflake ni Koch ang may hangganang lugar. At ito sa kabila ng katotohanan na ang perimeter nito ay walang hanggan. Ang ari-arian na ito ay maaaring mukhang kabalintunaan, ngunit ito ay halata - ang isang snowflake ay ganap na umaangkop sa isang bilog, kaya ang lugar nito ay malinaw na limitado. Ang lugar ay maaaring kalkulahin, at hindi mo na kailangan ng espesyal na kaalaman para dito - ang mga formula para sa lugar ng isang tatsulok at ang kabuuan ng isang geometric na pag-unlad ay itinuro sa paaralan. Para sa mga interesado, ang pagkalkula ay nakalista sa ibaba sa fine print.
Hayaan ang gilid ng orihinal na regular na tatsulok ay katumbas ng a. Tapos ang area nito ay . Una ang gilid ay 1 at ang lugar ay: . Ano ang mangyayari habang tumataas ang pag-ulit? Maaari nating ipagpalagay na ang mga maliliit na equilateral triangle ay nakakabit sa isang umiiral na polygon. Sa unang pagkakataon ay mayroon lamang 3 sa kanila, at sa bawat susunod na pagkakataon ay may 4 na beses na mas marami kaysa sa nauna. Iyon ay, sa n ang ika-hakbang ay matatapos Tn= 3 4 n-1 tatsulok. Ang haba ng gilid ng bawat isa sa kanila ay isang ikatlo ng gilid ng tatsulok na natapos sa nakaraang hakbang. Kaya ito ay katumbas ng (1/3) n. Ang mga lugar ay proporsyonal sa mga parisukat ng mga gilid, kaya ang lugar ng bawat tatsulok ay ![]() . Para sa malalaking halaga n Sa pamamagitan ng paraan, ito ay napakaliit. Ang kabuuang kontribusyon ng mga tatsulok na ito sa lugar ng snowflake ay Tn · S n= 3/4 · (4/9) n · S 0 . Samakatuwid pagkatapos n-hakbang, ang lugar ng figure ay magiging katumbas ng kabuuan S 0 + T 1 · S 1 + T 2 · S 2 + ... +Tn S n =
. Para sa malalaking halaga n Sa pamamagitan ng paraan, ito ay napakaliit. Ang kabuuang kontribusyon ng mga tatsulok na ito sa lugar ng snowflake ay Tn · S n= 3/4 · (4/9) n · S 0 . Samakatuwid pagkatapos n-hakbang, ang lugar ng figure ay magiging katumbas ng kabuuan S 0 + T 1 · S 1 + T 2 · S 2 + ... +Tn S n = ![]() . Ang isang snowflake ay nakuha pagkatapos ng isang walang katapusang bilang ng mga hakbang, na tumutugma sa n→ ∞. Ang resulta ay isang walang katapusang kabuuan, ngunit ito ang kabuuan ng isang bumababang geometric na pag-unlad; mayroong isang pormula para dito:
. Ang isang snowflake ay nakuha pagkatapos ng isang walang katapusang bilang ng mga hakbang, na tumutugma sa n→ ∞. Ang resulta ay isang walang katapusang kabuuan, ngunit ito ang kabuuan ng isang bumababang geometric na pag-unlad; mayroong isang pormula para dito: ![]() . Ang lugar ng snowflake ay .
. Ang lugar ng snowflake ay .
4. Ang dimensyon ng fractal ay katumbas ng log4/log3 = log 3 4 ≈ 1.261859... . Ang tumpak na pagkalkula ay mangangailangan ng malaking pagsisikap at mga detalyadong paliwanag, kaya narito ang isang paglalarawan ng kahulugan ng fractal na dimensyon. Mula sa formula ng batas ng kapangyarihan N(δ ) ~ (1/δ )D, Saan N- bilang ng mga intersecting na parisukat, δ - ang kanilang laki, at D ay ang dimensyon, nakuha namin iyon D= log 1/ δ N. Ang pagkakapantay-pantay na ito ay totoo hanggang sa pagdaragdag ng isang pare-pareho (pareho para sa lahat δ ). Ang mga figure ay nagpapakita ng ikalimang pag-ulit ng pagbuo ng Koch curve; ang mga parisukat na grid na bumalandra dito ay may kulay berde. Ang haba ng orihinal na segment ay 1, kaya sa itaas na pigura ang haba ng gilid ng mga parisukat ay 1/9. 12 parisukat ay may kulay, log 9 12 ≈ 1.130929... . Hindi pa masyadong katulad ng 1.261859... . Tingnan pa natin. Sa gitnang larawan, ang mga parisukat ay kalahati ng laki, ang kanilang sukat ay 1/18, may kulay na 30. log 18 30 ≈ 1.176733... . Mas maganda na. Sa ibaba, kalahati pa rin ang laki ng mga parisukat; 72 piraso na ang napinturahan. log 72 30 ≈ 1.193426... . Mas malapit pa. Pagkatapos ay kailangan mong dagdagan ang numero ng pag-ulit at sa parehong oras bawasan ang mga parisukat, kung gayon ang "empirical" na halaga ng dimensyon ng Koch curve ay patuloy na lalapit sa log 3 4, at sa limitasyon ay ganap itong magkakasabay.

Ang Koch snowflake "sa kabaligtaran" ay nakukuha kung gagawa tayo ng mga Koch curves sa loob ng orihinal na equilateral triangle.

Mga linya ng Cesaro. Sa halip na equilateral triangles, isosceles triangles na may base angle mula 60° hanggang 90° ang ginagamit. Sa figure, ang anggulo ay 88°.

Opsyon na parisukat. Dito nakumpleto ang mga parisukat.
|
Snowflake Koch
canvas(
hangganan: 1px dashed black;
}
var cos = 0.5,
kasalanan = Math.sqrt(3) / 2,
deg = Math.PI / 180;
canv, ctx;
function rebro(n, len) (
ctx.save(); // I-save ang kasalukuyang pagbabago
if (n == 0) ( // Non-recursive case - gumuhit ng linya
ctx.lineTo(len, 0);
}
iba pa(
ctx.scale(1 / 3, 1 / 3); // Mag-zoom out nang 3 beses
rebro(n-1, len); //RECUURSION sa gilid
ctx.rotate(60 * deg);
rebro(n-1, len);
ctx.rotate(-120 * deg);
rebro(n-1, len);
ctx.rotate(60 * deg);
rebro(n-1, len);
}
ctx.restore(); // Ibalik ang pagbabago
ctx.translate(len, 0); // pumunta sa dulo ng gilid
}
function drawKochSnowflake(x, y, len, n) (
x = x - len / 2;
y = y + len / 2 * Math.sqrt(3)/3;
ctx.save();
ctx.beginPath();
ctx.translate(x, y);
ctx.moveTo(0, 0);
rebro(n, len); ctx.rotate(-120 * deg); //RECUUUURSION ay isa nang tatsulok
rebro(n, len); ctx.rotate(-120 * deg);
rebro(n, len); ctx.closePath();
ctx.strokeStyle = "#000";
ctx.stroke();
ctx.restore();
}
function clearcanvas())( //clear ang canvas
ctx.save();
ctx.beginPath();
// Gamitin ang identity matrix habang nililinis ang canvas
ctx.setTransform(1, 0, 0, 1, 0, 0);
ctx.clearRect(0, 0, canvas1.width, canvas1.height);
// Ibalik ang pagbabago
ctx.restore();
}
function run() (
canv = document.getElementById("canvas1");
ctx = canv.getContext("2d");
var numberiter = document.getElementById("qty").value;
drawKochSnowflake(canv.width/2, canv.height/2, 380, numberiter);
Ctx.stroke(); //pag-render
}
Ang snowflake ni Koch - halimbawa
Ito ay isang hindi karaniwang mainit na taglamig sa Boston, ngunit naghintay pa rin kami para sa unang ulan ng niyebe. Sa pagmamasid sa pagbagsak ng snow sa bintana, naisip ko ang tungkol sa mga snowflake at kung paano ang kanilang istraktura ay hindi madaling ilarawan sa matematika. Gayunpaman, mayroong isang espesyal na uri ng snowflake, na kilala bilang ang Koch snowflake, na maaaring ilarawan nang simple. Ngayon ay titingnan natin kung paano mabubuo ang hugis nito gamit ang COMSOL Multiphysics Application Builder.
Ang Paggawa ng Snowflake ni KochTulad ng nabanggit na namin sa aming blog, ang mga fractals ay maaaring gamitin sa . Snowflake Koch ay isang fractal, na kapansin-pansin na mayroong isang napakasimpleng umuulit na proseso upang mabuo ito:
Ang pamamaraang ito ay inilalarawan sa figure sa ibaba para sa unang apat na pag-ulit ng pagguhit ng snowflake.
Ang unang apat na pag-ulit ng Koch snowflake. Larawan ni Wxs - Sariling gawa. Lisensyado sa ilalim ng CC BY-SA 3.0, sa pamamagitan ng Wikimedia Commons.
Konstruksyon ng Koch snowflake geometryDahil alam na natin ngayon kung aling algorithm ang gagamitin, tingnan natin kung paano gumawa ng ganitong istraktura gamit ang COMSOL Multiphysics Application Builder. Magbubukas kami ng bagong file at lilikha ng 2D object bahagi ng geometry sa node Mga pandaigdigang kahulugan. Para sa bagay na ito, magtatakda kami ng limang input parameter: ang haba ng gilid ng isang equilateral triangle; X- At y- mga coordinate ng midpoint ng base; at mga bahagi ng normal na vector na nakadirekta mula sa gitna ng base hanggang sa kabaligtaran ng vertex, tulad ng ipinapakita sa mga figure sa ibaba.

Limang parameter ang ginamit upang itakda ang laki, posisyon, at oryentasyon ng isang equilateral triangle.

Pagtatakda ng mga parameter ng input ng geometric na bahagi.  Ang isang polygon primitive ay ginagamit upang bumuo ng isang equilateral triangle.
Ang isang polygon primitive ay ginagamit upang bumuo ng isang equilateral triangle.

Ang bagay ay maaaring paikutin sa paligid ng gitna ng ilalim na gilid.

Ang isang bagay ay maaaring ilipat kaugnay sa pinagmulan.
Ngayon na tinukoy namin ang geometric na bahagi, ginagamit namin ito nang isang beses sa seksyon Geometry. Ang solong tatsulok na ito ay katumbas ng zeroth iteration ng Koch snowflake, at ngayon ay gamitin natin ang Application Builder upang lumikha ng mas kumplikadong mga snowflake.
Markup ng App UI sa Application BuilderAng application ay may napakasimpleng user interface. Naglalaman lamang ito ng dalawang bahagi kung saan maaaring makipag-ugnayan ang user: Slider (Slider)(minarkahan bilang 1 sa figure sa ibaba), kung saan maaari mong itakda ang bilang ng mga pag-ulit na kailangan upang lumikha ng snowflake, at Pindutan(label 2), sa pamamagitan ng pag-click kung saan nilikha at ipinapakita ang resultang geometry. Meron din Inskripsyon ng teksto(label 3) at Pagpapakita (Display) ng data(label 4), na nagpapakita ng bilang ng mga tinukoy na pag-ulit, pati na rin ang window Mga tsart(label 5), na nagpapakita ng panghuling geometry.

Ang application ay may isang solong form na may limang bahagi.
Ang application ay may dalawa Mga Kahulugan, ang isa ay tumutukoy sa isang integer na halaga na tinatawag na Mga Pag-uulit, na nagde-default sa zero ngunit maaaring baguhin ng user. Ang isang 1D na hanay ng mga double na tinatawag na Center ay tinukoy din. Ang nag-iisang elemento sa array ay may halaga na 0.5, na ginagamit upang mahanap ang sentrong punto ng bawat gilid. Ang halagang ito ay hindi kailanman nagbabago.

Mga setting para sa dalawang Depinisyon.
Kinokontrol ng bahagi ng Slider sa UI ang halaga ng integer, parameter ng Mga Pag-ulit. Ipinapakita ng screenshot sa ibaba ang mga setting para sa "Slider" at ang mga value, na itinakda bilang mga integer sa hanay sa pagitan ng 0 at 5. Ang parehong pinagmulan (tulad ng para sa slider) ay pinili din para sa bahagi Pagpapakita ng Data upang ipakita ang bilang ng mga tinukoy na pag-ulit sa screen ng application. Nililimitahan namin ang potensyal na user sa limang pag-ulit dahil ang algorithm na ginamit ay suboptimal at hindi masyadong mahusay, ngunit sapat na simple upang ipatupad at ipakita.

Mga setting para sa bahaging "Slider".
Susunod, tingnan natin ang mga setting para sa aming button, na ipinapakita sa screenshot sa ibaba. Kapag pinindot ang pindutan, dalawang utos ang ipapatupad. Una, ang CreateSnowFlake method ay tinatawag. Ang resultang geometry ay ipinapakita sa window ng graphics.

Mga setting ng button.
Tiningnan namin ngayon ang user interface ng aming application at makikita namin na ang paglikha ng anumang snowflake geometry ay dapat mangyari sa pamamagitan ng tinatawag na pamamaraan. Tingnan natin ang code para sa pamamaraang ito, na may line numbering na idinagdag sa kaliwa at string constants na naka-highlight sa pula:
1 model.geom("geom1" ).feature().clear(); 2 model.geom("geom1" ).create("pi1" , "PartInstance" ); 3 model.geom("geom1" ).run("fin" ); 4 para sa (int iter = 1; iter "geom1" ).getNEdges()+1; 6 UnionList = "pi" + iter; 7 para sa (int edge = 1; edge "geom1" ).getNEdges(); edge++) ( 8 String newPartInstance = "pi" + iter + edge; 9 model.geom("geom1" ).create(newPartInstance, "PartInstance" ).set("part" , "part1" ); 10 with(model. geom("geom1" ).feature(newPartInstance)); 11 setEntry("inputexpr" , "Length" , toString(Math.pow(1.0/3.0, iter))); 12 setEntry("inputexpr" , "px" , model.geom("geom1" ).edgeX(edge, Center)); 13 setEntry("inputexpr" , "py" , model.geom("geom1" ).edgeX(edge, Center)); 14 setEntry("inputexpr " , "nx" , model.geom("geom1" ).edgeNormal(edge, Center)); 15 setEntry("inputexpr" , "ny" , model.geom("geom1" ).edgeNormal(edge, Center)) ; 16 endwith(); 17 UnionList = newPartInstance; 18 ) 19 model.geom("geom1" ).create("pi" +(iter+1), "Union" ).selection("input" ).set(UnionList ); 20 model.geom("geom1" ).feature("pi" +(iter+1)).set("intbnd" , "off" ); 21 model.geom("geom1" ).run("fin" ); 22)
Dumaan tayo sa linya ng code sa bawat linya upang maunawaan kung anong function ang ginagawa ng bawat linya:
Kaya, nasaklaw namin ang lahat ng aspeto at elemento ng aming aplikasyon. Tingnan natin ang mga resulta!

Ang aming simpleng application para sa pagbuo ng Koch snowflake.
Maaari naming palawigin ang aming aplikasyon upang magsulat ng geometry sa isang file, o kahit na direktang magsagawa ng mga karagdagang pagsusuri. Halimbawa, maaari tayong magdisenyo ng fractal antenna. Kung interesado ka sa disenyo ng antenna, tingnan ang aming halimbawa, o kahit na gawin ang layout nito mula sa simula.
Subukan ito sa iyong sariliKung gusto mong buuin ang application na ito sa iyong sarili, ngunit hindi mo pa nakumpleto ang Application Builder, maaari mong makitang kapaki-pakinabang ang mga sumusunod na mapagkukunan:
- I-download ang gabay Panimula sa Application Development Environment sa English
- Panoorin ang mga video na ito at alamin kung paano gamitin
- Basahin ang mga paksang ito upang maging pamilyar sa kung paano ginagamit ang mga application ng simulation
Kapag natalakay mo na ang materyal na ito, makikita mo kung paano mapalawak ang functionality ng app para baguhin ang laki ng snowflake, i-export ang ginawang geometry, tantiyahin ang lugar at perimeter, at marami pang iba.
Anong uri ng application ang gusto mong gawin sa COMSOL Multiphysics? para sa tulong.
Ang fractal snowflake, isa sa pinakatanyag at mahiwagang geometric na bagay, ay inilarawan ni Helga von Koch sa simula ng ating siglo. Ayon sa tradisyon, sa ating panitikan ito ay tinatawag na snowflake ni Koch. Ito ay isang napaka-"spiky" na geometric na figure, na maaaring matalinghagang makikita bilang resulta ng Star of David na paulit-ulit na "multiplied" sa kanyang sarili. Ang anim na pangunahing sinag nito ay natatakpan ng walang katapusang bilang ng malalaki at maliliit na "karayom" na vertices. Ang bawat mikroskopikong fragment ng contour ng snowflake ay parang dalawang gisantes sa isang pod, at ang malaking beam, naman, ay naglalaman ng walang katapusang bilang ng parehong mga microscopic na fragment.
Sa isang internasyonal na simposyum sa pamamaraan ng matematikal na pagmomolde sa Varna noong 1994, nakita ko ang gawain ng mga may-akda ng Bulgaria na inilarawan ang kanilang karanasan sa paggamit ng mga snowflake ni Koch at iba pang katulad na mga bagay sa mga aralin sa mataas na paaralan upang ilarawan ang problema ng divisibility ng espasyo at ang mga pilosopong aporia ni Zeno. Bilang karagdagan, mula sa isang pang-edukasyon na pananaw, sa palagay ko, ang mismong prinsipyo ng pagbuo ng mga regular na fractal geometric na istruktura ay napaka-interesante - ang prinsipyo ng recursive multiplication ng pangunahing elemento. Ito ay hindi para sa wala na ang kalikasan ay "nagmamahal" sa mga fractal form. Ito ay tiyak na ipinaliwanag sa pamamagitan ng katotohanan na ang mga ito ay nakuha sa pamamagitan ng simpleng pagpaparami at pagbabago ng laki ng isang tiyak na bloke ng gusali ng elementarya. Tulad ng alam mo, ang kalikasan ay hindi nag-uumapaw sa iba't ibang mga kadahilanan at, kung posible, ay gumagawa ng mga pinakasimpleng algorithmic na solusyon. Tingnang mabuti ang mga contour ng mga dahon, at sa maraming mga kaso ay makakahanap ka ng isang malinaw na kaugnayan sa hugis ng tabas ng isang snowflake ng Koch.
Ang visualization ng fractal geometric na mga istraktura ay posible lamang sa tulong ng isang computer. Napakahirap na gumawa ng isang Koch snowflake sa itaas ng ikatlong order nang manu-mano, ngunit gusto mo talagang tumingin sa infinity! Samakatuwid, bakit hindi subukan na bumuo ng isang naaangkop na programa sa computer. Sa RuNet makakahanap ka ng mga rekomendasyon para sa pagbuo ng isang Koch snowflake mula sa mga tatsulok. Ang resulta ng algorithm na ito ay mukhang isang paghalu-halo ng mga intersecting na linya. Mas kawili-wiling pagsamahin ang figure na ito mula sa "mga piraso". Ang tabas ng isang Koch snowflake ay binubuo ng pantay na haba na mga segment na nakahilig sa 0°, 60°, at 120° na may paggalang sa pahalang na x-axis. Kung tinutukoy natin ang mga ito ng 1, 2 at 3 ayon sa pagkakabanggit, ang isang snowflake ng anumang pagkakasunud-sunod ay bubuo ng magkakasunod na triplets - 1, 2, 3, 1, 2, 3, 1, 2, 3... atbp. Ang bawat isa sa tatlong uri na ito ng mga segment ay maaaring ikabit sa nauna sa isa o sa kabilang dulo. Isinasaalang-alang ang sitwasyong ito, maaari nating ipagpalagay na ang tabas ng isang snowflake ay binubuo ng mga segment ng anim na uri. Tukuyin natin ang mga ito 0, 1, 2, 3, 4, 5. Kaya, nakakakuha tayo ng pagkakataong mag-encode ng contour ng anumang pagkakasunod-sunod gamit ang 6 na numero (tingnan ang figure).
Ang isang mas mataas na ayos na snowflake ay nakukuha mula sa isang lower-order na hinalinhan sa pamamagitan ng pagpapalit sa bawat gilid ng apat, na konektado tulad ng mga nakatiklop na palad (_/\_). Ang uri ng gilid 0 ay pinalitan ng apat na gilid 0, 5, 1, 0 at iba pa ayon sa talahanayan:
| 0 | 0 1 5 0 |
| 1 | 1 2 0 1 |
| 2 | 2 3 1 2 |
| 3 | 3 4 2 3 |
| 4 | 4 5 3 4 |
| 5 | 5 0 4 5 |
Ang isang simpleng equilateral triangle ay maaaring isipin bilang isang zero-order Koch snowflake. Sa inilarawan na sistema ng pag-encode, tumutugma ito sa entry 0, 4, 2. Lahat ng iba pa ay maaaring makuha ng inilarawan na mga kapalit. Hindi ko ibibigay ang procedure code dito at sa gayon ay aalisan ka ng kasiyahan sa pagbuo ng iyong sariling programa. Kapag isinusulat ito, hindi na kailangang gumamit ng tahasang recursive na tawag. Maaari itong mapalitan ng isang regular na cycle. Sa proseso ng trabaho, magkakaroon ka ng isa pang dahilan upang isipin ang tungkol sa recursion at ang papel nito sa pagbuo ng mga quasi-fractal na anyo ng mundo sa paligid natin, at sa dulo ng landas (kung, siyempre, hindi ka masyadong tamad. upang dumaan dito hanggang sa dulo) magagawa mong humanga ang kumplikadong pattern ng mga contour ng isang fractal snowflake, at tumingin din sa wakas sa harap ng kawalang-hanggan.
Paksa: Fractals.
1. Panimula. Maikling makasaysayang background sa fractals. 2. Ang mga fractals ay mga elemento ng geometry sa kalikasan.
3. Mga bagay na may mga katangian ng fractal sa kalikasan. 4. Kahulugan ng terminolohiyang "fractals".
5.Mga klase ng fractals.
6.Paglalarawan ng mga proseso ng fractal. 7. Mga pamamaraan para sa pagkuha ng mga fractal set.
8.1 Sirang Kokha (pagkuha ng pamamaraan).
8.2 Koch Snowflake (Koch Fractal).
8.3 Mga espongha ng Menger.
9. Mga halimbawa ng paggamit ng fractals.
Panimula. Maikling makasaysayang background sa fractals.Ang mga fractals ay isang batang sangay ng discrete mathematics.
Noong 1904, ang Swede Koch ay nakabuo ng isang tuluy-tuloy na kurba na walang tangent kahit saan - ang Koch curve.
Noong 1918, inilarawan ng Pranses na si Julia ang isang buong pamilya ng mga fractals.
Noong 1938, inilathala ni Pierre Levy ang artikulong “Eroplano at spatial na mga kurba at ibabaw na binubuo ng mga bahaging katulad ng kabuuan.”
Noong 1982, inilathala ni Benoit Mandelbrot ang aklat na "The Fractal Geometry of Nature."
Gamit ang mga simpleng constructions at formula, ang mga imahe ay nilikha. Lumitaw ang "Fractal painting".
Mula noong 1993, inilathala ng World Scientific ang journal na "Fractals".
Ang mga fractals ay mga elemento ng geometry sa kalikasan.Ang mga fractals ay isang paraan para sa paglalarawan ng mga bagay tulad ng mga modelo ng mga bulubundukin, masungit na baybayin, mga sistema ng sirkulasyon ng maraming mga capillary at sisidlan, mga korona ng puno, mga cascading waterfalls, mga pattern ng frosty sa salamin.
O ang mga ito: dahon ng pako, ulap, blot.
Ang mga imahe ng naturang mga bagay ay maaaring katawanin gamit ang fractal graphics.
Mga bagay na may mga katangian ng fractal sa kalikasan.CoralsStarfish at UrchinsSea Shells
Bulaklak at halaman (broccoli, repolyo) Mga prutas (pinya)
Mga korona ng mga puno at dahon ng mga halaman Sistema ng sirkulasyon at bronchi ng mga tao at hayop Sa walang buhay na kalikasan:
Mga hangganan ng mga heograpikal na bagay (mga bansa, rehiyon, lungsod) Mga baybayin Mga hanay ng bundok Snowflakes Ulap Kidlat
Mga pattern na nabuo sa salamin Mga kristal Stalactites, stalagmites, helictites.
Kahulugan ng terminolohiya na "fractals".Ang mga fractals ay mga geometric na hugis na nakakatugon sa isa o higit pa sa mga sumusunod na katangian:
Ito ay may isang kumplikadong di-maliit na istraktura sa anumang pagpapalaki (sa lahat ng mga antas); Ito ay (humigit-kumulang) kapareho sa sarili.
Mayroon itong fractional na Hausdorff (fractal) na dimensyon o lumampas sa topological na dimensyon; Maaaring mabuo sa pamamagitan ng recursive procedure.
Para sa mga regular na figure tulad ng isang bilog, ellipse, o ang graph ng isang makinis na function, ang isang maliit na fragment sa isang napakalaking sukat ay katulad ng isang fragment ng isang tuwid na linya. Para sa isang fractal, ang pagtaas ng sukat ay hindi humahantong sa isang pagpapasimple ng istraktura; para sa lahat ng mga kaliskis ay makikita natin ang pantay na kumplikadong mga larawan.
Mga klase ng fractalAng fractal ay isang istraktura na binubuo ng mga bahagi (substructure) na katulad ng kabuuan.
Ang ilang mga fractals, bilang mga elemento ng kalikasan, ay maaaring uriin bilang geometric (constructive) fractals.
Ang natitira ay maaaring uriin bilang mga dynamic na fractals (algebraic).

Ito ay isang simpleng recursive procedure para sa pagkuha ng fractal curves: tukuyin ang isang di-makatwirang putol na linya na may hangganan na bilang ng mga link - isang generator. Susunod, ang bawat segment ng generator ay pinalitan dito. Pagkatapos ang bawat segment sa loob nito ay muling papalitan ng generator, at iba pa ang ad infinitum.
Ipinapakita: paghahati ng isang segment ng yunit sa 3 bahagi (a), isang yunit na parisukat na lugar sa 9 na bahagi (b), isang unit cube sa 27 bahagi (c) at 64 na bahagi (d). Ang bilang ng mga bahagi ay n, ang scaling factor ay k, at ang dimensyon ng espasyo ay d. Mayroon kaming mga sumusunod na relasyon: n = kd,
kung n = 3, k = 3, kung gayon d = 1; kung n = 9, k = 3, kung gayon d = 2; kung n = 27, k = 3, kung gayon d = 3.
kung n = 4, k = 4, kung gayon d = 1; kung n = 16, k = 4, kung gayon d = 2; kung n = 64, k = 4, kung gayon d = 3. Ang dimensyon ng espasyo ay ipinahayag sa mga integer: d = 1, 2, 3; para sa n = 64, ang halaga ng d ay

Limang hakbang ng pagbuo ng isang Koch polyline ay ipinapakita: isang segment ng haba ng yunit (a), nahahati sa tatlong bahagi (k = 3), mula sa apat na bahagi (n = 4) - isang putol na linya (b); bawat tuwid na segment ay nahahati sa tatlong bahagi (k2 = 9) at ng 16 na bahagi (n2 = 16) - isang putol na linya (c); ang pamamaraan ay paulit-ulit para sa k3 = 27 at n3 = 64 - sirang linya (g); para sa k5 = 243 at n5 = 1024 – putol na linya (e).
Dimensyon
Ito ay isang fractional o fractal na dimensyon.
Ang Koch polyline, na iminungkahi ni Helg von Koch noong 1904, ay gumaganap bilang isang fractal na angkop para sa pagmomodelo ng ruggedness ng isang baybayin. Ipinakilala ni Mandelbrot ang isang elemento ng randomness sa coastline construction algorithm, na, gayunpaman, ay hindi nakakaapekto sa pangunahing konklusyon tungkol sa haba ng coastline. Dahil ang limitasyon
Ang haba ng baybayin ay may posibilidad na infinity dahil sa walang katapusang kagaspangan ng baybayin.
Ang pamamaraan para sa pagpapakinis ng baybayin kapag lumilipat mula sa isang mas detalyadong sukat patungo sa isang hindi gaanong detalyado, i.e.

Bilang batayan para sa pagtatayo, hindi ka maaaring kumuha ng mga segment ng haba ng yunit, ngunit isang equilateral triangle, sa bawat panig kung saan maaari mong pahabain ang pamamaraan ng pagpaparami ng mga iregularidad. Sa kasong ito, nakakakuha kami ng isang Koch snowflake (Fig.), at ng tatlong uri: ang mga bagong nabuo na tatsulok ay nakadirekta lamang palabas mula sa nakaraang tatsulok (a) at (b); sa loob lamang (sa); sapalaran alinman sa labas o paloob (d) at (e). Paano mo maitakda ang pamamaraan para sa pagbuo ng isang Koch fractal.
kanin. Snowflake Koch
Sa Fig. dalawang diagram ng vector ang ipinapakita; Ang mga numero sa itaas ng mga arrow ay malamang na magtataas ng tanong: ano ang ibig sabihin ng mga ito? Ang Vector 0 ay tumutugma sa positibong direksyon ng abscissa axis, dahil ang phase factor exp (i2πl/6) nito sa l = 0 ay nagpapanatili ng direksyon nito. Ang Vector 1 ay pinaikot kaugnay sa vector 0 sa pamamagitan ng isang anggulo na 2π/6, kapag l= 1. Ang Vector 5 ay may phase factor exp (i2π5/6), l = 5. Ang huling vector ay may parehong phase factor gaya ng una ( l = 0). Ang mga integer l ay nagpapakilala sa anggulo ng phase factor ng unit vector.
Ang unang hakbang (Fig.) ay tumutukoy sa isang recursive procedure para sa lahat ng kasunod na hakbang at, lalo na, para sa pangalawang hakbang (Fig.). Paano pumunta mula sa isang set ng mga numero φ1 = (0 1 5 0) hanggang φ2 = (0 1 5 0 1 2 0 1 5 0 4 5 0 1 5 0)? Sagot: sa pamamagitan ng direktang pagpaparami ng matrix, kapag ang bawat elemento ng isang matrix ay pinarami ng orihinal na matrix. Dahil sa kasong ito kami ay nakikitungo sa isang one-dimensional array, i.e. Dahil ang mga matrice ay mga vector, ang bawat elemento ng isang matrix-vector ay pinarami ng lahat ng mga elemento ng isa pang matrix-vector. Bilang karagdagan, ang mga elemento ng matrix-vector φ1 ay binubuo ng mga exponential function exp (i2πl/6), samakatuwid, 10 kapag pina-multiply ang bilang h kakailanganing idagdag ayon sa mod (6), at hindi paramihin.
Ang geometric na hugis ng Koch snowflake ay ganito ang hitsura

Paano gumuhit ng snowflake ng Koch

At mayroon ding Koch pyramid

Maaari mong malaman nang mas detalyado kung paano gumuhit ng isang Koch snowflake mula sa video sa ibaba. Baka may makaintindi, sumuko na ako.
Una, tingnan natin itong Koch snowflake. Ang diagram sa ibaba ay pinakamahusay na magpapakita sa amin.

Iyon ay, upang gumuhit ng isang naibigay na snowflake, kailangan mong gumamit ng mga indibidwal na geometric na hugis, na bumubuo sa geometric fractal na ito.

Ang batayan ng aming pagguhit ay isang equilateral triangle. Ang bawat panig ay nahahati sa tatlong mga segment, mula sa kung saan ang susunod, mas maliit, equilateral triangles ay binuo. Ang parehong operasyon ay ginaganap sa mga nagresultang tatsulok nang maraming beses.
Ang snowflake ni Koch ay isa sa mga unang fractals na pinag-aralan ng mga siyentipiko. Ang isang snowflake ay nakuha mula sa tatlong kopya ng Koch curve, ang impormasyon tungkol sa pagtuklas na ito ay lumitaw noong 1904 sa isang artikulo ng Swedish mathematician na si Helge von Koch. Sa esensya, ang isang kurba ay naimbento bilang isang halimbawa ng isang tuloy-tuloy na linya kung saan ang isang tangent na linya ay hindi maaaring iguguhit sa anumang punto. Ang Koch curve ay simple sa disenyo nito.
Isang halimbawa, isang pagguhit ng larawan ng isang larawan ng isang snowflake ng Koch na may sunud-sunod na pagguhit.

Sa diagram na ito maaari mong suriin nang detalyado ang mga linya na gagawa ng Koch snowflake.
At ito ay isang interpretasyon ng isang bagong snowflake batay sa snowflake ni Koch.

Bago mo maunawaan kung paano gumuhit ng isang snowflake ng Koch, kailangan mong matukoy kung ano ito.
Kaya, ang isang Koch snowflake ay isang geometric na imahe - isang fractal.
Ang buong kahulugan ng snowflake ni Koch ay ibinigay sa larawan sa ibaba.