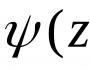Mitä kutsutaan funktion nollaksi? Funktion nollasääntö
Argumenttiarvot z jossa f(z) menee nollaan kutsuttuun. nolla piste, eli Jos f(a) = 0 siis a - nollapiste.
Def. Piste A nimeltään nolla järjestysn
, Jos
FKP voidaan esittää muodossa f(z) = , missä 
analyyttinen toiminta ja 
0.
Tässä tapauksessa Taylor-sarjan funktion (43) laajennus on ensimmäinen n kertoimet ovat nolla
=
=
Jne. Määritä nollan järjestys 
ja (1 – cos z) klo z
=
0
=
=
nolla 1. järjestys
1 – cos z
=
=
nolla 2. järjestys
Def. Piste z
=
nimeltään piste äärettömyyteen Ja nolla toimintoja f(z), Jos f(
) = 0. Tällainen funktio voidaan laajentaa sarjaksi negatiivisella potenssilla z
: f(z)
=
. Jos
ensimmäinen n
kertoimet ovat yhtä suuret kuin nolla, niin päästään nolla järjestys n
pisteessä äärettömyydessä: f(z)
= z
-
n
.
Eristetyt yksittäiset pisteet jaetaan: a) irrotettavat yksittäispisteet; b) järjestyksen pylväätn; V) pohjimmiltaan yksittäisiä pisteitä.
Piste A nimeltään irrotettava yksittäinen piste toimintoja f(z) jos klo z 
a
lim f(z)
= Kanssa - lopullinen numero .
Piste A nimeltään järjestyksen napan
(n
1) toiminnot f(z), jos käänteisfunktio 
=
1/
f(z) on nollajärjestys n pisteessä A. Tällainen funktio voidaan aina esittää muodossa f(z)
=
, Missä 
- analyyttinen toiminta ja 
.
Piste A nimeltään pohjimmiltaan erityinen kohta toimintoja f(z), jos klo z 
a
lim f(z) ei ole olemassa.
Laurent-sarja
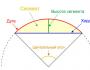
Tarkastellaan renkaan konvergenssialueen tapausta r < | z 0 – a| < R keskitetty johonkin pisteeseen A toimintoa varten f(z). Esitellään kaksi uutta piiriä L 1 (r) Ja L 2 (R) lähellä renkaan rajoja, jossa on piste z 0 heidän välillään. Tehdään renkaasta leikkaus, yhdistetään ympyrät leikkauksen reunoja pitkin, siirrytään yksinkertaisesti yhdistetylle alueelle ja sisään
Cauchyn integraalikaava (39) saa kaksi integraalia muuttujan z päälle
f(z 0)
=
+
,
(42)
jossa integraatio tapahtuu vastakkaisiin suuntiin.
Sillä integraali ohi L 1 ehto täyttyy | z 0 – a | > | z – a |, ja integraalin yli L 2 käänteinen ehto | z 0 – a | < | z – a |. Siksi kerroin 1/( z – z 0) laajenee sarjaksi (a) integraalissa over L 2 ja sarjassa (b) integraalissa yli L 1 . Tuloksena saamme laajennuksen f(z) rengasalueella Laurent-sarja positiivisilla ja negatiivisilla voimilla ( z 0 – a)
f(z 0)
=
A n
(z 0 -a) n
(43)
Missä A n
=
=
;A -n
=
Positiivisten voimien laajentaminen (z 0 - A) nimeltään oikea osa Laurent-sarja (Taylor-sarja), ja negatiivisten voimien laajenemista kutsutaan. pääosa Laurent-sarja.
Jos ympyrän sisällä L 1:ssä ei ole singulaaripisteitä ja funktio on analyyttinen, silloin (44):ssä ensimmäinen integraali on Cauchyn lauseen mukaan nolla ja vain oikea osa jää funktion laajennukseen. Negatiiviset voimat laajennuksessa (45) näkyvät vain, kun analyyttisyys rikotaan sisäympyrän sisällä, ja ne kuvaavat toimintoa lähellä eristettyjä yksittäispisteitä.
Laurent-sarjan (45) rakentamiseen f(z) voit laskea laajennuskertoimia yleisen kaavan avulla tai käyttää perusfunktioiden laajennuksia, jotka sisältyvät f(z).
Termien määrä ( n) Laurent-sarjan pääosassa riippuu singulaaripisteen tyypistä: irrotettava yksittäinen piste
(n
=
0)
; pohjimmiltaan yksittäinen kohta
(n 
);
napan- vau tilaus(n
-
lopullinen numero).
ja varten f(z)
=
piste z
= 0 irrotettava yksittäinen piste, koska ei ole pääosaa. f(z)
=
(z
-
) = 1 -
b) varten f(z)
=
piste z
= 0 -
1. asteen napa
f(z)
=
(z
-
) =
-
c) varten f(z) = e 1 / z piste z = 0 - pohjimmiltaan yksittäinen kohta
f(z)
=
e 1 /
z =
Jos f(z) on analyyttinen alalla D lukuunottamatta m yksittäisiä yksittäispisteitä 
ja | z 1 |
< |z 2 |
< . . . < |z m| , sitten kun laajennat funktiota tehoissa z koko kone on jaettu m+ 1 rengas | z i |
< | z
| < | z i+ 1 | ja Laurent-sarjalla on erilainen ulkonäkö jokaiselle sormukselle. Kun laajenee valtuuksiaan ( z
–
z i
) Laurent-sarjan konvergenssialue on ympyrä | z
–
z i
| < r, Missä r
– etäisyys lähimpään yksittäispisteeseen.
Jne. Laajennamme toimintoa f(z)
=
Laurent-sarjassa voimissa z Ja ( z
-
1).
Ratkaisu. Esitetään funktio muodossa f(z)
= - z 2
. Käytämme geometrisen progression summan kaavaa 
. Ympyrässä |z|< 1 ряд сходится и f(z)
= - z 2
(1 + z
+ z 2
+ z 3
+ z 4
+ . . .) = - z 2
- z 3
- z 4 - . . . , eli hajoaminen sisältää vain oikea Osa. Siirrytään ympyrän |z| ulommalle alueelle > 1. Esitetään funktio muodossa 
, jossa 1/| z|
< 1, и получим разложение f(z)
= z
=z
+ 1 +
Koska , funktion laajennus potenssien ( z
-
1) sillä on muoto f(z)
= (z
-
1) -1
+ 2 + (z
-
1) kaikille 
1.
Jne. Laajenna toiminto Laurent-sarjaksi f(z)
=
:
a) asteittain z ympyrässä | z|
< 1; b)
по степеням z
rengas 1<
|z|
< 3 ; c)
по степеням (z
–
2). Ratkaisu. Jaetaan funktio yksinkertaisiksi murtoluvuiksi
=
=
+
=
.
Ehtojen perusteella z
=1
A
= -1/2 , z
=3
B
= ½.
A) f(z)
=
½ [ 
]
= ½ [ 
-(1/3)
], jossa | z|<
1.
b) f(z)
= - ½ [ 
+
]
= -
(
), klo 1< |z|
< 3.
Kanssa) f(z)
=
½ [ 
]= -
½
[ 
]
=
=
- ½
= -
, kanssa |2 - z|
< 1
Se on ympyrä, jonka säde on 1 ja jonka keskipiste on z = 2 .
Joissakin tapauksissa potenssisarjat voidaan pelkistää geometristen progressioiden joukkoon, ja tämän jälkeen on helppo määrittää niiden konvergenssialue.
Jne. Tutki sarjan konvergenssia
.
. . +
+
+
+
1
+ ()
+ ()
2
+ ()
3
+ . . .
Ratkaisu. Tämä on kahden geometrisen progression summa q 1
=
, q 2 = () . Niiden lähentymisen ehdoista se seuraa 
< 1 ,
< 1 или |z|
> 1 , |z|
< 2 , т.е. область сходимости ряда кольцо
1 < |z|
< 2 .
Toimintojen nollia ovat argumenttiarvoja, joissa funktio on yhtä suuri kuin nolla.
Kaavan y=f(x) antaman funktion nollien löytämiseksi sinun on ratkaistava yhtälö f(x)=0.
Jos yhtälöllä ei ole juuria, funktiolla ei ole nollia.
Esimerkkejä.
1) Etsi lineaarifunktion y=3x+15 nollat.
Löytääksesi funktion nollat ratkaise yhtälö 3x+15=0.
Siten funktion y=3x+15 nolla on x= -5.
Vastaus: x= -5.
2) Etsi neliöfunktion f(x)=x²-7x+12 nollat.
Löydä funktion nollakohdat ratkaisemalla toisen asteen yhtälö
Sen juuret x1=3 ja x2=4 ovat tämän funktion nollia.
Vastaus: x=3; x=4.
Ohjeet
1. Funktion nolla on argumentin x arvo, jossa funktion arvo on nolla. Kuitenkin vain ne argumentit, jotka sisältyvät tutkittavan funktion määritelmäalueeseen, voivat olla nollia. Eli on paljon arvoja, joille funktio f(x) on hyödyllinen. 2. Kirjoita annettu funktio muistiin ja vertaa se nollaan, sano f(x) = 2x?+5x+2 = 0. Ratkaise saatu yhtälö ja etsi sen todelliset juuret. Neliöyhtälön juuret lasketaan erottajan löytämisen tuella. 2x?+5x+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0,5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. Näin tässä tapauksessa saadaan kaksi toisen asteen yhtälön juuria, jotka vastaavat alkufunktion f(x) argumentit. 3. Tarkista, että kaikki havaitut x-arvot kuuluvat annetun funktion määritelmäalueeseen. Selvitä OOF, tehdäksesi tämän tarkistamalla alkulausekkeen muodon?f (x) parillisten juurien esiintymisen, murtolukujen esiintymisen funktiossa argumentin nimittäjässä, logaritmisen tai trigonometrisen ilmaisuja. 4. Kun tarkastellaan funktiota, jonka lauseke on parillisen asteen juuren alla, ota määritelmän alueeksi kaikki argumentit x, joiden arvot eivät muuta radikaalilauseketta negatiiviseksi luvuksi (päinvastoin funktio tekee ei käy järkeen). Tarkista, ovatko funktion havaitut nollat tietyllä hyväksyttävien x-arvojen alueella. 5. Murtoluvun nimittäjä ei voi mennä nollaan, joten sulje pois argumentit x, jotka johtavat tällaiseen tulokseen. Logaritmisille suureille tulee ottaa huomioon vain ne argumentin arvot, joille itse lauseke on suurempi kuin nolla. Sublogaritmisen lausekkeen nollaksi tai negatiiviseksi luvuksi muuttavat funktion nollat on jätettävä pois lopputuloksesta. Huomautus! Kun yhtälön juuria löydetään, ylimääräisiä juuria saattaa ilmestyä. Tämä on helppo tarkistaa: korvaa vain tuloksena oleva argumentin arvo funktioon ja varmista, muuttuuko funktio nollaan. Hyödyllinen neuvo Joskus funktiota ei ilmaista ilmeisellä tavalla sen argumentin kautta, jolloin on helppo tietää, mikä tämä funktio on. Esimerkki tästä on ympyrän yhtälö.
Toimintojen nollia Kutsutaan abskissa-arvo, jossa funktion arvo on nolla.
Jos funktio on annettu sen yhtälöllä, niin funktion nollat ovat yhtälön ratkaisuja. Jos funktion kuvaaja on annettu, niin funktion nollat ovat arvoja, joilla kuvaaja leikkaa x-akselin.
Sisältö:
Funktion nolla on se x:n arvo, jossa funktion arvo on nolla. Tyypillisesti funktion nollien löytäminen tehdään ratkaisemalla polynomiyhtälö, kuten x 2 + 4x +3 = 0. Tässä on useita tapoja löytää funktion nollia.
Askeleet
1 Factorisointi
- 1
Kirjoita yhtälö niin, että se näyttää tältä x 2 + 5x + 4. Aloita korkeamman asteen termillä (kuten x 2) ja jatka sitten vapaaseen termiin (vakio ilman muuttujaa; luku). Yhdistä tuloksena oleva lauseke 0:aan.
- Oikein kirjoitetut polynomit (yhtälöt):
- x 2 + 5x + 6 = 0
- x 2 - 2x - 3 = 0
- Väärin kirjoitetut polynomit (yhtälöt):
- 5x + 6 = -x 2
- x 2 = 2x + 3
- Oikein kirjoitetut polynomit (yhtälöt):
- 2
a", "b", "c".
Tämä yksinkertaistaa faktorointiongelmaa. Kirjoita yhtälö tässä muodossa: a x 2 ± b x ± c = 0. Etsi nyt a, b, c sinulle annetusta yhtälöstä. Tässä on joitain esimerkkejä:
- x 2 + 5x + 6 = 0
- a
- b = 5
- c = 6
- x 2 - 2x - 3 = 0
- a= 1 (ei ole kerrointa ennen "x", joten kerroin = 1)
- b = -2
- c = -3
- x 2 + 5x + 6 = 0
- 3
Kirjoita muistiin kaikki kerrointekijöiden parit " Kanssa".
Tietyn luvun tekijäpari on kaksi lukua, jotka kerrottuna antavat kyseisen luvun. Kiinnitä erityistä huomiota negatiivisiin lukuihin. Kaksi negatiivista lukua kertovat positiivisen luvun. Kertolaskujärjestyksellä ei ole väliä ("1 x 4" on sama kuin "4 x 1").
- Yhtälö: x 2 + 5x + 6 = 0
- Kerroinparit 6 tai c:
- 1 x 6 = 6
- -1 x -6 = 6
- 2 x 3 = 6
- -2 x -3 = 6
- 4
Etsi tekijäpari, jonka summa on " b" .
Katso merkitystä b ja selvitä, mikä pareista summattaessa antaa tämän luvun.
- b = 5
- Kertoimien pari, jonka summa on 5, on 2 ja 3
- 2 + 3 = 5
- 5
Tee tästä tekijäparista 2 binomia ja yhdistä ne binomiiksi. Binomi on muotoa (x ± luku)(x ± luku) olevien binomien tulo. Mistä tiedät, mikä merkki (plus tai miinus) valita? Katso vain numeroiden etumerkkiä tekijäparista: positiivinen luku on plusmerkki, negatiivinen luku on miinusmerkki. Tässä on pari tekijää, joilla teimme binomiaalin:
- (x + 2) (x + 3) = 0
- 6
Ratkaise jokainen binomi siirtämällä tuntematon yhtälön toiselle puolelle. Yhdistä jokainen binomi arvoon 0: (x + 2) = 0 ja (x + 3) = 0, ja ratkaise sitten yhtälö:
- (x + 2) = 0; x = -2
- (x + 3) = 0; x = -3
- 7 Nämä ovat funktion nollia.
2 Neliöyhtälön ratkaiseminen
- 1 Toisen asteen yhtälö näyttää tältä:
- 2 Merkitse kertoimet yhtälössäsi " a", "b", "c". Tämä yksinkertaistaa yhtälön ratkaisuongelmaa. Kirjoita yhtälö tässä muodossa: a x 2 ± b x ± c = 0.
- 3 Nyt löytää a, b, c sinulle annetusta yhtälöstä.
- 4
Ratkaise yhtälö. Toisen yhtälön ratkaisemiseksi sinun on tiedettävä kaava tällaisen yhtälön ratkaisemiseksi. Kaikki muu on vain korvaamista ja laskemista.
- Toinen vaihtoehto toisen asteen yhtälön ratkaisemiseksi on täydellinen neliö. Jotkut ihmiset pitävät tätä menetelmää yksinkertaisempana kuin kaavan mukaan ratkaisemista.
- 5 Kaavan avulla tapahtuvan toisen asteen yhtälön ratkaisemisen tulos on etsimäsi funktion "nollat". Kaava antaa vastauksen kahden luvun muodossa, jotka ovat tämän funktion ratkaisu (nollat).
3 Toisen yhtälön kuvaaja
- 1 Piirrä funktio. Funktio kirjoitetaan muodossa x 2 + 8x + 12 = 0.
- 2 Etsi x-leikkaukset. Nämä kaksi pistettä ovat funktion nollia.
- 3 Käytä kuvaajaa tapana tarkistaa, ei tapana ratkaista yhtälö. Jos piirrät funktion nollien näyttämistä, käytä tätä tulosten tarkistamiseen.
- Voit tarkistaa laskelmasi korvaamalla löydetyt ratkaisut alkuyhtälöön. Jos yhtälö on nolla, niin ratkaisut ovat oikein.
Funktion matemaattinen esitys osoittaa selvästi, kuinka yksi suure määrittää kokonaan toisen suuren arvon. Perinteisesti katsotaan numeerisia funktioita, jotka antavat numeron toiselle. Funktion nolla on yleensä argumentin arvo, jossa funktiosta tulee nolla.
Ohjeet
1. Funktion nollien havaitsemiseksi sinun on rinnastettava sen oikea puoli nollaan ja ratkaistava tuloksena oleva yhtälö. Oletetaan, että sinulle annetaan funktio f(x)=x-5.
2. Löytääksemme tämän funktion nollat otetaan ja rinnastetaan sen oikea puoli nollaan: x-5=0.
3. Kun tämä yhtälö on ratkaistu, huomaamme, että x=5 ja tämä argumentin arvo on funktion nolla. Eli kun argumentin arvo on 5, funktio f(x) muuttuu nollaksi.
Näkymän alla toimintoja matematiikassa ymmärrämme joukkojen elementtien välisen yhteyden. Oikein sanottuna tämä on "laki", jonka mukaan yhden joukon koko elementti (kutsutaan määritelmäalueeksi) liitetään toisen joukon tiettyyn elementtiin (kutsutaan arvoalueeksi).
Tarvitset
- Algebran ja matemaattisen katsauksen tuntemus.
Ohjeet
1. Arvot toimintoja Tämä on tietty alue, josta funktio voi ottaa arvoja. Sanotaanko arvoalue toimintoja f(x)=|x| 0:sta äärettömään. Löytääkseen merkitys toimintoja jossain vaiheessa sinun on korvattava argumentti toimintoja sen numeerinen vastine, tuloksena oleva luku on merkitys m toimintoja. Olkoon funktio f(x)=|x| – 10 + 4x. Otetaan selvää merkitys toimintoja pisteessä x=-2. Korvataan x luvulla -2: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16. Tuo on merkitys toimintoja pisteessä -2 on yhtä suuri kuin -16.
Huomautus!
Ennen kuin etsit funktion arvoa pisteestä, varmista, että se on funktion toimialueen sisällä.
Hyödyllinen neuvo
Samanlainen menetelmä mahdollistaa useiden argumenttien funktion merkityksen selvittämisen. Erona on, että yhden numeron sijasta sinun on korvattava useita - funktion argumenttien lukumäärän mukaan.
Funktio edustaa muodostettua yhteyttä muuttujan y ja muuttujan x välillä. Lisäksi kaikki x:n arvot, joita kutsutaan argumentiksi, vastaavat y:n poikkeuksellista arvoa - funktiota. Graafisessa muodossa funktio on kuvattu suorakulmaisessa koordinaatistossa graafin muodossa. Kuvaajan ja abskissa-akselin leikkauspisteitä, joille argumentit x piirretään, kutsutaan funktion nolliksi. Hyväksyttyjen nollien löytäminen on yksi tietyn funktion löytämisen tehtävistä. Tässä tapauksessa kaikki itsenäisen muuttujan x sallitut arvot, jotka muodostavat funktion (DOF) määrittelyalueen, otetaan huomioon.
Ohjeet
1. Funktion nolla on argumentin x arvo, jossa funktion arvo on nolla. Kuitenkin vain ne argumentit, jotka sisältyvät tutkittavan funktion määritelmäalueeseen, voivat olla nollia. Eli on paljon arvoja, joille funktio f(x) on hyödyllinen.
2. Kirjoita annettu funktio muistiin ja vertaa se nollaan, sano f(x) = 2x?+5x+2 = 0. Ratkaise saatu yhtälö ja etsi sen todelliset juuret. Neliöyhtälön juuret lasketaan erottajan löytämisen tuella. 2x?+5x+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0,5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. Näin tässä tapauksessa saadaan kaksi toisen asteen yhtälön juuria, jotka vastaavat alkufunktion f(x) argumentit.
3. Tarkista, että kaikki havaitut x-arvot kuuluvat annetun funktion määritelmäalueeseen. Selvitä OOF, tehdäksesi tämän tarkistamalla alkulausekkeen muodon?f (x) parillisten juurien esiintymisen, murtolukujen esiintymisen funktiossa argumentin nimittäjässä, logaritmisen tai trigonometrisen ilmaisuja.
4. Kun tarkastellaan funktiota, jonka lauseke on parillisen asteen juuren alla, ota määritelmän alueeksi kaikki argumentit x, joiden arvot eivät muuta radikaalilauseketta negatiiviseksi luvuksi (päinvastoin funktio tekee ei käy järkeen). Tarkista, ovatko funktion havaitut nollat tietyllä hyväksyttävien x-arvojen alueella.
5. Murtoluvun nimittäjä ei voi mennä nollaan, joten sulje pois argumentit x, jotka johtavat tällaiseen tulokseen. Logaritmisille suureille tulee ottaa huomioon vain ne argumentin arvot, joille itse lauseke on suurempi kuin nolla. Sublogaritmisen lausekkeen nollaksi tai negatiiviseksi luvuksi muuttavat funktion nollat on jätettävä pois lopputuloksesta.
Huomautus!
Kun yhtälön juuria löydetään, ylimääräisiä juuria saattaa ilmestyä. Tämä on helppo tarkistaa: korvaa vain tuloksena oleva argumentin arvo funktioon ja varmista, muuttuuko funktio nollaan.
Hyödyllinen neuvo
Joskus funktiota ei ilmaista ilmeisellä tavalla sen argumentin kautta, jolloin on helppo tietää, mikä tämä funktio on. Esimerkki tästä on ympyrän yhtälö.
Jossa se saa arvon nolla. Esimerkiksi kaavan antamalle funktiolle
On nolla, koska
.Kutsutaan myös funktion nollia toiminnon juuret.
Toiminnon nollien käsitettä voidaan harkita kaikille funktioille, joiden arvoalue sisältää nollan tai vastaavan algebrallisen rakenteen nollaelementin.
Reaalimuuttujan funktiolle nollat ovat arvoja, joissa funktion kuvaaja leikkaa x-akselin.
Funktion nollien löytäminen vaatii usein numeeristen menetelmien käyttöä (esim. Newtonin menetelmä, gradienttimenetelmät).
Yksi ratkaisemattomista matemaattisista ongelmista on Riemannin zeta-funktion nollien löytäminen.
Polynomin juuri
Katso myös
Kirjallisuus
Wikimedia Foundation. 2010.
Katso, mitä "Function Zero" on muissa sanakirjoissa:
Piste, jossa annettu funktio f(z) katoaa; siis N. f. f (z) on sama kuin yhtälön f (z) = 0 juuret. Esimerkiksi pisteet 0, π, π, 2π, 2π,... ovat funktion sinz nollia. Analyyttisen funktion nollat (katso Analyyttinen... ...
Nollatoiminto, nollafunktio... Oikeinkirjoitussanakirja-viitekirja
Tällä termillä on muita merkityksiä, katso Zero. Tämän artikkelin sisältö on siirrettävä artikkeliin "Nullafunktio". Voit auttaa projektia yhdistämällä artikkeleita. Jos on tarpeen keskustella yhdistämisen toteutettavuudesta, korvaa tämä ... Wikipedia
Tai C-merkkijono (C-kielen nimestä) tai ASCIZ-merkkijono (assembler-direktiivin nimestä.asciz) menetelmä merkkijonojen esittämiseksi ohjelmointikielissä, jossa sen sijaan, että ottaisi käyttöön erityistä merkkijonotyyppiä, on joukko merkkejä. käytetty, ja lopussa ... ... Wikipedia
Kvanttikenttäteoriassa kytkentävakion renormalisointikertoimen katoamisominaisuuden hyväksytty (salasana) nimi on missä g0 on paljas kytkentävakio Lagrangin fysikaalista vuorovaikutuksesta. kytkentävakio pukeutuneena vuorovaikutukseksi. Tasa-arvo Z... Fyysinen tietosanakirja
Nollamutaatio n-alleeli- Nollamutaatio, n. alleeli * nollamutaatio, n. alleeli * nollamutaatio tai n. alleeli tai hiljainen a. mutaatio, joka johtaa täydelliseen toiminnan menettämiseen DNA-sekvenssissä, jossa se tapahtui... Genetiikka. tietosanakirja
Todennäköisyysteorian väite, jonka mukaan millä tahansa tapahtumalla (ns. jäännöstapahtuma), jonka esiintymisen määräävät vain mielivaltaisesti kaukana olevat itsenäisten satunnaistapahtumien tai satunnaismuuttujien sarjan elementit, on... ... Matemaattinen tietosanakirja
1) Luku, jolla on ominaisuus, että mikään (reaali- tai kompleksiluku) ei muutu, kun se lisätään siihen. Merkitään symbolilla 0. Minkä tahansa luvun tulo N:llä on yhtä suuri kuin N.: Jos kahden luvun tulo on yhtä suuri kuin N., niin yksi tekijöistä ... Matemaattinen tietosanakirja
Funktiot, jotka määritellään riippumattomien muuttujien välisillä suhteilla, joita ei ole ratkaistu suhteessa jälkimmäiseen; nämä suhteet ovat yksi tavoista määrittää funktio. Esimerkiksi relaatio x2 + y2 1 = 0 määrittää N.f. ... Suuri Neuvostoliiton tietosanakirja
Joukko niistä ja vain niistä pisteistä, joissa mikään yleisen funktion läheisyydestä ei katoa. Yleistetty funktio katoaa avoimessa joukossa, jos kaikille. Käyttämällä yhtenäisyyden laajennusta osoitetaan, että jos yleistetty funktio ... Matemaattinen tietosanakirja
