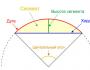
Horner-piirin määritelmä. Yhtälöt korkeammassa matematiikan polynomien rationaaliset juuret

Dia 3

Horner Williams George (1786-22.9.1837) - englantilainen matemaatikko. Syntynyt Bristolissa. Hän opiskeli ja työskenteli siellä, sitten Bathin kouluissa. Algebran perusteoksia. Vuonna 1819 julkaisi menetelmän polynomin todellisten juurien likimääräiseen laskemiseen, jota nykyään kutsutaan Ruffini-Horner-menetelmäksi (tämä menetelmä tunnettiin kiinalaisten jo 1200-luvulla). Hornerin jälkeen.

Dia 4

HORNER JÄRJESTELMÄ

Menetelmä n:nnen asteen polynomin jakamiseksi lineaarisella binomilla - a, joka perustuu siihen, että epätäydellisen osamäärän ja jäännöksen kertoimet liittyvät jaettavan polynomin kertoimiin ja kaavoilla:

Dia 5

Hornerin kaavion mukaiset laskelmat on sijoitettu taulukkoon:

Esimerkki 1. Jaa Osaosamäärä on x3-x2+3x - 13 ja jakojäännös on 42=f(-3).

Dia 6

Tämän menetelmän tärkein etu on merkinnän kompaktisuus ja kyky jakaa polynomi nopeasti binomiiksi. Itse asiassa Hornerin järjestelmä on toinen tapa tallentaa ryhmittelymenetelmä, vaikka toisin kuin jälkimmäinen, se on täysin ei-visuaalinen. Vastaus (faktorointi) saadaan tästä itsestään, emmekä näe sen saamisprosessia. Emme osallistu Hornerin suunnitelman tiukkaan perustelemiseen, vaan näytämme vain, kuinka se toimii.

Dia 7

Esimerkki 2.

Osoitetaan, että polynomi P(x)=x4-6x3+7x-392 on jaollinen x-7:llä, ja lasketaan jaon osamäärä. Ratkaisu. Hornerin kaaviota käyttämällä saadaan P(7): Tästä saadaan P(7)=0, ts. jäännös, kun polynomi jaetaan x-7:llä, on nolla ja siksi polynomi P(x) on (x-7) kerrannainen. Lisäksi taulukon toisella rivillä olevat luvut ovat polynomin kertoimia P(x):n osamäärä jaettuna arvolla (x-7), joten P(x)=(x-7)(x3+x2+7x+56).

Dia 8

Kerroin polynomin x3 – 5x2 – 2x + 16.

Tällä polynomilla on kokonaislukukertoimet. Jos kokonaisluku on tämän polynomin juuri, niin se on luvun 16 jakaja. Näin ollen, jos tietyllä polynomilla on kokonaislukujuuret, niin nämä voivat olla vain luvut ±1; ±2; ±4; ±8; ±16. Suoralla tarkastuksella olemme vakuuttuneita siitä, että luku 2 on tämän polynomin juuri, eli x3 – 5x2 – 2x + 16 = (x – 2)Q(x), missä Q(x) on toisen asteen polynomi.

Dia 9

Tuloksena olevat luvut 1, −3, −8 ovat kertoimia polynomille, joka saadaan jakamalla alkuperäinen polynomi x – 2:lla. Tämä tarkoittaa, että jaon tulos on: 1 x2 + (–3)x + ( –8) = x2 – 3x – 8. Jaosta johtuvan polynomin aste on aina 1 pienempi kuin alkuperäisen aste. Joten: x3 – 5x2 – 2x + 16 = (x – 2) (x2 – 3x – 8).

Jne. on yleissivistävä luonteeltaan ja sillä on suuri merkitys koko korkeamman matematiikan kurssin opiskelulle. Tänään toistamme "koulu"-yhtälöitä, mutta emme vain "koulu" - vaan niitä, joita löytyy kaikkialta erilaisissa vyshmat-ongelmissa. Tarina kerrotaan tuttuun tapaan sovelletulla tavalla, ts. En keskity määritelmiin ja luokitteluihin, vaan jaan kanssasi henkilökohtaisen kokemukseni sen ratkaisemisesta. Tieto on tarkoitettu ensisijaisesti aloittelijoille, mutta myös kokeneemmat lukijat löytävät monia mielenkiintoisia kohtia itselleen. Ja tietysti tulee uutta materiaalia, joka menee lukion ulkopuolelle.

Eli yhtälö…. Monet muistavat tämän sanan vapina. Mitä arvokkaat ovat "hienotetut" juuret sisältävät yhtälöt... ...unohda ne! Koska silloin tapaat tämän lajin vaarattomimmat "edustajat". Tai tylsiä trigonometrisiä yhtälöitä kymmenillä ratkaisumenetelmillä. Rehellisesti sanottuna en itse oikein pitänyt niistä... Älä hätäänny! – silloin enimmäkseen "voikukka" odottaa sinua ilmeisellä ratkaisulla 1-2 vaiheessa. Vaikka "takainen" varmasti takertuu, sinun on oltava objektiivinen tässä.

Kummallista kyllä, korkeammassa matematiikassa on paljon yleisempää käsitellä hyvin primitiivisiä yhtälöitä, kuten lineaarinen yhtälöt

Mitä tämän yhtälön ratkaiseminen tarkoittaa? Tämä tarkoittaa SEN arvon löytämistä "x":lle (juuri), joka muuttaa sen todelliseksi tasa-arvoksi. Heitetään "kolme" oikealle merkin muutoksella:

ja pudota "kaksi" oikealle puolelle (tai sama asia - kerro molemmat puolet) :

Tarkistaaksesi, korvataan voitettu pokaali alkuperäiseen yhtälöön:

Saadaan oikea yhtälö, mikä tarkoittaa, että löydetty arvo on todellakin tämän yhtälön juuri. Tai, kuten he myös sanovat, täyttää tämän yhtälön.

Huomaa, että juuri voidaan kirjoittaa myös desimaalilukuna:
Ja yritä olla pitämättä kiinni tästä huonosta tyylistä! Toistin syyn useammin kuin kerran, erityisesti ensimmäisellä oppitunnilla korkeampi algebra.

Muuten, yhtälö voidaan ratkaista myös "arabiaksi":

Ja mikä mielenkiintoisinta on, että tämä tallenne on täysin laillinen! Mutta jos et ole opettaja, on parempi olla tekemättä tätä, koska omaperäisyys on rangaistavaa täällä =)

Ja nyt vähän aiheesta

graafinen ratkaisumenetelmä

Yhtälöllä on muoto ja juuri on "X" koordinaatti risteyspisteet lineaarinen funktiokaavio lineaarisen funktion kuvaajalla (x-akseli):

Näyttää siltä, ​​​​että esimerkki on niin alkeellinen, ettei tässä ole enää mitään analysoitavaa, mutta siitä voidaan "puristaa" vielä yksi odottamaton vivahde: ​​esitetään sama yhtälö muodossa ja rakennetaan funktioiden graafit:

Jossa, älä sekoita kahta käsitettä: yhtälö on yhtälö ja toiminto– tämä on toiminto! Toiminnot vain apua löytää yhtälön juuret. Niitä voi olla kaksi, kolme, neljä tai jopa äärettömän monta. Lähin esimerkki tässä mielessä on tunnettu toisen asteen yhtälö, jonka ratkaisualgoritmi sai erillisen kappaleen "kuumia" koulukaavoja. Ja tämä ei ole sattumaa! Jos pystyt ratkaisemaan toisen asteen yhtälön ja tiedät Pythagoraan lause, silloin voisi sanoa, että "puolet korkeammasta matematiikasta on jo taskussa" =) Tietysti liioiteltua, mutta ei niin kaukana totuudesta!

Älä siis ole laiskoja ja ratkaise jokin toisen asteen yhtälö käyttämällä vakioalgoritmi:

, mikä tarkoittaa, että yhtälössä on kaksi erilaista pätevä juuri:

On helppo varmistaa, että molemmat löydetyt arvot todella täyttävät tämän yhtälön:

Mitä tehdä, jos yhtäkkiä unohdat ratkaisualgoritmin, eikä keinoja/apukäsiä ole käsillä? Tämä tilanne voi syntyä esimerkiksi kokeen tai kokeen aikana. Käytämme graafista menetelmää! Ja on kaksi tapaa: voit rakentaa kohta kohdalta paraabeli , jolloin saadaan selville, missä se leikkaa akselin (jos se ylittää ollenkaan). Mutta on parempi tehdä jotain ovelampaa: kuvitella yhtälö muodossa, piirtää kaavioita yksinkertaisemmista funktioista - ja "X" koordinaatit niiden leikkauspisteet ovat selvästi näkyvissä!


Jos käy ilmi, että suora koskettaa paraabelia, yhtälöllä on kaksi vastaavaa (useita) juuria. Jos käy ilmi, että suora ei leikkaa paraabelia, todellisia juuria ei ole.

Tätä varten sinun on tietysti osattava rakentaa perusfunktioiden kaavioita, mutta toisaalta koululainenkin osaa näitä taitoja.

Ja jälleen - yhtälö on yhtälö, ja funktiot ovat funktioita, joita vain auttoi ratkaise yhtälö!

Ja tässä muuten olisi paikallaan muistaa vielä yksi asia: jos kaikki yhtälön kertoimet kerrotaan muulla kuin nollalla, niin sen juuret eivät muutu.

Joten esimerkiksi yhtälö on samat juuret. Yksinkertaisena "todisteena" poistan vakion suluista:
ja poistan sen kivuttomasti (Jaan molemmat osat "miinus kahdella"):

MUTTA! Jos otetaan huomioon funktio , silloin et pääse eroon vakiosta täällä! Kertoimen poistaminen suluista on sallittua vain: .

Monet ihmiset aliarvioivat graafisen ratkaisumenetelmän pitäen sitä "epäarvoisena", ja jotkut jopa unohtavat tämän mahdollisuuden. Ja tämä on pohjimmiltaan väärin, koska kaavioiden piirtäminen joskus vain pelastaa tilanteen!

Toinen esimerkki: oletetaan, että et muista yksinkertaisimman trigonometrisen yhtälön juuria: . Yleinen kaava on koulun oppikirjoissa, kaikissa perusmatematiikan hakuteoksissa, mutta ne eivät ole saatavillasi. Yhtälön ratkaiseminen on kuitenkin kriittinen (alias "kaksi"). Siellä on uloskäynti! – rakentaa funktioiden kuvaajia:


jonka jälkeen kirjoitamme rauhallisesti muistiin niiden leikkauspisteiden "X"-koordinaatit:

Juureja on äärettömän monta, ja algebrassa hyväksytään niiden tiivistetty merkintä:
, Missä ( – joukko kokonaislukuja) .

Ja "poistumatta", muutama sana graafisesta menetelmästä epäyhtälöiden ratkaisemiseksi yhdellä muuttujalla. Periaate on sama. Joten esimerkiksi ratkaisu epäyhtälöön on mikä tahansa "x", koska Sinusoidi on lähes kokonaan suoran alla. Epäyhtälön ratkaisu on joukko intervalleja, joissa siniaallon palat ovat tiukasti suoran yläpuolella (x-akseli):

tai lyhyesti sanottuna:

Mutta tässä on monia ratkaisuja eriarvoisuuteen: tyhjä, koska mikään sinusoidin piste ei ole suoran yläpuolella.

Onko jotain mitä et ymmärrä? Tutustu kiireellisesti aiheisiin sarjat Ja funktiokaavioita!

Lämmitetään:

Harjoitus 1

Ratkaise seuraavat trigonometriset yhtälöt graafisesti:

Vastaukset oppitunnin lopussa

Kuten näet, eksaktien tieteiden opiskeluun ei ole ollenkaan välttämätöntä tukahduttaa kaavoja ja hakukirjoja! Lisäksi tämä on pohjimmiltaan virheellinen lähestymistapa.

Kuten jo vakuutin sinulle aivan oppitunnin alussa, monimutkaisia ​​trigonometrisiä yhtälöitä korkeamman matematiikan vakiokurssilla on ratkaistava erittäin harvoin. Kaikki monimutkaisuus pääsääntöisesti päättyy yhtälöihin kuten , joiden ratkaisu on kaksi juuriryhmää, jotka ovat peräisin yksinkertaisimmista yhtälöistä ja . Älä murehdi liikaa jälkimmäisen ratkaisemisesta – katso kirjasta tai löydä se Internetistä =)

Graafinen ratkaisumenetelmä voi auttaa myös vähemmän triviaalisissa tapauksissa. Harkitse esimerkiksi seuraavaa "rägtag"-yhtälöä:

Sen ratkaisunäkymät näyttävät... eivät näytä yhtään miltään, mutta sinun täytyy vain kuvitella yhtälö muodossa , rakentaa funktiokaavioita ja kaikki tulee olemaan uskomattoman yksinkertaista. Artikkelin keskellä on piirros aiheesta äärettömän pienet funktiot (avautuu seuraavassa välilehdessä).

Samaa graafista menetelmää käyttämällä voit selvittää, että yhtälöllä on jo kaksi juuria, joista toinen on nolla ja toinen ilmeisesti irrationaalinen ja kuuluu segmenttiin . Tämä juuri voidaan laskea suunnilleen esim. tangenttimenetelmä. Muuten, joissakin ongelmissa tapahtuu, että sinun ei tarvitse löytää juuria, vaan selvittää onko niitä ollenkaan olemassa?. Ja tässäkin piirustus voi auttaa - jos kaaviot eivät leikkaa, niin juuria ei ole.

Polynomien rationaaliset juuret kokonaislukukertoimilla.
Hornerin kaava

Ja nyt kutsun sinut kääntämään katseesi keskiaikaan ja tuntemaan klassisen algebran ainutlaatuisen tunnelman. Materiaalin ymmärtämiseksi paremmin suosittelen, että luet ainakin vähän kompleksiluvut.

He ovat parhaita. Polynomit.

Kiinnostuksen kohteena ovat muodon yleisimmät polynomit koko kertoimet Luonnollista lukua kutsutaan polynomin aste, numero – korkeimman asteen kerroin (tai vain korkein kerroin), ja kerroin on vapaa jäsen.

Merkitsen tätä polynomia lyhyesti .

Polynomin juuret kutsua yhtälön juuria

Rakastan rautaista logiikkaa =)

Esimerkkejä löydät artikkelin alusta:

1. ja 2. asteen polynomien juurien löytämisessä ei ole ongelmia, mutta kasvaessa tämä tehtävä muuttuu yhä vaikeammaksi. Vaikka toisaalta kaikki on mielenkiintoisempaa! Ja juuri tälle oppitunnin toinen osa on omistettu.

Ensinnäkin kirjaimellisesti puolet teorian näytöstä:

1) Seurauksen mukaan algebran peruslause, astepolynomilla on täsmälleen monimutkainen juuret. Jotkut juuret (tai jopa kaikki) voivat olla erityisen pätevä. Lisäksi todellisten juurien joukossa voi olla identtisiä (useita) juuria (vähintään kaksi, enintään kappaletta).

Jos jokin kompleksiluku on polynomin juuri, niin konjugaatti sen numero on myös välttämättä tämän polynomin juuri (konjugoitujen kompleksisten juurien muoto on ).

Yksinkertaisin esimerkki on toisen asteen yhtälö, joka löydettiin ensimmäisen kerran 8 (Kuten) luokassa, ja jonka vihdoin "päätimme" aiheessa kompleksiluvut. Muistutan teitä: toisen asteen yhtälöllä on joko kaksi erilaista reaalijuurta tai useita juuria tai konjugoituja kompleksisia juuria.

2) Alkaen Bezoutin lause Tästä seuraa, että jos luku on yhtälön juuri, niin vastaava polynomi voidaan kertoa:
, missä on astepolynomi.

Ja jälleen vanha esimerkkimme: koska on yhtälön juuri, niin . Sen jälkeen ei ole vaikeaa saada tunnettua "koulu"-laajennusta.

Bezoutin lauseen seurauksella on suuri käytännön arvo: jos tiedämme 3. asteen yhtälön juuren, voimme esittää sen muodossa ja toisen asteen yhtälöstä on helppo selvittää jäljellä olevat juuret. Jos tunnemme 4. asteen yhtälön juuren, on mahdollista laajentaa vasen puoli tuotteeksi jne.

Ja tässä on kaksi kysymystä:

Kysymys yksi. Kuinka löytää juuri tämä juuri? Ensinnäkin määritellään sen luonne: monissa korkeamman matematiikan ongelmissa se on löydettävä järkevää, erityisesti koko polynomien juuret, ja tässä suhteessa olemme edelleen kiinnostuneita pääasiassa niistä.... ...ne ovat niin hyviä, niin pörröisiä, että haluat vain löytää ne! =)

Ensimmäinen asia, joka tulee mieleen, on valintamenetelmä. Harkitse esimerkiksi yhtälöä . Tässä saalis on vapaalla termillä - jos se olisi yhtä suuri kuin nolla, niin kaikki olisi hyvin - otamme "x":n pois suluista ja juuret itse "pudottavat" pintaan:

Mutta vapaa termimme on yhtä suuri kuin "kolme", ​​ja siksi alamme korvata yhtälöön erilaisia ​​numeroita, jotka väittävät olevansa "juuri". Ensinnäkin yksittäisten arvojen korvaaminen viittaa itsestään. Korvataan:

Otettu vastaan väärä tasa-arvo, joten yksikkö "ei sopinut". No, okei, korvataan:

Otettu vastaan totta tasa-arvo! Eli arvo on tämän yhtälön juuri.

Kolmannen asteen polynomin juurien löytämiseksi on olemassa analyyttinen menetelmä (ns. Cardano-kaavat), mutta nyt olemme kiinnostuneita hieman erilaisesta tehtävästä.

Koska - on polynomimme juuri, polynomi voidaan esittää muodossa ja syntyy Toinen kysymys: kuinka löytää "nuorempi veli"?

Yksinkertaisimmat algebralliset näkökohdat viittaavat siihen, että tätä varten meidän on jaettava luvulla . Kuinka jakaa polynomi polynomilla? Sama koulumenetelmä, joka jakaa tavalliset numerot - "sarake"! Käsittelin tätä menetelmää yksityiskohtaisesti oppitunnin ensimmäisissä esimerkeissä. Monimutkaiset rajat, ja nyt tarkastelemme toista menetelmää, jota kutsutaan Hornerin kaava.

Ensin kirjoitetaan "korkein" polynomi kaikkien kanssa , mukaan lukien nollakertoimet:
, jonka jälkeen syötämme nämä kertoimet (tiukasti järjestyksessä) taulukon ylimmälle riville:

Kirjoitamme juuren vasemmalle:

Teen heti varauksen, että Hornerin järjestelmä toimii myös, jos "punainen" numero Ei on polynomin juuri. Älkäämme kuitenkaan kiirettäkö asioita.

Poistamme johtavan kertoimen ylhäältä:

Alempien solujen täyttöprosessi muistuttaa hieman kirjontaa, jossa "miinus yksi" on eräänlainen "neula", joka läpäisee seuraavat vaiheet. Kerromme "alennettu" luvun (-1) ja lisäämme tuotteeseen yläsolun numeron:

Kerromme löydetyn arvon "punaisella neulalla" ja lisäämme tuotteeseen seuraavan yhtälökertoimen:

Ja lopuksi tuloksena oleva arvo "käsitellään" jälleen "neulalla" ja ylemmällä kertoimella:

Viimeisen solun nolla kertoo, että polynomi on jaettu jälkeä jättämättä (kuten pitääkin), kun taas laajennuskertoimet "poistetaan" suoraan taulukon alimmalta riviltä:

Siten siirryimme yhtälöstä vastaavaan yhtälöön ja kaikki on selvää kahdella jäljellä olevalla juurilla (tässä tapauksessa saamme konjugoidut monimutkaiset juuret).

Yhtälö voidaan muuten ratkaista myös graafisesti: plot "salama" ja katso, että kuvaaja ylittää x-akselin () kohdassa. Tai sama "ovela" temppu - kirjoitamme yhtälön uudelleen muotoon , piirrämme peruskaavioita ja havaitsemme niiden leikkauspisteen "X"-koordinaatin.

Muuten minkä tahansa 3. asteen funktiopolynomin kuvaaja leikkaa akselin vähintään kerran, mikä tarkoittaa, että vastaavalla yhtälöllä on vähintään yksi pätevä juuri. Tämä tosiasia pätee mille tahansa parittoman asteen polynomifunktiolle.

Ja tässä haluaisin myös jäädä tärkeä pointti mikä koskee terminologiaa: polynomi Ja polynomifunktio – se ei ole sama asia! Mutta käytännössä he usein puhuvat esimerkiksi "polynomin kaaviosta", joka tietysti on huolimattomuutta.

Palataan kuitenkin Hornerin suunnitelmaan. Kuten äskettäin mainitsin, tämä järjestelmä toimii muille numeroille, mutta jos numero Ei on yhtälön juuri, niin nollasta poikkeava summa (jäännös) näkyy kaavassamme:

"Ajataan" "epäonnistunut" arvo Hornerin kaavion mukaan. Tässä tapauksessa on kätevää käyttää samaa taulukkoa - kirjoita uusi "neula" vasemmalle, siirrä johtava kerroin ylhäältä (vasen vihreä nuoli), ja mennään:

Tarkistaaksesi, avataan sulut ja esitetään samanlaiset termit:
, OK.

On helppo nähdä, että jäännös ("kuusi") on täsmälleen polynomin arvo . Ja itse asiassa - millaista se on:
, ja vielä hienompaa - kuten tämä:

Yllä olevista laskelmista on helppo ymmärtää, että Hornerin järjestelmä sallii polynomin ottamista huomioon, mutta myös juuren "sivistyneen" valinnan. Suosittelen, että vahvistat laskenta-algoritmin itse pienellä tehtävällä:

Tehtävä 2

Etsi Hornerin kaavion avulla yhtälön kokonaislukujuuri ja kerro vastaava polynomi

Toisin sanoen tässä sinun on tarkistettava numerot 1, –1, 2, –2, ... – peräkkäin, kunnes viimeiseen sarakkeeseen "piirretään" nollajäännös. Tämä tarkoittaa, että tämän rivin "neula" on polynomin juuri

Laskelmat on kätevää järjestää yhteen taulukkoon. Yksityiskohtainen ratkaisu ja vastaus oppitunnin lopussa.

Juurien valintamenetelmä on hyvä suhteellisen yksinkertaisiin tapauksiin, mutta jos polynomin kertoimet ja/tai aste ovat suuria, prosessi voi kestää kauan. Tai ehkä on joitain arvoja samasta listasta 1, -1, 2, -2, eikä niitä ole syytä harkita? Ja lisäksi juuret voivat osoittautua murto-osaisiksi, mikä johtaa täysin epätieteelliseen tönäisyyteen.

Onneksi on olemassa kaksi voimakasta lausetta, jotka voivat merkittävästi vähentää "ehdokas"-arvojen etsimistä rationaalisille juurille:

Lause 1 Harkitsemme vähentymätön murto-osa, missä. Jos luku on yhtälön juuri, niin vapaa termi jaetaan ja johtava kerroin jaetaan.

Erityisesti, jos johtava kerroin on , niin tämä rationaalinen juuri on kokonaisluku:

Ja alamme hyödyntää lausetta tällä maukkaalla yksityiskohdalla:

Palataan yhtälöön. Koska sen johtava kerroin on , hypoteettiset rationaaliset juuret voivat olla yksinomaan kokonaislukuja, ja vapaa termi on välttämättä jaettava näihin juuriin ilman jäännöstä. Ja "kolme" voidaan jakaa vain 1, -1, 3 ja -3. Eli meillä on vain 4 "juuriehdokasta". Ja sen mukaan Lause 1, muut rationaaliset luvut eivät voi olla tämän yhtälön juuria PERIAATTEESSA.

Yhtälössä on hieman enemmän "kilpailijoita": vapaa termi on jaettu 1, –1, 2, – 2, 4 ja –4.

Huomaa, että numerot 1, –1 ovat "säännöllisiä" mahdollisten juuriluettelossa (ilmeinen seuraus lauseesta) ja paras valinta prioriteettitestaukseen.

Jatketaan merkityksellisempiin esimerkkeihin:

Ongelma 3

Ratkaisu: koska johtava kerroin on , niin hypoteettiset rationaaliset juuret voivat olla vain kokonaislukuja, ja niiden on välttämättä oltava vapaan termin jakajia. "Miinus neljäkymmentä" on jaettu seuraaviin numeropareihin:
– yhteensä 16 "ehdokasta".

Ja tässä heti ilmestyy houkutteleva ajatus: onko mahdollista kitkeä pois kaikki negatiiviset vai kaikki positiiviset juuret? Joissain tapauksissa se on mahdollista! Muotoilen kaksi merkkiä:

1) Jos Kaikki Jos polynomin kertoimet eivät ole negatiivisia, sillä ei voi olla positiivisia juuria. Valitettavasti tämä ei ole meidän tapauksemme (Jos nyt meille annettaisiin yhtälö - niin kyllä, kun korvataan mikä tahansa polynomin arvo, polynomin arvo on ehdottomasti positiivinen, mikä tarkoittaa, että kaikki positiiviset luvut (ja irrationaalisia myös) eivät voi olla yhtälön juuria.

2) Jos parittomien potenssien kertoimet ovat ei-negatiivisia ja kaikille parillisille potenssille (mukaan lukien ilmainen jäsen) ovat negatiivisia, silloin polynomilla ei voi olla negatiivisia juuria. Tämä on meidän tapaus! Kun katsot hieman tarkemmin, voit nähdä, että kun yhtälössä korvataan mikä tahansa negatiivinen "X", vasen puoli on ehdottomasti negatiivinen, mikä tarkoittaa, että negatiiviset juuret katoavat

Tutkimusta varten on siis jäljellä 8 numeroa:

"Lataamme" ne peräkkäin Hornerin järjestelmän mukaan. Toivon, että olet jo oppinut henkiset laskelmat:

Onni odotti meitä "kahta" testattaessa. Siten on tarkasteltavan yhtälön juuri ja

On vielä tutkittava yhtälö . Tämä on helppo tehdä erottimen avulla, mutta teen suuntaa-antavan testin käyttäen samaa järjestelmää. Ensinnäkin huomioikaa, että vapaa termi on yhtä suuri kuin 20, mikä tarkoittaa Lause 1 luvut 8 ja 40 putoavat pois mahdollisten juurien luettelosta, jättäen arvot tutkimukseen (yksi eliminoitiin Hornerin kaavan mukaan).

Kirjoitamme trinomin kertoimet uuden taulukon yläriville ja Aloitamme tarkistamisen samalla "kahdella". Miksi? Ja koska juuret voivat olla kerrannaisia, ole hyvä: - tällä yhtälöllä on 10 identtistä juurta. Mutta älkäämme hämmentykö:

Ja tässä tietysti valehtelin vähän tietäen, että juuret ovat järkeviä. Loppujen lopuksi, jos ne olisivat irrationaalisia tai monimutkaisia, joutuisin kaikkien jäljellä olevien lukujen epäonnistuneen tarkastuksen. Käytä siis käytännössä syrjintää ohjaamaan.

Vastaus: rationaaliset juuret: 2, 4, 5

Analysoimassamme ongelmassa olimme onnekkaita, koska: a) negatiiviset arvot putosivat heti ja b) löysimme juuren hyvin nopeasti (ja teoriassa voisimme tarkistaa koko luettelon).

Mutta todellisuudessa tilanne on paljon pahempi. Kutsun sinut katsomaan jännittävää peliä nimeltä "The Last Hero":

Ongelma 4

Etsi yhtälön rationaaliset juuret

Ratkaisu: Tekijä Lause 1 hypoteettisten rationaalisten juurien osoittajien on täytettävä ehto (luemme "kaksitoista on jaettu el:llä"), ja nimittäjät vastaavat ehtoa . Tämän perusteella saamme kaksi listaa:

"lista el":
ja "lista um": (onneksi luvut ovat luonnollisia).

Tehdään nyt luettelo kaikista mahdollisista juurista. Ensin jaamme "el-listan" luvulla. On täysin selvää, että samat luvut saadaan. Laitetaan ne taulukkoon mukavuuden vuoksi:

Monia murto-osia on pienennetty, mikä johtaa arvoihin, jotka ovat jo "sankariluettelossa". Lisäämme vain "aloittelijat":

Samalla tavalla jaamme saman "luettelon" seuraavasti:

ja lopuksi päälle

Näin ollen pelimme osallistujaryhmä on valmis:


Valitettavasti tämän tehtävän polynomi ei täytä "positiivisen" tai "negatiivisen" kriteeriä, joten emme voi hylätä ylä- tai alariviä. Sinun on työskenneltävä kaikkien numeroiden kanssa.

Miten voit? No, pää pystyyn - on toinen lause, jota voidaan kuvainnollisesti kutsua "tappajalauseeksi"…. ..."ehdokkaat", tietysti =)

Mutta ensin sinun täytyy selata Hornerin kaaviota ainakin yhden kohdalla koko numeroita. Perinteisesti otetaan yksi. Yläriville kirjoitamme polynomin kertoimet ja kaikki on kuten tavallisesti:

Koska neljä ei selvästikään ole nolla, arvo ei ole kyseessä olevan polynomin juuri. Mutta hän auttaa meitä paljon.

Lause 2 Jos joillekin yleisesti polynomin arvo on nollasta poikkeava: , sitten sen rationaaliset juuret (jos he ovat) tyydyttää ehtoa

Meidän tapauksessamme ja siksi kaikkien mahdollisten juurten on täytettävä ehto (kutsutaanko sitä tilaksi nro 1). Tämä neljä on monien "ehdokkaiden" "tappaja". Esittelynä katson muutamaa tarkistusta:

Tarkastetaan "ehdokas". Tätä varten on esitettävä se keinotekoisesti murto-osan muodossa, josta näkyy selvästi, että . Lasketaan testiero: . Neljä on jaettu "miinus kahdella": , mikä tarkoittaa, että mahdollinen juuri on läpäissyt testin.

Tarkastetaan arvo. Tässä testin ero on: . Tietenkin, ja siksi myös toinen "aihe" pysyy luettelossa.

Ammatillisen matematiikan tutor -sivusto jatkaa opetusta käsittelevien metodologisten artikkelien sarjaa. Julkaisen kuvauksia työmenetelmistäni koulun opetussuunnitelman monimutkaisimpien ja ongelmallisimpien aiheiden parissa. Tämä materiaali on hyödyllinen 8-11-luokkien opiskelijoiden kanssa työskenteleville matematiikan opettajille ja ohjaajille sekä tavallisessa ohjelmassa että matematiikan tuntien ohjelmassa.

Matematiikan ohjaaja ei voi aina selittää oppikirjassa huonosti esitettyä materiaalia. Valitettavasti tällaisia ​​aiheita tulee yhä enemmän ja esitysvirheitä tapahtuu käsikirjojen tekijöiden mukaan. Tämä ei koske vain aloittelevia matematiikan tutoreita ja osa-aikaisia ​​tutoreita (tuutorit ovat opiskelijoita ja yliopistotuoreita), vaan myös kokeneita opettajia, ammatillisia tutoreita, tuutoreita, joilla on kokemusta ja pätevyyttä. Kaikilla matematiikan ohjaajilla ei ole kykyä korjata koulujen oppikirjojen karkeita reunoja. Kaikki eivät myöskään ymmärrä, että nämä korjaukset (tai lisäykset) ovat välttämättömiä. Harvat lapset osallistuvat materiaalin mukauttamiseen lasten laadulliseen havaintoon. Valitettavasti aika on ohi, jolloin matematiikan opettajat yhdessä metodologien ja julkaisujen tekijöiden kanssa keskustelivat massalla jokaisesta oppikirjan kirjaimesta. Aiemmin ennen oppikirjan julkaisua kouluihin tehtiin vakavia analyyseja ja oppimistuloksia koskevia tutkimuksia. On tullut aika amatööreille, jotka pyrkivät tekemään oppikirjoista yleismaailmallisia mukauttamalla ne vahvojen matematiikan luokkien standardiin.

Kilpailu informaation määrän lisäämisestä johtaa vain sen assimilaation laadun heikkenemiseen ja sen seurauksena matematiikan todellisen tiedon tason laskuun. Mutta kukaan ei kiinnitä tähän huomiota. Ja lapsemme pakotetaan jo 8. luokalla opiskelemaan sitä, mitä opiskelimme instituutissa: todennäköisyysteoriaa, korkean asteen yhtälöiden ratkaisemista ja jotain muuta. Kirjojen materiaalin mukauttaminen lapsen täyteen havaintoon jättää paljon toivomisen varaa, ja matematiikan ohjaajan on pakko käsitellä tätä jotenkin.

Puhutaanpa menetelmästä, jolla opetetaan niin erityistä aihetta kuin "polynomin jakaminen polynomilla kulmalla", joka tunnetaan aikuismatematiikassa paremmin nimellä "Bezoutin lause ja Hornerin kaavio". Vielä pari vuotta sitten kysymys ei ollut niin painava matematiikan tutorille, koska se ei kuulunut koulun pääopetusohjelmaan. Nyt Teljakovskyn toimittaman oppikirjan arvostetut kirjoittajat ovat tehneet muutoksia mielestäni parhaan oppikirjan uusimpaan painokseen ja pilattuaan sen kokonaan lisänneet opettajalle turhaa huolta. Kirjoittajien innovaatioihin keskittyvien koulujen ja luokkien opettajat, joilla ei ole matematiikan asemaa, alkoivat sisällyttää tunneilleen useammin lisäkappaleita, ja uteliaat lapset, jotka katsovat matematiikan oppikirjansa kauniita sivuja, kysyvät yhä useammin ohjaaja: "Mikä tämä kulman jako on? Käymmekö tämän läpi? Kuinka jakaa nurkka? Ei voi enää piiloutua sellaisilta suorilta kysymyksiltä. Opettajan on kerrottava lapselle jotain.

Mutta kuten? En luultavasti olisi kuvaillut tapaa työskennellä aiheen kanssa, jos se olisi pätevästi esitelty oppikirjoissa. Miten meillä kaikki menee? Oppikirjat pitää tulostaa ja myydä. Ja tätä varten ne on päivitettävä säännöllisesti. Valittavatko yliopiston opettajat, että lapset tulevat heidän luokseen tyhjäpäisin, ilman tietoja ja taitoja? Ovatko matemaattisen tiedon vaatimukset lisääntymässä? Loistava! Poistetaan joitakin harjoituksia ja lisätään sen sijaan aiheita, joita opitaan muissa ohjelmissa. Miksi oppikirjamme on huonompi? Lisäämme joitakin lisälukuja. Koululaiset eivät tiedä kulman jakamisen sääntöä? Tämä on perusmatematiikkaa. Tästä kappaleesta tulisi tehdä valinnainen otsikko "niille, jotka haluavat tietää enemmän". Tutorit sitä vastaan? Miksi välitämme ohjaajista yleensä? Metodologit ja koulun opettajat ovat myös sitä vastaan? Emme monimutkaista materiaalia ja harkitsemme sen yksinkertaisinta osaa.

Ja tästä se alkaa. Aiheen yksinkertaisuus ja sen assimiloinnin laatu piilee ennen kaikkea sen logiikan ymmärtämisessä, ei siinä, että tehdään oppikirjan tekijöiden ohjeiden mukaisesti tietty joukko toimintoja, jotka eivät liity selvästi toisiinsa. . Muuten opiskelijan päässä on sumua. Jos kirjoittajat ovat suunnattu suhteellisen vahvoille opiskelijoille (mutta opiskelevat tavallisessa ohjelmassa), sinun ei pitäisi esittää aihetta komentomuodossa. Mitä näemme oppikirjassa? Lapset, meidän on jaettava tämän säännön mukaan. Ota polynomi kulman alle. Siten alkuperäinen polynomi kerrotaan. Ei kuitenkaan ole selvää, miksi kulman alla olevat termit on valittu juuri tällä tavalla, miksi ne täytyy kertoa kulman yläpuolella olevalla polynomilla ja sitten vähentää nykyisestä jäännöksestä. Ja mikä tärkeintä, ei ole selvää, miksi valitut monomit on lopulta lisättävä ja miksi tuloksena olevat hakasulkeet ovat alkuperäisen polynomin laajennus. Jokainen pätevä matemaatikko laittaa lihavoitun kysymysmerkin oppikirjassa annettujen selitysten päälle.

Tuon ohjaajien ja matematiikan opettajien tietoon ratkaisuni ongelmaan, joka käytännössä tekee kaiken oppikirjassa sanotun itsestään selväksi opiskelijalle. Itse asiassa todistamme Bezoutin lauseen: jos luku a on polynomin juuri, niin tämä polynomi voidaan jakaa tekijöiksi, joista yksi on x-a ja toinen saadaan alkuperäisestä jollakin kolmesta tavasta: eristämällä lineaarinen tekijä muunnoksilla, jakamalla kulmalla tai Hornerin kaavalla. Juuri tällä muotoilulla matematiikan ohjaajan on helpompi työskennellä.

Mikä on opetusmetodologia? Ensinnäkin tämä on selkeä järjestys selitysten ja esimerkkien järjestyksessä, jonka perusteella matemaattiset johtopäätökset tehdään. Tämä aihe ei ole poikkeus. On erittäin tärkeää, että matematiikan opettaja esittelee lapsen Bezoutin lauseeseen ennen jakamista kulmalla. Se on erittäin tärkeää! On parasta saada ymmärrystä käyttämällä tiettyä esimerkkiä. Otetaan jokin polynomi valitulla juurilla ja esitellään tekniikka, jolla se lasketaan tekijöiksi identiteettimuunnosmenetelmällä, joka on tuttu koululaisille 7. luokalta lähtien. Asianmukaisilla mukana olevilla selityksillä, painotuksella ja matematiikan ohjaajan vinkeillä on täysin mahdollista välittää materiaali ilman yleisiä matemaattisia laskelmia, mielivaltaisia ​​kertoimia ja asteita.

Tärkeä neuvo matematiikan opettajalle- noudata ohjeita alusta loppuun äläkä muuta tätä järjestystä.

Oletetaan siis, että meillä on polynomi. Jos korvaamme luvun 1 sen X:n sijaan, polynomin arvo on nolla. Siksi x=1 on sen juuri. Yritetään jakaa se kahdeksi termiksi siten, että toinen niistä on lineaarisen lausekkeen ja jonkin monomiaalin tulos ja toisen aste on yksi pienempi kuin . Eli esitetään se muodossa

Valitsemme punaisen kentän monominin niin, että kun se kerrotaan johtavalla termillä, se on täysin sama kuin alkuperäisen polynomin johtava termi. Jos opiskelija ei ole heikoin, hän pystyy hyvin kertomaan matematiikan ohjaajalle vaaditun lausekkeen: . Ohjaajaa tulee välittömästi pyytää lisäämään se punaiseen kenttään ja näyttämään, mitä tapahtuu, kun ne avataan. Tämä virtuaalinen väliaikainen polynomi on parasta allekirjoittaa nuolien alle (pienen kuvan alle), korostaen sitä jollain värillä, esimerkiksi sinisellä. Tämä auttaa sinua valitsemaan termin punaiselle kenttään, jota kutsutaan valinnan loppuosaksi. Suosittelen ohjaajia huomauttamaan tässä, että tämä jäännös voidaan löytää vähentämällä. Suorittamalla tämän toiminnon saamme:

Matematiikan ohjaajan tulee kiinnittää opiskelijan huomio siihen, että korvaamalla yksi tähän yhtälään, saamme taatusti nollan sen vasemmalle puolelle (koska 1 on alkuperäisen polynomin juuri), ja oikealla puolella, tietysti nollaa myös ensimmäisen lukukauden. Tämä tarkoittaa, että ilman minkäänlaista vahvistusta voimme sanoa, että yksi on "vihreän jäännöksen" juuri.

Käsittelemme sitä samalla tavalla kuin teimme alkuperäisen polynomin kanssa, eristäen siitä saman lineaarisen tekijän. Matematiikan ohjaaja piirtää kaksi kehystä oppilaan eteen ja pyytää häntä täyttämään vasemmalta oikealle.

Opiskelija valitsee ohjaajalle punaisen kentän monominin niin, että se kerrottuna lineaarisen lausekkeen päätermillä antaa laajenevan polynomin alkutermin. Sovitamme sen kehykseen, avaa heti kiinnike ja korosta sinisellä lauseke, joka on vähennettävä taitettavasta. Suorittamalla tämän operaation saamme

Ja lopuksi tehdä sama viimeisellä jäljellä olevalla osalla

saamme sen vihdoin

Otetaan nyt lauseke pois suluista ja näemme alkuperäisen polynomin hajoamisen tekijöiksi, joista yksi on "x miinus valittu juuri".

Jotta opiskelija ei ajattelisi, että viimeinen "vihreä jäännös" hajosi vahingossa vaadituiksi tekijöiksi, matematiikan ohjaajan tulee osoittaa kaikkien vihreiden jäännösten tärkeä ominaisuus - jokaisella niistä on juuri 1. Koska nämä jäännökset pienenevät, niin mikä tahansa alkuluvun aste tahansa, riippumatta siitä, kuinka paljon polynomia meille annetaan, ennemmin tai myöhemmin saamme lineaarisen "vihreän jäännöksen", jonka juuri on 1, ja siksi se välttämättä hajoaa tietyn arvon tuloksi. numero ja lauseke.

Tällaisen valmistelutyön jälkeen matematiikan ohjaajan ei ole vaikea selittää opiskelijalle, mitä tapahtuu kulmalla jaettaessa. Tämä on sama prosessi, vain lyhyemmässä ja tiiviimmässä muodossa, ilman yhtäläisyysmerkkejä ja kirjoittamatta uudelleen samoja korostettuja termejä. Polynomi, josta lineaarinen tekijä erotetaan, kirjoitetaan kulman vasemmalle puolelle, valitut punaiset monomit kerätään kulmassa (nyt käy selväksi, miksi niiden pitäisi laskea yhteen), jotta saadaan "siniset polynomit", "punaiset". ” luvut on kerrottava x-1:llä ja vähennettävä sitten valitusta, kuinka tämä tehdään tavallisessa lukujen jakamisessa sarakkeeseen (tässä on analogia aiemmin tutkitun kanssa). Tuloksena olevat "vihreät jäännökset" joutuvat uuteen eristykseen ja "punaisten monomien" valintaan. Ja niin edelleen, kunnes saat nollan "vihreän tasapainon". Tärkeintä on, että opiskelija ymmärtää kulman ylä- ja alapuolella olevien kirjoitettujen polynomien jatkokohtalon. Ilmeisesti nämä ovat hakasulkuja, joiden tulo on yhtä suuri kuin alkuperäinen polynomi.

Seuraava vaihe matematiikan ohjaajan työssä on Bezoutin lauseen muotoilu. Itse asiassa sen muotoilu tällä ohjaajan lähestymistavalla tulee ilmeiseksi: jos luku a on polynomin juuri, niin se voidaan kertoilla, joista toinen on , ja toinen saadaan alkuperäisestä jollakin kolmesta tavasta. :

• suora hajoaminen (analogisesti ryhmittelymenetelmän kanssa)
• jakamalla kulmalla (sarakkeessa)
• Hornerin piirin kautta

On sanottava, että kaikki matematiikan tutorit eivät näytä sarvikaaviota oppilailleen, eivätkä kaikki koulun opettajat (onneksi tutorien itsensäkin kannalta) mene niin syvälle aiheeseen tunneilla. Matematiikan luokan opiskelijalle en kuitenkaan näe mitään syytä pysähtyä pitkiin jakoon. Lisäksi kätevin ja nopeasti Hajotustekniikka perustuu juuri Hornerin kaavioon. Selittääkseen lapselle, mistä se tulee, riittää, että jäljitetään kulmalla jakamisen esimerkillä korkeampien kertoimien esiintyminen vihreissä jäännöksissä. On selvää, että alkuperäisen polynomin johtava kerroin siirretään ensimmäisen "punaisen monomin" kertoimeen ja edelleen nykyisen ylemmän polynomin toisesta kertoimesta vähennetään tulos kertomalla "punaisen monomin" virtakerroin . Siksi se on mahdollista lisätä luvulla kertomisen tulos. Keskitettyään opiskelijan huomion kertoimilla tehtävien toimien erityispiirteisiin, matematiikan ohjaaja voi näyttää, kuinka nämä toiminnot yleensä suoritetaan ilman itse muuttujien tallentamista. Tätä varten on kätevää syöttää alkuperäisen polynomin juuri ja kertoimet tärkeysjärjestyksessä seuraavaan taulukkoon:

Jos polynomista puuttuu jokin aste, sen nollakerroin pakotetaan taulukkoon. "Punaisten polynomien" kertoimet kirjoitetaan vuorotellen alimmalle riville "koukku" -säännön mukaisesti:

Juuri kerrotaan viimeisellä punaisella kertoimella, lisätään seuraavaan kertoimeen ylärivillä ja tulos kirjoitetaan alariville. Viimeisessä sarakkeessa saamme taatusti viimeisen "vihreän jäännöksen" suurimman kertoimen, eli nollan. Kun prosessi on valmis, numerot sovitetun juuren ja nollajäännöksen väliin ovat toisen (epälineaarisen) tekijän kertoimia.

Koska juuri a antaa alimman rivin lopussa nollan, Hornerin mallia voidaan käyttää polynomin juuren otsikon lukujen tarkistamiseen. Jos erityinen lause rationaalisen juuren valinnasta. Kaikki tämän avulla saadut ehdokkaat tähän titteliin lisätään yksinkertaisesti vuorotellen vasemmalta Hornerin kaavioon. Heti kun saamme nollan, testattava luku on juuri ja samalla saamme sen suoralle alkuperäisen polynomin kertoimet. Erittäin mukavasti.

Lopuksi haluan todeta, että Hornerin järjestelmän tarkan esittelyn ja aiheen käytännön lujittamiseksi matematiikan ohjaajalla on oltava käytettävissään riittävä määrä tunteja. "Kerran viikossa" -järjestelmän kanssa työskentelevän tutorin ei tulisi osallistua nurkkajakoon. Matematiikan yhtenäisestä valtionkokeesta ja valtion matematiikan matematiikan akatemiasta on epätodennäköistä, että ensimmäisessä osassa kohtaat kolmannen asteen yhtälön, joka voidaan ratkaista sellaisilla keinoilla. Jos ohjaaja valmistelee lasta matematiikan kokeeseen Moskovan valtionyliopistossa, aiheen opiskelusta tulee pakollista. Yliopiston opettajat, toisin kuin yhtenäisen valtionkokeen laatijat, todella haluavat testata hakijan tietämyksen syvyyttä.

Kolpakov Alexander Nikolaevich, matematiikan ohjaaja Moskova, Strogino

Hornerin kaavio - menetelmä polynomin jakamiseksi

$$P_n(x)=\sum\limits_(i=0)^(n)a_(i)x^(n-i)=a_(0)x^(n)+a_(1)x^(n-1) )+a_(2)x^(n-2)+\ldots+a_(n-1)x+a_n$$

binomiaalissa $x-a$. Sinun on työskenneltävä taulukon kanssa, jonka ensimmäisellä rivillä on tietyn polynomin kertoimet. Toisen rivin ensimmäinen elementti on luku $a$, joka on otettu binomista $x-a$:

Kun n:nnen asteen polynomi on jaettu binomiaalilla $x-a$, saadaan polynomi, jonka aste on yksi pienempi kuin alkuperäinen, ts. on yhtä suuri kuin $n-1$. Hornerin järjestelmän suora soveltaminen on helpointa osoittaa esimerkein.

Esimerkki nro 1

Jaa $5x^4+5x^3+x^2-11$ $x-1$:lla Hornerin kaavaa käyttäen.

Tehdään kahden rivin taulukko: ensimmäiselle riville kirjoitetaan polynomin $5x^4+5x^3+x^2-11$ kertoimet, jotka on järjestetty muuttujan $x$ potenssien laskevaan järjestykseen. Huomaa, että tämä polynomi ei sisällä $x$ ensimmäisessä asteessa, ts. $x$:n kerroin ensimmäiseen potenssiin on 0. Koska jaamme arvolla $x-1$, kirjoitamme toiselle riville yhden:

Aloitetaan toisen rivin tyhjien solujen täyttäminen. Toisen rivin toiseen soluun kirjoitetaan numero $5$ siirtämällä se yksinkertaisesti ensimmäisen rivin vastaavasta solusta:

Täytä seuraava solu tällä periaatteella: $1\cdot 5+5=10$:

Täytetään toisen rivin neljäs solu samalla tavalla: $1\cdot 10+1=11$:

Viidennelle solulle saamme: $1\cdot 11+0=11$:

Ja lopuksi, viimeinen, kuudes solu, meillä on: $1\cdot 11+(-11)=0$:

Ongelma on ratkaistu, jäljellä on vain kirjoittaa vastaus muistiin:

Kuten näette, toisella rivillä (yhden ja nollan välillä) sijaitsevat luvut ovat polynomin kertoimia, jotka saadaan, kun $5x^4+5x^3+x^2-11$ jaetaan $x-1$:lla. Luonnollisesti, koska alkuperäisen polynomin $5x^4+5x^3+x^2-11$ aste oli neljä, tuloksena olevan polynomin $5x^3+10x^2+11x+11$ aste on yksi vähemmän, ts. vastaa kolmea. Toisen rivin viimeinen luku (nolla) tarkoittaa jäännöstä, kun polynomi $5x^4+5x^3+x^2-11$ jaetaan $x-1$:lla. Meidän tapauksessamme jäännös on nolla, ts. polynomit ovat tasaisesti jaollisia. Tätä tulosta voidaan luonnehtia myös seuraavasti: polynomin $5x^4+5x^3+x^2-11$ arvo $x=1$:lle on yhtä suuri kuin nolla.

Johtopäätös voidaan muotoilla myös tässä muodossa: koska polynomin $5x^4+5x^3+x^2-11$ arvo kohdassa $x=1$ on nolla, niin yksikkö on polynomin juuri $5x^4+5x^3+ x^2-11$.

Esimerkki nro 2

Jaa polynomi $x^4+3x^3+4x^2-5x-47$ $x+3$:lla Hornerin kaavaa käyttäen.

Määrätään heti, että lauseke $x+3$ on esitettävä muodossa $x-(-3)$. Hornerin ohjelmaan kuuluu täsmälleen -3 dollaria. Koska alkuperäisen polynomin $x^4+3x^3+4x^2-5x-47$ aste on neljä, niin jaon tuloksena saadaan kolmannen asteen polynomi:

Tulos tarkoittaa sitä

$$x^4+3x^3+4x^2-5x-47=(x+3)(x^3+0\cdot x^2 +4x-17)+4=(x+3)(x^ 3+4x-17)+4$$

Tässä tilanteessa jäännös, kun jaetaan $x^4+3x^3+4x^2-5x-47$ $x+3$:lla, on $4$. Tai mikä on sama, polynomin $x^4+3x^3+4x^2-5x-47$ arvo $x=-3$ on yhtä suuri kuin $4$. Muuten, tämä on helppo tarkistaa korvaamalla suoraan $x=-3$ annettuun polynomiin:

$$x^4+3x^3+4x^2-5x-47=(-3)^4+3 \cdot (-3)^3-5 \cdot (-3)-47=4.$$

Nuo. Hornerin kaaviota voidaan käyttää, jos sinun on löydettävä polynomin arvo muuttujan tietylle arvolle. Jos tavoitteenamme on löytää polynomin kaikki juuret, niin Hornerin kaaviota voidaan soveltaa useita kertoja peräkkäin, kunnes olemme käyttäneet kaikki juuret, kuten esimerkissä 3 on käsitelty.

Esimerkki nro 3

Etsi kaikki polynomin $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ kokonaislukujuuret Hornerin mallilla.

Kyseisen polynomin kertoimet ovat kokonaislukuja ja muuttujan suurimman potenssin kerroin (eli $x^6$) on yhtä suuri kuin yksi. Tässä tapauksessa polynomin kokonaislukujuuret on etsittävä vapaan termin jakajien joukosta, ts. luvun 45 jakajien joukossa. Tietylle polynomille sellaiset juuret voivat olla luvut $45; \; 15; \; 9; \; 5; \; 3; \; 1 $ ja -45 $; \; -15; \; -9; \; -5; \; -3; \; -1 $. Tarkastetaan esimerkiksi luku $1$:

Kuten näet, polynomin $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ arvo $x=1$ on yhtä suuri kuin $192$ (viimeinen luku toisella rivillä), eikä $0 $, joten yksikkö ei ole tämän polynomin juuri. Koska yhden tarkistus epäonnistui, tarkistetaan arvo $x=-1$. Emme luo tätä varten uutta taulukkoa, vaan jatkamme taulukon käyttöä. nro 1, lisäämällä siihen uuden (kolmannen) rivin. Toinen rivi, jossa $1$:n arvo tarkistettiin, korostetaan punaisella, eikä sitä käytetä jatkokeskusteluissa.

Voit tietysti kirjoittaa taulukon uudelleen uudelleen, mutta sen manuaalinen täyttäminen vie paljon aikaa. Lisäksi voi olla useita lukuja, joiden vahvistus epäonnistuu, ja uuden taulukon kirjoittaminen joka kerta on vaikeaa. Kun lasketaan "paperilla", punaiset viivat voidaan yksinkertaisesti ylittää.

Joten polynomin $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ arvo kohdassa $x=-1$ on yhtä suuri kuin nolla, ts. luku $-1$ on tämän polynomin juuri. Kun polynomi $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ on jaettu binomilla $x-(-1)=x+1$, saadaan polynomi $x ^5+x ^4-22x^3+2x^2+69x+45$, jonka kertoimet on otettu taulukon kolmannelta riviltä. nro 2 (katso esimerkki nro 1). Laskelmien tulos voidaan esittää myös tässä muodossa:

\begin(yhtälö)x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)(x^5+x^4-22x^3+2x^2 +69x+45)\end(yhtälö)

Jatketaan kokonaislukujuurien hakua. Nyt meidän täytyy etsiä polynomin $x^5+x^4-22x^3+2x^2+69x+45$ juuret. Jälleen tämän polynomin kokonaislukujuuria etsitään sen vapaan termin, lukujen $45$ jakajista. Yritetään tarkistaa numero $-1$ uudelleen. Emme luo uutta taulukkoa, vaan jatkamme edellisen taulukon käyttöä. nro 2, ts. Lisätään tähän vielä yksi rivi:

Joten luku $-1$ on polynomin $x^5+x^4-22x^3+2x^2+69x+45$ juuri. Tämä tulos voidaan kirjoittaa näin:

\begin(yhtälö)x^5+x^4-22x^3+2x^2+69x+45=(x+1)(x^4-22x^2+24x+45) \end(yhtälö)

Tasa-arvo (2) huomioon ottaen tasa-arvo (1) voidaan kirjoittaa uudelleen seuraavaan muotoon:

\begin(yhtälö)\begin(tasattu) & x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)(x^5+x^4-22x ^2+2x^2+69x+45)=\\ & =(x+1)(x+1)(x^4-22x^2+24x+45)=(x+1)^2(x^ 4-22x^2+24x+45)\end(tasattu)\end(yhtälö)

Nyt täytyy etsiä polynomin $x^4-22x^2+24x+45$ juuret - luonnollisesti sen vapaan termin jakajien joukosta (luvut $45$). Tarkistetaan numero $-1$ uudelleen:

Luku $-1$ on polynomin $x^4-22x^2+24x+45$ juuri. Tämä tulos voidaan kirjoittaa näin:

\begin(yhtälö)x^4-22x^2+24x+45=(x+1)(x^3-x^2-21x+45) \end(yhtälö)

Ottaen huomioon tasa-arvon (4), kirjoitamme tasa-arvon (3) uudelleen seuraavaan muotoon:

\begin(yhtälö)\begin(tasattu) & x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)^2(x^4-22x^3 +24x+45)= \\ & =(x+1)^2(x+1)(x^3-x^2-21x+45)=(x+1)^3(x^3-x^ 2-21x+45)\end(tasattu)\end(yhtälö)

Nyt etsitään polynomin $x^3-x^2-21x+45$ juuria. Tarkistetaan numero $-1$ uudelleen:

Tarkastus päättyi epäonnistumiseen. Korostetaan kuudes rivi punaisella ja yritetään tarkistaa toinen numero, esimerkiksi numero $3$:

Jäännös on nolla, joten luku $3$ on kyseessä olevan polynomin juuri. Joten $x^3-x^2-21x+45=(x-3)(x^2+2x-15)$. Nyt yhtäläisyys (5) voidaan kirjoittaa uudelleen seuraavasti.

Takaisin eteenpäin

Huomio! Diojen esikatselut ovat vain tiedoksi, eivätkä ne välttämättä edusta kaikkia esityksen ominaisuuksia. Jos olet kiinnostunut tästä työstä, lataa täysversio.

Oppitunnin tyyppi: Oppitunti perustiedon hallitsemisesta ja lujittamisesta.

Oppitunnin tarkoitus:

• Esittele opiskelijat polynomin juurten käsitteestä ja opeta heitä löytämään ne. Paranna taitojasi käyttää Hornerin menetelmää polynomin laajentamiseksi potenssien perusteella ja polynomin jakamiseksi binomiaalilla.
• Opi löytämään yhtälön juuret Hornerin kaavion avulla.
• Kehitä abstraktia ajattelua.
• Edistää tietojenkäsittelykulttuuria.
• Tieteidenvälisten yhteyksien kehittäminen.

Tuntien aikana

1. Organisatorinen hetki.

Ilmoita oppitunnin aihe, muotoile tavoitteet.

2. Kotitehtävien tarkistaminen.

3. Uuden materiaalin opiskelu.

Olkoon Fn(x) = a n x n +a n-1 x n-1 +...+ a 1 x +a 0 - n-asteen polynomi x:lle, jossa a 0, a 1,...,a n on annettu lukuja ja a 0 ei ole yhtä suuri kuin 0. Jos polynomi F n (x) jaetaan jäännöksellä binomialla x-a , niin osamäärä (epätäydellinen osamäärä) on polynomi Q n-1 (x) asteen n-1, jakoosa R on luku ja yhtälö on tosi Fn(x)=(x-a) Qn-1 (x) +R. Polynomi F n (x) on jaollinen binomilla (x-a) vain, jos R=0.

Bezoutin lause: Polynomin F n (x) jakamisesta binomilla (x-a) jäävä jäännös R on yhtä suuri kuin polynomin F n (x) arvo kohdassa x=a, ts. R = Pn(a).

Hieman historiaa. Bezoutin lause on ilmeisestä yksinkertaisuudestaan ​​ja ilmeisyydestään huolimatta yksi polynomiteorian peruslauseista. Tämä lause yhdistää polynomien algebralliset ominaisuudet (jotka sallivat polynomien käsittelemisen kokonaislukuina) niiden funktionaalisiin ominaisuuksiin (jotka sallivat polynomien käsittelemisen funktioina). Yksi tapa ratkaista korkeamman asteen yhtälöitä on kertoa yhtälön vasemmalla puolella oleva polynomi. Polynomin ja jäännöksen kertoimien laskenta kirjoitetaan Horner-kaavioksi kutsutun taulukon muodossa.

Hornerin kaavio on algoritmi polynomien jakamiseen, joka on kirjoitettu sitä erikoistapausta varten, kun osamäärä on yhtä suuri kuin binomi x–a.

Horner William George (1786 - 1837), englantilainen matemaatikko. Päätutkimus koskee algebrallisten yhtälöiden teoriaa. Kehittänyt menetelmän minkä tahansa asteen yhtälöiden likimääräiseen ratkaisuun. Vuonna 1819 hän esitteli tärkeän menetelmän algebralle polynomin jakamiseksi binomiaalisella x - a (Hornerin malli).

Hornerin kaavion yleiskaavan johtaminen.

Polynomin f(x) jakaminen jäännöksellä binomilla (x-c) tarkoittaa polynomin q(x) ja luvun r löytämistä siten, että f(x)=(x-c)q(x)+r

Kirjoitetaan tämä yhtäläisyys yksityiskohtaisesti:

f 0 x n + f 1 x n-1 + f 2 x n-2 + ...+f n-1 x + f n = (x-c) (q 0 x n-1 + q 1 x n-2 + q 2 x n-3 +...+ q n-2 x + q n-1)+r

Yhdistäkäämme kertoimet samoilla asteikoilla:

xn:	f 0 = q 0	=> q 0 = f 0
xn-1:	f 1 = q 1 - c q 0	=> q 1 = f 1 + c q 0
xn-2:	f 2 = q 2 - c q 1	=> q 2 = f 2 + c q 1
...		...
x0:	fn = q n - c q n-1	=> q n = f n + c q n-1.

Hornerin piirin esittely esimerkin avulla.

Harjoitus 1. Hornerin kaavaa käyttäen jaetaan polynomi f(x) = x 3 - 5x 2 + 8 jäännöksellä binomiaalilla x-2.

f(x) = x 3 - 5x 2 + 8 =(x-2)(x 2 -3x-6) -4, missä g(x)= (x 2 -3x-6), r = -4 jäännös.

Polynomin laajennus binomilin potenssiin.

Laajennamme Hornerin kaavaa käyttäen polynomia f(x)=x 3 +3x 2 -2x+4 binomin (x+2) potenssiina.

Tuloksena pitäisi saada laajennus f(x) = x 3 +3x 2 -2x+4 = (x+2)(x 2 +x-4)+12 = (x+2)((x-1) )(x+ 2)-2)+12 = (((1*(x+2)-3)(x+2)-2)(x+2))+12 = (x+2) 3 -3( x+2) 2 -2(x+2)+12

Hornerin kaaviota käytetään usein ratkaistaessa kolmannen, neljännen ja korkeamman asteen yhtälöitä, kun polynomi on kätevää laajentaa binomiaaliksi x-a. Määrä a nimeltään polynomin juuri F n (x) = f 0 x n + f 1 x n-1 + f 2 x n-2 + ...+ f n-1 x + f n, jos x=a polynomin F n (x) arvo on nolla: F n (a)=0, ts. jos polynomi on jaollinen binomilla x-a.

Esimerkiksi luku 2 on polynomin F 3 (x)=3x 3 -2x-20 juuri, koska F 3 (2) = 0. se tarkoittaa. Että tämän polynomin kertoimella on tekijä x-2.

F3 (x)=3x3 -2x-20=(x-2)(3x2 +6x+10).

Mikä tahansa astepolynomi F n(x). n 1 ei voi olla enempää n todelliset juuret.

Mikä tahansa yhtälön kokonaislukujuuri, jossa on kokonaislukukertoimia, on sen vapaan termin jakaja.

Jos yhtälön johtava kerroin on 1, niin kaikki yhtälön rationaaliset juuret, jos ne ovat olemassa, ovat kokonaislukuja.

Tutkitun materiaalin konsolidointi.

Uuden aineiston vahvistamiseksi oppilaita pyydetään täydentämään lukuja oppikirjoista 2.41 ja 2.42 (s. 65).

(2 oppilasta ratkaisee taululla, ja loput päätettyään tarkistavat tehtävät vihkosta taululla olevien vastausten kanssa).

Yhteenveto.

Kun Horner-kaavion rakenne ja toimintaperiaate on ymmärretty, sitä voidaan käyttää myös tietojenkäsittelyn tunneilla, kun tarkastellaan kokonaislukujen muuntamista desimaalilukujärjestelmästä binäärijärjestelmään ja päinvastoin. Perusta numerojärjestelmästä toiseen siirtymiselle on seuraava yleinen lause

Lause. Muuntaa kokonaisluvun Ap alkaen s-aarilukujärjestelmä peruslukujärjestelmään d tarpeellista Ap jaa peräkkäin jäännöksellä numerolla d, kirjoitettu samassa s-aarinen järjestelmä, kunnes tuloksena oleva osamäärä on yhtä suuri kuin nolla. Loput jaosta ovat d- numeeriset numerot Ilmoitus, alkaen nuorimmasta luokasta vanhimpaan. Kaikki toimet on suoritettava sisään s-aarilukujärjestelmä. Henkilölle tämä sääntö on kätevä vain silloin s= 10, ts. käännettäessä alkaen desimaalijärjestelmä. Mitä tulee tietokoneeseen, päinvastoin, sen on "kätevämpää" suorittaa laskelmia binäärijärjestelmässä. Siksi "2:n" muuntamiseksi 10:ksi käytetään peräkkäistä jakoa kymmenellä binäärijärjestelmässä, ja "10 - 2" on kymmenen potenssien yhteenlasku. "10 in 2" -menettelyn laskelmien optimoimiseksi tietokone käyttää Hornerin taloudellista laskentatapaa.

Kotitehtävät. Ehdotetaan suoritettavaksi kaksi tehtävää.

1. Jaa polynomi f(x)=2x 5 -x 4 -3x 3 +x-3 binomiaalilla (x-3) Hornerin mallia käyttäen.

2. Etsi polynomin f(x)=x 4 -2x 3 +2x 2 -x-6 kokonaislukujuuret (ottaen huomioon, että mikä tahansa yhtälön kokonaislukujuuri, jolla on kokonaislukukerroin, on sen vapaan termin jakaja)

Kirjallisuus.

1. Kurosh A.G. "Korkeamman algebran kurssi."
2. Nikolsky S.M., Potapov M.K. luokka 10 "Algebra ja matemaattisen analyysin alku".
3. http://inf.1september.ru/article.php?ID=200600907.