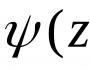Kuinka löytää funktion nollat ​​murtoluvusta. Kuinka löytää funktion nollia

Toimintojen nollia ovat argumenttiarvoja, joissa funktio on yhtä suuri kuin nolla.

Kaavan y=f(x) antaman funktion nollien löytämiseksi sinun on ratkaistava yhtälö f(x)=0.

Jos yhtälöllä ei ole juuria, funktiolla ei ole nollia.

Esimerkkejä.

1) Etsi lineaarifunktion y=3x+15 nollat.

Löytääksesi funktion nollat ​​ratkaise yhtälö 3x+15=0.

Siten funktion y=3x+15 nolla on x= -5.

Vastaus: x= -5.

2) Etsi neliöfunktion f(x)=x²-7x+12 nollat.

Löydä funktion nollakohdat ratkaisemalla toisen asteen yhtälö

Sen juuret x1=3 ja x2=4 ovat tämän funktion nollia.

Vastaus: x=3; x=4.

Ohjeet

1. Funktion nolla on argumentin x arvo, jossa funktion arvo on nolla. Kuitenkin vain ne argumentit, jotka kuuluvat tutkittavan funktion määritelmän piiriin, voivat olla nollia. Eli on paljon arvoja, joille funktio f(x) on hyödyllinen. 2. Kirjoita annettu funktio muistiin ja vertaa se nollaan, sano f(x) = 2x?+5x+2 = 0. Ratkaise saatu yhtälö ja etsi sen todelliset juuret. Neliöyhtälön juuret lasketaan erottajan löytämisen tuella. 2x?+5x+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0,5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. Näin tässä tapauksessa saadaan kaksi toisen asteen yhtälön juuria, jotka vastaavat alkufunktion f(x) argumentit. 3. Tarkista, että kaikki havaitut x-arvot kuuluvat annetun funktion määritelmäalueeseen. Selvitä OOF, tehdäksesi tämän tarkistamalla alkulausekkeen muodon?f (x) parillisten juurien esiintymisen, murtolukujen esiintymisen funktiossa argumentin nimittäjässä, logaritmisen tai trigonometrisen ilmaisuja. 4. Kun tarkastellaan funktiota, jonka lauseke on parillisen asteen juuren alla, ota määritelmän alueeksi kaikki argumentit x, joiden arvot eivät muuta radikaalilauseketta negatiiviseksi luvuksi (päinvastoin funktio tekee ei käy järkeen). Tarkista, ovatko funktion havaitut nollat ​​tietyllä hyväksyttävien x-arvojen alueella. 5. Murtoluvun nimittäjä ei voi mennä nollaan, joten sulje pois argumentit x, jotka johtavat tällaiseen tulokseen. Logaritmisille suureille tulee ottaa huomioon vain ne argumentin arvot, joille itse lauseke on suurempi kuin nolla. Sublogaritmisen lausekkeen nollaksi tai negatiiviseksi luvuksi muuttavat funktion nollat ​​on jätettävä pois lopputuloksesta. Huomautus! Kun yhtälön juuria löydetään, ylimääräisiä juuria saattaa ilmestyä. Tämä on helppo tarkistaa: korvaa vain tuloksena oleva argumentin arvo funktioon ja varmista, muuttuuko funktio nollaan. Hyödyllinen neuvo Joskus funktiota ei ilmaista ilmeisellä tavalla sen argumentin kautta, jolloin on helppo tietää, mikä tämä funktio on. Esimerkki tästä on ympyrän yhtälö.

Toimintojen nollia Kutsutaan abskissa-arvo, jossa funktion arvo on nolla.

Jos funktio on annettu sen yhtälöllä, niin funktion nollat ​​ovat yhtälön ratkaisuja. Jos funktion kuvaaja on annettu, niin funktion nollat ​​ovat arvoja, joilla kuvaaja leikkaa x-akselin.

Toiminto on yksi tärkeimmistä matemaattisista käsitteistä. Toiminto - muuttuva riippuvuus klo muuttujasta x, jos jokainen arvo X vastaa yhtä arvoa klo. Muuttuva X jota kutsutaan itsenäiseksi muuttujaksi tai argumentiksi. Muuttuva klo kutsutaan riippuvaiseksi muuttujaksi. Kaikki riippumattoman muuttujan arvot (muuttuja x) muodostavat funktion määritelmäalueen. Kaikki arvot, jotka riippuva muuttuja ottaa (muuttuja y), muodostavat funktion arvoalueen.

Funktiokaavio kutsua koordinaattitason kaikkien pisteiden joukkoa, joiden abskissat ovat yhtä suuret kuin argumentin arvot ja ordinaatit ovat yhtä suuria kuin funktion vastaavat arvot, eli muuttuja piirretään pitkin abskissa-akselia x, ja muuttujan arvot piirretään ordinaatta-akselia pitkin y. Jotta voit piirtää funktion, sinun on tiedettävä funktion ominaisuudet. Toiminnon pääominaisuuksia käsitellään alla!

Funktion kaavion rakentamiseen suosittelemme käyttämään ohjelmaamme - Graphing functions verkossa. Jos sinulla on kysyttävää tämän sivun materiaalia tutkiessasi, voit aina kysyä niitä foorumillamme. Myös foorumilla he auttavat sinua ratkaisemaan matematiikan, kemian, geometrian, todennäköisyysteorian ja monien muiden aiheiden ongelmia!

Funktioiden perusominaisuudet.

1) Toimintoalue ja funktioalue.

Funktion toimialue on kaikkien kelvollisten argumenttiarvojen joukko x(muuttuja x), jolle toiminto y = f(x) päättänyt.
Funktioalue on kaikkien reaaliarvojen joukko y, jonka funktio hyväksyy.

Alkeismatematiikassa funktioita tutkitaan vain reaalilukujoukolla.

2) Funktion nollat.

Funktio nolla on argumentin arvo, jossa funktion arvo on nolla.

3) Funktion vakiomerkin intervallit.

Funktion vakiomerkkien välit ovat argumenttiarvojen joukkoja, joissa funktion arvot ovat vain positiivisia tai vain negatiivisia.

4) Toiminnon monotonisuus.

Kasvava funktio (tietyllä aikavälillä) on funktio, jossa suurempi argumentin arvo tästä intervallista vastaa suurempaa funktion arvoa.

Pienevä funktio (tietyllä aikavälillä) on funktio, jossa suurempi argumentin arvo tästä intervallista vastaa funktion pienempää arvoa.

5) Parillinen (pariton) funktio.

Parillinen funktio on funktio, jonka määritelmäalue on symmetrinen origon suhteen ja minkä tahansa X määritelmän alueelta tasa-arvo f(-x) = f(x). Parillisen funktion kuvaaja on symmetrinen ordinaatan suhteen.

Pariton funktio on funktio, jonka määritelmäalue on symmetrinen origon suhteen ja minkä tahansa X määritelmäalueelta tasa-arvo on tosi f(-x) = - f(x). Parittoman funktion kuvaaja on symmetrinen origon suhteen.

6) Rajoitetut ja rajoittamattomat toiminnot.

Funktiota kutsutaan rajatuksi, jos on olemassa positiivinen luku M siten, että |f(x)| ≤ M kaikille x:n arvoille. Jos tällaista numeroa ei ole, toiminto on rajoittamaton.

7) Toiminnon jaksollisuus.

Funktio f(x) on jaksollinen, jos on nollasta poikkeava luku T siten, että mille tahansa x:lle f(x+T) = f(x). Tätä pienintä lukua kutsutaan funktion jaksoksi. Kaikki trigonometriset funktiot ovat jaksollisia. (Trigonometriset kaavat).

Kun olet tutkinut nämä funktion ominaisuudet, voit helposti tutkia funktiota ja funktion ominaisuuksia käyttämällä voit rakentaa funktiosta kuvaajan. Katso myös materiaalia totuustaulukosta, kertotaulukosta, jaksollisesta taulukosta, derivaattataulukosta ja integraalitaulukosta.

Toimintojen nollia

Mitä ovat funktion nollat? Kuinka määrittää funktion nollat ​​analyyttisesti ja graafisesti?

Toimintojen nollia- nämä ovat argumenttiarvoja, joilla funktio on yhtä suuri kuin nolla.

Kaavan y=f(x) antaman funktion nollien löytämiseksi sinun on ratkaistava yhtälö f(x)=0.

Jos yhtälöllä ei ole juuria, funktiolla ei ole nollia.

1) Etsi lineaarifunktion y=3x+15 nollat.

Löytääksesi funktion nollat, ratkaise yhtälö 3x+15 =0.

Siten funktion nolla on y=3x+15 - x= -5.

2) Etsi neliöfunktion f(x)=x²-7x+12 nollat.

Löydä funktion nollakohdat ratkaisemalla toisen asteen yhtälö

Sen juuret x1=3 ja x2=4 ovat tämän funktion nollia.

3) Etsi funktion nollat

Murtoluku on järkevä, jos nimittäjä ei ole nolla. Siksi x²-1≠0, x² ≠ 1, x ≠±1. Eli tietyn funktion (DO) määritelmäalue

Yhtälön x²+5x+4=0 x1=-1 x2=-4 juurista vain x=-4 sisältyy määritelmäalueeseen.

Graafisesti annetun funktion nollien löytämiseksi sinun on löydettävä funktiokaavion ja abskissa-akselin leikkauspisteet.

Jos kuvaaja ei leikkaa Ox-akselia, funktiolla ei ole nollia.

funktiossa, jonka graafi on esitetty kuvassa, on neljä nollaa -

Algebrassa funktion nollien löytämisongelma esiintyy sekä itsenäisenä tehtävänä että muita ongelmia ratkaistaessa, esimerkiksi tutkittaessa funktiota, ratkaistaessa epäyhtälöitä jne.

www.algebraclass.ru

Funktion nollasääntö

Funktioiden peruskäsitteet ja ominaisuudet

Sääntö kirjeenvaihtolaki. Monotoninen toiminto .

Rajoitetut ja rajattomat toiminnot. Jatkuva ja

epäjatkuvat toiminnot . Parilliset ja parittomat funktiot.

Jaksottainen toiminto. Toiminnan aika.

Toimintojen nollia . Asymptootti .

Määritelmäalue ja funktion arvoalue. Alkeismatematiikassa funktioita tutkitaan vain reaalilukujoukolla R . Tämä tarkoittaa, että funktion argumentti voi ottaa vain ne todelliset arvot, joille funktio on määritelty, ts. se hyväksyy myös vain todelliset arvot. Joukko X kaikki kelvolliset argumenttiarvot x, jolle toiminto y = f (x) määritellään, kutsutaan toiminnon toimialue. Joukko Y kaikki todelliset arvot y, jonka funktio hyväksyy, kutsutaan toimintoalue. Nyt voimme antaa funktion tarkemman määritelmän: sääntö (laki) joukkojen välisestä vastaavuudesta X Ja Y , jonka mukaan jokaiselle joukon elementille X Löydät sarjasta yhden ja vain yhden elementin Y, kutsutaan funktioksi .

Tästä määritelmästä seuraa, että funktio katsotaan määritellyksi, jos:

— funktion määrittelyalue on määritelty X ;

— toimintoalue on määritetty Y ;

— kirjeenvaihdon sääntö (laki) tunnetaan ja sellainen, että jokaiselle

argumenttiarvo, vain yksi funktion arvo löytyy.

Tämä funktion yksilöllisyyden vaatimus on pakollinen.

Monotoninen toiminto. Jos jollekin kahdelle argumentin arvolle x 1 ja x 2 ehdosta x 2 > x 1 seuraa f (x 2) > f (x 1), sitten funktio f (x) kutsutaan lisääntyy; jos jollekin x 1 ja x 2 ehdosta x 2 > x 1 seuraa f (x 2)

Kuvassa 3 esitetty toiminto on rajoitettu, mutta ei monotoninen. Kuvan 4 toiminto on juuri päinvastainen, monotoninen, mutta rajoittamaton. (Selitä tämä!).

Jatkuvat ja epäjatkuvat toiminnot. Toiminto y = f (x) kutsutaan jatkuva pisteessä x = a, Jos:

1) funktio määritellään milloin x = a, eli f (a) olemassa;

2) on olemassa rajallinen raja lim f (x) ;

Jos ainakin yksi näistä ehdoista ei täyty, funktiota kutsutaan räjähtävä pisteessä x = a .

Jos toiminto on jatkuva aikana kaikille määrittelyalueensa kohdat, niin sitä kutsutaan jatkuva toiminto.

Parilliset ja parittomat funktiot. Jos varten minkä tahansa x funktion määritelmäalueesta seuraava pätee: f (— x) = f (x), funktiota kutsutaan jopa; jos se tapahtuu: f (— x) = — f (x), funktiota kutsutaan outo. Parillisen funktion kuvaaja symmetrisesti Y-akselin suhteen(Kuva 5), ​​parittoman funktion kaavio Sim metristä alkuperän suhteen(Kuva 6).

Jaksottainen toiminto. Toiminto f (x) — määräajoin, jos sellainen on olemassa ei-nolla määrä T mitä varten minkä tahansa x funktion määritelmäalueesta seuraava pätee: f (x + T) = f (x). Tämä vähiten numeroon soitetaan toiminnon ajanjakso. Kaikki trigonometriset funktiot ovat jaksollisia.

Esimerkki 1. Todista synti x jakso on 2.

Ratkaisu: Tiedämme sen synnin ( x+ 2 n) = synti x, Missä n= 0, ± 1, ± 2, …

Siksi lisäys 2 n ei sini-argumentille

muuttaa arvoaan e. Onko tähän joku muu numero?

Teeskennetäänpä sitä P– sellainen numero, ts. tasa-arvo:

voimassa mille tahansa arvolle x. Mutta sitten on

paikka ja klo x= / 2, ts.

synti(/2 + P) = sin / 2 = 1.

Mutta pelkistyskaavan mukaan synti (/ 2 + P) = cos P. Sitten

kahdesta viimeisestä yhtälöstä seuraa, että cos P= 1, mutta me

tiedämme, että tämä on totta vain silloin P = 2 n. Pienimmistä lähtien

nollasta poikkeava luku 2:sta n on 2, niin tämä luku

ja siellä on jaksosynti x. Se voidaan todistaa samalla tavalla, että 2

on myös aika cos x .

Todista, että funktiot tan x ja pinnasänky x on kausi.

Esimerkki 2. Mikä luku on funktion sin 2 jakso x ?

Ratkaisu: Harkitse syntiä 2 x= sin(2 x+ 2 n) = synti [ 2 ( x + n) ] .

Näemme tämän lisäyksen n argumenttiin x, ei muutu

funktion arvo. Pienin nollasta poikkeava luku

alkaen n on , joten tämä on jakso sin 2 x .

Toimintojen nollia. Kutsutaan argumenttiarvo, jolla funktio on yhtä suuri kuin 0 nolla ( juuri) -toiminto. Funktiolla voi olla useita nollia. Esimerkiksi funktio y = x (x + 1) (x- 3) sisältää kolme nollaa: x = 0, x = — 1, x= 3. Geometrisesti nollatoiminto – tämä on funktiokuvaajan ja akselin leikkauspisteen abskissa X .

Kuvassa 7 on kaavio funktiosta, jossa on nollia: x = a , x = b Ja x = c .

Asymptootti. Jos funktion kuvaaja lähestyy rajattomasti tiettyä suoraa siirtyessään pois origosta, niin tätä suoraa kutsutaan ns. asymptootti.

Aihe 6. "Intervallimenetelmä."

Jos f (x) f (x 0) x x 0:lle, kutsutaan funktiota f (x). jatkuva pisteessä x 0.

Jos funktio on jatkuva jonkin intervallin I jokaisessa pisteessä, sitä kutsutaan jatkuva väliajoin I (väliä I kutsutaan funktion jatkuvuusväli). Tämän intervallin funktion kaavio on jatkuva viiva, joka voidaan heidän mukaansa "piirtää nostamatta kynää paperilta".

Jatkuvien funktioiden ominaisuus.

Jos välillä (a ; b) funktio f on jatkuva eikä katoa, niin se säilyttää vakiomerkin tällä välillä.

Tähän ominaisuuteen perustuu menetelmä yhden muuttujan epäyhtälöiden ratkaisemiseksi, intervallimenetelmä. Olkoon funktio f(x) jatkuva välillä I ja häviävä äärellisessä määrässä tämän välin pisteitä. Jatkuvien funktioiden ominaisuudella nämä pisteet jakavat I:n intervalleiksi, joissa jokaisessa jatkuva funktio f(x) c säilyttää vakiomerkin. Tämän merkin määrittämiseksi riittää, että lasketaan funktion f(x) arvo missä tahansa pisteessä kustakin tällaisesta intervallista. Tämän perusteella saadaan seuraava algoritmi epäyhtälöiden ratkaisemiseksi intervallimenetelmällä.

Intervallimenetelmä muotoepäyhtälöille

Intervallimenetelmä. Keskitaso.

Haluatko testata voimaasi ja saada selville, kuinka valmis olet Unified State -kokeeseen tai Unified State -kokeeseen?

Lineaarinen funktio

Muodon funktiota kutsutaan lineaariseksi. Otetaan esimerkkinä funktio. Se on positiivinen kohdassa 3″> ja negatiivinen kohdassa. Piste on funktion () nolla. Esitetään tämän funktion merkit numeroakselilla:

Sanotaan, että "funktio vaihtaa merkkiä kulkiessaan pisteen läpi".

Voidaan nähdä, että funktion etumerkit vastaavat funktiokaavion sijaintia: jos kuvaaja on akselin yläpuolella, merkki on " ", jos sen alapuolella on " ".

Jos yleistämme tuloksena olevan säännön mielivaltaiseksi lineaarifunktioksi, saamme seuraavan algoritmin:

Neliöllinen toiminto

Toivottavasti muistat kuinka ratkaista neliöllinen epätasa-arvo? Jos ei, lue aihe "Kvadraattiset epätasa-arvot". Muistutan teitä neliöfunktion yleisestä muodosta: .

Muistetaan nyt, mitä merkkejä neliöfunktio ottaa. Sen kuvaaja on paraabeli, ja funktio ottaa merkin " " niille, joissa paraabeli on akselin yläpuolella, ja " " - jos paraabeli on akselin alapuolella:

Jos funktiolla on nollia (arvoja, joissa), paraabeli leikkaa akselin kahdessa pisteessä - vastaavan toisen asteen yhtälön juurissa. Siten akseli on jaettu kolmeen väliin, ja funktion merkit vaihtelevat vuorotellen kulkiessaan jokaisen juuren läpi.

Onko mahdollista määrittää merkit jotenkin piirtämättä paraabelia joka kerta?

Muista, että neliötrinomi voidaan kertoa:

Merkitään juuret akselille:

Muistamme, että funktion etumerkki voi muuttua vain, kun se kulkee juuren kautta. Käytetään tätä tosiasiaa: kullekin kolmelle aikavälille, joihin akseli on jaettu juurilla, riittää, että määritetään funktion etumerkki vain yhdessä mielivaltaisesti valitussa pisteessä: välin muissa pisteissä etumerkki on sama .

Esimerkissämme: kohdassa 3″> molemmat suluissa olevat lausekkeet ovat positiivisia (korvaa esimerkiksi: 0″>). Laitamme " " -merkin akselille:

No, kun (korvaa esimerkiksi), molemmat sulut ovat negatiivisia, mikä tarkoittaa, että tuote on positiivinen:

Sitä se on intervallimenetelmä: Kun tiedämme kunkin intervallin tekijöiden merkit, määritämme koko tuotteen etumerkin.

Tarkastellaan myös tapauksia, joissa funktiossa ei ole nollia tai vain yksi.

Jos niitä ei ole, ei ole juuria. Tämä tarkoittaa, että "juuren läpi" ei tapahdu. Tämä tarkoittaa, että funktio ottaa vain yhden merkin koko lukurivillä. Se voidaan määrittää helposti korvaamalla se funktiona.

Jos juuria on vain yksi, paraabeli koskettaa akselia, joten funktion etumerkki ei muutu juuren läpi kulkiessaan. Millaisen säännön voimme keksiä tällaisiin tilanteisiin?

Jos otat huomioon tällaisen funktion, saat kaksi identtistä tekijää:

Ja mikä tahansa neliölauseke ei ole negatiivinen! Siksi funktion etumerkki ei muutu. Tällaisissa tapauksissa korostamme juuren, jonka läpi kulkee merkki ei muutu, ympyröimällä sen neliöllä:

Kutsumme tällaista juuria kerrannaisina.

Intervallimenetelmä epäyhtälöissä

Nyt mikä tahansa neliöllinen epäyhtälö voidaan ratkaista ilman paraabelia. Riittää vain sijoittaa neliöfunktion etumerkit akselille ja valita välit epäyhtälön merkin mukaan. Esimerkiksi:

Mittaataan juuret akselilla ja laitetaan merkit:

Tarvitsemme sen akselin osan, jossa on " " -merkki; koska epätasa-arvo ei ole tiukka, myös juuret itse sisältyvät ratkaisuun:

Harkitse nyt rationaalista epäyhtälöä - epätasa-arvoa, jonka molemmat puolet ovat rationaalisia lausekkeita (katso "Rationaaliset yhtälöt").

Esimerkki:

Kaikki tekijät yhtä lukuun ottamatta ovat tässä "lineaarisia", eli ne sisältävät muuttujan vain ensimmäiseen potenssiin. Tarvitsemme tällaisia ​​lineaarisia tekijöitä intervallimenetelmän soveltamiseen - merkki muuttuu kulkeessaan niiden juurien läpi. Mutta kertoimella ei ole juuria ollenkaan. Tämä tarkoittaa, että se on aina positiivinen (tarkista tämä itse), eikä siksi vaikuta koko epätasa-arvon merkkiin. Tämä tarkoittaa, että voimme jakaa epäyhtälön vasemman ja oikean puolen sillä ja siten päästä eroon siitä:

Nyt kaikki on sama kuin neliöeräisillä: määritämme missä kohdissa kukin tekijä muuttuu nollaksi, merkitse nämä pisteet akselille ja järjestä merkit. Haluaisin kiinnittää huomionne erittäin tärkeään seikkaan:

Parillisen luvun tapauksessa teemme samoin kuin ennen: ympyröimme pisteen neliöllä emmekä vaihda etumerkkiä juuren läpi kulkiessaan. Mutta parittoman luvun tapauksessa tämä sääntö ei päde: merkki muuttuu silti, kun se kulkee juuren läpi. Siksi emme tee mitään ylimääräistä sellaisella juurilla, ikään kuin se ei olisi kerrannainen. Yllä olevat säännöt koskevat kaikkia parillisia ja parittomia tehoja.

Mitä meidän pitäisi kirjoittaa vastaukseen?

Jos merkkien vuorottelua rikotaan, on oltava erittäin varovainen, koska jos epätasa-arvo ei ole tiukka, vastauksen tulee sisältää kaikki varjostetut kohdat. Mutta jotkut niistä eroavat usein toisistaan, eli ne eivät sisälly varjostettuun alueeseen. Tässä tapauksessa lisäämme ne vastaukseen yksittäisinä pisteinä (kiharaisissa aaltosulkeissa):

Esimerkkejä (päätä itse):

Vastaukset:

1. Jos tekijöiden joukossa se on yksinkertainen, se on juuri, koska se voidaan esittää muodossa.
   .

2. Etsitään funktion nollat.

f(x) x:ssä .

Vastaa f(x) kohdassa x .

2) x 2 > -4x-5;

x 2 +4x +5>0;

Olkoon f(x)=x 2 +4x +5 niin etsitään sellainen x, jolle f(x)>0,

D=-4 Ei nollia.

4. Epätasa-arvojärjestelmät. Epäyhtälöt ja epäyhtälöjärjestelmät kahdella muuttujalla

1) Epäyhtälöjärjestelmän ratkaisujoukko on siihen sisältyvien eriarvoisuuksien ratkaisujoukkojen leikkauspiste.

2) Epäyhtälön f(x;y)>0 ratkaisujoukko voidaan kuvata graafisesti koordinaattitasolla. Tyypillisesti yhtälön f(x;y) = 0 määrittelemä suora jakaa tason 2 osaan, joista toinen on epäyhtälön ratkaisu. Määrittääksesi, mikä osa, sinun on korvattava epäyhtälöllä mielivaltaisen pisteen M(x0;y0), joka ei ole suoralla f(x;y)=0, koordinaatit. Jos f(x0;y0) > 0, niin epäyhtälön ratkaisu on se osa tasosta, joka sisältää pisteen M0. jos f(x0;y0)<0, то другая часть плоскости.

3) Epäyhtälöjärjestelmän ratkaisujoukko on siihen sisältyvien epäyhtälöiden ratkaisujoukkojen leikkauspiste. Oletetaan esimerkiksi epätasa-arvojärjestelmä:

.

Ensimmäiselle epäyhtälölle ratkaisujoukko on ympyrä, jonka säde on 2 ja jonka keskipiste on origossa, ja toiselle se on puolitaso, joka sijaitsee suoran 2x+3y=0 yläpuolella. Tämän järjestelmän ratkaisujoukko on näiden joukkojen leikkauspiste, ts. puoliympyrä.

4) Esimerkki. Ratkaise epäyhtälöjärjestelmä:

Ensimmäisen epäyhtälön ratkaisu on joukko , 2. on joukko (2;7) ja kolmas on joukko .

Näiden joukkojen leikkauspiste on intervalli (2;3]), joka on epäyhtälöjärjestelmän ratkaisujen joukko.

5. Rationaalisten epäyhtälöiden ratkaiseminen intervallimenetelmällä

Intervallimenetelmä perustuu seuraavaan binomiaalin (x-a) ominaisuuteen: piste x=α jakaa lukuakselin kahteen osaan - pisteen α oikealla puolella binomiaali (x-α)>0 ja vasemmalla pisteestä α (x-α)<0.

Olkoon tarpeen ratkaista epäyhtälö (x-α 1)(x-α 2)...(x-α n)>0, missä α 1, α 2 ...α n-1, α n ovat kiinteitä lukuja, joiden joukossa ei ole yhtäläisiä ja sellaisia, että α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 intervallimenetelmää käyttäen etene seuraavasti: luvut α 1, α 2 ... α n-1, α n piirretään numeeriselle akselille; välissä niistä suurimman oikealla puolella, ts. numerot α n, laita plusmerkki, laita sitä seuraavaan väliin oikealta vasemmalle miinusmerkki, sitten plusmerkki, sitten miinusmerkki jne. Tällöin epäyhtälön (x-α 1)(x-α 2)...(x-α n)>0 ratkaisujen joukko on kaikkien niiden välien liitto, joihin plusmerkki on sijoitettu, ja joukko epäyhtälön (x-α 1 )(x-α 2)...(x-α n) ratkaisuista<0 будет объединение всех промежутков, в которых поставлен знак «минус».

1) Rationaalisten epäyhtälöiden (eli muodon epäyhtälöiden) ratkaiseminen P(x) Q(x) missä ovat polynomit) perustuu seuraavaan jatkuvan funktion ominaisuuteen: jos jatkuva funktio katoaa pisteistä x1 ja x2 (x1; x2) eikä sillä ole muita juuria näiden pisteiden välillä, niin välein (x1; x2) funktio säilyttää etumerkkinsä.

Siksi, jotta voit löytää funktion y=f(x) vakiomerkkivälit lukuviivalta, merkitse kaikki pisteet, joissa funktio f(x) katoaa tai kärsii epäjatkuvuudesta. Nämä pisteet jakavat lukujonon useisiin väliin, joiden sisällä funktio f(x) on jatkuva eikä katoa, ts. tallentaa merkin. Tämän merkin määrittämiseksi riittää, kun löytää funktion etumerkki mistä tahansa numeroviivan tarkastellun intervallin kohdasta.

2) Määrittää rationaalisen funktion vakiomerkkivälit, ts. Rationaalisen epäyhtälön ratkaisemiseksi merkitsemme numeroviivalle osoittajan juuret ja nimittäjän juuret, jotka ovat myös rationaalisen funktion juuria ja taitepisteitä.

Epäyhtälöiden ratkaiseminen intervallimenetelmällä

3. < 20.

Ratkaisu. Hyväksyttyjen arvojen alue määräytyy epäyhtälöjärjestelmällä:

Funktiolle f(x) = – 20. Etsi f(x):

jossa x = 29 ja x = 13.

f(30) = – 20 = 0,3 > 0,

f(5) = – 1 – 20 = – 10< 0.

Vastaus:. Perusmenetelmät rationaalisten yhtälöiden ratkaisemiseen. 1) Yksinkertaisin: ratkaistaan ​​tavallisilla yksinkertaistuksilla - pelkistys yhteiseen nimittäjään, samanlaisten termien vähentäminen ja niin edelleen. Neliöyhtälöt ax2 + bx + c = 0 ratkaistaan...

X muuttuu välillä (0,1] ja pienenee välillä = ½ [
-(1/3)
], jossa | z|< 1.

b) f(z) = - ½ [
+
] = - (
), klo 1< |z| < 3.

Kanssa) f(z) = ½ [
]= - ½ [
] =

= - ½ = -
, |2 - z| < 1

Se on ympyrä, jonka säde on 1 ja jonka keskipiste on z = 2 .

Joissakin tapauksissa potenssisarjat voidaan pelkistää geometristen progressioiden joukkoon, ja tämän jälkeen on helppo määrittää niiden konvergenssialue.

Jne. Tutki sarjan konvergenssia

. . . + + + + 1 + () + () 2 + () 3 + . . .

Ratkaisu. Tämä on kahden geometrisen progression summa q 1 = , q 2 = () . Niiden lähentymisen ehdoista se seuraa < 1 , < 1 или |z| > 1 , |z| < 2 , т.е. область сходимости ряда кольцо 1 < |z| < 2 .