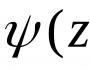Ako sa nazývajú nuly funkcie? Pravidlo funkčných núl

Hodnoty argumentov z na ktorom f(z) ide na nulu. nulový bod, t.j. Ak f(a) = 0 teda a - nulový bod.

Def. Bodka A volal nultého rádun , Ak FKP môže byť zastúpený vo forme f(z) = , kde
analytická funkcia a
0.

V tomto prípade v Taylorovom rade expanzie funkcie (43), prvej n koeficienty sú nulové

= =

Atď. Určite poradie nuly pre
a (1 – cos z) pri z = 0

=
=

nula 1. rádu

1 – kos z =
=

nula 2. rádu

Def. Bodka z =
volal bod v nekonečne A nula funkcie f(z), Ak f(
) = 0. Takáto funkcia môže byť rozšírená na rad v záporných mocninách z : f(z) =
. Ak najprv n koeficienty sa rovnajú nule, potom dospejeme k nultého rádu n v bode v nekonečne: f(z) = z - n
.

Izolované singulárne body sa delia na: a) odnímateľné singulárne body; b) póly poriadkun; V) v podstate singulárne body.

Bodka A volal odnímateľný singulárny bod funkcie f(z) ak o z
a lim f(z) = s - konečné číslo .

Bodka A volal pól poriadkun (n 1) funkcie f(z), ak je inverzná funkcia
= 1/ f(z) má nulové poradie n v bode A. Takáto funkcia môže byť vždy reprezentovaná ako f(z) =
, Kde
- analytická funkcia a
.

Bodka A volal v podstate zvláštny bod funkcie f(z), ak o z
a lim f(z) neexistuje.

Laurentova séria

Uvažujme o prípade oblasti prstencovej konvergencie r < | z 0 – a| < R sústredený v bode A pre funkciu f(z). Predstavme si dva nové kruhy L 1 (r) A L 2 (R) v blízkosti hraníc kruhu s hrotom z 0 medzi nimi. Urobme rez prsteňa, spojíme kruhy pozdĺž okrajov rezu, prejdeme na jednoducho spojenú oblasť a v

Cauchyho integrálny vzorec (39) dostaneme dva integrály nad premennou z

f(z 0) =
+
, (42)

kde integrácia ide opačným smerom.

Pre integrál preč L 1 podmienka je splnená | z 0 – a | > | z – a |, a pre integrál nad L 2 inverzná podmienka | z 0 – a | < | z – a |. Preto faktor 1/( z – z 0) expandovať do radu (a) v integrálnom nad L 2 av sérii (b) v integrálnom prepočte L 1. V dôsledku toho získame expanziu f(z) v oblasti prstenca v Laurentova séria pozitívnymi a negatívnymi silami ( z 0 – a)

f(z 0) =
A n (z 0 -a) n (43)

Kde A n =
=
;A -n =

Rozšírenie pozitívnych síl (z 0 - A) tzv pravá časť Laurentova séria (séria Taylor) a expanzia v negatívnych silách sa nazýva. Hlavná časť Séria Laurent.

Ak vo vnútri kruhu L 1 nie sú singulárne body a funkcia je analytická, potom v (44) je prvý integrál rovný nule podľa Cauchyho vety a v expanzii funkcie zostáva len správna časť. Záporné mocniny v expanzii (45) sa objavujú iba vtedy, keď je analyticita narušená vo vnútornom kruhu a slúžia na opis funkcie v blízkosti izolovaných singulárnych bodov.

Na konštrukciu série Laurent (45) pre f(z) môžete vypočítať koeficienty expanzie pomocou všeobecného vzorca alebo použiť expanzie elementárnych funkcií zahrnutých v f(z).

Počet výrazov ( n) hlavnej časti Laurentovho radu závisí od typu singulárneho bodu: odnímateľný singulárny bod (n = 0) ; v podstate singulárny bod (n
); póln- wow objednávka(n - konečné číslo).

a pre f(z) = bodka z = 0 odnímateľný singulárny bod, pretože nie je tam žiadna hlavná časť. f(z) = (z -
) = 1 -

b) Pre f(z) = bodka z = 0 - pól 1. rádu

f(z) = (z -
) = -

c) Pre f(z) = e 1 / z bodka z = 0 - v podstate singulárny bod

f(z) = e 1 / z =

Ak f(z) je v doméne analytický D s výnimkou m izolované singulárne body a | z 1 | < |z 2 | < . . . < |z m| , potom pri rozširovaní funkcie v mocninách z celá rovina je rozdelená na m+ 1 krúžok | z i | < | z | < | z i+ 1 | a séria Laurent má pre každý prsteň iný vzhľad. Pri rozširovaní právomocí ( z – z i ) oblasťou konvergencie Laurentovho radu je kruh | z – z i | < r, Kde r – vzdialenosť k najbližšiemu singulárnemu bodu.

Atď. Rozšírime funkciu f(z) =v sérii Laurent v mocnostiach z a ( z - 1).

Riešenie. Predstavme si funkciu vo forme f(z) = - z 2 . Použijeme vzorec pre súčet geometrickej postupnosti
. V kruhu |z|< 1 ряд сходится и f(z) = - z 2 (1 + z + z 2 + z 3 + z 4 + . . .) = - z 2 - z 3 - z 4 - . . . , t.j. rozklad obsahuje len správneČasť. Presuňme sa do vonkajšej oblasti kruhu |z| > 1. Predstavme si funkciu vo forme
, kde 1/| z| < 1, и получим разложение f(z) = z
=z + 1 +

Pretože , rozšírenie funkcie v mocninách ( z - 1) vyzerá f(z) = (z - 1) -1 + 2 + (z - 1) pre všetkých
1.

Atď. Rozšírte funkciu na Laurentovu sériu f(z) =
: a) podľa stupňov z v kruhu | z| < 1; b) по степеням z prsteň 1< |z| < 3 ; c) по степеням (z – 2).Riešenie. Rozložme funkciu na jednoduché zlomky
= =+=
. Z podmienok z =1
A = -1/2 , z =3
B = ½.

A) f(z) = ½ [
] = ½ [
-(1/3)
], s | z|< 1.

b) f(z) = - ½ [
+
] = - (
), o 1< |z| < 3.

s) f(z) = ½ [
]= - ½ [
] =

= - ½ = -
, s |2 - z| < 1

Je to kruh s polomerom 1 so stredom z = 2 .

V niektorých prípadoch môžu byť mocninné rady redukované na množinu geometrických progresií a potom je ľahké určiť oblasť ich konvergencie.

Atď. Preskúmajte konvergenciu radu

. . . + + + + 1 + () + () 2 + () 3 + . . .

Riešenie. Toto je súčet dvoch geometrických postupností s q 1 = , q 2 = () . Z podmienok ich konvergencie to vyplýva < 1 , < 1 или |z| > 1 , |z| < 2 , т.е. область сходимости ряда кольцо 1 < |z| < 2 .

Funkčné nuly sú hodnoty argumentov, pri ktorých sa funkcia rovná nule.

Ak chcete nájsť nuly funkcie danej vzorcom y=f(x), musíte vyriešiť rovnicu f(x)=0.

Ak rovnica nemá korene, funkcia nemá nuly.

Príklady.

1) Nájdite nuly lineárnej funkcie y=3x+15.

Ak chcete nájsť nuly funkcie, vyriešte rovnicu 3x+15=0.

Nula funkcie y=3x+15 je teda x= -5.

Odpoveď: x= -5.

2) Nájdite nuly kvadratickej funkcie f(x)=x²-7x+12.

Ak chcete nájsť nuly funkcie, vyriešte kvadratickú rovnicu

Jej korene x1=3 a x2=4 sú nuly tejto funkcie.

Odpoveď: x=3; x=4.

Inštrukcie

1. Nula funkcie je hodnota argumentu x, pri ktorej sa hodnota funkcie rovná nule. Nulové však môžu byť len tie argumenty, ktoré sú v rámci definície skúmanej funkcie. To znamená, že existuje veľa hodnôt, pre ktoré je funkcia f(x) užitočná. 2. Zapíšte si danú funkciu a prirovnajte ju k nule, povedzme f(x) = 2x?+5x+2 = 0. Vyriešte výslednú rovnicu a nájdite jej skutočné korene. Korene kvadratickej rovnice sú vypočítané s podporou hľadania diskriminantu. 2x?+5x+2 = 0;D = b?-4ac = 5a-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0,5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. V tomto prípade sa teda získajú dva korene kvadratickej rovnice zodpovedajúce argumenty počiatočnej funkcie f(x). 3. Skontrolujte, či všetky zistené hodnoty x patria do domény definície danej funkcie. Zistite OOF, aby ste to urobili, skontrolujte počiatočný výraz na prítomnosť párnych koreňov tvaru?f (x), na prítomnosť zlomkov vo funkcii s argumentom v menovateli, na prítomnosť logaritmických alebo trigonometrických výrazov. 4. Pri zvažovaní funkcie s výrazom pod odmocninou párneho stupňa vezmite ako definičný obor všetky argumenty x, ktorých hodnoty nemenia radikálny výraz na záporné číslo (naopak, funkcia áno nedáva zmysel). Skontrolujte, či zistené nuly funkcie spadajú do určitého rozsahu prijateľných hodnôt x. 5. Menovateľ zlomku nemôže ísť na nulu, preto vylúčte tie argumenty x, ktoré vedú k takémuto výsledku. Pre logaritmické veličiny by sa mali brať do úvahy iba tie hodnoty argumentu, pre ktoré je samotný výraz väčší ako nula. Nuly funkcie, ktorá mení sublogaritmický výraz na nulu alebo záporné číslo, musia byť z konečného výsledku vyradené. Poznámka! Pri hľadaní koreňov rovnice sa môžu objaviť ďalšie korene. To sa dá ľahko skontrolovať: stačí nahradiť výslednú hodnotu argumentu do funkcie a uistiť sa, že sa funkcia zmení na nulu. Užitočné rady Niekedy funkcia nie je vyjadrená zrejmým spôsobom prostredníctvom svojho argumentu, potom je ľahké vedieť, čo je táto funkcia. Príkladom toho je rovnica kruhu.

Funkčné nuly Zavolá sa hodnota vodorovnej osi, pri ktorej sa hodnota funkcie rovná nule.

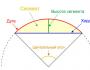
Ak je funkcia daná svojou rovnicou, potom nuly funkcie budú riešením rovnice. Ak je daný graf funkcie, potom nuly funkcie sú hodnoty, pri ktorých graf pretína os x.

Obsah:

Nula funkcie je hodnota x, pri ktorej je hodnota funkcie nula. Zvyčajne sa nájdenie núl funkcie vykonáva riešením polynómovej rovnice, napríklad x 2 + 4x +3 = 0. Tu je niekoľko spôsobov, ako nájsť nuly funkcie.

Kroky

1 Faktorizácia

1. 1 Napíšte rovnicu tak, aby vyzerala niečo ako x 2 + 5x + 4. Začnite s výrazom vyššieho rádu (napríklad x 2) a potom prejdite na voľný výraz (konštanta bez premennej; číslo). Výsledný výraz prirovnajte k 0.
   • Správne napísané mnohočleny (rovnice):
     • x 2 + 5 x + 6 = 0
     • x 2 – 2 x – 3 = 0
   • Nesprávne napísané polynómy (rovnice):
     • 5x + 6 = -x 2
     • x 2 = 2 x + 3
2. 2 a", "b", "c". To zjednoduší problém faktorizácie. Napíšte rovnicu v tomto formáte: a x 2 ± b x ± c = 0. Teraz nájdite a, b, c z rovnice, ktorú ste dostali. Tu je niekoľko príkladov:
   • x 2 + 5 x + 6 = 0
     • a
     • b = 5
     • c = 6
   • x 2 – 2 x – 3 = 0
     • a= 1 (pred „x“ nie je žiadny koeficient, takže koeficient = 1)
     • b = -2
     • c = -3
3. 3 Zapíšte si všetky dvojice koeficientových faktorov " s". Dvojica faktorov daného čísla sú dve čísla, ktoré po vynásobení dávajú dané číslo. Venujte zvláštnu pozornosť záporným číslam. Dve záporné čísla po vynásobení dávajú kladné číslo. Na poradí násobenia nezáleží ("1 x 4" je to isté ako "4 x 1").
   • Rovnica: x 2 + 5 x + 6 = 0
   • Násobiteľ párov 6, príp c:
     • 1 x 6 = 6
     • -1 x -6 = 6
     • 2 x 3 = 6
     • -2 x -3 = 6
4. 4 Nájdite pár faktorov, ktorých súčet je " b" . Pozrite sa na význam b a zistite, ktorý z párov po sčítaní dá toto číslo.
   • b = 5
   • Dvojica násobiteľov, ktorých súčet je 5, je 2 a 3
     • 2 + 3 = 5
5. 5 Z tejto dvojice faktorov vytvorte 2 dvojčleny a spojte ich do dvojčlena. Dvojčlen je súčinom dvojčlenov v tvare (x ± číslo) (x ± číslo). Ako viete, ktoré znamienko (plus alebo mínus) si vybrať? Stačí sa pozrieť na znamienko čísel z dvojice faktorov: kladné číslo je znamienko plus, záporné číslo je znamienko mínus. Tu je niekoľko faktorov, pomocou ktorých sme vytvorili binomický znak:
   • (x + 2) (x + 3) = 0
6. 6 Vyriešte každú dvojčlenku presunutím neznámej na druhú stranu rovnice. Prirovnajte každý dvojčlen k 0: (x + 2) = 0 a (x + 3) = 0 a potom vyriešte rovnicu:
   • (x + 2) = 0; x = -2
   • (x + 3) = 0; x = -3
7. 7 Toto sú nuly funkcie.

2 Riešenie kvadratickej rovnice

1. 1 Kvadratická rovnica vyzerá takto:
2. 2 Koeficienty vo svojej rovnici označte „ a", "b", "c". Tým sa zjednoduší problém riešenia rovnice. Napíšte rovnicu v tomto formáte: a x 2 ± b x ± c = 0.
3. 3 Teraz nájdite a, b, c z rovnice, ktorú ste dostali.
4. 4 Vyriešte rovnicu. Ak chcete vyriešiť kvadratickú rovnicu, musíte poznať vzorec na riešenie takejto rovnice. Všetko ostatné je len nahrádzanie a kalkulácia.
   • Ďalšou možnosťou riešenia kvadratickej rovnice je dokonalý štvorec. Niektorí ľudia považujú túto metódu za jednoduchšiu ako riešenie podľa vzorca.
5. 5 Výsledkom riešenia kvadratickej rovnice pomocou vzorca budú „nuly“ funkcie, ktorú hľadáte. Vzorec dáva odpoveď vo forme dvoch čísel, ktoré sú riešením (nulami) tejto funkcie.

3 Graf kvadratickej rovnice

1. 1 Graf funkcie. Funkcia je napísaná ako x 2 + 8x + 12 = 0.
2. 2 Nájdite priesečníky x. Tieto dva body budú nulami funkcie.
3. 3 Použite graf ako spôsob kontroly, nie ako spôsob riešenia rovnice. Ak vykresľujete na zobrazenie núl funkcie, použite to na dvojitú kontrolu výsledkov.

• Svoje výpočty môžete skontrolovať nahradením nájdených riešení do počiatočnej rovnice. Ak sa rovnica rovná nule, riešenia sú správne.

Matematické znázornenie funkcie jasne ukazuje, ako jedna veličina úplne určuje hodnotu inej veličiny. Tradične sa za numerické funkcie považujú tie, ktoré priraďujú jedno číslo druhému. Nula funkcie je zvyčajne hodnota argumentu, pri ktorej sa funkcia stáva nulou.

Inštrukcie

1. Ak chcete zistiť nuly funkcie, musíte prirovnať jej pravú stranu k nule a vyriešiť výslednú rovnicu. Predstavme si, že máte funkciu f(x)=x-5.

2. Aby sme našli nuly tejto funkcie, zoberme a prirovnajme jej pravú stranu k nule: x-5=0.

3. Po vyriešení tejto rovnice zistíme, že x=5 a táto hodnota argumentu bude nula funkcie. To znamená, že keď je hodnota argumentu 5, funkcia f(x) sa stane nulou.

Pod výhľadom funkcie v matematike chápeme súvislosť medzi prvkami množín. Správnejšie povedané, ide o „zákon“, podľa ktorého je celý prvok jednej množiny (nazývaný doména definície) spojený s určitým prvkom inej množiny (nazývaný doménou hodnôt).

Budete potrebovať

• Znalosť algebry a matematického prehľadu.

Inštrukcie

1. hodnoty funkcie Ide o určitú oblasť, z ktorej môže funkcia nadobúdať hodnoty. Povedzme rozsah hodnôt funkcie f(x)=|x| od 0 do nekonečna. S cieľom objaviť význam funkcie v určitom bode musíte argument nahradiť funkcie jeho číselný ekvivalent, výsledné číslo bude význam m funkcie. Nech funkcia f(x)=|x| - 10 + 4x. Poďme zistiť význam funkcie v bode x=-2. Nahradíme x číslom -2: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16. Teda význam funkcie v bode -2 sa rovná -16.

Poznámka!
Pred hľadaním hodnoty funkcie v bode sa uistite, že je v doméne funkcie.

Užitočné rady
Podobná metóda umožňuje objaviť význam funkcie viacerých argumentov. Rozdiel je v tom, že namiesto jedného čísla budete musieť nahradiť niekoľko - podľa počtu argumentov funkcie.

Funkcia predstavuje vytvorené spojenie medzi premennou y a premennou x. Navyše všetky hodnoty x, nazývané argument, zodpovedajú výnimočnej hodnote y - funkcii. V grafickej forme je funkcia znázornená na karteziánskom súradnicovom systéme vo forme grafu. Priesečníky grafu s osou x, na ktorých sú vynesené argumenty x, sa nazývajú nuly funkcie. Nájdenie prijateľných núl je jednou z úloh hľadania danej funkcie. V tomto prípade sa berú do úvahy všetky prípustné hodnoty nezávislej premennej x, ktoré tvoria doménu definície funkcie (DOF).

Inštrukcie

1. Nula funkcie je hodnota argumentu x, pri ktorej sa hodnota funkcie rovná nule. Nulové však môžu byť len tie argumenty, ktoré sú v rámci definície skúmanej funkcie. To znamená, že existuje veľa hodnôt, pre ktoré je funkcia f(x) užitočná.

2. Zapíšte si danú funkciu a prirovnajte ju k nule, povedzme f(x) = 2x?+5x+2 = 0. Vyriešte výslednú rovnicu a nájdite jej skutočné korene. Korene kvadratickej rovnice sú vypočítané s podporou hľadania diskriminantu. 2x?+5x+2 = 0;D = b?-4ac = 5a-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0,5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. V tomto prípade sa teda získajú dva korene kvadratickej rovnice zodpovedajúce argumenty počiatočnej funkcie f(x).

3. Skontrolujte, či všetky zistené hodnoty x patria do domény definície danej funkcie. Zistite OOF, aby ste to urobili, skontrolujte počiatočný výraz na prítomnosť párnych koreňov tvaru?f (x), na prítomnosť zlomkov vo funkcii s argumentom v menovateli, na prítomnosť logaritmických alebo trigonometrických výrazov.

4. Pri zvažovaní funkcie s výrazom pod odmocninou párneho stupňa vezmite ako definičný obor všetky argumenty x, ktorých hodnoty nemenia radikálny výraz na záporné číslo (naopak, funkcia áno nedáva zmysel). Skontrolujte, či zistené nuly funkcie spadajú do určitého rozsahu prijateľných hodnôt x.

5. Menovateľ zlomku nemôže ísť na nulu, preto vylúčte tie argumenty x, ktoré vedú k takémuto výsledku. Pre logaritmické veličiny by sa mali brať do úvahy iba tie hodnoty argumentu, pre ktoré je samotný výraz väčší ako nula. Nuly funkcie, ktorá mení sublogaritmický výraz na nulu alebo záporné číslo, musia byť z konečného výsledku vyradené.

Poznámka!
Pri hľadaní koreňov rovnice sa môžu objaviť ďalšie korene. To sa dá ľahko skontrolovať: stačí nahradiť výslednú hodnotu argumentu do funkcie a uistiť sa, že sa funkcia zmení na nulu.

Užitočné rady
Niekedy funkcia nie je vyjadrená zrejmým spôsobom prostredníctvom svojho argumentu, potom je ľahké vedieť, čo je táto funkcia. Príkladom toho je rovnica kruhu.

V ktorom nadobúda hodnotu nula. Napríklad pre funkciu danú vzorcom

Je nulový, pretože

Volajú sa aj nuly funkcie korene funkcie.

Koncept núl funkcie možno zvážiť pre všetky funkcie, ktorých rozsah hodnôt obsahuje nulu alebo nulový prvok zodpovedajúcej algebraickej štruktúry.

Pre funkciu reálnej premennej sú nuly hodnoty, pri ktorých graf funkcie pretína os x.

Hľadanie núl funkcie často vyžaduje použitie numerických metód (napríklad Newtonova metóda, gradientové metódy).

Jedným z nevyriešených matematických problémov je hľadanie núl Riemannovej zeta funkcie.

Koreň polynómu

pozri tiež

Literatúra

Nadácia Wikimedia. 2010.

Pozrite si, čo je „Function Zero“ v iných slovníkoch:

Bod, v ktorom daná funkcia f(z) zaniká; teda N. f. f (z) je to isté ako korene rovnice f (z) = 0. Napríklad body 0, π, π, 2π, 2π,... sú nuly funkcie sinz. Nuly analytickej funkcie (Pozri Analytické... ...

Nulová funkcia, nulová funkcia... Slovník pravopisu-príručka

Tento výraz má iné významy, pozri Nula. Je potrebné presunúť obsah tohto článku do článku „Null Function“. Projektu môžete pomôcť kombinovaním článkov. Ak je potrebné diskutovať o uskutočniteľnosti zlúčenia, nahraďte toto ... Wikipedia

Alebo reťazec C (z názvu jazyka C) alebo reťazec ASCIZ (z názvu smernice assembleru.asciz) metóda reprezentácie reťazcov v programovacích jazykoch, pri ktorej sa namiesto zavedenia špeciálneho typu reťazca použije pole znakov. použité, a na konci ... ... Wikipedia

V kvantovej teórii poľa je akceptovaným (žargónovým) názvom pre vlastnosť miznutia renormalizačného faktora väzbovej konštanty, kde g0 je holá väzbová konštanta z interakcie Lagrangian, fyzika. väzbová konštanta oblečená ako interakcia. Rovnosť Z... Fyzická encyklopédia

Nulová mutácia n-alely- Nulová mutácia, n. alela * nulová mutácia, n. alela * nulová mutácia alebo n. alel alebo tichý a. mutácia vedúca k úplnej strate funkcie v sekvencii DNA, v ktorej sa vyskytla... genetika. encyklopedický slovník

Tvrdenie v teórii pravdepodobnosti, že každá udalosť (tzv. reziduálna udalosť), ktorej výskyt je určený len ľubovoľne vzdialenými prvkami postupnosti nezávislých náhodných udalostí alebo náhodných premenných, má... ... Matematická encyklopédia

1) Číslo, ktoré má tú vlastnosť, že žiadne (reálne alebo komplexné) číslo sa po pridaní nemení. Označuje sa symbolom 0. Súčin ľubovoľného čísla pomocou N. sa rovná N.: Ak sa súčin dvoch čísel rovná N., potom jeden z faktorov ... Matematická encyklopédia

Funkcie definované vzťahmi medzi nezávislými premennými, ktoré nie sú vyriešené vo vzťahu k nezávislým premenným; tieto vzťahy sú jedným zo spôsobov, ako špecifikovať funkciu. Napríklad vzťah x2 + y2 1 = 0 definuje N.f. ... Veľká sovietska encyklopédia

Množina tých a len tých bodov, v ktorých nezaniká v žiadnom okolí zovšeobecnená funkcia Zovšeobecnená funkcia mizne v otvorenej množine ak pre všetkých. Pomocou expanzie jednoty sa ukazuje, že ak zovšeobecnená funkcia ... Matematická encyklopédia