ஆன்லைன் கால்குலேட்டர். கொடுக்கப்பட்ட புள்ளியில் ஒரு செயல்பாட்டின் வரைபடத்திற்கு நேரான தொடுகோடு சமன்பாடு

வழித்தோன்றலின் அடையாளத்திற்கும் செயல்பாட்டின் மோனோடோனிசிட்டியின் தன்மைக்கும் இடையிலான தொடர்பைக் காட்டுகிறது.

பின்வருவனவற்றில் மிகவும் கவனமாக இருக்கவும். பாருங்கள், உங்களுக்கு என்ன கொடுக்கப்பட்டுள்ளது! செயல்பாடு அல்லது அதன் வழித்தோன்றல்

வழித்தோன்றலின் வரைபடம் கொடுக்கப்பட்டால், பின்னர் நாம் செயல்பாட்டு அறிகுறிகள் மற்றும் பூஜ்ஜியங்களில் மட்டுமே ஆர்வமாக இருப்போம். கொள்கையளவில் எந்த "மலைகள்" அல்லது "வெள்ளைகள்" மீது எங்களுக்கு ஆர்வம் இல்லை!

பணி 1.

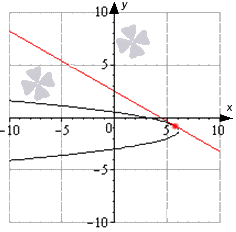
படம் இடைவெளியில் வரையறுக்கப்பட்ட செயல்பாட்டின் வரைபடத்தைக் காட்டுகிறது. செயல்பாட்டின் வழித்தோன்றல் எதிர்மறையாக இருக்கும் முழு எண் புள்ளிகளின் எண்ணிக்கையைத் தீர்மானிக்கவும்.

தீர்வு:

படத்தில், செயல்பாடு குறையும் பகுதிகள் நிறத்தில் சிறப்பிக்கப்பட்டுள்ளன:

செயல்பாட்டின் இந்த குறையும் பகுதிகள் 4 முழு எண் மதிப்புகளைக் கொண்டிருக்கின்றன.

பணி 2.

படம் இடைவெளியில் வரையறுக்கப்பட்ட செயல்பாட்டின் வரைபடத்தைக் காட்டுகிறது. செயல்பாட்டின் வரைபடத்தின் தொடுகோடு இணையாக அல்லது கோட்டுடன் இணைந்திருக்கும் புள்ளிகளின் எண்ணிக்கையைக் கண்டறியவும்.

தீர்வு:

ஒரு செயல்பாட்டின் வரைபடத்திற்கான தொடுகோடு ஒரு நேர்கோட்டுடன் இணையாக (அல்லது ஒத்துப்போகும்) ஒருமுறை (அல்லது, அதே விஷயம்), சாய்வு , பூஜ்ஜியத்திற்கு சமம், பின்னர் தொடுவானம் ஒரு கோண குணகத்தைக் கொண்டுள்ளது.

இதையொட்டி, தொடுவானம் அச்சுக்கு இணையாக உள்ளது, ஏனெனில் சாய்வு என்பது தொடுவானின் சாய்வின் கோணத்தின் தொடுகோடு ஆகும்.

எனவே, வரைபடத்தில் தீவிர புள்ளிகளை (அதிகபட்ச மற்றும் குறைந்தபட்ச புள்ளிகள்) காண்கிறோம் - இந்த புள்ளிகளில்தான் வரைபடத்தின் தொடுகோடு செயல்பாடுகள் அச்சுக்கு இணையாக இருக்கும்.

அத்தகைய 4 புள்ளிகள் உள்ளன.

பணி 3.

படம் இடைவெளியில் வரையறுக்கப்பட்ட செயல்பாட்டின் வழித்தோன்றலின் வரைபடத்தைக் காட்டுகிறது. செயல்பாட்டின் வரைபடத்தின் தொடுகோடு இணையாக அல்லது கோட்டுடன் இணைந்திருக்கும் புள்ளிகளின் எண்ணிக்கையைக் கண்டறியவும்.

தீர்வு:

ஒரு செயல்பாட்டின் வரைபடத்திற்கான தொடுகோடு ஒரு சாய்வைக் கொண்ட ஒரு கோட்டுடன் இணையாக (அல்லது ஒத்துப்போகிறது) என்பதால், தொடுவானமும் ஒரு சாய்வைக் கொண்டுள்ளது.

இதையொட்டி தொடு புள்ளிகளில் என்று அர்த்தம்.

எனவே, வரைபடத்தில் எத்தனை புள்ளிகளுக்கு சமமான ஆர்டினேட் உள்ளது என்பதைப் பார்க்கிறோம்.

நீங்கள் பார்க்க முடியும் என, அத்தகைய நான்கு புள்ளிகள் உள்ளன.

பணி 4.

படம் இடைவெளியில் வரையறுக்கப்பட்ட செயல்பாட்டின் வரைபடத்தைக் காட்டுகிறது. செயல்பாட்டின் வழித்தோன்றல் 0 ஆக இருக்கும் புள்ளிகளின் எண்ணிக்கையைக் கண்டறியவும்.

தீர்வு:

வழித்தோன்றல் தீவிர புள்ளிகளில் பூஜ்ஜியத்திற்கு சமம். அவற்றில் 4 எங்களிடம் உள்ளன:

பணி 5.

படம் ஒரு செயல்பாட்டின் வரைபடம் மற்றும் x- அச்சில் பதினொரு புள்ளிகளைக் காட்டுகிறது :. இதில் எத்தனை புள்ளிகளில் செயல்பாட்டின் வழித்தோன்றல் எதிர்மறையாக உள்ளது?

தீர்வு:

செயல்பாடு குறையும் இடைவெளியில், அதன் வழித்தோன்றல் எதிர்மறை மதிப்புகளை எடுக்கும். மற்றும் செயல்பாடு புள்ளிகளில் குறைகிறது. அத்தகைய 4 புள்ளிகள் உள்ளன.

பணி 6.

படம் இடைவெளியில் வரையறுக்கப்பட்ட செயல்பாட்டின் வரைபடத்தைக் காட்டுகிறது. செயல்பாட்டின் உச்ச புள்ளிகளின் கூட்டுத்தொகையைக் கண்டறியவும்.

தீர்வு:

தீவிர புள்ளிகள்- இவை அதிகபட்ச புள்ளிகள் (-3, -1, 1) மற்றும் குறைந்தபட்ச புள்ளிகள் (-2, 0, 3).

தீவிர புள்ளிகளின் கூட்டுத்தொகை: -3-1+1-2+0+3=-2.

பணி 7.

இடைவெளியில் வரையறுக்கப்பட்ட செயல்பாட்டின் வழித்தோன்றலின் வரைபடத்தை படம் காட்டுகிறது. செயல்பாட்டின் அதிகரிப்புக்கான இடைவெளிகளைக் கண்டறியவும். உங்கள் பதிலில், இந்த இடைவெளியில் சேர்க்கப்பட்டுள்ள முழு எண் புள்ளிகளின் கூட்டுத்தொகையைக் குறிப்பிடவும்.

தீர்வு:

செயல்பாட்டின் வழித்தோன்றல் எதிர்மறையாக இல்லாத இடைவெளிகளை படம் எடுத்துக்காட்டுகிறது.

அதிகரித்து வரும் சிறிய இடைவெளியில் முழு எண் புள்ளிகள் இல்லை: , , மற்றும் .

அவற்றின் கூட்டுத்தொகை:

பணி 8.

இடைவெளியில் வரையறுக்கப்பட்ட செயல்பாட்டின் வழித்தோன்றலின் வரைபடத்தை படம் காட்டுகிறது. செயல்பாட்டின் அதிகரிப்புக்கான இடைவெளிகளைக் கண்டறியவும். உங்கள் பதிலில், அவற்றில் பெரியவற்றின் நீளத்தைக் குறிப்பிடவும்.

தீர்வு:

படத்தில், வழித்தோன்றல் நேர்மறையாக இருக்கும் அனைத்து இடைவெளிகளும் நிறத்தில் முன்னிலைப்படுத்தப்படுகின்றன, அதாவது இந்த இடைவெளிகளில் செயல்பாடு அதிகரிக்கிறது.

அவற்றில் மிகப்பெரிய நீளம் 6 ஆகும்.

பணி 9.

இடைவெளியில் வரையறுக்கப்பட்ட செயல்பாட்டின் வழித்தோன்றலின் வரைபடத்தை படம் காட்டுகிறது. பிரிவில் எந்த கட்டத்தில் அது மிகப்பெரிய மதிப்பைப் பெறுகிறது?

தீர்வு:

நாம் ஆர்வமாக உள்ள பிரிவில் வரைபடம் எவ்வாறு செயல்படுகிறது என்பதைப் பார்ப்போம் வழித்தோன்றலின் அடையாளம் மட்டுமே .

இந்த பிரிவில் உள்ள வரைபடம் அச்சுக்குக் கீழே இருப்பதால், on வழித்தோன்றலின் அடையாளம் கழித்தல் ஆகும்.

ஒரு சார்பு f கொடுக்கப்பட வேண்டும், இது ஒரு கட்டத்தில் x 0 ஆனது f (x 0) வரையறுக்கப்பட்ட வழித்தோன்றலைக் கொண்டுள்ளது. பின்னர் கோணக் குணகம் f'(x 0) கொண்ட புள்ளி (x 0 ; f (x 0)) வழியாக செல்லும் நேர்கோடு தொடுகோடு எனப்படும்.

x 0 புள்ளியில் வழித்தோன்றல் இல்லை என்றால் என்ன நடக்கும்? இரண்டு விருப்பங்கள் உள்ளன:

1. வரைபடத்திற்கும் தொடுகோடு இல்லை. கிளாசிக் உதாரணம்- செயல்பாடு y = |x | புள்ளியில் (0; 0).
2. தொடுகோடு செங்குத்தாக மாறுகிறது. எடுத்துக்காட்டாக, புள்ளியில் (1; π /2) y = arcsin x செயல்பாட்டிற்கு இது உண்மை.

தொடு சமன்பாடு

எந்த செங்குத்து அல்லாத நேர்கோடும் y = kx + b வடிவத்தின் சமன்பாட்டால் வழங்கப்படுகிறது, இங்கு k என்பது சாய்வாகும். தொடுவானம் விதிவிலக்கல்ல, மேலும் அதன் சமன்பாட்டை x 0 புள்ளியில் உருவாக்க, இந்த கட்டத்தில் செயல்பாட்டின் மதிப்பையும் வழித்தோன்றலையும் அறிந்தால் போதும்.

எனவே, ஒரு சார்பு y = f (x) கொடுக்கப்பட வேண்டும், இது பிரிவில் y = f ’(x) என்ற வழித்தோன்றலைக் கொண்டுள்ளது. பின்னர் எந்தப் புள்ளியிலும் x 0 ∈ (a; b) இந்தச் செயல்பாட்டின் வரைபடத்திற்கு ஒரு தொடுகோடு வரையப்படலாம், இது சமன்பாட்டால் வழங்கப்படுகிறது:

y = f ’(x 0) (x - x 0) + f (x 0)

இங்கே f ’(x 0) என்பது x 0 புள்ளியில் உள்ள வழித்தோன்றலின் மதிப்பாகும், மேலும் f (x 0) என்பது செயல்பாட்டின் மதிப்பாகும்.

பணி. y = x 3 செயல்பாடு கொடுக்கப்பட்டது. x 0 = 2 என்ற புள்ளியில் இந்தச் சார்பின் வரைபடத்திற்கு தொடுவானுக்கான சமன்பாட்டை எழுதவும்.

தொடு சமன்பாடு: y = f ’(x 0) · (x - x 0) + f (x 0). புள்ளி x 0 = 2 எங்களுக்கு வழங்கப்படுகிறது, ஆனால் மதிப்புகள் f (x 0) மற்றும் f '(x 0) கணக்கிடப்பட வேண்டும்.

முதலில், செயல்பாட்டின் மதிப்பைக் கண்டுபிடிப்போம். இங்கே எல்லாம் எளிது: f (x 0) = f (2) = 2 3 = 8;
இப்போது வழித்தோன்றலைக் கண்டுபிடிப்போம்: f '(x) = (x 3)' = 3x 2;
x 0 = 2 ஐ வழித்தோன்றலில் மாற்றுகிறோம்: f ’(x 0) = f ’(2) = 3 2 2 = 12;
மொத்தத்தில் நாம் பெறுவது: y = 12 · (x - 2) + 8 = 12x - 24 + 8 = 12x - 16.
இது தொடுகோடு சமன்பாடு.

பணி. x 0 = π /2 என்ற புள்ளியில் f (x) = 2sin x + 5 செயல்பாட்டின் வரைபடத்திற்கு தொடுகோடு ஒரு சமன்பாட்டை எழுதவும்.

இந்த முறை ஒவ்வொரு செயலையும் விரிவாக விவரிக்க மாட்டோம் - முக்கிய படிகளை மட்டுமே நாங்கள் குறிப்பிடுவோம். எங்களிடம் உள்ளது:

f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f ’(x) = (2sin x + 5)’ = 2cos x;
f ’(x 0) = f ’(π /2) = 2cos (π /2) = 0;

தொடு சமன்பாடு:

y = 0 · (x - π /2) + 7 ⇒ y = 7

IN பிந்தைய வழக்குநேர் கோடு கிடைமட்டமாக மாறியது, ஏனெனில் அதன் கோணக் குணகம் k = 0. இதில் எந்தத் தவறும் இல்லை - நாம் ஒரு தீவிர புள்ளியில் தடுமாறினோம்.

கட்டுரை வரையறைகள் பற்றிய விரிவான விளக்கத்தை வழங்குகிறது, உடன் வழித்தோன்றலின் வடிவியல் பொருள் வரைகலை சின்னங்கள். தொடுகோட்டின் சமன்பாடு எடுத்துக்காட்டுகளுடன் பரிசீலிக்கப்படும், 2வது வரிசை வளைவுகளுக்கு ஒரு தொடுகோடு சமன்பாடுகள் காணப்படும்.

Yandex.RTB R-A-339285-1 வரையறை 1

y = k x + b என்ற நேர்க்கோட்டின் சாய்வு கோணம் கோணம் α என அழைக்கப்படுகிறது, இது x அச்சின் நேர்கோட்டில் இருந்து நேர்கோட்டில் y = k x + b வரை அளவிடப்படுகிறது.

படத்தில், x திசை பச்சை அம்பு மற்றும் பச்சை வில் மற்றும் சாய்வின் கோணம் சிவப்பு வில் மூலம் குறிக்கப்படுகிறது. நீலக் கோடு நேர் கோட்டைக் குறிக்கிறது.

வரையறை 2

y = k x + b நேர்க்கோட்டின் சாய்வு எண் குணகம் k எனப்படும்.

கோண குணகம் நேர் கோட்டின் தொடுகோடு சமமாக உள்ளது, வேறுவிதமாகக் கூறினால் k = t g α.

• ஒரு நேர்கோட்டின் சாய்வின் கோணம் x க்கு இணையாக இருந்தால் மட்டுமே 0 க்கு சமமாக இருக்கும் மற்றும் பூஜ்ஜியத்தின் தொடுகோடு 0 க்கு சமமாக இருக்கும். இதன் பொருள் சமன்பாட்டின் வடிவம் y = b ஆக இருக்கும்.
• y = k x + b நேர்க்கோட்டின் சாய்வின் கோணம் கடுமையானதாக இருந்தால், நிபந்தனைகள் 0 திருப்தி அடையும்< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается நேர்மறை எண், டேன்ஜென்ட் மதிப்பு t g α > 0 நிபந்தனையை பூர்த்தி செய்வதால், வரைபடத்தில் அதிகரிப்பு உள்ளது.
• α = π 2 எனில், கோட்டின் இடம் x க்கு செங்குத்தாக இருக்கும். சமத்துவம் x = c ஆல் குறிப்பிடப்படுகிறது, இதன் மதிப்பு c உண்மையான எண்ணாக இருக்கும்.
• y = k x + b நேர்க்கோட்டின் சாய்வின் கோணம் மழுங்கியதாக இருந்தால், அது π 2 நிபந்தனைகளுக்கு ஒத்திருக்கும்.< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

secant என்பது f (x) செயல்பாட்டின் 2 புள்ளிகள் வழியாக செல்லும் ஒரு கோடு. வேறு வார்த்தைகளில் கூறுவதானால், ஒரு செகண்ட் என்பது கொடுக்கப்பட்ட செயல்பாட்டின் வரைபடத்தில் ஏதேனும் இரண்டு புள்ளிகள் வழியாக வரையப்பட்ட ஒரு நேர் கோடு.

A B என்பது ஒரு செக்கன்ட் என்றும், f (x) என்பது கருப்பு வளைவு என்றும், α என்பது சிவப்பு வளைவு என்றும், இது செக்கன்ட்டின் சாய்வின் கோணத்தைக் குறிக்கிறது.

ஒரு நேர்கோட்டின் கோணக் குணகம் சாய்வின் கோணத்தின் தொடுகோடு சமமாக இருக்கும் போது, ​​A B C வலது முக்கோணத்தின் தொடுகோடு எதிரெதிர் பக்கத்தின் விகிதத்தில் அருகில் உள்ள ஒன்றின் விகிதத்தால் கண்டறியப்படலாம் என்பது தெளிவாகிறது.

வரையறை 4

படிவத்தின் செகண்ட்டைக் கண்டறிவதற்கான சூத்திரத்தைப் பெறுகிறோம்:

k = t g α = B C A C = f (x B) - f x A x B - x A, இதில் A மற்றும் B புள்ளிகளின் abscissas x A, x B மற்றும் f (x A), f (x B) இந்த புள்ளிகளில் மதிப்புகள் செயல்பாடுகள்.

வெளிப்படையாக, secant இன் கோணக் குணகம் k = f (x B) - f (x A) x B - x A அல்லது k = f (x A) - f (x B) x A - x B என்ற சமத்துவத்தைப் பயன்படுத்தி தீர்மானிக்கப்படுகிறது. , மற்றும் சமன்பாடு y = f (x B) - f (x A) x B - x A x - x A + f (x A) அல்லது
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

secant வரைபடத்தை பார்வைக்கு 3 பகுதிகளாகப் பிரிக்கிறது: புள்ளி A க்கு இடப்புறம், A முதல் B வரை, B க்கு வலப்புறம். கீழே உள்ள படம், தற்செயலாகக் கருதப்படும் மூன்று செகண்டுகள் இருப்பதைக் காட்டுகிறது, அதாவது, அவை a ஐப் பயன்படுத்தி அமைக்கப்பட்டுள்ளன. ஒத்த சமன்பாடு.

வரையறையின்படி, இந்த வழக்கில் நேர் கோடு மற்றும் அதன் செகண்ட் ஒத்துப்போகின்றன என்பது தெளிவாகிறது.

கொடுக்கப்பட்ட செயல்பாட்டின் வரைபடத்தை ஒரு செகண்ட் பலமுறை வெட்டலாம். ஒரு நொடிக்கு y = 0 என்ற வடிவத்தின் சமன்பாடு இருந்தால், சைனூசாய்டுடன் வெட்டும் புள்ளிகளின் எண்ணிக்கை எல்லையற்றது.

வரையறை 5

x 0 புள்ளியில் f (x) செயல்பாட்டின் வரைபடத்திற்கு டேன்ஜென்ட்; f (x 0) என்பது கொடுக்கப்பட்ட புள்ளி x 0 வழியாக செல்லும் ஒரு நேர்கோடு; f (x 0), x 0 க்கு நெருக்கமான பல x மதிப்புகளைக் கொண்ட ஒரு பிரிவின் முன்னிலையில்.

எடுத்துக்காட்டு 1

கீழே உள்ள உதாரணத்தை இன்னும் விரிவாகப் பார்ப்போம். y = x + 1 செயல்பாட்டால் வரையறுக்கப்பட்ட கோடு ஆய (1; 2) புள்ளியில் y = 2 x க்கு தொடுவாகக் கருதப்படுகிறது என்பது தெளிவாகிறது. தெளிவுக்காக, (1; 2) க்கு நெருக்கமான மதிப்புகளைக் கொண்ட வரைபடங்களைக் கருத்தில் கொள்வது அவசியம். செயல்பாடு y = 2 x கருப்பு நிறத்தில் காட்டப்பட்டுள்ளது, நீலக் கோடு தொடுகோடு மற்றும் சிவப்பு புள்ளி வெட்டும் புள்ளியாகும்.

வெளிப்படையாக, y = 2 x என்பது y = x + 1 என்ற வரியுடன் இணைகிறது.

தொடுவானைத் தீர்மானிக்க, A B புள்ளியின் நடத்தையை நாம் கருத்தில் கொள்ள வேண்டும்.

நீலக் கோட்டால் குறிக்கப்படும் செக்கன்ட் A B, தொடுகோட்டின் நிலையையே நோக்கிச் செல்கிறது, மேலும் secant α இன் சாய்வின் கோணம் α x என்ற தொடுகோட்டின் சாய்வின் கோணத்தை நோக்கிச் செல்லத் தொடங்கும்.

வரையறை 6

A புள்ளியில் உள்ள y = f (x) செயல்பாட்டின் வரைபடத்திற்கான தொடுவானம், B ஆனது A க்கு முனைவதால், A B இன் வரம்பிடும் நிலையாகக் கருதப்படுகிறது, அதாவது B → A.

இப்போது ஒரு கட்டத்தில் ஒரு செயல்பாட்டின் வழித்தோன்றலின் வடிவியல் பொருளைக் கருத்தில் கொள்ள செல்லலாம்.

x 0, f (x 0) மற்றும் x 0 + ∆ x, f (x 0 + ∆ x) மற்றும் ∆ x ஆயத்தொகுப்புகளுடன் A மற்றும் B ஆனது f (x) செயல்பாட்டிற்கான A B ஐப் பரிசீலிப்போம். வாதத்தின் அதிகரிப்பாகக் குறிக்கப்படுகிறது. இப்போது செயல்பாடு ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) வடிவத்தை எடுக்கும். தெளிவுக்காக, ஒரு வரைபடத்தின் உதாரணத்தைக் கொடுப்போம்.

முடிவைக் கருத்தில் கொள்வோம் வலது முக்கோணம் A B C. தொடுகோட்டின் வரையறையைப் பயன்படுத்தி தீர்க்கிறோம், அதாவது, ∆ y ∆ x = t g α உறவைப் பெறுகிறோம். தொடுகோட்டின் வரையறையிலிருந்து லிம் ∆ x → 0 ∆ y ∆ x = t g α x . ஒரு புள்ளியில் உள்ள வழித்தோன்றலின் விதியின்படி, x 0 புள்ளியில் உள்ள derivative f (x) வாதத்தின் அதிகரிப்புக்கான செயல்பாட்டின் அதிகரிப்பின் விகிதத்தின் வரம்பு என்று அழைக்கப்படுகிறது, அங்கு ∆ x → 0 , பின்னர் அதை f (x 0) = lim ∆ x → 0 ∆ y ∆ x எனக் குறிக்கிறோம்.

இது f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, இங்கு k x என்பது தொடுகோட்டின் சாய்வாகக் குறிக்கப்படுகிறது.

அதாவது, f ' (x) என்பது x 0 புள்ளியில் இருக்க முடியும் என்பதையும், x 0, f 0 (x 0) க்கு சமமான டேன்ஜென்சி புள்ளியில் செயல்பாட்டின் கொடுக்கப்பட்ட வரைபடத்தின் தொடுகோடு போல, இதன் மதிப்பு புள்ளியில் உள்ள தொடுகோட்டின் சாய்வு புள்ளி x 0 இல் உள்ள வழித்தோன்றலுக்கு சமம். பிறகு k x = f " (x 0) என்று கிடைக்கும்.

வடிவியல் பொருள்ஒரு புள்ளியில் ஒரு செயல்பாட்டின் வழித்தோன்றல், அதே புள்ளியில் வரைபடத்திற்கு ஒரு தொடுகோடு இருப்பது பற்றிய கருத்து வழங்கப்படுகிறது.

ஒரு விமானத்தில் ஏதேனும் நேர்கோட்டின் சமன்பாட்டை எழுத, அது கடந்து செல்லும் புள்ளியுடன் ஒரு கோண குணகம் இருப்பது அவசியம். குறுக்குவெட்டில் அதன் குறியீடானது x 0 ஆக எடுக்கப்படுகிறது.

x 0, f 0 (x 0) புள்ளியில் உள்ள y = f (x) செயல்பாட்டின் வரைபடத்திற்கான தொடு சமன்பாடு y = f "(x 0) x - x 0 + f (x 0) வடிவத்தை எடுக்கும்.

இதன் பொருள் f "(x 0) என்ற வழித்தோன்றலின் இறுதி மதிப்பு தொடுகின் நிலையை தீர்மானிக்க முடியும், அதாவது செங்குத்தாக, லிம் x → x 0 + 0 f "(x) = ∞ மற்றும் lim x → x 0 - 0 f "(x ) = ∞ அல்லது இல்லாத நிலை lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .

தொடுகோட்டின் இருப்பிடம் அதன் கோணக் குணகம் k x = f "(x 0) மதிப்பைப் பொறுத்தது. o x அச்சுக்கு இணையாக இருக்கும் போது, ​​k k = 0, o y - k x = ∞ க்கு இணையாக இருக்கும்போது, ​​மற்றும் அதன் வடிவத்தைப் பெறுகிறோம். தொடுகோடு சமன்பாடு x = x 0 k x > 0 உடன் அதிகரிக்கிறது, k x ஆக குறைகிறது< 0 .

எடுத்துக்காட்டு 2

y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 என்ற செயல்பாட்டின் வரைபடத்திற்கு தொடுவானுக்கான சமன்பாட்டை ஆயத்தொகுப்புகளுடன் (1; 3) தொகுத்து, சாய்வின் கோணத்தைத் தீர்மானிக்கவும்.

தீர்வு

நிபந்தனையின்படி, அனைத்து உண்மையான எண்களுக்கும் செயல்பாடு வரையறுக்கப்பட்டுள்ளது. நிபந்தனையால் குறிப்பிடப்பட்ட ஆயங்களைக் கொண்ட புள்ளி, (1; 3) தொடுநிலையின் ஒரு புள்ளியாகும், பின்னர் x 0 = - 1, f (x 0) = - 3.

மதிப்பு - 1 உடன் புள்ளியில் வழித்தோன்றலைக் கண்டறிவது அவசியம். நமக்கு அது கிடைக்கும்

y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

தொடுநிலைப் புள்ளியில் f' (x) இன் மதிப்பு தொடுகோட்டின் சாய்வாகும், இது சாய்வின் தொடுகோடு சமமாக இருக்கும்.

பின்னர் k x = t g α x = y " (x 0) = 3 3

இது α x = a r c t g 3 3 = π 6

பதில்:தொடுகோடு சமன்பாடு வடிவம் பெறுகிறது

y = f "(x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

தெளிவுக்காக, கிராஃபிக் விளக்கப்படத்தில் ஒரு உதாரணம் தருகிறோம்.

அசல் செயல்பாட்டின் வரைபடத்திற்கு கருப்பு நிறம் பயன்படுத்தப்படுகிறது, நீல நிறம்- ஒரு தொடுகோடு படம், சிவப்பு புள்ளி - தொடு புள்ளி. வலதுபுறத்தில் உள்ள படம் பெரிதாக்கப்பட்ட காட்சியைக் காட்டுகிறது.

எடுத்துக்காட்டு 3

கொடுக்கப்பட்ட செயல்பாட்டின் வரைபடத்திற்கு ஒரு தொடுகோடு இருப்பதைத் தீர்மானிக்கவும்
y = 3 · x - 1 5 + 1 ஆய (1 ; 1) உடன் புள்ளியில். ஒரு சமன்பாட்டை எழுதி சாய்வின் கோணத்தை தீர்மானிக்கவும்.

தீர்வு

நிபந்தனையின்படி, கொடுக்கப்பட்ட செயல்பாட்டின் வரையறையின் டொமைன் அனைத்து உண்மையான எண்களின் தொகுப்பாகக் கருதப்படுகிறது.

வழித்தோன்றலைக் கண்டுபிடிப்பதற்குச் செல்லலாம்

y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

x 0 = 1 எனில், f' (x) வரையறுக்கப்படவில்லை, ஆனால் வரம்புகள் லிம் x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 என எழுதப்படும். · 1 + 0 = + ∞ மற்றும் லிம் x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , அதாவது புள்ளியில் இருப்பு செங்குத்து தொடுகோடு (1; 1).

பதில்:சமன்பாடு x = 1 வடிவத்தை எடுக்கும், அங்கு சாய்வின் கோணம் π 2 க்கு சமமாக இருக்கும்.

தெளிவுக்காக, அதை வரைபடமாக சித்தரிக்கலாம்.

எடுத்துக்காட்டு 4

y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 செயல்பாட்டின் வரைபடத்தில் உள்ள புள்ளிகளைக் கண்டறியவும்.

1. தொடுகோடு இல்லை;
2. தொடுகோடு x க்கு இணையாக உள்ளது;
3. தொடுகோடு y = 8 5 x + 4 என்ற கோட்டிற்கு இணையாக உள்ளது.

தீர்வு

வரையறையின் நோக்கத்திற்கு கவனம் செலுத்த வேண்டியது அவசியம். நிபந்தனையின்படி, அனைத்து உண்மையான எண்களின் தொகுப்பிலும் செயல்பாடு வரையறுக்கப்பட்டுள்ளது. தொகுதியை விரிவுபடுத்தி கணினியை x ∈ - ∞ இடைவெளியுடன் தீர்க்கிறோம் ; 2 மற்றும் [ - 2 ; +∞) . நமக்கு அது கிடைக்கும்

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; +∞)

செயல்பாட்டை வேறுபடுத்துவது அவசியம். எங்களிடம் அது இருக்கிறது

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; +∞)

x = − 2 ஆக இருக்கும் போது, ​​ஒரு பக்க வரம்புகள் அந்த புள்ளியில் சமமாக இல்லாததால், வழித்தோன்றல் இல்லை:

லிம் x → - 2 - 0 y " (x) = லிம் x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 லிம் x → - 2 + 0 y " (x) = லிம் x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

செயல்பாட்டின் மதிப்பை x = - 2 புள்ளியில் கணக்கிடுகிறோம், அங்கு நாம் அதைப் பெறுகிறோம்

1. y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, அதாவது புள்ளியில் உள்ள தொடுகோடு ( - 2; - 2) இருக்காது.
2. சாய்வு பூஜ்ஜியமாக இருக்கும்போது தொடுகோடு x க்கு இணையாக இருக்கும். பின்னர் k x = t g α x = f "(x 0). அதாவது, செயல்பாட்டின் வழித்தோன்றல் பூஜ்ஜியமாக மாறும் போது அத்தகைய x இன் மதிப்புகளைக் கண்டறிய வேண்டும். அதாவது, f' இன் மதிப்புகள். (x) தொடுநிலை புள்ளிகளாக இருக்கும், அங்கு தொடுவானம் x க்கு இணையாக இருக்கும்.

எப்போது x ∈ - ∞ ; - 2, பின்னர் - 1 5 (x 2 + 12 x + 35) = 0, மற்றும் x ∈ (- 2; + ∞) க்கு 1 5 (x 2 - 4 x + 3) = 0 கிடைக்கும்.

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

தொடர்புடைய செயல்பாட்டு மதிப்புகளைக் கணக்கிடுங்கள்

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

எனவே - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 செயல்பாட்டு வரைபடத்தின் தேவையான புள்ளிகளாகக் கருதப்படுகிறது.

கருத்தில் கொள்வோம் வரைகலை படம்தீர்வுகள்.

கருப்பு கோடு செயல்பாட்டின் வரைபடம், சிவப்பு புள்ளிகள் தொடு புள்ளிகள்.

1. கோடுகள் இணையாக இருக்கும்போது, ​​கோண குணகங்கள் சமமாக இருக்கும். சரிவு மதிப்பு 8 5 க்கு சமமாக இருக்கும் செயல்பாட்டு வரைபடத்தில் புள்ளிகளைத் தேடுவது அவசியம். இதைச் செய்ய, y "(x) = 8 5 படிவத்தின் சமன்பாட்டை நீங்கள் தீர்க்க வேண்டும். பின்னர், x ∈ - ∞; - 2 எனில், நாம் அதைப் பெறுகிறோம் - 1 5 (x 2 + 12 x + 35) = 8 5, மற்றும் x ∈ ( - 2 ; + ∞) என்றால் 1 5 (x 2 - 4 x + 3) = 8 5.

முதல் சமன்பாடு பாரபட்சம் என்பதால் வேர்கள் இல்லை பூஜ்ஜியத்தை விட குறைவாக. அதை எழுதுவோம்

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

மற்றொரு சமன்பாட்டில் இரண்டு உண்மையான வேர்கள் உள்ளன

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

செயல்பாட்டின் மதிப்புகளைக் கண்டுபிடிப்பதற்குச் செல்லலாம். நமக்கு அது கிடைக்கும்

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

மதிப்புகள் கொண்ட புள்ளிகள் - 1; 4 15, 5; 8 3 என்பது y = 8 5 x + 4 என்ற கோட்டிற்கு இணையாக தொடுகோடுகள் இருக்கும் புள்ளிகள்.

பதில்:கருப்புக் கோடு – செயல்பாட்டின் வரைபடம், சிவப்புக் கோடு – y = 8 5 x + 4 வரைபடம், நீலக் கோடு – புள்ளிகளில் உள்ள தொடுகோடுகள் - 1; 4 15, 5; 8 3.

கொடுக்கப்பட்ட செயல்பாடுகளுக்கு எண்ணற்ற தொடுகோடுகள் இருக்கலாம்.

எடுத்துக்காட்டு 5

y = 3 cos 3 2 x - π 4 - 1 3 செயல்பாட்டின் கிடைக்கக்கூடிய அனைத்து தொடுகோடுகளின் சமன்பாடுகளை எழுதவும், அவை y = - 2 x + 1 2 என்ற நேர் கோட்டிற்கு செங்குத்தாக அமைந்துள்ளன.

தீர்வு

தொடு சமன்பாட்டை தொகுக்க, கோடுகளின் செங்குத்தாக இருக்கும் நிபந்தனையின் அடிப்படையில், தொடு புள்ளியின் குணகம் மற்றும் ஒருங்கிணைப்புகளைக் கண்டறிவது அவசியம். வரையறை பின்வருமாறு: நேர் கோடுகளுக்கு செங்குத்தாக இருக்கும் கோண குணகங்களின் தயாரிப்பு சமம் - 1, அதாவது k x · k ⊥ = - 1 என எழுதப்பட்டுள்ளது. கோண குணகம் கோட்டிற்கு செங்குத்தாக அமைந்துள்ளது மற்றும் k x = - 1 k ⊥ = - 1 - 2 = 1 2 க்கு சமமாக இருக்கும் நிபந்தனையிலிருந்து.

இப்போது நீங்கள் தொடு புள்ளிகளின் ஆயங்களை கண்டுபிடிக்க வேண்டும். கொடுக்கப்பட்ட செயல்பாட்டிற்கான x மற்றும் அதன் மதிப்பைக் கண்டறிய வேண்டும். புள்ளியில் உள்ள வழித்தோன்றலின் வடிவியல் அர்த்தத்திலிருந்து என்பதைக் கவனியுங்கள்
x 0 நாம் k x = y "(x 0) ஐப் பெறுகிறோம். இந்த சமத்துவத்திலிருந்து தொடர்பு புள்ளிகளுக்கான x இன் மதிப்புகளைக் காண்கிறோம்.

நமக்கு அது கிடைக்கும்

y "(x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 sin 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9

இது முக்கோணவியல் சமன்பாடுதொடு புள்ளிகளின் ஆர்டினேட்டுகளை கணக்கிட பயன்படும்.

3 2 x 0 - π 4 = a r c பாவம் - 1 9 + 2 πk அல்லது 3 2 x 0 - π 4 = π - a r c பாவம் - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk அல்லது 3 2 x 0 - π 4 = π + a r c பாவம் 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk அல்லது x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z என்பது முழு எண்களின் தொகுப்பாகும்.

x தொடர்பு புள்ளிகள் கண்டறியப்பட்டுள்ளன. இப்போது நீங்கள் y இன் மதிப்புகளைத் தேடுவதற்குச் செல்ல வேண்டும்:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 அல்லது y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 அல்லது y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 அல்லது y 0 = - 4 5 + 1 3

இதிலிருந்து நாம் 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3, 2 3 5 π 4 + a r c sin 1 9 + 2 πk; - 4 5 + 1 3 ஆகியவை தொடுநிலையின் புள்ளிகள்.

பதில்:தேவையான சமன்பாடுகள் என எழுதப்படும்

y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c பாவம் 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

ஒரு காட்சிப் பிரதிநிதித்துவத்திற்கு, ஒரு ஆயக் கோட்டில் ஒரு செயல்பாடு மற்றும் ஒரு தொடுகோடு.

செயல்பாடு இடைவெளியில் அமைந்திருப்பதை படம் காட்டுகிறது [ - 10 ; 10 ], இதில் கருப்பு நேர் கோடு செயல்பாட்டின் வரைபடம், நீல கோடுகள்– y = - 2 x + 1 2 வடிவத்தின் கொடுக்கப்பட்ட வரிக்கு செங்குத்தாக அமைந்துள்ள தொடுகோடுகள். சிவப்பு புள்ளிகள் தொடு புள்ளிகள்.

2வது வரிசை வளைவுகளின் நியதிச் சமன்பாடுகள் ஒற்றை-மதிப்புச் செயல்பாடுகள் அல்ல. அவற்றுக்கான தொடு சமன்பாடுகள் அறியப்பட்ட திட்டங்களின்படி தொகுக்கப்படுகின்றன.

ஒரு வட்டத்திற்கு தொடுகோடு

x c e n t e r புள்ளியில் மையத்துடன் ஒரு வட்டத்தை வரையறுக்க; y c e n t e r மற்றும் R ஆரம், x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 என்ற சூத்திரத்தைப் பயன்படுத்தவும்.

இந்த சமத்துவத்தை இரண்டு செயல்பாடுகளின் ஒன்றியமாக எழுதலாம்:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

படத்தில் காட்டப்பட்டுள்ளபடி முதல் செயல்பாடு மேலேயும், இரண்டாவது கீழேயும் அமைந்துள்ளது.

x 0 புள்ளியில் ஒரு வட்டத்தின் சமன்பாட்டை தொகுக்க; y 0 , மேல் அல்லது கீழ் அரை வட்டத்தில் அமைந்துள்ளது, y = R 2 - x - x c e n t e r 2 + y c e n t e r அல்லது y = - R 2 - x - x c e n t சுட்டிக்காட்டப்பட்ட புள்ளியில் y c e n t e r.

x c e n t e r என்ற புள்ளிகளில் இருக்கும்போது; y c e n t e r + R மற்றும் x c e n t e r; y c e n t e r - R தொடுகோடுகளை y = y c e n t e r + R மற்றும் y = y c e n t e r - R , மற்றும் புள்ளிகள் x c e n t e r + R ஆகிய சமன்பாடுகள் மூலம் கொடுக்கலாம்; y c e n t e r மற்றும்
x c e n t e r - R; y c e n t e r என்பது o y க்கு இணையாக இருக்கும், பின்னர் x = x c e n t e r + R மற்றும் x = x c e n t e r - R வடிவத்தின் சமன்பாடுகளைப் பெறுகிறோம்.

நீள்வட்டத்தின் தொடுகோடு

நீள்வட்டம் x c e n t e r இல் ஒரு மையத்தைக் கொண்டிருக்கும் போது; y c e n t e r உடன் அரை அச்சுகள் a மற்றும் b, பின்னர் அதை x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 என்ற சமன்பாட்டைப் பயன்படுத்தி குறிப்பிடலாம்.

மேல் மற்றும் கீழ் அரை நீள்வட்டம் என இரண்டு செயல்பாடுகளை இணைப்பதன் மூலம் நீள்வட்டத்தையும் வட்டத்தையும் குறிக்கலாம். பின்னர் நாம் அதைப் பெறுகிறோம்

y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

தொடுகோடுகள் நீள்வட்டத்தின் உச்சியில் அமைந்திருந்தால், அவை x அல்லது y க்கு இணையாக இருக்கும். கீழே, தெளிவுக்காக, உருவத்தைக் கவனியுங்கள்.

எடுத்துக்காட்டு 6

x = 2 க்கு சமமான x மதிப்புகள் கொண்ட புள்ளிகளில் x - 3 2 4 + y - 5 2 25 = 1 நீள்வட்டத்திற்கு தொடுகோடு சமன்பாட்டை எழுதவும்.

தீர்வு

x = 2 மதிப்புடன் தொடர்புடைய தொடு புள்ளிகளைக் கண்டறிவது அவசியம். நீள்வட்டத்தின் தற்போதைய சமன்பாட்டில் நாம் மாற்றியமைத்து அதைக் கண்டுபிடிப்போம்

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

பின்னர் 2; 5 3 2 + 5 மற்றும் 2; - 5 3 2 + 5 என்பது மேல் மற்றும் கீழ் அரை நீள்வட்டத்தைச் சேர்ந்த தொடு புள்ளிகள்.

y ஐப் பொறுத்து நீள்வட்டத்தின் சமன்பாட்டைக் கண்டுபிடித்து தீர்ப்பதற்குச் செல்லலாம். நமக்கு அது கிடைக்கும்

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

வெளிப்படையாக, மேல் அரை நீள்வட்டம் y = 5 + 5 2 4 - x - 3 2 வடிவத்தின் செயல்பாட்டைப் பயன்படுத்தி குறிப்பிடப்படுகிறது, மேலும் கீழ் அரை நீள்வட்டம் y = 5 - 5 2 4 - x - 3 2.

ஒரு புள்ளியில் ஒரு செயல்பாட்டின் வரைபடத்திற்கு ஒரு தொடுகோடு ஒரு சமன்பாட்டை உருவாக்க ஒரு நிலையான அல்காரிதத்தைப் பயன்படுத்துவோம். புள்ளி 2 இல் முதல் தொடுகோடுக்கான சமன்பாடு என்று எழுதுவோம்; 5 3 2 + 5 போல் இருக்கும்

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

புள்ளியில் உள்ள மதிப்புடன் இரண்டாவது தொடுகோட்டின் சமன்பாடு இருப்பதைக் காண்கிறோம்
2 ; - 5 3 2 + 5 வடிவம் எடுக்கிறது

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

வரைபட ரீதியாக, தொடுகோடுகள் பின்வருமாறு குறிப்பிடப்படுகின்றன:

மிகைப்புரைக்கு தொடுகோடு

ஒரு ஹைபர்போலா x c e n t e r இல் ஒரு மையத்தைக் கொண்டிருக்கும் போது; y c e n t e r மற்றும் vertices x c e n t e r + α ; y c e n t e r மற்றும் x c e n t e r - α ; y c e n t e r, சமத்துவமின்மை x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 நடைபெறுகிறது, செங்குத்துகளுடன் இருந்தால் x c e n t e r; y c e n t e r + b மற்றும் x c e n t e r; y c e n t e r -b , பின்னர் சமத்துவமின்மை x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 ஐப் பயன்படுத்தி குறிப்பிடப்படுகிறது.

ஒரு ஹைபர்போலாவை படிவத்தின் இரண்டு ஒருங்கிணைந்த செயல்பாடுகளாக குறிப்பிடலாம்

y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r அல்லது y = y + 2 n t e r y = - b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r

முதல் வழக்கில், தொடுகோடுகள் y க்கு இணையாக உள்ளன, இரண்டாவதாக அவை x க்கு இணையாக இருக்கும்.

ஒரு ஹைப்பர்போலாவிற்கான தொடுகோட்டின் சமன்பாட்டைக் கண்டறிய, தொடுநிலைப் புள்ளி எந்தச் செயல்பாட்டைச் சேர்ந்தது என்பதைக் கண்டறிய வேண்டியது அவசியம். இதைத் தீர்மானிக்க, சமன்பாடுகளுக்குப் பதிலாக அடையாளத்தை சரிபார்க்க வேண்டியது அவசியம்.

எடுத்துக்காட்டு 7

புள்ளி 7 இல் ஹைப்பர்போல x - 3 2 4 - y + 3 2 9 = 1 க்கு தொடுகோடு ஒரு சமன்பாட்டை எழுதுங்கள்; - 3 3 - 3 .

தீர்வு

2 செயல்பாடுகளைப் பயன்படுத்தி ஹைப்பர்போலாவைக் கண்டறிவதற்கான தீர்வு பதிவை மாற்றுவது அவசியம். நமக்கு அது கிடைக்கும்

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 மற்றும் y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

7 ஆயத்தொலைவுகளுடன் கொடுக்கப்பட்ட புள்ளி எந்தச் செயல்பாட்டைச் சேர்ந்தது என்பதைக் கண்டறிவது அவசியம்; - 3 3 - 3 .

வெளிப்படையாக, முதல் செயல்பாட்டைச் சரிபார்க்க இது அவசியம் y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, பின்னர் புள்ளி வரைபடத்திற்கு சொந்தமானது அல்ல, ஏனெனில் சமத்துவம் இல்லை.

இரண்டாவது செயல்பாட்டிற்கு y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, அதாவது புள்ளி கொடுக்கப்பட்ட வரைபடத்திற்கு சொந்தமானது. இங்கிருந்து நீங்கள் சாய்வைக் கண்டுபிடிக்க வேண்டும்.

நமக்கு அது கிடைக்கும்

y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

பதில்:தொடுகோடு சமன்பாட்டை இவ்வாறு குறிப்பிடலாம்

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

இது தெளிவாக இவ்வாறு சித்தரிக்கப்பட்டுள்ளது:

பரவளையத்தின் தொடுகோடு

x 0, y (x 0) புள்ளியில் பரவளைய y = a x 2 + b x + c க்கு தொடுகோடு ஒரு சமன்பாட்டை உருவாக்க, நீங்கள் ஒரு நிலையான அல்காரிதத்தைப் பயன்படுத்த வேண்டும், பின்னர் சமன்பாடு y = y "(x) வடிவத்தை எடுக்கும் 0) x - x 0 + y ( x 0) உச்சியில் உள்ள தொடுகோடு x க்கு இணையாக உள்ளது

நீங்கள் பரவளைய x = a y 2 + b y + c இரண்டு செயல்பாடுகளின் ஒன்றியமாக வரையறுக்க வேண்டும். எனவே, y க்கான சமன்பாட்டை நாம் தீர்க்க வேண்டும். நமக்கு அது கிடைக்கும்

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

அதை வரைபடமாக இவ்வாறு சித்தரிக்கலாம்:

ஒரு புள்ளி x 0, y (x 0) ஒரு செயல்பாட்டிற்குச் சொந்தமானதா என்பதைக் கண்டறிய, நிலையான அல்காரிதம் படி மெதுவாக தொடரவும். பரவளையத்துடன் ஒப்பிடும்போது அத்தகைய தொடுகோடு இணையாக இருக்கும்.

எடுத்துக்காட்டு 8

x - 2 y 2 - 5 y + 3 வரையிலான தொடுகோணத்தின் சமன்பாட்டை நாம் 150 ° என்ற தொடுகோணத்தைக் கொண்டிருக்கும் போது எழுதவும்.

தீர்வு

பரவளையத்தை இரண்டு செயல்பாடுகளாகக் குறிப்பிடுவதன் மூலம் தீர்வைத் தொடங்குகிறோம். நமக்கு அது கிடைக்கும்

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

சாய்வின் மதிப்பு இந்த செயல்பாட்டின் x 0 புள்ளியில் உள்ள வழித்தோன்றலின் மதிப்புக்கு சமம் மற்றும் சாய்வின் கோணத்தின் தொடுகோடு சமமாக இருக்கும்.

நாங்கள் பெறுகிறோம்:

k x = y "(x 0) = t g α x = t g 150 ° = - 1 3

இங்கிருந்து நாம் தொடர்பு புள்ளிகளுக்கான x மதிப்பை தீர்மானிக்கிறோம்.

முதல் செயல்பாடு என எழுதப்படும்

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

வெளிப்படையாக, எங்களுக்கு எதிர்மறை மதிப்பு கிடைத்ததால், உண்மையான வேர்கள் இல்லை. அத்தகைய செயல்பாட்டிற்கு 150° கோணத்துடன் தொடுகோடு இல்லை என்று முடிவு செய்கிறோம்.

இரண்டாவது செயல்பாடு என எழுதப்படும்

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

தொடர்பு புள்ளிகள் 23 4 என்று எங்களிடம் உள்ளது; - 5 + 3 4 .

பதில்:தொடுகோடு சமன்பாடு வடிவம் பெறுகிறது

y = - 1 3 x - 23 4 + - 5 + 3 4

அதை வரைபடமாக இந்த வழியில் சித்தரிக்கலாம்:

உரையில் பிழையைக் கண்டால், அதை முன்னிலைப்படுத்தி Ctrl+Enter ஐ அழுத்தவும்

வீடியோ பாடம் "ஒரு செயல்பாட்டின் வரைபடத்திற்கு ஒரு தொடுகோடு சமன்பாடு" என்பதை நிரூபிக்கிறது கல்வி பொருள்தலைப்பில் தேர்ச்சி பெற. வழங்கப்பட்ட வீடியோ பாடத்தின் போது தத்துவார்த்த பொருள், ஒரு குறிப்பிட்ட புள்ளியில் ஒரு செயல்பாட்டின் வரைபடத்திற்கு ஒரு தொடுகோடு சமன்பாடு என்ற கருத்தை உருவாக்குவதற்குத் தேவையானது, அத்தகைய தொடுநிலையைக் கண்டறிவதற்கான ஒரு வழிமுறை, ஆய்வு செய்யப்பட்ட கோட்பாட்டுப் பொருளைப் பயன்படுத்தி சிக்கல்களைத் தீர்ப்பதற்கான எடுத்துக்காட்டுகள் விவரிக்கப்பட்டுள்ளன.

வீடியோ டுடோரியல் பொருளின் தெளிவை மேம்படுத்தும் முறைகளைப் பயன்படுத்துகிறது. விளக்கக்காட்சியில் வரைபடங்கள், வரைபடங்கள், முக்கியமான குரல் கருத்துகள், அனிமேஷன், தனிப்படுத்துதல் மற்றும் பிற கருவிகள் உள்ளன.

வீடியோ பாடம் பாடத்தின் தலைப்பின் விளக்கக்காட்சி மற்றும் M(a;f(a)) என்ற புள்ளியில் உள்ள சில செயல்பாட்டின் y=f(x) வரைபடத்திற்கு ஒரு தொடுகோடு படத்துடன் தொடங்குகிறது. கொடுக்கப்பட்ட புள்ளியில் வரைபடத்தில் வரையப்பட்ட தொடுகோட்டின் கோண குணகம் இந்த புள்ளியில் f΄(a) செயல்பாட்டின் வழித்தோன்றலுக்கு சமம் என்பது அறியப்படுகிறது. மேலும் இயற்கணித பாடத்தில் இருந்து y=kx+m என்ற நேர்கோட்டின் சமன்பாட்டை நாம் அறிவோம். ஒரு புள்ளியில் தொடுகோடு சமன்பாட்டைக் கண்டறிவதில் உள்ள சிக்கலுக்கான தீர்வு திட்டவட்டமாக வழங்கப்படுகிறது, இது குணகங்களைக் கண்டறிவதைக் குறைக்கிறது k, m. செயல்பாட்டின் வரைபடத்தைச் சேர்ந்த ஒரு புள்ளியின் ஆயங்களை அறிந்து, ஆய மதிப்பை f(a)=ka+m என்ற தொடு சமன்பாட்டில் மாற்றுவதன் மூலம் m ஐக் கண்டறியலாம். அதிலிருந்து நாம் m=f(a)-ka என்று காண்கிறோம். இவ்வாறு, கொடுக்கப்பட்ட புள்ளியில் உள்ள வழித்தோன்றலின் மதிப்பையும், புள்ளியின் ஆயத்தொலைவுகளையும் தெரிந்துகொள்வதன் மூலம், நாம் தொடு சமன்பாட்டை y=f(a)+f΄(a)(x-a) என்று குறிப்பிடலாம்.

வரைபடத்தைத் தொடர்ந்து தொடுகோடு சமன்பாட்டை உருவாக்குவதற்கான ஒரு எடுத்துக்காட்டு கீழே உள்ளது. y=x 2, x=-2 சார்பு கொடுக்கப்பட்டது. a=-2ஐ எடுத்துக் கொண்டால், கொடுக்கப்பட்ட புள்ளியில் f(a)= f(-2)=(-2) 2 =4 இல் செயல்பாட்டின் மதிப்பைக் காண்கிறோம். f΄(x)=2x செயல்பாட்டின் வழித்தோன்றலை நாங்கள் தீர்மானிக்கிறோம். இந்த கட்டத்தில் வழித்தோன்றல் f΄(a)= f΄(-2)=2·(-2)=-4 க்கு சமம். சமன்பாட்டை உருவாக்க, அனைத்து குணகங்களும் a=-2, f(a)=4, f΄(a)=-4 கண்டுபிடிக்கப்பட்டன, எனவே தொடு சமன்பாடு y=4+(-4)(x+2) ஆகும். சமன்பாட்டை எளிதாக்கினால், நாம் y = -4-4x ஐப் பெறுகிறோம்.

பின்வரும் எடுத்துக்காட்டு, y=tgx செயல்பாட்டின் வரைபடத்தின் தொடக்கத்தில் உள்ள தொடுகோடு ஒரு சமன்பாட்டை உருவாக்க பரிந்துரைக்கிறது. கொடுக்கப்பட்ட புள்ளியில் a=0, f(0)=0, f΄(x)=1/cos 2 x, f΄(0)=1. எனவே தொடுகோடு சமன்பாடு y=x போல் தெரிகிறது.

ஒரு பொதுமைப்படுத்தலாக, ஒரு குறிப்பிட்ட புள்ளியில் ஒரு செயல்பாட்டின் வரைபடத்திற்கு ஒரு சமன்பாடு தொடுகோடு உருவாக்கும் செயல்முறை 4 படிகளைக் கொண்ட ஒரு வழிமுறையின் வடிவத்தில் முறைப்படுத்தப்படுகிறது:

• தொடு புள்ளியின் abscissa க்கான பதவியை உள்ளிடவும்;
• f(a) கணக்கிடப்படுகிறது;
• f΄(x) தீர்மானிக்கப்படுகிறது மற்றும் f΄(a) கணக்கிடப்படுகிறது. a, f(a), f΄(a) இன் கண்டுபிடிக்கப்பட்ட மதிப்புகள் y=f(a)+f΄(a)(x-a) என்ற தொடுநிலை சமன்பாட்டின் சூத்திரத்தில் மாற்றியமைக்கப்படுகின்றன.

எடுத்துக்காட்டு 1 புள்ளி x=1 இல் y=1/x செயல்பாட்டின் வரைபடத்துடன் தொடு சமன்பாட்டை உருவாக்குவதைக் கருதுகிறது. சிக்கலைத் தீர்க்க, நாங்கள் ஒரு வழிமுறையைப் பயன்படுத்துகிறோம். புள்ளி a=1 இல் கொடுக்கப்பட்ட செயல்பாட்டிற்கு, f(a)=-1 செயல்பாட்டின் மதிப்பு. f΄(x)=1/x 2 செயல்பாட்டின் வழித்தோன்றல். புள்ளி a=1 இல் derivative f΄(a)= f΄(1)=1. பெறப்பட்ட தரவைப் பயன்படுத்தி, தொடுகோடு சமன்பாடு y=-1+(x-1), அல்லது y=x-2 வரையப்பட்டது.

உதாரணம் 2 இல், y=x 3 +3x 2 -2x-2 செயல்பாட்டின் வரைபடத்திற்கு தொடுவானின் சமன்பாட்டைக் கண்டறிவது அவசியம். முக்கிய நிபந்தனை y=-2x+1 என்ற தொடுகோடு மற்றும் நேர்கோட்டின் இணையாக உள்ளது. முதலில், y=-2x+1 என்ற நேர்கோட்டின் கோணக் குணகத்திற்குச் சமமான, தொடுகோடுகளின் கோணக் குணகத்தைக் காண்கிறோம். கொடுக்கப்பட்ட வரிக்கு f΄(a)=-2 என்பதால், விரும்பிய டேன்ஜென்ட்டுக்கு k=-2. செயல்பாட்டின் வழித்தோன்றலைக் காண்கிறோம் (x 3 +3x 2 -2x-2)΄=3x 2 +6x-2. f΄(a)=-2 என்பதை அறிந்தால், புள்ளி 3a 2 +6a-2=-2 இன் ஆயத்தொலைவுகளைக் காண்கிறோம். சமன்பாட்டைத் தீர்த்த பிறகு, நாம் 1 =0 மற்றும் 2 =-2 ஐப் பெறுகிறோம். கண்டுபிடிக்கப்பட்ட ஆயங்களைப் பயன்படுத்தி, நன்கு அறியப்பட்ட அல்காரிதத்தைப் பயன்படுத்தி தொடு சமன்பாட்டைக் கண்டறியலாம். f(a 1)=-2, f(a 2)=-18 புள்ளிகளில் செயல்பாட்டின் மதிப்பைக் காண்கிறோம். f΄(а 1)= f΄(а 2)=-2 புள்ளியில் உள்ள வழித்தோன்றலின் மதிப்பு. கண்டுபிடிக்கப்பட்ட மதிப்புகளை தொடு சமன்பாட்டில் மாற்றினால், முதல் புள்ளிக்கு 1 =0 y=-2x-2 ஐப் பெறுகிறோம், இரண்டாவது புள்ளிக்கு ஒரு 2 =-2 தொடுகோடு சமன்பாடு y=-2x-22 ஐப் பெறுகிறோம்.

எடுத்துக்காட்டு 3, y=√x செயல்பாட்டின் வரைபடத்திற்கு (0;3) புள்ளியில் வரைவதற்கான தொடுகோடு சமன்பாட்டின் கலவையை விவரிக்கிறது. நன்கு அறியப்பட்ட அல்காரிதம் மூலம் தீர்வு செய்யப்படுகிறது. தொடு புள்ளியில் x=a ஆயத்தொகுதிகள் உள்ளன, இங்கு a>0. f(a)=√x புள்ளியில் உள்ள செயல்பாட்டின் மதிப்பு. f΄(х)=1/2√х செயல்பாட்டின் வழித்தோன்றல், எனவே கொடுக்கப்பட்ட புள்ளியில் f΄(а)=1/2√а. பெறப்பட்ட அனைத்து மதிப்புகளையும் தொடுகோடு சமன்பாட்டில் மாற்றினால், நாம் y=√a+(x-a)/2√a ஐப் பெறுகிறோம். சமன்பாட்டை மாற்றினால், நாம் y=x/2√а+√а/2 ஐப் பெறுகிறோம். தொடுகோடு புள்ளி (0;3) வழியாக செல்கிறது என்பதை அறிந்தால், a இன் மதிப்பைக் காண்கிறோம். 3=√a/2 இலிருந்து ஒரு ஐக் காண்கிறோம். எனவே √a=6, a=36. y=x/12+3 என்ற தொடுகோடு சமன்பாட்டைக் காண்கிறோம். பரிசீலனையில் உள்ள செயல்பாட்டின் வரைபடம் மற்றும் கட்டமைக்கப்பட்ட விரும்பிய தொடுகோடு படம் காட்டுகிறது.

தோராயமான சமத்துவங்கள் Δy=≈f΄(x)Δx மற்றும் f(x+Δx)-f(x)≈f΄(x)Δx ஆகியவை மாணவர்களுக்கு நினைவூட்டப்படுகின்றன. x=a, x+Δx=x, Δx=x-a என எடுத்துக் கொண்டால், f(x)- f(a)≈f΄(a)(x-a), எனவே f(x)≈f(a)+ f΄( a)(x-a).

எடுத்துக்காட்டு 4 இல், 2.003 6 என்ற வெளிப்பாட்டின் தோராயமான மதிப்பைக் கண்டறிவது அவசியம். x=2.003 என்ற புள்ளியில் f(x)=x 6 செயல்பாட்டின் மதிப்பைக் கண்டறிவது அவசியம் என்பதால், f(x)=x 6, a=2, f(a) ஆகியவற்றை எடுத்துக் கொண்டு நன்கு அறியப்பட்ட சூத்திரத்தைப் பயன்படுத்தலாம். )= f(2)=64, f ΄(x)=6x 5. f΄(2)=192 புள்ளியில் வழித்தோன்றல். எனவே, 2.003 6 ≈65-192·0.003. வெளிப்பாட்டைக் கணக்கிட்டால், நமக்கு 2.003 6 ≈64.576 கிடைக்கும்.

"ஒரு செயல்பாட்டின் வரைபடத்திற்கு ஒரு தொடுகோடு சமன்பாடு" என்ற வீடியோ பாடம் பள்ளியில் பாரம்பரிய கணித பாடத்தில் பயன்படுத்த பரிந்துரைக்கப்படுகிறது. தொலைதூரத்தில் கற்பிக்கும் ஆசிரியருக்கு, தலைப்பை இன்னும் தெளிவாக விளக்க வீடியோ பொருள் உதவும். பாடத்தைப் பற்றிய அவர்களின் புரிதலை ஆழப்படுத்த, தேவைப்பட்டால், சுயாதீனமாக மதிப்பாய்வு செய்ய வீடியோவைப் பரிந்துரைக்கலாம்.

உரை டிகோடிங்:

ஒரு புள்ளி M (a; f(a)) (a மற்றும் ef இலிருந்து ஆயத்தொகுப்புகளுடன்) y = f (x) செயல்பாட்டின் வரைபடத்தைச் சேர்ந்தது மற்றும் இந்த கட்டத்தில் ஒரு தொடுகோடு வரைய முடியும் என்பதை நாம் அறிவோம். அச்சு abscissa க்கு செங்குத்தாக இல்லாத செயல்பாட்டின் வரைபடத்திற்கு, தொடுகோட்டின் கோண குணகம் f"(a) (a இலிருந்து eff பிரைம்) க்கு சமமாக இருக்கும்.

ஒரு சார்பு y = f(x) மற்றும் ஒரு புள்ளி M (a; f(a)) கொடுக்கப்பட வேண்டும், மேலும் f´(a) உள்ளது என்பதும் அறியப்படுகிறது. கொடுக்கப்பட்ட செயல்பாட்டின் வரைபடத்திற்கான தொடுகோடு ஒரு சமன்பாட்டை உருவாக்குவோம் கொடுக்கப்பட்ட புள்ளி. இந்த சமன்பாடு, ஆர்டினேட் அச்சுக்கு இணையாக இல்லாத எந்த நேர்கோட்டின் சமன்பாடு போல, y = kx+m (y என்பது ka x plus em க்கு சமம்) வடிவத்தைக் கொண்டுள்ளது, எனவே இதன் மதிப்புகளைக் கண்டறிவதே பணியாகும். குணகங்கள் k மற்றும் m (ka மற்றும் em)

கோணக் குணகம் k= f"(a).m இன் மதிப்பைக் கணக்கிட, விரும்பிய நேர்கோடு M(a; f (a) என்ற புள்ளியின் வழியாக செல்கிறது என்ற உண்மையைப் பயன்படுத்துகிறோம். இதன் பொருள் நாம் ஆயங்களை மாற்றினால் நேர் கோட்டின் சமன்பாட்டில் புள்ளி M ஐப் பெறுகிறோம், நாம் சரியான சமத்துவத்தைப் பெறுகிறோம்: f(a) = ka+m, m = f(a) - ka.

ki மற்றும் m குணகங்களின் காணப்படும் மதிப்புகளை நேர் கோட்டின் சமன்பாட்டில் மாற்றுவதற்கு இது உள்ளது:

y = kx+(f(a) -ka);

y = f(a)+k(x-a);

ஒய்= f(அ)+ f"(அ) (எக்ஸ்- அ). ( y என்பது a இலிருந்து ஒரு கூட்டல் ef பிரைமில் இருந்து ef க்கு சமம், x கழித்தல் a ஆல் பெருக்கப்படுகிறது).

x=a என்ற புள்ளியில் உள்ள y = f(x) செயல்பாட்டின் வரைபடத்திற்கு தொடுவானுக்கான சமன்பாட்டைப் பெற்றுள்ளோம்.

y = x 2 மற்றும் x = -2 (அதாவது a = -2) என்றால், f (a) = f (-2) = (-2) 2 = 4; f´(x) = 2x, அதாவது f"(a) = f´(-2) = 2·(-2) = -4. (பின்னர் a இன் ef என்பது நான்கிற்குச் சமம், பிரைம் இன் ef x என்பது இரண்டு x க்கு சமம், அதாவது ef பிரைம் ஒரு சமம் கழித்தல் நான்கு)

கண்டுபிடிக்கப்பட்ட மதிப்புகள் a = -2, f(a) = 4, f"(a) = -4 ஆகியவற்றை சமன்பாட்டில் மாற்றினால், நாம் பெறுகிறோம்: y = 4+(-4)(x+2), அதாவது y = -4x -4.

(E என்பது கழித்தல் நான்கு x கழித்தல் நான்குக்கு சமம்)

y = tgx(கிரேக்கம்) செயல்பாட்டின் வரைபடத்திற்கான தொடுகோடு ஒரு சமன்பாட்டை உருவாக்குவோம் தொடுகோடு சமம் x) தோற்றத்தில். எங்களிடம் உள்ளது: a = 0, f(0) = tan0=0;

f"(x)= , அதாவது f"(0) = l. கண்டுபிடிக்கப்பட்ட மதிப்புகளான a=0, f(a)=0, f´(a) = 1 ஆகியவற்றை சமன்பாட்டில் மாற்றினால், நாம் பெறுகிறோம்: y=x.

ஒரு அல்காரிதத்தைப் பயன்படுத்தி x புள்ளியில் உள்ள சார்பின் வரைபடத்திற்கு தொடுவானின் சமன்பாட்டைக் கண்டறிவதில் நமது படிகளைச் சுருக்கமாகக் கூறுவோம்.

y = f(x) செயல்பாட்டின் வரைபடத்திற்கான டேன்ஜெண்டிற்கான சமன்பாட்டை உருவாக்குவதற்கான வழிமுறை

1) தொடுநிலை புள்ளியின் abscissa ஐ எழுத்து a உடன் குறிப்பிடவும்.

2) எஃப்(அ) கணக்கிடவும்.

3) f´(x) ஐக் கண்டுபிடித்து f´(a) ஐக் கணக்கிடுங்கள்.

4) கண்டுபிடிக்கப்பட்ட எண்களை a, f(a), f´(a) சூத்திரத்தில் மாற்றவும் ஒய்= f(அ)+ f"(அ) (எக்ஸ்- அ).

எடுத்துக்காட்டு 1. y = - இன் செயல்பாட்டின் வரைபடத்திற்கான தொடுகோடு ஒரு சமன்பாட்டை உருவாக்கவும்

புள்ளி x = 1.

தீர்வு. என்பதை கணக்கில் எடுத்துக்கொண்டு, அல்காரிதத்தைப் பயன்படுத்துவோம் இந்த எடுத்துக்காட்டில்

2) f(a)=f(1)=- =-1

3) f´(x)=; f´(a)= f´(1)= =1.

4) கண்டுபிடிக்கப்பட்ட மூன்று எண்களை மாற்றவும்: a = 1, f(a) = -1, f"(a) = 1 சூத்திரத்தில். நாம் பெறுவது: y = -1+(x-1), y = x-2 .

பதில்: y = x-2.

எடுத்துக்காட்டு 2. y = செயல்பாடு கொடுக்கப்பட்டால் x 3 +3x 2 -2x-2. y = -2x +1 என்ற நேர்கோட்டிற்கு இணையான y = f(x) செயல்பாட்டின் வரைபடத்திற்கு தொடுகோட்டின் சமன்பாட்டை எழுதவும்.

தொடுகோடு சமன்பாட்டை உருவாக்க அல்காரிதத்தைப் பயன்படுத்தி, இந்த எடுத்துக்காட்டில் f(x) = x 3 +3x 2 -2x-2, ஆனால் தொடு புள்ளியின் abscissa இங்கே குறிப்பிடப்படவில்லை.

இப்படி யோசிக்க ஆரம்பிப்போம். விரும்பிய தொடுகோடு y = -2x+1 என்ற நேர்கோட்டிற்கு இணையாக இருக்க வேண்டும். மற்றும் இணையான கோடுகள் சமமான கோண குணகங்களைக் கொண்டுள்ளன. இதன் பொருள், தொடுகோட்டின் கோண குணகம் கொடுக்கப்பட்ட நேர்கோட்டின் கோண குணகத்திற்கு சமம்: k தொடுகோடு. = -2. ஹோக் கேஸ். = f"(a) எனவே, f´(a) = -2 என்ற சமன்பாட்டிலிருந்து a இன் மதிப்பைக் கண்டறியலாம்.

செயல்பாட்டின் வழித்தோன்றலைக் கண்டுபிடிப்போம் y=f(எக்ஸ்):

f"(எக்ஸ்)= (x 3 +3x 2 -2x-2)´ =3x 2 +6x-2;f"(a)= 3a 2 +6a-2.

சமன்பாட்டிலிருந்து f"(a) = -2, i.e. 3a 2 +6a-2=-2 நாம் ஒரு 1 =0, a 2 =-2. இதன் பொருள், பிரச்சனையின் நிபந்தனைகளை பூர்த்தி செய்யும் இரண்டு தொடுகோடுகள் உள்ளன: ஒன்று அப்சிஸ்ஸா 0 உடன் புள்ளி, மற்றொன்று அப்சிஸ்ஸா -2 உடன்.

இப்போது நீங்கள் அல்காரிதத்தைப் பின்பற்றலாம்.

1) a 1 =0, மற்றும் 2 =-2.

2) f(a 1)= 0 3 +3·0 2 -2∙0-2=-2; f(a 2)= (-2) 3 +3·(-2) 2 -2·(-2)-2=6;

3) f"(a 1) = f"(a 2) = -2.

4) a 1 = 0, f(a 1) = -2, f"(a 1) = -2 மதிப்புகளை சூத்திரத்தில் மாற்றினால், நாம் பெறுகிறோம்:

y=-2-2(x-0), y=-2x-2.

சூத்திரத்தில் a 2 = -2, f(a 2) =6, f"(a 2) = -2 மதிப்புகளை மாற்றினால், நாம் பெறுகிறோம்:

y=6-2(x+2), y=-2x+2.

பதில்: y=-2x-2, y=-2x+2.

எடுத்துக்காட்டு 3. புள்ளியில் இருந்து (0; 3) y = செயல்பாட்டின் வரைபடத்திற்கு ஒரு தொடுகோடு வரையவும். தீர்வு. இந்த எடுத்துக்காட்டில் f(x) = என்பதை கணக்கில் எடுத்துக்கொண்டு, தொடுகோடு சமன்பாட்டை உருவாக்க அல்காரிதத்தைப் பயன்படுத்துவோம். இங்கே, உதாரணம் 2 இல், தொடு புள்ளியின் abscissa வெளிப்படையாகக் குறிப்பிடப்படவில்லை என்பதை நினைவில் கொள்ளவும். இருப்பினும், நாங்கள் அல்காரிதத்தைப் பின்பற்றுகிறோம்.

1) x = a என்பது தொடு புள்ளியின் abscissa ஆக இருக்கட்டும்; ஒரு >0 என்பது தெளிவாகிறது.

3) f´(x)=()´=; f´(a) =.

4) a, f(a) = , f"(a) = இன் மதிப்புகளை சூத்திரத்தில் மாற்றுதல்

y=f (a) +f "(a) (x-a), நாங்கள் பெறுகிறோம்:

நிபந்தனையின்படி, தொடுகோடு புள்ளி (0; 3) வழியாக செல்கிறது. சமன்பாட்டில் x = 0, y = 3 மதிப்புகளை மாற்றினால், நாம் பெறுகிறோம்: 3 = , பின்னர் =6, a =36.

நீங்கள் பார்க்க முடியும் என, இந்த எடுத்துக்காட்டில், அல்காரிதத்தின் நான்காவது படியில் மட்டுமே தொடு புள்ளியின் abscissa ஐக் கண்டுபிடிக்க முடிந்தது. சமன்பாட்டில் மதிப்பு a =36 ஐ மாற்றினால், நாம் பெறுகிறோம்: y=+3

படத்தில். 1 வழங்கப்பட்டது வடிவியல் விளக்கம்உதாரணமாக கருதப்படுகிறது: செயல்பாட்டின் வரைபடம் y = கட்டமைக்கப்பட்டது, ஒரு நேர் கோடு வரையப்பட்டது y = +3.

பதில்: y = +3.

x புள்ளியில் ஒரு வழித்தோன்றலைக் கொண்ட y = f(x) செயல்பாட்டிற்கு, தோராயமான சமத்துவம் செல்லுபடியாகும் என்பதை நாங்கள் அறிவோம்: Δyf´(x)Δx (டெல்டா y என்பது டெல்டா x ஆல் பெருக்கப்படும் x இன் eff பிரைமுக்கு தோராயமாக சமம்)

அல்லது, இன்னும் விரிவாக, f(x+Δx)-f(x) f´(x) Δx (x இலிருந்து எஃப் பிளஸ் டெல்டா x மைனஸ் எஃப் x இலிருந்து டெல்டா x ஆல் x இலிருந்து eff பிரைம்க்கு தோராயமாக சமம்).

மேலும் பகுத்தறிவின் வசதிக்காக, குறியீட்டை மாற்றுவோம்:

x க்கு பதிலாக நாம் எழுதுவோம் ஏ,

x+Δxக்கு பதிலாக x என்று எழுதுவோம்

Δx க்கு பதிலாக x-a என்று எழுதுவோம்.

மேலே எழுதப்பட்ட தோராயமான சமத்துவம் வடிவம் எடுக்கும்:

f(x)-f(a)f´(a)(x-a)

f(x)f(a)+f´(a)(x-a). (x இலிருந்து eff என்பது, a இலிருந்து ஒரு கூட்டல் ef ப்ரைம் இலிருந்து தோராயமாக சமம், x மற்றும் a இடையே உள்ள வேறுபாட்டால் பெருக்கப்படுகிறது).

எடுத்துக்காட்டு 4. எண் வெளிப்பாட்டின் தோராயமான மதிப்பைக் கண்டறியவும் 2.003 6.

தீர்வு. இது பற்றி x = 2.003 புள்ளியில் y = x 6 செயல்பாட்டின் மதிப்பைக் கண்டறிவது பற்றி. f(x)f(a)+f´(a)(x-a), இந்த எடுத்துக்காட்டில் f(x)=x 6, a = 2,f(a) = f(2) என்ற சூத்திரத்தைப் பயன்படுத்துவோம். = 2 6 =64; x = 2.003, f"(x) = 6x 5 மற்றும், எனவே, f"(a) = f"(2) = 6 2 5 =192.

இதன் விளைவாக நாம் பெறுகிறோம்:

2.003 6 64+192· 0.003, அதாவது. 2.003 6 =64.576.

நாம் ஒரு கால்குலேட்டரைப் பயன்படுத்தினால், நாம் பெறுவோம்:

2,003 6 = 64,5781643...

நீங்கள் பார்க்க முடியும் என, தோராயமான துல்லியம் மிகவும் ஏற்றுக்கொள்ளத்தக்கது.

பின்வரும் உருவத்தைக் கவனியுங்கள்:

இது ஒரு குறிப்பிட்ட செயல்பாட்டை y = f(x) சித்தரிக்கிறது, இது புள்ளி a இல் வேறுபடுகிறது. ஆய (a; f(a)) உடன் புள்ளி M குறிக்கப்பட்டுள்ளது. ஒரு செகண்ட் எம்ஆர் வரைபடத்தின் தன்னிச்சையான புள்ளி P(a + ∆x; f(a + ∆x)) மூலம் வரையப்படுகிறது.

இப்போது புள்ளி P ஆனது வரைபடத்துடன் M புள்ளிக்கு மாற்றப்பட்டால், MR என்ற நேர்கோடு M புள்ளியை சுற்றி சுழலும். இந்த நிலையில், ∆x பூஜ்ஜியமாக இருக்கும். இங்கிருந்து நாம் ஒரு செயல்பாட்டின் வரைபடத்திற்கு ஒரு தொடுகோடு வரையறையை உருவாக்கலாம்.

ஒரு செயல்பாட்டின் வரைபடத்தின் தொடுகோடு

ஒரு செயல்பாட்டின் வரைபடத்திற்கான தொடுகோடு என்பது, வாதத்தின் அதிகரிப்பு பூஜ்ஜியமாக இருப்பதால், செகண்டின் வரையறுக்கப்பட்ட நிலையாகும். x0 புள்ளியில் f செயல்பாட்டின் வழித்தோன்றல் இருப்பது வரைபடத்தின் இந்த புள்ளியில் உள்ளது என்பதை புரிந்து கொள்ள வேண்டும். தொடுகோடுஅவனுக்கு.

இந்த வழக்கில், தொடுகோட்டின் கோணக் குணகம் இந்தச் செயல்பாட்டின் வழித்தோன்றலுக்குச் சமமாக இருக்கும். இது வழித்தோன்றலின் வடிவியல் பொருள். புள்ளி x0 இல் வேறுபடுத்தக்கூடிய ஒரு சார்பின் வரைபடத்திற்கான தொடுகோடு என்பது புள்ளியின் வழியாக செல்லும் ஒரு குறிப்பிட்ட நேர்கோடு (x0;f(x0)) மற்றும் ஒரு கோண குணகம் f'(x0).

தொடு சமன்பாடு

புள்ளி A(x0; f(x0)) சில சார்பு f இன் வரைபடத்திற்கு தொடுகோட்டின் சமன்பாட்டைப் பெற முயற்சிப்போம். சாய்வு k உடன் நேர்கோட்டின் சமன்பாடு உள்ளது அடுத்த பார்வை:

எங்கள் சாய்வு குணகம் வழித்தோன்றலுக்கு சமமாக இருப்பதால் f'(x0), பின்னர் சமன்பாடு பின்வரும் வடிவத்தை எடுக்கும்: y = f'(x0)*x + b.

இப்போது b இன் மதிப்பைக் கணக்கிடுவோம். இதைச் செய்ய, செயல்பாடு புள்ளி A வழியாக செல்கிறது என்ற உண்மையைப் பயன்படுத்துகிறோம்.

f(x0) = f'(x0)*x0 + b, இங்கிருந்து நாம் b ஐ வெளிப்படுத்துகிறோம் மற்றும் b = f(x0) - f'(x0)*x0 ஐப் பெறுகிறோம்.

இதன் விளைவாக வரும் மதிப்பை நாம் தொடுகோடு சமன்பாட்டில் மாற்றுகிறோம்:

y = f'(x0)*x + b = f'(x0)*x + f(x0) - f'(x0)*x0 = f(x0) + f'(x0)*(x - x0).

y = f(x0) + f’(x0)*(x - x0).

பின்வரும் எடுத்துக்காட்டைக் கவனியுங்கள்: x = 2 என்ற புள்ளியில் f(x) = x 3 - 2*x 2 + 1 செயல்பாட்டின் வரைபடத்திற்கான தொடுகோட்டின் சமன்பாட்டைக் கண்டறியவும்.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f’(x) = 3*x 2 - 4*x.

4. f’(x0) = f’(2) = 3*2 2 - 4*2 = 4.

5. பெறப்பட்ட மதிப்புகளை தொடுகோடு சூத்திரத்தில் மாற்றவும், நாம் பெறுகிறோம்: y = 1 + 4*(x - 2). அடைப்புக்குறிகளைத் திறந்து, ஒத்த சொற்களைக் கொண்டு வரும்போது நமக்குக் கிடைக்கும்: y = 4*x - 7.

பதில்: y = 4*x - 7.

தொடுகோடு சமன்பாட்டை உருவாக்குவதற்கான பொதுவான திட்டம் y = f(x) செயல்பாட்டின் வரைபடத்திற்கு:

1. x0 ஐ தீர்மானிக்கவும்.

2. f(x0) கணக்கிடவும்.

3. f'(x) கணக்கிடு