Online-laskin. Toiminnon kuvaajan suoran tangentin yhtälö tietyssä pisteessä

Osoittaa derivaatan etumerkin ja funktion monotonisuuden luonteen välisen yhteyden.

Ole erittäin varovainen seuraavissa asioissa. Katso, aikataulu MITÄ sinulle annetaan! Funktio tai sen johdannainen

Jos annetaan derivaatan kaavio, niin meitä kiinnostavat vain funktiomerkit ja nollat. Meitä ei periaatteessa kiinnosta mikään "kukkula" tai "ontto"!

Tehtävä 1.

Kuvassa on kaavio välille määritetystä funktiosta. Määritä niiden kokonaislukupisteiden lukumäärä, joissa funktion derivaatta on negatiivinen.

Ratkaisu:

Kuvassa pienenevän toiminnon alueet on korostettu värillä:

Nämä funktion pienenevät alueet sisältävät 4 kokonaislukuarvoa.

Tehtävä 2.

Kuvassa on kaavio välille määritetystä funktiosta. Selvitä niiden pisteiden lukumäärä, joissa funktion kaavion tangentti on yhdensuuntainen suoran kanssa tai osuu yhteen sen kanssa.

Ratkaisu:

Kun funktion kaavion tangentti on yhdensuuntainen (tai osuu yhteen) suoran kanssa (tai, mikä on sama asia), jolla on kaltevuus , on yhtä suuri kuin nolla, silloin tangentilla on kulmakerroin .

Tämä puolestaan ​​tarkoittaa, että tangentti on yhdensuuntainen akselin kanssa, koska kaltevuus on tangentin kaltevuuskulman tangentti akseliin nähden.

Siksi löydämme kaaviosta ääripisteet (maksimi- ja minimipisteet) - juuri näissä pisteissä kuvaajan tangentit ovat yhdensuuntaisia ​​akselin kanssa.

Tällaisia ​​pisteitä on 4.

Tehtävä 3.

Kuvassa on kaavio välille määritellyn funktion derivaatasta. Selvitä niiden pisteiden lukumäärä, joissa funktion kaavion tangentti on yhdensuuntainen suoran kanssa tai osuu yhteen sen kanssa.

Ratkaisu:

Koska funktion kaavion tangentti on yhdensuuntainen (tai osuu yhteen) suoran kanssa, jolla on kaltevuus, tangentilla on myös kulmakerroin.

Tämä puolestaan ​​tarkoittaa, että kosketuspisteissä.

Siksi tarkastelemme kuinka monen kaavion pisteen ordinaatit ovat yhtä suuria kuin .

Kuten näet, tällaisia ​​kohtia on neljä.

Tehtävä 4.

Kuvassa on kaavio välille määritetystä funktiosta. Etsi pisteiden lukumäärä, joissa funktion derivaatta on 0.

Ratkaisu:

Derivaata on yhtä suuri kuin nolla ääripisteissä. Meillä on niitä 4:

Tehtävä 5.

Kuvassa on kaavio funktiosta ja 11 pisteestä x-akselilla:. Kuinka monessa näistä pisteistä funktion derivaatta on negatiivinen?

Ratkaisu:

Laskevan funktion aikaväleillä sen derivaatta saa negatiiviset arvot. Ja funktio pienenee pisteissä. Tällaisia ​​pisteitä on 4.

Tehtävä 6.

Kuvassa on kaavio välille määritetystä funktiosta. Etsi funktion ääripisteiden summa.

Ratkaisu:

Äärimmäiset pisteet– nämä ovat maksimipisteet (-3, -1, 1) ja vähimmäispisteet (-2, 0, 3).

Ääripisteiden summa: -3-1+1-2+0+3=-2.

Tehtävä 7.

Kuvassa on kaavio välille määritellyn funktion derivaatasta. Etsi funktion kasvuvälit. Ilmoita vastauksessasi näiden välien sisältämien kokonaislukupisteiden summa.

Ratkaisu:

Kuvassa on korostettu intervallit, joissa funktion derivaatta on ei-negatiivinen.

Pienellä kasvavalla välillä ei ole kokonaislukupisteitä, vaan kasvavalla välillä on neljä kokonaislukuarvoa: , , ja .

Niiden summa:

Tehtävä 8.

Kuvassa on kaavio välille määritellyn funktion derivaatasta. Etsi funktion kasvuvälit. Ilmoita vastauksessasi niistä suurimman pituus.

Ratkaisu:

Kuvassa kaikki intervallit, joilla derivaatta on positiivinen, on korostettu värein, mikä tarkoittaa, että funktio itse kasvaa näillä intervalleilla.

Niistä suurimman pituus on 6.

Tehtävä 9.

Kuvassa on kaavio välille määritellyn funktion derivaatasta. Missä segmentin kohdassa se saa suurimman arvon?

Ratkaisu:

Katsotaan kuinka kaavio käyttäytyy segmentillä, mistä olemme kiinnostuneita vain johdannaisen merkki .

Derivaatan etumerkki on miinus, koska tämän segmentin kuvaaja on akselin alapuolella.

Olkoon annettu funktio f, jolla on jossain pisteessä x 0 äärellinen derivaatta f (x 0). Sitten pisteen (x 0 ; f (x 0)) läpi kulkevaa suoraa, jolla on kulmakerroin f ’(x 0), kutsutaan tangentiksi.

Mitä tapahtuu, jos derivaatta ei ole olemassa pisteessä x 0? Vaihtoehtoja on kaksi:

1. Graafilla ei myöskään ole tangenttia. Klassinen esimerkki- funktio y = |x | pisteessä (0; 0).
2. Tangentti muuttuu pystysuoraksi. Tämä pätee esimerkiksi funktiolle y = arcsin x pisteessä (1; π /2).

Tangenttiyhtälö

Mikä tahansa ei-pystysuora viiva saadaan yhtälöllä muotoa y = kx + b, missä k on kaltevuus. Tangentti ei ole poikkeus, ja sen yhtälön luomiseksi jossain kohdassa x 0 riittää, että tietää funktion ja derivaatan arvo tässä pisteessä.

Olkoon siis annettu funktio y = f (x), jolla on derivaatta y = f ’(x) segmentillä. Sitten mihin tahansa pisteeseen x 0 ∈ (a ; b) voidaan piirtää tangentti tämän funktion kuvaajalle, joka saadaan yhtälöstä:

y = f ’(x 0) (x − x 0) + f (x 0)

Tässä f ’(x 0) on derivaatan arvo pisteessä x 0 ja f (x 0) on itse funktion arvo.

Tehtävä. Annettu funktio y = x 3 . Kirjoita yhtälö tämän funktion kaavion tangentille pisteessä x 0 = 2.

Tangenttiyhtälö: y = f ’(x 0) · (x − x 0) + f (x 0). Piste x 0 = 2 on meille annettu, mutta arvot f (x 0) ja f '(x 0) on laskettava.

Ensin selvitetään funktion arvo. Täällä kaikki on helppoa: f (x 0) = f (2) = 2 3 = 8;
Etsitään nyt derivaatta: f '(x) = (x 3)' = 3x 2;
Korvaamme x 0 = 2 derivaatta: f '(x 0) = f '(2) = 3 2 2 = 12;
Yhteensä saadaan: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Tämä on tangenttiyhtälö.

Tehtävä. Kirjoita yhtälö funktion f (x) = 2sin x + 5 kaavion tangentille pisteessä x 0 = π /2.

Tällä kertaa emme kuvaile jokaista toimintaa yksityiskohtaisesti - osoitamme vain tärkeimmät vaiheet. Meillä on:

f (x 0) = f (π/2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f '(x) = (2sin x + 5)' = 2cos x;
f '(x 0) = f '(π /2) = 2cos (π /2) = 0;

Tangenttiyhtälö:

y = 0 · (x − π /2) + 7 ⇒ y = 7

SISÄÄN jälkimmäinen tapaus suora viiva osoittautui vaakasuoraksi, koska sen kulmakerroin k = 0. Tässä ei ole mitään väärää - törmäsimme juuri ääripisteeseen.

Artikkeli tarjoaa yksityiskohtaisen selityksen johdannaisen määritelmistä, geometrisesta merkityksestä graafiset symbolit. Tangenttiviivan yhtälöä tarkastellaan esimerkein, 2. kertaluvun käyrien tangentin yhtälöt löytyvät.

Yandex.RTB R-A-339285-1 Määritelmä 1

Suoran y = k x + b kaltevuuskulmaa kutsutaan kulmaksi α, joka mitataan x-akselin positiivisesta suunnasta suoralle y = k x + b positiivisessa suunnassa.

Kuvassa x-suunta on merkitty vihreällä nuolella ja vihreällä kaarella ja kaltevuuskulma punaisella kaarella. Sininen viiva viittaa suoraan viivaan.

Määritelmä 2

Suoran y = k x + b jyrkkyyttä kutsutaan numeeriseksi kertoimeksi k.

Kulmakerroin on yhtä suuri kuin suoran tangentti, toisin sanoen k = t g α.

• Suoran viivan kaltevuuskulma on 0 vain, jos se on yhdensuuntainen x:n suhteen ja kaltevuus on yhtä suuri kuin nolla, koska nollan tangentti on yhtä suuri kuin 0. Tämä tarkoittaa, että yhtälön muoto on y = b.
• Jos suoran kaltevuuskulma y = k x + b on terävä, niin ehdot 0 täyttyvät< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается positiivinen luku, koska tangentin arvo täyttää ehdon t g α > 0, ja kaaviossa on kasvua.
• Jos α = π 2, niin suoran sijainti on kohtisuorassa x:ää vastaan. Yhtälö määritellään kaavalla x = c, jolloin arvo c on reaaliluku.
• Jos suoran y = k x + b kaltevuuskulma on tylppä, niin se vastaa ehtoja π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Sekantti on suora, joka kulkee funktion f (x) 2 pisteen kautta. Toisin sanoen sekantti on suora viiva, joka vedetään minkä tahansa kahden pisteen läpi tietyn funktion kaaviossa.

Kuvasta näkyy, että A B on sekantti ja f (x) on musta käyrä, α on punainen kaari, joka osoittaa sekantin kaltevuuskulman.

Kun suoran kulmakerroin on yhtä suuri kuin kaltevuuskulman tangentti, on selvää, että suorakulmaisen kolmion tangentti A B C löytyy vastakkaisen sivun suhteesta viereiseen.

Määritelmä 4

Saamme kaavan lomakkeen sekantin löytämiseksi:

k = t g α = B C A C = f (x B) - f x A x B - x A, missä pisteiden A ja B abskissat ovat arvot x A, x B ja f (x A), f (x) B) ovat arvofunktiot näissä pisteissä.

Ilmeisesti sekantin kulmakerroin määritetään yhtälöllä k = f (x B) - f (x A) x B - x A tai k = f (x A) - f (x B) x A - x B , ja yhtälö on kirjoitettava muodossa y = f (x B) - f (x A) x B - x A x - x A + f (x A) tai
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

Sekantti jakaa graafin visuaalisesti kolmeen osaan: pisteen A vasemmalla puolella, pisteestä A paikkaan B, pisteen B oikealla puolella. Alla olevasta kuvasta näkyy, että kolme sekanttia katsotaan sattumanvaraisiksi, eli ne on asetettu käyttämällä samanlainen yhtälö.

Määritelmän mukaan on selvää, että suora ja sen sekantti ovat tässä tapauksessa samat.

Sekantti voi leikata tietyn funktion kuvaajan useita kertoja. Jos sekantille on yhtälö muotoa y = 0, niin siniaallon leikkauspisteiden määrä on ääretön.

Määritelmä 5

Tangentti funktion f (x) kuvaajalle pisteessä x 0 ; f (x 0) on tietyn pisteen x 0 kautta kulkeva suora; f (x 0), jossa on segmentti, jolla on useita x-arvoja lähellä x 0.

Esimerkki 1

Katsotaanpa tarkemmin alla olevaa esimerkkiä. Tällöin on selvää, että funktion y = x + 1 määrittelemää suoraa pidetään y = 2 x:n tangenttina koordinaattipisteessä (1; 2). Selvyyden vuoksi on tarpeen tarkastella kaavioita, joiden arvot ovat lähellä (1; 2). Funktio y = 2 x näkyy mustana, sininen viiva on tangenttiviiva ja punainen piste on leikkauspiste.

Ilmeisesti y = 2 x sulautuu linjaan y = x + 1.

Tangentin määrittämiseksi tulee ottaa huomioon tangentin A B käyttäytyminen pisteen B lähestyessä pistettä A äärettömästi. Selvyyden vuoksi esitämme piirustuksen.

Sekantti A B, joka on merkitty sinisellä viivalla, pyrkii itse tangentin asentoon, ja sekantin kaltevuuskulma α alkaa taipua itse tangentin kaltevuuskulmaan α x.

Määritelmä 6

Funktion y = f (x) kaavion tangenttia pisteessä A pidetään sekantin A B raja-asemana, koska B pyrkii A:han, eli B → A.

Siirrytään nyt tarkastelemaan funktion derivaatan geometrista merkitystä pisteessä.

Siirrytään tarkastelemaan funktion f (x) sekanttia A B, jossa A ja B koordinaatteilla x 0, f (x 0) ja x 0 + ∆ x, f (x 0 + ∆ x) ja ∆ x on ilmaistaan ​​argumentin lisäyksenä. Nyt funktio saa muotoa ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Selvyyden vuoksi annetaan esimerkki piirroksesta.

Mietitäänpä tulosta suorakulmainen kolmio A B C. Ratkaisemiseen käytetään tangentin määritelmää, eli saadaan relaatio ∆ y ∆ x = t g α . Tangentin määritelmästä seuraa, että lim ∆ x → 0 ∆ y ∆ x = t g α x . Pisteen derivaatan säännön mukaan derivaatta f (x) pisteessä x 0 kutsutaan funktion inkrementin ja argumentin inkrementin suhteen rajaksi, missä ∆ x → 0 , niin se merkitään f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

Tästä seuraa, että f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, missä k x on merkitty tangentin kulmakertoimeksi.

Toisin sanoen havaitsemme, että f ' (x) voi olla pisteessä x 0, ja kuten funktion tietyn kaavion tangentti tangenttipisteessä, joka on yhtä suuri kuin x 0, f 0 (x 0), jossa tangentin jyrkkyys pisteessä on yhtä suuri kuin derivaatta pisteessä x 0 . Sitten saadaan, että k x = f " (x 0) .

Geometrinen merkitys funktion derivaatta pisteessä on se, että on annettu käsite graafin tangentin olemassaolosta samassa pisteessä.

Minkä tahansa suoran yhtälön kirjoittamiseksi tasolle tarvitaan kulmakerroin sen pisteen kanssa, jonka läpi se kulkee. Sen merkintä on x 0 leikkauspisteessä.

Funktion y = f (x) kaavion tangenttiyhtälö pisteessä x 0, f 0 (x 0) on muodossa y = f "(x 0) x - x 0 + f (x 0).

Tämä tarkoittaa, että derivaatan f "(x 0) lopullinen arvo voi määrittää tangentin sijainnin, eli pystysuorassa, mikäli lim x → x 0 + 0 f "(x) = ∞ ja lim x → x 0 - 0 f "(x ) = ∞ tai poissaolo ollenkaan ehdolla lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .

Tangentin sijainti riippuu sen kulmakertoimen arvosta k x = f "(x 0). Kun se on yhdensuuntainen o x -akselin kanssa, saadaan, että k k = 0, kun se on yhdensuuntainen o y:n kanssa - k x = ∞, ja sen muoto tangenttiyhtälö x = x 0 kasvaa kun k x > 0, pienenee kun k x< 0 .

Esimerkki 2

Muodosta yhtälö funktion y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 kaavion tangentille koordinaattipisteessä (1; 3) ja määritä kaltevuuskulma.

Ratkaisu

Ehdolla meillä on, että funktio on määritelty kaikille reaaliluvuille. Havaitsemme, että ehdon (1; 3) määrittämien koordinaattien piste on tangenttipiste, jolloin x 0 = - 1, f (x 0) = - 3.

On tarpeen löytää derivaatta pisteestä, jonka arvo on -1. Me ymmärrämme sen

y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

F'(x):n arvo tangenttipisteessä on tangentin kulmakerroin, joka on yhtä suuri kuin kulmakertoimen tangentti.

Sitten k x = t g α x = y " (x 0) = 3 3

Tästä seuraa, että α x = a r c t g 3 3 = π 6

Vastaus: tangenttiyhtälö saa muodon

y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

Selvyyden vuoksi annamme esimerkin graafisessa kuvassa.

Mustaa väriä käytetään alkuperäisen funktion kaaviossa, Sininen väri– tangentin kuva, punainen piste – kosketuspiste. Oikealla oleva kuva näyttää suurennettuna.

Esimerkki 3

Määritä tietyn funktion kaavion tangentin olemassaolo
y = 3 · x - 1 5 + 1 pisteessä, jonka koordinaatit (1 ; 1) . Kirjoita yhtälö ja määritä kaltevuuskulma.

Ratkaisu

Ehdolla meillä on, että tietyn funktion määritelmäalueen katsotaan olevan kaikkien reaalilukujen joukko.

Siirrytään johdannaisen etsimiseen

y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

Jos x 0 = 1, niin f' (x) on määrittelemätön, mutta rajat kirjoitetaan muodossa lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ ja lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , mikä tarkoittaa pystytangentin olemassaolo pisteessä (1; 1).

Vastaus: yhtälö on muodossa x = 1, jossa kaltevuuskulma on yhtä suuri kuin π 2.

Selvyyden vuoksi kuvataan se graafisesti.

Esimerkki 4

Etsi funktion y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 kaaviosta pisteet, missä

1. Tangenttia ei ole;
2. Tangentti on yhdensuuntainen x:n kanssa;
3. Tangentti on yhdensuuntainen suoran y = 8 5 x + 4 kanssa.

Ratkaisu

On tarpeen kiinnittää huomiota määritelmän laajuuteen. Ehdolla meillä on, että funktio on määritelty kaikkien reaalilukujen joukossa. Laajennamme moduulia ja ratkaisemme järjestelmän intervalleilla x ∈ - ∞ ; 2 ja [-2; + ∞) . Me ymmärrämme sen

y = -1 15 x 3 + 18 x 2 + 105 x + 176, x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)

On tarpeen erottaa toiminto. Meillä se on

y" = -1 15 x 3 + 18 x 2 + 105 x + 176", x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35), x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)

Kun x = − 2, niin derivaatta ei ole olemassa, koska yksipuoliset rajat eivät ole samat tässä pisteessä:

lim x → - 2 - 0 y " (x) = raja x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = raja x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

Laskemme funktion arvon pisteessä x = - 2, josta saamme sen

1. y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, eli tangentti pisteessä ( - 2; - 2) ei ole olemassa.
2. Tangentti on yhdensuuntainen x:n kanssa, kun kaltevuus on nolla. Silloin k x = t g α x = f "(x 0). Eli on tarpeen löytää sellaisen x:n arvot, kun funktion derivaatta muuttaa sen nollaksi. Eli f':n arvot (x) ovat tangenttipisteitä, joissa tangentti on yhdensuuntainen x:n kanssa.

Kun x ∈ - ∞ ; - 2, sitten - 1 5 (x 2 + 12 x + 35) = 0, ja x ∈ (- 2; + ∞) saa 1 5 (x 2 - 4 x + 3) = 0.

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

Laske vastaavat funktioarvot

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

Tästä syystä - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 katsotaan funktiokaavion vaadituiksi pisteiksi.

Harkitsemme graafinen kuva ratkaisuja.

Musta viiva on funktion kaavio, punaiset pisteet ovat tangenttipisteitä.

1. Kun suorat ovat yhdensuuntaiset, kulmakertoimet ovat yhtä suuret. Sitten on tarpeen etsiä funktiokaaviosta pisteitä, joissa kaltevuus on yhtä suuri kuin arvo 8 5. Tätä varten sinun on ratkaistava yhtälö, jonka muoto on y "(x) = 8 5. Sitten, jos x ∈ - ∞; - 2, saadaan, että - 1 5 (x 2 + 12 x + 35) = 8 5, ja jos x ∈ ( - 2 ; + ∞), niin 1 5 (x 2 - 4 x + 3) = 8 5.

Ensimmäisellä yhtälöllä ei ole juuria, koska diskriminantti alle nolla. Kirjoitetaan se ylös

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

Toisella yhtälöllä on siis kaksi todellista juuria

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

Siirrytään funktion arvojen etsimiseen. Me ymmärrämme sen

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Pisteet arvoilla - 1; 4 15, 5; 8 3 ovat pisteet, joissa tangentit ovat yhdensuuntaisia ​​suoran y = 8 5 x + 4 kanssa.

Vastaus: musta viiva – funktion kuvaaja, punainen viiva – y:n käyrä = 8 5 x + 4, sininen viiva – tangentit pisteissä - 1; 4 15, 5; 8 3.

Annetuille funktioille voi olla ääretön määrä tangentteja.

Esimerkki 5

Kirjoita funktion y = 3 cos 3 2 x - π 4 - 1 3 kaikkien käytettävissä olevien tangenttien yhtälöt, jotka sijaitsevat kohtisuorassa suoraa y = - 2 x + 1 2 vastaan.

Ratkaisu

Tangenttiyhtälön laatimiseksi on tarpeen löytää tangentin pisteen kerroin ja koordinaatit suorien kohtisuoran ehdon perusteella. Määritelmä on seuraava: kulmakertoimien tulo, jotka ovat kohtisuorassa suoria viivoja vastaan, on yhtä suuri kuin -1, eli kirjoitettuna k x · k ⊥ = - 1. Ehdosta saadaan, että kulmakerroin sijaitsee kohtisuorassa suoraa vastaan ​​ja on yhtä suuri kuin k ⊥ = - 2, jolloin k x = - 1 k ⊥ = - 1 - 2 = 1 2.

Nyt sinun on löydettävä kosketuspisteiden koordinaatit. Sinun on löydettävä x ja sitten sen arvo tietylle funktiolle. Huomaa, että derivaatan geometrisesta merkityksestä pisteessä
x 0 saadaan, että k x = y "(x 0). Tästä yhtälöstä saamme x:n arvot kosketuspisteille.

Me ymmärrämme sen

y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 sin 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9

Tämä trigonometrinen yhtälö käytetään tangenttipisteiden ordinaattien laskemiseen.

3 2 x 0 - π 4 = arc sin - 1 9 + 2 πk tai 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk tai 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - arc sin 1 9 + 2 πk tai x 0 = 2 3 5 π 4 + arc sin 1 9 + 2 πk , k ∈ Z

Z on joukko kokonaislukuja.

x yhteyspisteitä on löydetty. Nyt sinun on siirryttävä y:n arvojen etsimiseen:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 tai y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 tai y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 tai y 0 = - 4 5 + 1 3

Tästä saadaan, että 2 3 π 4 - arc sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + arc sin 1 9 + 2 πk ; - 4 5 + 1 3 ovat kosketuspisteitä.

Vastaus: tarvittavat yhtälöt kirjoitetaan muodossa

y = 1 2 x - 2 3 π 4 - arc sin 1 9 + 2 πk + 4 5 - 1 3, y = 1 2 x - 2 3 5 π 4 + arc sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

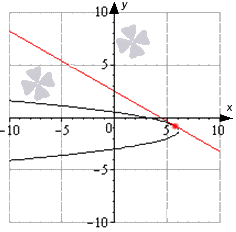
Visuaalista esitystä varten harkitse koordinaattiviivan funktiota ja tangenttia.

Kuvasta näkyy, että funktio sijaitsee intervallilla [-10; 10 ], jossa musta suora on funktion kuvaaja, siniset viivat– tangentit, jotka sijaitsevat kohtisuorassa tiettyä muotoa y = - 2 x + 1 2 olevaa suoraa vastaan. Punaiset pisteet ovat kosketuspisteitä.

Toisen asteen käyrien kanoniset yhtälöt eivät ole yksiarvoisia funktioita. Niiden tangenttiyhtälöt kootaan tunnettujen kaavioiden mukaisesti.

Tangentti ympyrää

Ympyrän määrittäminen, jonka keskipiste on pisteessä x c e n t e r ; y c e n t e r ja säde R, käytä kaavaa x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 .

Tämä yhtäläisyys voidaan kirjoittaa kahden funktion liitoksi:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

Ensimmäinen toiminto sijaitsee ylhäällä ja toinen alhaalla, kuten kuvassa.

Ympyrän yhtälön laatiminen pisteessä x 0; y 0 , joka sijaitsee ylemmässä tai alemmassa puoliympyrässä, sinun tulee löytää muotoa y = R 2 - x - x c e n t e r 2 + y c e n t e r tai y = - R 2 - x - x c e n t e r 2 + olevan funktion kaavion yhtälö. y c e n t e r osoitetussa kohdassa.

Kun pisteissä x c e n t e r ; y c e n t e r + R ja x c e n t e r; y c e n t e r - R tangentit voidaan antaa yhtälöillä y = y c e n t e r + R ja y = y c e n t e r - R ja pisteissä x c e n t e r + R ; y c e n t e r ja
x c e n t e r-R; y c e n t e r on yhdensuuntainen o y:n kanssa, jolloin saadaan yhtälöt muotoa x = x c e n t e r + R ja x = x c e n t e r - R .

Tangentti ellipsille

Kun ellipsin keskipiste on x c e n t e r ; y c e n t e r puoliakseleilla a ja b, niin se voidaan määrittää yhtälöllä x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.

Ellipsi ja ympyrä voidaan merkitä yhdistämällä kaksi funktiota, nimittäin ylempi ja alempi puoliellipsi. Sitten saamme sen

y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

Jos tangentit sijaitsevat ellipsin kärjessä, ne ovat yhdensuuntaisia ​​x:n tai y:n suhteen. Harkitse alla olevaa kuvaa selvyyden vuoksi.

Esimerkki 6

Kirjoita ellipsin tangentin yhtälö x - 3 2 4 + y - 5 2 25 = 1 pisteissä, joiden x arvo on yhtä suuri kuin x = 2.

Ratkaisu

On tarpeen löytää tangenttipisteet, jotka vastaavat arvoa x = 2. Korvaamme olemassa olevan ellipsin yhtälön ja löydämme sen

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

Sitten 2; 5 3 2 + 5 ja 2; - 5 3 2 + 5 ovat tangenttipisteitä, jotka kuuluvat ylempään ja alempaan puoliellipsiin.

Jatketaan ellipsin yhtälön löytämiseen ja ratkaisemiseen y:n suhteen. Me ymmärrämme sen

x - 3 2 4 + y - 5 2 25 = 1 v - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 v - 5 = ± 5 1 - x - 3 2 4 v = 5 ± 5 2 4 - x - 3 2

Ilmeisesti ylempi puoliellipsi määritellään funktiolla, jonka muoto on y = 5 + 5 2 4 - x - 3 2, ja alempi puoliellipsi y = 5 - 5 2 4 - x - 3 2.

Luodaan yhtälö funktion kaavion tangentille pisteessä vakioalgoritmin avulla. Kirjoitetaan, että ensimmäisen tangentin yhtälö pisteessä 2; 5 3 2 + 5 näyttää siltä

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

Huomaamme, että yhtälö toisen tangentin arvolla pisteessä
2; - 5 3 2 + 5 saa muodon

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Graafisesti tangentit on merkitty seuraavasti:

Tangentti hyperbolille

Kun hyperbelin keskus on x c e n t e r :ssä; y c e n t e r ja kärjet x c e n t e r + α ; y c e n t e r ja x c e n t e r - α ; y c e n t e r , epäyhtälö x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 tapahtuu, jos pisteillä x c e n t e r ; y c e n t e r + b ja x c e n t e r ; y c e n t e r - b , määritetään sitten käyttämällä epäyhtälöä x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Hyperbola voidaan esittää muodon kahtena yhdistettynä funktiona

y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r tai y = b a · (x - x c e r e) n = - b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r

Ensimmäisessä tapauksessa tangentit ovat yhdensuuntaisia ​​y:n kanssa ja toisessa samansuuntaisia ​​x:n kanssa.

Tästä seuraa, että hyperbelin tangentin yhtälön löytämiseksi on selvitettävä, mihin funktioon tangenttipiste kuuluu. Tämän määrittämiseksi on välttämätöntä korvata yhtälöt ja tarkistaa identiteetti.

Esimerkki 7

Kirjoita yhtälö hyperbolin tangentille x - 3 2 4 - y + 3 2 9 = 1 pisteessä 7; - 3 3 - 3 .

Ratkaisu

On tarpeen muuttaa ratkaisutietue hyperbelin löytämiseksi kahdella funktiolla. Me ymmärrämme sen

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 ja y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

On tarpeen tunnistaa mihin funktioon tietty piste koordinaatilla 7 kuuluu; - 3 3 - 3 .

Ilmeisesti ensimmäisen funktion tarkistamiseen tarvitaan y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, jolloin piste ei kuulu kuvaajaan, koska tasa-arvo ei päde.

Toiselle funktiolle on, että y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, mikä tarkoittaa, että piste kuuluu annettuun kuvaajaan. Täältä sinun pitäisi löytää rinne.

Me ymmärrämme sen

y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

Vastaus: tangenttiyhtälö voidaan esittää muodossa

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

Se on selvästi kuvattu näin:

Tangentti paraabelille

Jos haluat luoda yhtälön paraabelin tangentille y = a x 2 + b x + c pisteessä x 0, y (x 0), sinun on käytettävä standardialgoritmia, jolloin yhtälö saa muotoa y = y "(x) 0) x - x 0 + y ( x 0). Tällainen tangentti kärjessä on x:n suuntainen.

Sinun tulisi määritellä paraabeli x = a y 2 + b y + c kahden funktion liitoksi. Siksi meidän on ratkaistava yhtälö y:lle. Me ymmärrämme sen

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

Graafisesti kuvattu näin:

Selvittääksesi kuuluuko piste x 0, y (x 0) funktioon, etene varovasti vakioalgoritmin mukaan. Tällainen tangentti on yhdensuuntainen o y:n kanssa suhteessa paraabeliin.

Esimerkki 8

Kirjoita graafin x - 2 y 2 - 5 y + 3 tangentin yhtälö, kun meillä on tangenttikulma 150 °.

Ratkaisu

Aloitamme ratkaisun esittämällä paraabelin kahtena funktiona. Me ymmärrämme sen

2 v 2 - 5 v + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

Kulmakertoimen arvo on yhtä suuri kuin derivaatan arvo tämän funktion pisteessä x 0 ja on yhtä suuri kuin kaltevuuskulman tangentti.

Saamme:

k x = y "(x 0) = t g α x = t g 150 ° = - 1 3

Tästä määritämme kosketuspisteiden x-arvon.

Ensimmäinen funktio kirjoitetaan muodossa

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Varsinaisia ​​juuria ei tietenkään ole, koska saimme negatiivisen arvon. Päättelemme, että tällaiselle funktiolle ei ole tangenttia, jonka kulma on 150°.

Toinen funktio kirjoitetaan muodossa

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

Meillä on, että kosketuspisteet ovat 23 4 ; - 5 + 3 4 .

Vastaus: tangenttiyhtälö saa muodon

y = -1 3 x - 23 4 + - 5 + 3 4

Kuvataan se graafisesti näin:

Jos huomaat tekstissä virheen, korosta se ja paina Ctrl+Enter

Videotunti "Funktion kaavion tangentin yhtälö" osoittaa koulutusmateriaalia hallitsemaan aihetta. Esitetyn videotunnin aikana teoreettista materiaalia, tarvitaan funktion kaavion tangentin yhtälön käsitteen muodostamiseen tietyssä pisteessä, algoritmi tällaisen tangentin löytämiseksi, kuvataan esimerkkejä ongelmien ratkaisemisesta tutkitun teoreettisen materiaalin avulla.

Video-opetusohjelmassa käytetään menetelmiä, jotka parantavat materiaalin selkeyttä. Esitys sisältää piirroksia, kaavioita, tärkeitä äänikommentteja, animaatioita, korostuksia ja muita työkaluja.

Videotunti alkaa oppitunnin aiheen esittelyllä ja kuvalla jonkin funktion y=f(x) kaavion tangentista pisteessä M(a;f(a)). Tiedetään, että kaavioon piirretyn tangentin kulmakerroin tietyssä pisteessä on yhtä suuri kuin funktion f΄(a) derivaatta tässä pisteessä. Myös algebran kurssista tunnemme suoran y=kx+m yhtälön. Ongelman ratkaisu tangenttiyhtälön löytämiseksi pisteestä on esitetty kaavamaisesti, mikä pelkistyy kertoimien k, m löytämiseen. Kun tiedämme funktion kuvaajaan kuuluvan pisteen koordinaatit, voidaan löytää m korvaamalla koordinaattiarvo tangenttiyhtälöön f(a)=ka+m. Siitä saadaan m=f(a)-ka. Näin ollen, kun tiedetään derivaatan arvo tietyssä pisteessä ja pisteen koordinaatit, voimme esittää tangenttiyhtälön tällä tavalla y=f(a)+f΄(a)(x-a).

Seuraavassa on esimerkki tangenttiyhtälön muodostamisesta kaavion mukaisesti. Kun funktio y=x 2 , x=-2. Ottaen a=-2, löydämme funktion arvon annetusta pisteestä f(a)= f(-2)=(-2) 2 =4. Määritetään funktion derivaatta f΄(x)=2x. Tässä vaiheessa derivaatta on f΄(a)= f΄(-2)=2·(-2)=-4. Yhtälön muodostamiseksi löydettiin kaikki kertoimet a=-2, f(a)=4, f΄(a)=-4, joten tangenttiyhtälö on y=4+(-4)(x+2). Yksinkertaistamalla yhtälöä saadaan y = -4-4x.

Seuraava esimerkki ehdottaa yhtälön muodostamista tangentille funktion y=tgx kaavion origossa. Tietyssä pisteessä a=0, f(0)=0, f΄(x)=1/cos 2 x, f΄(0)=1. Joten tangenttiyhtälö näyttää y=x.

Yleistyksenä funktion kuvaajalle tietyssä kohdassa tangentin yhtälön muodostamisprosessi formalisoidaan neljästä vaiheesta koostuvan algoritmin muodossa:

• Kirjoita tangenttipisteen abskissalle merkintä a;
• f(a) lasketaan;
• f΄(x) määritetään ja f΄(a) lasketaan. Löydetyt arvot a, f(a), f΄(a) korvataan tangenttiyhtälön kaavalla y=f(a)+f΄(a)(x-a).

Esimerkki 1 harkitsee tangenttiyhtälön muodostamista funktion y=1/x kuvaajaan pisteessä x=1. Ongelman ratkaisemiseksi käytämme algoritmia. Tietylle funktiolle pisteessä a=1 funktion arvo f(a)=-1. Toiminnon f΄(x)=1/x 2 derivaatta. Pisteessä a=1 derivaatta f΄(a)= f΄(1)=1. Saatujen tietojen avulla laaditaan tangenttiyhtälö y=-1+(x-1) tai y=x-2.

Esimerkissä 2 on tarpeen löytää funktion y=x 3 +3x 2 -2x-2 kuvaajan tangentin yhtälö. Pääehto on tangentin ja suoran y=-2x+1 yhdensuuntaisuus. Ensin löydetään tangentin kulmakerroin, joka on yhtä suuri kuin suoran y=-2x+1 kulmakerroin. Koska f΄(a)=-2 tietylle suoralle, niin k=-2 halutulle tangentille. Löydämme funktion (x 3 +3x 2 -2x-2)΄=3x 2 +6x-2 derivaatan. Tietäen, että f΄(a)=-2, löydämme pisteen 3a 2 +6a-2=-2 koordinaatit. Kun yhtälö on ratkaistu, saadaan 1 =0 ja 2 =-2. Löydetyistä koordinaateista voit löytää tangenttiyhtälön tunnetulla algoritmilla. Löydämme funktion arvon pisteistä f(a 1)=-2, f(a 2)=-18. Derivaatan arvo pisteessä f΄(а 1)= f΄(а 2)=-2. Korvaamalla löydetyt arvot tangenttiyhtälöön, saadaan ensimmäiselle pisteelle a 1 =0 y=-2x-2 ja toiselle pisteelle a 2 =-2 tangenttiyhtälö y=-2x-22.

Esimerkki 3 kuvaa tangenttiyhtälön koostumusta sen piirtämiseksi funktion y=√x kaavion pisteeseen (0;3). Ratkaisu tehdään tunnetulla algoritmilla. Tangenttipisteen koordinaatit x=a, missä a>0. Funktion arvo pisteessä f(a)=√x. Toiminnon derivaatta f΄(х)=1/2√х, siis tietyssä pisteessä f΄(а)=1/2√а. Korvaamalla kaikki saadut arvot tangenttiyhtälöön, saadaan y = √a + (x-a)/2√a. Muuttamalla yhtälö saadaan y=x/2√а+√а/2. Tietäen, että tangentti kulkee pisteen (0;3) läpi, löydämme a:n arvon. Löydämme a:sta 3=√a/2. Tästä syystä √a=6, a=36. Löydämme tangenttiyhtälön y=x/12+3. Kuvassa on kaavio tarkasteltavasta funktiosta ja muodostettu haluttu tangentti.

Opiskelijoita muistutetaan likimääräisistä yhtälöistä Δy=≈f΄(x)Δxja f(x+Δx)-f(x)≈f΄(x)Δx. Kun otetaan x=a, x+Δx=x, Δx=x-a, saadaan f(x)- f(a)≈f΄(a)(x-a), joten f(x)≈f(a)+ f΄( a)(x-a).

Esimerkissä 4 on tarpeen löytää lausekkeen 2.003 6 likimääräinen arvo. Koska funktion f(x)=x 6 arvo on löydettävä pisteestä x=2.003, voidaan käyttää hyvin tunnettua kaavaa, jossa f(x)=x 6, a=2, f(a )= f(2)=64, f ΄(x)=6x5. Derivaata pisteessä f΄(2)=192. Siksi 2,003 6 ≈65-192·0,003. Laskettuamme lausekkeen saamme 2.003 6 ≈64.576.

Videotuntia "Funktion kaavion tangentin yhtälö" suositellaan käytettäväksi perinteisellä matematiikan tunnilla koulussa. Etäopettajalle videomateriaali auttaa selventämään aihetta selkeämmin. Videota voidaan suositella opiskelijoille katsottavaksi tarvittaessa itsenäisesti syventääkseen ymmärrystä aiheesta.

TEKSTIN DEKOODAUS:

Tiedämme, että jos piste M (a; f(a)) (em koordinaattein a ja ef a:sta) kuuluu funktion y = f (x) kuvaajaan ja jos tässä kohdassa on mahdollista piirtää tangentti funktion kuvaajalle, joka ei ole kohtisuorassa abskissa-akselia vastaan, tangentin kulmakerroin on yhtä suuri kuin f"(a) (eff alkuluku a:sta).

Olkoon funktio y = f(x) ja piste M (a; f(a)), ja tiedetään myös, että f´(a) on olemassa. Luodaan yhtälö annetun funktion kaavion tangentille in annettu piste. Tämä yhtälö, kuten minkä tahansa suoran yhtälö, joka ei ole yhdensuuntainen ordinaatta-akselin kanssa, on muotoa y = kx+m (y on yhtä kuin ka x plus em), joten tehtävänä on löytää kertoimet k ja m. (ka ja em)

Kulmakerroin k= f"(a). M:n arvon laskemiseen käytämme sitä tosiasiaa, että haluttu suora kulkee pisteen M(a; f (a) kautta). Tämä tarkoittaa, että jos korvaamme pisteen koordinaatit pisteen M suoran yhtälöön, saadaan oikea yhtälö : f(a) = ka+m, josta saadaan m = f(a) - ka.

On vielä korvattava kertoimien ki ja m löydetyt arvot suoran yhtälöön:

y = kx+(f(a)-ka);

y = f(a)+k(x-a);

y= f(a)+ f"(a) (x- a). ( y on yhtä suuri kuin ef plus ef alkuluvusta a, kerrottuna x miinus a).

Olemme saaneet yhtälön funktion y = f(x) kaavion tangentille pisteessä x=a.

Jos esimerkiksi y = x 2 ja x = -2 (eli a = -2), niin f (a) = f (-2) = (-2) 2 = 4; f´(x) = 2x, mikä tarkoittaa f"(a) = f´(-2) = 2·(-2) = -4. (silloin a:n ef on yhtä kuin neljä, alkuluvun ef x on yhtä suuri kuin kaksi x, mikä tarkoittaa ef alkulukua yhtä kuin miinus neljä)

Korvaamalla löydetyt arvot a = -2, f(a) = 4, f"(a) = -4 yhtälöön saadaan: y = 4+(-4)(x+2), eli y = -4x -4.

(E on yhtä suuri kuin miinus neljä x miinus neljä)

Luodaan yhtälö funktion y = tgx(kreikka) kaavion tangentille yhtä suuri kuin tangentti x) alkuperässä. Meillä on: a = 0, f(0) = tan0 = 0;

f"(x)= , mikä tarkoittaa f"(0) = l. Korvaamalla löydetyt arvot a=0, f(a)=0, f´(a) = 1 yhtälöön, saadaan: y=x.

Tehdään yhteenveto vaiheistamme löytääksemme funktion kaavion tangentin yhtälön pisteessä x käyttämällä algoritmia.

ALGORITMI YHTÄLÖN KEHITTÄMISEKSI FUNKTION y = f(x) KAAVION TANTENTILLE:

1) Merkitse tangentin pisteen abskissa kirjaimella a.

2) Laske f(a).

3) Etsi f´(x) ja laske f´(a).

4) Korvaa löydetyt luvut a, f(a), f´(a) kaavaan y= f(a)+ f"(a) (x- a).

Esimerkki 1. Luo yhtälö funktion y = - in kaavion tangentille

piste x = 1.

Ratkaisu. Käytämme algoritmia ottaen huomioon, että in tässä esimerkissä

2) f(a)=f(1)=- =-1

3) f'(x)=; f´(a)= f´(1)= =1.

4) Korvaa kaavaan löydetyt kolme lukua: a = 1, f(a) = -1, f"(a) = 1. Saadaan: y = -1+(x-1), y = x-2 .

Vastaus: y = x-2.

Esimerkki 2. Annettu funktio y = x 3 +3x 2 -2x-2. Kirjoita funktion y = f(x) kuvaajaan tangentin yhtälö, joka on yhdensuuntainen suoran y = -2x +1 kanssa.

Käyttämällä tangenttiyhtälön muodostamisalgoritmia otamme huomioon, että tässä esimerkissä f(x) = x 3 +3x 2 -2x-2, mutta tangentin pisteen abskissaa ei ole ilmoitettu tässä.

Alotetaan ajatella näin. Halutun tangentin tulee olla yhdensuuntainen suoran y = -2x+1 kanssa. Ja yhdensuuntaisilla viivoilla on samat kulmakertoimet. Tämä tarkoittaa, että tangentin kulmakerroin on yhtä suuri kuin annetun suoran kulmakerroin: k tangentti. = -2. Hok cas. = f"(a). Siten voimme löytää a:n arvon yhtälöstä f ´(a) = -2.

Etsitään funktion derivaatta y=f(x):

f"(x)= (x 3 +3x 2 -2x-2)' =3x 2 +6x-2;f"(a) = 3a2 +6a-2.

Yhtälöstä f"(a) = -2, ts. 3a 2 +6a-2=-2 löydämme 1 =0, a 2 =-2. Tämä tarkoittaa, että on olemassa kaksi tangenttia, jotka täyttävät ongelman ehdot: yksi pisteessä, jossa on abskissa 0, toinen pisteessä, jossa on abskissa -2.

Nyt voit seurata algoritmia.

1) a 1 = 0 ja 2 = -2.

2) f(a 1) = 0 3 +3·0 2 -2∙0-2=-2; f(a 2)= (-2) 3 +3·(-2) 2-2·(-2)-2=6;

3) f"(a 1) = f"(a 2) = -2.

4) Korvaamalla kaavaan arvot a 1 = 0, f(a 1) = -2, f"(a 1) = -2, saadaan:

y = -2-2(x-0), y = -2x-2.

Korvaamalla kaavaan arvot a 2 = -2, f(a 2) =6, f"(a 2) = -2, saadaan:

y = 6-2 (x+2), y = -2x+2.

Vastaus: y=-2x-2, y=-2x+2.

Esimerkki 3. Piirrä pisteestä (0; 3) tangentti funktion y = kuvaajalle. Ratkaisu. Käytetään algoritmia tangenttiyhtälön muodostamiseen ottaen huomioon, että tässä esimerkissä f(x) = . Huomaa, että tässä, kuten esimerkissä 2, tangentin pisteen abskissaa ei ole nimenomaisesti osoitettu. Noudatamme kuitenkin algoritmia.

1) Olkoon x = a tangenttipisteen abskissa; on selvää, että >0.

3) f'(x)=()'=; f´(a) =.

4) Korvaa kaavaan arvot a, f(a) = , f"(a) =

y=f (a) +f "(a) (x-a), saamme:

Ehdon mukaan tangentti kulkee pisteen (0; 3) läpi. Korvaamalla yhtälöön arvot x = 0, y = 3, saadaan: 3 = , ja sitten =6, a =36.

Kuten näet, tässä esimerkissä onnistuimme löytämään tangentin pisteen abskissan vasta algoritmin neljännessä vaiheessa. Korvaamalla yhtälöön arvon a =36, saadaan: y=+3

Kuvassa 1 esitetty geometrinen kuva harkittu esimerkki: muodostetaan funktion y = kuvaaja, piirretään suora y = +3.

Vastaus: y = +3.

Tiedämme, että funktiolle y = f(x), jolla on derivaatta pisteessä x, likimääräinen yhtälö on voimassa: Δyf´(x)Δx (delta y on suunnilleen yhtä suuri kuin x:n eff-alkuluku kerrottuna delta x:llä)

tai yksityiskohtaisemmin f(x+Δx)-f(x) f´(x) Δx (eff x:stä plus delta x miinus ef x:stä on suunnilleen yhtä suuri kuin eff alkuluku x:stä delta x:llä).

Jatkokeskustelun helpottamiseksi muutetaan merkintää:

x:n sijasta kirjoitamme A,

x+Δx:n sijasta kirjoitetaan x

Δx:n sijasta kirjoitetaan x-a.

Sitten yllä kirjoitettu likimääräinen yhtäläisyys saa muotoa:

f(x)-f(a)f´(a)(x-a)

f(x)f(a)+f´(a)(x-a). (eff x:stä on suunnilleen yhtä suuri kuin ef plus ef alkuluvusta a:sta, kerrottuna x:n ja a:n erolla).

Esimerkki 4. Etsi numeerisen lausekkeen 2.003 6 likimääräinen arvo.

Ratkaisu. Se on noin funktion y = x 6 arvon löytämisestä pisteessä x = 2.003. Käytetään kaavaa f(x)f(a)+f´(a)(x-a) ottaen huomioon, että tässä esimerkissä f(x)=x 6, a = 2,f(a) = f(2) = 2 6 = 64; x = 2,003, f"(x) = 6x 5 ja siten f"(a) = f"(2) = 6 2 5 =192.

Tuloksena saamme:

2,003 6 64+192· 0,003, so. 2,003 6 = 64,576.

Jos käytämme laskinta, saamme:

2,003 6 = 64,5781643...

Kuten näette, likimääräinen tarkkuus on melko hyväksyttävä.

Harkitse seuraavaa kuvaa:

Se kuvaa tiettyä funktiota y = f(x), joka on differentioituva pisteessä a. Piste M koordinaatteineen (a; f(a)) on merkitty. Sekantti MR piirretään graafin mielivaltaisen pisteen P(a + ∆x; f(a + ∆x)) läpi.

Jos nyt piste P siirretään kuvaajaa pitkin pisteeseen M, niin suora MR pyörii pisteen M ympäri. Tässä tapauksessa ∆x pyrkii nollaan. Tästä voimme muotoilla funktion kaavion tangentin määritelmän.

Tangentti funktion kuvaajalle

Funktion kaavion tangentti on sekantin raja-asema, koska argumentin lisäys pyrkii nollaan. On ymmärrettävä, että funktion f derivaatan olemassaolo pisteessä x0 tarkoittaa, että tässä kaavion kohdassa on tangentti hänelle.

Tässä tapauksessa tangentin kulmakerroin on yhtä suuri kuin tämän funktion derivaatta tässä pisteessä f’(x0). Tämä on derivaatan geometrinen merkitys. Pisteessä x0 differentioituvan funktion f kaavion tangentti on tietty suora, joka kulkee pisteen (x0;f(x0)) läpi ja jolla on kulmakerroin f’(x0).

Tangenttiyhtälö

Yritetään saada jonkin funktion f kuvaajan tangentin yhtälö pisteessä A(x0; f(x0)). Suoran ja kaltevuuden k yhtälöllä on seuraava näkymä:

Koska kaltevuuskertoimemme on yhtä suuri kuin derivaatta f'(x0), yhtälö saa seuraavan muodon: y = f'(x0)*x + b.

Lasketaan nyt b:n arvo. Tätä varten käytämme sitä tosiasiaa, että funktio kulkee pisteen A kautta.

f(x0) = f’(x0)*x0 + b, tästä ilmaisemme b ja saamme b = f(x0) - f’(x0)*x0.

Korvaamme saadun arvon tangenttiyhtälöön:

y = f'(x0)*x + b = f'(x0)*x + f(x0) - f'(x0)*x0 = f(x0) + f'(x0)*(x - x0).

y = f(x0) + f’(x0)*(x - x0).

Tarkastellaan seuraavaa esimerkkiä: etsi funktion f(x) = x 3 - 2*x 2 + 1 kaavion tangentin yhtälö pisteessä x = 2.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f’(x) = 3*x 2 - 4*x.

4. f’(x0) = f’(2) = 3*2 2 - 4*2 = 4.

5. Korvaa saadut arvot tangenttikaavaan, saamme: y = 1 + 4*(x - 2). Avaamalla sulut ja tuomalla samanlaiset termit saamme: y = 4*x - 7.

Vastaus: y = 4*x - 7.

Yleinen kaavio tangenttiyhtälön muodostamiseksi funktion y = f(x) kuvaajaan:

1. Määritä x0.

2. Laske f(x0).

3. Laske f'(x)